Unravelling Morphological and Topological Energy Contributions of Metal Nanoparticles
Abstract
:1. Introduction
2. Computational Details
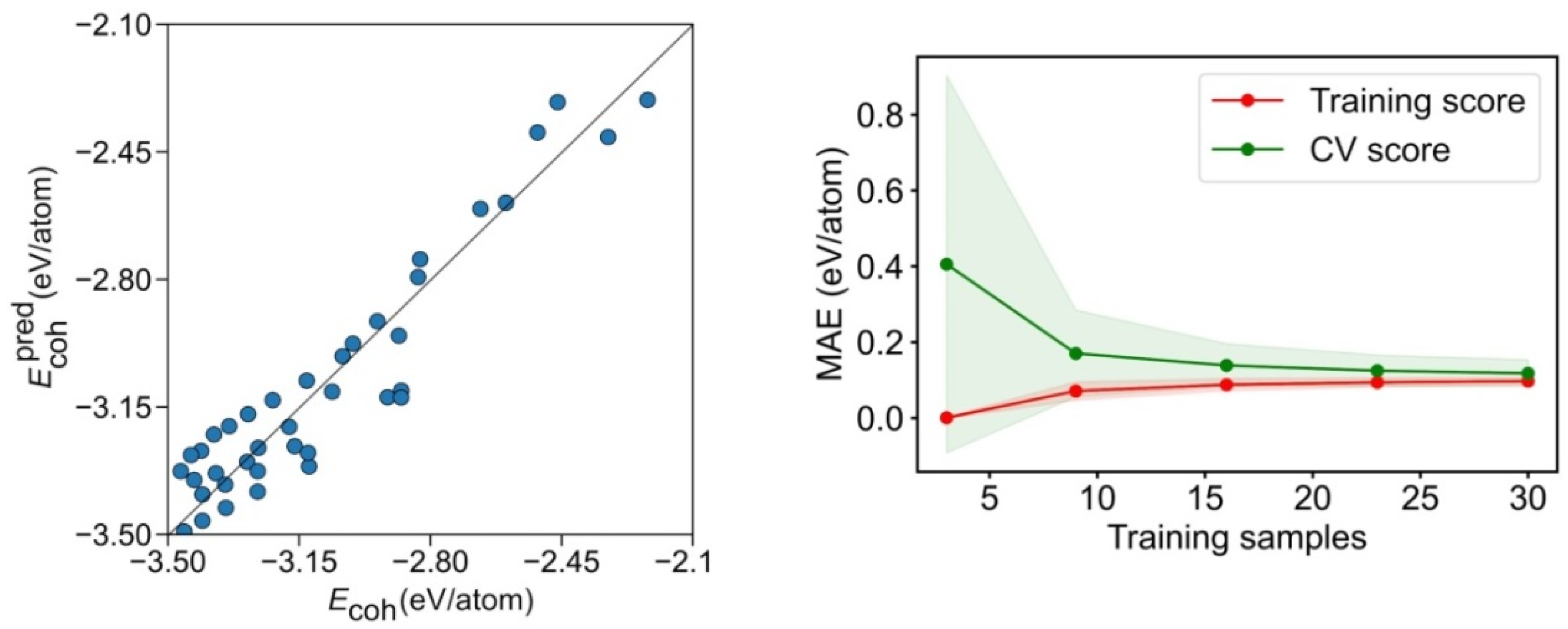
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pomerantseva, E.; Bonaccorso, F.; Feng, X.; Cui, Y.; Gogotsi, Y. Energy storage: The future enabled by nanomaterials. Science 2019, 366, eaan8285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raghunath, A.; Perumal, E. Metal oxide nanoparticles as antimicrobial agents. Int. J. Antimicrob. Agents 2017, 49, 137–152. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Raza, K. C60-fullerenes as drug delivery carriers for anticancer agents: Promises and hurdles. Pharm. Nanotechnol. 2017, 5, 169–179. [Google Scholar] [CrossRef]
- Viñes, F.; Gomes, J.R.B.; Illas, F. Understanding the reactivity of metallic nanoparticles: Beyond the extended surface model for catalysis. Chem. Soc. Rev. 2014, 43, 4922–4939. [Google Scholar] [CrossRef] [PubMed]
- Medford, A.J.; Vojvodic, A.; Hummelshøj, J.S.; Voss, J.; Abild-Pedersen, F.; Studt, F.; Bligaard, T.; Nilsson, A.; Nørskov, J.K. From the Sabatier principle to a predictive theory of transition-metal heterogeneous catalysis. J. Catal. 2015, 328, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Haruta, M.; Yamada, N.; Kobayashi, T.; Iijima, S. Gold catalysts prepared by coprecipitation for low-temperature oxidation of hydrogen and of carbon monoxide. J. Catal. 1989, 115, 301–309. [Google Scholar] [CrossRef]
- Kuhn, J.N.; Huang, W.; Tsung, C.; Zhang, Y.; Somorjai, G.A. Structure sensitivity of carbon−nitrogen ring opening: Impact of platinum particle size from below 1 to 5 nm upon pyrrole hydrogenation product electivity over monodisperse platinum nanoparticles loaded onto mesoporous silica. J. Am. Chem. Soc. 2008, 130, 14026–14027. [Google Scholar] [CrossRef] [Green Version]
- Corma, A.; Boronat, M.; González, S.; Illas, F. On the activation of molecular hydrogen by gold: A theoretical approximation to the nature of potential active sites. Chem. Commun. 2007, 3371–3373. [Google Scholar] [CrossRef] [PubMed]
- Baletto, F.; Ferrando, R.; Fortunelli, A.; Montalenti, F.; Mottet, C. Crossover among structural motifs in transition and noble-metal clusters. J. Chem. Phys. 2002, 116, 3856–3863. [Google Scholar] [CrossRef]
- Krüger, S.; Vent, S.; Rösch, N. Size dependence of bond length and binding energy in palladium and gold clusters. Bunsenges. Für Phys. Chem. 1997, 101, 1640–1643. [Google Scholar] [CrossRef]
- Sánchez-Sánchez, C.M.; Solla-Gullón, J.; Vidal-Iglesias, F.J.; Aldaz, A.; Montiel, V.; Herrero, E. Imaging structure sensitive catalysis on different shape-controlled platinum nanoparticles. J. Am. Chem. Soc. 2010, 132, 5622–5624. [Google Scholar] [CrossRef]
- Mitchell, S.; Qin, R.; Zheng, N.; Pérez-Ramírez, J. Nanoscale engineering of catalytic materials for sustainable technologies. Nat. Nanotechnol. 2021, 16, 129–139. [Google Scholar] [CrossRef]
- Barnard, A.S.; Curtiss, L.A. Predicting the shape and structure of face-centered cubic gold nanocrystals smaller than 3 nm. ChemPhysChem 2006, 7, 1544–1553. [Google Scholar] [CrossRef] [PubMed]
- Maeda, Y.; Okumura, M.; Tsubota, S.; Kohyama, M.; Haruta, M. Local barrier height of Au nanoparticles on a TiO2(110)-(1 × 2) surface. Appl. Surf. Sci. 2004, 222, 409–414. [Google Scholar] [CrossRef]
- Pakarinen, O.H.; Barth, C.; Foster, A.S.; Nieminen, R.M.; Henry, C.R. High-resolution scanning force microscopy of gold nanoclusters on the KBr (001) surface. Phys. Rev. B 2006, 73, 235428. [Google Scholar] [CrossRef] [Green Version]
- Akita, T.; Okumura, M.; Tanaka, K.; Kohyama, M.; Haruta, M. TEM observation of gold nanoparticles deposited on cerium oxide. J. Mater. Sci. 2005, 40, 3101–3106. [Google Scholar] [CrossRef]
- Heiz, U.; Sanchez, A.; Abbet, S.; Schneider, W.-D. Catalytic oxidation of carbon monoxide on monodispersed platinum clusters: Each atom counts. J. Amer. Chem. Soc. 1999, 121, 3214–3217. [Google Scholar] [CrossRef]
- Aprà, E.; Ferrando, R.; Fortunelli, A. Density-functional global optimization of gold nanoclusters. Phys. Rev. B 2006, 73, 205414. [Google Scholar] [CrossRef]
- Yang, X.; Cai, W.; Shao, X. Structural variation of silver clusters from Ag13 to Ag160. J. Phys. Chem. A 2007, 111, 5048–5056. [Google Scholar] [CrossRef]
- McKenna, K.P.; Sushko, P.V.; Shluger, A.L. Dynamics of low-coordinated surface atoms on gold nanocrystallites. J. Chem. Phys. 2007, 126, 154704. [Google Scholar] [CrossRef] [PubMed]
- Ricci, D.; Bongiorno, A.; Pacchioni, G.; Landman, U. Bonding trends and dimensionality crossover of gold nanoclusters on metal-supported MgO thin films. Phys. Rev. Lett. 2006, 97, 36106. [Google Scholar] [CrossRef] [Green Version]
- Wilson, N.T.; Johnston, R.L. A theoretical study of atom ordering in copper–gold nanoalloy clusters. J. Mater. Chem. 2002, 12, 2913–2922. [Google Scholar] [CrossRef]
- Kozlov, S.M.; Aleksandrov, H.A.; Goniakowski, J.; Neyman, K.M. Effect of MgO(100) support on structure and properties of Pd and Pt nanoparticles with 49–155 atoms. J. Chem. Phys. 2013, 139, 084701. [Google Scholar] [CrossRef] [PubMed]
- Prats, H.; Gutiérrez, R.A.; Piñero, J.J.; Viñes, F.; Bromley, S.T.; Ramírez, P.J.; Rodriguez, J.A.; Illas, F. Room temperature methane capture and activation by Ni clusters supported on TiC(001): Effects of metal–carbide interactions on the cleavage of the C–H bond. J. Am. Chem. Soc. 2019, 141, 5303–5313. [Google Scholar] [CrossRef]
- Ko, C.; Bromley, S.T.; Lee, J.Y.; Illas, F. Size-dependent level alignment between rutile and anatase TiO2 nanoparticles: Implications for photocatalysis. J. Phys. Chem. Lett. 2017, 8, 5593–5598. [Google Scholar] [CrossRef] [PubMed]
- Viñes, F.; Lamiel-Garcia, O.; Illas, F.; Bromley, S. T Size dependent structural and polymorphic transitions in ZnO: From nanocluster to bulk. Nanoscale 2017, 9, 10067–10074. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vega, L.; Ruvireta, J.; Viñes, F.; Illas, F. Jacob’s ladder as sketched by Escher: Assessing the performance of broadly used density functionals on transition metal surface properties. J. Chem. Theory Comput. 2018, 14, 395–403. [Google Scholar] [CrossRef]
- Vega, L.; Viñes, F. Generalized gradient approximation adjusted to transition metals properties: Key roles of exchange and local spin density. J. Comput. Chem. 2020, 41, 2598–2603. [Google Scholar] [CrossRef]
- Yudanov, I.V.; Sahnoun, R.; Neyman, K.M.; Rösch, N. Metal nanoparticles as models of single crystal surfaces and supported catalysts: Density functional study of size effects for CO on Pd(111). J. Chem. Phys. 2002, 117, 9887–9896. [Google Scholar] [CrossRef]
- Viñes, F.; Illas, F.; Neyman, K.M. Density functional calculations of Pd nanoparticles using a plane-wave method. J. Phys. Chem. A 2008, 112, 8911–8915. [Google Scholar] [CrossRef] [PubMed]
- Roldán, A.; Viñes, F.; Illas, F.; Ricart, J.M.; Neyman, K.M. Density functional studies of coinage metal nanoparticles: Scalability of their properties to bulk. Theor. Chem. Acc. 2008, 120, 565–573. [Google Scholar] [CrossRef]
- Kozlov, S.M.; Neyman, K.M. Catalysis from first principles: Towards accounting for the effects of nanostructuring. Top. Catal. 2013, 56, 867–873. [Google Scholar] [CrossRef]
- Viñes, F.; Lykhach, Y.; Staudt, T.; Lorenz, M.P.A.; Papp, C.; Steinrück, H.-P.; Libuda, J.; Neyman, K.M.; Görling, A. Methane activation by platinum: Critical role of edge and corner sites of metal nanoparticles. Chem. Eur. J. 2010, 16, 6530–6539. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, S.M.; Neyman, K.M. Insights from methane decomposition on nanostructured palladium. J. Catal. 2016, 337, 111–121. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, J.; Zhang, B.; Shi, W.; Guo, Y.; Cui, F. Insight into the size effect of Pd nanoparticles on the catalytic reduction of nitrite in water over Pd/C catalysts. Environ. Sci. Nano 2020, 7, 2117–2129. [Google Scholar] [CrossRef]
- Pérez-Lorenzo, M. Palladium nanoparticles as efficient catalysts for Suzuki cross-coupling reactions. J. Phys. Chem. Lett. 2012, 3, 167–174. [Google Scholar] [CrossRef]
- Ruvireta, J.; Vega, L.; Viñes, F. Cohesion and coordination effects on transition metal surface energies. Surf. Sci. 2017, 664, 45–49. [Google Scholar] [CrossRef]
- Yang, S.; Shen, C.; Tian, Y.; Zhang, X.; Gao, H.-J. Synthesis of cubic and spherical Pd nanoparticles on graphene and their electrocatalytic performance in the oxidation of formic acid. Nanoscale 2014, 6, 13154–13162. [Google Scholar] [CrossRef]
- Norimatsu, F.Y.; Mizokoshi, Y.; Mori, K.; Mizugaki, T.; Ebitani, K.; Kaneda, K. Shape- and size-controlled synthesis of tetrahedral Pd nanoparticles using tetranuclear Pd cluster as precursor. Chem. Lett. 2006, 35, 276–277. [Google Scholar] [CrossRef]
- Zhao, H.; Qi, W.; Ji, W.; Wang, T.; Peng, H.; Wang, Q.; Jia, Y.; He, J. Large Marks-decahedral Pd nanoparticles synthesized by a modified hydrothermal method using a homogeneous reactor. J. Nanopart. Res. 2017, 19, 162. [Google Scholar] [CrossRef]
- Zhang, Q.; Xie, J.; Yang, J.; Lee, J.Y. Monodisperse icosahedral Ag, Au, and Pd nanoparticles: Size control strategy and superlattice formation. ACS Nano 2009, 3, 139–148. [Google Scholar] [CrossRef]
- Johnston, R.L. Atomic and Molecular Clusters; Taylor and Francis: London, UK, 2002. [Google Scholar]
- Dietze, E.M.; Plessow, P.N.; Studt, F. Modeling the size dependency of the stability of metal nanoparticles. J. Phys. Chem. C 2019, 123, 25464–25469. [Google Scholar] [CrossRef]
- Farkaš, B.; Leeuw, N.H. Towards a morphology of cobalt nanoparticles: Size and strain effects. Nanotechnology 2020, 31, 195711. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, S.M.; Viñes, F.; Nilius, N.; Shaikhutdinov, S.; Neyman, K.M. Absolute surface step energies: Accurate theoretical methods applied to ceria nanoislands. J. Phys. Chem. Lett. 2012, 3, 1956–1961. [Google Scholar] [CrossRef]
- Álvarez-Falcón, L.; Viñes, F.; Notario-Estévez, A.; Illas, F. On the hydrogen adsorption and dissociation on Cu surfaces and nanorows. Surf. Sci. 2016, 646, 221–229. [Google Scholar] [CrossRef]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Reuter, K.; Scheffler, M. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef] [Green Version]
- Havu, V.; Blum, V.; Havu, P.; Scheffler, M. Efficient O(N) integration for all-electron electronic structure calculation using numeric basis functions. J. Comput. Phys. 2009, 228, 8367–8379. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- Chang, C.; Pelissier, M.; Durand, P. Regular two-component Pauli-like effective Hamiltonians in Dirac theory. Phys. Scr. 1986, 34, 394–404. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer: New York, NY, USA, 2006. [Google Scholar]
- Rapps, T.; Ahlrichs, R.; Waldt, E.; Kappes, M.M.; Schooss, D. On the Structures of 55-Atom Transition-Metal Clusters and Their Relationship to the Crystalline Bulk. Angew. Chem. Int. Ed. 2013, 52, 6102–6105. [Google Scholar] [CrossRef]
- Piotrowski, M.J.; Ungureanu, C.G.; Tereshchuk, P.; Batista, K.E.; Chaves, A.S.; Guedes-Sobrinho, D.; Da Silva, J.L.F. Theoretical study of the structural, energetic, and electronic properties of 55-atom metal nanoclusters: A DFT investigation within van der Waals corrections, spin–orbit coupling, and PBE+U of 42 metal systems. J. Phys. Chem. C 2016, 120, 28844–28856. [Google Scholar] [CrossRef]
- Viñes, F.; Görling, A. Explaining Cu@Pt bimetallic nanoparticles activity based on NO adsorption. Chem. Eur. J. 2020, 26, 11478–11491. [Google Scholar] [CrossRef] [PubMed]
- Engel, J.; Francis, S.; Roldan, A. The Influence of support materials on the structural and electronic properties of gold nanoparticles—A DFT study. Phys. Chem. Chem. Phys. 2019, 21, 19011–19025. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stone, M. Cross-validatory choice and assessment of statistical prediction (with discussion). J. R. Stat. Soc. Ser. B Stat. Methodol. 1974, 36, 111–147. [Google Scholar] [CrossRef]

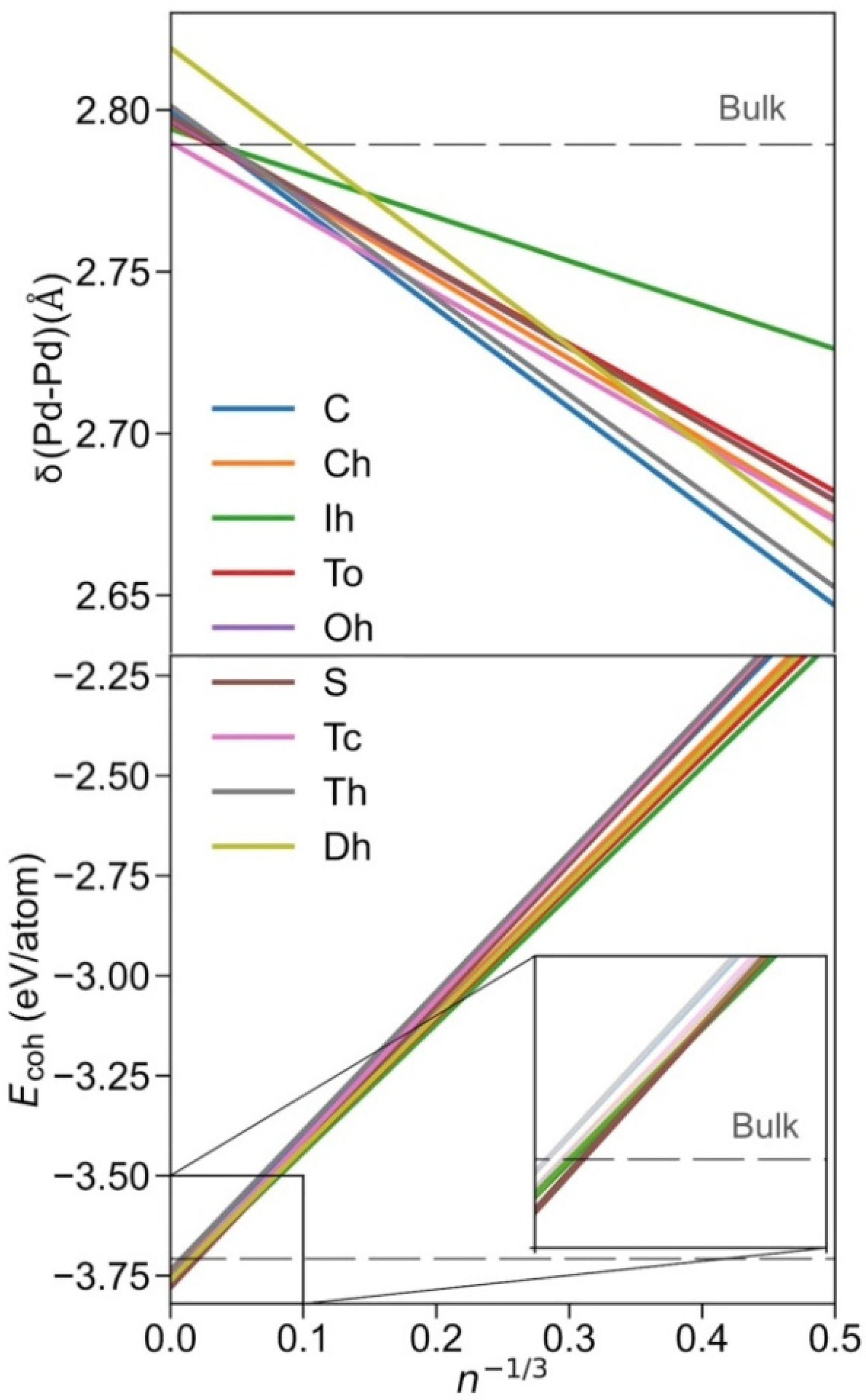
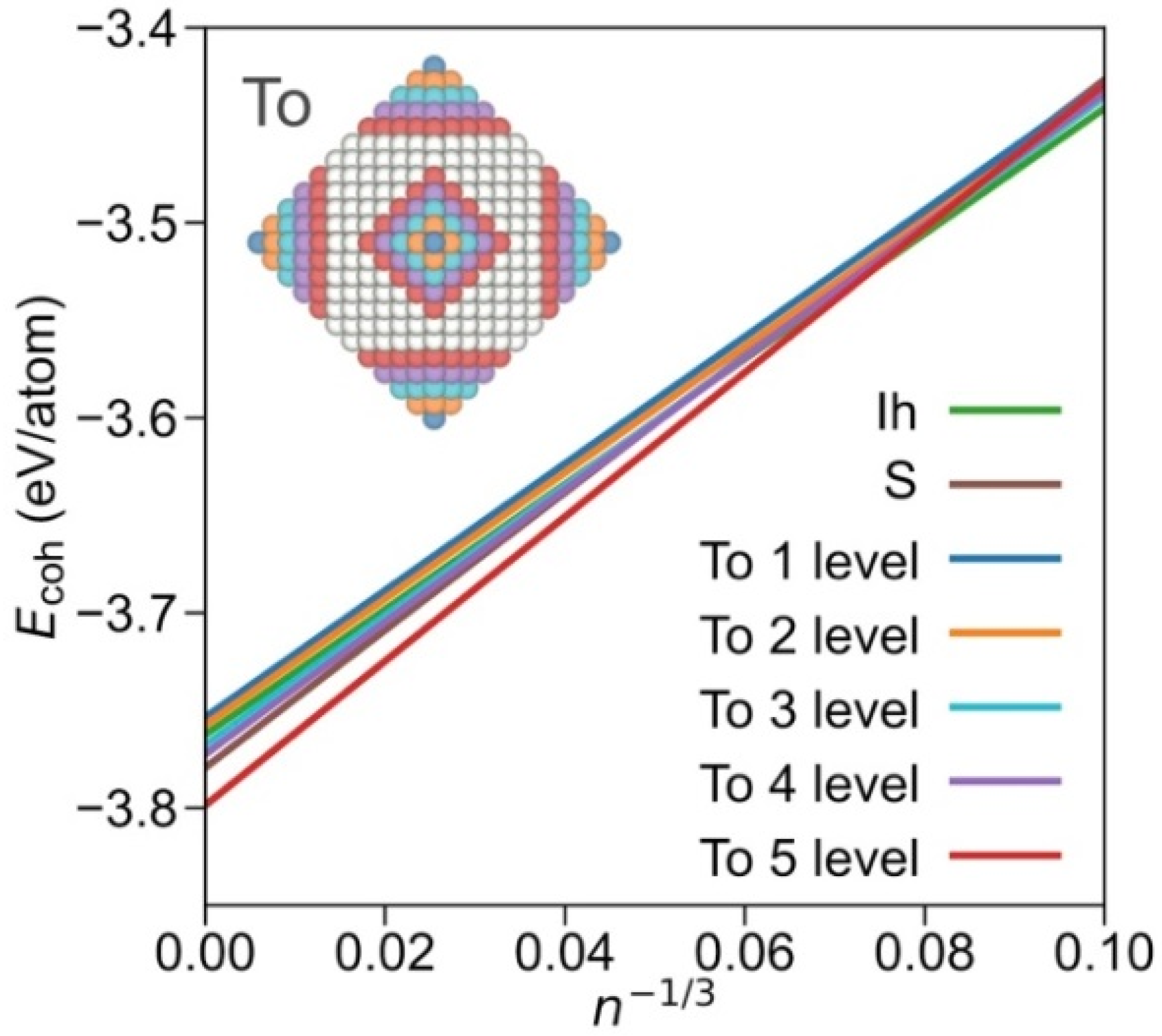
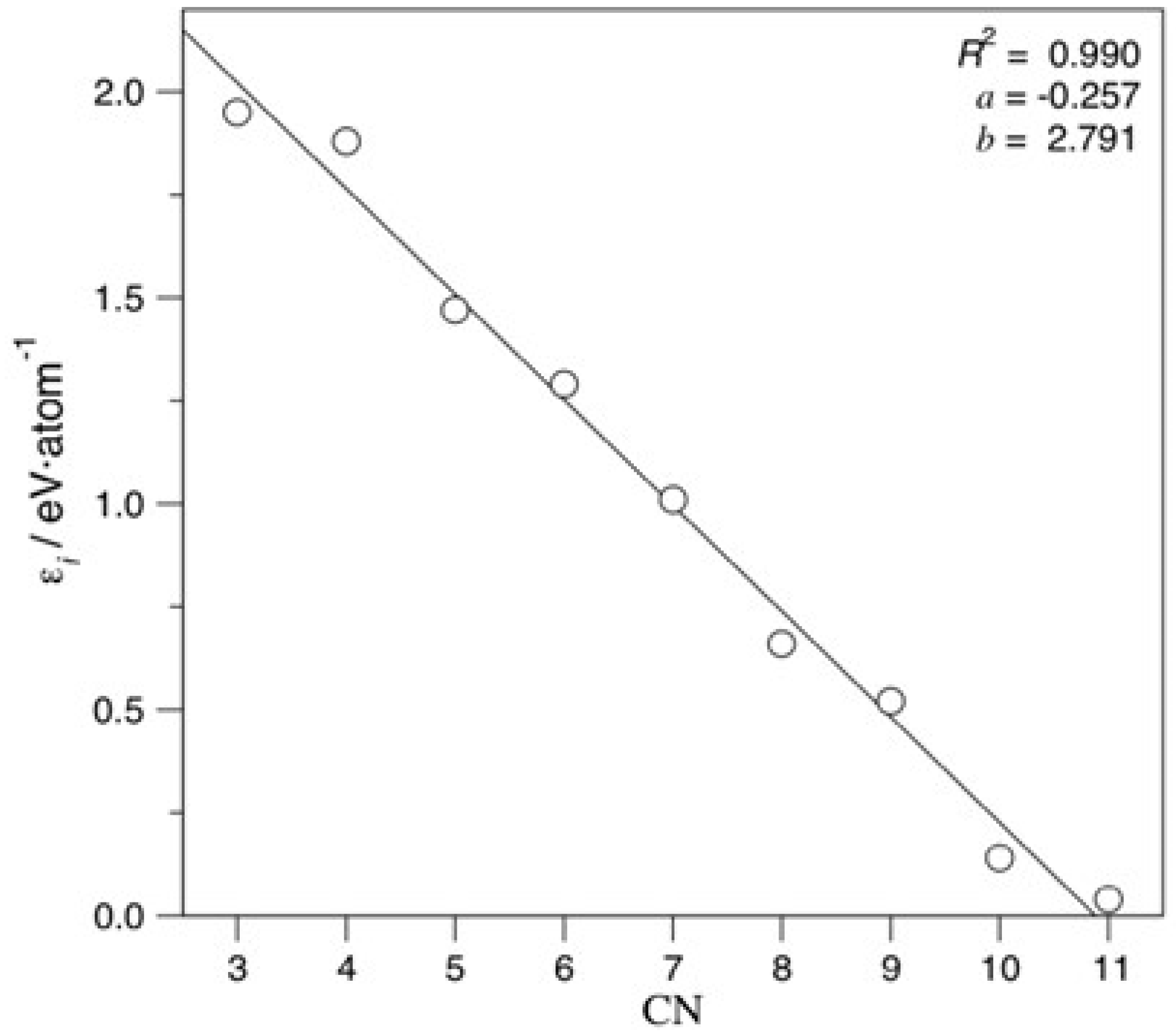
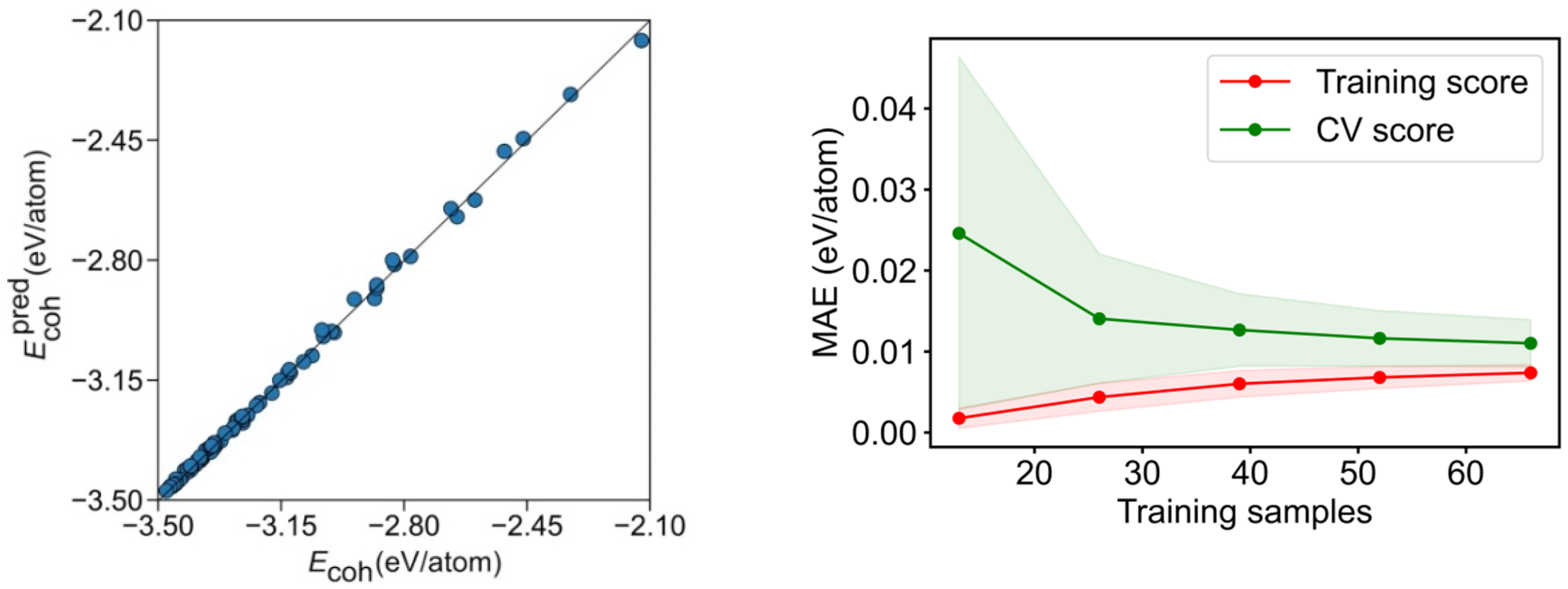
| NPs | γ(001) | γ(111) | β(001) | β(111) | ξ |
|---|---|---|---|---|---|
| C | 0.09 | — | 0.27 | — | 0.07 |
| Oh | — | 0.08 | — | 0.27 | −0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vega, L.; Viñes, F.; Neyman, K.M. Unravelling Morphological and Topological Energy Contributions of Metal Nanoparticles. Nanomaterials 2022, 12, 17. https://doi.org/10.3390/nano12010017
Vega L, Viñes F, Neyman KM. Unravelling Morphological and Topological Energy Contributions of Metal Nanoparticles. Nanomaterials. 2022; 12(1):17. https://doi.org/10.3390/nano12010017
Chicago/Turabian StyleVega, Lorena, Francesc Viñes, and Konstantin M. Neyman. 2022. "Unravelling Morphological and Topological Energy Contributions of Metal Nanoparticles" Nanomaterials 12, no. 1: 17. https://doi.org/10.3390/nano12010017
APA StyleVega, L., Viñes, F., & Neyman, K. M. (2022). Unravelling Morphological and Topological Energy Contributions of Metal Nanoparticles. Nanomaterials, 12(1), 17. https://doi.org/10.3390/nano12010017









