Abstract
In recent years, there has been a growing demand for renewable energy that is free of power generation by products to address the global climate and resource limitation crises. Wind power generation is maximizing efficiency through constant research and development, and as the use of large capacity turbines increases, the scale of supporting structure also increases. The structural maintenance of hollow towers, the supporting structure of wind turbines, requires the installation of an opening through which workers can access the tower to check corrosion, cracks, and damage to the tower body. However, these access points can affect the buckling strength of the tower structures due to section loss. In this study, the effects of the opening on the structural stability and ultimate strength of a large diameter cylindrical shell, which could be used as a wind turbine supporting tower structure, were studied through elastic buckling and nonlinear analyses. Based on the analytical results, the effects of the thickness of a collar stiffener around the opening on the structure’s ultimate strength were investigated. The results were compared to the design criteria, and through regression analysis, an effective equation to determine the collar stiffener’s thickness for large diameter cylindrical shells was proposed based on an opening that satisfied the design strength criteria.
1. Introduction
The continued use of fossil fuels has exacerbated the global warming crisis, making the development of alternative energy applications using natural energy an important new undertaking for humanity—consequently, research on various alternative energy resources is being actively conducted in various regions such as Europe and the United States. The result is the potential use of alternative energy from sustainable, clean resources such as biomass, hydropower, geothermal, solar, and wind resources. These resources are classified as renewable energy without generation byproducts, and their use has been recommended at a global level in recent years. Among them, wind energy has been developed and delivered in earnest in European countries such as Denmark and Germany since the early 1990s, having the advantages of high-power generation efficiency and independent energy production in any areas where the wind-direction conditions can be met (open, hill, coast etc.).
Consequently, since the 2010s, the demand for tower support structures has been increasing with the development of large-scale wind turbines of 5 MW or more that maximize power generation efficiency and increase power generation capacity [1]. As shown in Figure 1, as wind turbine capacity increases, the supporting structure dimensions also increase. Research has shown that the diameters of tower bases supporting turbines of 2 MW or more range from a minimum of 4 m to more than 10 m [2,3,4,5,6,7].

Figure 1.
Comparison of resources by turbine capacity and tower base diameter, adapted from refs [2,3,4,5,6,7].
In general, maintenance is essential to support the continuous operation of wind power generators and power generational efficiency—in particular, because the lifespan of wind turbines is known to be more than 20 yr—so tower structural maintenance should be conducted regularly. Any defect that could affect the structural health and safety—such as corrosion, cracks, and tower damage—should be detected through consistent monitoring and inspection. Therefore, it is essential to install an access point to the tower for the maintenance of parts, power cables, and other devices inside the wind turbine, as shown in Figure 2.

Figure 2.
Wind tower segments: (a) installed openings; (b) the tower interior.
The access point installed in a tower—itself a cylindrical shell—is an opening made in the thin tower shell, which creates several structural problems. Various studies on these structural defects have been conducted. Guz et al. [8], Zirka et al. [9], Golling [10], and Reyno et al. [11] conducted stress concentration tests of cylindrical shells considering the opening. Tennyson [12], Starnes [13], Jullien et al. [14], Shariati et al. [15,16], Ghazijahani et al. [17], and Alsalah et al. [18] analyzed the effect on the opening of a cylindrical shell under axial load but did not deal with the effect of reinforcement using a surrounding stiffener.
Regarding reinforcement around the opening, Hilburger et al. [19] identified the behavior based on the thickness of the opening stiffener and Reyno [20] studied the effect of the stiffener geometry, proposing a reinforcement design formula for an open installation angle of 20° or more. Cho [21] and Santos et al. [22] analyzed the effect of ultimate strength and reinforcement on a large-diameter cylindrical shell with an opening installation angle of 20° or less through finite element analysis, modifying the strength reduction factor of the design criteria. However, even when the installation angle is less than 20°, the strength reduction factor has already been provided for in the design standard. Moreover, if the opening design satisfies the limits provided for by the design standards, the influence of the cross-sectional loss of a cylindrical shell with an opening of the same size has been shown to decrease as the diameter increases.
In this study, the effects of the opening on the structural stability and ultimate strength of a large-diameter cylindrical shell that could be used for a wind turbine supporting tower structure were studied through elastic buckling and nonlinear analyses. Based on the analytical results, the effects of the thickness of a collar stiffener around the opening on the ultimate strength were investigated. The results were compared with the design criteria, and through regression analysis, an effective equation to determine the collar stiffener thickness for a large-diameter cylindrical shell was proposed, considering an opening that satisfied design strength standards.
2. Current Design Standard for a Cylindrical Shell with Opening
For a cylindrical shell, Timoshenko and James M. Gere [23] proposed an equation to evaluate the elastic buckling strength () by solving the differential equation of an infinite length cylindrical shell subjected to an axial force, as expressed in Equation (1).
where is the modulus of elasticity, is the shell thickness, is the shell radius, and is Poisson’s ratio.
The EN1993-1-6 standard [24] proposes an elastic buckling strength equation as shown in Equation (2), based on the strength of the cylindrical shell provided by the design criteria. Variables along the shell length are considered , with length types being divided into short, medium, and long, as shown in Table 1.

Table 1.
Classification of cylinders and factor by length type [24].
DNV-RP-C202 [25] also provides the elastic buckling strength () of the unstiffened cylindrical shell as shown in Equation (3).
where is modulus of elasticity, is thickness of shell, is radius of shell, is Poisson’s ratio, and is the reduced buckling coefficient.
In the recommended practice document, DNVGL-ST-0126 [26], the design buckling stress () is proposed by applying the strength reduction factor () as shown in Equation (4) for a cylindrical shell with an opening, as shown in Figure 3.
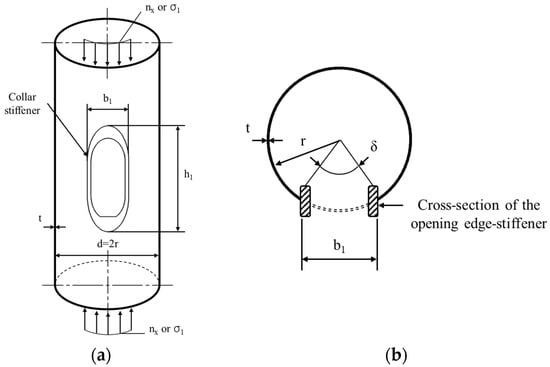
Figure 3.
Circumferentially edge-stiffened openings [26]: (a) overview; (b) plan view.

Table 2.
Coefficients and for reduction factor [26].
To apply the strength reduction factor for an opening design to the design strength of a cylindrical shell without an opening, all the following conditions must be met:
- The ratio of tower thickness to tower radius () must not be more than 160.
- The angle () occupied by the width of the shell opening must be 60° or less.
- The ratio of opening width to opening height () must be three or less.
- A stiffener of specific cross-section should be installed on the centerline of the center surface of the wall.
- The cross-sectional area of the reinforcement to be installed must be at least 1/3 of the area of the wall lost due to the installation of the opening.
- The cross-section of the stiffener must satisfy the limit value () of the EN1993-1-1 standard [27].
Figure 4 shows changes in the strength reduction coefficient () based on the opening () installation angle of a cylindrical shell using S355 steel for differing shell thicknesses (). The shape and dimension of the opening used in the calculation that satisfies the limit range of the design criteria were selected for the collar stiffener opening used in wind power towers.
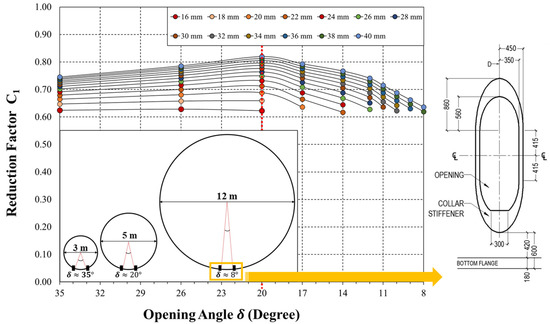
Figure 4.
Trend of the strength reduction factor () based on the opening angle ().
As the angle of installation of the cylindrical shell opening decreases, the reduction factor increases linearly. However, when the angle is less than 20°, the reduction factor gradually decreases. Consequently, in the design standard, when the angle of installation of the cylindrical shell opening is 20° or less, the influence of the section loss is considered to be small. Based on this, a large tower with a small opening angle should have a different collar stiffener design. However, the design standard does not deal with stiffener thickness.
3. Analysis Method for Investigating the Structural Stability and Ultimate Behavior of a Cylindrical Shell with Opening
For thin-walled structures with large radius-to-thickness ratios, such as cylindrical shells, it is important to examine the safety of compressive forces due to axial forces and bending moments [28]. For cylindrical shells with openings, the strength is reduced due to stress concentration and loss of section, so accurate analysis of the structure and review of the design strength is essential. Consequently, the structural analysis application ABAQUS (2020) and the finite element analysis guide provided by the design standards [24,25,27,29] were used. Through this, the model was selected to minimize errors by length by comparing the eigenvalue analysis results according to the shell length of the numerical analysis model with the elastic buckling strength provided by the design standards and theoretical Equations (1)–(3). Based on these results, an analysis considering the opening was performed, and the effect of the thickness of the reinforcement on the elastic buckling strength of the opening was investigated compared with the cylindrical shell without an opening. Finally, the results of LBA and GMNA of the selected variable analysis model were compared with the design Equations (4) and (5) considering the opening effect provided by DNV-GL-ST-0126.
3.1. Material Property
Typical properties used in wind towers are provided by the EN1993-1-10 standard [29]. Based on the grade of steel, S235 is used for normal strength steel (NS) and S355 is used for high strength steel (HS). Since the HS grade is suitable for large-diameter cylindrical shells with large r/t ratios, S355 steel was used in this study, as shown in Table 3 and Figure 5. A bi-linear material model was applied in the analysis to reflect the material nonlinearity.

Table 3.
Material properties for S355 [30].
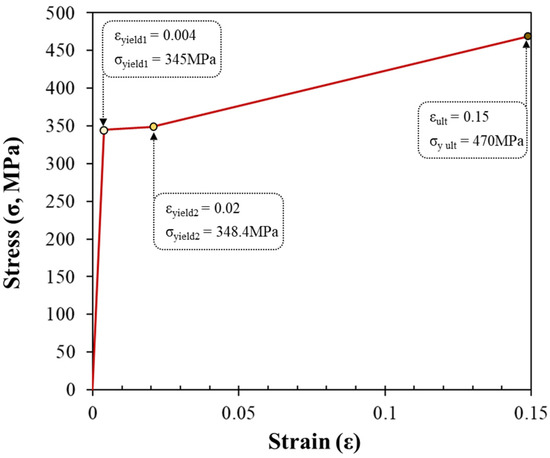
Figure 5.
Stress-strain curve (S355 Steel, ).
3.2. Parametric Modeling
To implement an accurate finite element analysis model, the theoretical strength of a cylindrical shell without an opening was compared with the ABAQUS analysis results. The model for error verification was a cylindrical shell of diameter 4 m () to 12 m () and thickness 40 mm. The length of the cylinder was set to a range from 4 to 12 m in consideration of the installation height of the opening, the model satisfying all the design standard restrictions.
The boundary conditions of the analysis model were applied, as shown in Table 4, and reference points were constructed at the top (RP1) and bottom (RP2) and connected to the rigid body (via interaction option-pins). Step-buckle analysis was conducted using ABAQUS. Through the analysis, the 1st order buckling mode of the cylindrical shell models, which is the governing buckling mode, was obtained. Figure 6 shows the 1st order buckling mode’s shape and the effect of the length of the models on the 1st order buckling strength.

Table 4.
Boundary conditions.
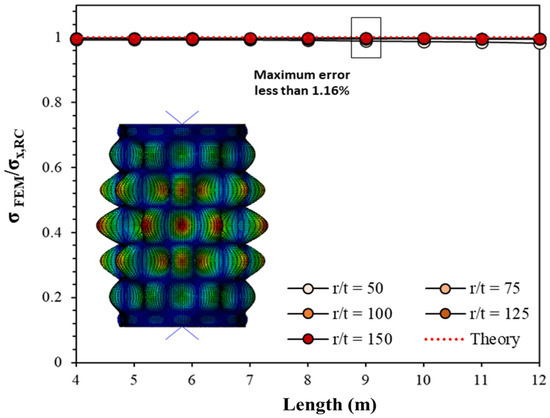
Figure 6.
Comparison of eigenvalue results and theoretical strength (1st order mode).
Table 5 shows the results in the first order buckling mode, the maximum error of which was 1.82% when and L = 12 m. To minimize the maximum error along the length to within 1.16%, the length of the cylindrical shell was limited to 9 m or less.

Table 5.
Comparison of elastic buckling stress (L = 9).
For finite element analysis modeling of the cylindrical shell considering the opening, the same modeling method as the previous analysis result was applied, the analysis variables considering the opening based on the diameter being set as shown in Table 6.

Table 6.
Comparison of elastic buckling stress (L = 9).
The diameter of the cylindrical shell used for modeling was 4–12 m, the resources of the tower supporting the turbine investigated in Figure 1 being used. The thickness of the shell was selected to be 40 mm, the maximum value within the thickness range of S355 steel (). The dimensions of the collar stiffener and the opening are shown in Figure 7. The ratio is 2.83 and the width of the stiffener varies from 100mm to 300mm. The inner width of the opening is 700 mm, and the opening angle of the shell along the girth varies from 8° to 26° depending on the cylindrical shell diameter. The dimensions of the openings used in this study were modeled to meet the design criteria presented by EN1993-1-1 standard.
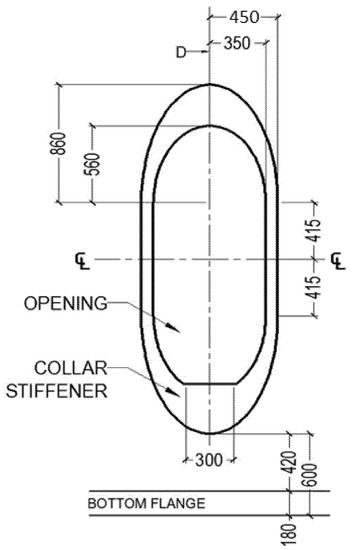
Figure 7.
Collar stiffener and opening dimensions (unit: mm).
Figure 8a shows the structural analysis model used in this study. It was sketched in a form similar to the drawing to reflect the effect of the opening as accurately as possible. Figure 8b shows the mesh for finite element analysis, the mesh being divided based on the curvature of the periphery of the opening. Figure 8c shows the boundary conditions and loads used in the analysis, with the critical load obtained from the eigenvalue analysis being applied to the GMNA load.
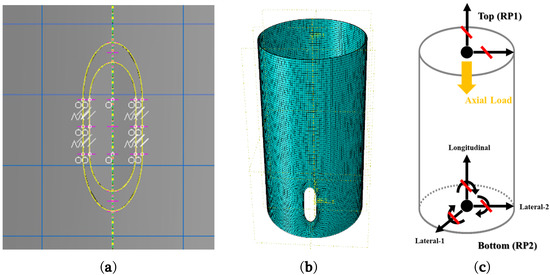
Figure 8.
Modeling of a cylindrical shell with openings: (a) parts sketch; (b) application of the mesh; (c) loading and boundary conditions.
4. Discussion: Analytical Investigation of the Structural Behavior and Proposed Equation for Collar Stiffener Thickness Design
4.1. The Effects of a Collar Stiffener around the Opening on the Elastic Buckling Strength of a Cylindrical Shell with Opening
LBA considering the opening was conducted by changing the thickness of the collar stiffener around the opening based on the ratio, after which the elastic analysis results of the circular cylindrical shell were compared with those of the cylindrical shell considering the opening.

Table 7.
Comparison of linear buckling analysis results by parameter.
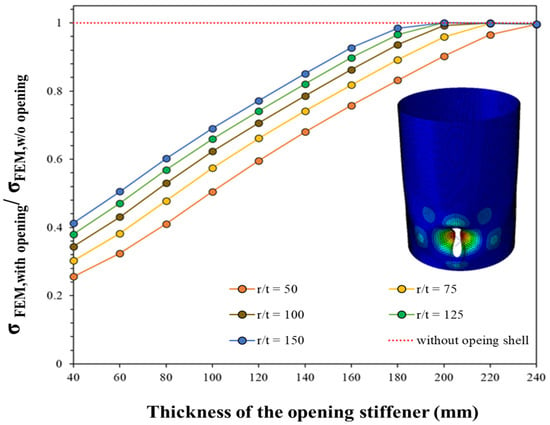
Figure 9.
Comparison of linear buckling analysis results based on collar stiffener thickness.
- (1)
- When = 40 mm (t = 40 mm, unstiffened opening), the effect of the opening on the elastic buckling strength was smaller as r/t increased.
- (2)
- If the thickness of the collar stiffener continuously increased at all ratios, it approached the elastic buckling strength of a cylindrical shell with no cross-sectional loss over a certain thickness.
- (3)
- At all ratios, the reinforcement effect based on the thickness of the collar stiffener exhibited a similar slope.
4.2. Ultimate Behavior of the Stiffened Cylindrical Shells with Opening Investigated Using Geometric and Material Nonlinear Analysis
To investigate the ultimate behavioral characteristics of the large-diameter cylindrical shell with opening, the nonlinear analysis GMNA, considering the main geometric and material nonlinearities such as the inelastic and large displacement and deformation effects, was carried out. To validate the numerical model and nonlinear analysis method performed in this study, the cylindrical shells without opening were analyzed by GMNA and the ultimate stresses evaluated were directly compared to the stress calculated by Equation (4) presented by DNVGL-ST-0126. As shown in Table 8, the differences between GMNA results and the stress calculated by Equation (4) for the cylindrical shells without opening were less than 5%, so it is concluded that the nonlinear analysis method is acceptable.

Table 8.
Comparison of geometric and material nonlinear analysis results by parameter.
Like the LBA results, the GMNA results were compared with the design strength of the cylindrical shell without opening and the finite element analysis results of the cylindrical shell considering the opening.
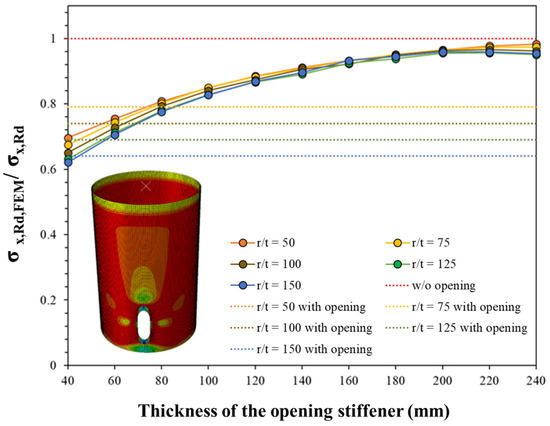
Figure 10.
Comparison of geometric and material nonlinear analysis results based on collar stiffener thickness.
- (1)
- The larger the ratio, the greater the reinforcement effect based on the thickness of the stiffener, but when = 180 mm, the design strength for all ratios converges to one point.
- (2)
- Comparing the analysis results with the design strength () applied with a strength reduction factor based on , the larger the ratio, the smaller the required design thickness of the stiffener. In other words, the effect of section loss due to the installation of openings is reduced.
- (3)
- To optimize the design of the collar stiffener for large-diameter cylindrical shells accounting for the opening, the reinforcement thickness should be applied differently based on the ratio.
4.3. Proposed Equation for Collar Stiffener Thickness Design
As shown in the finite element analysis results, it was confirmed that as the diameter of the cylindrical shell increased, the effect on elasticity and design strength due to the loss of the section due to the installation of the opening decreased. To understand the design strength trend based on the installation angle of the cylindrical shell considering the opening, the results of analyzing the thickness of the reinforcement around the opening as a variable are shown in Figure 11.
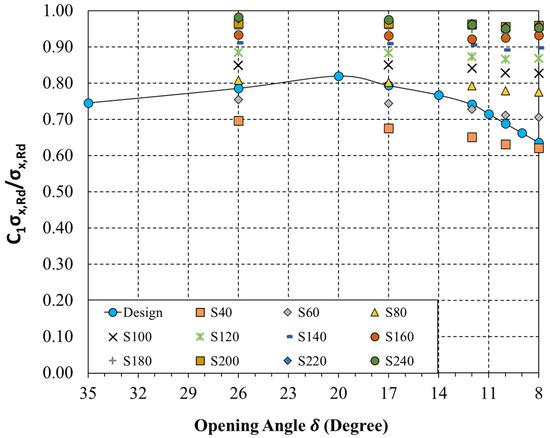
Figure 11.
Comparison of analysis results based on design strength and opening angle.
If the opening installation angle was more than 20°, the design strength decreased linearly considering the strength reduction factor provided by the design criteria. However, if the installation angle of the opening was less than 20°, the design strength accounting for the strength reduction factor sharply decreased, making it necessary to reflect this effect in the design of the stiffener thickness around the opening.
An economical design can be derived by optimizing the design of the peripheral stiffener thickness of a large-diameter cylindrical shell. Consequently, Equation (6) for the optimal design of a collar stiffener for large-diameter cylindrical shells was derived through power regression (R^2 = 0.9994) based on the design equation presented by DNVGL-ST-0126 with the finite element analysis results as follows:
where is the shell thickness and is the strength reduction factor provided by DNVGL-ST-0126 [26]. The proposed formula considers the ratio and within the target thickness and the strength reduction factor of a large-diameter cylindrical shell, making it possible to calculate the minimum collar stiffener thickness that meets the limits specified by the design standards.
5. Conclusions
In this study, the strength of a large-diameter cylindrical shell supporting a wind generator considering the opening was compared with the design strength provided by results that use the finite element analysis application ABAQUS and the design standard. Moreover, using the strength reduction factor provided by DNVGL-ST-0126 [26], a formula for calculating the thickness of a collar stiffener for a large-diameter cylindrical shell with an opening installation angle of 20° or less was proposed. Based on these results, the following conclusions were drawn.
- The eigenvalue analysis results of a cylindrical shell were compared with the elastic strength provided by the theory and design standards, and a parametric model with a maximum error of 1.16% was established.
- As a result of the LBA of a cylindrical shell considering the opening, the effect on the elastic buckling strength by the opening was small as increased. In the variable model for all ratios, the elastic buckling strength of the cylindrical shell converged to a certain thickness as the collar stiffener thickness increased.
- As a result of the GMNA of the cylindrical shell considering the opening, the effect of reinforcing the collar stiffener increased as increased, tending to converge when the thickness reached 180 mm. Comparing the analysis results with the design buckling strength to which the strength reduction factor was applied, the larger the ratio, the smaller the required design thickness of the stiffener, indicating that the cross-sectional loss effect due to the opening being installed in a large-diameter cylindrical shell was reduced.
- The design could thus be optimized by reducing the thickness of the collar stiffener based on the ratio when the opening installation angle was 20° or less. A formula for calculating the minimum collar stiffener thickness was proposed using the finite element analysis results and regression analysis of the design buckling strength.
- The proposed collar stiffener thickness calculation formula could only be used within the limits of the design standard. Therefore, if a follow-up experimental study considers the defects caused by fabrication imperfections (Q, Class A, B, C) and the cylindrical shell strength is verified and supplemented, the proposed formula could be applied to various designs of cylindrical shell structures with openings.
- In this study, the structural behaviors of the large-diameter cylindrical shell with stiffened opening subjected to the uniformly applied compressive force were investigated. However, the non-uniformed compressive force could be applied to the section of the wind turbine tower due to the characteristics of the structures and various loading conditions. Therefore, further study of the investigation of the structural behaviors of the cylindrical shell with an opening under the non-uniformly applied forces should be carried out.
Author Contributions
Conceptualization, Y.-J.K. and J.-S.P.; methodology, S.-Y.K., D.W., Y.-J.K. and S.K.; software, Y.-J.K.; validation, S.-Y.K. and S.K.; formal analysis, S.-Y.K.; investigation, S.-Y.K. and J.-S.P.; resources, Y.-J.K. and S.K.; data curation, S.-Y.K.; writing—original draft preparation, S.-Y.K.; writing—review and editing, S.K.; visualization, S.-Y.K. and D.W.; supervision, Y.-J.K., J.-S.P. and S.K.; project administration, Y.-J.K.; funding acquisition, Y.-J.K. and S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Pohang Iron and Steel Co., Ltd. (POSCO). This research was also funded by the National Research Foundation of Korea (NRF).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This research was conducted by the research project POSCO (Code 2020Z032). This work was also supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. NRF-2021R1A5A1032433).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mehmanparast, A.; Lotfian, S.; Vipin, S.P. A Review of Challenges and Opportunities Associated with Bolted Flange Connections in the Offshore Wind Industry. Metals 2020, 10, 732. [Google Scholar] [CrossRef]
- POWER TECHNOLOGY. “Horns Rev Offshore Wind Farm, Denmark” Projects. Available online: https://www.power-technology.com/projects/hornsreefwind/ (accessed on 14 July 2021).
- Domenico, L. Dynamics of Offshore Wind Turbines. Master’s Thesis, University of Bristol, Bristol, UK, 2010. [Google Scholar]
- Sørensen, J.D. Structural Reliability Aspects in Design of Wind Turbines; The Rackwitz Symposium Technical University: Munich, Germany, 24 November 2006. [Google Scholar]
- Zhao, Z.; Li, X.; Wang, W.; Shi, W. Analysis of Dynamic Characteristics of an Ultra-Large Semi-Submersible Floating Wind Turbine. J. Mar. Sci. Eng. 2019, 7, 169. [Google Scholar] [CrossRef] [Green Version]
- Desmond, C.; Murphy, J.; Blonk, L.; Haans, W. Description of an 8 MW reference wind turbine. J. Phys. Conf. Ser. 2016, 753, 092013. [Google Scholar] [CrossRef] [Green Version]
- NREL Transforming ENERGY. New Reference Turbine Gives Offshore Wind an Upward Draft; NREL: Golden, CO, USA, 2020.
- Guz, A.N.; Chernyshenko, I.S.; Shnerenko, K.I. Stress Concentration Near Openings in Composite Shells. Int. Appl. Mech. 2001, 37, 139–181. [Google Scholar] [CrossRef]
- Zirka, A.I.; Chernopiskii, D.I. Stress Concentration in an Axially Compressed Cylindrical Shell of Medium Thickness with an Elliptic Opening. Int. Appl. Mech. 2003, 39, 1335–1338. [Google Scholar] [CrossRef]
- Golling, S. Stress Concentration at the Door Opening of Steel Towers for Wind Turbine. Master’s Thesis, Lulea University of Technology, Luleå, Sweden, 2009. [Google Scholar]
- Reyno, H.; Park, J.; Kang, S.; Kang, Y.A. Numerical Analysis for Stress Concentration of Openings in Offshore Tubular Steel Tower under Design Loading Condition. J. Korea Acad. Ind. Coop. Soc. 2015, 16, 1516–1523. [Google Scholar]
- Tennyson, R. The effects of unreinforced circular cutouts on the buckling of circular cylindrical shells under axial compression. J. Eng. Ind. 1968, 90, 541–546. [Google Scholar] [CrossRef]
- Starnes, J. Effect of a slot on the buckling load of a cylindrical shell with a circular cutout. AAIA J. 1972, 10, 227–229. [Google Scholar] [CrossRef]
- Jullien, J.F.; Limam, A. Effects of openings of the buckling of cylindrical shells subjected to axial compression. Thin-Walled Struct. 1998, 31, 187–202. [Google Scholar] [CrossRef]
- Shariati, M.; Rokhi, M. Numerical and experimental investigations on buckling of steel cylindrical shells with elliptical cutout subject to axial compression. Thin-Walled Struct. 2008, 46, 1251–1261. [Google Scholar] [CrossRef]
- Shariati, M.; Rokhi, M. Buckling of steel cylindrical shells with an elliptical cutout. Int. J. Steel Struct. 2010, 10, 193–205. [Google Scholar] [CrossRef]
- Ghazijahani, T.G.; Jiao, H.; Holloway, D. Structural behavior of shells with different cutouts under compression: An experimental study. J. Constr. Steel Res. 2015, 105, 129–137. [Google Scholar] [CrossRef]
- Alsalah, A.; Holloway, D.; Ghazijahani, T.G. Recovery of capacity lost due to openings in cylindrical shells under compression. J. Constr. Steel Res. 2017, 137, 169–179. [Google Scholar] [CrossRef]
- Hilburger, M.W.; Starnes, J.H., Jr. Buckling behavior of compression-loaded composite cylindrical shells with reinforced cutouts. Int. J. Non-Linear Mech. 2005, 40, 1005–1021. [Google Scholar]
- Reyno, H. The ultimate strength for the lower segment of tubular steel wind tower with opening. Master’s Thesis, Sangmyung University, Seoul, South Korea, 2016. [Google Scholar]
- Cho, S.J. The Ultimate Strength of Cylindrical Steel Wind Turbine Tower with Opening. Master’s Thesis, Sangmyung University, Seoul, South Korea, 2017. [Google Scholar]
- Santos, R.; Cho, S.J.; Park, J.S. Ultimate Strength of 10 MW Wind Turbine Tower Considering Opening, Stiffener, and Initial Imperfection. Int. J. Steel Struct. 2018, 18, 1318–1324. [Google Scholar] [CrossRef]
- Timoshenko, S.; Gere, J. Theory of Elastic Stability, 2nd ed.; Dover Publications, Incorporated, McGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- BSI (British Standards Institution). Eurocode 3: Design of Steel Structures-Part 1–6: Strength and Stability of Shell Structures; BSI: London, UK, 2007. [Google Scholar]
- DNV (Det Norske Veritas). DNV-RP-C202: Buckling Strength of Shells; DNVGL: Oslo, Norway, 2017. [Google Scholar]
- DNV (Det Norske Veritas). DNVGL-ST-0126: Support Structures For Wind Turbines; DNVGL: Oslo, Norway, 2018. [Google Scholar]
- BSI (British Standards Institution). Eurocode 3: Design of Steel Structures-Part 1-1: General Rules; BSI: London, UK, 2005. [Google Scholar]
- Ahn, J.T.; Shin, D.K. Ultimate Flexural Strength of Cylindrical Steel Shell for Wind Tower. Korean Soc. Steel Constr. 2015, 27, 109–118. [Google Scholar] [CrossRef]
- BSI (British Standards Institution). Eurocode 3: Design of Steel Structures-Part 1–10: Material Toughness and Through-Thickness Properties; BSI: London, UK, 2007. [Google Scholar]
- DNV (Det Norske Veritas). DNV-RP-C208: Determination of Structural Capacity by Non-Linear FE Analysis Methods; DNVGL: Oslo, Norway, 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).