Modified Flower Pollination Algorithm for Global Optimization
Abstract
:1. Introduction
- ➢
- Proposes a modified variant of the classical FPA, namely MFPA, with various updating schemes to tackle both global optimization and NESs.
- ➢
- Improves the exploration operator of MFPA using the DE with the “DE/rand/1” scheme to propose a new hybrid variant, called HFPA, with strong attributes.
- ➢
- The experimental findings show that HFPA has superior performance for tackling global optimization and NESs compared to eight rival algorithms and MFPA.
2. Literature Review: NESs
3. Overview of Used Metaheuristic Techniques
3.1. Flower Pollination Algorithm (FPA)
- Biotic and cross-pollination can be defined as global pollination used to explore the regions of the search space for finding the most promising regions. This stage is based on the levy distribution.
- The abiotic self-pollination describes the local pollination utilized to exploit the regions around the current solution for accelerating the convergence speed.
- The flower constancy property can be regarded as a reproduction ratio that is proportional to the degree of similarity between two flowers.
- Local pollination has a slight advantage in comparison to global pollination due to the physical proximity and wind. In specific, the local and global pollinations are controlled by a control variable P having a value between 0 and 1.
3.2. Differential Evolution
3.2.1. Mutation Operator
3.2.2. Crossover Operator
3.2.3. Selection Operator
4. Proposed Algorithm: Hybrid Modified FPA (HMFPA)
4.1. Initialization
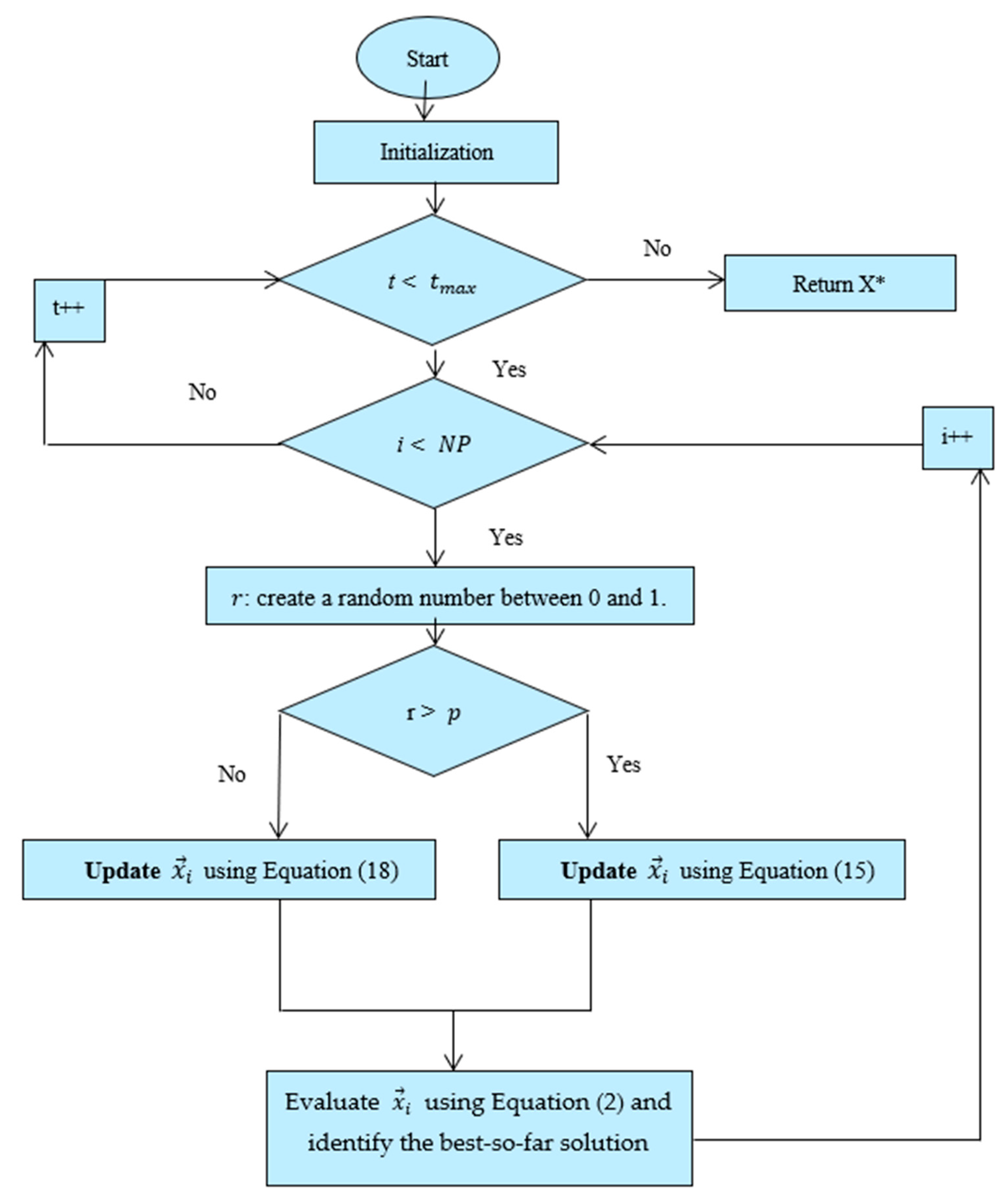
4.2. Modified Flower Pollination Algorithm (MFPA)
4.2.1. Global Pollination
4.2.2. Local Pollination
| Algorithm 1 The Steps of MFPA |
| 1. Initialization step. |
| 2. Evaluation. |
| 3. while (t < ) |
| 4. For (I = 1: NP) |
| 5. : create a random number between 0 and 1. |
| 6. if (r > p) |
| 7. Update using Equation (15) |
| 8. Else |
| 9. Update using Equation (18) |
| 10. End if |
| 11. End for |
| 12. Evaluation step. |
| 13. t = t + 1; |
| 14. end while |
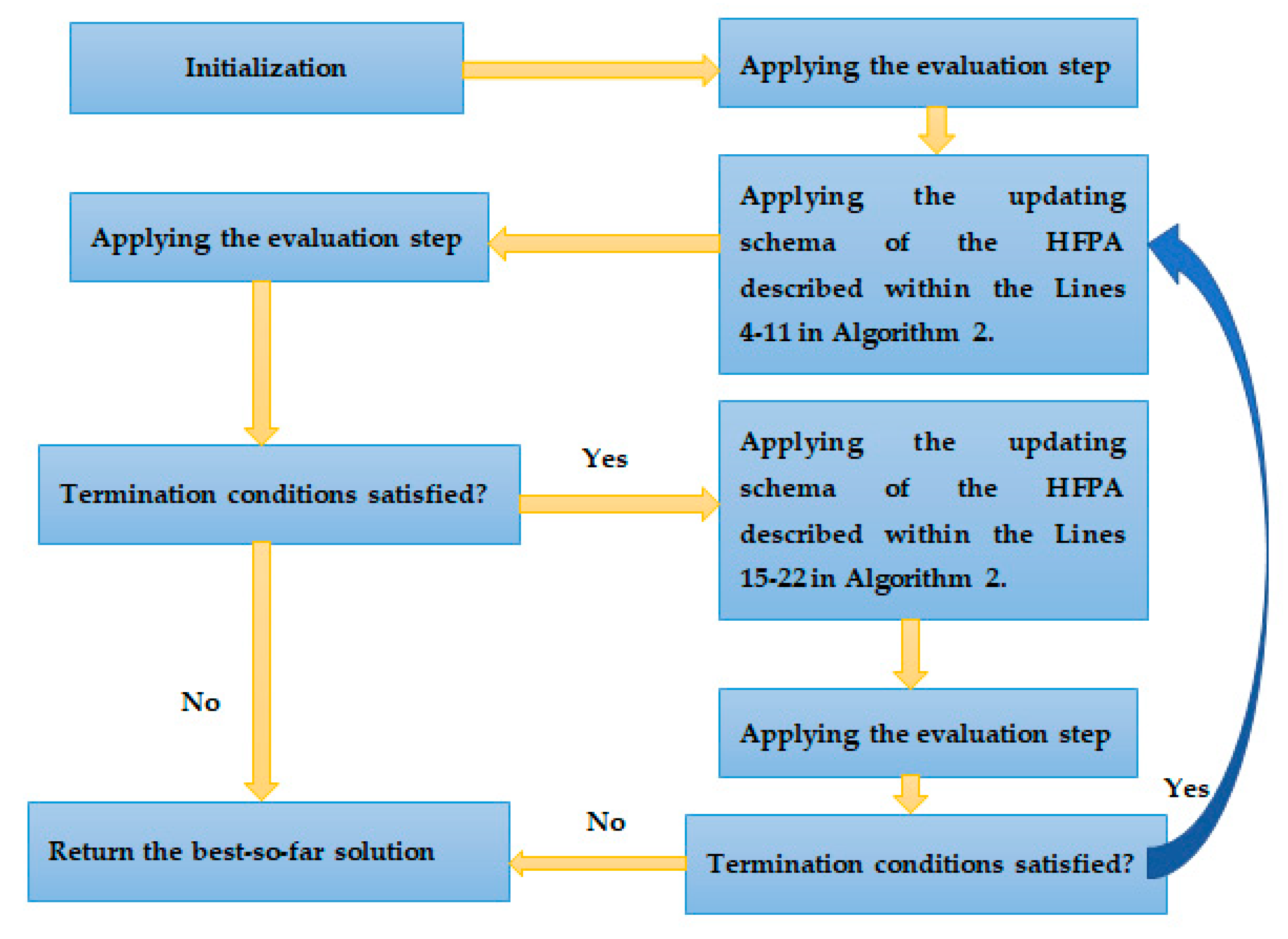
4.3. Hybridization of MFPA with DE(HFPA)
| Algorithm 2 The Steps of HFPA |
| 1. Initialization step. |
| 2.Evaluation. |
| 3.while (t < ) |
| 4. For (i = 1: NP) |
| 5. : create a random number between 0 and 1. |
| 6. if (r > p) |
| 7. Update using Equation (15) |
| 8. Else |
| 9. Update using Equation (18) |
| 10. End if |
| 11. End for |
| 12. Evaluation step. |
| 13. t = t + 1; |
| 14. /// Applying differential evolution |
| 15. if r< |
| 16. For (i=1: NP) |
| 17. Creating a mutant vector for using Equation (5) |
| 18. Applying crossover operator. |
| 19. Applying selection operator |
| 20. End for |
| 21. t = t + 1; |
| 22. End if |
| 23. end while |
5. Outcomes and Discussion
- ➢
- Section 5.1 shows the parameter settings and benchmark test functions.
- ➢
- Section 5.2 presents validation and comparison under 23 global optimization problems.
- ➢
- Section 5.3 presents validation and comparison under 27 NESs.
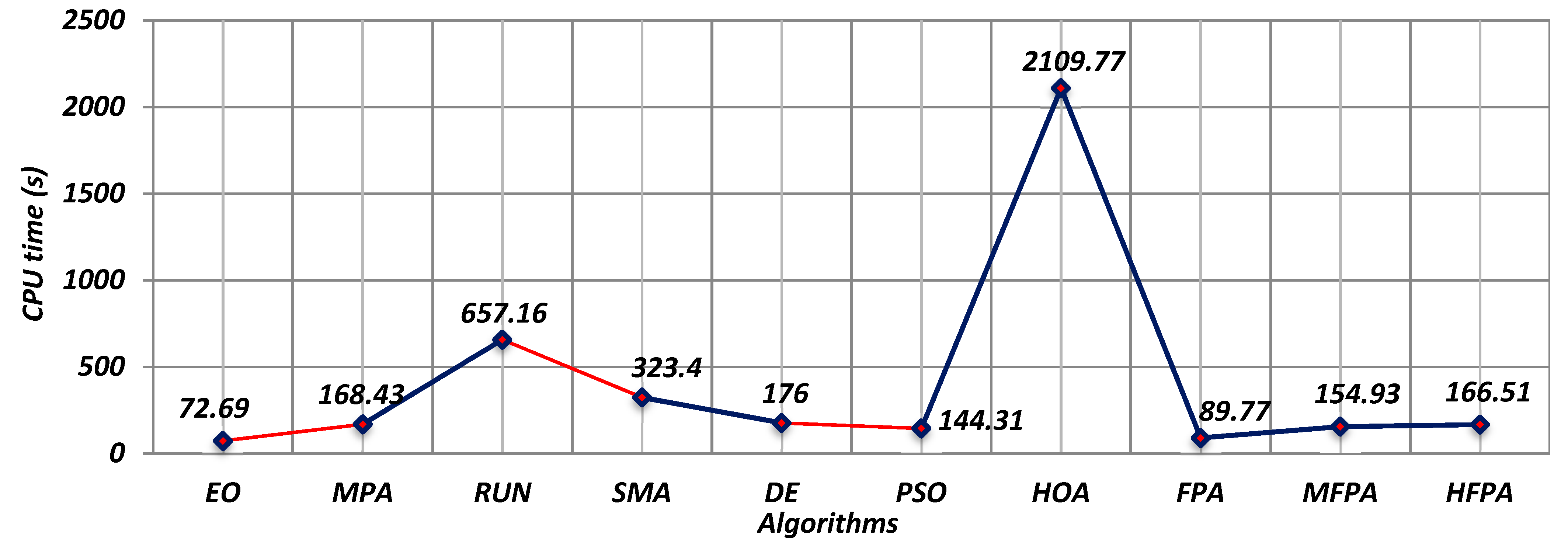
5.1. Parameter Settings
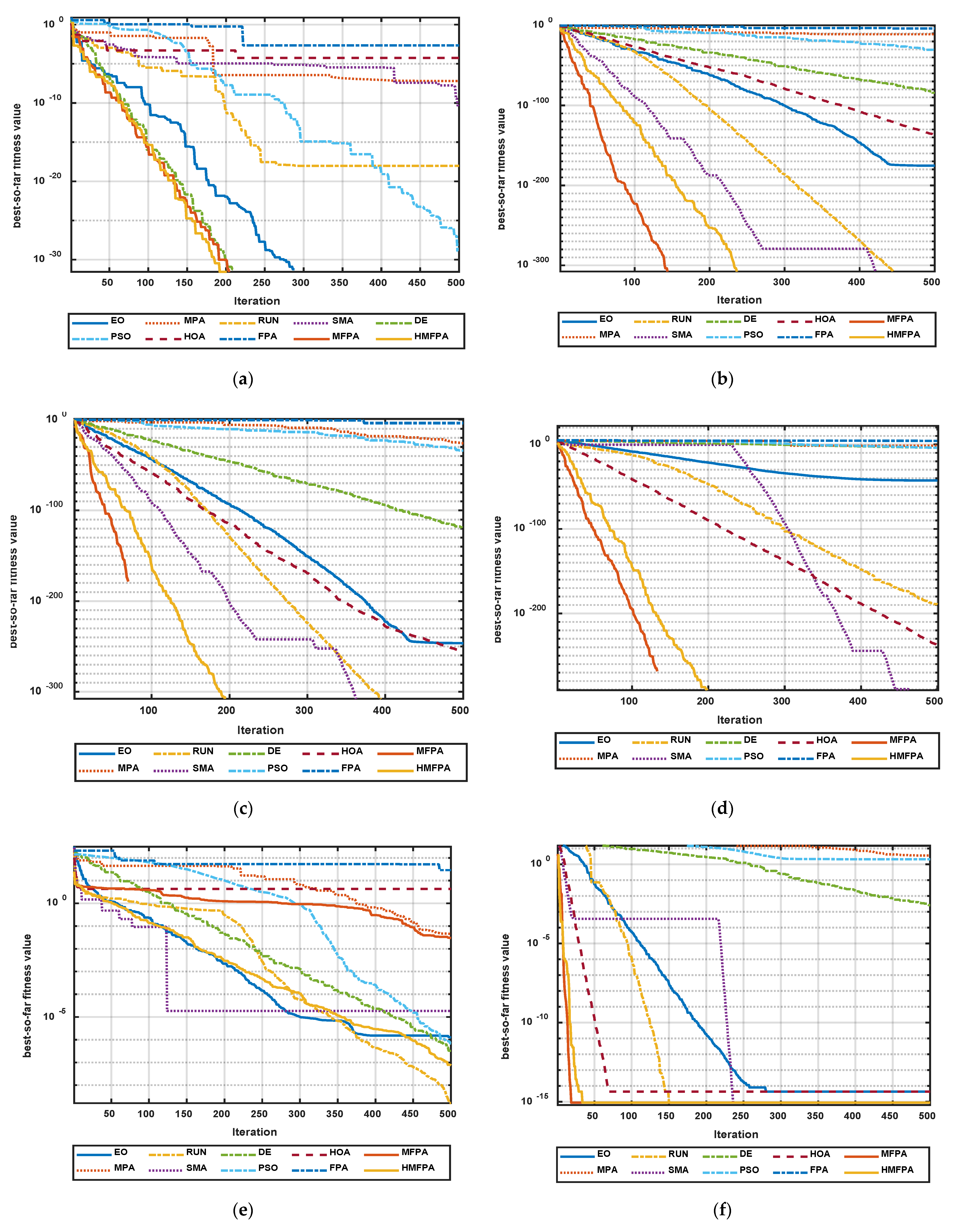
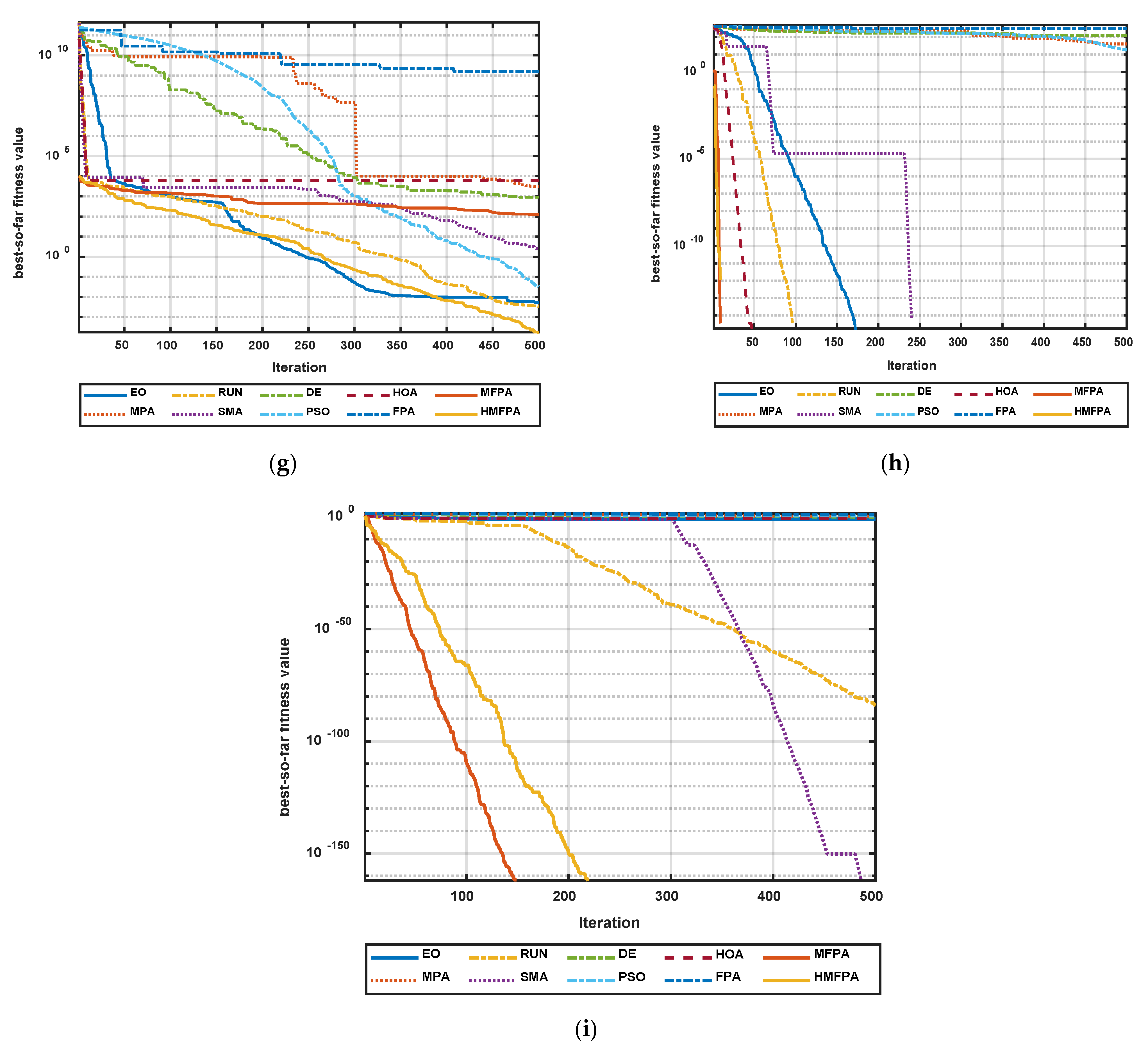
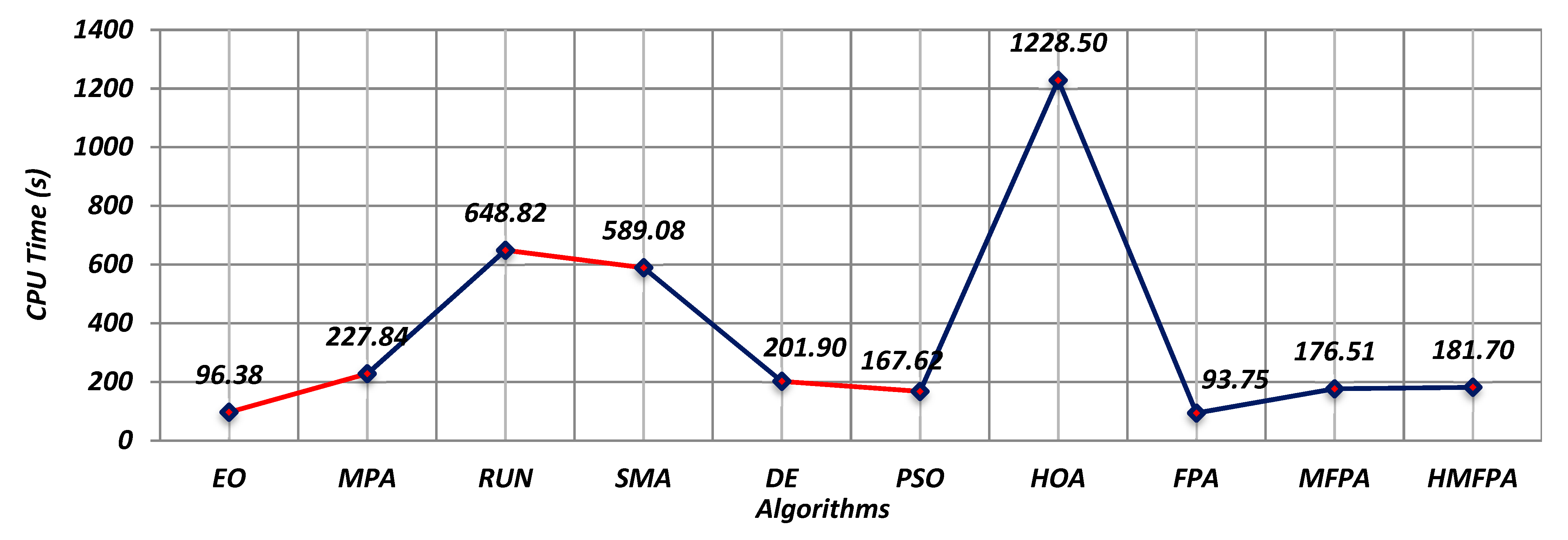
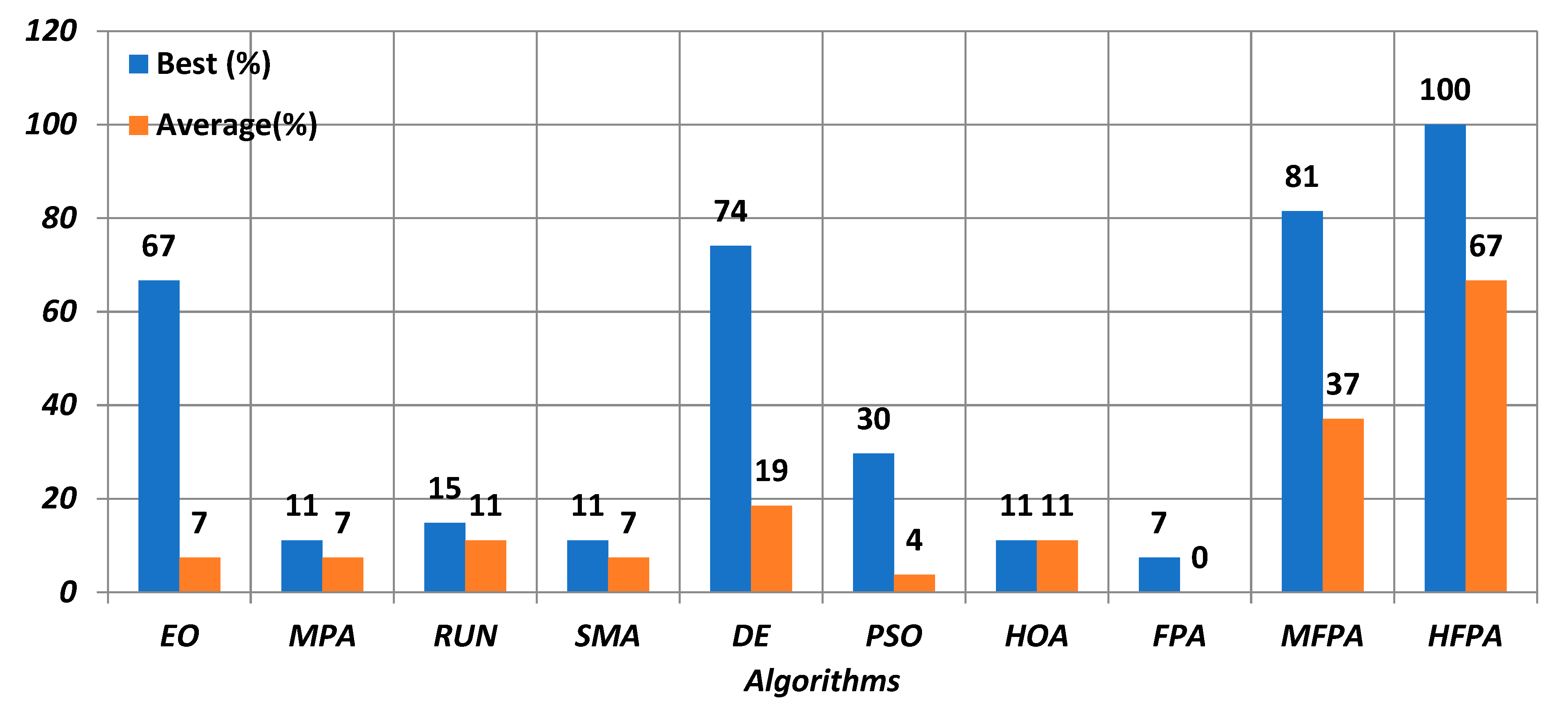
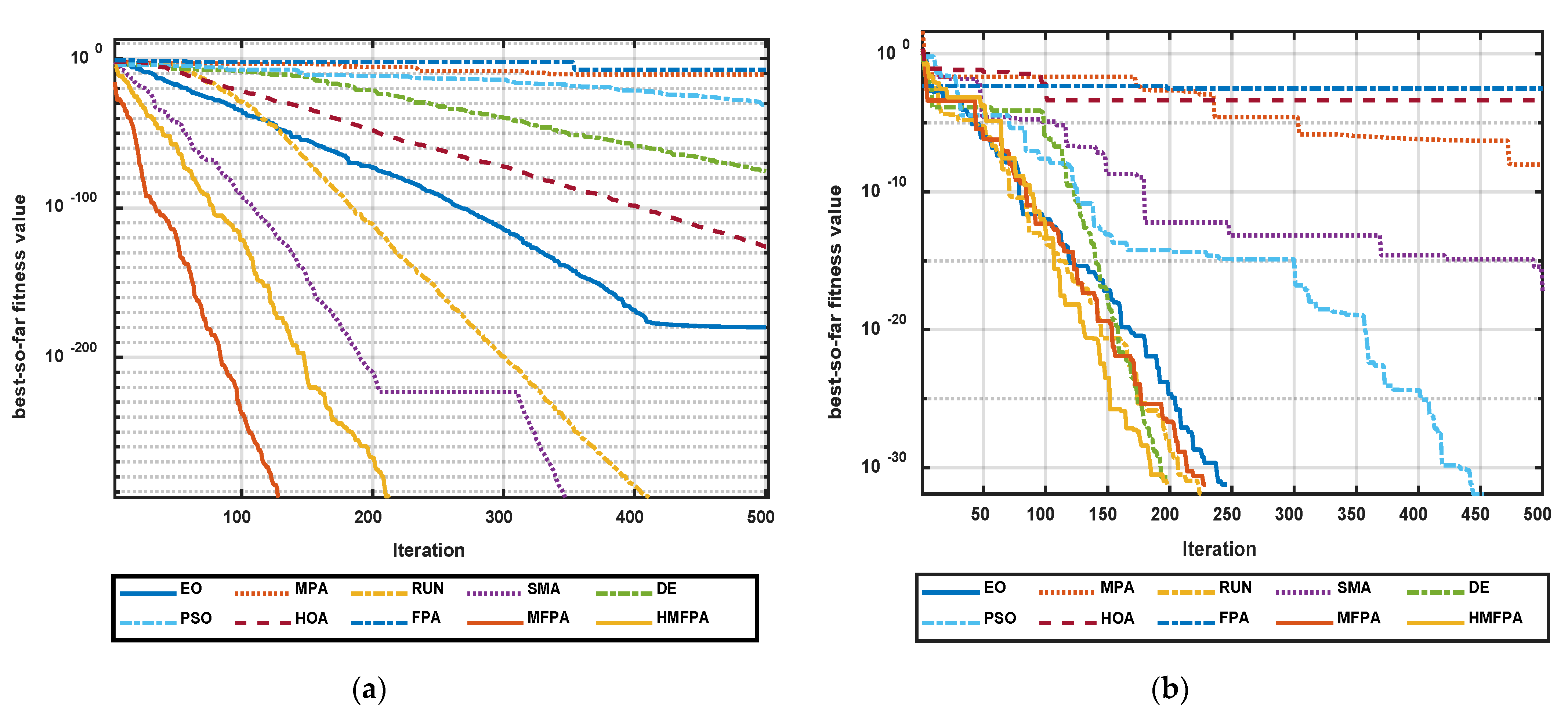
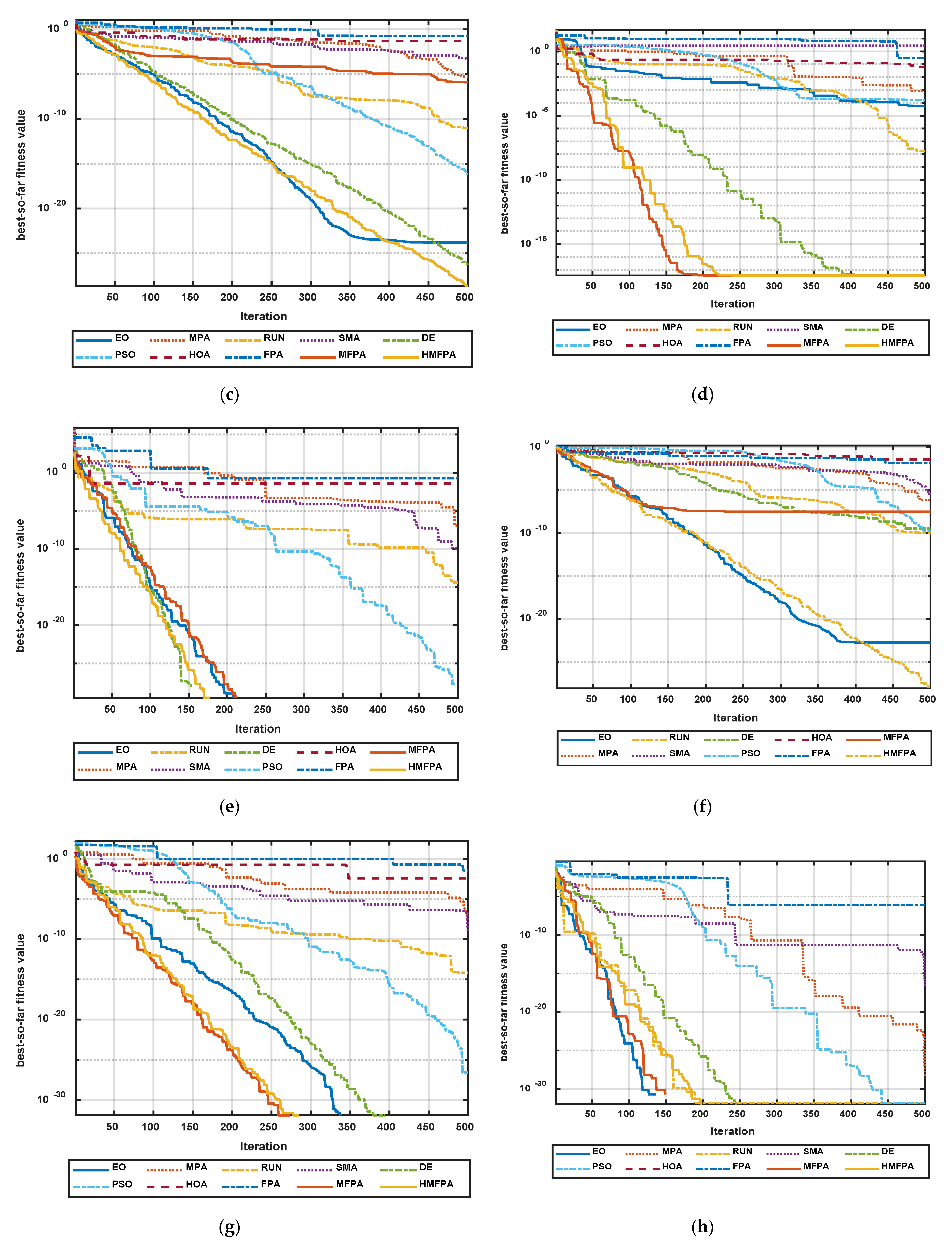
5.2. Comparison of the Global Optimization
5.3. Comparison of the NESs
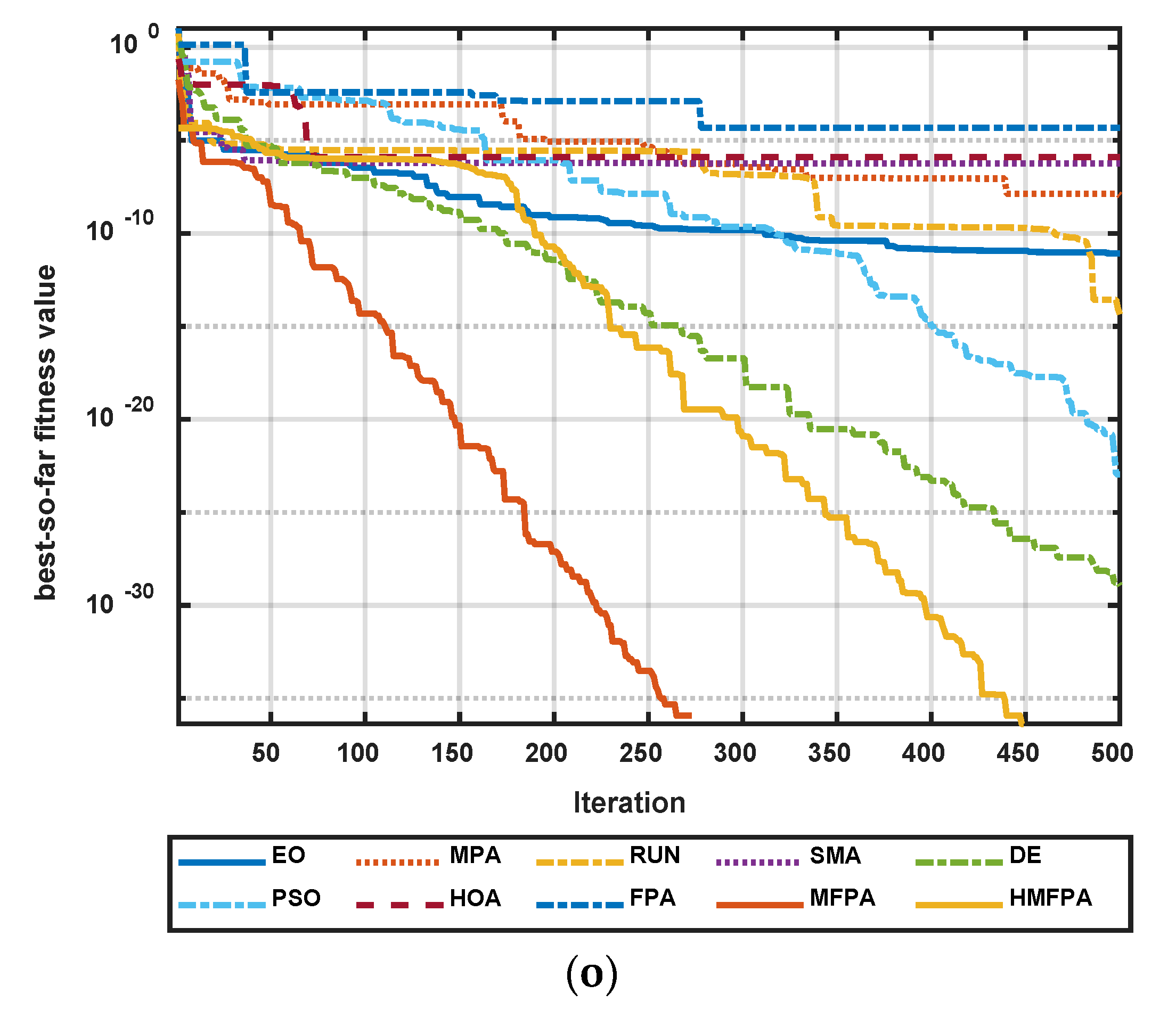
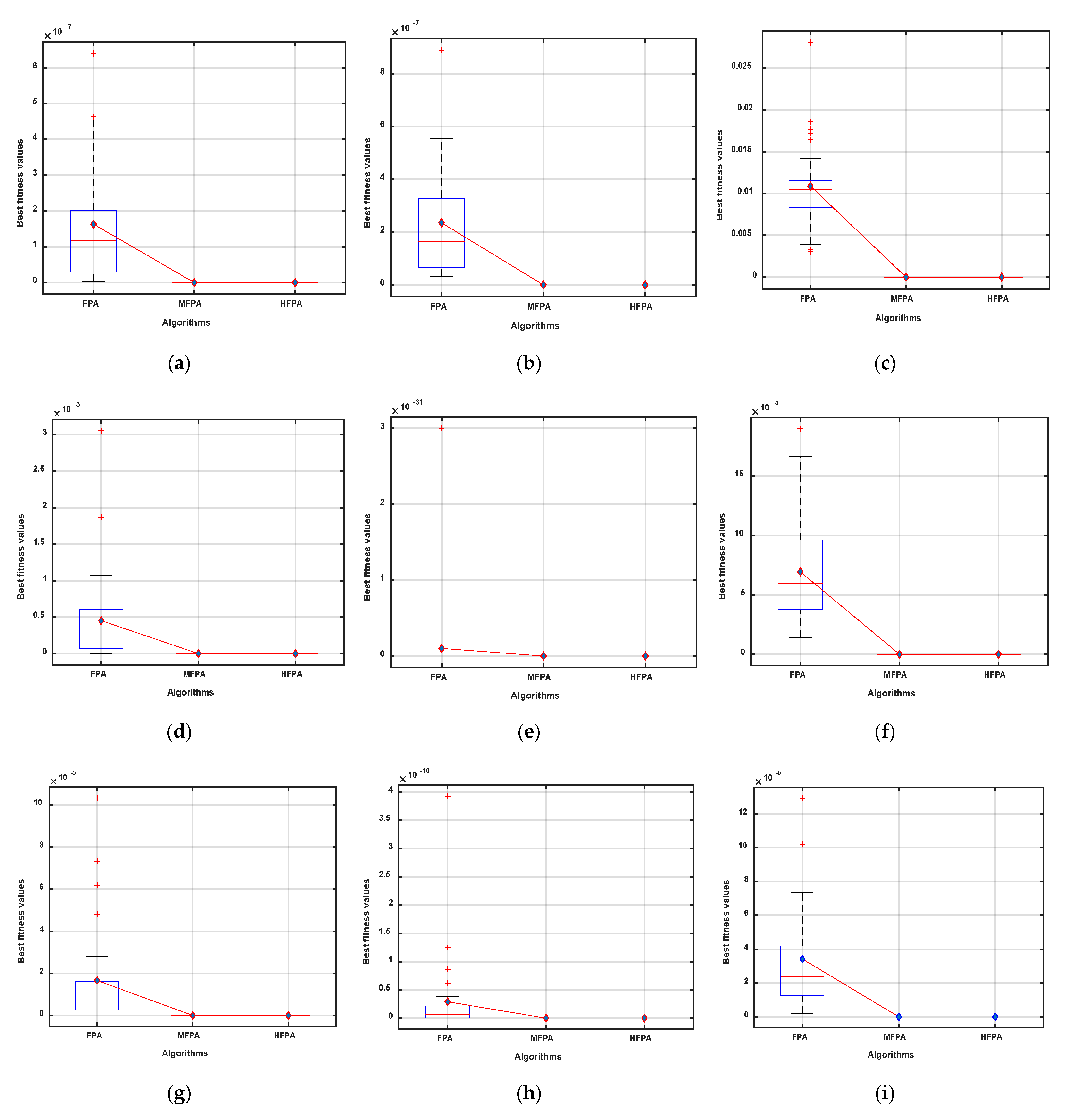
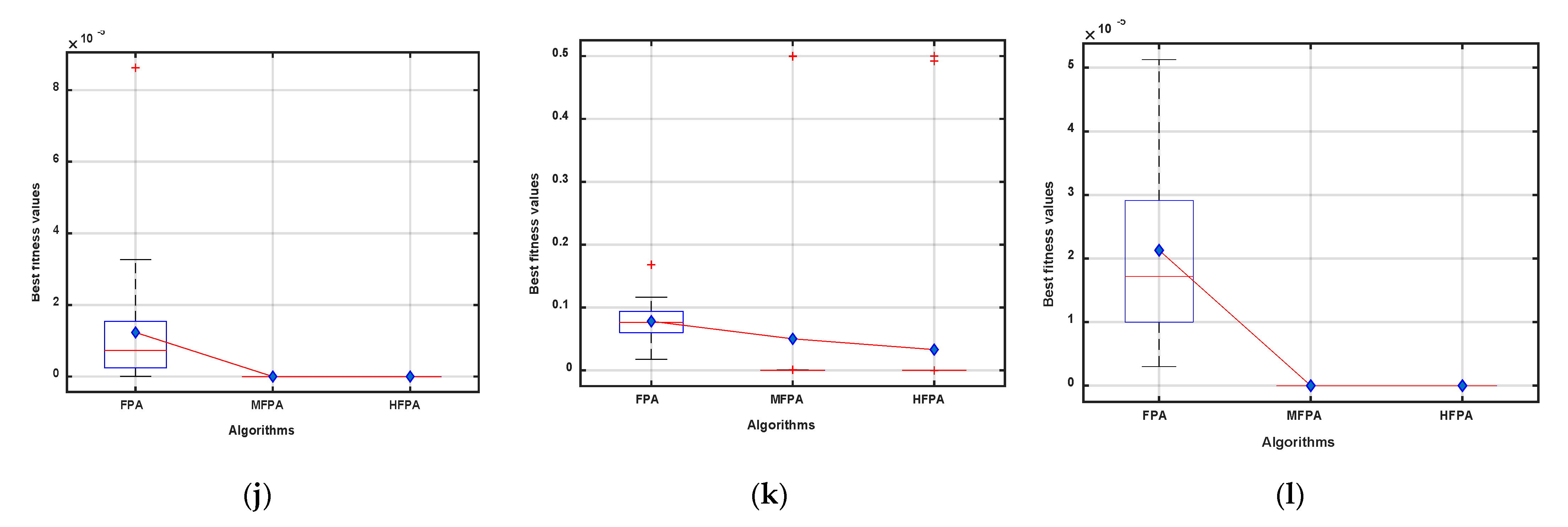
5.4. Comparison between FPA Variants on NESs
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Rechenberg, I. Evolutionsstrategien, in Simulationsmethoden in der Medizin und Biologie; Springer: Berlin/Heidelberg, Germany, 1978; pp. 83–114. [Google Scholar]
- Banzhaf, W.; Nordin, P.; Keller, R.E.; Francone, F.D. Genetic Programming: An Introduction; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1998; Volume 1. [Google Scholar]
- Dasgupta, D.; Michalewicz, Z. Evolutionary Algorithms in Engineering Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef] [Green Version]
- Van Laarhoven, P.J.M.; Aarts, E.H.L. Simulated Annealing: Theory and Applications; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1987; pp. 7–15. [Google Scholar]
- Erol, O.K.; Eksin, I. A New Optimization Method: Big Bang–Big Crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Du, H.; Wu, X.; Zhuang, J. Small-World Optimization Algorithm for Function Optimization. In Proceedings of the Transactions on Petri Nets and Other Models of Concurrency XV; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2006; pp. 264–273. [Google Scholar]
- Moghaddam, F.F.; Moghaddam, R.F.; Cheriet, M. Curved Space Optimization: A Random Search Based on General Relativity Theory. arXiv 2012, arXiv:1208.2214. [Google Scholar]
- Hosseini, H.S. Principal Components Analysis by the Galaxy-Based Search Algorithm: A Novel Metaheuristic for Continuous Optimisation. Int. J. Comput. Sci. Eng. 2011, 6, 132. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A Novel Heuristic Optimization Method: Charged System Search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Van Tran, T.; Wang, Y. Informatics, Artificial Chemical Reaction Optimization Algorithm and Neural Network Based Adaptive Control for Robot Manipulator. J. Control. Eng. Appl. Inform. 2017, 19, 61–70. [Google Scholar]
- Kaveh, A.; Khayatazad, M. A New Meta-Heuristic Method: Ray Optimization. Comput. Struct. 2012, 112-113, 283–294. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Kaveh, A.; Khanzadi, M.; Moghaddam, M.R. Billiards-Inspired Optimization Algorithm; A New Meta-Heuristic Method. Structures 2020, 27, 1722–1739. [Google Scholar] [CrossRef]
- Hatamlou, A. Black Hole: A New Heuristic Optimization Approach for Data Clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95 International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Futur. Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A Nature-Inspired Metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime Mould Algorithm: A New Method for Stochastic Optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Erratum to: Cuckoo Search Algorithm: A Metaheuristic Approach to Solve Structural Optimization Problems. Eng. Comput. 2013, 29, 245. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.-S.; He, X. Bat Algorithm: Literature Review and Applications. Int. J. Bio-Inspired Comput. 2013, 5, 141–149. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.-S. Flower Pollination Algorithm for Global Optimization. In Proceedings of the Transactions on Petri Nets and Other Models of Concurrency XV; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2012; pp. 240–249. [Google Scholar]
- Khishe, M.; Mosavi, M. Chimp Optimization Algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Chu, S.-C.; Tsai, P.-W.; Pan, J.-S. Cat Swarm Optimization. In Proceedings of the 9th Pacific Rim International Conference on Artificial Intelligence, Guilin, China, 7–11 August 2006. [Google Scholar]
- Meng, X.-B.; Liu, Y.; Gao, X.; Zhang, H. A New Bio-inspired Algorithm: Chicken Swarm Optimization. In Proceedings of the 5th International Conference (ICSI 2014), Hefei, China, 17–20 October 2014; pp. 86–94. [Google Scholar]
- Bansal, J.C.; Sharma, H.; Jadon, S.S.; Clerc, M. Spider Monkey Optimization Algorithm for Numerical Optimization. Memetic Comput. 2014, 6, 31–47. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill Herd: A New Bio-Inspired Optimization Algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Xing, B.; Gao, W.-J. Innovative Computational Intelligence: A Rough Guide to 134 Clever Algorithms; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2014; pp. 167–170. [Google Scholar]
- Kaveh, A.; Farhoudi, N. A New Optimization Method: Dolphin Echolocation. Adv. Eng. Softw. 2013, 59, 53–70. [Google Scholar] [CrossRef]
- Oftadeh, R.; Mahjoob, M.; Shariatpanahi, M. A Novel Meta-Heuristic Optimization Algorithm Inspired by Group Hunting of Animals: Hunting Search. Comput. Math. Appl. 2010, 60, 2087–2098. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization. In International Symposium on Stochastic Algorithms; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Shiqin, Y.; Jianjun, J.; Guangxing, Y. A Dolphin Partner Optimization. In Proceedings of the 2009 WRI Global Congress on Intelligent Systems, Xiamen, China, 19–21 May 2009; Volume 1, pp. 124–128. [Google Scholar] [CrossRef]
- Lu, X.; Zhou, Y. A Novel Global Convergence Algorithm: Bee Collecting Pollen Algorithm. In Proceedings of the 4th International Conference on Intelligent Computing, ICIC 2008, Shanghai, China, 15–18 September 2008; pp. 518–525. [Google Scholar]
- Wu, H.; Zhang, F.-M. Wolf Pack Algorithm for Unconstrained Global Optimization. Math. Probl. Eng. 2014, 2014, 465082. [Google Scholar] [CrossRef] [Green Version]
- Pilat, M.L. Wasp-Inspired Construction Algorithms; University of Calgary: Calgary, AB, Canda, 2006. [Google Scholar]
- Rao, R.V. Teaching-Learning-Based Optimization Algorithm. In Teaching Learning Based Optimization Algorithm; Springer: Berlin/Heidelberg, Germany, 2016; pp. 9–39. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Kashan, A.H. League Championship Algorithm: A New Algorithm for Numerical Function Optimization. In Proceedings of the 2009 International Conference of Soft Computing and Pattern Recognition, Malacca, Malaysia, 4–7 December 2009; pp. 43–48. [Google Scholar]
- Eita, M.; Fahmy, M. Group Counseling Optimization. Appl. Soft Comput. 2014, 22, 585–604. [Google Scholar] [CrossRef]
- Eita, M.A.; Fahmy, M.M. Group Counseling Optimization: A Novel Approach. In Research and Development in Intelligent Systems XXVI; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2009; pp. 195–208. [Google Scholar]
- Sadollah, A.; Bahreininejad, A.; Eskandar, H.; Hamdi, M. Mine Blast Algorithm: A New Population Based Algorithm for Solving Constrained Engineering Optimization Problems. Appl. Soft Comput. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Dai, C.; Zhu, Y.; Chen, W. Seeker Optimization Algorithm. In International Conference on Computational and Information Science; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Moosavian, N.; Roodsari, B.K.J. Soccer League Competition Algorithm, A New Method for Solving Systems of Nonlinear Equations. Int. J. Intell. Sci. 2013, 4, 7. [Google Scholar] [CrossRef]
- Moosavian, N.; Roodsari, B.K. Soccer League Competition Algorithm: A Novel Meta-Heuristic Algorithm for Optimal Design of Water Distribution Networks. Swarm Evol. Comput. 2014, 17, 14–24. [Google Scholar] [CrossRef]
- Tan, Y.; Zhu, Y. Fireworks Algorithm for Optimization. In Proceedings of the Transactions on Petri Nets and Other Models of Concurrency XV; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2010; pp. 355–364. [Google Scholar]
- Moosavi, S.H.S.; Bardsiri, V.K. Poor and Rich Optimization Algorithm: A New Human-Based and Multi Populations Algorithm. Eng. Appl. Artif. Intell. 2019, 86, 165–181. [Google Scholar] [CrossRef]
- Liao, Z.; Gong, W.; Wang, L. Memetic Niching-Based Evolutionary Algorithms for Solving Nonlinear Equation System. Expert Syst. Appl. 2020, 149, 113261. [Google Scholar] [CrossRef]
- Wetweerapong, J.; Puphasuk, P. An Improved Differential Evolution Algorithm with a Restart Technique to Solve Systems of Nonlinear Equations. Int. J. Optim. Control. Theor. Appl. 2020, 10, 118–136. [Google Scholar] [CrossRef] [Green Version]
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A Survey on Optimization Metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Siddique, N.H.; Adeli, H. Nature Inspired Computing: An Overview and Some Future Directions. Cogn. Comput. 2015, 7, 706–714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nabil, E. A Modified Flower Pollination Algorithm for Global Optimization. Expert Syst. Appl. 2016, 57, 192–203. [Google Scholar] [CrossRef]
- Yang, X.-S.; Karamanoglu, M.; He, X. Flower Pollination Algorithm: A Novel Approach for Multiobjective Optimization. Eng. Optim. 2014, 46, 1222–1237. [Google Scholar] [CrossRef] [Green Version]
- Nigdeli, S.M.; Bekdaş, G.; Yang, X.-S. Application of the Flower Pollination Algorithm in Structural Engineering. In Internet of Things (IoT) in 5G Mobile Technologies; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2016; pp. 25–42. [Google Scholar]
- Rodrigues, D.; Yang, X.-S.; de Souza, A.N.; Papa, J.P. Binary Flower Pollination Algorithm and Its Application to Feature Selection. In Econometrics for Financial Applications; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2015; pp. 85–100. [Google Scholar]
- Salgotra, R.; Singh, U. Application of Mutation Operators to Flower Pollination Algorithm. Expert Syst. Appl. 2017, 79, 112–129. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, Y.; Qiao, S.; Huang, K. Flower Pollination Algorithm with Bee Pollinator for Cluster Analysis. Inf. Process. Lett. 2016, 116, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Storn, R. On the Usage of Differential Evolution for Function Optimization. In Proceedings of the North American Fuzzy Information Processing, Berkeley, CA, USA, 19–22 June 1996; pp. 519–523. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Sabry, H.Z.; Khorshid, M. An Alternative Differential Evolution Algorithm for Global Optimization. J. Adv. Res. 2012, 3, 149–165. [Google Scholar] [CrossRef] [Green Version]
- Karaboğa, D.; Ökdem, S.J.; Sciences, C. A Simple and Global Optimization Algorithm for Engineering Problems: Differential Evolution Algorithm. Turk. J. Electr. Eng. Comput. Sci. 2004, 12, 53–60. [Google Scholar]
- Das, S.; Mandal, A.; Mukherjee, R. An Adaptive Differential Evolution Algorithm for Global Optimization in Dynamic Environments. IEEE Trans. Cybern. 2013, 44, 966–978. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, C.-E.; Ma, M. A Robust Archived Differential Evolution Algorithm for Global Optimization Problems. J. Comput. 2009, 4, 160–167. [Google Scholar] [CrossRef]
- Pant, M.; Ali, M.; Singh, V.P. Parent-Centric Differential Evolution Algorithm for Global Optimization Problems. Opsearch 2009, 46, 153–168. [Google Scholar] [CrossRef]
- Choi, T.J.; Ahn, C.W.; An, J. An Adaptive Cauchy Differential Evolution Algorithm for Global Numerical Optimization. Sci. World J. 2013, 2013, 969734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, P.; Pant, M. A Self Adaptive Differential Evolution Algorithm for Global Optimization. In Proceedings of the Computer Vision; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2010; Volume 6466, pp. 103–110. [Google Scholar]
- Sun, J.; Zhang, Q.; Tsang, E.P.K. DE/EDA: A New Evolutionary Algorithm for Global Optimization. Inf. Sci. 2005, 169, 249–262. [Google Scholar] [CrossRef]
- Brest, J.; Zamuda, A.; Fister, I.; Maucec, M.S. Large Scale Global Optimization Using Self-Adaptive Differential Evolution Algorithm. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Yi, W.; Gao, L.; Li, X.; Zhou, Y. A New Differential Evolution Algorithm with a Hybrid Mutation Operator and Self-Adapting Control Parameters for Global Optimization Problems. Appl. Intell. 2014, 42, 642–660. [Google Scholar] [CrossRef]
- Brest, J.; Zumer, V.; Maucec, M. Self-Adaptive Differential Evolution Algorithm in Constrained Real-Parameter Optimization. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006. [Google Scholar]
- Ramadas, G.C.; Fernandes, E.M.d.G. Solving Systems of Nonlinear Equations by Harmony Search. In Proceedings of the 13th International Conference on Mathematical Methods in Science and Engineering, Almeria, Spain, 24–27 June 2013. [Google Scholar]
- Wu, J.; Cui, Z.; Liu, J. Using Hybrid Social Emotional Optimization Algorithm with Metropolis Rule to Solve Nonlinear Equations. In Proceedings of the IEEE 10th International Conference on Cognitive Informatics and Cognitive Computing (ICCI-CC’11), Banff, AB, Canada, 18–20 August 2011; pp. 405–411. [Google Scholar]
- Chang, W.-D. An Improved Real-Coded Genetic Algorithm for Parameters Estimation of Nonlinear Systems. Mech. Syst. Signal. Process. 2006, 20, 236–246. [Google Scholar] [CrossRef]
- Grosan, C.; Abraham, A. A New Approach for Solving Nonlinear Equations Systems. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2008, 38, 698–714. [Google Scholar] [CrossRef]
- Ren, H.; Wu, L.; Bi, W.; Argyros, I.K. Solving Nonlinear Equations System via an Efficient Genetic Algorithm with Symmetric and Harmonious Individuals. Appl. Math. Comput. 2013, 219, 10967–10973. [Google Scholar] [CrossRef]
- Mo, Y.; Liu, H.; Wang, Q. Conjugate Direction Particle Swarm Optimization Solving Systems of Nonlinear Equations. Comput. Math. Appl. 2009, 57, 1877–1882. [Google Scholar] [CrossRef] [Green Version]
- Jaberipour, M.; Khorram, E.; Karimi, B. Particle Swarm Algorithm for Solving Systems of Nonlinear Equations. Comput. Math. Appl. 2011, 62, 566–576. [Google Scholar] [CrossRef] [Green Version]
- Ariyaratne, M.; Fernando, T.; Weerakoon, S. Solving Systems of Nonlinear Equations Using a Modified Firefly Algorithm (MODFA). Swarm Evol. Comput. 2019, 48, 72–92. [Google Scholar] [CrossRef]
- Wu, Z.; Kang, L. A Fast and Elitist Parallel Evolutionary Algorithm for Solving Systems of Non-Linear Equations. In Proceedings of the 2003 Congress on Evolutionary Computation, CEC ’03, Canberra, Australia, 8–12 December 2003. [Google Scholar]
- El-Shorbagy, M.A.; El-Refaey, A.M. Hybridization of Grasshopper Optimization Algorithm With Genetic Algorithm for Solving System of Non-Linear Equations. IEEE Access 2020, 8, 220944–220961. [Google Scholar] [CrossRef]
- Ibrahim, A.M.; Tawhid, M.A. A Hybridization of Differential Evolution and Monarch Butterfly Optimization for Solving Systems of Nonlinear Equations. J. Comput. Des. Eng. 2018, 6, 354–367. [Google Scholar] [CrossRef]
- Pant, S.; Kumar, A.; Ram, M. Solution of Nonlinear Systems of Equations via Metaheuristics. Int. J. Math. Eng. Manag. Sci. 2019, 4, 1108–1126. [Google Scholar] [CrossRef]
- Ibrahim, A.M.; Tawhid, M.A. Conjugate Direction DE Algorithm for Solving Systems of Nonlinear Equations. Appl. Math. Inf. Sci. 2017, 11, 339–352. [Google Scholar] [CrossRef]
- Zhang, X.; Wan, Q.; Fan, Y. Applying Modified Cuckoo Search Algorithm for Solving Systems of Nonlinear Equations. Neural Comput. Appl. 2017, 31, 553–576. [Google Scholar] [CrossRef]
- Ibrahim, A.M.; Tawhid, M.A. A Hybridization of Cuckoo Search and Particle Swarm Optimization for Solving Nonlinear Systems. Evol. Intell. 2019, 12, 541–561. [Google Scholar] [CrossRef]
- Xie, J.; Zhou, Y.; Chen, H. A Novel Bat Algorithm Based on Differential Operator and Lévy Flights Trajectory. Comput. Intell. Neurosci. 2013, 2013, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hassan, O.F.; Jamal, A.; Abdel-Khalek, S. Genetic Algorithm and Numerical Methods for Solving Linear and Nonlinear System of Equations: A Comparative Study. J. Intell. Fuzzy Syst. 2020, 38, 2867–2872. [Google Scholar] [CrossRef]
- Tawhid, M.A.; Ibrahim, A.M. A Hybridization of Grey Wolf Optimizer and Differential Evolution for Solving Nonlinear Systems. Evol. Syst. 2019, 11, 65–87. [Google Scholar] [CrossRef]
- Luo, Y.-Z.; Tang, G.-J.; Zhou, L.-N. Hybrid Approach for Solving Systems of Nonlinear Equations Using Chaos Optimization and Quasi-Newton Method. Appl. Soft Comput. 2008, 8, 1068–1073. [Google Scholar] [CrossRef]
- Wu, J.; Gong, W.; Wang, L. A Clustering-Based Differential Evolution with Different Crowding Factors for Nonlinear Equations system. Appl. Soft Comput. 2021, 98, 106733. [Google Scholar] [CrossRef]
- Mangla, C.; Ahmad, M.; Uddin, M. Optimization of Complex Nonlinear Systems Using Genetic Algorithm. Int. J. Inf. Technol. 2020. [Google Scholar] [CrossRef]
- Pourjafari, E.; Mojallali, H. Solving Nonlinear Equations Systems with a New Approach Based on Invasive Weed Optimization Algorithm and Clustering. Swarm Evol. Comput. 2012, 4, 33–43. [Google Scholar] [CrossRef]
- Storn, R. Differrential Evolution-A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; Technical report; International Computer Science Institute: Berkeley, CA, USA, 1995; p. 11. [Google Scholar]
- MiarNaeimi, F.; Azizyan, G.; Rashki, M. Horse Herd Optimization Algorithm: A Nature-Inspired Algorithm for High-Dimensional Optimization Problems. Knowl. Based Syst. 2021, 213, 106711. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN Beyond the Metaphor: An Efficient Optimization Algorithm Based on Runge Kutta Method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Brest, J.; Maučec, M.S. Population Size Reduction for the Differential Evolution Algorithm. Appl. Intell. 2007, 29, 228–247. [Google Scholar] [CrossRef]
- Song, W.; Wang, Y.; Li, H.-X.; Cai, Z. Locating Multiple Optimal Solutions of Nonlinear Equation Systems Based on Multiobjective Optimization. IEEE Trans. Evol. Comput. 2015, 19, 414–431. [Google Scholar] [CrossRef]
- Sacco, W.; Henderson, N. Finding All Solutions of Nonlinear Systems Using a Hybrid Metaheuristic with Fuzzy Clustering Means. Appl. Soft Comput. 2011, 11, 5424–5432. [Google Scholar] [CrossRef]
- Hirsch, M.J.; Pardalos, P.M.; Resende, M.G. Solving Systems of Nonlinear Equations with Continuous GRASP. Nonlinear Anal. Real World Appl. 2009, 10, 2000–2006. [Google Scholar] [CrossRef]
- Sharma, J.R.; Arora, H. On Efficient Weighted-Newton Methods for Solving Systems of Nonlinear Equations. Appl. Math. Comput. 2013, 222, 497–506. [Google Scholar] [CrossRef]
- Junior, H.A.E.O.; Ingber, L.; Petraglia, A.; Petraglia, M.R.; Machado, M.A.S. Stochastic Global Optimization and Its Applications with Fuzzy Adaptive Simulated Annealing; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2012; pp. 33–62. [Google Scholar]
- Morgan, A.; Shapiro, V. Box-Bisection for Solving Second-Degree Systems and the Problem of Clustering. ACM Trans. Math. Softw. 1987, 13, 152–167. [Google Scholar] [CrossRef]
- Grau-Sánchez, M.; Grau, À.; Noguera, M. Frozen Divided Difference Scheme for Solving Systems of Nonlinear Equations. J. Comput. Appl. Math. 2011, 235, 1739–1743. [Google Scholar] [CrossRef]
- Waziri, M.; Leong, W.J.; Hassan, M.A.; Monsiet, M. An Efficient Solver for Systems of Nonlinear Equations with Singular Jacobian via Diagonal Updating. Appl. Math. Sci. 2010, 4, 3403–3412. [Google Scholar]





| Name | Formula | D | |
|---|---|---|---|
| Unimodal Test Functions | |||
| Beale | 2 | ||
| Matyas | 2 | ||
| Three-hump camel | 2 | ||
| Exponential | 30 | ||
| Ridge | 30 | ||
| Sphere | 30 | ||
| Step | 30 | ||
| Multimodal Test Functions | |||
| Drop wave | 2 | ||
| Egg holder | 2 | ||
| Himmelblau | 2 | ||
| Levi 13 | 2 | ||
| Ackley 1 | 20 | ||
| Griewank | 5 | ||
| Happy cat | 30 | ||
| Michalewicz | 10 | ||
| Penalized 1 | 30 | ||
| Penalized 2 | 30 | ||
| Periodic | 30 | ||
| Qing | 30 | ||
| Rastrigin | 30 | ||
| Rosenbrock | 30 | ||
| Salomon | 30 | ||
| Yang 4 | 30 | ||
| Function | Formulas | D | References | |
|---|---|---|---|---|
| f1 | 2 | [100] | ||
| f2 | 2 | [100] | ||
| f3 | 10 | [77] | ||
| f4 | 4 | [95] | ||
| f5 | 2 | [101] | ||
| f6 | 2 | [102] | ||
| f7 | 8 | [52] | ||
| f8 | 3 | [103] | ||
| f9 | 2 | [95] | ||
| f10 | 2 | [104] | ||
| f11 | 2 | [104] | ||
| f12 | 20 | [100] | ||
| f13 | 5 | [105] | ||
| f14 | 5 | [106] | ||
| f15 | 20 | [106] | ||
| f16 | 2 | [106] | ||
| f17 | 3 | [106] | ||
| f18 | 3 | [107] | ||
| f19 | 2 | [52] | ||
| f20 | 2 | [52] | ||
| f21 | 2 | [52] | ||
| f22 | 3 | [52] | ||
| f23 | 2 | [52] | ||
| f24 | 2 | [52] | ||
| f25 | 2 | [52] | ||
| f26 | 2 | [52] | ||
| f27 | 2 | [52] |
| F | EO | MPA | RUN | SMA | DE | PSO | HOA | FPA | MFPA | HFPA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 0 | 6.34 × 10−8 | 9.23 × 10−19 | 3.07 × 10−11 | 0 | 1.26 × 10−29 | 5.64 × 10−5 | 2.23 × 10−3 | 0 | 0 |
| Avg | 9.24 × 10−34 | 2.37 × 10−5 | 2.36 × 10−13 | 1.28 × 10−8 | 0 | 1.02 × 10−1 | 2.33 × 10−2 | 1.47 × 10−1 | 0 | 0 | |
| Worst | 2.77 × 10−32 | 1.94 × 10−4 | 2.19 × 10−12 | 1.17 × 10−7 | 0 | 7.62 × 10−1 | 1.02 × 10−1 | 1.01 | 0 | 0 | |
| SD | 5.06 × 10−33 | 3.91 × 10−5 | 4.56 × 10−13 | 2.70 × 10−8 | 0 | 2.63 × 10−1 | 2.71 × 10−2 | 2.90 × 10−1 | 0 | 0 | |
| F2 | Best | 4.14 × 10−176 | 8. × 10−12 | 0 | 0 | 7.09 × 10−85 | 1.01 × 10−31 | 2.79 × 10−137 | 1.54 × 10−4 | 0 | 0 |
| Avg | 4.60 × 10−130 | 1.78 × 10−8 | 0 | 1.1 × 10−318 | 1.06 × 10−80 | 2.01 × 10−27 | 5.71 × 10−5 | 8.98 × 10−3 | 0 | 0 | |
| Worst | 1.38 × 10−128 | 1.11 × 10−7 | 0 | 3.5 × 10−317 | 2.12 × 10−79 | 2.40 × 10−26 | 1.37 × 10−3 | 3.70 × 10−2 | 0 | 0 | |
| SD | 2.52 × 10−129 | 2.37 × 10−8 | 0 | 0 | 3.90 × 10−80 | 5.21 × 10−27 | 2.50 × 10−4 | 8.90 × 10−3 | 0 | 0 | |
| F3 | Best | 4.12 × 10−247 | 1.56 × 10−26 | 0 | 0 | 4.61 × 10−120 | 1.09 × 10−34 | 3.10 × 10−256 | 1.26 × 10−4 | 0 | 0 |
| Avg | 1.61 × 10−198 | 2.66 × 10−9 | 0 | 0 | 6.20 × 10−112 | 9.95 × 10−3 | 5.04 × 10−77 | 3.53 × 10−2 | 0 | 0 | |
| Worst | 4.83 × 10−197 | 1.79 × 10−8 | 0 | 0 | 7.57 × 10−111 | 2.99 × 10−1 | 1.51 × 10−75 | 2.36 × 10−1 | 0 | 0 | |
| SD | 0 | 4.48 × 10−9 | 0 | 0 | 1.97 × 10−111 | 5.45 × 10−2 | 2.76 × 10−76 | 5.18 × 10−2 | 0 | 0 | |
| F4 | Best | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −6.58 × 10−1 | −1.0000 | −1.0000 |
| Avg | −1.0000 | −9.90 × 10−1 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −2.92 × 10−1 | −1.0000 | −1.0000 | |
| Worst | −1.0000 | −9.68 × 10−1 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −6.46 × 10−2 | −1.0000 | −1.0000 | |
| SD | 5.45 × 10−17 | 9.64 × 10−3 | 0 | 0 | 6.94 × 10−9 | 1.21 × 10−8 | 6.84 × 10−17 | 1.50 × 10−1 | 0 | 0 | |
| F5 | Best | −5.0000 | −3.42 | −5.0000 | −4.98 | −4.57 | −4.47 | −3.14 | −1.85 | −4.51 | −4.75 |
| Avg | −5.0000 | −2.86 | −5.0000 | −4.96 | −4.54 | −4.22 | −2.85 | −1.67 | −4.22 | −4.67 | |
| Worst | −5.0000 | −2.40 | −5.0000 | −4.93 | −4.48 | −2.85 | −2.70 | −1.54 | −3.86 | −4.61 | |
| SD | 5.79 × 10−4 | 2.63 × 10−1 | 5.73 × 10−7 | 1.61 × 10−2 | 2.34 × 10−2 | 3.39 × 10−1 | 1.12 × 10−1 | 7.98 × 10−2 | 1.55 × 10−1 | 3.60 × 10−2 | |
| F6 | Best | 1.97 × 10−43 | 2.83 × 10−2 | 3.33 × 10−190 | 0 | 1.05 × 10−4 | 9.15 × 10−5 | 3.03 × 10−238 | 1.39 × 104 | 0 | 0 |
| Avg | 1.94 × 10−40 | 3.52 × 102 | 1.56 × 10−163 | 1.3 × 10−319 | 3.50 × 10−4 | 6.96 × 10−4 | 1.11 × 10−125 | 2.67 × 104 | 0 | 0 | |
| Worst | 1.65 × 10−39 | 1.39 × 103 | 4.67 × 10−162 | 4.0 × 10−318 | 8.85 × 10−4 | 2.72 × 10−3 | 3.34 × 10−124 | 6.19 × 104 | 0 | 0 | |
| SD | 3.57 × 10−40 | 3.95 × 102 | 0 | 0 | 1.86 × 10−4 | 6.35 × 10−4 | 6.10 × 10−125 | 1.00 × 104 | 0 | 0 | |
| F7 | Best | 1.24 × 10−6 | 4.61 × 10−2 | 1.62 × 10−7 | 1.65 × 10−5 | 3.24 × 10−7 | 6.89 × 10−7 | 4.33 | 2.89 × 10 | 2.98 × 10−2 | 7.44 × 10−8 |
| Avg | 5.33 × 10−6 | 6.91 × 10−1 | 3.28 × 10−7 | 9.95 × 10−4 | 8.90 × 10−7 | 7.39 × 10−6 | 6.04 | 8.50 × 10 | 5.76 × 10−1 | 2.83 × 10−6 | |
| Worst | 1.39 × 10−5 | 3.57 | 5.43 × 10−7 | 2.91 × 10−3 | 2.24 × 10−6 | 3.72 × 10−5 | 7.02 | 1.51 × 102 | 1.23 | 2.15 × 10−5 | |
| SD | 3.11 × 10−6 | 8.92 × 10−1 | 8.52 × 10−8 | 8.20 × 10−4 | 4.67 × 10−7 | 9.04 × 10−6 | 7.18 × 10−1 | 3.08 × 10 | 2.97 × 10−1 | 4.36 × 10−6 | |
| F8 | Best | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −9.92 × 10−1 | −1.0000 | −1.0000 |
| Avg | −1.0000 | −9.98 × 10−1 | −1.0000 | −1.0000 | −1.0000 | −9.88 × 10−1 | −9.99 × 10−1 | −9.11 × 10−1 | −1.0000 | −1.0000 | |
| Worst | −1.0000 | −9.36 × 10−1 | −1.0000 | −1.0000 | −1.0000 | −9.36 × 10−1 | −9.77 × 10−1 | −7.82 × 10−1 | −1.0000 | −1.0000 | |
| SD | 0 | 1.16 × 10−2 | 0 | 0 | 0 | 2.18 × 10−2 | 4.39 × 10−3 | 4.71 × 10−2 | 0 | 0 |
| F | EO | MPA | RUN | SMA | DE | PSO | HOA | FPA | MFPA | HFPA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F9 | Best | −9.60 × 102 | −9.60 × 102 | −9.60 × 102 | −9.60 × 102 | −9.60 × 102 | −9.60 × 102 | −9.60 × 102 | −9.60 × 102 | −9.60 × 102 | −9.60 × 102 |
| Avg | −9.52 × 102 | −9.60 × 102 | −9.60 × 102 | −9.60 × 102 | −9.53 × 102 | −7.60 × 102 | −8.98 × 102 | −9.18 × 102 | −9.10 × 102 | −9.28 × 102 | |
| Worst | −7.87 × 102 | −9.60 × 102 | −9.60 × 102 | −9.60 × 102 | −8.21 × 102 | −5.25 × 102 | −7.18 × 102 | −7.79 × 102 | −7.17 × 102 | −7.18 × 102 | |
| SD | 3.34 × 10 | 5.78 × 10−13 | 1.47 × 10−9 | 1.47 × 10−8 | 2.71 × 10 | 1.04 × 102 | 6.77 × 10 | 5.60 × 10 | 7.41 × 10 | 6.25 × 10 | |
| F10 | Best | 0 | 2.88 × 10−9 | 1.17 × 10−18 | 1.24 × 10−9 | 0 | 0 | 0 | 3.76 × 10−3 | 0 | 0 |
| Avg | 1.15 × 10−31 | 8.24 × 10−6 | 2.90 × 10−11 | 1.82 × 10−7 | 1.05 × 10−31 | 6.27 × 10−27 | 1.57 × 10−3 | 2.68 × 10−1 | 3.16 × 10−31 | 1.05 × 10−31 | |
| Worst | 7.89 × 10−31 | 8.05 × 10−5 | 1.94 × 10−10 | 6.35 × 10−7 | 7.89 × 10−31 | 1.16 × 10−25 | 1.05 × 10−2 | 1.87 | 7.89 × 10−31 | 7.89 × 10−31 | |
| SD | 2.77 × 10−31 | 1.74 × 10−5 | 4.73 × 10−11 | 2.00 × 10−7 | 2.73 × 10−31 | 2.17 × 10−26 | 2.45 × 10−3 | 4.04 × 10−1 | 3.93 × 10−31 | 2.73 × 10−31 | |
| F11 | Best | 1.35 × 10−31 | 1.97 × 10−10 | 1.61 × 10−17 | 5.03 × 10−13 | 1.35 × 10−31 | 2.23 × 10−30 | 2.72 × 10−3 | 3.75 × 10−3 | 1.35 × 10−31 | 1.35 × 10−31 |
| Avg | 1.35 × 10−31 | 4.65 × 10−6 | 1.26 × 10−11 | 3.68 × 10−9 | 1.35 × 10−31 | 2.30 × 10−25 | 1.74 × 10−1 | 3.15 × 10−1 | 1.35 × 10−31 | 1.35 × 10−31 | |
| Worst | 1.35 × 10−31 | 6.73 × 10−5 | 8.72 × 10−11 | 2.31 × 10−8 | 1.35 × 10−31 | 6.62 × 10−24 | 3.63 × 10−1 | 7.91 × 10−1 | 1.35 × 10−31 | 1.35 × 10−31 | |
| SD | 6.68 × 10−47 | 1.26 × 10−5 | 2.13 × 10−11 | 5.21 × 10−9 | 6.68 × 10−47 | 1.21 × 10−24 | 9.32 × 10−2 | 2.28 × 10−1 | 6.68 × 10−47 | 6.68 × 10−47 | |
| F12 | Best | 4.44 × 10−15 | 3.65 | 8.88 × 10−16 | 8.88 × 10−16 | 2.64 × 10−3 | 2.12 | 4.44 × 10−15 | 1.59 × 10 | 8.88 × 10−16 | 8.88 × 10−16 |
| Avg | 9.06 × 10−15 | 6.60 | 8.88 × 10−16 | 8.88 × 10−16 | 5.25 × 10−3 | 6.28 | 6.57 × 10−15 | 1.89 × 10 | 8.88 × 10−16 | 8.88 × 10−16 | |
| Worst | 1.51 × 10−14 | 1.15 × 10 | 8.88 × 10−16 | 8.88 × 10−16 | 9.38 × 10−3 | 8.91 | 1.51 × 10−14 | 2.06 × 10 | 8.88 × 10−16 | 8.88 × 10−16 | |
| SD | 2.97 × 10−15 | 2.22 | 0 | 0 | 1.74 × 10−3 | 1.61 | 2.57 × 10−15 | 1.46 | 0 | 0 | |
| F13 | Best | 4.38 × 10−3 | 1.24 | 9.44 × 10−5 | 3.45 × 10−2 | 3.54 × 10−4 | 3.71 × 10−3 | 1.06 × 10 | 1.41 × 102 | 1.11 | 1.87 × 10−4 |
| Avg | 2.61 × 10−2 | 7.75 | 1.25 × 10−2 | 5.54 × 10−1 | 1.57 × 10−2 | 6.23 × 10−2 | 3.69 × 10 | 2.69 × 102 | 5.17 | 2.89 × 10−2 | |
| Worst | 8.88 × 10−2 | 2.54 × 10 | 4.67 × 10−2 | 9.88 × 10−1 | 1.18 × 10−1 | 4.49 × 10−1 | 6.61 × 10 | 4.64 × 102 | 1.32 × 10 | 1.18 × 10−1 | |
| SD | 2.44 × 10−2 | 5.84 | 1.32 × 10−2 | 3.57 × 10−1 | 2.85 × 10−2 | 9.00 × 10−2 | 1.88 × 10 | 7.68 × 10 | 2.69 | 2.60 × 10−2 | |
| F14 | Best | 2.04 × 10−1 | 3.88 × 10−1 | 1.26 × 10−1 | 1.59 × 10−1 | 3.54 × 10−1 | 5.05 × 10−1 | 1.05 | 8.42 × 10−1 | 4.52 × 10−1 | 2.67 × 10−1 |
| Avg | 3.42 × 10−1 | 7.10 × 10−1 | 2.48 × 10−1 | 4.12 × 10−1 | 5.38 × 10−1 | 7.09 × 10−1 | 1.45 | 1.37 | 6.93 × 10−1 | 5.19 × 10−1 | |
| Worst | 5.61 × 10−1 | 9.08 × 10−1 | 3.85 × 10−1 | 7.12 × 10−1 | 6.73 × 10−1 | 9.82 × 10−1 | 1.99 | 1.76 | 1.01 | 7.29 × 10−1 | |
| SD | 8.06 × 10−2 | 1.08 × 10−1 | 6.57 × 10−2 | 1.54 × 10−1 | 7.85 × 10−2 | 1.20 × 10−1 | 2.33 × 10−1 | 2.23 × 10−1 | 1.51 × 10−1 | 1.01 × 10−1 | |
| F15 | Best | −9.58 | −7.86 | −9.36 | −9.36 | −9.60 | −9.14 | −6.00 | −5.47 | −8.95 | −9.66 |
| Avg | −8.50 | −5.99 | −8.06 | −7.73 | −9.20 | −7.53 | −5.17 | −3.72 | −7.30 | −9.39 | |
| Worst | −7.07 | −4.61 | −6.74 | −6.32 | −8.15 | −5.05 | −4.46 | −2.97 | −5.53 | −8.71 | |
| SD | 7.23 × 10−1 | 8.40 × 10−1 | 7.53 × 10−1 | 9.51 × 10−1 | 2.30 × 10−1 | 1.14 | 4.37 × 10−1 | 5.62 × 10−1 | 9.19 × 10−1 | 2.00 × 10−1 | |
| F16 | Best | 3.77 × 10−8 | 3.27 × 10−1 | 6.52 × 10−9 | 2.00 × 10−6 | 6.79 × 10−5 | 2.62 × 10−5 | 8.64 × 10−1 | 1.12 × 106 | 9.66 × 10−3 | 6.40 × 10−9 |
| Avg | 3.46 × 10−3 | 3.25 × 103 | 2.06 × 10−7 | 5.17 × 10−3 | 5.44 × 10−4 | 1.17 | 1.30 | 1.08 × 108 | 3.40 × 10−2 | 6.97 × 10−8 | |
| Worst | 1.04 × 10−1 | 9.37 × 104 | 4.16 × 10−6 | 2.50 × 10−2 | 4.66 × 10−3 | 3.42 | 3.22 | 4.46 × 108 | 5.97 × 10−2 | 2.61 × 10−7 | |
| SD | 1.89 × 10−2 | 1.71 × 104 | 8.19 × 10−7 | 6.63 × 10−3 | 8.57 × 10−4 | 9.25 × 10−1 | 4.17 × 10−1 | 1.20 × 108 | 1.41 × 10−2 | 8.19 × 10−8 | |
| F17 | Best | 2.69 × 10−6 | 4.17 × 10−1 | 1.31 × 10−8 | 1.84 × 10−4 | 1.90 × 10−4 | 5.41 × 10−1 | 2.86 | 1.24 × 107 | 2.58 | 1.18 |
| Avg | 4.26 × 10−2 | 4.73 × 103 | 6.13 × 10−3 | 4.25 × 10−3 | 1.71 × 10−3 | 1.26 × 10 | 3.04 | 1.69 × 108 | 2.80 | 2.28 | |
| Worst | 1.96 × 10−1 | 5.57 × 104 | 2.10 × 10−2 | 1.62 × 10−2 | 8.23 × 10−3 | 2.87 × 10 | 3.46 | 8.03 × 108 | 2.97 | 2.97 | |
| SD | 5.47 × 10−2 | 1.37 × 104 | 7.25 × 10−3 | 3.44 × 10−3 | 1.75 × 10−3 | 6.13 | 1.28 × 10−1 | 1.67 × 108 | 1.22 × 10−1 | 4.94 × 10−1 | |
| F18 | Best | 2.74 | 2.07 | 9.00 × 10−1 | 9.00 × 10−1 | 1.71 | 5.73 | 2.95 | 3.02 | 9.00 × 10−1 | 9.00 × 10−1 |
| Avg | 2.86 | 2.47 | 1.10 | 9.11 × 10−1 | 2.02 | 7.40 | 3.05 | 4.64 | 9.00 × 10−1 | 9.00 × 10−1 | |
| Worst | 3.00 | 2.74 | 2.91 | 1.00 | 2.34 | 9.37 | 3.07 | 7.11 | 9.00 × 10−1 | 9.00 × 10−1 | |
| SD | 5.08 × 10−2 | 1.57 × 10−1 | 5.27 × 10−1 | 3.05 × 10−2 | 1.40 × 10−1 | 8.65 × 10−1 | 2.87 × 10−2 | 1.36 | 4.52 × 10−16 | 4.52 × 10−16 | |
| F19 | Best | 5.38 × 10−3 | 3.05 × 103 | 3.52 × 10−3 | 2.41 | 8.69 × 102 | 3.27 × 10−2 | 6.23 × 103 | 1.59 × 109 | 1.22 × 102 | 1.79 × 10−4 |
| Avg | 5.44 × 10−1 | 4.50 × 107 | 3.37 × 10−1 | 5.82 | 1.38 × 103 | 5.20 × 10−1 | 7.46 × 103 | 4.63 × 1010 | 5.97 × 102 | 1.05 × 10−1 | |
| Worst | 8.69 | 4.76 × 108 | 3.90 | 1.71 × 10 | 1.81 × 103 | 8.14 | 8.54 × 103 | 1.87 × 1011 | 1.49 × 103 | 2.78 | |
| SD | 1.70 | 9.89 × 107 | 9.68 × 10−1 | 3.59 | 2.45 × 102 | 1.47 | 5.83 × 102 | 3.87 × 1010 | 3.96 × 102 | 5.06 × 10−1 | |
| F20 | Best | 0 | 4.05 × 10 | 0 | 0 | 1.22 × 102 | 1.82 × 10 | 0 | 2.97 × 102 | 0 | 0 |
| Avg | 0 | 9.56 × 10 | 0 | 0 | 1.54 × 102 | 9.48 × 10 | 2.28 × 10 | 3.69 × 102 | 0 | 0 | |
| Worst | 0 | 1.63 × 102 | 0 | 0 | 1.74 × 102 | 2.29 × 102 | 2.44 × 102 | 4.26 × 102 | 0 | 0 | |
| SD | 0 | 3.11 × 10 | 0 | 0 | 1.16 × 10 | 7.06 × 10 | 7.00 × 10 | 3.73 × 10 | 0 | 0 | |
| F21 | Best | 2.48 × 10 | 2.53 × 102 | 2.41 × 10 | 6.95 × 10−3 | 2.55 × 10 | 6.15 × 10−2 | 2.87 × 10 | 1.35 × 105 | 2.58 × 10 | 2.23 × 10 |
| Avg | 2.54 × 10 | 2.12 × 103 | 2.56 × 10 | 3.88 × 10−1 | 3.03 × 10 | 8.14 × 10 | 2.89 × 10 | 4.40 × 105 | 2.68 × 10 | 2.36 × 10 | |
| Worst | 2.60 × 10 | 5.16 × 103 | 2.87 × 10 | 1.35 | 9.32 × 10 | 3.17 × 102 | 2.90 × 10 | 1.08 × 106 | 2.84 × 10 | 2.50 × 10 | |
| SD | 3.19 × 10−1 | 1.53 × 103 | 1.13 | 3.44 × 10−1 | 1.30 × 10 | 7.43 × 10 | 6.73 × 10−2 | 2.36 × 105 | 6.16 × 10−1 | 7.38 × 10−1 | |
| F22 | Best | 9.99 × 10−2 | 1.30 | 1.14 × 10−84 | 0 | 6.21 × 10−1 | 3.10 | 2.00 × 10−1 | 8.89 | 0 | 0 |
| Avg | 1.03 × 10−1 | 4.28 | 8.72 × 10−64 | 6.30 × 10−145 | 7.94 × 10−1 | 4.43 | 8.42 × 10−1 | 1.74 × 10 | 0 | 0 | |
| Worst | 2.00 × 10−1 | 9.00 | 2.61 × 10−62 | 1.89 × 10−143 | 1.01 | 5.70 | 2.47 | 2.50 × 10 | 0 | 0 | |
| SD | 1.83 × 10−2 | 1.93 | 4.76 × 10−63 | 3.45 × 10−144 | 9.74 × 10−2 | 7.60 × 10−1 | 4.76 × 10−1 | 3.42 | 0 | 0 | |
| F23 | Best | 1.78 × 10−17 | 3.70 × 10−15 | −1.0000 | −1.0000 | 2.50 × 10−12 | 5.99 × 10−14 | 1.36 × 10−12 | 3.34 × 10−10 | −1.0000 | −1.0000 |
| Avg | 2.08 × 10−16 | 6.68 × 10−13 | −1.0000 | −1.0000 | 5.60 × 10−12 | 7.81 × 10−12 | 9.00 × 10−12 | 5.45 × 10−9 | −1.0000 | −1.0000 | |
| Worst | 5.79 × 10−16 | 4.66 × 10−12 | −1.0000 | −1.0000 | 1.21 × 10−11 | 5.97 × 10−11 | 2.45 × 10−11 | 2.36 × 10−8 | −1.0000 | −1.0000 | |
| SD | 1.59 × 10−16 | 1.16 × 10−12 | 0 | 0 | 2.04 × 10−12 | 1.43 × 10−11 | 4.89 × 10−12 | 6.06 × 10−9 | 0 | 0 |
| F | EO | MPA | RUN | SMA | DE | PSO | HOA | FPA | MFPA | HFPA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| f1 | Best | 8.0 × 10−183 | 3.39 × 10−14 | 0 | 0 | 9.75 × 10−86 | 5.55 × 10−32 | 1.1 × 10−128 | 4.31 × 10−5 | 0 | 0 |
| Avg | 1.36 × 10−10 | 2.15 × 10−6 | 1.21 × 10−47 | 9.3 × 10−312 | 1.73 × 10−32 | 3.78 × 10−15 | 3.71 × 10−5 | 1.42 × 10−3 | 0 | 0 | |
| Worst | 4.09 × 10−9 | 2.93 × 10−5 | 3.63 × 10−46 | 2.7 × 10−310 | 2.47 × 10−32 | 1.06 × 10−13 | 1.72 × 10−4 | 1.05 × 10−2 | 0 | 0 | |
| SD | 7.46 × 10−10 | 5.70 × 10−6 | 6.63 × 10−47 | 0 | 1.09 × 10−32 | 1.93 × 10−14 | 4.96 × 10−5 | 2.08 × 10−3 | 0 | 0 | |
| f2 | Best | 0 | 2.93 × 10−9 | 0 | 1.25 × 10−17 | 0 | 0 | 2.54 × 10−5 | 2.49 × 10−4 | 0 | 0 |
| Avg | 4.63 × 10−25 | 4.09 × 10−6 | 4.78 × 10−12 | 3.16 × 10−9 | 5.81 × 10−32 | 4.45 × 10−25 | 4.11 × 10−3 | 7.00 × 10−2 | 5.87 × 10−32 | 3.52 × 10−32 | |
| Worst | 1.39 × 10−23 | 2.73 × 10−5 | 6.41 × 10−11 | 6.15 × 10−8 | 2.74 × 10−31 | 1.24 × 10−23 | 2.28 × 10−2 | 2.55 × 10−1 | 3.08 × 10−31 | 2.74 × 10−31 | |
| SD | 2.54 × 10−24 | 6.37 × 10−6 | 1.48 × 10−11 | 1.12 × 10−8 | 1.10 × 10−31 | 2.26 × 10−24 | 4.67 × 10−3 | 6.37 × 10−2 | 1.06 × 10−31 | 8.20 × 10−32 | |
| f3 | Best | 2.11 × 10−23 | 1.76 × 10−6 | 9.38 × 10−12 | 1.30 × 10−4 | 3.62 × 10−27 | 1.25 × 10−16 | 8.89 × 10−2 | 6.91 × 10−1 | 1.80 × 10−6 | 8.65 × 10−30 |
| Avg | 1.44 × 10−19 | 5.60 × 10−5 | 7.91 × 10−10 | 2.53 × 10−3 | 1.12 × 10−25 | 1.50 × 10−14 | 1.83 × 10−1 | 1.68 | 4.31 × 10−5 | 1.96 × 10−26 | |
| Worst | 3.00 × 10−18 | 3.32 × 10−4 | 5.00 × 10−9 | 8.72 × 10−3 | 1.09 × 10−24 | 1.39 × 10−13 | 3.89 × 10−1 | 3.76 | 1.81 × 10−4 | 3.20 × 10−25 | |
| SD | 5.54 × 10−19 | 7.18 × 10−5 | 1.15 × 10−9 | 2.35 × 10−3 | 2.19 × 10−25 | 2.92 × 10−14 | 7.34 × 10−2 | 8.07 × 10−1 | 5.15 × 10−5 | 5.87 × 10−26 | |
| f4 | Best | 1.56 × 10−5 | 3.48 × 10−5 | 7.08 × 10−9 | 3.69 × 10−1 | 3.61 × 10−18 | 1.14 × 10−4 | 4.36 × 10−2 | 2.47 × 10−1 | 3.61 × 10−18 | 3.61 × 10−18 |
| Avg | 9.20 × 10−3 | 5.92 × 10−2 | 1.78 × 10−3 | 4.06 | 2.34 × 10−3 | 5.20 × 10−2 | 2.10 | 2.98 | 1.54 × 10−1 | 6.46 × 10−2 | |
| Worst | 1.36 × 10−2 | 1.72 × 10−1 | 1.75 × 10−2 | 4.36 | 4.92 × 10−2 | 3.29 × 10−1 | 9.07 | 8.89 | 6.64 × 10−1 | 6.64 × 10−1 | |
| SD | 4.58 × 10−3 | 4.96 × 10−2 | 4.60 × 10−3 | 8.05 × 10−1 | 9.36 × 10−3 | 1.02 × 10−1 | 2.89 | 2.34 | 2.53 × 10−1 | 1.76 × 10−1 | |
| f5 | Best | 0 | 5.15 × 10−6 | 7.07 × 10−15 | 7.44 × 10−11 | 0 | 2.02 × 10−28 | 2.78 × 10−1 | 5.50 × 10−1 | 0 | 0 |
| Avg | 0 | 1.07 × 10−2 | 1.08 × 10−8 | 3.12 × 10−8 | 1.35 × 10−29 | 5.22 × 10−23 | 2.03 × 10 | 7.81 × 10 | 6.06 × 10−29 | 0 | |
| Worst | 0 | 1.88 × 10−1 | 3.21 × 10−7 | 4.29 × 10−7 | 2.02 × 10−28 | 1.40 × 10−21 | 2.32 × 102 | 3.59 × 102 | 8.08 × 10−28 | 0 | |
| SD | 0 | 3.49 × 10−2 | 5.87 × 10−8 | 7.83 × 10−8 | 5.12 × 10−29 | 2.55 × 10−22 | 4.22 × 10 | 8.36 × 10 | 1.60 × 10−28 | 0 | |
| f6 | Best | 0 | 0 | 0 | 0 | 0 | 6.17 × 10−32 | 0 | 0 | 0 | 0 |
| Avg | 1.36 × 10−32 | 0 | 0 | 0 | 1.00 × 10−32 | 1.14 × 10−22 | 0 | 2.04 × 10−31 | 0 | 0 | |
| Worst | 3.00 × 10−31 | 0 | 0 | 0 | 3.00 × 10−31 | 3.43 × 10−21 | 0 | 1.08 × 10−30 | 0 | 0 | |
| SD | 5.76 × 10−32 | 0 | 0 | 0 | 5.48 × 10−32 | 6.26 × 10−22 | 0 | 3.69 × 10−31 | 0 | 0 | |
| f7 | Best | 9.99 × 10−25 | 2.62 × 10−7 | 2.23 × 10−10 | 2.63 × 10−6 | 3.35 × 10−8 | 2.84 × 10−12 | 3.04 × 10−2 | 2.13 × 10−2 | 1.39 × 10−8 | 1.69 × 10−27 |
| Avg | 1.87 × 10−15 | 6.47 × 10−3 | 3.17 × 10−7 | 4.14 × 10−3 | 2.04 × 10−4 | 2.85 × 10−2 | 2.48 × 10−1 | 1.96 × 10−1 | 2.16 × 10−5 | 8.08 × 10−20 | |
| Worst | 2.00 × 10−14 | 1.03 × 10−1 | 4.48 × 10−6 | 1.23 × 10−1 | 3.27 × 10−3 | 1.42 × 10−1 | 6.40 × 10−1 | 3.87 × 10−1 | 1.76 × 10−4 | 2.38 × 10−18 | |
| SD | 4.78 × 10−15 | 2.35 × 10−2 | 1.03 × 10−6 | 2.25 × 10−2 | 6.17 × 10−4 | 4.13 × 10−2 | 1.54 × 10−1 | 9.36 × 10−2 | 3.97 × 10−5 | 4.34 × 10−19 | |
| f8 | Best | 0 | 2.51 × 10−8 | 6.11 × 10−15 | 5.69 × 10−10 | 0 | 4.28 × 10−26 | 1.94 × 10−3 | 6.35 × 10−2 | 0 | 0 |
| Avg | 9.44 × 10−24 | 2.65 × 10−5 | 6.26 × 10−13 | 6.37 × 10−8 | 1.19 × 10−32 | 6.72 × 10−1 | 1.05 × 10−1 | 3.03 | 6.98 × 10−33 | 9.04 × 10−33 | |
| Worst | 2.83 × 10−22 | 2.07 × 10−4 | 3.20 × 10−12 | 3.35 × 10−7 | 1.23 × 10−32 | 4.03 | 3.87 × 10−1 | 1.56 × 10 | 2.47 × 10−32 | 1.23 × 10−32 | |
| SD | 5.17 × 10−23 | 4.80 × 10−5 | 7.56 × 10−13 | 1.01 × 10−7 | 2.25 × 10−33 | 1.53 | 8.55 × 10−2 | 4.09 | 7.01 × 10−33 | 5.54 × 10−33 | |
| f9 | Best | 0 | 9.03 × 10−27 | 2.21 × 10−29 | 1.27 × 10−16 | 0 | 0 | 0 | 4.96 × 10−7 | 0 | 0 |
| Avg | 4.50 × 10−33 | 8.78 × 10−8 | 5.63 × 10−11 | 4.34 × 10−12 | 1.50 × 10−33 | 1.94 × 10−22 | 0 | 7.69 × 10−4 | 5.00 × 10−34 | 2.00 × 10−33 | |
| Worst | 1.50 × 10−32 | 2.63 × 10−6 | 1.06 × 10−9 | 9.75 × 10−11 | 1.50 × 10−32 | 2.80 × 10−21 | 0 | 6.15 × 10−3 | 1.50 × 10−32 | 1.50 × 10−32 | |
| SD | 6.99 × 10−33 | 4.80 × 10−7 | 2.19 × 10−10 | 1.78 × 10−11 | 4.58 × 10−33 | 6.78 × 10−22 | 0 | 1.31 × 10−3 | 2.74 × 10−33 | 5.19 × 10−33 | |
| f10 | Best | 0 | 1.88 × 10−7 | 1.82 × 10−16 | 4.56 × 10−11 | 0 | 0 | 2.66 × 10−3 | 2.22 × 10−2 | 0 | 0 |
| Avg | 1.31 × 10−30 | 2.01 × 10−4 | 8.36 × 10−12 | 4.02 × 10−8 | 0 | 8.71 × 10−25 | 3.83 × 10−1 | 4.46 | 1.31 × 10−31 | 1.05 × 10−31 | |
| Worst | 3.16 × 10−29 | 2.15 × 10−3 | 5.86 × 10−11 | 4.08 × 10−7 | 0 | 2.54 × 10−23 | 2.48 | 7.80 × 10 | 7.89 × 10−31 | 7.89 × 10−31 | |
| SD | 5.76 × 10−30 | 4.20 × 10−4 | 1.36 × 10−11 | 8.94 × 10−8 | 0 | 4.64 × 10−24 | 5.88 × 10−1 | 1.41 × 10 | 2.99 × 10−31 | 2.73 × 10−31 | |
| f11 | Best | 2.95 × 10−32 | 2.75 × 10−8 | 8.91 × 10−17 | 1.03 × 10−10 | 2.95 × 10−32 | 7.57 × 10−30 | 4.37 × 10−5 | 4.11 × 10−3 | 2.95 × 10−32 | 2.95 × 10−32 |
| Avg | 1.09 × 10−31 | 5.68 × 10−5 | 2.35 × 10−12 | 3.74 × 10−8 | 1.08 × 10−31 | 9.96 × 10−18 | 4.16 × 10−2 | 8.53 × 10−2 | 1.20 × 10−31 | 1.07 × 10−31 | |
| Worst | 2.50 × 10−31 | 5.37 × 10−4 | 1.49 × 10−11 | 2.40 × 10−7 | 2.25 × 10−31 | 2.99 × 10−16 | 2.56 × 10−1 | 3.81 × 10−1 | 2.25 × 10−31 | 2.25 × 10−31 | |
| SD | 9.70 × 10−32 | 1.01 × 10−4 | 3.67 × 10−12 | 6.26 × 10−8 | 9.74 × 10−32 | 5.46 × 10−17 | 6.97 × 10−2 | 8.82 × 10−2 | 9.92 × 10−32 | 9.74 × 10−32 | |
| f12 | Best | 1.91 × 10−14 | 1.75 × 10−5 | 1.31 × 10−14 | 5.64 × 10−12 | 2.10 × 10−14 | 6.46 × 10−13 | 1.92 × 10−3 | 8.53 × 10−1 | 1.75 × 10−5 | 7.87 × 10−18 |
| Avg | 8.62 × 10−11 | 2.35 × 10−3 | 2.75 × 10−8 | 5.56 × 10−9 | 9.79 × 10−6 | 3.36 × 10−2 | 4.66 × 10−2 | 3.89 | 1.20 × 10−3 | 5.48 × 10−14 | |
| Worst | 1.16 × 10−9 | 1.71 × 10−2 | 3.32 × 10−7 | 6.55 × 10−8 | 2.92 × 10−4 | 5.00 × 10−1 | 5.06 × 10−1 | 1.18 × 10 | 5.34 × 10−3 | 7.13 × 10−13 | |
| SD | 2.24 × 10−10 | 3.80 × 10−3 | 7.38 × 10−8 | 1.29 × 10−8 | 5.33 × 10−5 | 1.27 × 10−1 | 1.22 × 10−1 | 3.01 | 1.20 × 10−3 | 1.53 × 10−13 | |
| f13 | Best | 2.74 × 10−11 | 5.45 × 10−6 | 4.57 × 10−11 | 1.91 × 10−6 | 1.38 × 10−11 | 4.70 × 10−11 | 1.54 × 10−3 | 7.63 × 10−2 | 0 | 0 |
| Avg | 2.03 × 10−5 | 9.56 × 10−4 | 9.15 × 10−9 | 5.60 × 10−5 | 2.05 × 10−8 | 1.12 × 10−1 | 1.43 × 10−2 | 4.91 × 10−1 | 0 | 0 | |
| Worst | 2.12 × 10−4 | 5.33 × 10−3 | 6.05 × 10−8 | 3.01 × 10−4 | 3.24 × 10−7 | 3.05 | 3.66 × 10−2 | 2.01 | 0 | 0 | |
| SD | 5.02 × 10−5 | 1.45 × 10−3 | 1.47 × 10−8 | 8.92 × 10−5 | 6.21 × 10−8 | 5.58 × 10−1 | 8.44 × 10−3 | 4.22 × 10−1 | 0 | 0 |
| F | EO | MPA | RUN | SMA | DE | PSO | HOA | FPA | MFPA | HFPA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| f14 | Best | 1.51 × 10−32 | 6.13 × 10−8 | 4.29 × 10−13 | 1.43 × 10−9 | 1.51 × 10−32 | 9.17 × 10−29 | 3.41 × 10−3 | 7.09 × 10−3 | 1.51 × 10−32 | 1.51 × 10−32 |
| Avg | 3.12 × 10−32 | 4.39 × 10−5 | 2.15 × 10−6 | 9.31 × 10−7 | 2.66 × 10−32 | 7.48 × 10−17 | 4.11 × 10−2 | 1.16 × 10−1 | 2.62 × 10−32 | 3.50 × 10−32 | |
| Worst | 1.60 × 10−31 | 2.40 × 10−4 | 4.93 × 10−5 | 1.32 × 10−5 | 1.60 × 10−31 | 2.24 × 10−15 | 1.02 × 10−1 | 4.08 × 10−1 | 1.59 × 10−31 | 1.59 × 10−31 | |
| SD | 3.85 × 10−32 | 6.03 × 10−5 | 9.08 × 10−6 | 2.56 × 10−6 | 3.07 × 10−32 | 4.10 × 10−16 | 2.95 × 10−2 | 9.63 × 10−2 | 3.70 × 10−32 | 4.60 × 10−32 | |
| f15 | Best | 9.78 × 10−13 | 1.49 × 10−18 | 1.30 × 10−13 | 1.98 × 10−8 | 1.84 × 10−4 | 1.10 × 10−6 | 7.44 × 10−1 | 4.03 × 10−1 | 0 | 0 |
| Avg | 2.21 × 10−5 | 1.06 × 10−5 | 2.47 × 10−4 | 3.47 × 10−5 | 4.35 × 10−2 | 2.65 × 103 | 2.63 × 10 | 1.40 × 102 | 1.93 × 10−32 | 2.27 × 10−14 | |
| Worst | 2.35 × 10−4 | 7.90 × 10−5 | 4.06 × 10−3 | 3.12 × 10−4 | 1.26 × 10−1 | 1.43 × 104 | 5.29 × 102 | 3.75 × 103 | 1.97 × 10−31 | 5.14 × 10−12 | |
| SD | 5.27 × 10−5 | 2.04 × 10−5 | 8.37 × 10−4 | 6.06 × 10−5 | 3.57 × 10−2 | 4.22 × 103 | 9.96 × 10 | 6.84 × 102 | 4.18 × 10−32 | 9.31 × 10−13 | |
| f16 | Best | 6.16 × 10−32 | 6.79 × 10−8 | 2.10 × 10−19 | 5.10 × 10−2 | 6.16 × 10−32 | 3.46 × 10−30 | 3.67 × 10−5 | 1.59 × 10−4 | 6.16 × 10−32 | 6.16 × 10−32 |
| Avg | 6.16 × 10−32 | 3.36 × 10−5 | 6.23 × 10−13 | 9.80 × 10−2 | 6.16 × 10−32 | 1.29 × 10−24 | 2.70 × 10−3 | 1.63 × 10−1 | 6.16 × 10−32 | 6.16 × 10−32 | |
| Worst | 6.16 × 10−32 | 1.90 × 10−4 | 3.59 × 10−12 | 2.33 × 10−1 | 6.16 × 10−32 | 1.59 × 10−23 | 8.80 × 10−3 | 2.12 | 6.16 × 10−32 | 6.16 × 10−32 | |
| SD | 0 | 4.36 × 10−5 | 9.88 × 10−13 | 2.90 × 10−2 | 0 | 3.12 × 10−24 | 2.69 × 10−3 | 3.96 × 10−1 | 0 | 0 | |
| f17 | Best | 3.79 × 10−12 | 1.57 × 10−7 | 5.75 × 10−15 | 3.94 × 10−7 | 2.84 × 10−27 | 9.15 × 10−21 | 1.76 × 10−6 | 1.92 × 10−4 | 0 | 0 |
| Avg | 7.33 × 10−6 | 3.03 × 10−5 | 5.54 × 10−7 | 5.22 × 10−6 | 3.66 × 10−7 | 4.14 × 10−5 | 5.80 × 10−4 | 6.06 × 10−3 | 0 | 0 | |
| Worst | 1.09 × 10−4 | 2.32 × 10−4 | 9.99 × 10−7 | 1.22 × 10−4 | 9.99 × 10−7 | 1.22 × 10−4 | 7.91 × 10−3 | 3.73 × 10−2 | 0 | 0 | |
| SD | 2.75 × 10−5 | 5.73 × 10−5 | 4.94 × 10−7 | 2.22 × 10−5 | 4.65 × 10−7 | 5.03 × 10−5 | 1.53 × 10−3 | 8.08 × 10−3 | 0 | 0 | |
| f18 | Best | 4.93 × 10−32 | 5.20 × 10−11 | 4.52 × 10−18 | 1.22 × 10−10 | 4.93 × 10−32 | 1.23 × 10−31 | 2.84 × 10−5 | 7.32 × 10−6 | 4.93 × 10−32 | 4.93 × 10−32 |
| Avg | 1.33 × 10−2 | 4.78 × 10−6 | 9.25 × 10−12 | 2.38 × 10−8 | 6.25 × 10−32 | 3.79 × 10−25 | 3.88 × 10−3 | 2.96 × 10−2 | 6.25 × 10−32 | 6.41 × 10−32 | |
| Worst | 9.94 × 10−2 | 3.73 × 10−5 | 1.08 × 10−10 | 1.82 × 10−7 | 1.23 × 10−31 | 5.77 × 10−24 | 3.04 × 10−2 | 1.24 × 10−1 | 1.23 × 10−31 | 1.23 × 10−31 | |
| SD | 3.44 × 10−2 | 8.19 × 10−6 | 2.09 × 10−11 | 4.28 × 10−8 | 2.73 × 10−32 | 1.31 × 10−24 | 6.29 × 10−3 | 3.62 × 10−2 | 2.48 × 10−32 | 2.79 × 10−32 | |
| f19 | Best | 0 | 1.13 × 10−10 | 1.88 × 10−18 | 1.13 × 10−12 | 0 | 0 | 1.22 × 10−6 | 1.09 × 10−6 | 0 | 0 |
| Avg | 2.05 × 10−34 | 4.21 × 10−7 | 1.43 × 10−14 | 1.80 × 10−10 | 0 | 1.45 × 10−28 | 7.66 × 10−5 | 1.33 × 10−3 | 0 | 0 | |
| Worst | 3.08 × 10−33 | 2.82 × 10−6 | 1.55 × 10−13 | 1.03 × 10−9 | 0 | 1.52 × 10−27 | 2.49 × 10−4 | 7.62 × 10−3 | 0 | 0 | |
| SD | 7.82 × 10−34 | 7.62 × 10−7 | 3.41 × 10−14 | 2.31 × 10−10 | 0 | 3.97 × 10−28 | 6.82 × 10−5 | 1.91 × 10−3 | 0 | 0 | |
| f20 | Best | 0 | 1.26 × 10−9 | 1.72 × 10−19 | 2.02 × 10−12 | 0 | 0 | 2.09 × 10−5 | 1.37 × 10−3 | 0 | 0 |
| Avg | 2.97 × 10−32 | 4.53 × 10−6 | 2.52 × 10−8 | 1.50 × 10−8 | 3.93 × 10−32 | 2.65 × 10−26 | 9.80 × 10−3 | 3.97 × 10−2 | 2.39 × 10−32 | 2.35 × 10−32 | |
| Worst | 1.97 × 10−31 | 6.41 × 10−5 | 3.83 × 10−7 | 2.14 × 10−7 | 2.47 × 10−31 | 7.89 × 10−25 | 1.17 × 10−1 | 1.43 × 10−1 | 1.97 × 10−31 | 1.97 × 10−31 | |
| SD | 5.73 × 10−32 | 1.28 × 10−5 | 8.06 × 10−8 | 4.07 × 10−8 | 7.37 × 10−32 | 1.44 × 10−25 | 2.13 × 10−2 | 3.67 × 10−2 | 4.77 × 10−32 | 4.78 × 10−32 | |
| f21 | Best | 0 | 0 | 0 | 0 | 0 | 1.56 × 10−26 | 0 | 0 | 0 | 0 |
| Avg | 3.43 × 10−14 | 0 | 0 | 0 | 3.29 × 10−24 | 3.83 × 10−12 | 0 | 1.45 × 10−2 | 0 | 0 | |
| Worst | 1.03 × 10−12 | 0 | 0 | 0 | 9.87 × 10−23 | 9.46 × 10−11 | 0 | 1.12 × 10−1 | 0 | 0 | |
| SD | 1.88 × 10−13 | 0 | 0 | 0 | 1.80 × 10−23 | 1.75 × 10−11 | 0 | 2.81 × 10−2 | 0 | 0 | |
| f22 | Best | 0 | 5.73 × 10−22 | 1.60 × 10−18 | 2.74 × 10−11 | 0 | 8.01 × 10−31 | 1.38 × 10−3 | 2.53 × 10−2 | 0 | 0 |
| Avg | 3.71 × 10−18 | 1.59 × 10−4 | 4.63 × 10−11 | 2.44 × 10−8 | 1.65 × 10−31 | 3.61 × 10−23 | 2.85 × 10−2 | 2.31 | 2.29 × 10−31 | 1.48 × 10−31 | |
| Worst | 1.11 × 10−16 | 1.05 × 10−3 | 3.68 × 10−10 | 3.44 × 10−7 | 8.01 × 10−31 | 6.96 × 10−22 | 1.59 × 10−1 | 1.13 × 10 | 8.01 × 10−31 | 8.01 × 10−31 | |
| SD | 2.03 × 10−17 | 2.57 × 10−4 | 8.74 × 10−11 | 6.72 × 10−8 | 3.24 × 10−31 | 1.32 × 10−22 | 3.38 × 10−2 | 3.44 | 3.55 × 10−31 | 3.02 × 10−31 | |
| f23 | Best | 0 | 1.94 × 10−8 | 1.13 × 10−17 | 3.11 × 10−11 | 0 | 0 | 5.67 × 10−4 | 3.13 × 10−4 | 0 | 0 |
| Avg | 3.42 × 10−31 | 7.74 × 10−6 | 5.01 × 10−12 | 2.56 × 10−8 | 0 | 1.47 × 10−25 | 3.38 × 10−2 | 1.56 × 10−1 | 5.26 × 10−32 | 1.05 × 10−31 | |
| Worst | 3.16 × 10−30 | 6.94 × 10−5 | 3.11 × 10−11 | 3.14 × 10−7 | 0 | 3.69 × 10−24 | 5.07 × 10−1 | 9.85 × 10−1 | 7.89 × 10−31 | 3.16 × 10−30 | |
| SD | 9.65 × 10−31 | 1.45 × 10−5 | 8.26 × 10−12 | 5.91 × 10−8 | 0 | 6.75 × 10−25 | 9.18 × 10−2 | 2.25 × 10−1 | 2.00 × 10−31 | 5.76 × 10−31 | |
| f24 | Best | 0 | 1.02 × 10−21 | 3.36 × 10−18 | 1.69 × 10−11 | 0 | 0 | 7.41 × 10−4 | 2.20 × 10−2 | 0 | 0 |
| Avg | 1.05 × 10−2 | 7.27 × 10−3 | 2.45 × 10−2 | 7.01 × 10−3 | 3.51 × 10−3 | 1.05 × 10−2 | 1.59 × 10−1 | 1.69 | 2.45 × 10−2 | 1.40 × 10−2 | |
| Worst | 1.05 × 10−1 | 1.05 × 10−1 | 1.05 × 10−1 | 1.05 × 10−1 | 1.05 × 10−1 | 1.05 × 10−1 | 9.21 × 10−1 | 6.58 | 1.05 × 10−1 | 1.05 × 10−1 | |
| SD | 3.21 × 10−2 | 2.67 × 10−2 | 4.53 × 10−2 | 2.67 × 10−2 | 1.92 × 10−2 | 3.21 × 10−2 | 2.13 × 10−1 | 1.80 | 4.53 × 10−2 | 3.64 × 10−2 | |
| f25 | Best | 0 | 2.06 × 10−9 | 4.33 × 10−18 | 1.25 × 10−11 | 0 | 1.11 × 10−31 | 4.69 × 10−4 | 7.49 × 10−3 | 0 | 0 |
| Avg | 2.47 × 10−3 | 1.89 × 10−3 | 1.21 × 10−3 | 1.24 × 10−3 | 1.45 × 10−4 | 7.78 × 10−21 | 1.16 × 10−2 | 7.73 × 10−2 | 9.18 × 10−14 | 8.55 × 10−30 | |
| Worst | 7.27 × 10−3 | 7.27 × 10−3 | 7.27 × 10−3 | 7.27 × 10−3 | 4.36 × 10−3 | 2.27 × 10−19 | 3.97 × 10−2 | 3.13 × 10−1 | 3.22 × 10−13 | 1.28 × 10−29 | |
| SD | 3.46 × 10−3 | 3.07 × 10−3 | 2.75 × 10−3 | 2.75 × 10−3 | 7.97 × 10−4 | 4.14 × 10−20 | 1.06 × 10−2 | 7.78 × 10−2 | 1.22 × 10−14 | 3.24 × 10−30 | |
| f26 | Best | 0 | 7.06 × 10−10 | 1.11 × 10−18 | 1.12 × 10−10 | 0 | 1.97 × 10−31 | 4.70 × 10−6 | 4.06 × 10−4 | 0 | 0 |
| Avg | 7.85 × 10−2 | 6.12 × 10−6 | 3.17 × 10−12 | 7.16 × 10−8 | 6.57 × 10−32 | 2.76 × 10−25 | 1.67 × 10−2 | 1.33 × 10−1 | 2.04 × 10−31 | 5.89 × 10−32 | |
| Worst | 1.18 | 3.72 × 10−5 | 2.65 × 10−11 | 6.12 × 10−7 | 1.58 × 10−30 | 3.90 × 10−24 | 2.27 × 10−1 | 1.31 | 1.58 × 10−30 | 1.58 × 10−30 | |
| SD | 2.99 × 10−1 | 1.07 × 10−5 | 6.39 × 10−12 | 1.26 × 10−7 | 2.90 × 10−31 | 8.29 × 10−25 | 4.12 × 10−2 | 3.13 × 10−1 | 4.73 × 10−31 | 2.41 × 10−31 | |
| f27 | Best | 0 | 1.36 × 10−9 | 1.57 × 10−19 | 6.09 × 10−12 | 0 | 9.12 × 10−31 | 5.52 × 10−3 | 1.01 × 10−3 | 0 | 0 |
| Avg | 2.15 × 10−2 | 8.90 × 10−6 | 1.26 × 10−2 | 2.33 × 10−2 | 2.54 × 10−2 | 1.44 × 10−2 | 5.72 × 10−2 | 6.87 × 10−2 | 3.05 × 10−2 | 3.05 × 10−2 | |
| Worst | 5.39 × 10−2 | 9.55 × 10−5 | 5.39 × 10−2 | 5.39 × 10−2 | 5.39 × 10−2 | 5.39 × 10−2 | 1.26 × 10−1 | 1.91 × 10−1 | 5.39 × 10−2 | 5.39 × 10−2 | |
| SD | 2.68 × 10−2 | 1.95 × 10−5 | 2.32 × 10−2 | 2.72 × 10−2 | 2.71 × 10−2 | 2.42 × 10−2 | 2.48 × 10−2 | 4.38 × 10−2 | 2.72 × 10−2 | 2.72 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Basset, M.; Mohamed, R.; Saber, S.; Askar, S.S.; Abouhawwash, M. Modified Flower Pollination Algorithm for Global Optimization. Mathematics 2021, 9, 1661. https://doi.org/10.3390/math9141661
Abdel-Basset M, Mohamed R, Saber S, Askar SS, Abouhawwash M. Modified Flower Pollination Algorithm for Global Optimization. Mathematics. 2021; 9(14):1661. https://doi.org/10.3390/math9141661
Chicago/Turabian StyleAbdel-Basset, Mohamed, Reda Mohamed, Safaa Saber, S. S. Askar, and Mohamed Abouhawwash. 2021. "Modified Flower Pollination Algorithm for Global Optimization" Mathematics 9, no. 14: 1661. https://doi.org/10.3390/math9141661






