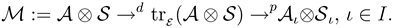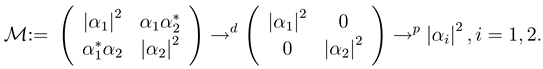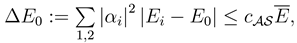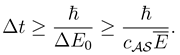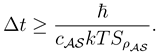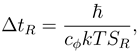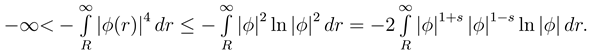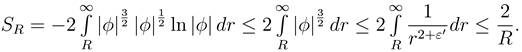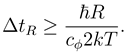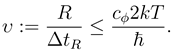2.2.1 Scope
In the sequel we would like to look at the question of minimal measurement time from an intrinsic angle. By intrinsic we mean that we abstract from a conscious observer. We solely base on elements given by our model, namely on the system , the environment , the sequence (1) and the corresponding physical consequences (2). For the sequence (1) the word "realization" would probably be more accurate than "measurement" in this context. The projection and registering of the definite outcome with the necessary erasure of other/former states of the memory is an integral part of this measurement process. The information gained by decoherence has to be offset.
The connection between the environement
and the system
which, from the intrinsic perspective of
, gives proof of the definite outcome of
, is only the dissipated energy. In first order approximation the dissipation can be described by some Hamiltonian
which is in our intrinsic sense unknown to the detector. In this situation we can apply the time-energy inequality [
1]. Let us assume that the true energy is
EO. Following [
1] , the intrinsic energy uncertainty on the basis of quantities given in our model is
where
> 0 depends upon the system
.
By the time-energy inequality [
1] and (3) there holds for the lower bound on Δ
t
The lower bound holding for all possible measurements is therefore by (2)
This result can be interpreted that the process
takes, from the perspective of a generic detector in the environment
, minimally a time interval
to happen.
2.2.2 Application
Let us assume that in empty Euclidean space there is a free particle, represented by a wave packet with fairly well defined momentum. Since its momentum is well known, by the Heisenberg uncertainty relation, its position is highly unprecise in . Classical theory, however, would say that this particle moves with constant velocity v along a straight line in the direction of the momentum vector. There is no way, given the uncertainty principle, to reconstruct directly the concept of classical trajectory and hence velocity defined by in the quantum realm.
By the help of our model, however, we will define a quantitiy which can be interpreted as the time Δt the particle needs to "reach" a point at distance R. This way we will come close to a reconstruction of classical velocity .
We will use some technical facts: 1) −c ≤ x ln x ≤ x2 for some fixed and all x ≥ 0, 2) L4() ⊂ L2(), 3) limx→0 xs ln x → 0, s, x > 0.
Let there be a free particle,
φ(
x) ≡
φ(
r), in an environment which is in thermal equilibrium of temperature
T. According to our model, the minimal time Δ
tR needed to measure our particle at a distance of at least
R would by (4) be
where
SR is defined as
and
cφ > 0 denotes the constant depending upon the set up (3).
The intuitive interpretation of ΔtR is the minimal time it takes for the particle to "reach" a point at distance R or further.
Note that, since SR → 0 as R → ∞, the intuitive fact that it takes longer to reach more distant regions, is assured.
Next we want to better understand the dependency of
SR from
R. Since
φ ∈
L2(ℝ
3) we have for some
R0 > 0,
ε > 0
By the technical facts we have for any
s ∈ ℝ,
s > 0
If we set
, we get for
R >
R0 big enough
If we put the last result into the expression for time we get for
R > 0 big enough
We now can define the analouge of classical velocity by
(6) gives us an upper bound which is independent of the distance
R, for
R big enough.
Interpretation We try to reconstruct as closely as possible an analogue of classical velocity from quantum mechanics. Thereby we focus on the reconstruction of the most simple situation where there is a free particle in space of temperature T. Due to the probabilistic nature of quantum mechanics it is clear that the reconstruction can only be done by using quantities which are at most analogous to the classical notions of "distance passed on a straight line" and "time to pass through that distance" which form the definition of classical velocity.
For the analogue of a classical particle moving on a straight line we use the radial symmetry of a free wave packet with fairly well defined momentum. Our model gives an estimate for the minimal time it takes to measure the position of this particle at a distance bigger or equal to R. It turns out that, if R is big enough, we find an estimate for the minimal time needed which is proportionate to the distance R, exactly what we would expect in the classical case. Note also that if R is big the value of the integral (5) is concentrated in an annulus around R. So the probability that the particle is detected outside an annulus [R, R + δ] , δ > 0 gets smaller as R gets bigger. We then interpret this time as the minimal time needed for our particle φ to "reach" a distance R and can reconstruct classical velocity. The fact that classically the particle moves with constant velocity is mirrored by an upper bound for the reconstructed velocity.
Note that estimate (6) can certainly be refined and is probably not the best estimate possible. If we could find an upper bound for cϕ , (6) would give a general bound on the velocity of a free particle.