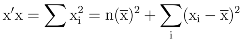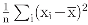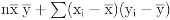Symmetry Studies and Decompositions of Entropy
Abstract
:1 Introduction
2 Symmetry Studies
3 The Standard Decomposition of Entropy
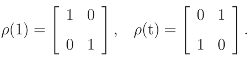
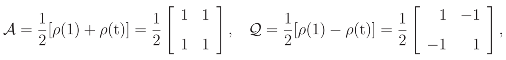
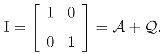
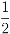 log(p1p2)
log(p1p2)
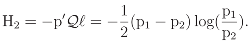
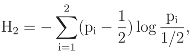
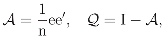
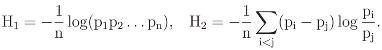
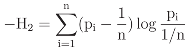
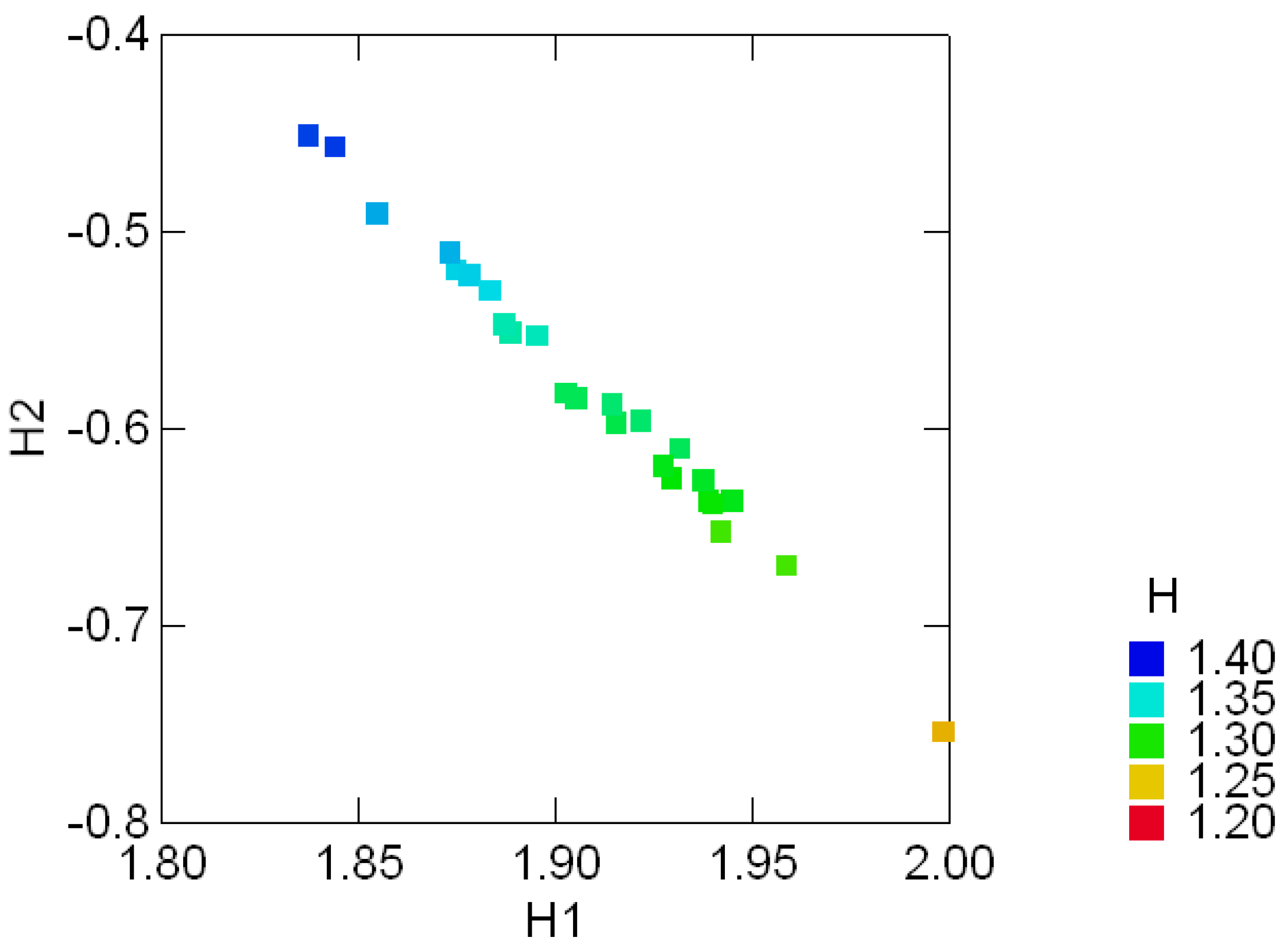
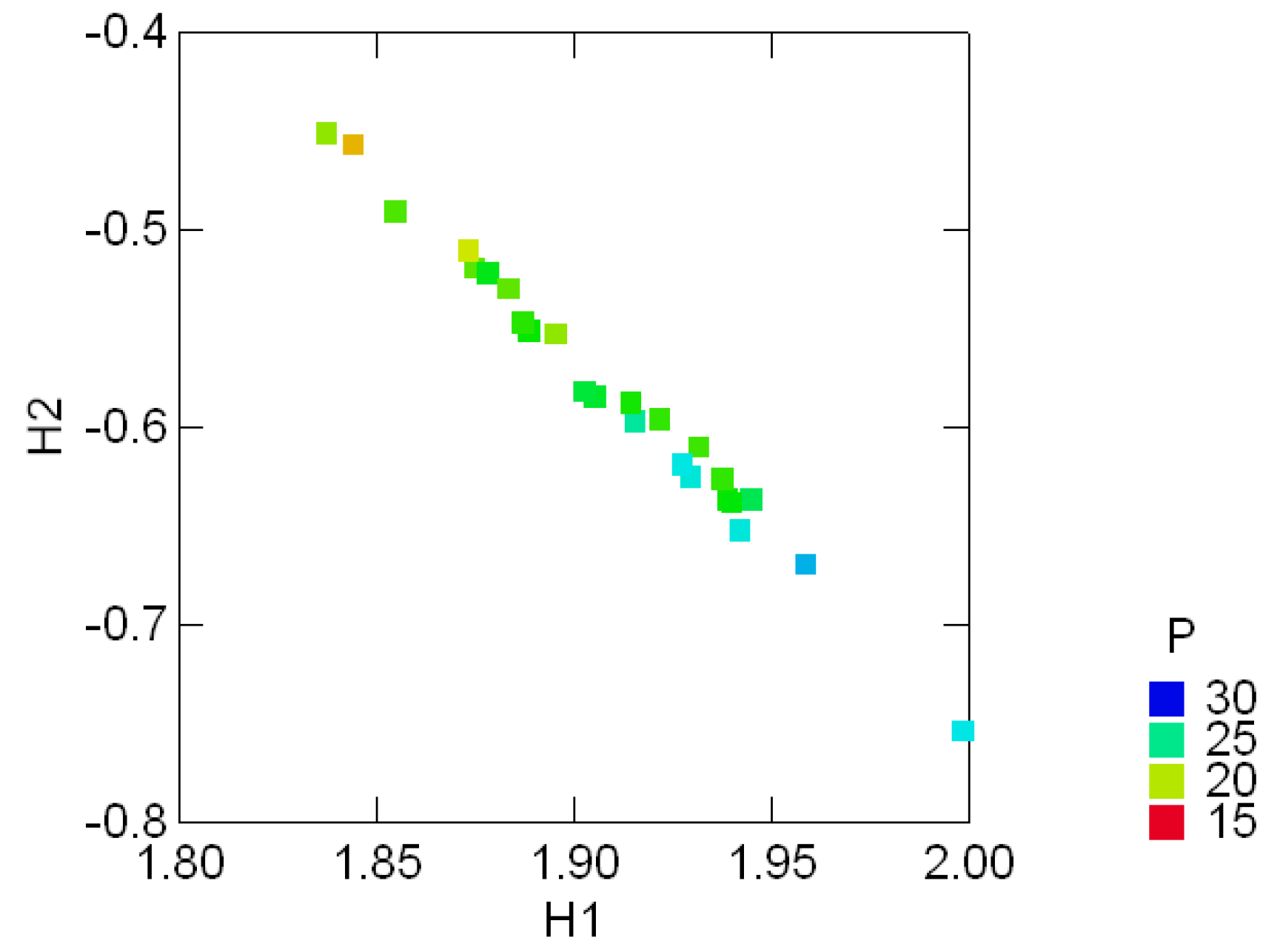
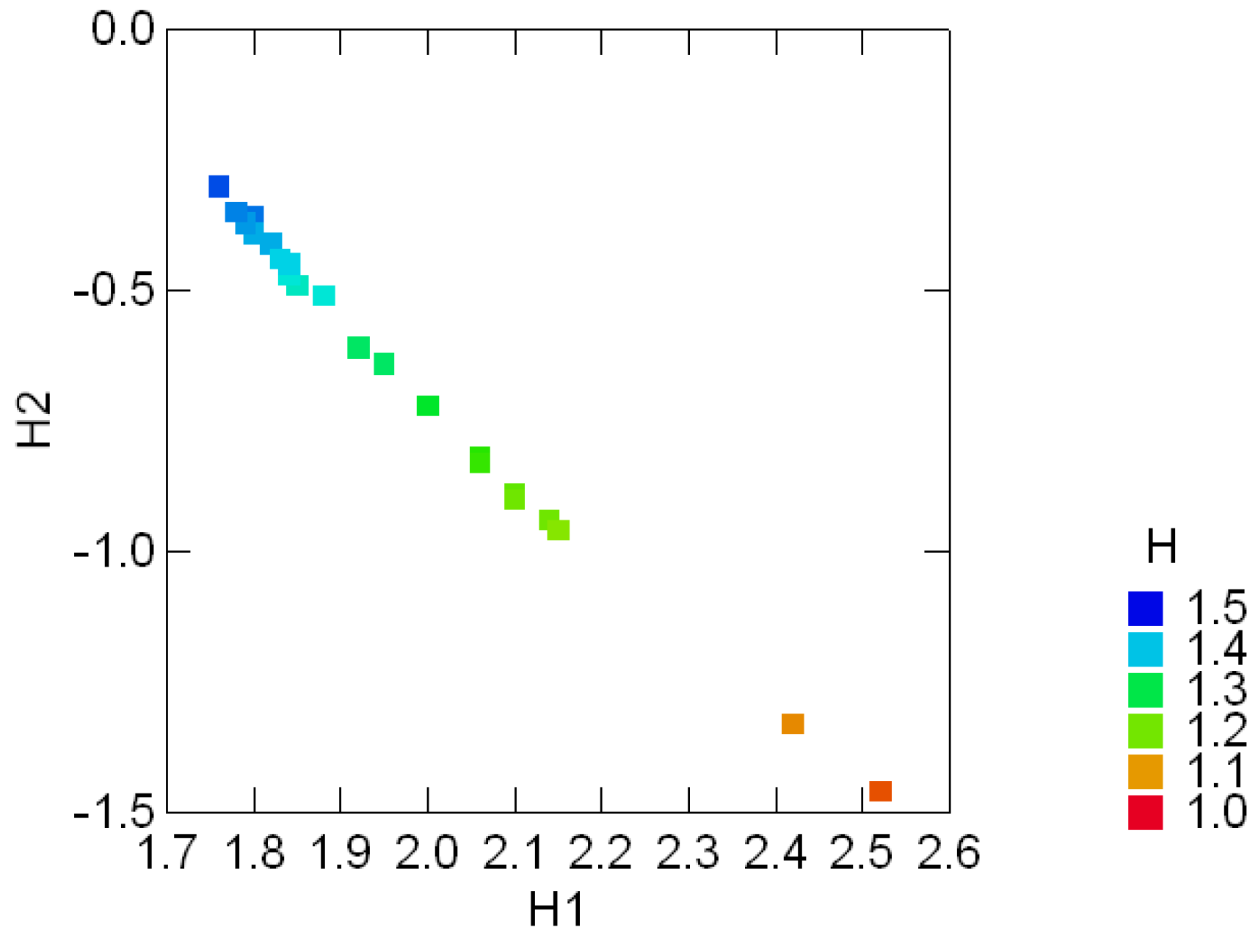
3.1 Graphical displays of {H1, H2}
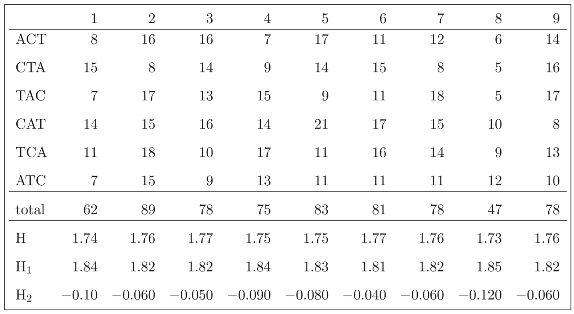
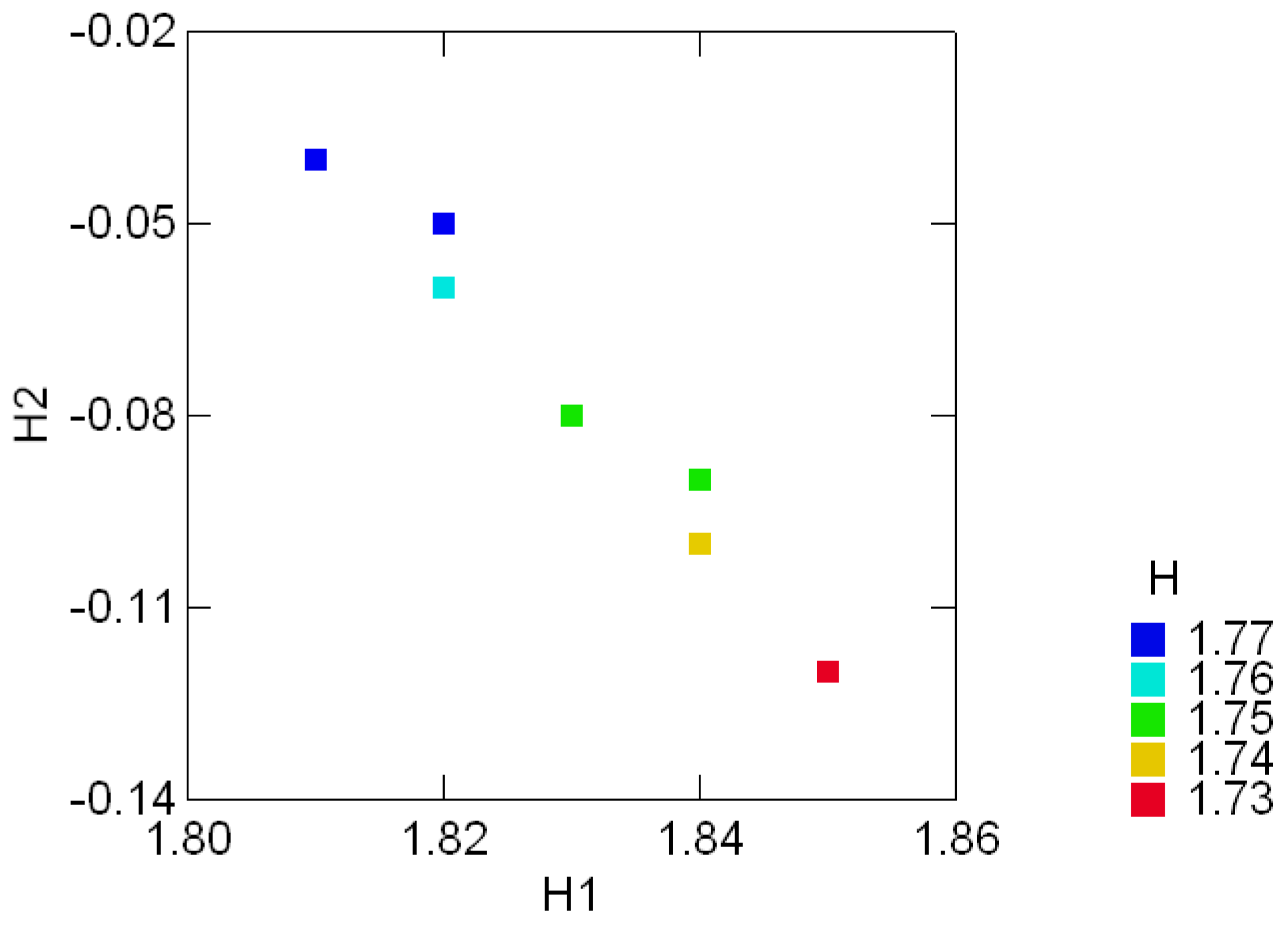
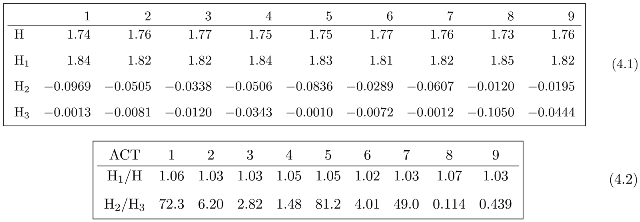
3.2 The standard decomposition of the entropy of the Sloan fonts
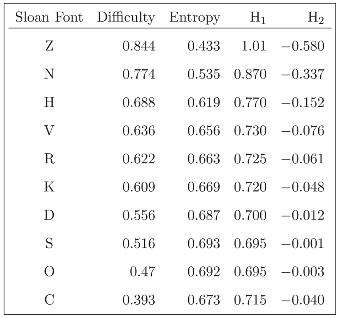
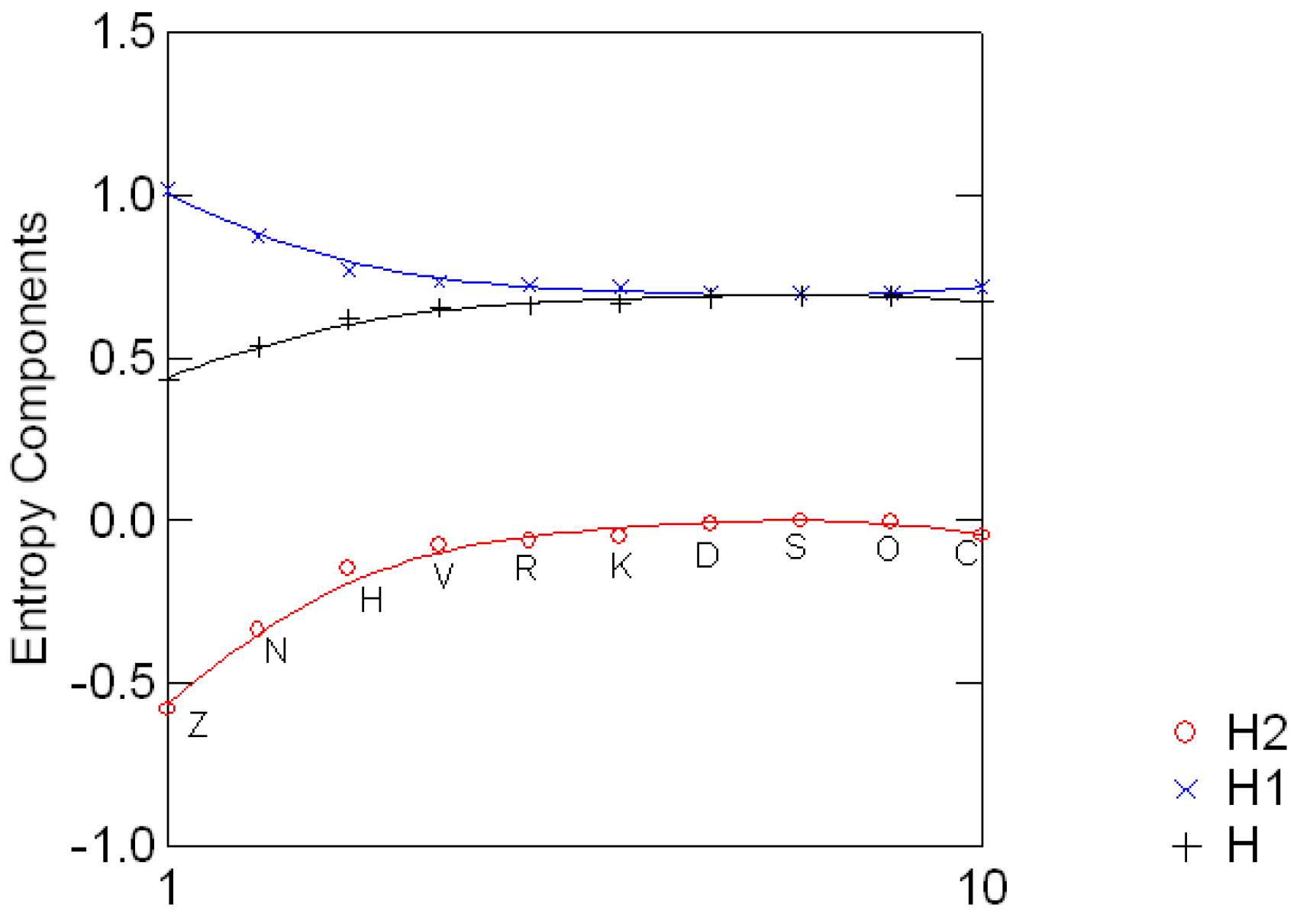
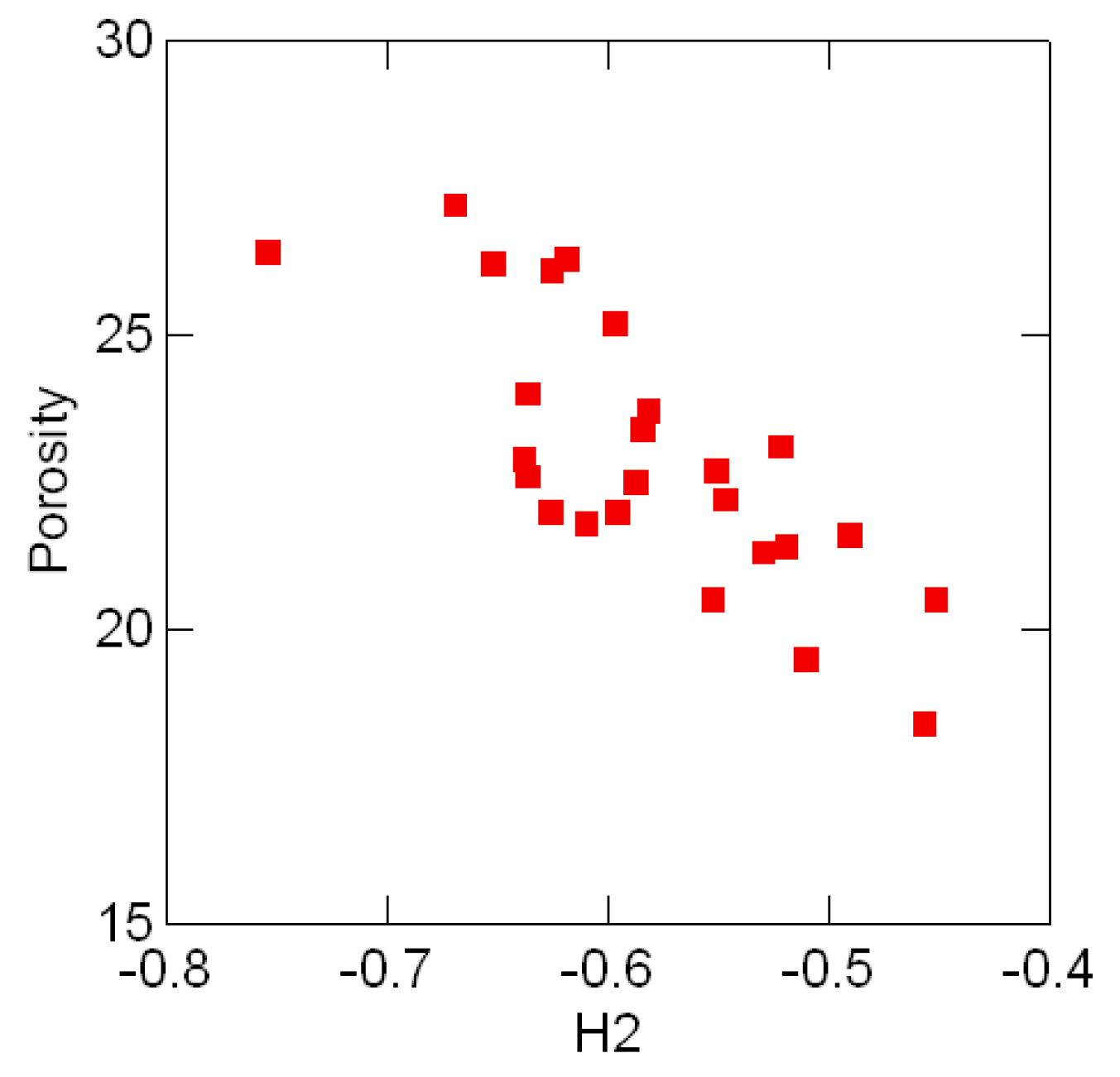
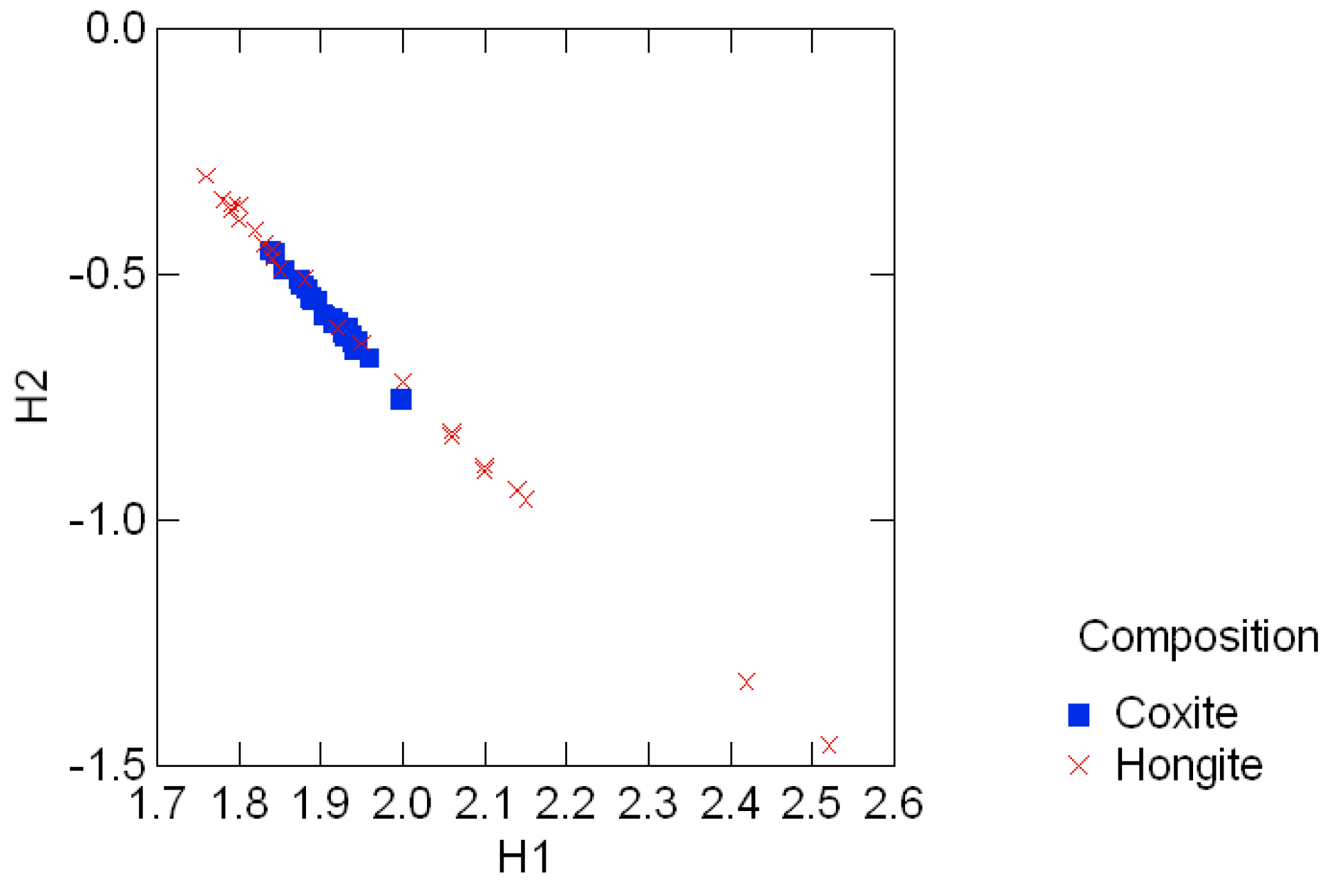
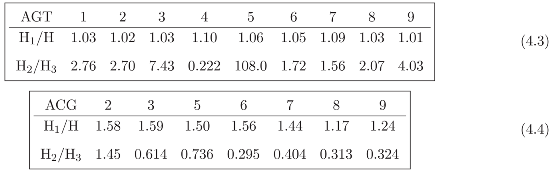
3.3 Geological compositions
4 Regular Decompositions of Entropy
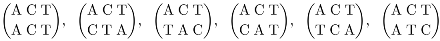
4.1 The regular decomposition
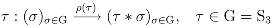
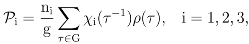
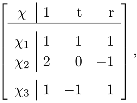
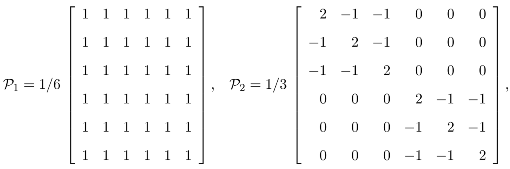

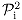 = i, i = 1, 2, 3 and I = 1 + 2 + 3. The underlying invariant image subspaces ix, x ∈ ℝ6, are in dimension of 1, 4, 1 respectively.
= i, i = 1, 2, 3 and I = 1 + 2 + 3. The underlying invariant image subspaces ix, x ∈ ℝ6, are in dimension of 1, 4, 1 respectively.
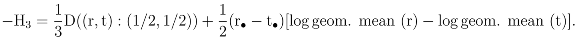
5 A Symmetry Study of Sloan Charts
5.1 The Sloan Charts and the Sloan Fonts symmetries

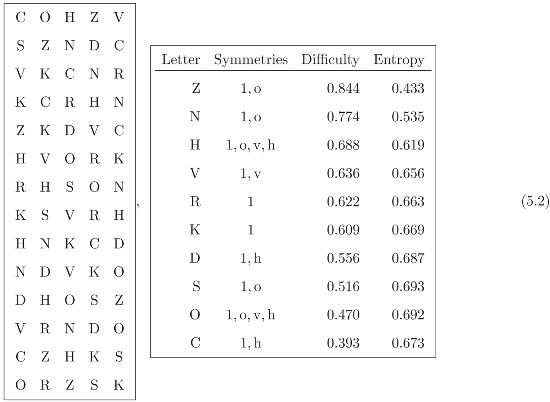
5.2 The regular decomposition
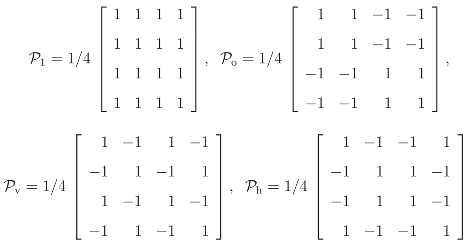
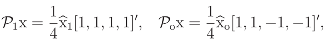
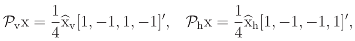
 are the Fourier transforms
are the Fourier transforms
 1 = 1 + o + v + h,
1 = 1 + o + v + h,  o = 1 +o − v − h,
o = 1 +o − v − h,
 v = 1 + v − o − h,
v = 1 + v − o − h,  h = 1 + h − o − v,
h = 1 + h − o − v,
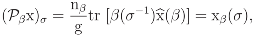
 (β)]/g. Consequently, the data assignment xβ identifies the properties of the regular canonical projection β with the properties of the Fourier transform
(β)]/g. Consequently, the data assignment xβ identifies the properties of the regular canonical projection β with the properties of the Fourier transform  (β) evaluated at β. In that sense, the indexing xβ should retain the interpretations associated with the invariant subspace of β, and, jointly, the data vectors {xβ, β ∈
(β) evaluated at β. In that sense, the indexing xβ should retain the interpretations associated with the invariant subspace of β, and, jointly, the data vectors {xβ, β ∈ 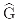 } should fully describe the regular symmetry invariants. Here
} should fully describe the regular symmetry invariants. Here 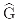 indicates the set of all irreducible representations of G. Any indexing x of G decomposes (via the Fourier inverse formula) as the linear superposition ), ∑β∈
indicates the set of all irreducible representations of G. Any indexing x of G decomposes (via the Fourier inverse formula) as the linear superposition ), ∑β∈ 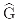 xβ(τ) of regular invariants xβ of G. Shortly, then x = ∑β∈
xβ(τ) of regular invariants xβ of G. Shortly, then x = ∑β∈ 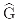 )xβ.
)xβ.5.3 Sorting the line entropy by font symmetry type
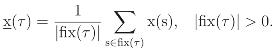

 o, EINVV ≡
o, EINVV ≡  v and EINVH≡
v and EINVH≡  h for the entropy data indexed by font symmetries.
h for the entropy data indexed by font symmetries.
 o, EINVV ≡
o, EINVV ≡  v and EINVH≡
v and EINVH≡  h for the entropy data indexed by font symmetries.
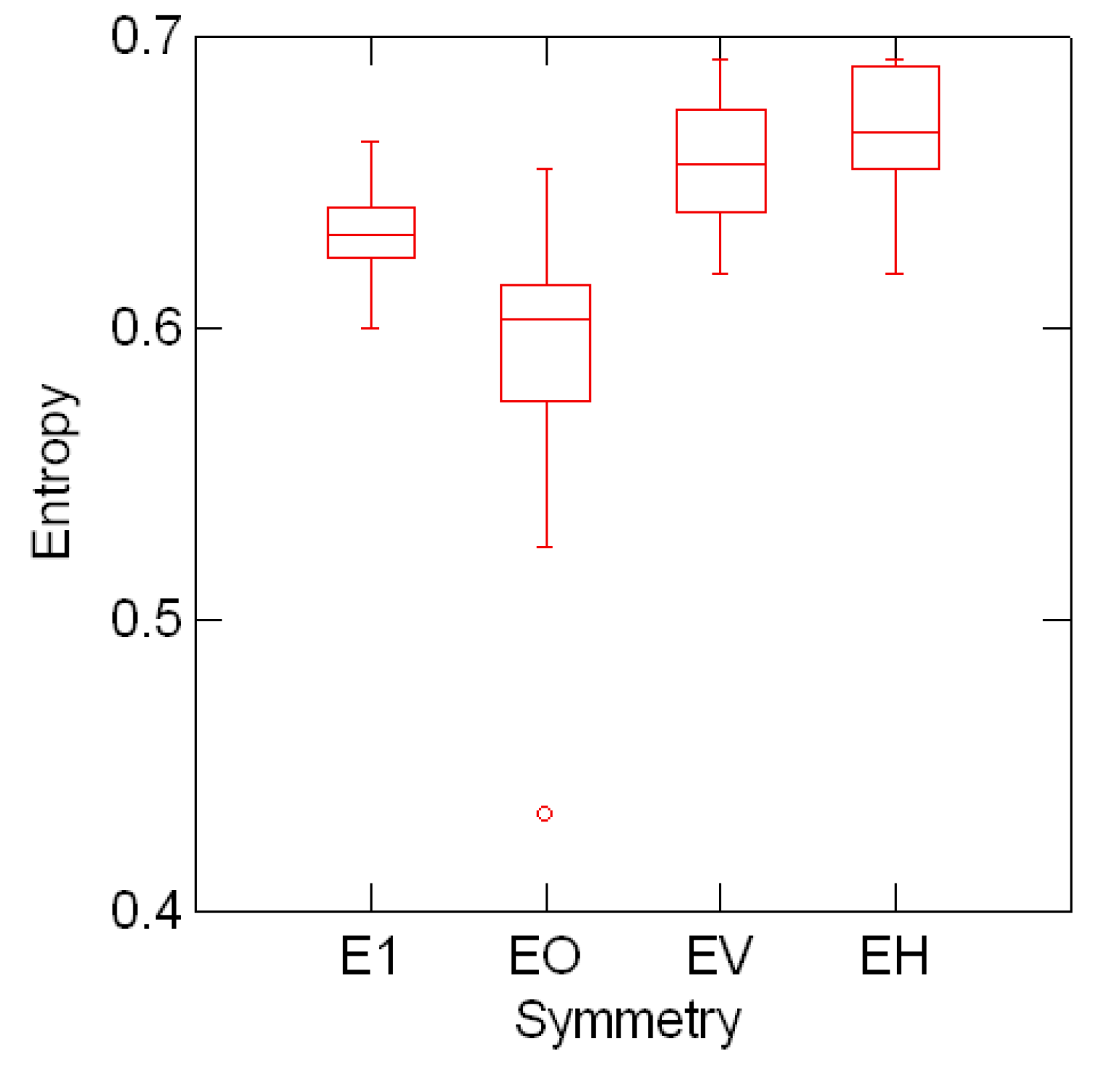
h for the entropy data indexed by font symmetries.
 2,
2,  3 and
3 and  4 (second, third and fourth invariants) for the entropy data
4 (second, third and fourth invariants) for the entropy data
 o is markedly shifted from the distributions of
o is markedly shifted from the distributions of  v and
v and  h.
h.6 Summary and Comments
- The standard decomposition appears in analogy with the decomposition of the sum of squares, or, more specifically, to the decomposition of an inner product (y|x) of two vector x and y in the same finite-dimensional vector space. In fact, the standard decomposition I = 𝒜 + has a well-known role in statistics. It leads to the usual decompositionof the sum of squares in terms of the sample average and the sample variance
. Similarly, it decomposes x’y into the sum
;
- The methodology presented in this paper should provide an additional tool to study the entropy in distributions of nucleotide sequences in molecular biology data. This case is also of statistical and algebraic interest because it extends the decompositions introduced in the present paper to the case in which the probability distributions are indexed by the short nucleotide sequences upon which a group may act by symbol symmetry or by position symmetry [5, p.40];
- Two-dimensional invariant plots for the regular decomposition of the entropy by S3 can be obtained by jointly displaying the three pairwise combinations of the invariant components {H1, H2, H3}. The characteristic of the regions of constant entropy in these planes needs to be investigated;
- The large-sample theory for multinomial distributions, described in detail, for example, in [27, p.469], can be applied to derive the moments of the entropy components.
Appendix A
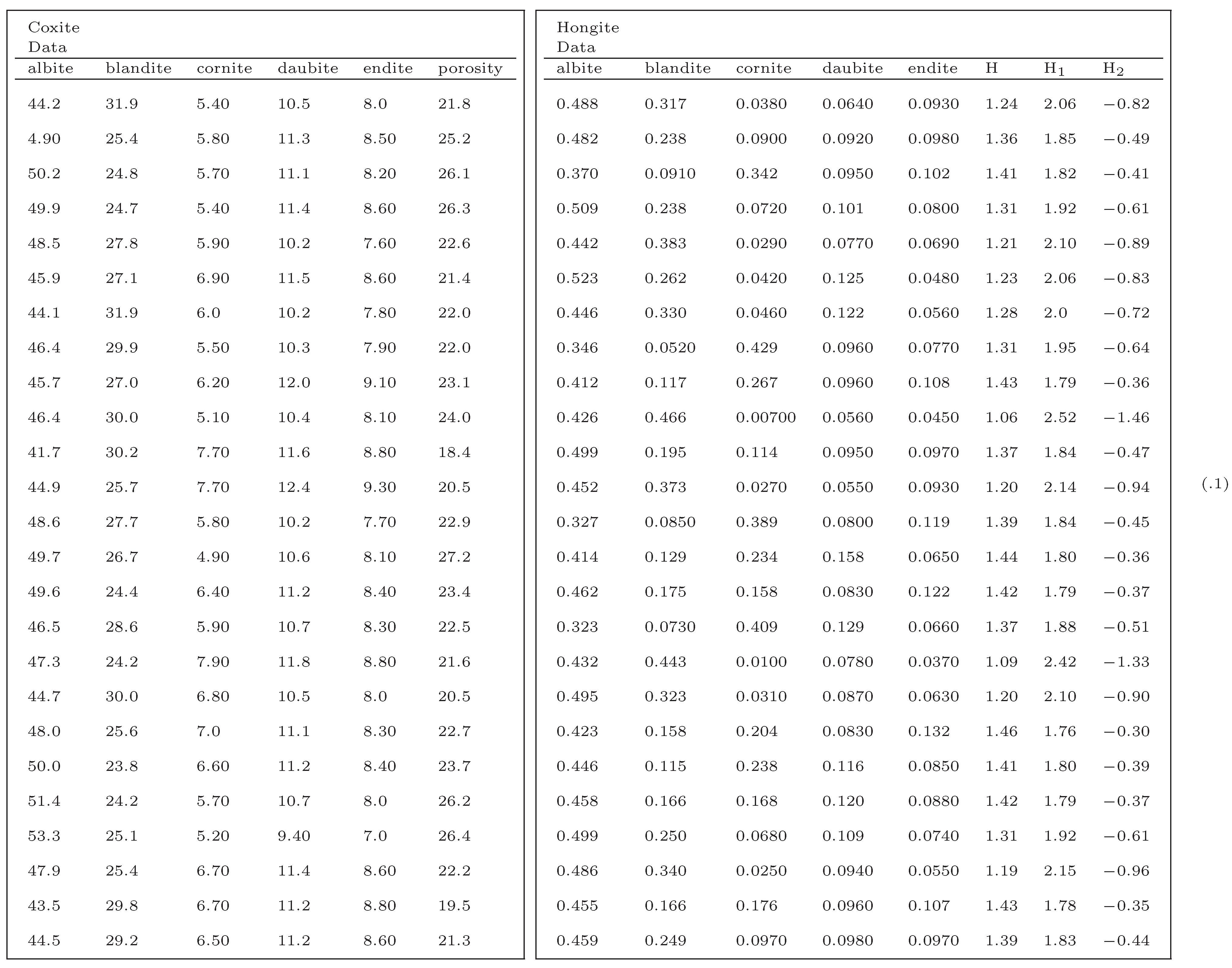
Appendix B
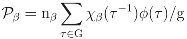
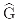 .
. (β) = ∑τ ∈G x(τ)β(τ) of the scalar function x is also an element in
(β) = ∑τ ∈G x(τ)β(τ) of the scalar function x is also an element in 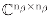 , the indexing xβ(τ) = nβ tr [β(τ−1)
, the indexing xβ(τ) = nβ tr [β(τ−1)  (β)]/g is well-defined. The following proposition shows that it reduces as β.
(β)]/g is well-defined. The following proposition shows that it reduces as β. (β)]/g is an invariant of β.
(β)]/g is an invariant of β.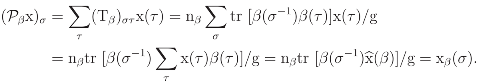
 (β)]/g.
(β)]/g.Acknowledgments
References
- Khinchin, A. I. Information theory; Dover: New York, NY, 1957. [Google Scholar]
- Kullback, S. Information theory and statistics; Dover: New York, NY, 1968. [Google Scholar]
- Jean-Pierre Serre. Linear representations of finite groups; Springer-Verlag: New York, 1977. [Google Scholar]
- Viana, M. Symmetry studies- an introduction; IMPA Institute for Pure and Applied Mathematics Press: Rio de Janeiro, Brazil, 2003. [Google Scholar]
- ——, Lecture notes on symmetry studies, Technical Report 2005-027, EURANDOM, Eindhoven University of Technology, Eindhoven, The Netherlands. 2005. Electronic version http://www.eurandom.tue.nl.
- Eaton, M. L. Multivariate statistics- a vector space approach; Wiley: New York, NY, 1983. [Google Scholar]
- Muirhead, R. J. Aspects of multivariate statistical theory; Wiley: New York, 1982. [Google Scholar]
- Lakshminarayanan, V.; Viana, M. Dihedral representations and statistical geometric optics I: Spherocylindrical lenses. J. Optical Society of America A 2005, 22, no. 11. 2843–89. [Google Scholar]
- Viana, M. Invariance conditions for random curvature models. Methodology and Computing in Applied Probability 2003, 5, 439–453. [Google Scholar]
- Viana, M.; Lakshminarayanan, V. Dihedral representations and statistical geometric optics II: Elementary instruments. J. Modern Optics To appear. 2006. [Google Scholar]
- Hannan, E. J. Group representations and applied probability. Journal of Applied Probability 1965, 2, 1–68. [Google Scholar]
- James, A.T. The relationship algebra of an experimental design. Annals of Mathematical Statistics 1957, 28, 993–1002. [Google Scholar]
- Grenander, U. Probabilities on algebraic structures; Wiley: New York, NY, 1963. [Google Scholar]
- Bailey, R. A. Strata for randomized experiments. Journal of the Royal Statistical Society B 1991, no. 53. 27–78. [Google Scholar]
- Dawid, A. P. Symmetry models and hypothesis for structured data layouts. Journal of the Royal Statistical Society B 1988, no. 50. 1–34. [Google Scholar]
- Diaconis, P. Group representation in probability and statistics; IMS: Hayward, California, 1988. [Google Scholar]
- Eaton, M. L. Group invariance applications in statistics; IMS-ASA: Hayward, California, 1989. [Google Scholar]
- Farrell, R. H. (Ed.) Multivariate calculation; Springer-Verlag: New York, NY, 1985.
- Wijsman, R. A. Invariant measures on groups and their use in statistics; Vol. 14, IMS: Hayward, California, 1990. [Google Scholar]
- Nachbin, L. The Haar integral; Van Nostrand: Princeton, N.J., 1965. [Google Scholar]
- Andersson, S. Invariant normal models. Annals of Statistics 1975, 3, no. 1. 132–154. [Google Scholar]
- Perlman, M. D. Group symmetry covariance models. Statistical Science 1987, 2, 421–425. [Google Scholar]
- Viana, M.; Richards, D. Viana, M., Richards, D., Eds.; Vol. 287, American Mathematical Society: Providence, RI, 2001.
- Ferris, F.L., 3rd; Freidlin, V.; Kassoff, A.; Green, S.B.; Milton, R.C. Relative letter and position difficulty on visual acuity charts from the early treatment diabetic retinopathy study. Am J Ophthalmol 1993, 15, 735–40. [Google Scholar]
- Aitchison, J. The statistical analysis of compositional data; Chapman and Hall: New York, NY, 1986. [Google Scholar]
- Doi, H. Importance of purine and pyrimidine content of local nucleotide sequences (six bases long) for evolution of human immunodeficiency virus type 1. Evolution 1991, 88, no. 3. 9282–9286. [Google Scholar]
- Bishop, Y.M.M.; Fienberg, S.E.; Holland, P.W. Discrete multivariate analysis: Theory and practice; MIT Press: Cambridge, Massachusetts, 1975. [Google Scholar]
© 2006 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Viana, M. Symmetry Studies and Decompositions of Entropy. Entropy 2006, 8, 88-109. https://doi.org/10.3390/e8020088
Viana M. Symmetry Studies and Decompositions of Entropy. Entropy. 2006; 8(2):88-109. https://doi.org/10.3390/e8020088
Chicago/Turabian StyleViana, Marlos. 2006. "Symmetry Studies and Decompositions of Entropy" Entropy 8, no. 2: 88-109. https://doi.org/10.3390/e8020088
APA StyleViana, M. (2006). Symmetry Studies and Decompositions of Entropy. Entropy, 8(2), 88-109. https://doi.org/10.3390/e8020088