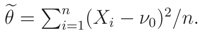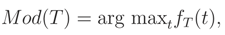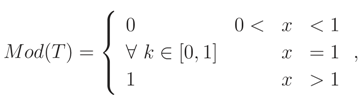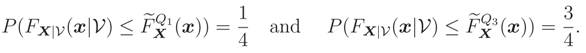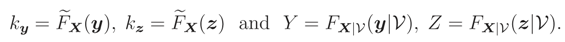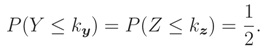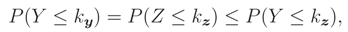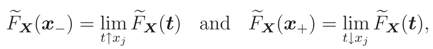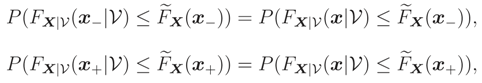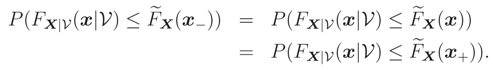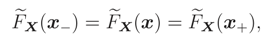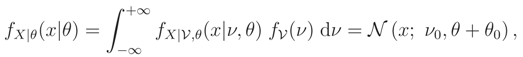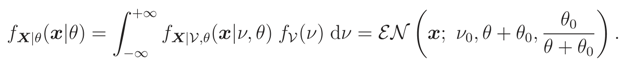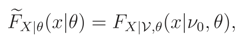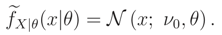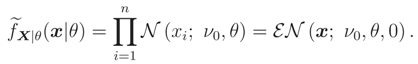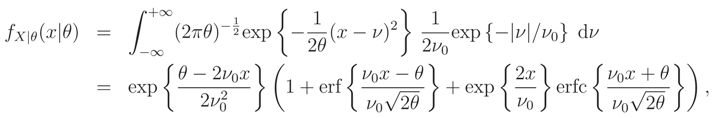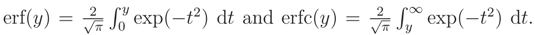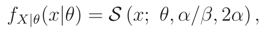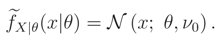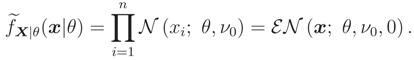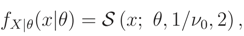1 Introduction
We consider the problem of inference on a parameter of interest
θ of a probability distribution when we have some prior information on a nuisance parameter
ν from a finite number of samples of this probability distribution. Assume that we know the expressions of either the cumulative distribution function (cdf)
FX|ν,θ(
x|ν, θ) or its corresponding probability density function (pdf)
fX|ν,θ(
x|ν, θ),
X = (
X1, … ,
Xn)′ and
x = (
x1, … ,
xn)′.
is a random parameter on which we have an
a priori information and
θ is a fixed unknown parameter. This prior information can either be of the form of a prior cdf
F(
ν) (or a pdf
f(
ν)) or, for example, only the knowledge of a finite number of its moments. In the first case, the marginal cdf
is the classical tool for doing any inference on
θ. For example the Maximum Likelihood (ML) estimate,
of
θ is defined as
where
fX|θ(
x|θ) is the pdf corresponding to the cdf
FX|θ(
x|θ).
In the second case the Maximum Entropy (ME) principle ([
4,
5]), can be used for assigning the probability law
f(
ν) and thus go back to the previous case, e.g. [
1] page 90.
In this paper we consider the case where we only know the median of the nuisance parameter
. If we had a complementary knowledge about the finite support of pdf of
, then we could again use the ME principle to assign a prior and go back to the previous case, e.g. [
3]. But if we are given the median of
and if the support is not finite, then in our knowledge, there is not any solution for this case. The main object of this paper is to propose a solution for it. For this aim, in place of
FX|θ(
x|θ) in (1), we propose a new inference tool
(
x|θ) which can be used to infer on
θ (we will show that
(
x|θ) is a cdf under a few conditions). For example we can define
where
(
x|θ) is the pdf corresponding to the cdf
(
x|θ).
This new tool is deduced from the interpretation of
FX|θ(
x|θ) as the mean value of the random variable
T =
T (
; x) =
FX|θ(
x|θ) as given by (1). Now, if in place of the mean value, we take the median, we obtain this new inference tool
(
x|θ) which is defined as
and can be used in the same way to infer on
θ.
As far as the authors know, there is no work on this subject except recently presented conference papers by the authors, [
9,
8,
7]. In the first article we introduced an alternative inference tool to total probability formula, which is called a new inference tool in this paper. We calculated directly this new inference tool (such as Example A in
Section 2) and a numerical method suggested for its approximation. In the second one, we used this new tool for parameter estimation. Finally, in the last one, we reviewed the content of two previous papers and mentioned its use for the estimation of a parameter with incomplete knowledge on a nuisance parameter in the one dimensional case. In this paper we give more details and more results with proofs using weaker conditions, with a new overlook on the problem. We also extend the idea to the multivariate case. In the following, first we give more precise definition of
(
x|θ). Then we present some of its properties. For example, we show that under some conditions,
(
x|θ) has all the properties of a cdf, its calculation is very easy and depends only on the median of prior distribution. Then, we give a few examples and finally, we compare the relative performances of these two tools for the inference on
θ. Extensions and conclusion are given in the last two sections.
2 A New Inference Tool
Hereafter in this section to simplify the notations we omit the parameter θ, and we assume that the random variables Xi, i = 1, … , n and random parameter are continuous and real. We also use increasing and decreasing instead of non-decreasing and non-increasing respectively.
Definition 1 Let X = (
X1, … ,
Xn)′
have a cdf FX|ν(
x|ν)
depending on a random parameter with pdf f(
ν),
and let the random variable T =
T(
;
x) =
FX|ν(
x|)
have a unique median for each fixed x. The new inference tool,
,
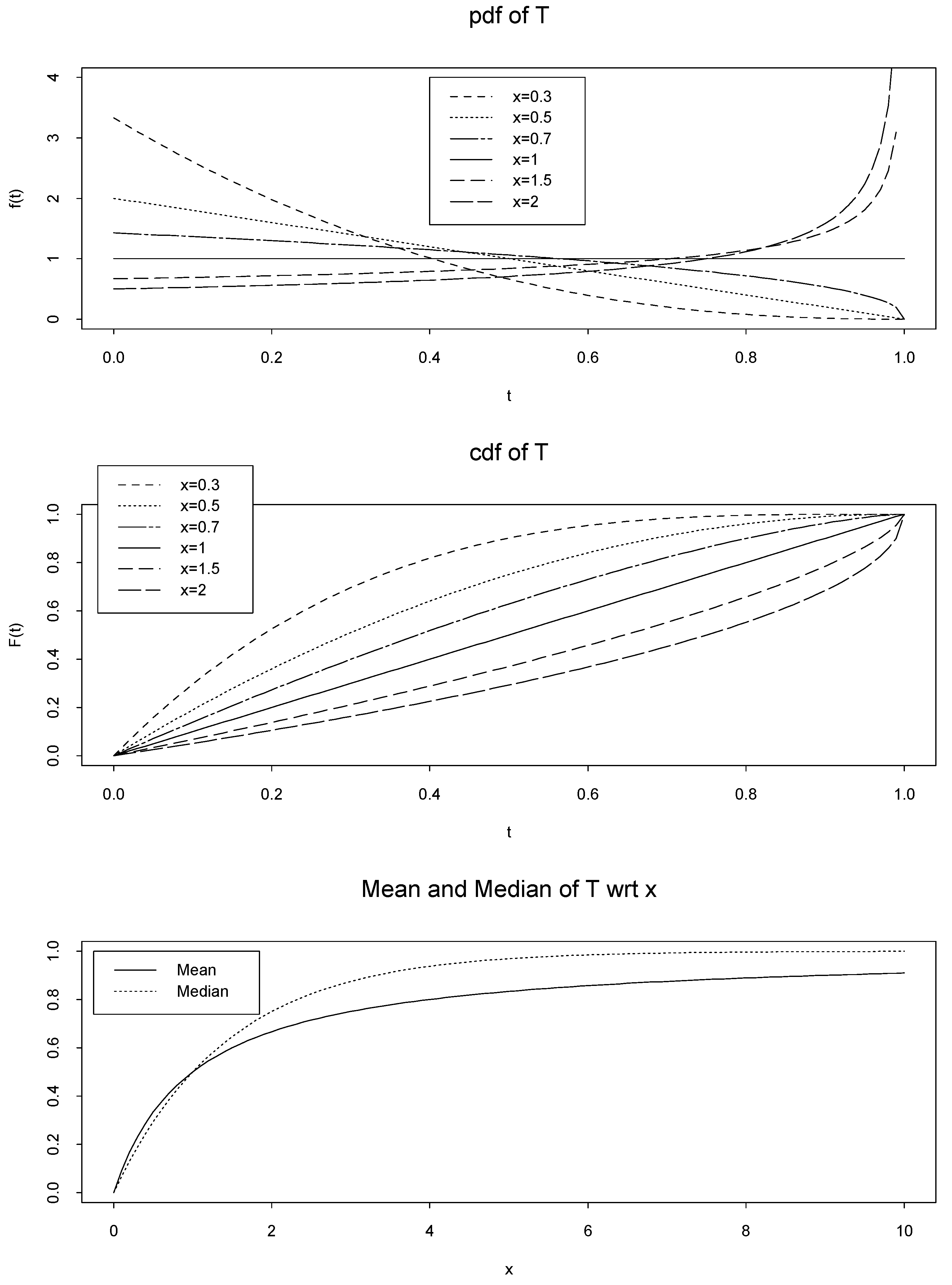
is defined as the median of T: To make our point clear we begin with the following simple example, called
Example A. Let
FX|(
x|
ν) = 1 −
e−νx,
x > 0, be the cdf of an exponential random variable with scale parameter
ν > 0. We assume that the prior pdf of
is known and also is exponential with parameter 1, i.e.
fν(
ν) =
e−ν,
ν > 0. We define the random variable
T =
FX|(
x|
) = 1 −
e−x, for any fixed value
x > 0. The random variable 0 ≤
T ≤ 1 has the following cdf
Therefore, pdf of
T is
fT(
t) =
(1 −
t)
( − 1), 0 ≤
t ≤ 1. Now, we can calculate the mean of the random variable
T as follow
Let
Med(
T) be the median of the random variable
T, then it can be calculated by
Mean value of the random variable
T is a cdf with respect to (wrt)
x. This fact is always true; because
E(
T) is the marginal cdf of random variable
X, i.e.
FX(
x). The marginal cdf is well known, well defined and can also be calculated directly by (1). On the other hand, in this example, it is obvious that
Med(
T) is a cdf wrt
x, which is called
(
x) in Definition 1, see
Figure 1. However, we have not a short cut for calculating
(
x) such as
FX(
x) in (1).
In the following theorem and remark, first we show that under a few conditions, (x) has all the properties of a cdf. Then, in Theorem 2, we drive a simple expression for calculating (x) and show that, in many cases, the expression of (x) depends only on the median of the prior and can be calculated simply, see Remark 2. In Theorem 3 we state separability property of (x) versus exchangeability of FX(x).
Theorem 1 Let X have a cdf FX|ν(
x|ν)
depending on a random parameter with pdf f(
ν)
and the real random variable T =
FX|ν(
x|)
have a unique median for each fixed x. Then:- 1.
(x) is an increasing function in each of its arguments.
- 2.
If FX|ν(x|ν) and F(ν) are continuous cdfs then (x) is a continuous function in each of its arguments.
- 3.
0 ≤ (x) ≤ 1.
Proof: - 1.
Let
y = (
y1, … ,
yn)′,
z = (
z1, … ,
zn)′,
yj <
zj for fixed
j and
yi =
zi for
i ≠
j, 1 ≤
i,
j ≤
n and take
Then using (2) we have
We also have
Y ≤
Z, because
FX| is an increasing function in each of its arguments. Therefore,
ky is the unique median of
Y and so
ky ≤
kz or equivalently
(
x) is increasing in its
j-th argument.
- 2.
Let
x. = (
x1, … ,
xj − 1,
x.,
xj + 1, … ,
xn)′ and
t = (
x1, … ,
xj − 1,
t,
xj + 1, … ,
xn)′. By part 1,
(
x) is an increasing function in each of its arguments. Therefore,
exist and are finite, e.g. [
11].
Further,
FX|(
x|
) is continuous wrt
xj, and so
and by (2) we have
But
(
x) is the unique median of
FX|(
x|
), therefore by (3),
and thus
(
x) is continuous.
- 3.
(x) is the median of random variable T, where T = FX|(x|) and 0 ≤ T ≤ 1, and so 0 ≤ (x) ≤ 1. ☐
Remark 1 By part 1 of Theorem 1, lim
xj↑+∞ (
x)
and lim
xj↓−∞ (
x)
exist and are finite, [11]. Therefore (
x)
is a continuous cdf if conditions of Theorem 1 hold and- 1.
limxj↓−∞ (x) = 0 for any particular j,
- 2.
limx1↑+∞,… ,xn↑+∞ (x) = 1,
- 3.
∆b1a1 …∆bnan (x) ≥ 0, where ai ≤ bi, i = 1, … , n, and ∆bjaj (x) = ((x1, … , xj − 1, bj, xj + 1, … ,xn)′)−((x1, … , xj − 1, aj, xj + 1, … ,xn)′) ≥ 0.
In this case, we call (
x)
the marginal cdf of X based on median.
When (
x)
is a one dimensional cdf, the last condition follows from parts 1 and 3 of Theorem 1. Theorem 2 If L(ν) = FX|ν(x|ν) is a monotone function wrt ν and has a unique median , then (x) = L().
Proof: Let
be the generalized inverse of
L, e.g. [
10] page 39. Noting that
and by (2) we have,
where the last expression follows from
☐
Remark 2 If conditions of Theorem 2 hold, then (x) belongs to the family of distributions FX|(x|). Because, (x) = FX|ν(x|) Therefore (x) is a cdf and conditions in Remark 1 hold.
Remark 3 (x) depends only on the median of prior distribution, , while the expression of FX(x) needs the perfect knowledge of F(ν). Therefore, (x) is robust relative to prior distributions with the same median.
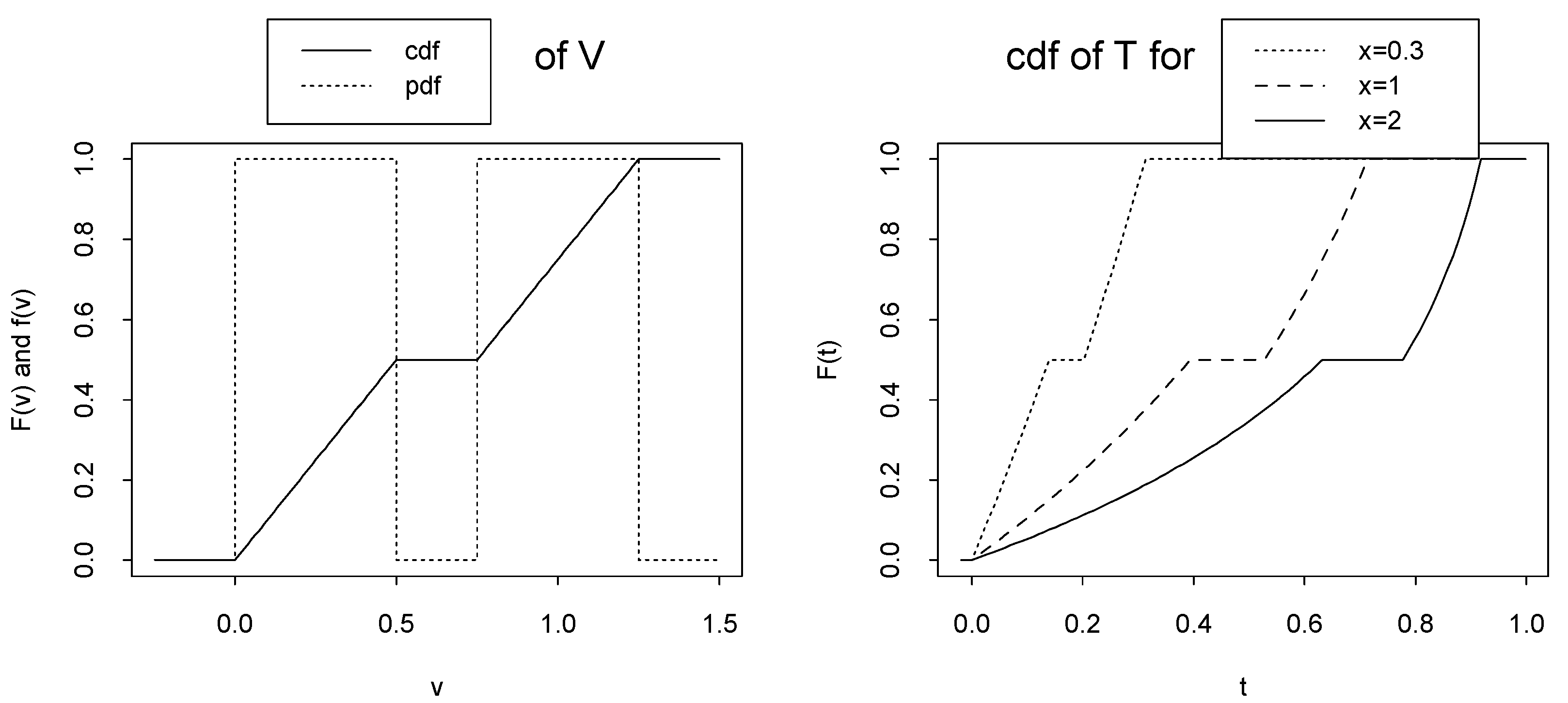
Remark 4 If median of T is not unique then (
x)
may not be a unique cdf wrt x. For example (called Example B
), assumethat has the following cdf, in Example A, Figure 2-left:Then, T =
T (
;
x) =
FX|(
x|
) = 1 −
e−x has the following cdfTherefore, the median of T is an arbitrary point in the following interval: (see Figure 2-right) Theorem 3 Let FX|ν(
x|ν)
be conditional cdf of X = (
X1, … ,
Xn)′
given =
ν and L(k1,… ,kr)(
ν) =
F(Xk1 ,… ,Xkr)|
(
xk1 , … ,
xkr|
ν)
be monotone function of ν for each {
k1, … ,
kr} ⊆ {1, … ,
n}.
Let also have a unique median .
If for each {
k1, … ,
kr} ⊆ {1, … ,
n},
i.e. X |
=
ν has independent components, then Proof: Conditions of Theorem 2 hold and so, for each {
k1, … ,
kr} ⊆ {1, … ,
n},
☐
Remark 5 If X |
=
ν has independent components, then the marginal distribution of X cannot have independent components. For example, in general case,It can be shown that, if X | = ν has Independent and Identically Distributed (iid) components, then the marginal distribution of X is exchangeable, see Example 1. We recall that for identically distributed random variables exchangeability is a weaker condition than independence. In the following we show that some families of distributions (e.g. [
6]) have a monotone distribution function wrt their parameters and so, calculation of
(
x) is very easy by using Theorem 2.
Lemma 1 Let L(ν) = FX|(x|). If ν is a real location parameter then L(ν) is decreasing wrt ν.
Proof: Let
ν1 <
ν2 and
ν be a location parameter. Then
☐
Lemma 2 Let L(ν) = FX|(x|ν). If ν is a scale parameter then L(ν) is monotone wrt ν.
Proof: Let
ν1 <
ν2. If
ν is a scale parameter,
ν > 0, then
Therefore,
L(
ν) is an increasing function if
x < 0 and is a decreasing function if
x > 0, i.e.
L(
ν) is a monotone function wrt
ν. ☐
The proof of the following lemma is straightforward.
Lemma 3 Let X1, … Xn given = ν beiid random variables and X = (X1, … , Xn)′. If L(ν) = FX1|(x|ν) is an increasing (a decreasing) function then L*(ν) = FX|ν(x|ν) is an increasing (a decreasing) function of ν.
In some cases we can show directly that
L(.) is a monotone function. For example, in the exponen-tial family this property can be proved by using differentiation. Let
X|
η be distributed according to an exponential family with pdf
where
η = (
η1, … ,
ηn)′ and
T = (
T1, … ,
Tn)′. It can be shown that
L(
η) =
FX|
η(
x|
η) is a monotone function wrt each of its arguments in many cases by the following method: Let
Iy≤x = 1 if
y1 ≤
x1, … ,
yn ≤
xn and 0 elsewhere; and note that the differentiation under the integral sign is true for exponential family. Then
The last equality follows from
![Entropy 08 00067 i031]()
, e.g. [
6] page 27.
On the other hand, we can use stochastic ordering property of a family of distributions for showing that
L(.) is a monotone function. A family of cdfs
where
V is an interval on the real line, is said to have Monotone Likelihood Ratio (MLR) property if, for every
ν1 <
ν2 in
V the likelihood ratio
is a monotone function of
x. The property of MLR defines a very strong ordering of a family of distributions.
Lemma 4 If is an MLR family wrt x then FX|(x|ν) is an increasing (or a decreasing) functionof ν for all x.
Proof: See e.g. [
12] page 124. ☐
A family of cdfs in (4) is said to be stochastically increasing (SI) if
ν1 <
ν2 implies
FX|(
x|
ν1) ≥
FX|(
x|
ν2) for all
x. For stochastically decreasing (SD) the inequality is reversed. This definition is a weaker property than MLR property (by Lemma 4), but is a stronger property than monotonicity of
L(
ν) =
FX|(
x|
ν) (because
L(
ν) is monotone for each fixed
x). Therefore, we have
It can be shown that the converse of the above relations are not true.
Remark 6 In Theorem 1, we prove that (
x)
is an increasing function. In the proof of this theorem we do not use the monotonicity property of L(
ν) =
FX|(
x|
ν)
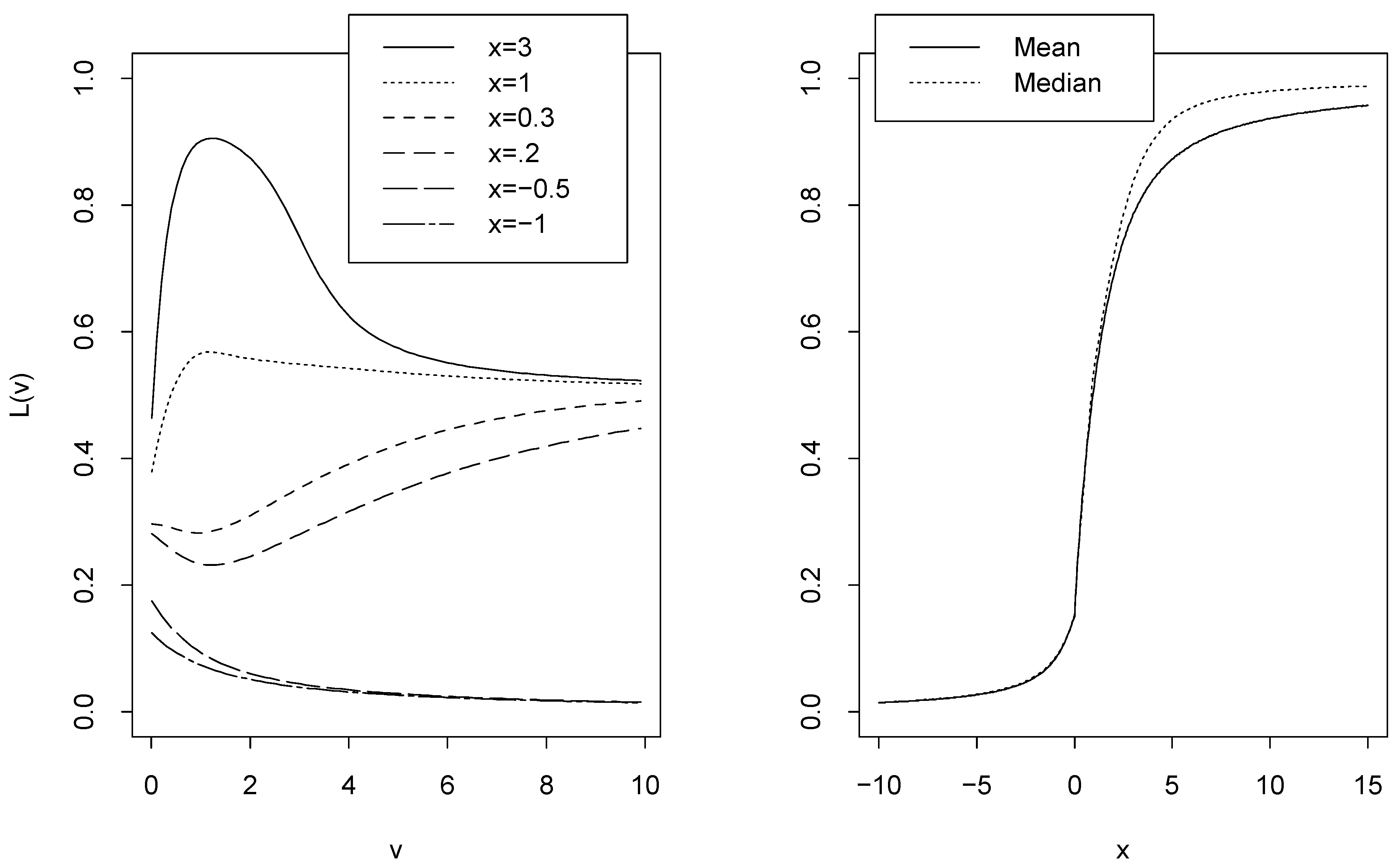
wrt ν.Forexample (called Example C
), assume thatbe mixture cdf of an exponential and a Cauchy cdf with parameter ν > 0.
Figure 3-left shows the graphs of L(
ν) =
FX|(
x|
ν)
for different x. L(
ν)
is not monotone for some of x values in this figure. If we assume that the prior pdf of is known and is also exponential with parameter 1, then, still median of random variable T is a cdf, see Figure 3-right. 4 Extensions
In this section, we show that the suggested new tool can be extended to other functions such as quantiles instead of median, but not to other functions such as mode. For example, mode of the random variable
T =
T (
;
x) =
FX|(
x|θ) in Definition 1, i.e.,
is not a cdf in Example A. The mode of
T is: (see
Figure 1 top)
which is not a distribution function. If we assume
k = 1, then
Mod(
T) is a degenerate cdf. In
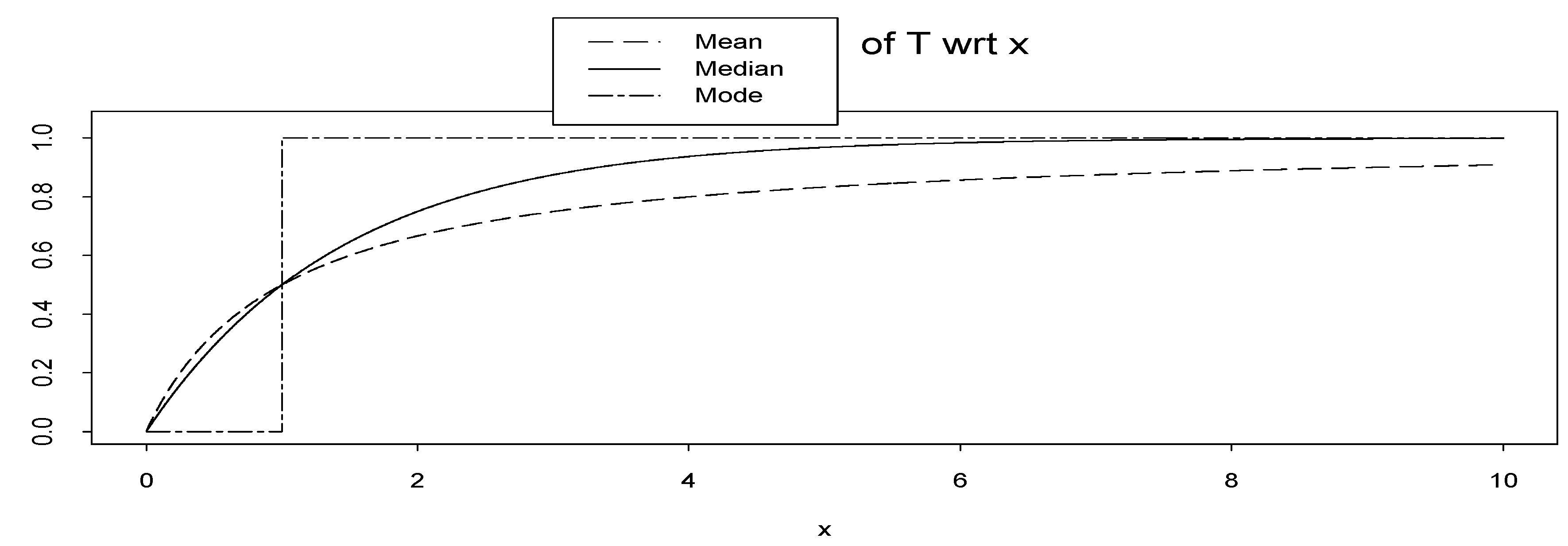
Figure 5 we plot the mean, median and mode of the random variable
T. We see that they are cdfs. However, the cdf based on mode is the extreme case of the two others.
As noted by one of the referees, the mode of prior pdf is useful for introducing a pseudo cdf similar to our new inference tool,
(
x). That is, instead of using the result of Theorem 2:
(
x|θ) =
FX|
ν,θ(
x|
Med(
),
θ), using
(
x|θ) =
FX|
ν,θ(
x|
Mod(
),
θ). This method was used for eliminating the nuisance parameter
ν. In this case, Theorem 3, i.e. separability property of pseudo marginal distribution, also holds for
(
x|θ). Note that, the mode of the random variable
T, defined in (7) is not equal to
(
x|θ) and may not be a cdf similar to the above illustration. However, it may be a cdf similar to the following example pointed out by the referee. In Example A, let
− 1 be a binomial distribution with parameters
(2,
), i.e.
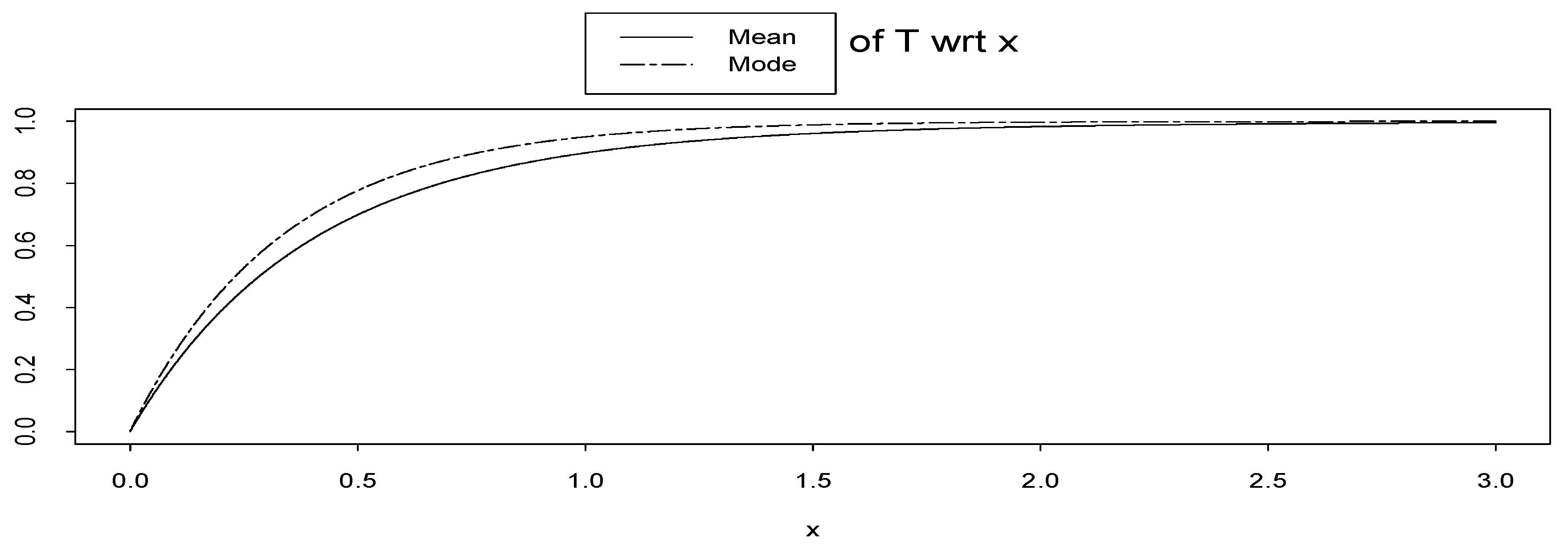
is a discrete random variable with support {1, 2, 3}. Then
E(
T) = 1 − (
e−x + 6
e−2x + 9
e−3x)/16 and
Mod(
T) = 1 −
e−3x are cdfs see
Figure 6.
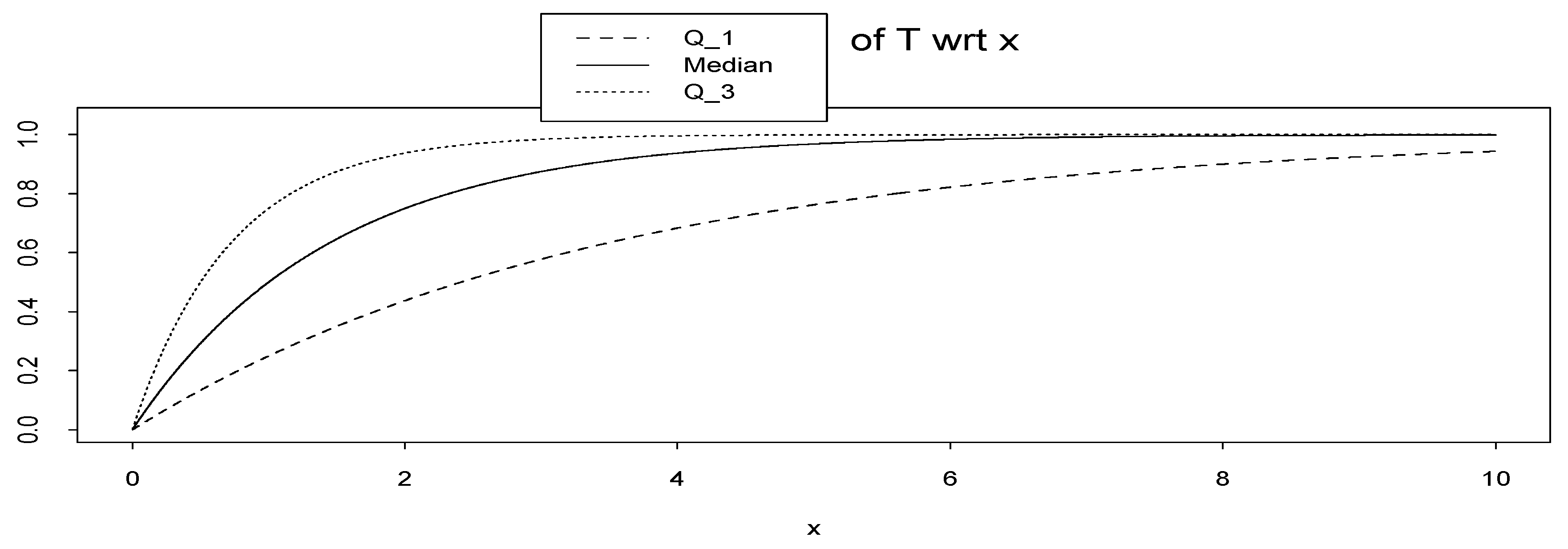
On the other hand, we may extend the method presented in this paper to the class of quantiles (e.g., quartiles or percentiles). To make our point clear we consider the first and third quartiles of random variable T in Example A (instead of median, which is the second quartile). We denote the new inference tools based on first and third quartiles by (x) and (x) respectively.
They can be calculated such as (2) by
It can be shown that, in Example A,
(
x) = 1 −
ex ln 0.75 and
(
x) = 1 −
ex ln 0.25. In
Figure 7 we plot them.
In conclusion, it seems that the method can be extended to any quantiles instead of median, but its extension to other functions may need more care.

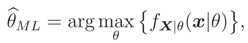
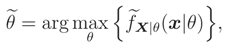
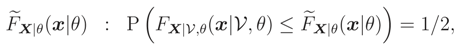
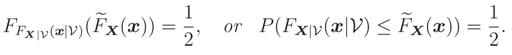
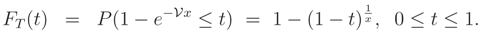
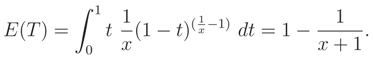
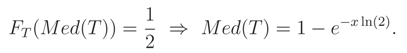
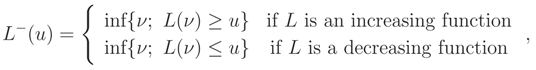
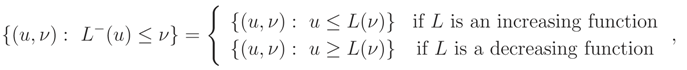

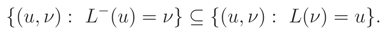
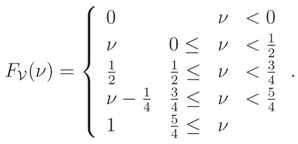
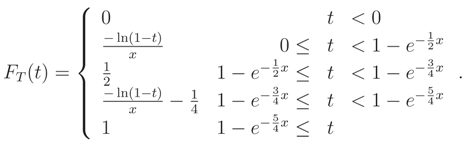
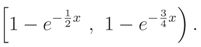
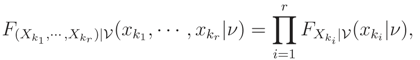
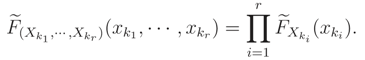
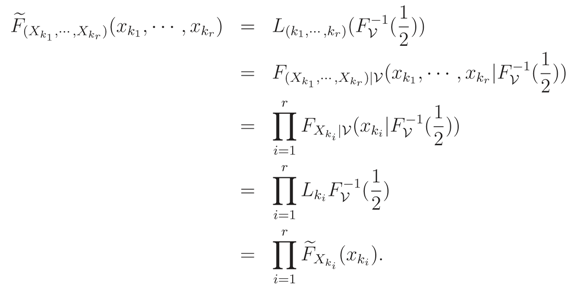

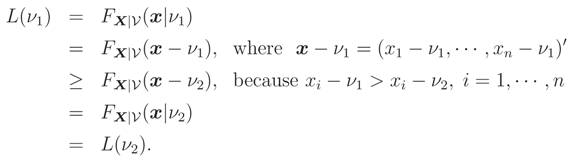
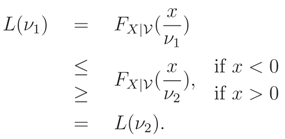
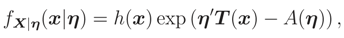
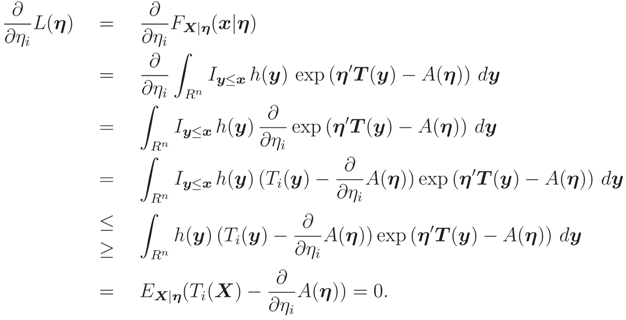
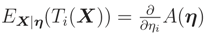 , e.g. [6] page 27.
, e.g. [6] page 27.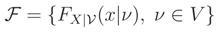
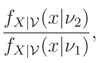
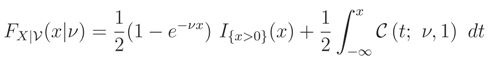
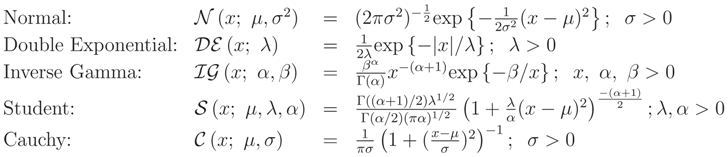
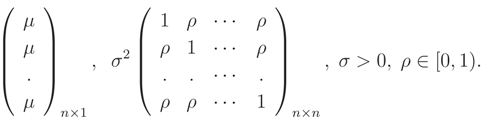
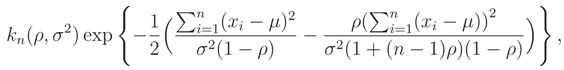
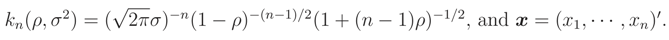
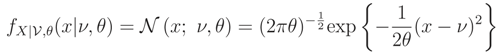
We recall that, if we know that E() = ν0 or Median {} = ν0 and the support of is R the ME pdf does not exist.
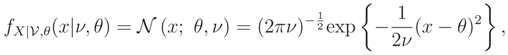
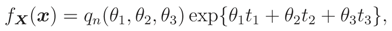
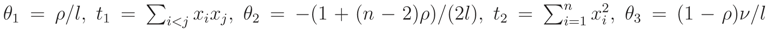 ,
, 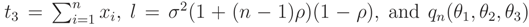 can be determined. This pdf is a monotone function wrt θ3 and so L(ν) is a monotone function. Let θ = (σ2, ρ) and the median of prior pdf be ν0, then
can be determined. This pdf is a monotone function wrt θ3 and so L(ν) is a monotone function. Let θ = (σ2, ρ) and the median of prior pdf be ν0, then
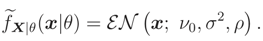
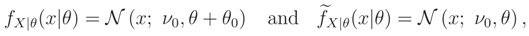
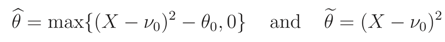
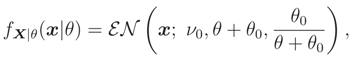
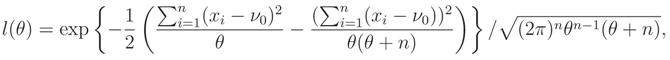
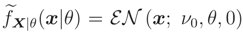 , is equal to
, is equal to