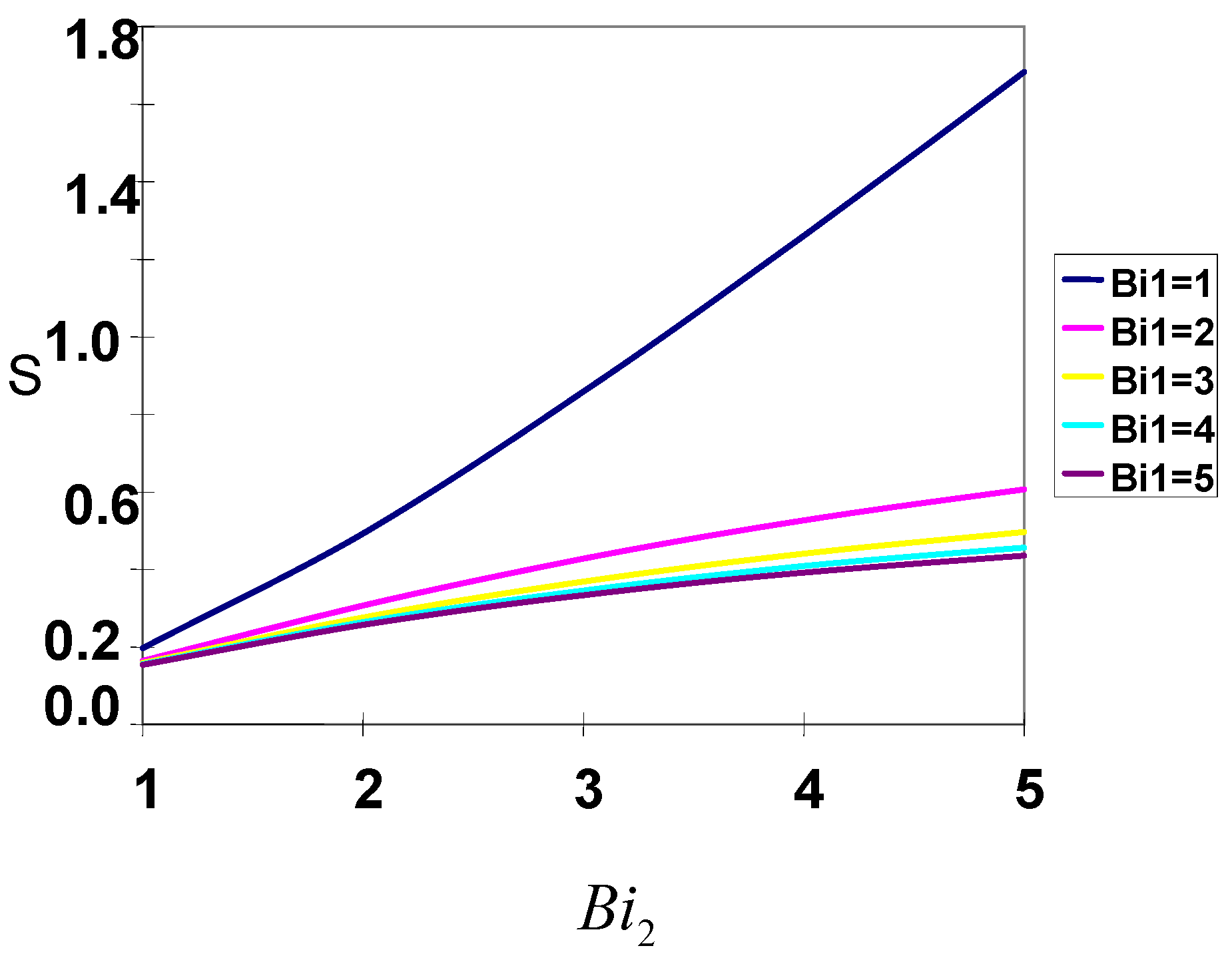Introduction
Since the pioneering work of Bejan [
1] on entropy generation in convective heat transfer, it is now widely recognized that convective heat transfer problems that were previously studied using the first law of thermodynamics be reexamined in the light of the second law of thermodynamics so that thermal systems can be designed with the objective of minimizing thermodynamic irreversibility. This design methodology, known as entropy generation minimization (EGM), is comprehensively covered in the book by Bejan [
2]. The popularity of EGM can be gauged from the number of papers on entropy generation in convective flows that continue to appear in the heat transfer literature e.g. [
3,
4]. We will refer only to the literature that deals with entropy generation for flow between parallel plates which is of immediate relevance to the present study.
The flow of a viscous, incompressible flow induced by a plate moving parallel to a stationary plate and assisted by a favorable pressure gradient situation, known as generalized Couette flow, is useful in many engineering applications and has been studied extensively both from fluid mechanics and heat transfer perspectives. However, studies of entropy generation in such flows have been limited. Ibanez et al [
5] have studied the entropy generation due to pressure gradient assisted viscous flow between two parallel stationary plates when the plates are subjected to convective boundary conditions. Their analysis assumes that the convective environment temperature is the same for both plates but the heat transfer coefficients and consequently the Biot numbers are different. They concluded that a minimum volumetric entropy generation rate can be achieved for certain combinations of Biot numbers. This work was later extended to the generalized Couette flow [
6].
The present paper is an analytical study of entropy generation in generalized Couette flow with focus on the effect of thermal boundary conditions imposed on the plates. Four different combinations of thermal boundary conditions are investigated: (a) both plates at different temperatures, (b) stationary plate at a fixed temperature and moving plate subjected to a constant heat flux, (c) stationary plate at a fixed temperature and convection at the moving plate, and (d) convection at both plates. The case (d) is a refinement of the analysis presented in [
6] because it allows both the environment temperatures and the convective heat transfer coefficients to be different. Analytical results for the velocity and temperature profiles, entropy generation due to heat transfer, entropy generation due to viscous dissipation, and the total entropy generation are presented and discussed.
Hydrodynamic and Thermal Analysis
Fig. 1 illustrates the Couette flow of a viscous, incompressible fluid confined between two parallel plates separated by a distance a. The fluid viscosity, µ, is assumed to be a constant. The bottom plate is stationary while the top plate moves with a uniform V. The fluid flow is also assisted by a favorable pressure gradient, dp/dx <0.
Fig.1.
Couette flow between parallel plates
Fig.1.
Couette flow between parallel plates
The momentum equation for the velocity u along the x direction may be written in dimensionless form as
where U = u / V, Y = y / a, and
is the dimensionless pressure gradient. The boundary conditions for equation (1) are
The solution of equations (1-2) is easily obtained as
The derivative of
U with respect to
Y which will be needed later in the entropy generation analysis is
With the inclusion of heat conduction in the y direction and the viscous dissipation term, the energy equation in dimensionless form is expressible as
where
θ=
kT/
μV2 is the dimensionless temperature and
k is the thermal conductivity of the fluid. The use of dimensionless temperature in this form eliminates the Eckert number Ec and Prandtl number Pr which appear in traditional analyses. The solution of equation (5) depends on the thermal boundary conditions imposed at the plates. We consider the solutions for four combinations of boundary conditions.
Entropy Generation Rate
Adapting the general result for the local volumetric entropy generation rate(
W/
m3K) provided by Bejan [
1,
2] to the present convective flow situation, we have
which may be expressed in dimensionless form as
Both in equations (18) and (19), the first term represents the entropy generation due to heat conduction (subscript h ) and the second term the entropy generation due to viscous or fluid friction effect (subscript f). Using equation (4) for
dU/
dY and the appropriate results (depending on the thermal boundary conditions) for
dθ/
dY, we can integrate equation (19) from
Y = −1/2 to
Y = 1/2 and obtain the entropy generation rate across the gap between the plates.
Results and Discussion
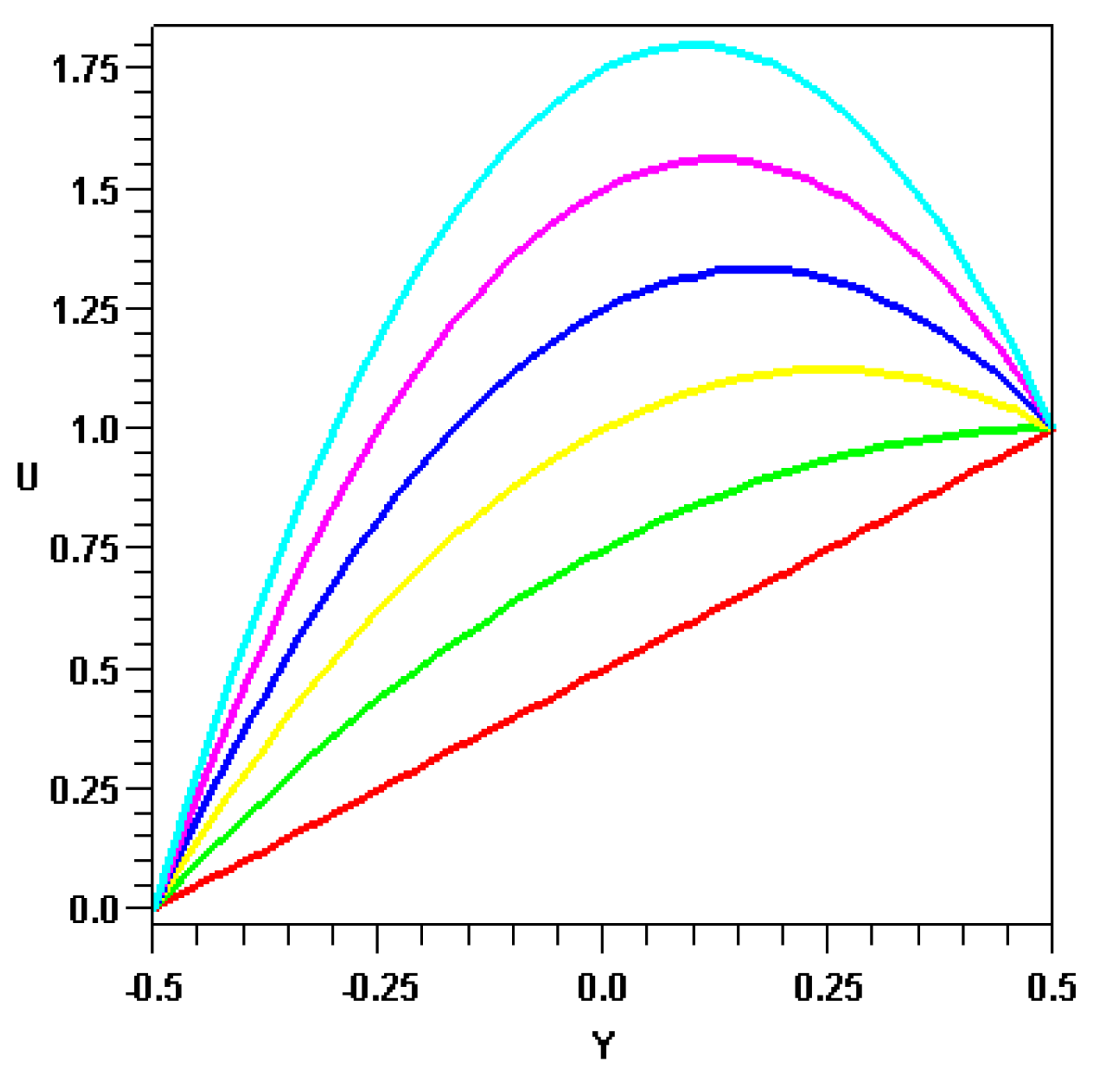
The dimensionless velocity distribution given by equation (3) is plotted in
Fig.2 for
P = 0 (red), 2 (green), 4 (yellow), 6 (blue), 8(pink), and 10 (aqua blue). For
P = 0 i.e. no axial pressure gradient, the velocity distribution is linear giving a constant velocity gradient
dU/
dY across the gap. As a consequence, the entropy generation due to fluid friction occurs at all locations across the gap. As the pressure gradient
P increases, the velocity profiles exhibit maxima indicating zero velocity gradients at certain locations across the gap and consequently zero entropy generation due to friction at those locations. The location of zero entropy generation due to friction moves closer to the center line
Y = 0 as the pressure gradient increases.
Fig.2.
Effect of pressure gradient P on velocity profiles
Fig.2.
Effect of pressure gradient P on velocity profiles
Constant Plates Temperatures
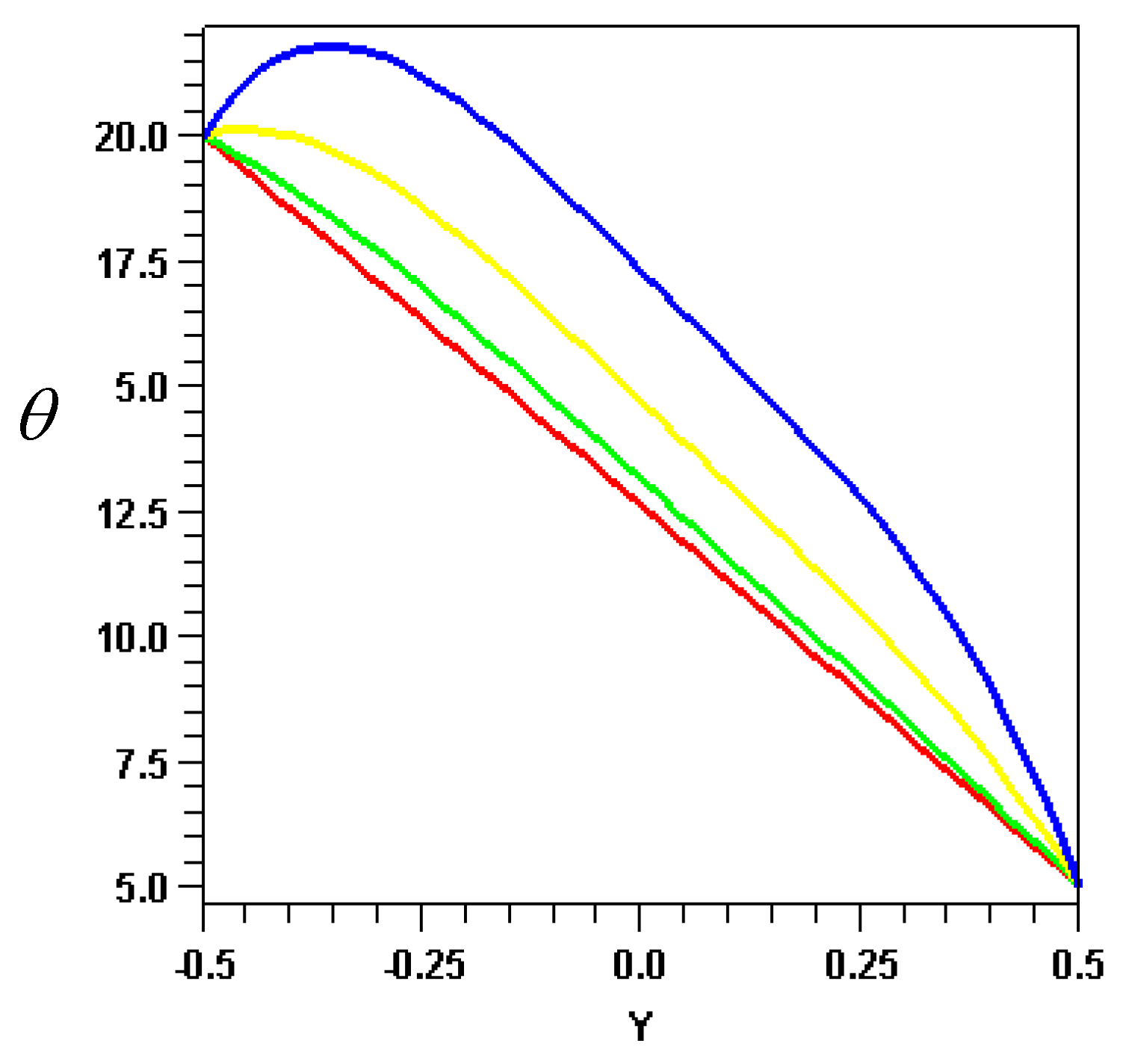
The effect of pressure gradient on the temperature distribution is illustrated in
Fig.3 for the case of constant plate temperatures (
θ1 = 20,
θ2 = 5). In the range from
P = 0-10, the temperature distribution changes only slightly. Since the temperature profiles do not exhibit any maxima, the entropy generation due to heat conduction occurs at all locations across the gap. However, a distinct maximum in temperature is observed at
P = 50 and indicates zero entropy generation due to heat conduction at that location.
Fig.3.
Effect of pressure gradient P on temperature profile
Fig.3.
Effect of pressure gradient P on temperature profile
Fig.4a.
Local entropy generation due to heat conduction
Fig.4a.
Local entropy generation due to heat conduction
Fig.4b.
Local entropy generation due to fluid friction
Fig.4b.
Local entropy generation due to fluid friction
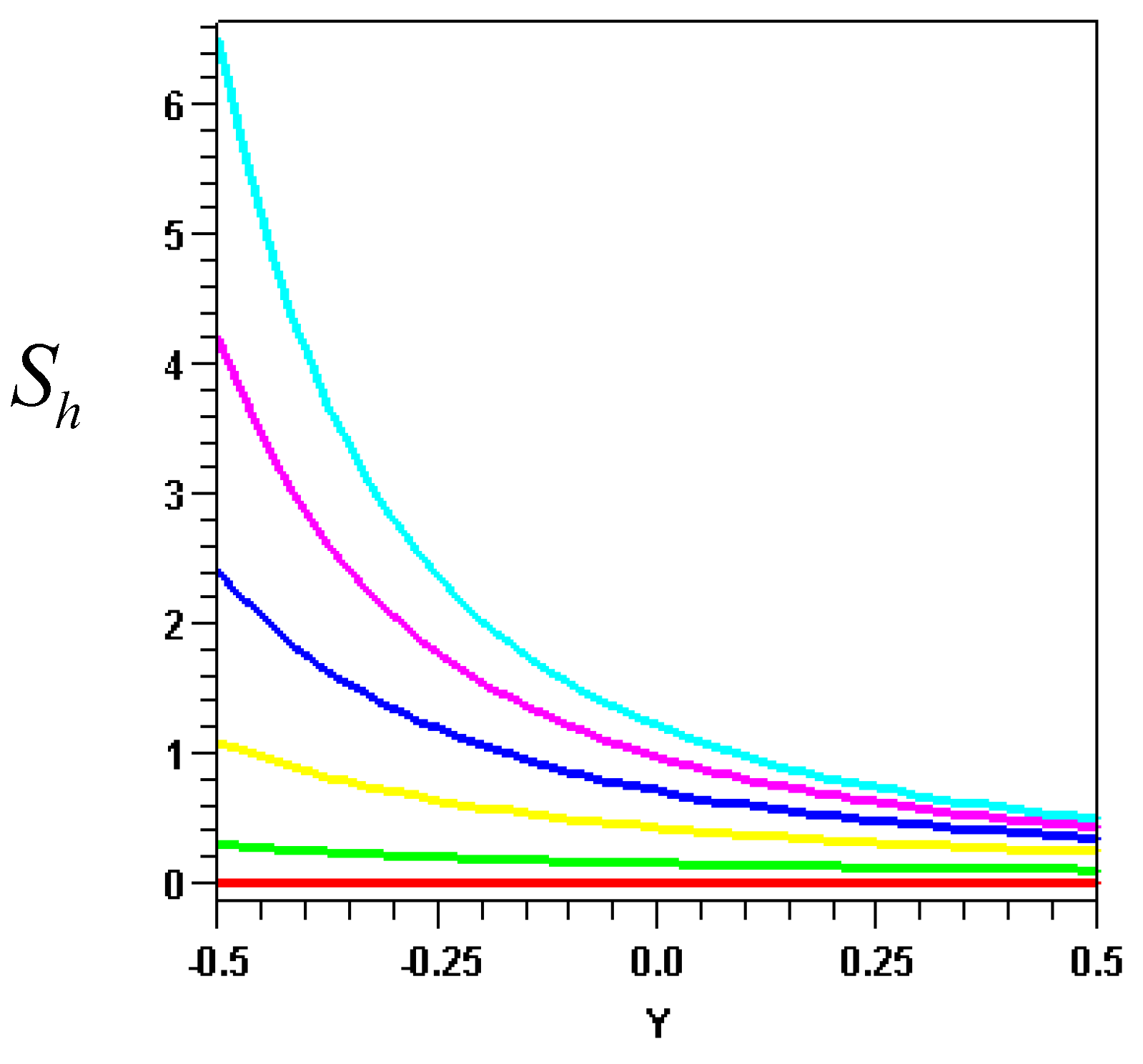
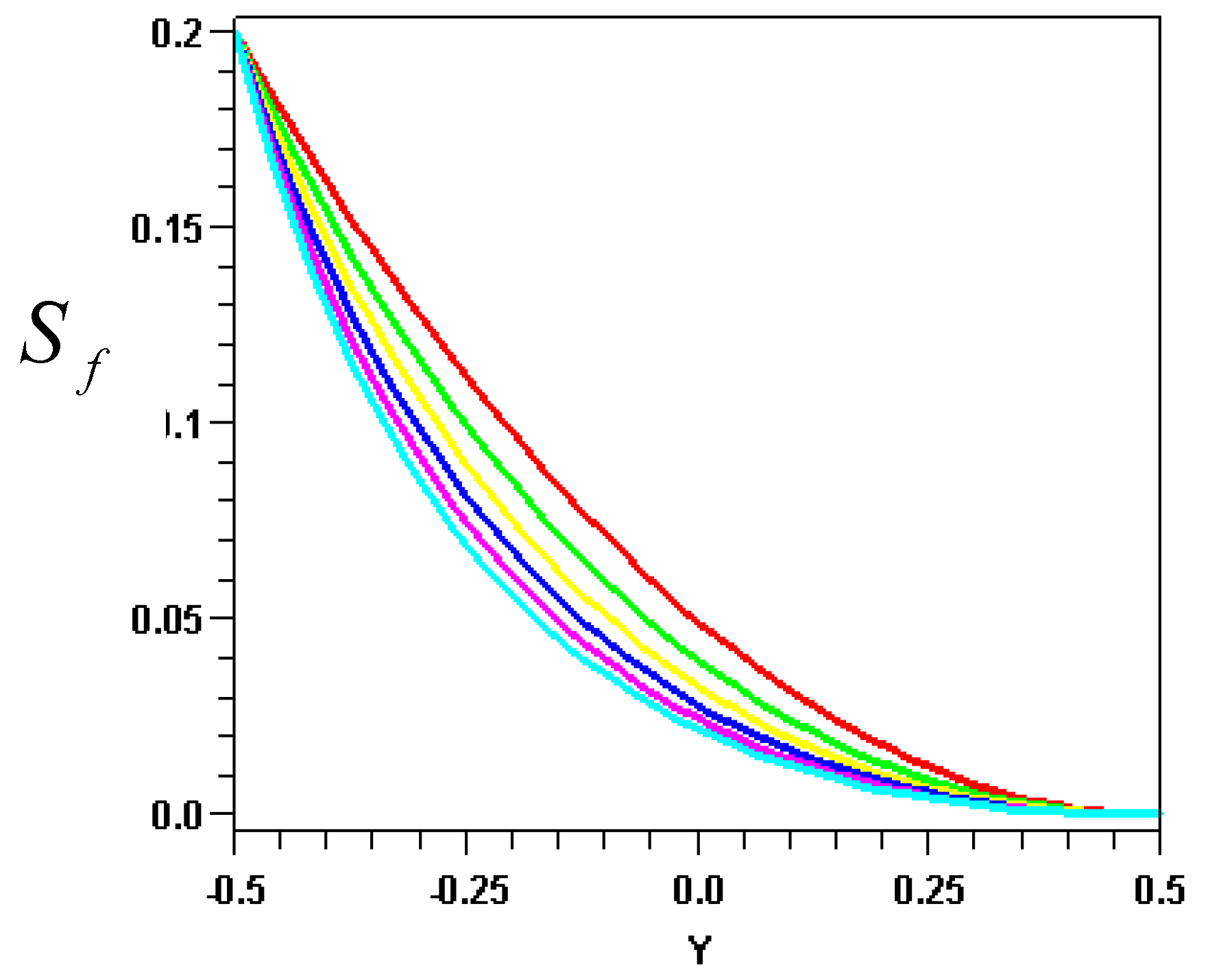
For fixed values of
θ1 = 20 and
P = 2, the effect of varying
θ2 on the entropy generation rate is depicted in
Fig.4.
Fig. 4a shows the entropy generated due to heat conduction i.e.
(denoted by
Sh ) while
Fig. 4b shows that due to fluid friction i.e
(denoted by
Sf). The temperature is varied from
θ2 = 20 (red curve) in increment of 10 to 70 (aqua curve). For
θ2 = 20, the local entropy generation due to heat conduction (
Fig 4a) is negligible. However, the entropy generation due heat conduction increases sharply as
θ2 is increased particularly at the stationary plate where the largest temperature gradients occur. The effect of
θ2 on the local entropy generation at the moving plate is rather small because the changes in
θ2 result in comparatively smaller changes in the temperature gradients at the moving plate. The local entropy generation due to fluid friction (
Fig. 4b) is maximum at the stationary plate and minimum at the moving plate. The highest entropy generation due to fluid friction occurs at the lowest value of
θ2 (red curve). This is due to the presence of
θ in the denominator of the fluid friction term in equation (19). A comparison of the results in
Fig. 4a and
Fig. 4b and the corresponding results for other pressure gradients reveals that the entropy generation due to fluid friction is much smaller than that due to heat conduction for the range of
P investigated i.e. from 0 to 50.
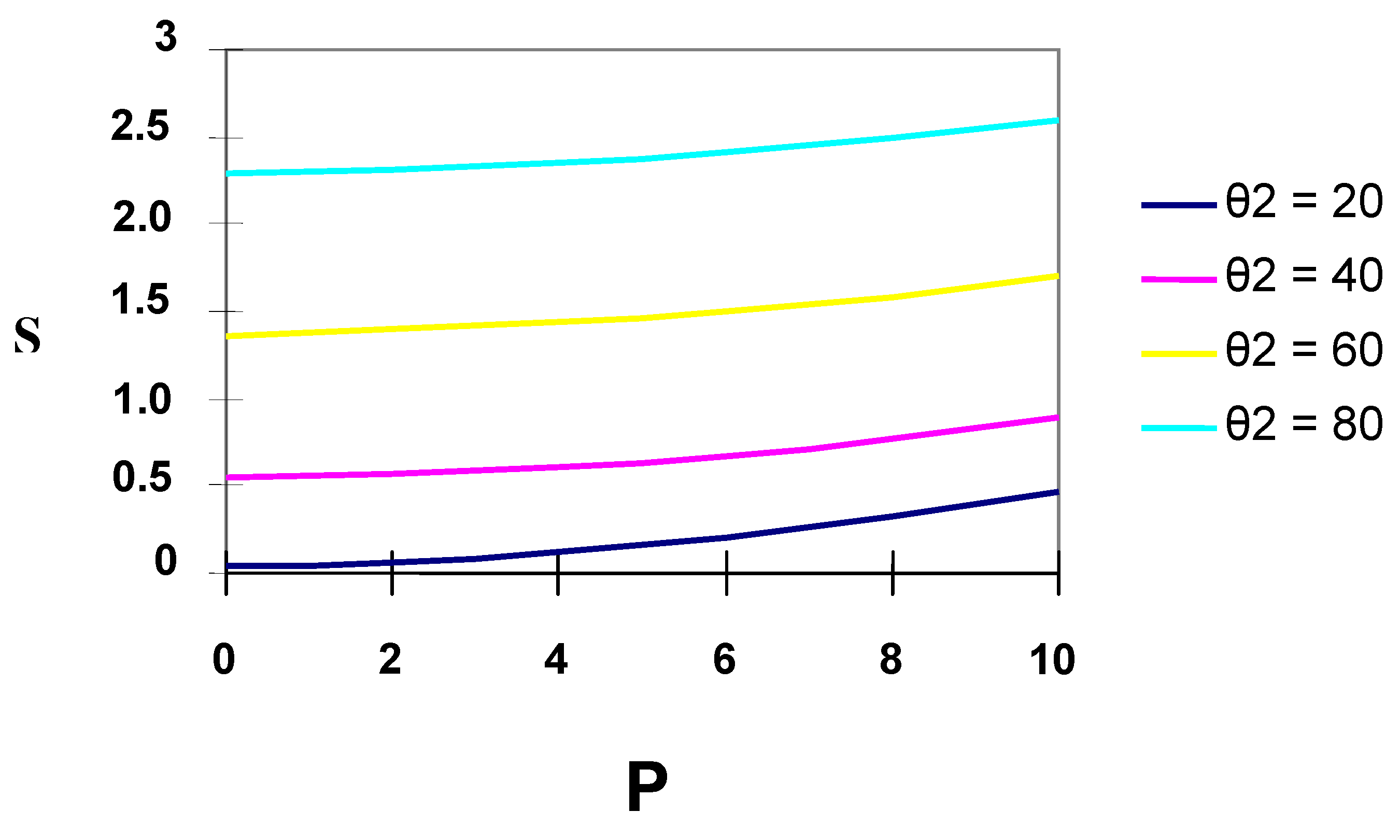
Fig.5 shows the integrated (across the gap) total entropy generation rate, denoted in the figure by
S =
Sh +
Sf for convenience, as a function of the pressure gradient
P for
θ2 = 20, 40, 60, and 80 with
θ1 fixed at a value of 20. The contribution of
Sf is much smaller than
Sh. The total entropy generation rate increases as
P increases and/or
θ2 increases. This is a consequence of the higher velocity and temperature gradients caused by the increase in
P and
θ2, respectively. From a system design perspective, the total entropy generation is minimized only when the plates are held at identical temperatures and the pressure gradient is zero, that is, when the flow is driven solely by the motion of the upper plate.
Fig.5.
Effect of pressure gradient P and θ2 on total entropy generation.
Fig.5.
Effect of pressure gradient P and θ2 on total entropy generation.
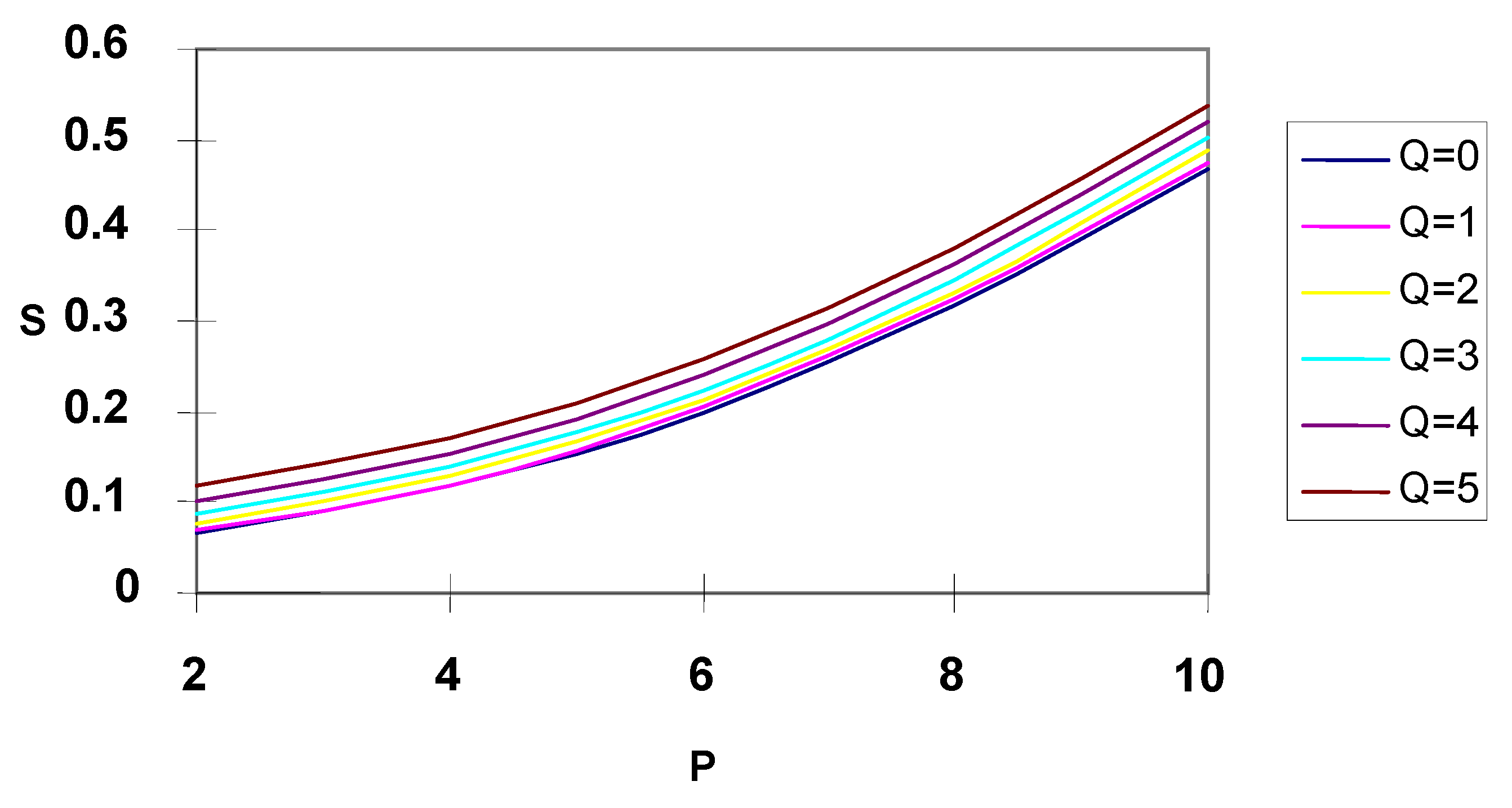
Constant Temperature at Stationary Plate and Constant Heat flux at the Moving Plate
For this case, the temperature at the stationary plate i.e.
θ1 was fixed at a value of 20. The effect of varying the pressure gradient
P and the heat flux
Q at the moving plate is illustrated in
Fig. 6. The total entropy generation rate increases significantly with increase in pressure gradient but is comparatively less affected by the changes in heat flux at the moving plate. The increase in entropy generation rate is due to the increase in velocity and temperature gradients that accompany the increase in
P and
Q. It may be noted that in this case the moving plate is colder than the stationary plate and extracts energy from the fluid. The entropy generation is minimized only when the moving plate is insulated, the pressure gradient is zero and the flow is induced solely by the motion of the plate. A comparison of
Fig.5 and
Fig.6 shows that by extracting heat at a constant rate from the moving plate, the entropy generation in the process can be significantly reduced.
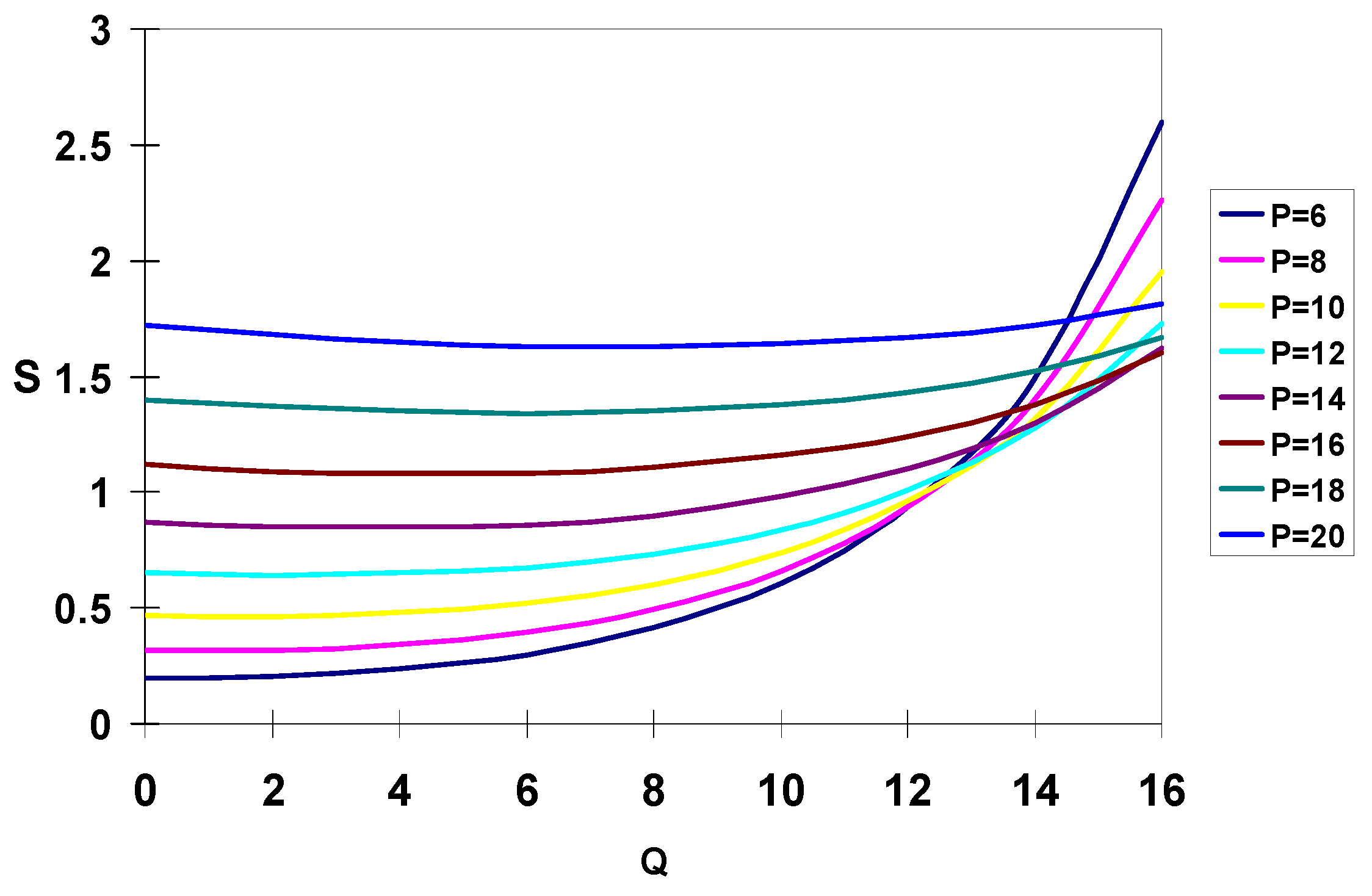
For the case where the moving plate is hotter than the stationary plate, the moving plate delivers energy to the fluid.
Fig.7 shows the results for this scenario. For low values of pressure gradient
P, the entropy generation rate increases rapidly as the heat flux increases beyond
Q ≈ 8. It is interesting to observe that at high values of the heat flux, the entropy curves for low values of
P cross over the curves for high values of
P . Thus, within the examined intervals of
P and
Q, the highest entropy generation is encountered at
P = 6 and
Q = 16. However, at higher pressure gradients, the increase in
Q affects the entropy generation rate moderately. Furthermore, at
P = 18 and 20, both curves exhibit a minimum in the neighborhood of
Q = 8 (discernible with numerical results). This result is important in flows driven by high pressure gradients in which the moving plate supplies heat to the fluid. If a system is to be designed under these operating conditions, the maximum energy input from the moving plate should be close to
Q = 8 to ensure minimum entropy generation.
Fig.6.
Effect of pressure gradient P and heat flux Q on total entropy generation when the moving plate delivers heat to the fluid.
Fig.6.
Effect of pressure gradient P and heat flux Q on total entropy generation when the moving plate delivers heat to the fluid.
Fig.7.
Effect of pressure gradient P and heat flux Q on total entropy generation rate when the moving plate extracts heat from the fluid.
Fig.7.
Effect of pressure gradient P and heat flux Q on total entropy generation rate when the moving plate extracts heat from the fluid.
Constant Temperature at the Stationary Plate and Convection at the Moving Plate
We choose
θ1 = 20 and
θa = 5 and illustrate in
Fig.8 the effect of Biot number on the total entropy generation rate for selected values of the pressure gradient. For each value of
P, the total entropy generation rate increases as Bi increases i.e. the convection at the moving plate gets stronger. The increase in heat removal from the fluid by the moving plate results in enhanced entropy generation rate. For a fixed Bi, the higher the pressure gradient and hence the larger the velocity gradients, the higher the entropy generation rate.
Fig.8.
Variation of entropy generation rate with Biot number Bi and pressure gradient P.
Fig.8.
Variation of entropy generation rate with Biot number Bi and pressure gradient P.
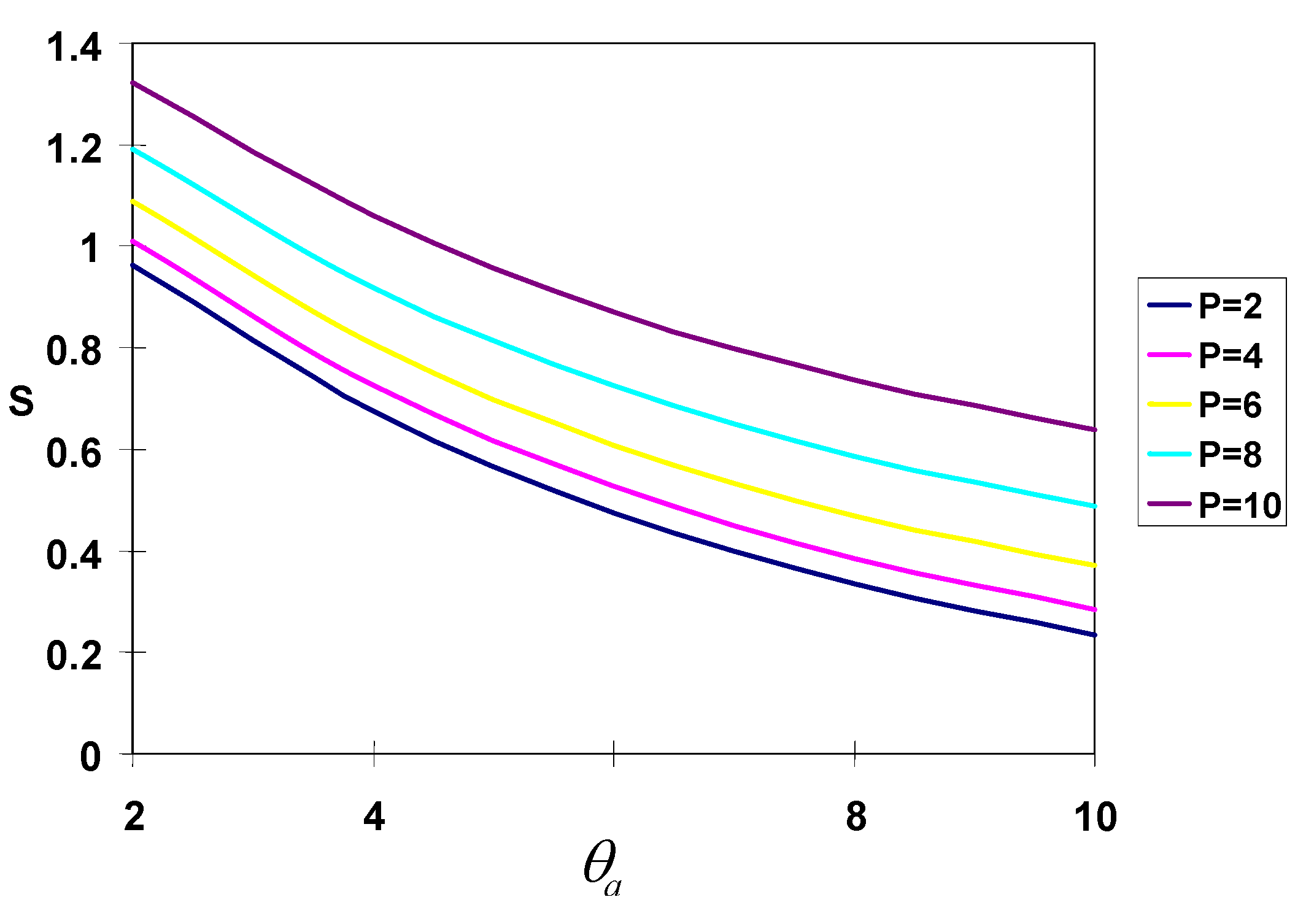
The effect of varying the convection environment temperature
θa on the entropy generation rate is depicted in
Fig. 9 for selected values of the pressure gradient
P. This figure was generated by fixing
θ1 = 20 and Bi = 2. As
θa increases, the convective heat removal from the moving plate decreases which leads to a reduction in entropy generation rate.
Fig.9.
Entropy generation rate as a function of θa and P with θ1 = 20 and Bi = 2.
Fig.9.
Entropy generation rate as a function of θa and P with θ1 = 20 and Bi = 2.
Convection at both plates
The variables in this case are
P,
θa,1,
θa,2,
Bi1 and
Bi2 . We fix the first three at
P = 2,
θa,1 = 20,
θa,2 = 10 and study the effect of varying
Bi1 and
Bi2 . In
Fig. 10, the entropy generation rate is plotted as a function of
Bi2 for parametric values of
Bi1 . At
Bi1 = 1, the entropy generation increases sharply as
Bi2 increases. However at
Bi1 = 2, 3, 4 and 5, the increase in entropy generation with
Bi2 is moderate. Also the effect of
Bi1 is significantly attenuated beyond
Bi1 = 3.
Fig.10.
Entropy generation rate as a function of Bi2 and Bi1 with P = 2, θa,1 = 20, θa,2 = 10.
Fig.10.
Entropy generation rate as a function of Bi2 and Bi1 with P = 2, θa,1 = 20, θa,2 = 10.
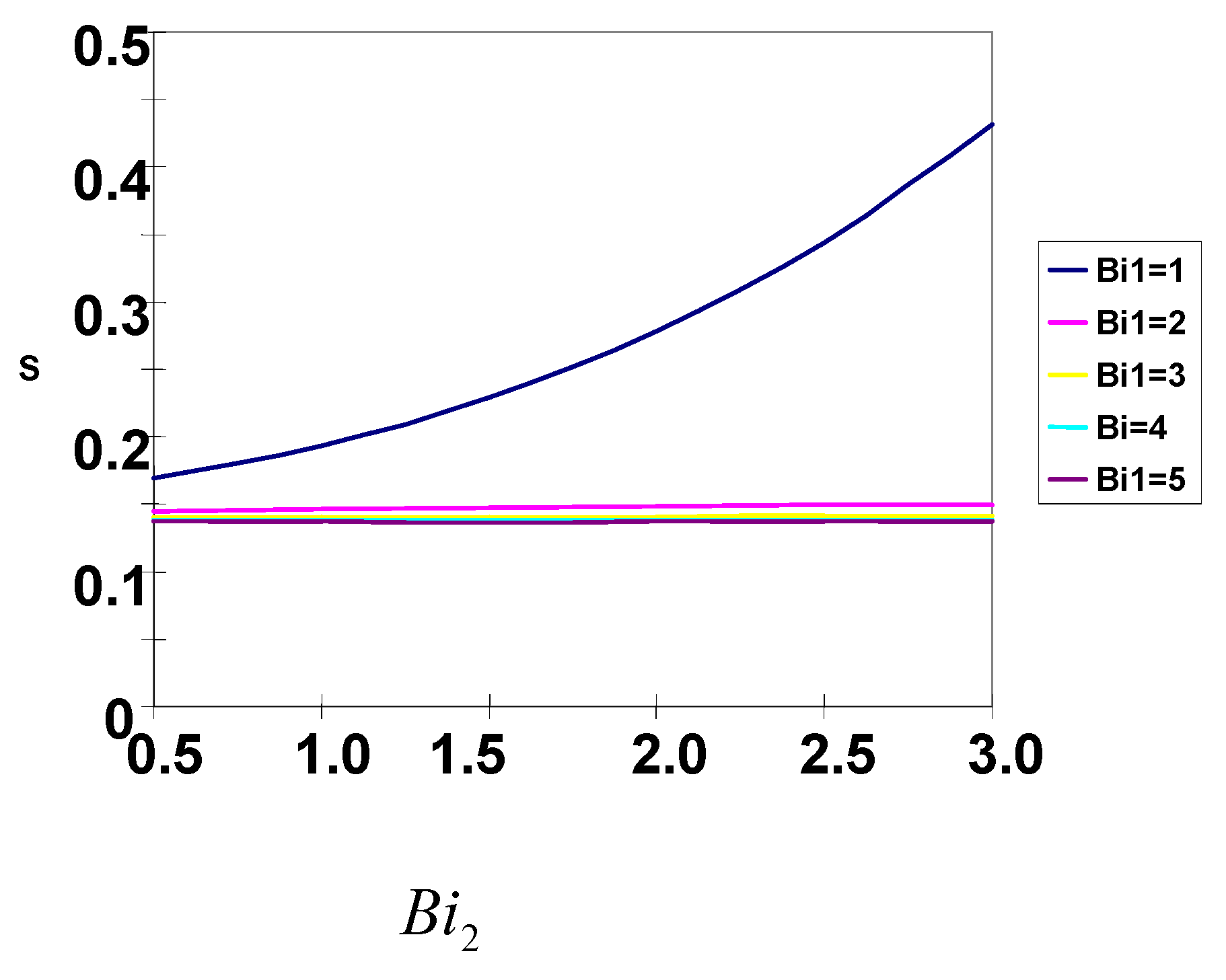
It has been pointed by Ibanez et al [
6] that for certain combinations of
Bi1 and
Bi2, the entropy generation attains a minimum. A close examination of their
Fig. 3 for G=2 (P = 2 in present work) indicates the variation in entropy generation as
Bi1 (
Bi2 in present work) increases from 0 to 6 is only about 0.2 percent for the three values of
Bi2 (
Bi1 in present work ) used namely 20, 25 and 30 with the minimum entropy generation occurring at
Bi1 (
Bi2 in present work) = 0.5. Because of the variation of 0.2 percent, the minimum could not be identified graphically without a large magnification of S axis. We use the values of
P,
θa,1,
θa,2,
Bi1 and
Bi2 on which their
Fig. 3 is based and present our results in
Fig.11. It can be observed that in the range of
Bi2 from 0.5-3.0 and
Bi1 ≥ 2, the entropy generation rate is virtually a minimum. A distinct minimum can be identified by magnifying the S axis or examining the numerical results but the exact determination of the minimum would appear to be of little practical use. The same conclusion was reached with the results for other values of
P,
θa,1, and
θa,2 .
The results of asymmetric convective cooling of the plates provide opportunity for minimum entropy design of Couette flow systems. For minimum entropy generation design, the cooling of the moving plate must provide a minimum Biot number of 2 for the operating condition of P = 2, θa,1 = 20, θa,2 = 10.The designer then has the flexibility of providing cooling at the stationary plate within Biot numbers in the range 0.5-3.
Fig.11.
Entropy generation rate as a function of Bi2 and Bi1 with P = 2, θa,1 = 10, θa,2 = 10.
Fig.11.
Entropy generation rate as a function of Bi2 and Bi1 with P = 2, θa,1 = 10, θa,2 = 10.