On Expansion of a Spherical Enclosure Bathed in Zero-Point Radiation

Abstract

In the present contribution a simple thought experiment made with an idealized spherical enclosure bathed in zero-point (ZP) electromagnetic radiation and having walls made of a material with an upper frequency cut-off has been qualitatively analysed. As a result, a possible mechanism of filling real cavities with ZP radiation based on Doppler’s effect has been suggested and corresponding entropy changes have been discussed.

Introduction

Contemporary view on the problem of black-body radiation in a cavity requires solving of a rather complex problem of interaction of a system of charged particles (fermions), e.g. electrons contained in the walls of the enclosure with the electromagnetic radiation represented by an ensemble of photons (bosons) with extremely large number of degrees of freedom. Simplification of the treatment of systems with a large number of degrees of freedom is traditionally achieved by applying thermodynamic methods. To the most powerful tools of classical thermodynamics used with appreciable success for the theoretical investigations of interaction between electromagnetic radiation and ordinary matter belong thought experiments with idealized Carnot’s engine. Quite a crucial role in these studies plays the concept of adiabatic wall (partition) which is, as a rule, realized by means of an absolutely reflecting mirror made of a “perfectly conducting material”. Application of such an abstraction to theoretical treatment of the properties of black-body radiation enclosed in a cavity enabled one to introduce the concepts of temperature and entropy of radiation into classical thermodynamics and, eventually, led to the derivation of the correct form for the dependence of the integral radiation density on temperature (Stefan-Boltzmann law). Among other results of these pioneering studies, an interesting theorem related to the subject of the present work should be mentioned [1], namely: “Expansion or compression of a cavity with adiabatic walls do not change the entropy of the radiation enclosed, regardless of its original spectral composition.” It is a typical feature of this approach that the electromagnetic radiation was considered to be a self-contained entity, which might be only slightly influenced by the shape of the cavity and which was essentially independent of the quality of its walls. The very importance of the physical nature of the walls of the cavity on the processes involved was first realized only later by Planck [2] who simulated the physical properties of the walls by a finite set of abstract “oscillators”. It was just his extensive research devoted to the black-body radiation which started the development of quantum mechanics and eventually led to the discovery of the so called zero-point (ZP) energy of his “oscillators”. It was recognized later that such a zero-point energy is an intrinsic property of any physical system and now this concept plays the central role in modern theories describing, e.g., the structure of quantum vacuum. Accordingly, there is a fluctuating electromagnetic field, existing quite independently of the source and thermal electromagnetic fields and persisting even in the absolute zero temperature limit where classically all motions cease [3, 4]. It is further assumed that this “all-pervasive” electromagnetic radiation of unknown origin is homogeneous, isotropic and that its spectrum is invariant with respect to the Lorentz transformations. It is interesting enough to notice that the latter property is decisive even for the analytical shape of the ZP electromagnetic spectrum. As was proposed by Boyer [5] on the basis of homogeneity arguments, there is only one possible form of spectral energy density ρ(ω) which is Lorentz invariant, namely:

$$\rho (\omega )=\frac{\hslash {\omega }^3}{2{\pi }^2{c}^3}.$$

(1)

A very unpleasant property of this spectral dependence is obviously its divergence with respect to the integration over the infinite frequency range. To obtain physically meaningful figures from it a rather laborious work with infinities is necessary, the aim of which is usually to evaluate finite differences between infinite ZP energy deposited in free space and infinite electromagnetic energy resulting from the redistribution of the ZP spectrum into normal modes corresponding to given boundaries. For example, an astonishingly good prediction of forces existing between two infinite perfectly conducting planes [6, 7] (so called Casimir’s effect) was obtained just by computing a finite difference of two infinite radiation forces acting on different sides of the said planes. It is a remarkable consequence of the vector character of electromagnetic field [5] that the corresponding mathematical procedure enables exact cancellation of high frequency modes without introduction of a frequency cut-off. In spite of this, we consider such reasoning in general somewhat unphysical. We are convinced that the incorporation of intrinsic material properties of the reflecting or absorbing partitions into the thought experiments with radiation, at least to a certain degree of approximation, is an inevitable part of such considerations.

Cut-off frequency

The physical reasons for the existence of the upper cut-off frequency for the interaction of the ZP electromagnetic radiation with ordinary matter can be explained as follows (cf. [4]). Setting aside the problem whether the electrodynamics can be extended to arbitrarily high frequencies or not (admitting e.g. formula (1) without limits), we consider only materials in which the response to the external electromagnetic radiation is mainly due to the electrons. It is obvious in this case that at very high frequencies ω ≥ c/b, where b represents the extent of the structure and c the velocity of light, the electrons are not able, because their speed is limited by c, to follow the electromagnetic vibrations and the field has to uncouple from them and the interaction ceases. Reasonable estimate for the upper frequency limit of such a decoupling is Compton’s frequency ω_C = mc²/ħ. Accordingly, it is assumed that all the mathematical boundaries considered are made of a material which is, up to a certain cut-off frequency ω_K ≤ ω_C , a perfect conductor (mirror) and is simultaneously fully transparent for frequencies > ω_K. The cut-off function can be introduced directly into the formula describing the ZP radiation as its intrinsic part. Every cut-off related frequency parameter ω_K must have, namely, a character of Lorentz invariant constitutive quantity, because in the opposite case, by measuring ω_K it would be possible to determine the absolute motion of a coordinate system firmly connected with the partition, which is in odds with the principle of relativity. The invariance of the ZP spectrum with respect to Lorentz’s transformation will be thus preserved also for the spectrum of the following shape,

$$\rho (\omega )=\frac{ħ{\omega }^3}{2{\pi }^2{c}^3}f\left(\omega /{\omega }_K\right),$$

(2)

where f(ω/ω_K) is a dimensionless Lorentz invariant function. Formula (2) may be interpreted in two different ways. It can be considered as a spectrum resulting from the interaction of free space ZP radiation (1) with a particular partition which is described by the cut-off function f(ω/ω_K). Alternatively, if we admit [4] that ZP radiation is a sum of incoherent radiation emitted by all charged particles in the Universe and ω_K is a universal cut-off parameter putting a limitation on such an emission of radiation by ordinary matter, formula (2), instead of (1), becomes a universal formula for the ZP radiation itself.

However, for the sake of simplicity, in the present contribution, we assume that the interaction between radiation and ordinary matter (partitions) is due only to electrons involved, so that the former interpretation of (2) must be used. Moreover, the cut-off function is reduced to the simplest possible form, i.e. cut-off at frequency ω_K.

Figure 1. Illustration of trapping of the ZP radiation by expanding spherical enclosure based on Doppler’s effect. The shell of the enclosure is made of reflecting material with the cut-off frequency ω_K.

Figure 1. Illustration of trapping of the ZP radiation by expanding spherical enclosure based on Doppler’s effect. The shell of the enclosure is made of reflecting material with the cut-off frequency ω_K.

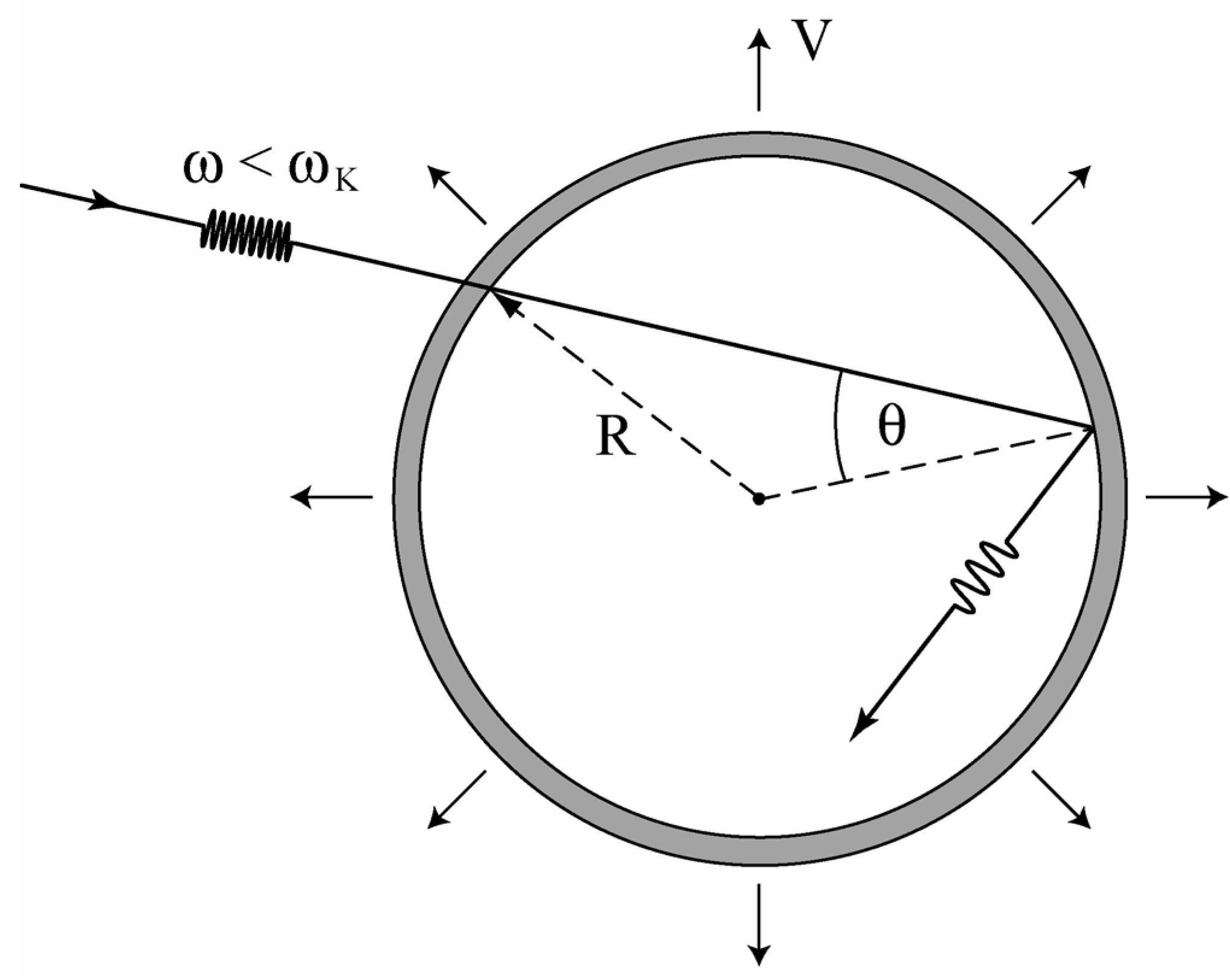
Heat engine with cut-off frequency

In the following we are trying to analyse a simple thermodynamic thought experiment performed with a heat engine containing ZP radiation, in which the reflecting walls are made of a material having an intrinsic upper cut-off frequency, more realistic than a “perfect conductor” is.

The engine itself consists of a thin spherical shell, the radius R of which can be changed without adding any work. The thought experiment is performed at T = 0 with an engine bathed in the ZP radiation. Let us now expand the cavity with a constant radial velocity V ` c. The beams belonging to a certain narrow frequency band just below ω_K, when meeting the outer side of the expanding sphere, will not reflect but they will penetrate inside the sphere because their frequencies observed from local moving coordinate system of the wall will be, due to Doppler’s effect, higher than ω_K (see Fig. 1). For similar reasons, the same beam falling on the inner side of the expanding shell will be reflected with the frequency shifted below its original value. It is obvious that all such penetrated and reflected beams will remain trapped within the cavity, moving to-and-fro with a gradually decreasing frequency.

Semi-quantitative relations

To be more specific, the frequency shift of a beam reflected from the moving mirror is given by the formula

ω₁ = K ω₀,

(3)

where ω₀  is the original frequency, ω₁ the frequency after the first reflection, K Doppler’s factor which depends on velocity V (or β = V/c) and incidence angle θ. (For the wall moving against the beam, i.e. approaching a source of radiation evidently K > 1 since for receding wall K < 1.) As the reflection belongs to Lorentz’s group of transformations, i.e. just to the group which preserves the spectral composition of the ZP radiation, relation (3) should map any band of ZP spectrum (1) onto another band of the same curve. Thus any narrow band of the ZP radiation lying just below ω_K can be transformed by a number of multiple reflections from the moving wall to the ZP radiation extended down to the gravest mode ω_G = 2.74 c/R of the cavity [8]. The process follows the formula:

ω_N = K^N ω₀,

(4)

where ω_N is the frequency of the original beam after N reflections from the inner side of the expanding spherical shell. To assess the limiting behaviour of the process just described some approximations are necessary. For example, for the quasi-stationary expansion of the shell (i.e. V → 0) the following estimate (for “inner side” K) is valid:

K ≈ (1 − 2β cosθ).

(5)

Taking into account the fact that the length of a chord corresponding to the incidence angle θ is ≈ 2R cosθ (see Fig. 1) and neglecting the relativistic change of θ, we can estimate the number of reflections from the inner side of the spherical cavity during the time corresponding to the displacement of dR as N ≈ cosθ dR/(2βR). Consequently, with increasing N, we obtain

$${\omega }_N={\omega }_0{\left(1-2\beta \cos \theta \right)}^N\to {\omega }_0\exp \left(-{\cos }^2\theta dR/R\right).$$

(6)

From this formula it is obvious that the explicit dependence of the limiting frequency on velocity disappears and that for a sufficiently large expansion dR the cavity is filled practically down to zero frequency by the ZP radiation. The process is, due to the time reversibility of beams, reversible also in the thermodynamic sense. Particularly, for an already filled large cavity (R ≺ c/ω_K, ω_G → 0) any change dR ` R is fully analogous to the classical reversible adiabatic process. Indeed, in this case because the spectral composition corresponding to the distribution of ZP fluctuations given by (1) is preserved during expansion or compression, the entropy change dS = 0 as well as dT = 0, which is fully in accordance with the definition of zero absolute temperature in classical thermodynamics [9].

ZP radiation in a small cavity

It was tacitly assumed in the previous paragraph that the density of normal modes in the cavity was sufficient to accommodate all the beams originated from the ZP spectrum. It is, of course, possible for a large cavity where Weyl’s normal mode density g₀(ω) = ω²/π²c³ [10] coincides with the mode density of the ZP radiation in free space = 2ρ(ω)/ħω. The redistribution of the ZP spectrum among normal modes in the cavity by multiple Lorentz’s invariant transformations, i.e. reflections, should lead to a spectrum which is with very high degree of accuracy identical with (1). The behaviour of small cavities (formally R ≈ c/ω_K) is, however, qualitatively different. In this case the lower cut–off frequency corresponding to the ground mode of the cavity (ω_G = 2.74 c/R) reaches values comparable with ω_K and the number of admissible normal modes within the interval (ω_G , ω_K) must be reduced appreciably. This reduction is given by the negative correction to Weyl’s free space density [11]

$$g(\omega )\approx \frac{{\omega }^2}{{\pi }^2{c}^3}-\frac{1}{2{\pi }^{2}c{R}^2},$$

(7)

hence, the density of normal modes will be reduced to zero if R√2 ≈ c/ω. Obviously, for ω ≈ ω_K this condition is practically identical with the definition of a small cavity. Hence, there will be, simply speaking, no room to settle the reflected beam within the small cavity without its appreciable disturbance. It can be qualitatively accounted for by the fact that the interference should play an essential role in this process of filling the cavity by radiation. The successive interactions of the beam with the wall of the sphere can no longer be treated as separate events and the “reflection” cannot be considered to be a Lorentz invariant transformation, either. Resulting spectrum inside the small cavity thus differs appreciably from the ZP spectrum (1) and being practically anchored to the coordinate system of the cavity as a whole it must be Lorentz non-invariant, resembling the purely thermal component of the black-body radiation. Moreover, the number of accessible modes in the small cavity within the interval (ω_G, ω_K) thus changes during its expansion or compression appreciably (i.e. dS ≠ 0) and the process is evidently non-adiabatic.

Conclusions

Summarizing, we have introduced a first-step approximation model of reflecting wall with a sharp upper cut-off frequency ω_K, which was used for the construction of an idealized heat engine in the form of reflecting spherical shell bathed in the ZP electromagnetic radiation.

Making a thought experiment with this engine a possible mechanism of filling real cavities with the ZP radiation based on Doppler’s effect was suggested. From the qualitative analysis of this thought process it becomes apparent that the walls with upper cut-off frequency are equivalent to the classical adiabatic partitions only if the cavity is large enough (ω_K ≺ ω_G). It has further been shown that the resulting spectrum in a large enclosure is practically identical with the ZP spectrum (1). On the other hand, for a small cavity where R ≈ c/ω it has been shown that the arising spectrum of normal modes must differ from the ZP spectrum substantially and that the expansion of such enclosure has to be strongly non-adiabatic process (entropy change dS ≠ 0).