Entropy Generation in Laminar Fluid Flow through a Circular Pipe
Abstract
:1. Introduction
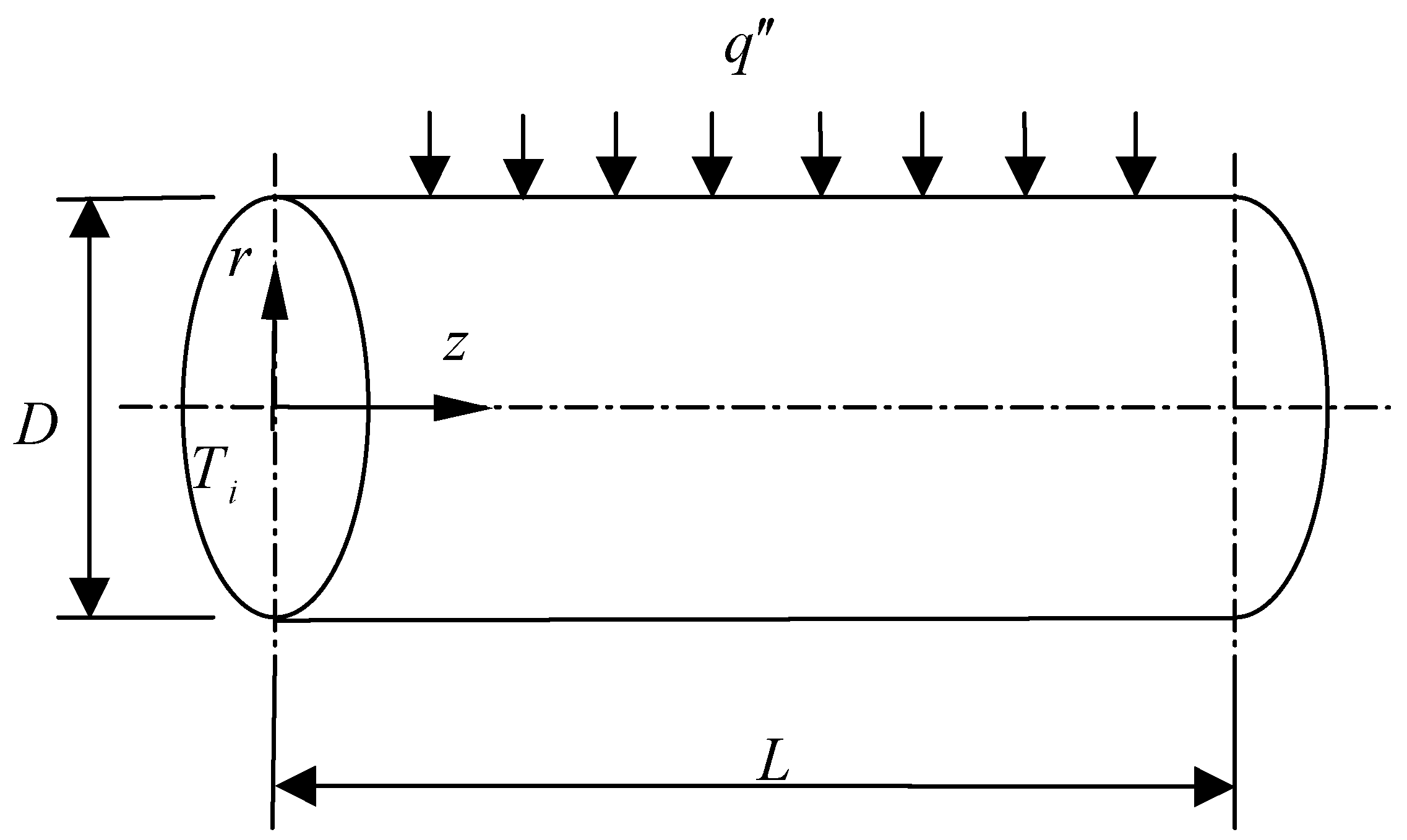
2. Analysis
- vr= 0, vz = 0 at the wall
- vr = 0, vz = vz 0 at the inlet where vz0 is a constant value.
- , at the outlet section providing a fully developed flow condition.
- A constant heat flux is imposed at the wall q” = q0 where q0 is a constant.
- T = Ti at the inlet section of the pipe where Ti is constant.
- at the outlet. This condition may not be fully valid as the thermal boundary layer is still developing, but it is necessary to limit the computational domain. This condition introduces some error in the last three nodes of the calculations which have been accounted for in the post-processing of the results.
3. Results and Discussion
4. Conclusions
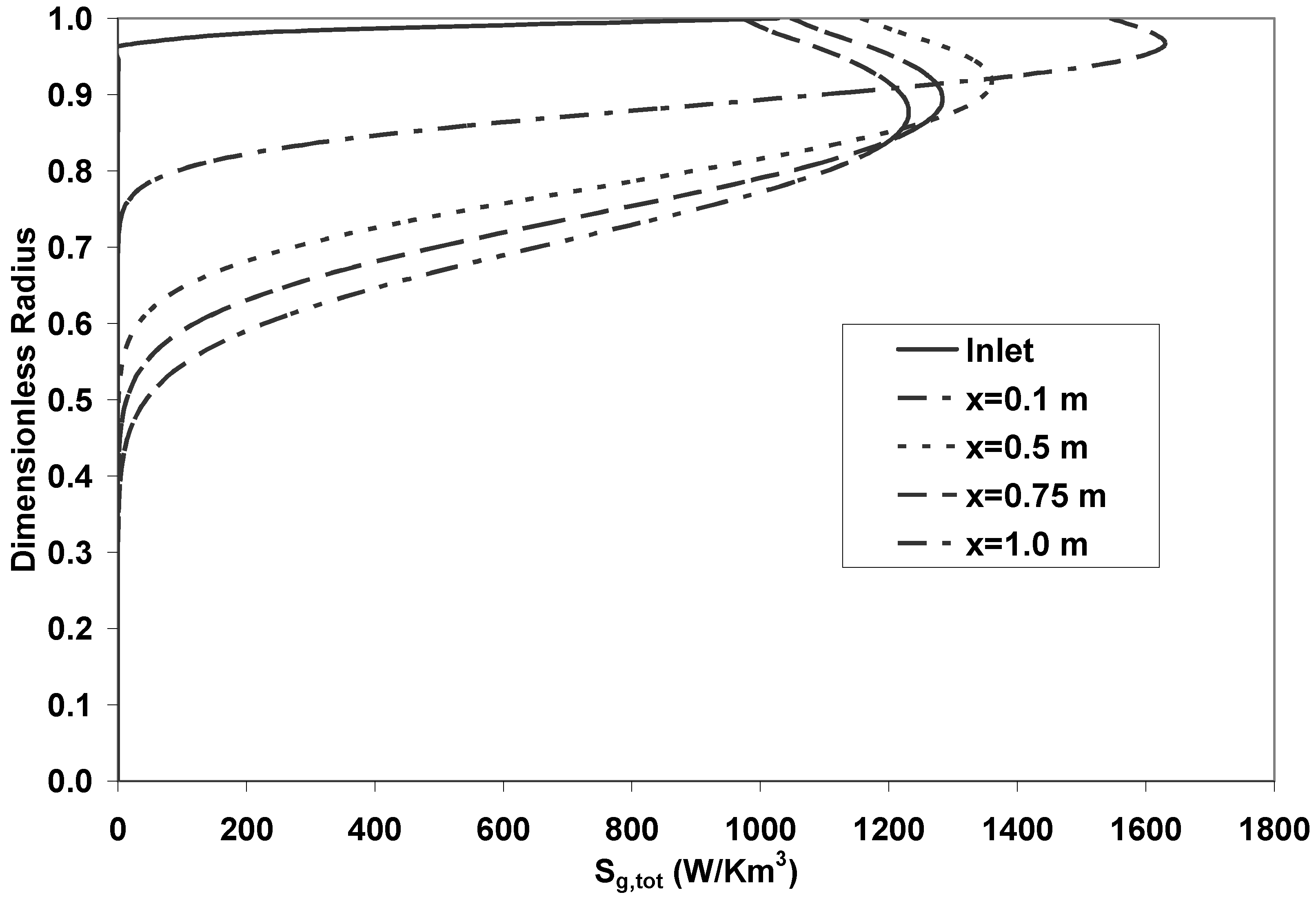
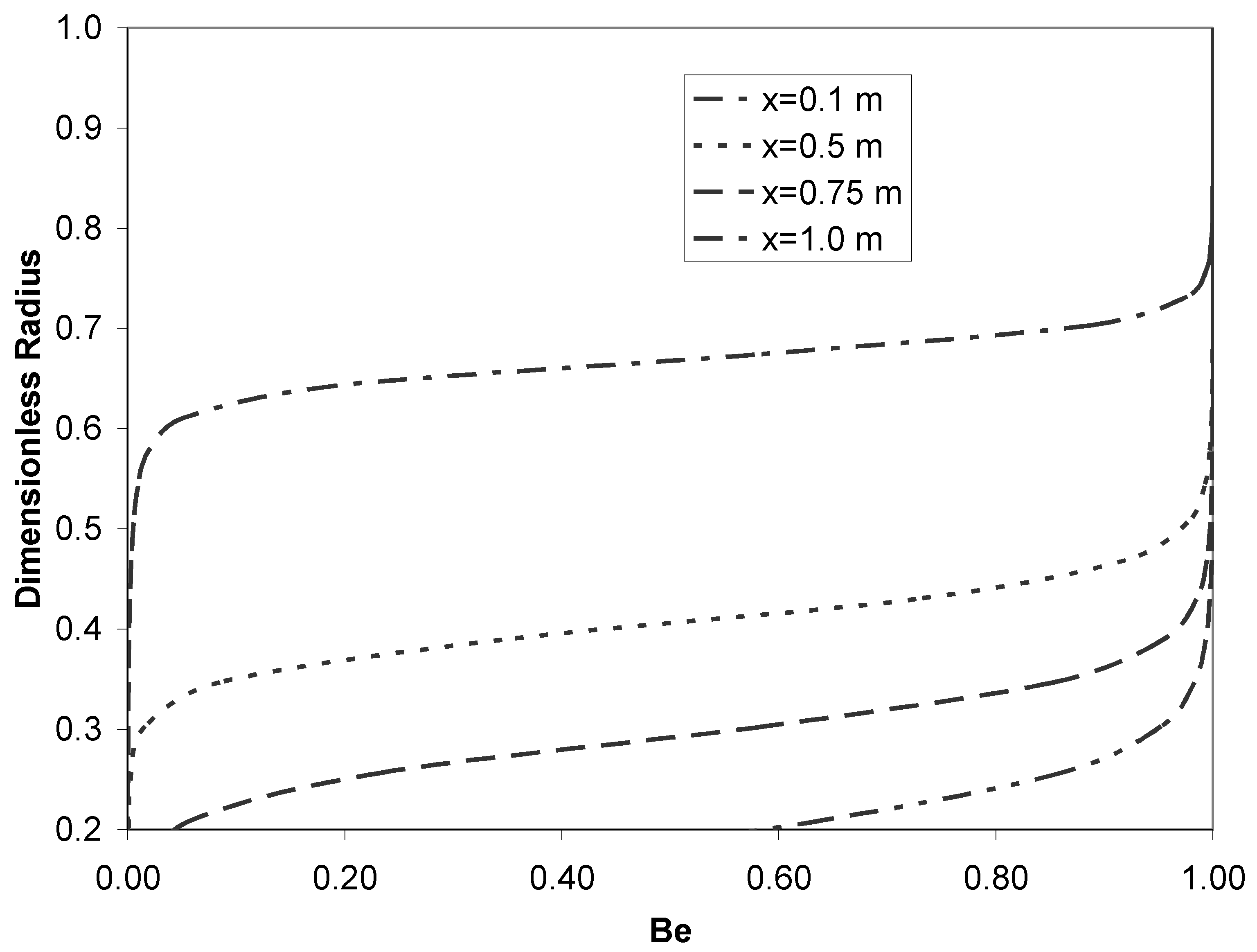
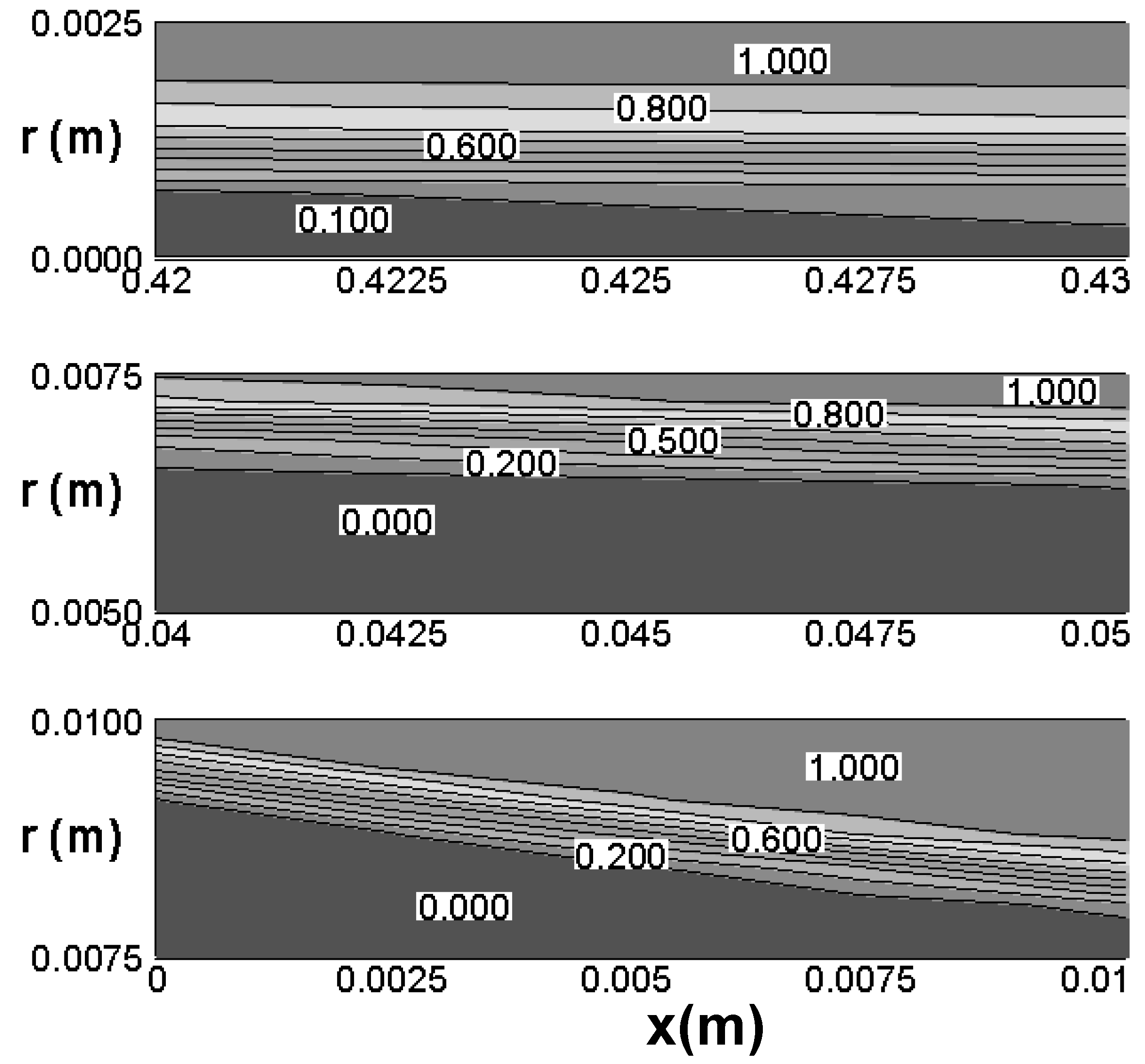
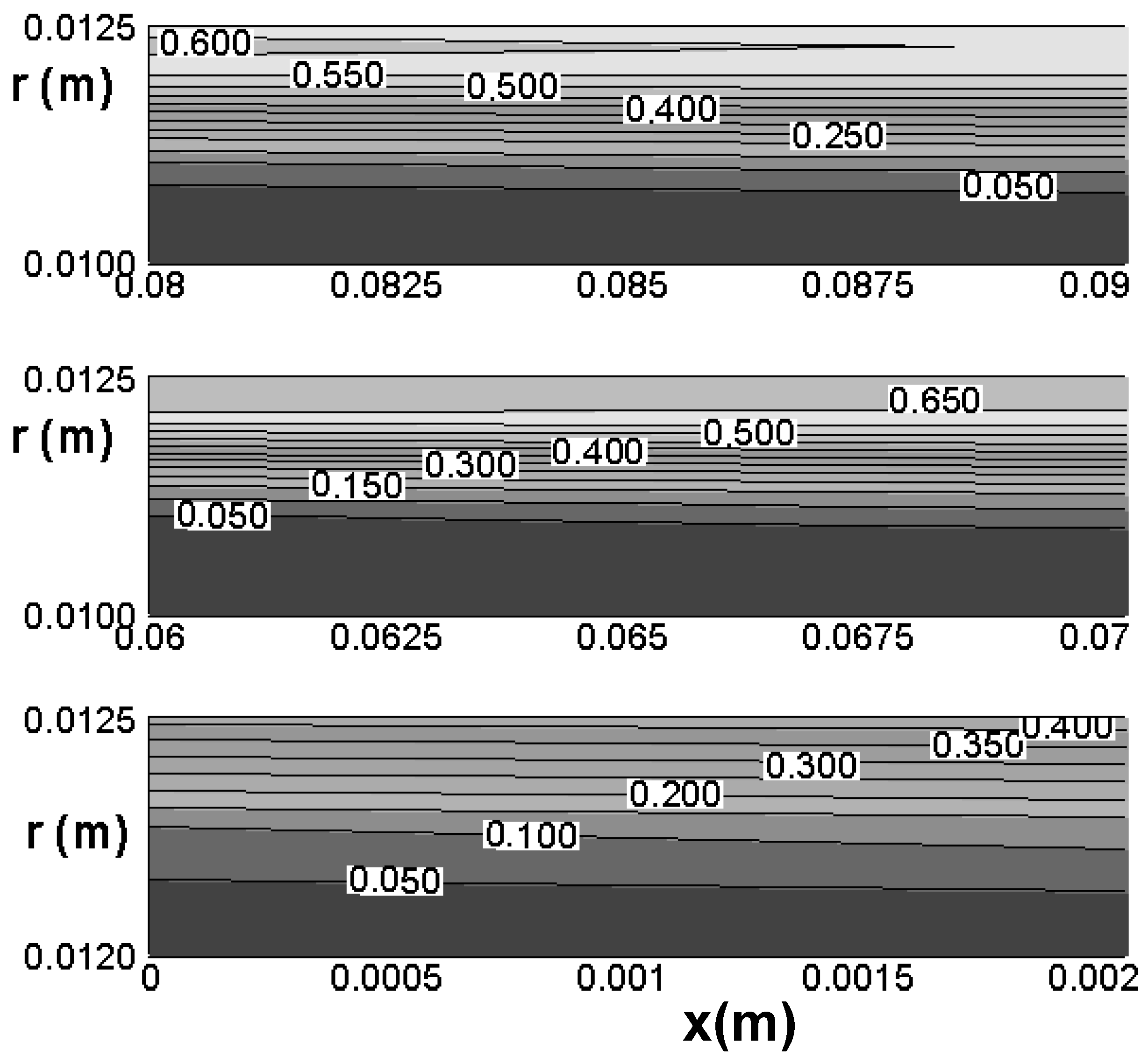
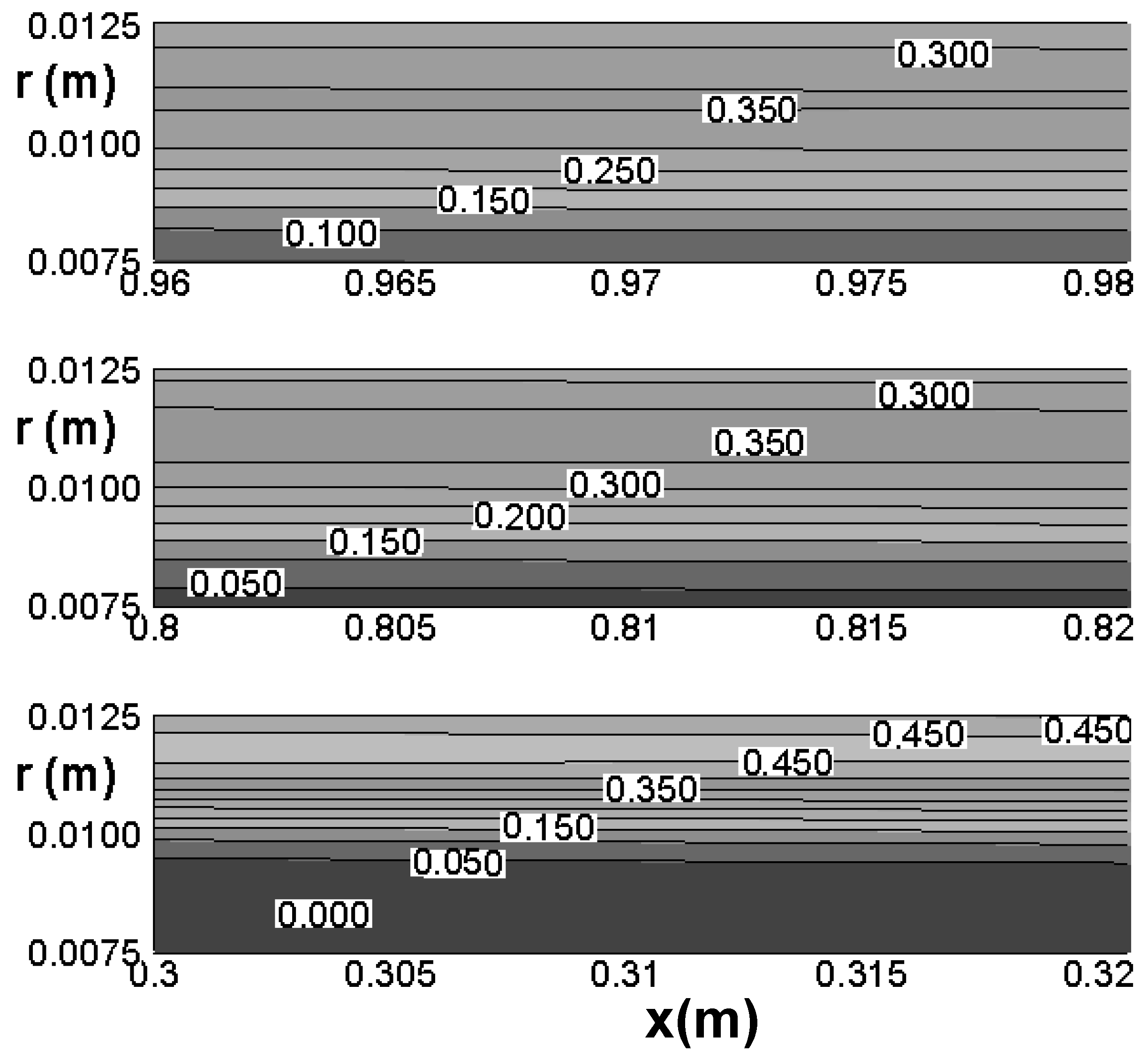
- The entropy generation rate is higher near the wall and sharply decreases along the radius away from the surface of the pipe. This is due to the existing temperature and velocity gradients in this region. Around the centerline these gradients are small and therefore the entropy generation is small. Thermal component is the major component in the entropy generation rate.
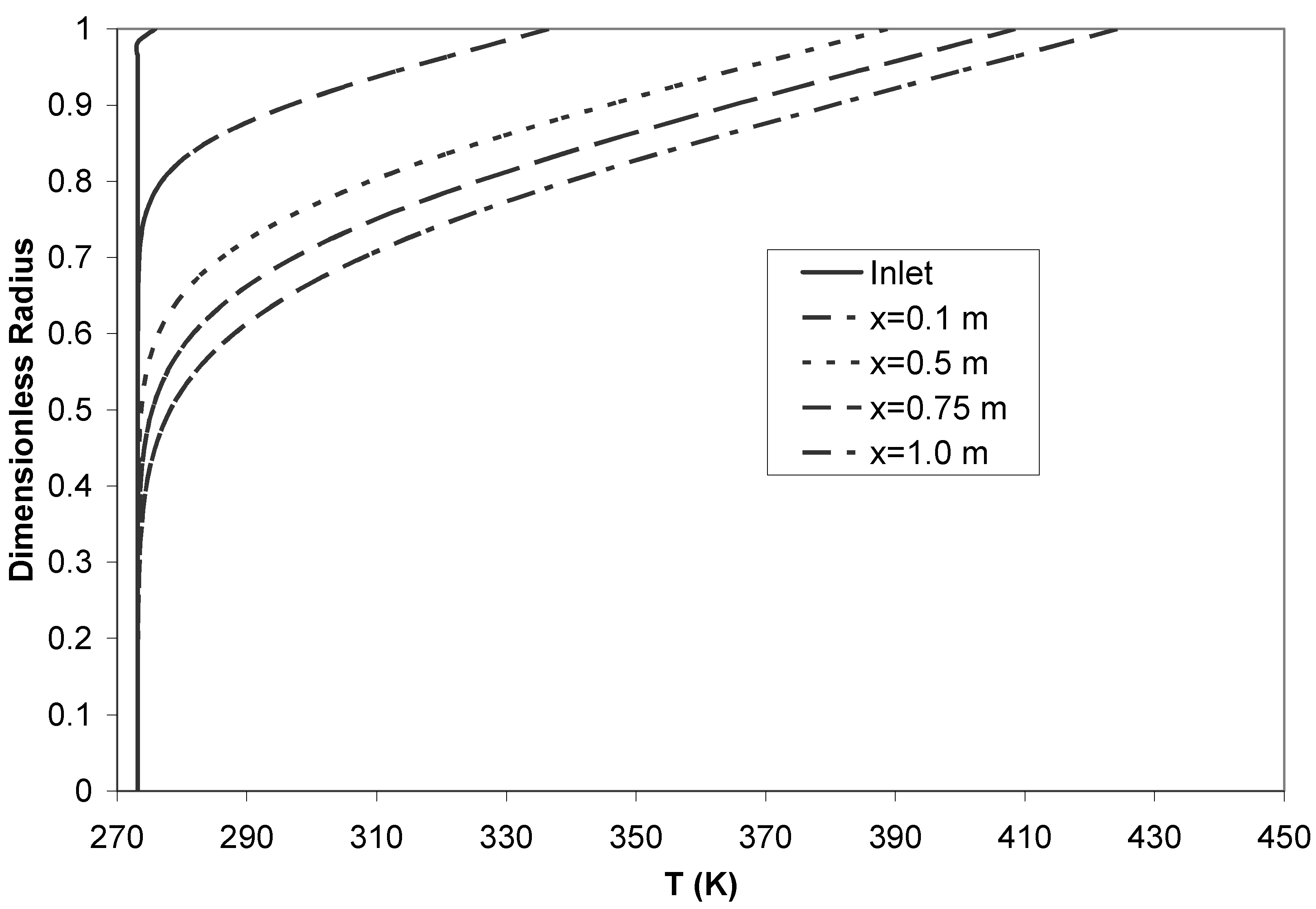
- The entropy generation along the axial direction near the wall increases sharply to a maximum and then decreases steadily. The integrated value of entropy generation rate over the cross-sectional area of the pipe along the axial direction show a steady increase that is due to the temperature penetration and the widening of the thermal as well as hydrodynamic boundary layers.
- The overall entropy generation rate calculated agrees with the result obtained by control volume thermodynamic analysis within a deviation of 20%. This deviation is attributed to the assumptions made for the thermophysical properties and boundary conditions. This indicated that consideration of variable thermophysical properties may provide more accurate results.
Acknowledgment
Nomenclature
| Cp | Specific heat (J/kg K) |
| D | Diameter (m) |
| he | Enthalpy at exit (J/kg) |
| hi | >Enthalpy at inlet (J/kg) |
| k | Thermal conductivity (W/m K) |
| L | Length of the duct (m) |
| m | Mass flow rate (kg/s) |
| P | Pressure (N/m2) |
| Pr | Prandtl number ( = µCp/k) |
| q" | Heat flux (W/m2) |
| Q | Total heat transfer rate (W) |
| r | Radial distance (m) |
| Re | Reynolds number ( = pVD / µ ) |
| s | Entropy (J/kg K) |
| se | Entropy at the exit (J/kg K) |
| si | Entropy at the inlet (J/kg K) |
Entropy generation rate (W/K) | |
| T | Temperature (K) |
| Te | Exit fluid temperature (K) |
| Ti | Inlet fluid temperature (K) |
| Tref | Reference temperature (=293 K) |
| Tw | Wall temperature of the duct (K) |
| vr | Radial velocity component (m/s) |
| vz | Axial velocity component (m/s) |
| vz0 | Inlet axial velocity (m/s) |
| V | Fluid bulk velocity (m/s) |
| z | Axial distance (m) |
| Greek Symbols | |
| µ | Viscosity (N s/m2) |
| µref | Viscosity of fluid at reference temperature (N s/m2) |
| ρ | Density (kg/m3) |
| Subscripts | |
| e | exit |
| I | inlet |
| ref | reference value |
| r | radial |
| w | wall |
| z | axial |
References
- Cengel, Y.A.; Boles, M.A. Thermodynamics an Engineering Approach, Second editionMcGraw Hill: New York, 1994. [Google Scholar]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. ASME Journal of Heat Transfer 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization. CRC Press: New York, 1996. [Google Scholar]
- Bejan, A. The concept of irreversibility in heat exchanger design: counterflow heat exchangers for gas-to-gas applications. ASME Journal of Heat Transfer 1977, 99, 374–380. [Google Scholar] [CrossRef]
- Shah, R. K. Compact Heat Exchanger Design Procedures. In Heat Exchangers, Thermal-Hydraulic Fundamentals and Design; Kakac, S., Bergles, A.E., Mayinger, F., Eds.; McGraw Hill: New York, 1981. [Google Scholar]
- Brinkman, H. C. Heat effects in capillary flow. Appl. Sci. Res. Sect. 1951, A2, 120–124. [Google Scholar] [CrossRef]
- Ou, J. W.; Cheng, K. C. Viscous dissipation effects on thermal entrance heat transfer in pipes flows with uniform wall heat flux. Appl. Sci. Res. 1973, 28, 289–301. [Google Scholar]
- Ou, J. W.; Cheng, K. C. Viscous dissipation effects on thermal entrance heat transfer in laminar and turbulent pipe flows with uniform wall temperature. Am. Soc. Mech. Eng. 1974. Pap. 74-HT-50. [Google Scholar]
- Kakac, S.; Bergles, A. E.; Mayinger, F. (Eds.) Heat Exchangers: Thermal-Hydraulic Fundamentals and Design. Hemisphere: Washington, DC, 1981.
- Fraas, A. P. Heat Exchanger Design, 2nd Ed. edWiley: New York, 1989. [Google Scholar]
- Schlunder, E. U. (Ed.) Heat Exchanger Design Handboo. Hemisphere: New York, 1983.
- San, J.-Y.; Jan, C.-L. Second-law analysis of a wet crossflow heat exchanger. Energy 2000, 25(10), 939–955. [Google Scholar] [CrossRef]
- Izquierdo, M.; de Vega, M.; Lecuona, A.; Rodriguez, P. Compressors driven by thermal solar energy: entropy generated, exergy destroyed and exergetic efficiency. Solar Energy 2002, 72(4), 363–375. [Google Scholar] [CrossRef]
- Mahmud, S.; Fraser, R.A. Inherent irreversibility of channel and pipe flows for non-Newtonian fluids. Int. Comm. Heat Mass Transfer 2002, 29, 577–587. [Google Scholar] [CrossRef]
- Nag, P.K.; Kumar, N. Second Law Optimization of Convective Heat Transfer Though a Duct with Constant Heat Flux. Int. J. of Energy Research 1989, 13, 537–543. [Google Scholar] [CrossRef]
- Sahin, A.Z. Second Law Analysis of Laminar Viscous Flow through a Duct Subjected to Constant Wall Temperature. ASME J. Heat Transfer 1998, 120, 76–83. [Google Scholar]
- Sahin, A.Z. The Effect of Variable Viscosity on the Entropy Generation and Pumping Power in a Laminar Fluid Flow through a Duct Subjected to Constant Heat Flux. Heat and Mass Transfer 1999, 35, 499–506. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena. John Wiley and Sons: New York, 1960. [Google Scholar]
- Mahmud, S.; Fraser, R.A. Irreversibility analysis of concentrically rotating annuli. Int. Comm. Heat Mass Transfer 2002, 29, 697–706. [Google Scholar] [CrossRef]
- Patankar, S. “Numerical Heat Transfer and fluid flow”. Hemisphere, MaGraw-Hill: Washington, 1980. [Google Scholar]



| Thermophysical parameter | Engine Oil | Water | Freon |
|---|---|---|---|
| Specific heat, Cp (J/ kg K) | 1845 | 4182 | 978.1 |
| Pipe diameter, D (m) | 0.025 | 0.025 | 0.025 |
| Thermal conductivity, k (W/m K) | 0.146 | 0.6 | 0.072 |
| Pipe length, L (m) | 1 | 1 | 1 |
| Wall heat flux, q” (W/m2) | 5000 | 5000 | 5000 |
| Inlet fluid temperature, Ti (K) | 273.15 | 273.16 | 273.16 |
| Reference temperature, Tref (K) | 288.16 | 293 | 300 |
| Inlet axial fluid velocity, vz0 (m/s) | 0.02 | 0.02 | 0.015 |
| Viscosity at reference temperature, µref (N s/m2) | 1.06 | 0.00103 | 0.000254 |
| Density of the fluid, p (kg/m3) | 889 | 998 | 1305.8 |
| Variable | Grid: 30x400 | Grid: 40x500 | % Diff. |
|---|---|---|---|
| Wall temperature at x=0.5m (K) | 388.7770 | 389.0570 | 0.07 |
| Centerline axial velocity at x=0.012 m (m/s) | 0.03861 | 0.03879 | 0.47 |
| Entropy generation on the cross-section at x=0.5m (W/m.K) | 1156.5500 | 1150.6300 | -0.51 |
| Total entropy generation (W/K) | 0.2537 | 0.2542 | 0.18 |
| Axial location, x(m) | Entropy Generation rate integrated over cross-sectional area, W/mK | ||
| Engine Oil | Water | Freon | |
| 0 | 0.01328 | 0.00365 | 0.02535 |
| 0.1 | 0.1833 | 0.05532 | 0.23930 |
| 0.5 | 0.2695 | 0.10130 | 0.35620 |
| 0.75 | 0.291 | 0.11527 | 0.37884 |
| 1 | 0.3055 | 0.12520 | 0.39123 |
© 2003 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Sahin, A.Z.; Ben-Mansour, R. Entropy Generation in Laminar Fluid Flow through a Circular Pipe. Entropy 2003, 5, 404-416. https://doi.org/10.3390/e5050404
Sahin AZ, Ben-Mansour R. Entropy Generation in Laminar Fluid Flow through a Circular Pipe. Entropy. 2003; 5(5):404-416. https://doi.org/10.3390/e5050404
Chicago/Turabian StyleSahin, Ahmet Z., and Rached Ben-Mansour. 2003. "Entropy Generation in Laminar Fluid Flow through a Circular Pipe" Entropy 5, no. 5: 404-416. https://doi.org/10.3390/e5050404
APA StyleSahin, A. Z., & Ben-Mansour, R. (2003). Entropy Generation in Laminar Fluid Flow through a Circular Pipe. Entropy, 5(5), 404-416. https://doi.org/10.3390/e5050404




