Introduction
Universal, entropic growth is a well established aspect of the Second Law of Thermodynamics. Despite this there are many examples of change where a system lowers its entropy. These are generally understood in terms of the accompanying, greater entropy increase of the local universe due to energy release accompanying the negative change. Common examples are the creation of more ordered structures as in the gravitational condensation of matter into stars and galaxies or the thermal freezing of water into ice. Here the tradeoff is between configurational and thermal entropies. It has been suggested [
1] that such local negative changes are a
necessary consequence of the dynamics of some system behavior.
In particular, students of life processes have long been troubled by the prevalence of the reduced entropy states of biological systems, created and maintained by the living metabolic processes: Schroedinger [
2] referred to this as production of “negentropy.” Historically this situation contributed to the assertion of a unique feature of living systems, an
elan vital, that defines life. While this has long been recognized as a retrogressive concept that lacks justification, it occasionally turns up hidden even in modern analyses [
3].
Since entropy is a measure of the randomness and uncertainty of the system or universe being considered, its relation to the information in the system description has been studied since Boltzmann related it to the density of microstates constituting that system. For distinct microstates of probability p
i the entropy is given by
where k is Boltzmann’s constant. The similarity of this to the engineering relation given by Shannon and Weaver, for the information content of a message whose elements have probability p
i,
has begged for comment. Modern analysis [
4] has closely related H to the missing information of S.
Unlike the universal growth of S, there is no analytic reason to expect a grand behavior of H, or of information in any more general sense. However, it is the intent of this paper to demonstrate that there is
empirical evidence for such a behavior, ranging from the earliest cosmic moments to the present. For this we will start with “logistics” a well-known, parameter free, description of system development. The sigmoid growth pattern exhibited by the logistic equation is widely accepted because it is, perhaps, the simplest description of a growing system, displaying an initial exponential increase, a linear middle range, and then approaching saturation at maturity. It has displayed great robustness in a wide variety of applications, ranging through the technological, cultural, physical, archeological, and biological [
5] [
6]. From its extension we extract a test for the existence of an evolutionary parameter that varies through cycles of change.
Well established historical events are shown to conform to that description and from their nature it is seen that information is the underlying parameter of the combined series. Since we will examine the entirety of evolution, the series consist of astronomical, paleontological, cultural, and technological events. The choice of particular events, out of the infinite possibilities is a daunting and questionable enterprise. However, without being expert with the criteria used we can proceed by reducing our total range to a number of subintervals. In each of these we can find and accept those events indicated by the group judgements of professionals who have established and agreed upon primary categories and criteria in their own specialty areas.
System Growth and Evolution
The logistic model of development describes an initial exponential change of some parameter, x, followed by its saturation at a limit, X. The resulting sigmoid growth curve is given by [
7]
where r
o is the initial growth rate. The time from initiation to termination of this growth can be estimated from the slope of the line through the sigmoid inflection point, extrapolated from initiation to saturation values of x. From the appendix it is ∆t = 4/r
o. The saturation at X is generally due to some natural limit of the process. For example, in the case that x represents the population number of a newly introduced species it may be food limits in the area of growth or the attraction of predators as x increases. In biological growth X may be the size ascribed to the limits of physical stress. In technology it can be taken to be an economic limit or fulfillment of the capabilities of a new approach.
In his study of logistic behaviors Derek de Solla Price [
5] pointed out that, after reaching saturation, i.e., attainment of the upper level of the “S” shaped growth curve, one frequently sees a behavior called “escalation.”
“If a slight change of definition of the thing that is being measured can be so allowed as to count a new phenomenon on equal terms with the old, [a] new logistic curve rises phoenix-like on the ashes of the old . . . “
He gives several examples, including the energy of particle accelerators, the number of universities, and the number of known elements. Successive escalations produce a staircase growth pattern of “the thing that is being measured.” The logistic equation (3) can be modified to include this phenomenology [
8 through the equation
where the higher terms are absent in earlier cycles but appear sequentially. The absolute value signs assure that the changes are positive. . Each term produces a successive sigmoid growth. As with the single logistic equation, one anticipates that the simplicity of this equation gives it a robustness that extends to cases where the individual steps are not precisely logistic.
From equation (4) it is shown in the Appendix that the ratio of two successive escalation transition times, from initiation to saturation of their cycles, is given by
R
k > 1 so that the series of escalations converges. If the R change slowly with cycle number then, from the appendix, the total time from the end of the sequence of escalations, back to the k-th transition t
k, is
On a plot of logtk(past) versus k, this is a straight line: the “Evolutionary Trajectory” of the phenomena being studied.
Escalation is an alternative view of what is referred to as “emergence” in the general systems theory of evolving systems [
9]. It refers to the appearance of a novel form, e.g., species, that derives from its predecessor. The underlying nature of the change is rarely apparent but the difference is generally easy to distinguish. We wish to apply equation 6 to the timing of escalation events of evolution on earth, in its broadest sense. For this we must determine the critical transitions of that process. It is important to recognize that such transitions are not the only important changes but, rather, represent those appearances
that are most significant for the parameter whose change is being examined i.e., which introduce new possibilities for further change. Since we have not yet established what is that parameter we will be guided, in the choice of events, by the evaluations of experts in related specialties.
Natural Evolution
As our topic is evolution of the universe it is natural to take
the origin of our escalation series, i.e., “Event 0,” to be The Big Bang. The consequent rapid expansion increased the maximum possible cosmic entropy because the growing volume of space increased the total number of possible configurations, and because early nucleosynthesis released energy and the growth of chemical entropy. For both of these mechanisms the actual entropy was less than its maximum possible value. In the first case, gravitational forces limited the attained volume, and in the second the lower density of particles and reduced temperature lowered nucleon interaction rates and, thereby, the realized chemical entropy. These entropy reductions are equivalent to the organization of stored information. As Layzer [
10] points out:
“The ultimate cause of order in the universe is the cosmic expansion.”To this event zero we can assign a date between the limits of 1.0 -2.0(10)10 BP, where we use the paleontologists notation “BP,” for years Before the Present.
Event 1 is then the formation of a substantial earthly surface on which it could exist and the initiation of life on that surface. The latter is the appearance of replicating molecules and of procaryotes, i.e., simple anuclear life forms such as algae. These events are in such close proximity, on the time scale we are using, that we take them together as a single event dated at about 3.4 - 3.6(10)9 BP. As with almost all the events we consider, there is a range of argued values for its age, due to differing criteria and sampling uncertainties. However, as we will be using the logarithm of that age this variance is greatly reduced on the scale we will employ. We recognize, of course, that the formation and reproduction of the first replicating molecule, and then cell, were major informational storage and transmission developments.
Appearance of the eucaryotic cell, some 1000 times larger than the earlier procaryotic cell, constituted a major advance and must be
Event 2. This cell contains diverse organelles, some representing a cooperation between formerly independent procaryotes. The appearance of eucaryotes brought such versatility that it engendered different tissue forms and marked the beginning of metazoan evolution, i.e., of multicellular creatures [
11]. There resulted an explosion of different life forms that filled every available niche, the Cambrian radiation, in 5-8(10)
8 BP.
With the advent of organic evolution the variety and multiplicity of changes has led to debates over the relative significances of subsequent events. The specific criteria of biologists and paleontologists cannot entirely coincide with what we will eventually see to be ours so we expect that important transitions, according to their reckoning, do not appear in ours, or vice-versa. However we can avoid these details by recognizing that they have agreed on the major divisions of the progress of each species when they give its specific phylogenetic history. While many object to elevating humans above other species we will adopt the phylogeny of Homo sapiens sapiens as having advanced the farthest and, as we will see, having controlled subsequent evolution. This phylogeny, which reflects the major stages and changes of development, can be found in almost any textbook on the subject [
12]. The divisions [
13], with their ages of first appearance, and brief discussions of some of their relevances, are given on Table I.
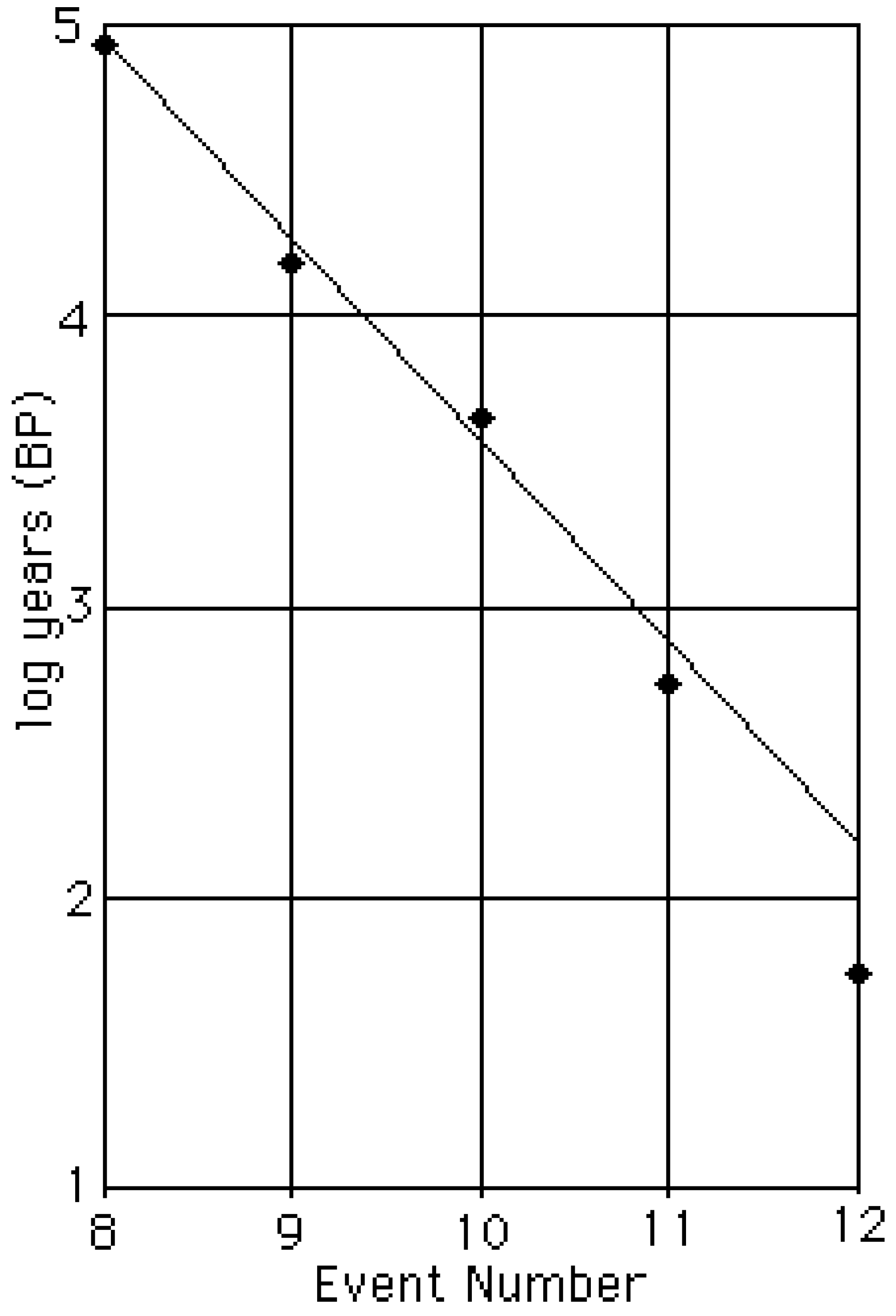
Following the lead of equation 6 we construct a semilogarithmic plot of the events 0 through 8, using the midpoints of the ranges shown for each. This is displayed on
figure 1. It is immediately seen that the points fall on an evolutionary trajectory. According to Price’s criteria this implies that each transition marks “a slight change of definition of the thing that is being measured,” which is common to the series events. That “thing” is not yet defined.
Figure 1.
Evolutionary trajectory of pre-eucaryotic and organic events.
Figure 1.
Evolutionary trajectory of pre-eucaryotic and organic events.
Post-Organic Evolution
In the common interpretation, evolution on earth is assumed to have ended with the appearance of H.s, sapiens. However scholars have long acknowledged that, while organic evolution may have ceased, or nearly so, a form of evolutionary change still continued, now with the guidance of that remarkable creature. We therefore turn to those events that are their common choice for the major accomplishments of humanity's cultural and intellectual growth. We are led to the inventions on table II.
After a long history of anatomical and physiological evolution this marks the appearance of the neocortex, the brain’s outside layer of gray matter, where memories are stored and reasoning takes place. Also, compared to earlier forms, mammals exhibit a unique interplay of parental gene selection during natal development. and a reordering of genetic information storage.
The living Hominoid apes are gibbons, orangutans, chimpanzees, and gorillas. These are in parallel families to the line of descent of humanity and its immediate ancestors.
Creatures that resemble man.
The first appearance of this Genus signifies a change of evolutionary emphasis from physical and anatomical change to the attainment of greater brain size.
Transitional Homo Sapiens have many of the attributes of modern H. Sapiens but are not fully evolved, e.g., in H. s. Neanderthalensis the ability of speech is not as well developed and the level of “industry” is lower.
This marks the arrival of modern mankind, with full ability to speak and with the associated mental powers [
14]. Subsequent evolutionary changes on earth are of its doing.
TABLE II: EVENTS OF POST-BIOLOGICAL EVOLUTION
This change involved communal villages, animal domestication, farming, control of surface water, and purposeful, cooperative behavior in the production of higher forms of organization; a unification of many minds and abilities. By this step mankind took charge of its own evolution, altering its survival and propagation modes [
15].
Event number 10: Writing
Date (BP): 3 - 5 (10)3
Rapid and sophisticated communication, begun with speech at event 8, is greatly enhanced, and moved to a higher level of accomplishment by this invention. Development included cuneiform, hieroglyphics and alphabet notation. Accompanying these were systems of weights and measures, and numerical and mathematical understanding for land and economic management. This has been called “the greatest intellectual achievement of mankind.” [
16]
This date is that of Gutenberg’s main production. Mechanical means for rapidly and inexpensively duplicating the written word, allowed broad dissemination of ideas and information. It has been pointed out that printing was as revolutionary in the fifteenth century as the computer in the twentieth. As late as the 1940’s it was said that "In the cultural history of mankind there is no event even approaching in importance the invention of printing with movable types.” [
17]
Historians acknowledge [
18] that modern electronics and the computer constitute a revolution in the conduct of our civilization, leading to world wide, instantaneous communication and vast computation power. The date is that of the close proximity of discovery of the transistor and development of the Eniac computer.
Figure 2.
Trajectory of post-organic events.
Figure 2.
Trajectory of post-organic events.
Following our previous procedure,
figure 2 shows a semilog graph of the events of Table II. For continuity we include event 8, from Table I and the line on this figure is the extension of that on
Figure 1. Events 9 and 10 fall on this line, indicating a continuity of the accomplishments of mankind with the earlier evolutionary events. A least- squares regression analysis on events 0 through 10, results in
where t is the time (BP) of event number k. From equation (6) this yields R=4.62
Events 11 and 12 fall below the trajectory line in a systematic way. The dates shown for these points on Table 2 are arbitrarily measured from the year 2000 and this raises the question of reference. When denoting times as "years Before the Present (BP)," exactly when, in this geological context, do we mean by the "Present"? An incorrect choice by, say, several hundred years makes no difference in points 0 through 10 because they are orders of magnitude greater and have large ranges of uncertainty. However, the matter is important for points 11 and 12 because they are recent and better defined. A backward shift of 135 years results in the optimum placement of these events to the straight line through the other points. This adjustment means that our reference for the "Present" should be that much in the future, i.e., approximately the year 2135 of our calendar. With it we arrive at the full Evolutionary Trajectory, shown as
figure 3. To fit on one figure the chart has been presented in two sections.
Figure 3.
Trajectory of Information on Earth.
Figure 3.
Trajectory of Information on Earth.
Discussion
The trajectory of information evolution on earth extends over 13 transitional events, spanning 8 orders of magnitude of time. Even for a logarithmic relation that is an impressive range. The wide success of the logistic model in many fields results from its descriptive simplicity, that seems to cut through complex details that accompany most system changes. The trajectory itself is based on the simple logarithmic relation that is also doubtlessly more robust than the derivation given here. It seems to depend primarily on the product of terms describing the stages.
As with any new theory, having the basic relation has lead to some culling of all the available data for the set that it satisfies. The points found then reveal the underlying features of the phenomenon itself, in this case leading to inference of the role of information. In this regard we note that there is no dearth of authors who have selected major events of evolution [
22]. These are generally based on the perspectives of their particular fields of specialty and, lacking a quantitative basis for choice, are unable to distinguish major from minor events. In our case the quantitative theory itself directed event selection, and the parameter they indicate is a result of their nature, not an
a priori bias. It is worth noting, however, that all other such selections have events that coincide with some of those found here.
In scientific analyses of physical behavior and properties, we are accustomed to having time as the independent variable and understand extrapolated behavior as time advances. There is an awkwardness to the results here because the extrapolation results in the specific expectation of broad, illdefined, societal-informational changes. In most cases such predictions are the result of questionable forecasting and are regarded with disdain because their bases are weak. However in this case it is impressive to realize that, in addition to its long duration and large number of points, the trajectory proceeds without deviation, at least on the scale with which we observe it, through events that should be expected to alter its timing. For example, it is estimated that the earth has experienced five impact induced mass extinctions in the last 600 million years [
20]. Neither these nor wars and epidemics have altered the timely progression of transition events, a fact that further leads one to suspect the informational development shown has a fundamental basis and broad significance.
An inherent difficulty of these findings lies in the fact that there is presently no generally useful definition of or distinction between the “information” aspect in each stage. In part this is due to there being “a slight change” between stages. In this regard it should be noted that some in the community of general systems theorists and cyberneticians have adopted “complexity” as their working parameter for the changes through evolution. If anything this is even more vaguely defined except, perhaps, where it can be associated with information [
21]