Fundamental Solutions to Fractional Heat Conduction in Two Joint Half-Lines Under Conditions of Nonperfect Thermal Contact
Abstract
1. Introduction
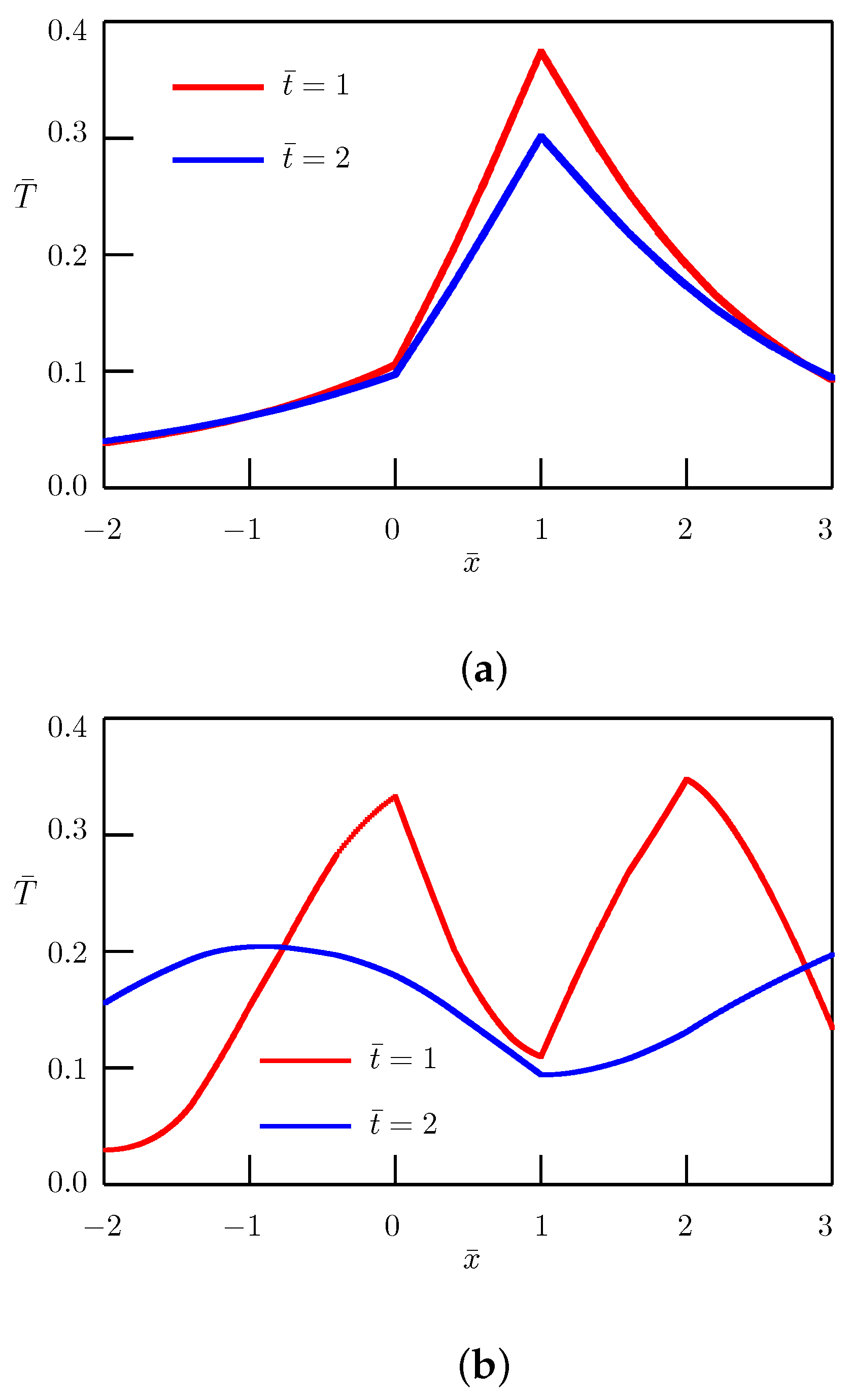
2. Fundamental Solution to the Cauchy Problem
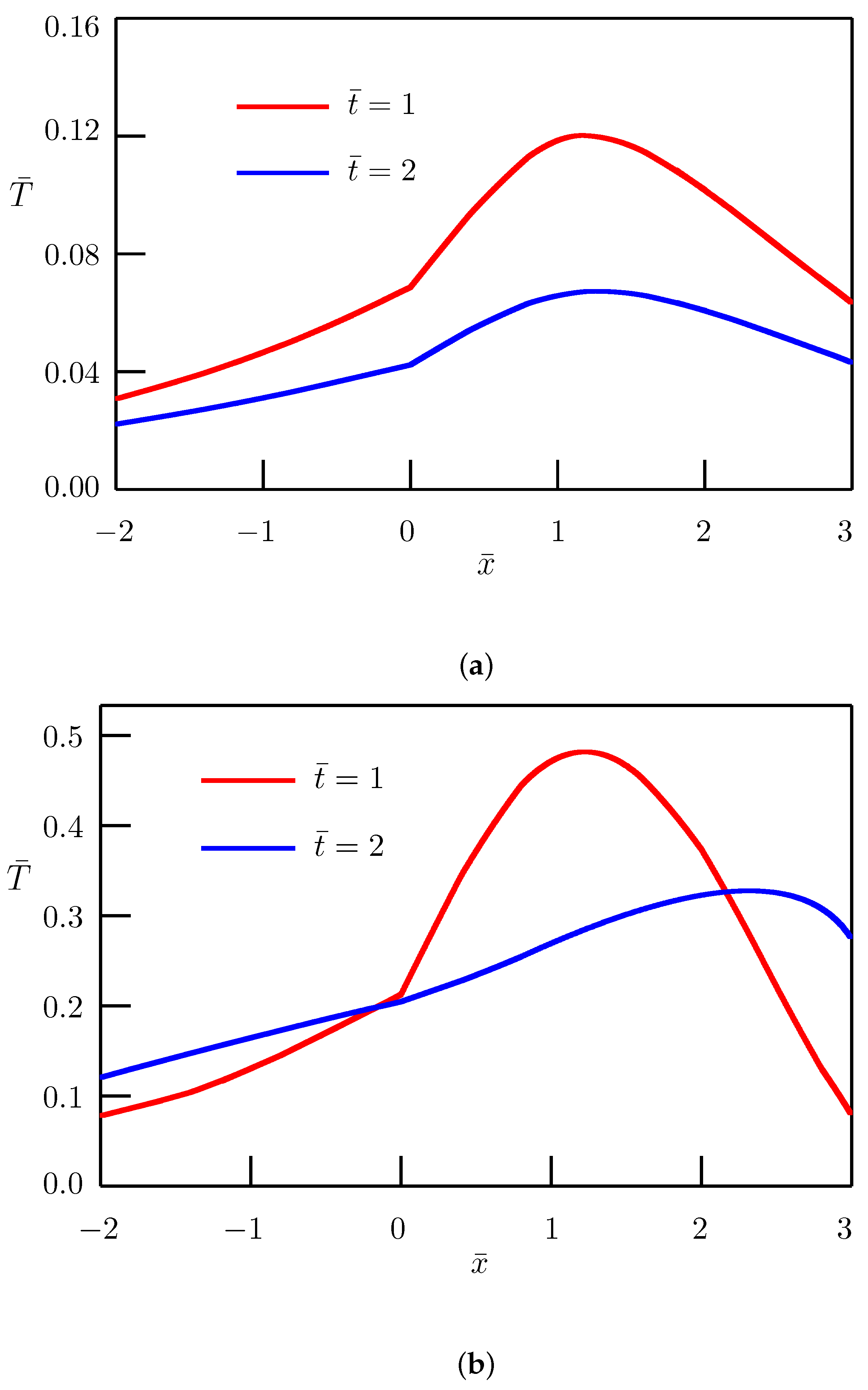
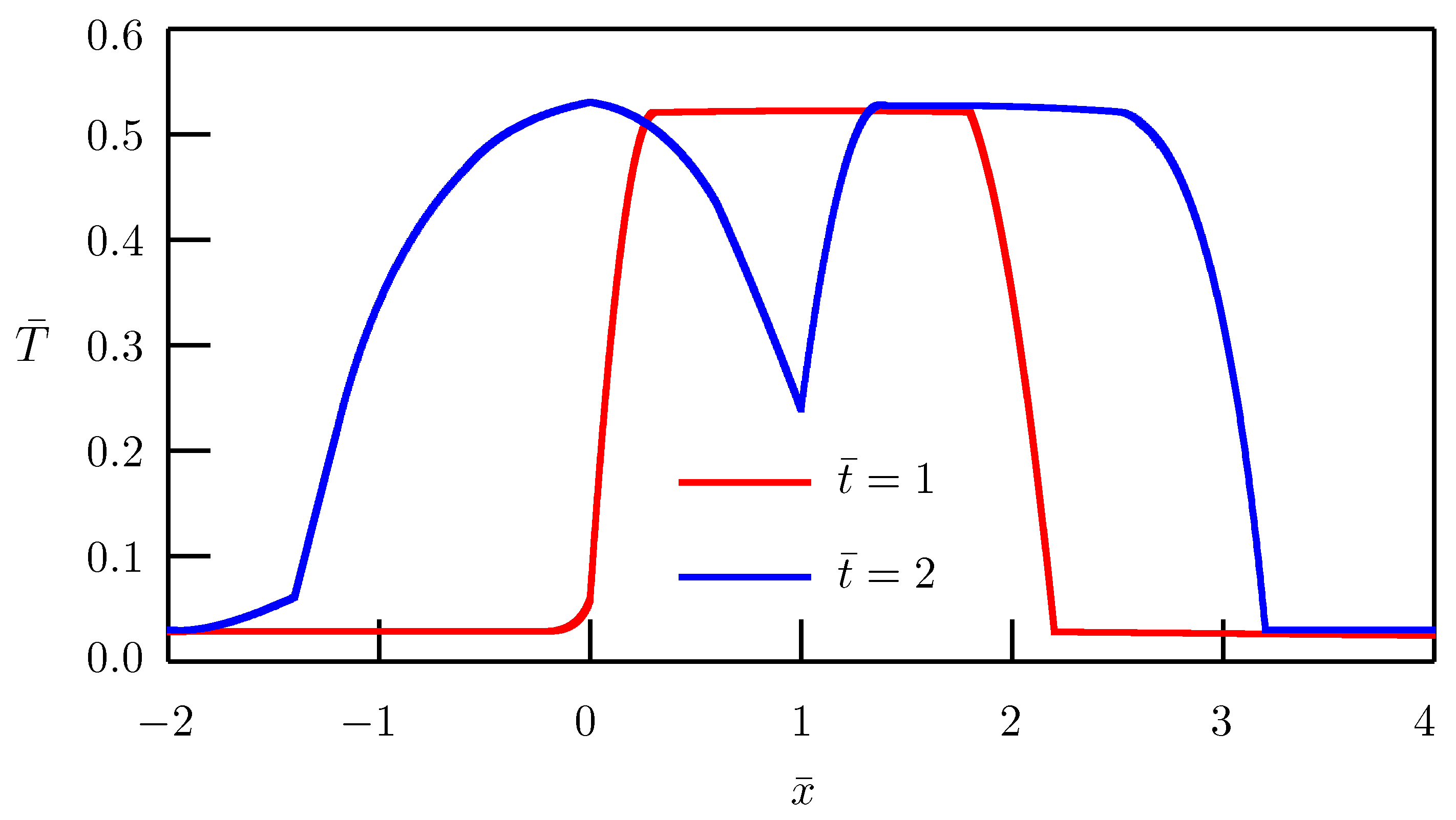
3. Fundamental Solution to the Source Problem
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Fractional Integrals and Derivatives
References
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Vibrations and Diffusion Processes; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Tarasov, V.E. Heat transfer in fractal materials. Int. J. Heat Mass Transf. 2016, 93, 427–430. [Google Scholar] [CrossRef]
- Pagnini, G. Fractional kinetics in random/complex media. In Handbook of Fractional Calculus with Applications, Volume 5: Applications in Physics, Part B; De Gruyter: Berlin, Germany, 2019; pp. 183–205. [Google Scholar]
- Zhmakin, A.I. Heat conduction beyond the Fourier law. Techn. Phys. 2021, 66, 1–22. [Google Scholar] [CrossRef]
- Zhmakin, A.I. Non-Fourier Heat Conduction: From Phase-Lag Models to Relativistic and Quantum Transport; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Zhou, Y. Fractional Diffusion and Wave Equations: Well-Posedness and Inverse Problems; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Kharrat, M.; Touafek, N.; Krichen, M. (Eds.) Modeling of Discrete and Continuous Systems: Ordinary, Partial and Fractional Derivatives; Springer: Singapore, 2025. [Google Scholar]
- Povstenko, Y.; Kyrylych, T. Fractional heat conduction in solids connected by thin intermediate layer: Nonperfect thermal contact. Continuum Mech. Thermodyn. 2019, 31, 1719–1731. [Google Scholar] [CrossRef]
- Podstrigach, Y.S. Temperature field in a system of solids conjugated by a thin intermediate layer. Inzh. Fiz. Zhurn. 1963, 6, 129–136. (In Russian) [Google Scholar]
- Povstenko, Y. Fractional heat conduction in infinite one-dimensional composite medium. J. Therm. Stress. 2013, 36, 351–363. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series, Volume 1: Elementary Functions; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Mainardi, F. The fundamental solutions for the fractional diffusion-wave equation. Appl. Math. Lett. 1996, 9, 23–28. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 1996, 7, 1461–1477. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Gorenflo, R.; Loutchko, J.; Luchko, Y. Computation of the Mittag-Leffler function Eα,β(z) and its derivatives. Fract. Calc. Appl. Anal. 2002, 5, 491–518, Erratum in Fract. Calc. Appl. Anal. 2003, 6, 111–112. [Google Scholar]
- Luchko, Y. Algorithms for evaluation of the Wright function for the real arguments’ values. Fract. Calc. Appl. Anal. 2008, 11, 57–75. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Povstenko, Y.; Kyrylych, T.; Dashkiiev, V.; Yatsko, A. Fundamental Solutions to Fractional Heat Conduction in Two Joint Half-Lines Under Conditions of Nonperfect Thermal Contact. Entropy 2025, 27, 965. https://doi.org/10.3390/e27090965
Povstenko Y, Kyrylych T, Dashkiiev V, Yatsko A. Fundamental Solutions to Fractional Heat Conduction in Two Joint Half-Lines Under Conditions of Nonperfect Thermal Contact. Entropy. 2025; 27(9):965. https://doi.org/10.3390/e27090965
Chicago/Turabian StylePovstenko, Yuriy, Tamara Kyrylych, Viktor Dashkiiev, and Andrzej Yatsko. 2025. "Fundamental Solutions to Fractional Heat Conduction in Two Joint Half-Lines Under Conditions of Nonperfect Thermal Contact" Entropy 27, no. 9: 965. https://doi.org/10.3390/e27090965
APA StylePovstenko, Y., Kyrylych, T., Dashkiiev, V., & Yatsko, A. (2025). Fundamental Solutions to Fractional Heat Conduction in Two Joint Half-Lines Under Conditions of Nonperfect Thermal Contact. Entropy, 27(9), 965. https://doi.org/10.3390/e27090965





