Detection of Significant Seismic Quiescence Patterns in the Mexican Subduction Zone Using Extended Schreider Algorithms
Abstract
1. Introduction
2. Methods
2.1. Schreider Algorithm
2.2. Analysis of Spatio-Temporal Series Using the Schreider Algorithm
2.3. Analysis of Pseudo-Velocity Series Using the Schreider Algorithm
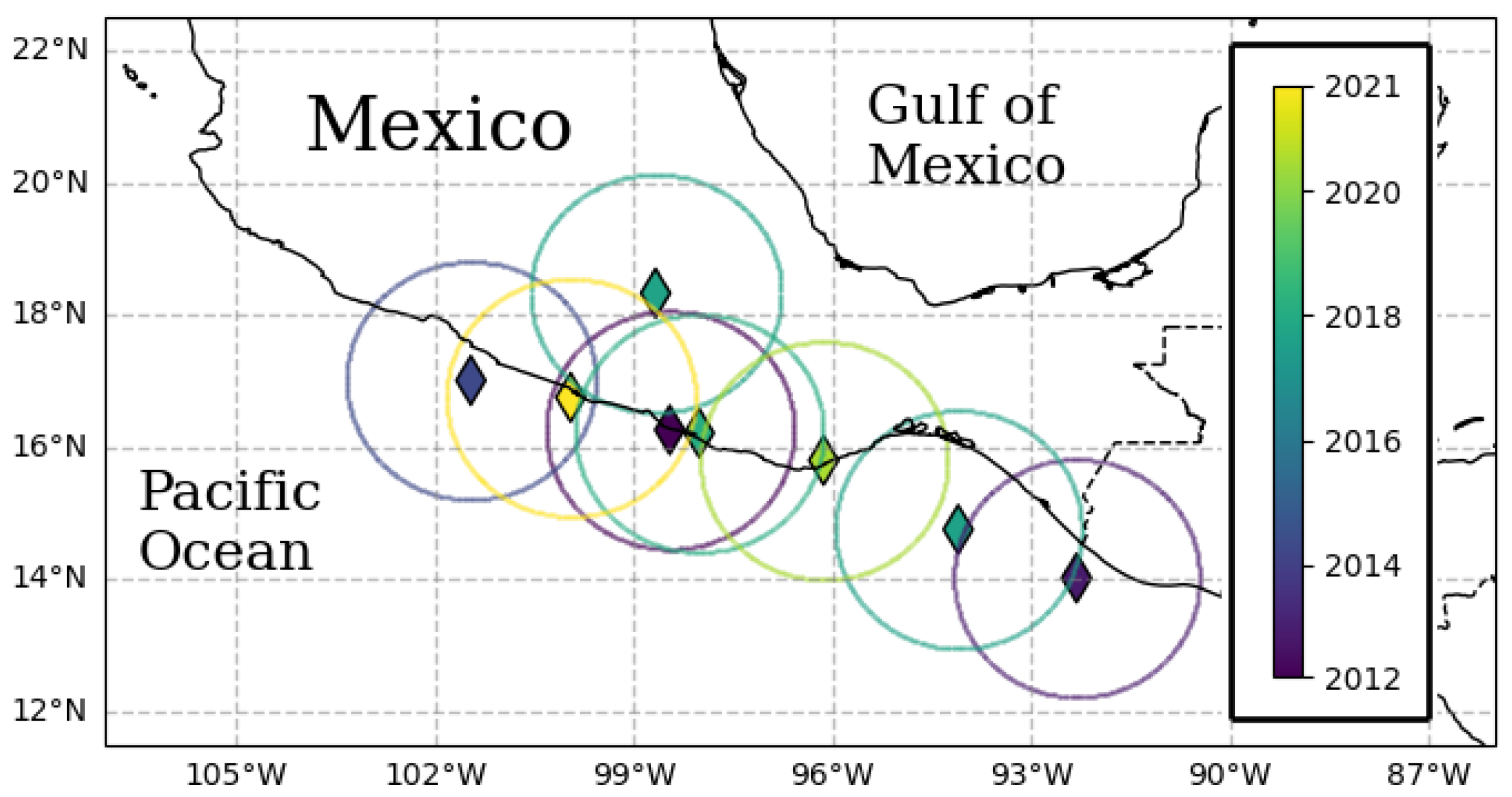
3. Data: Southern Mexican Pacific Seismic Zone
4. Seismic Quiescence of Mexico Mainshocks, Unmixed Patterns
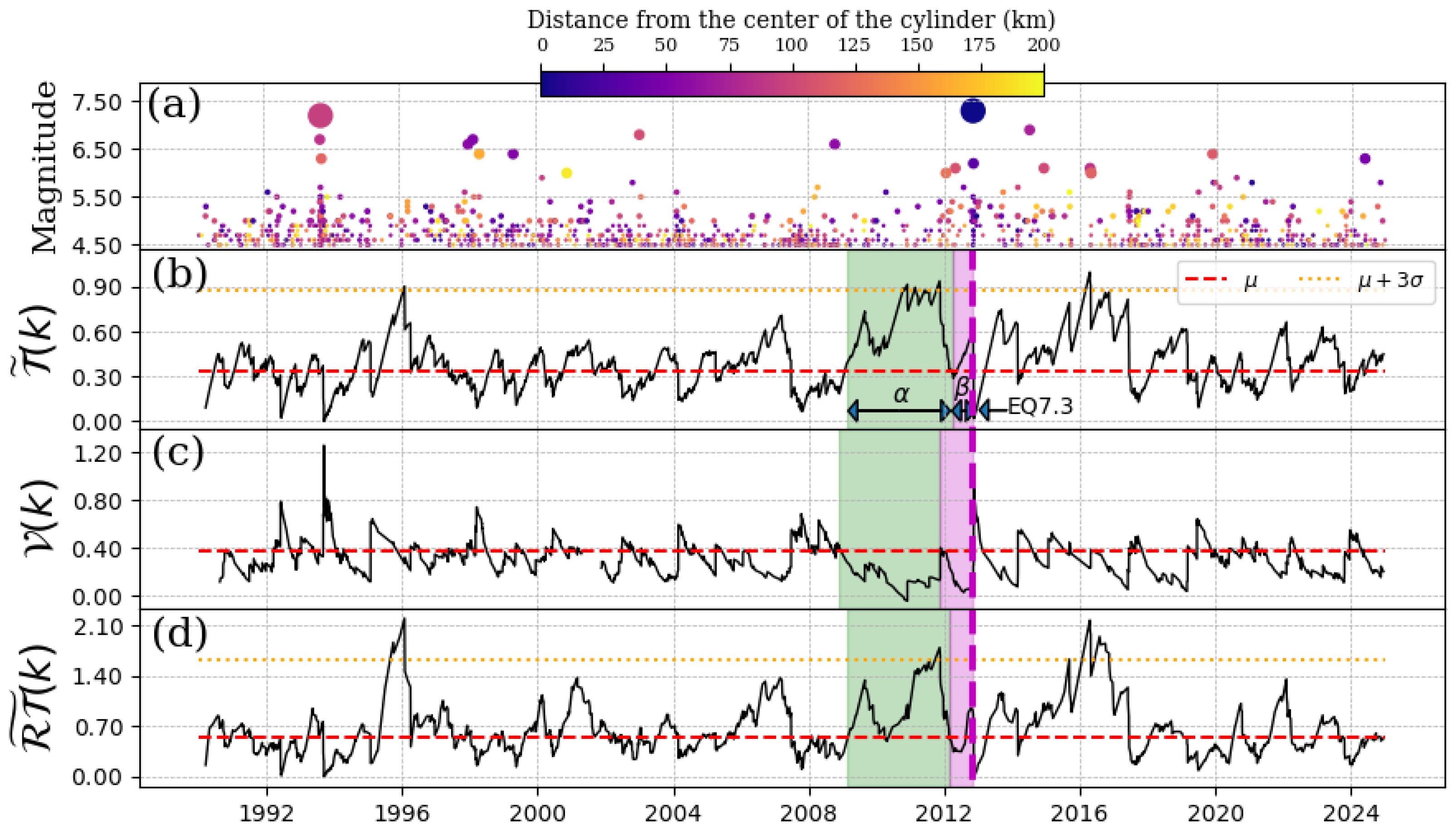
4.1. EQ 7.5, 20 March 2012
4.2. EQ 7.3, 7 November 2012
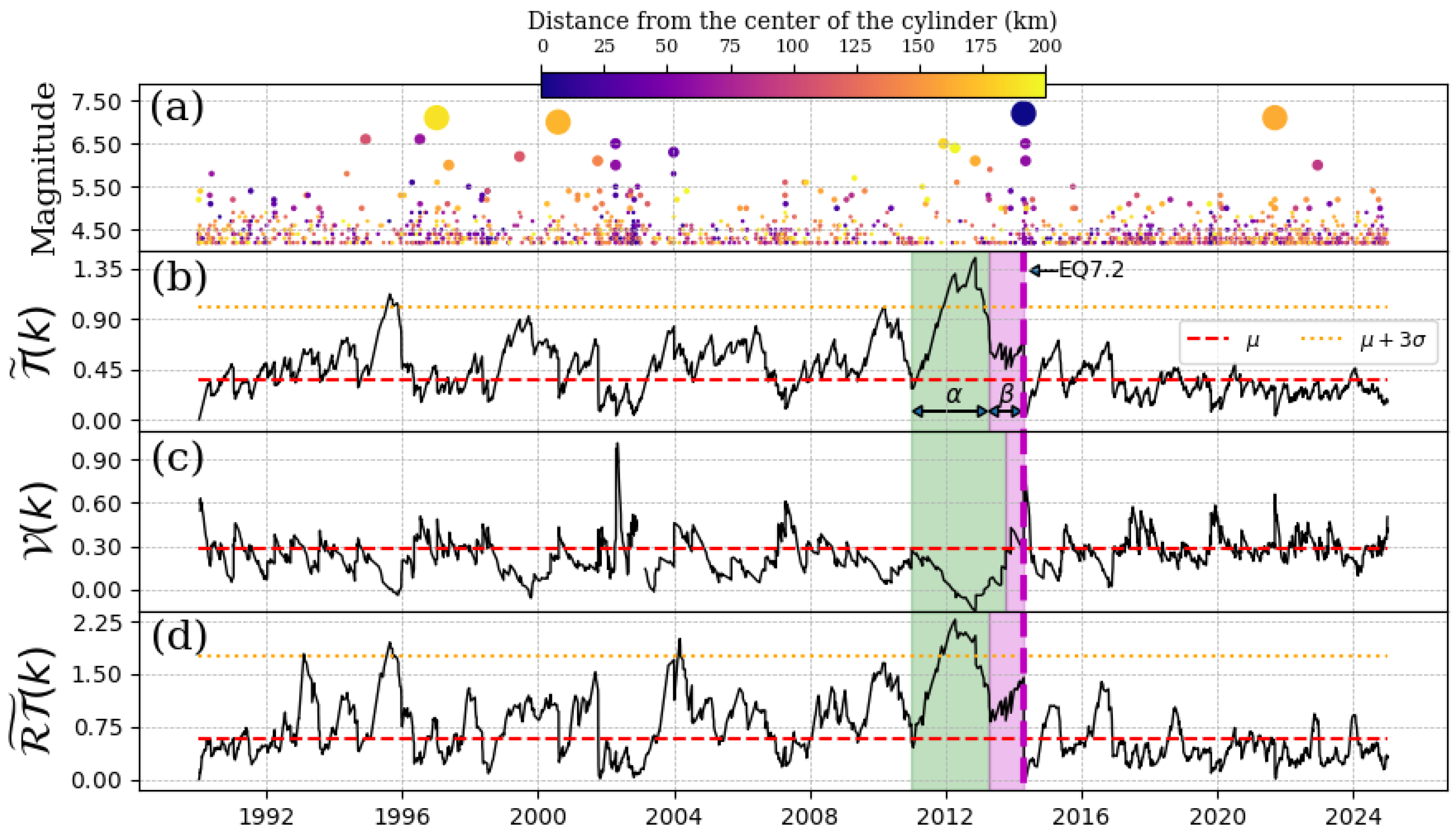
4.3. EQ 7.2, 18 April 2014
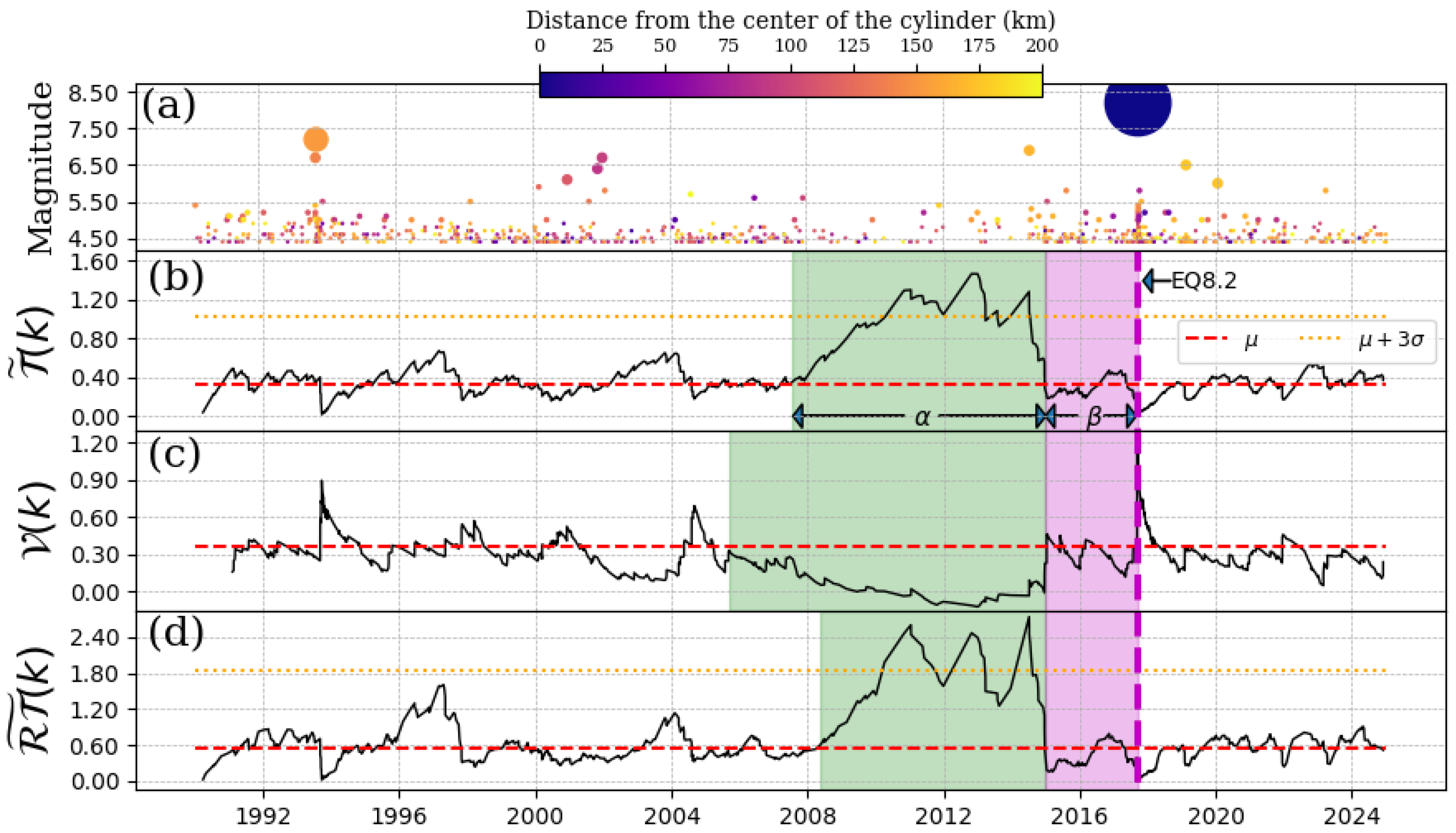
4.4. EQ8.2, 7 September 2017
4.5. EQ7.1, 19 September 2017
5. Seismic Quiescence of Mexico Mainshocks, Possibly Mixed Patterns
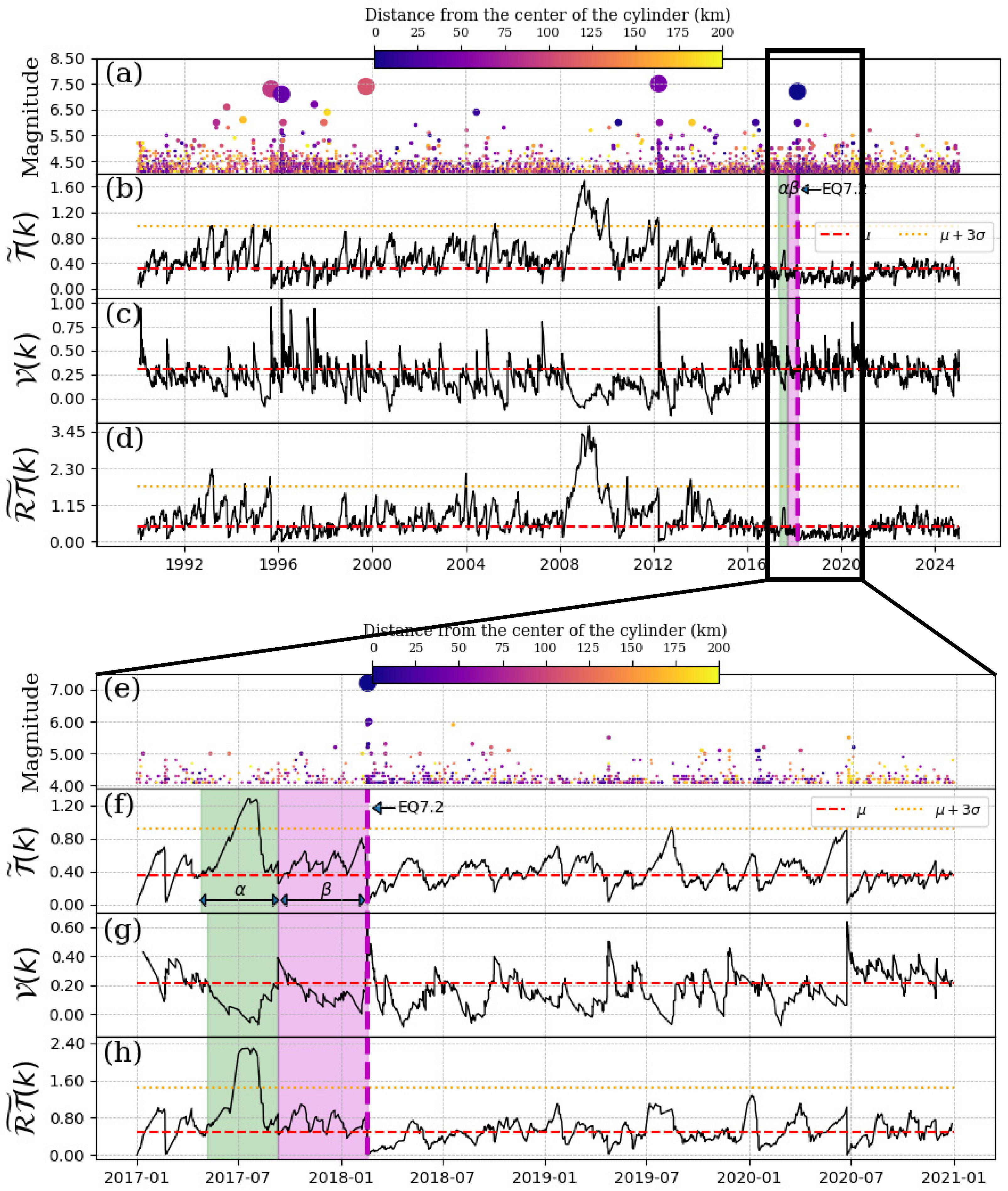
5.1. EQ7.2, 16 February 2018
5.2. EQ7.4, 23 June 2020
5.3. EQ7.1, 7 September 2021
5.4. Statistical Significance
6. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EQ(s) | Earthquake(s) |
References
- Richards, P.G.; Simpson, D.W. (Eds.) Earthquake Prediction: An International Review; American Geophysical Union: Washington, DC, USA, 1981. [Google Scholar]
- Keilis-Borok, V.; Shebalin, P. (Eds.) Dynamics of the Lithosphere and Earthquake Prediction; Elsevier: Amsterdam, The Netherlands, 1999; Volume 111, pp. 179–327. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Nagao, T. Complexity measure in natural time analysis identifying the accumulation of stresses before major earthquakes. Sci. Rep. 2024, 14, 30828. [Google Scholar] [CrossRef]
- Zaccagnino, D.; Telesca, L.; Tan, O.; Doglioni, C. Clustering analysis of seismicity in the Anatolian region with implications for seismic hazard. Entropy 2023, 25, 835. [Google Scholar] [CrossRef]
- Ohtake, M.; Matumoto, T.; Latham, G.V. Seismicity gap near Oaxaca, southern Mexico as a probable precursor to a large earthquake. In Stress in the Earth; Birkhäuser: Basel, Switzerland, 1977; pp. 375–385. [Google Scholar]
- Ohtake, M. Earthquake prediction based on the seismic gap with special reference to the 1978, Oaxaca, Mexico earthquake. Rept. Natl. Cent. Disaster Prev. 1980, 23, 65–110. [Google Scholar]
- Ohtake, M.; Matumoto, T.; Latham, G.V. Evaluation of the forecast of the 1978 Oaxaca, southern Mexico earthquake based on a precursory seismic quiescence. Earthq. Predict. Int. Rev. 1981, 4, 53–61. [Google Scholar]
- Schreider, S.Y. Formal definition of premonitory seismic quiescence. Phys. Earth Planet. Inter. 1990, 61, 113–127. [Google Scholar] [CrossRef]
- Lay, T.; Kanamori, H.; Ruff, L. The Asperity Model and the Nature of Large Subduction Zone Earthquakes; Terra Scientific Publishing Company: Tokyo, Japan, 1982. [Google Scholar]
- Wyss, M.; Habermann, R.E. Precursory seismic quiescence. Pure Appl. Geophys. 1988, 126, 319–332. [Google Scholar] [CrossRef]
- Chen, C.C.; Wu, Y.X. An improved region—Time—Length algorithm applied to the 1999 Chi-Chi, Taiwan earthquake. Geophys. J. Int. 2006, 166, 1144–1148. [Google Scholar] [CrossRef]
- Huang, Q. Seismicity changes prior to the Ms8.0 Wenchuan earthquake in Sichuan, China. Geophys. Res. Lett. 2008, 35, L23308. [Google Scholar] [CrossRef]
- Rudolf-Navarro, A.H.; Muñoz-Diosdado, A.; Angulo-Brown, F. Seismic quiescence patterns as possible precursors of great earthquakes in Mexico. Int. J. Phys. Sci 2010, 5, 651–670. [Google Scholar]
- Muñoz-Diosdado, A.; Rudolf-Navarro, A.; Angulo-Brown, F.; Barrera-Ferrer, A. Patterns of significant seismic quiescence on the Mexican Pacific coast. Phys. Chem. Earth Parts A/B/C 2015, 85, 119–130. [Google Scholar]
- Mogi, K. Two kinds of seismic gaps. Pure Appl. Geophys. 1979, 117, 1172–1186. [Google Scholar] [CrossRef]
- Mogi, K. Earthquake Prediction; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
- Wyss, M.; Sobolev, G.; Clippard, J.D. Seismic quiescence precursors to two M7 earthquakes on Sakhalin Island, measured by two methods. Earth Planets Space 2004, 56, 725–740. [Google Scholar] [CrossRef]
- Carrizales-Velazquez, C.; Rudolf-Navarro, A.; Reyes-Ramírez, I.; Muñoz-Diosdado, A.; Guzmán-Vargas, L.; Angulo-Brown, F. Multifractality of Pseudo-Velocities and Seismic Quiescence Associated with the Tehuantepec M8.2 EQ. Entropy 2018, 20, 961. [Google Scholar] [CrossRef] [PubMed]
- Servicio Sismologico Nacional. Universidad Nacional Autónoma de México. Available online: http://www.ssn.unam.mx/ (accessed on 13 November 2024).
- Singh, S.; Rodriguez, M.; Esteva, L. Statistics of small earthquakes and frequency of occurrence of large earthquakes along the Mexican subduction zone. Bull. Seismol. Soc. Am. 1983, 73, 1779–1796. [Google Scholar]
- Carretero-Campos, C.; Bernaola-Galván, P.; Ivanov, P.C.; Carpena, P. Phase transitions in the first-passage time of scale-invariant correlated processes. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2012, 85, 011139. [Google Scholar] [CrossRef]
- Guzmán-Vargas, L.; Carrizales-Velazquez, C.; Reyes-Ramírez, I.; Fonseca-Campos, J.; Rosa-Galindo, A.d.l.; Quintana-Moreno, V.O.; Peralta, J.A.; Angulo-Brown, F. A comparative study of geoelectric signals possibly associated with the occurrence of two Ms > 7 EQs in the South Pacific Coast of Mexico. Entropy 2019, 21, 1225. [Google Scholar] [CrossRef]
- Mirabedini, M.S.; Agh-Atabai, M.; Azimmohseni, M.; Zadeh, M.A. Temporal pattern of seismicity in the Zagros belt, SW Iran. Arab. J. Geosci. 2021, 14, 1707. [Google Scholar] [CrossRef]
- Wyss, M.; Wiemer, S. Two current seismic quiescences within 40 km of Tokyo. Geophys. J. Int. 1997, 128, 459–473. [Google Scholar] [CrossRef]
- Wyss, M.; Hasegawa, A.; Wiemer, S.; Umino, N. Quantitative mapping of precursory seismic quiescence before the 1989, M 7.1 off-Sanriku earthquake, Japan. Ann. Geophys. 1999, 42. [Google Scholar] [CrossRef]
- Huang, Q.; Nagao, T. Seismic quiescence before the 2000 M = 7.3 Tottori earthquake. Geophys. Res. Lett. 2002, 29, 19–21. [Google Scholar] [CrossRef]
- Huang, Q.; Sobolev, G.A.; Nagao, T. Characteristics of the seismic quiescence and activation patterns before the M= 7.2 Kobe earthquake, January 17, 1995. Tectonophysics 2001, 337, 99–116. [Google Scholar] [CrossRef]
- Aden-Antóniow, F.; Satriano, C.; Bernard, P.; Poiata, N.; Aissaoui, E.M.; Vilotte, J.P.; Frank, W.B. Statistical analysis of the preparatory phase of the M w 8.1 Iquique Earthquake, Chile. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019337. [Google Scholar] [CrossRef]
- Derode, B.; Madariaga, R.; Campos, J. Seismic rate variations prior to the 2010 Maule, Chile MW 8.8 giant megathrust earthquake. Sci. Rep. 2021, 11, 2705. [Google Scholar] [CrossRef]
- Das, R.; Das, A. Limitations of Mw and M Scales: Compelling evidence advocating for the das magnitude scale (Mwg)—A critical review and analysis. Indian Geotech. J. 2025, 1–19. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Sam, L.; Martin-Torres, F. The challenges and possibilities of earthquake predictions using non-seismic precursors. Eur. Phys. J. Spec. Top. 2021, 230, 367–380. [Google Scholar] [CrossRef]
- Guo, G.; Wang, B. Cloud anomaly before Iran earthquake. Int. J. Remote Sens. 2008, 29, 1921–1928. [Google Scholar] [CrossRef]
- Eleftheriou, A.; Filizzola, C.; Genzano, N.; Lacava, T.; Lisi, M.; Paciello, R.; Pergola, N.; Vallianatos, F.; Tramutoli, V. Long-term RST analysis of anomalous TIR sequences in relation with earthquakes occurred in Greece in the period 2004–2013. Pure Appl. Geophys. 2016, 173, 285–303. [Google Scholar] [CrossRef]
- Alvan, H.V.; Azad, F.H.; Mansor, S. Latent heat flux and air temperature anomalies along an active fault zone associated with recent Iran earthquakes. Adv. Space Res. 2013, 52, 1678–1687. [Google Scholar] [CrossRef]
- Borghi, A.; Aoudia, A.; Riva, R.E.; Barzaghi, R. GPS monitoring and earthquake prediction: A success story towards a useful integration. Tectonophysics 2009, 465, 177–189. [Google Scholar] [CrossRef]
- Cao, K.; Huang, Q. Geo-sensor (s) for potential prediction of earthquakes: Can earthquake be predicted by abnormal animal phenomena? Ann. GIS 2018, 24, 125–138. [Google Scholar] [CrossRef]
- Paudel, S.R.; Banjara, S.P.; Wagle, A.; Freund, F.T. Earthquake chemical precursors in groundwater: A review. J. Seismol. 2018, 22, 1293–1314. [Google Scholar] [CrossRef]
- Pulinets, S.; Herrera, V.M.V. Earthquake precursors: The physics, identification, and application. Geosciences 2024, 14, 209. [Google Scholar] [CrossRef]
- Picozza, P.; Conti, L.; Sotgiu, A. Looking for earthquake precursors from space: A critical review. Front. Earth Sci. 2021, 9, 676775. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Beroza, G.C. Machine learning in earthquake seismology. Annu. Rev. Earth Planet. Sci. 2023, 51, 105–129. [Google Scholar] [CrossRef]
- Xiong, P.; Tong, L.; Zhang, K.; Shen, X.; Battiston, R.; Ouzounov, D.; Iuppa, R.; Crookes, D.; Long, C.; Zhou, H. Towards advancing the earthquake forecasting by machine learning of satellite data. Sci. Total Environ. 2021, 771, 145256. [Google Scholar] [CrossRef]
- Kong, Q.; Trugman, D.T.; Ross, Z.E.; Bianco, M.J.; Meade, B.J.; Gerstoft, P. Machine learning in seismology: Turning data into insights. Seismol. Res. Lett. 2019, 90, 3–14. [Google Scholar] [CrossRef]
- Kubo, H.; Naoi, M.; Kano, M. Recent advances in earthquake seismology using machine learning. Earth Planets Space 2024, 76, 36. [Google Scholar] [CrossRef]
- Gitis, V.G.; Derendyaev, A.B. Machine learning methods for seismic hazards forecast. Geosciences 2019, 9, 308. [Google Scholar] [CrossRef]
- Johnson, P.A.; Rouet-Leduc, B.; Pyrak-Nolte, L.J.; Beroza, G.C.; Marone, C.J.; Hulbert, C.; Howard, A.; Singer, P.; Gordeev, D.; Karaflos, D.; et al. Laboratory earthquake forecasting: A machine learning competition. Proc. Natl. Acad. Sci. USA 2021, 118, e2011362118. [Google Scholar] [CrossRef] [PubMed]
- Velasco Herrera, V.M.; Rossello, E.A.; Orgeira, M.J.; Arioni, L.; Soon, W.; Velasco, G.; Rosique-De La Cruz, L.; Zúñiga, E.; Vera, C. Long-term forecasting of strong earthquakes in north America, south America, Japan, southern China and northern India with machine learning. Front. Earth Sci. 2022, 10, 905792. [Google Scholar] [CrossRef]
- Katsumata, K. A Long-Term Seismic Quiescence before the 2004 Sumatra (M w 9.1) Earthquake. Bull. Seismol. Soc. Am. 2015, 105, 167–176. [Google Scholar] [CrossRef]
- Katsumata, K.; Zhuang, J. A new method for imaging seismic quiescence and its application to the M w= 8.3 Kurile islands earthquake on 15 November 2006. Pure Appl. Geophys. 2020, 177, 3619–3630. [Google Scholar] [CrossRef]
- Chingtham, P.; Sharma, B. Detection of seismic quiescences before 1991 Uttarkashi (M w 6.8) and 1999 Chamoli M w (6.6) earthquakes and its implications for stress change sensor. Acta Geophys. 2022, 70, 509–523. [Google Scholar] [CrossRef]
- Gentili, S.; Di Giovambattista, R.; Peresan, A. Seismic quiescence preceding the 2016 central Italy earthquakes. Phys. Earth Planet. Int. 2017, 272, 27–33. [Google Scholar] [CrossRef]
- Nagao, T.; Takeuchi, A.; Nakamura, K. A new algorithm for the detection of seismic quiescence: Introduction of the RTM algorithm, a modified RTL algorithm. Earth Planets Space 2011, 63, 315–324. [Google Scholar] [CrossRef]
- Katsumata, K.; Nakatani, M. Testing the seismic quiescence hypothesis through retrospective trials of alarm-based earthquake prediction in the Kurile–Japan subduction zone. Earth Planets Space 2021, 73, 100. [Google Scholar] [CrossRef]
- Aki, K. A probabilistic synthesis of precursory phenomena. Earthq. Predict. Int. Rev. 1981, 4, 566–574. [Google Scholar]
- Perinelli, A.; Ricci, L.; Santis, A.D.; Iuppa, R. Earthquakes unveil the global-scale fractality of the lithosphere. Commun. Earth Environ. 2024, 5, 146. [Google Scholar] [CrossRef]
- Eluyemi, A.A.; Baruah, S.; Baruah, S. Empirical relationships of earthquake magnitude scales and estimation of guttenberg–richter parameters in gulf of guinea region. Sci. Afr. 2019, 6, e00161. [Google Scholar] [CrossRef]




| Date | Magnitude | Latitude | Longitude | Depth (km) |
|---|---|---|---|---|
| 20 March 2012 | 7.5 | 16.26 | −98.46 | 18.0 |
| 7 November 2012 | 7.3 | 14.03 | −92.32 | 17.1 |
| 18 April 2014 | 7.2 | 17.01 | −101.46 | 18.0 |
| 7 September 2017 | 8.2 | 14.76 | −94.10 | 45.9 |
| 19 September 2017 | 7.1 | 18.33 | −98.67 | 51.2 |
| 16 February 2018 | 7.2 | 16.22 | −98.01 | 16.0 |
| 23 June 2020 | 7.4 | 15.80 | −96.13 | 22.8 |
| 17 September 2021 | 7.1 | 16.75 | −99.95 | 15.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrizales-Velazquez, C.; Perez-Oregon, J.; Reyes-Ramírez, I.; Guzmán-Vargas, L.; Angulo-Brown, F. Detection of Significant Seismic Quiescence Patterns in the Mexican Subduction Zone Using Extended Schreider Algorithms. Entropy 2025, 27, 960. https://doi.org/10.3390/e27090960
Carrizales-Velazquez C, Perez-Oregon J, Reyes-Ramírez I, Guzmán-Vargas L, Angulo-Brown F. Detection of Significant Seismic Quiescence Patterns in the Mexican Subduction Zone Using Extended Schreider Algorithms. Entropy. 2025; 27(9):960. https://doi.org/10.3390/e27090960
Chicago/Turabian StyleCarrizales-Velazquez, Carlos, Jennifer Perez-Oregon, Israel Reyes-Ramírez, Lev Guzmán-Vargas, and Fernando Angulo-Brown. 2025. "Detection of Significant Seismic Quiescence Patterns in the Mexican Subduction Zone Using Extended Schreider Algorithms" Entropy 27, no. 9: 960. https://doi.org/10.3390/e27090960
APA StyleCarrizales-Velazquez, C., Perez-Oregon, J., Reyes-Ramírez, I., Guzmán-Vargas, L., & Angulo-Brown, F. (2025). Detection of Significant Seismic Quiescence Patterns in the Mexican Subduction Zone Using Extended Schreider Algorithms. Entropy, 27(9), 960. https://doi.org/10.3390/e27090960









