The Realization of One-to-Two-Port Beam Division in a Five-Channel Acoustic System
Abstract
1. Introduction
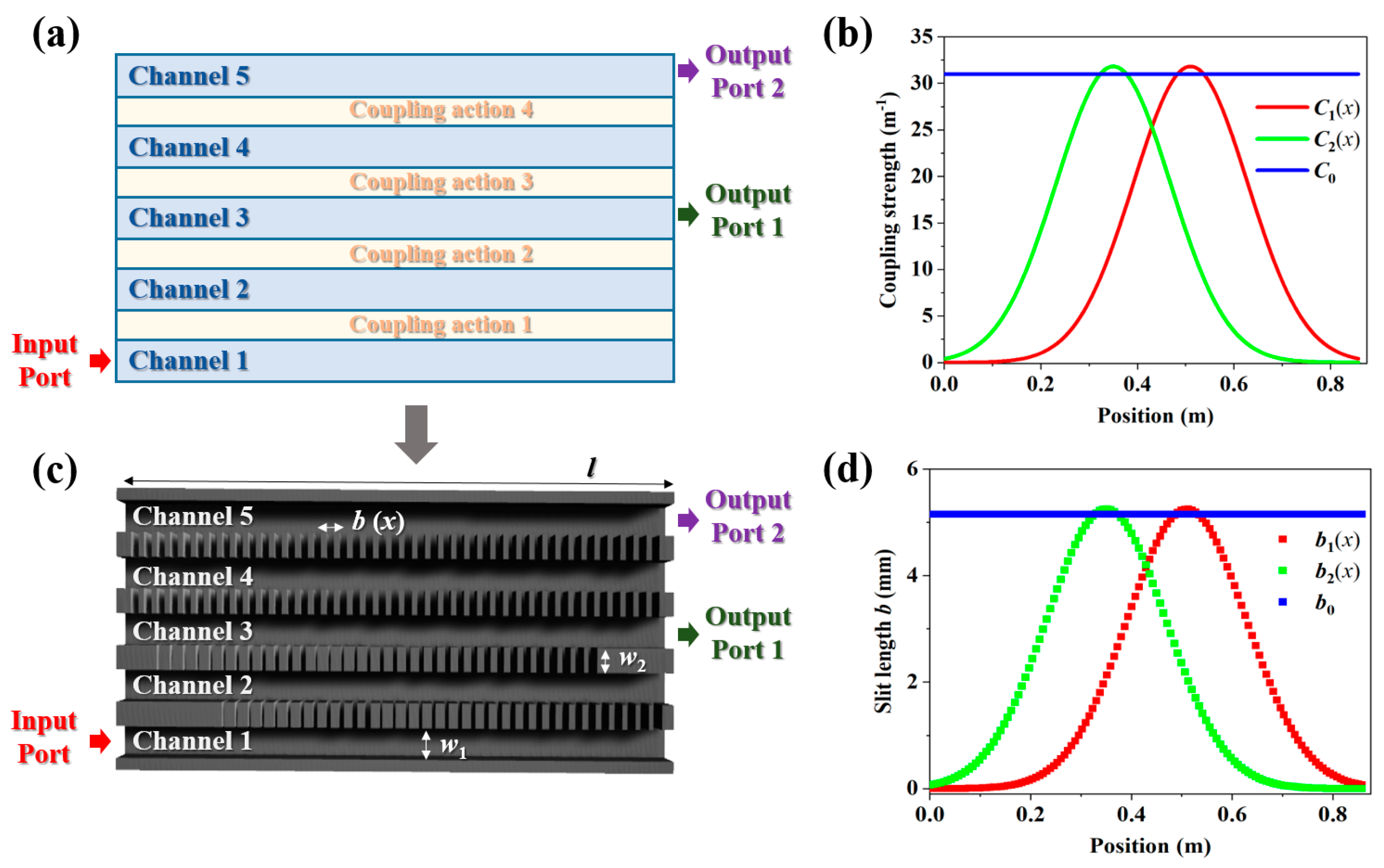
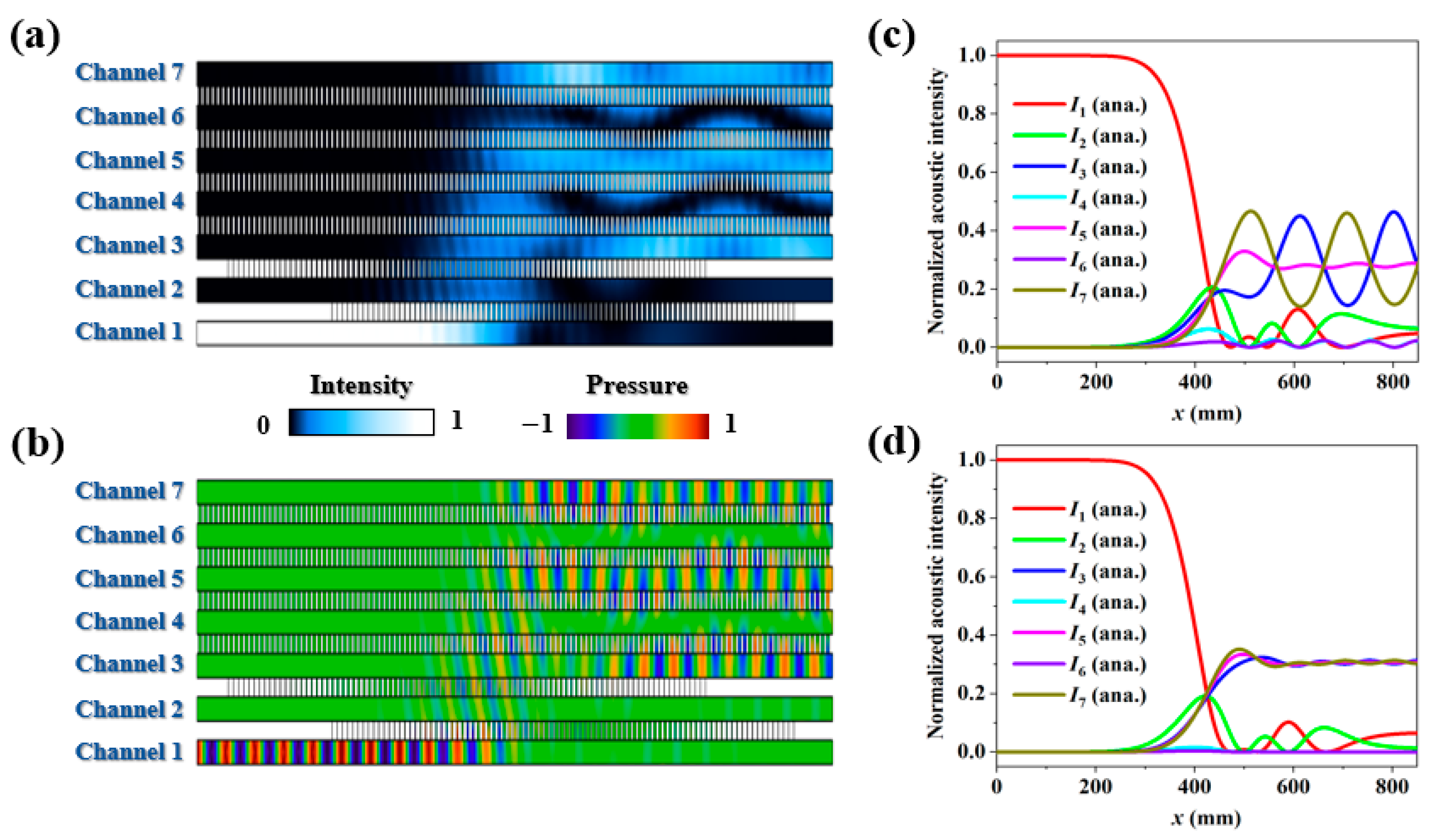
2. Design and Methods
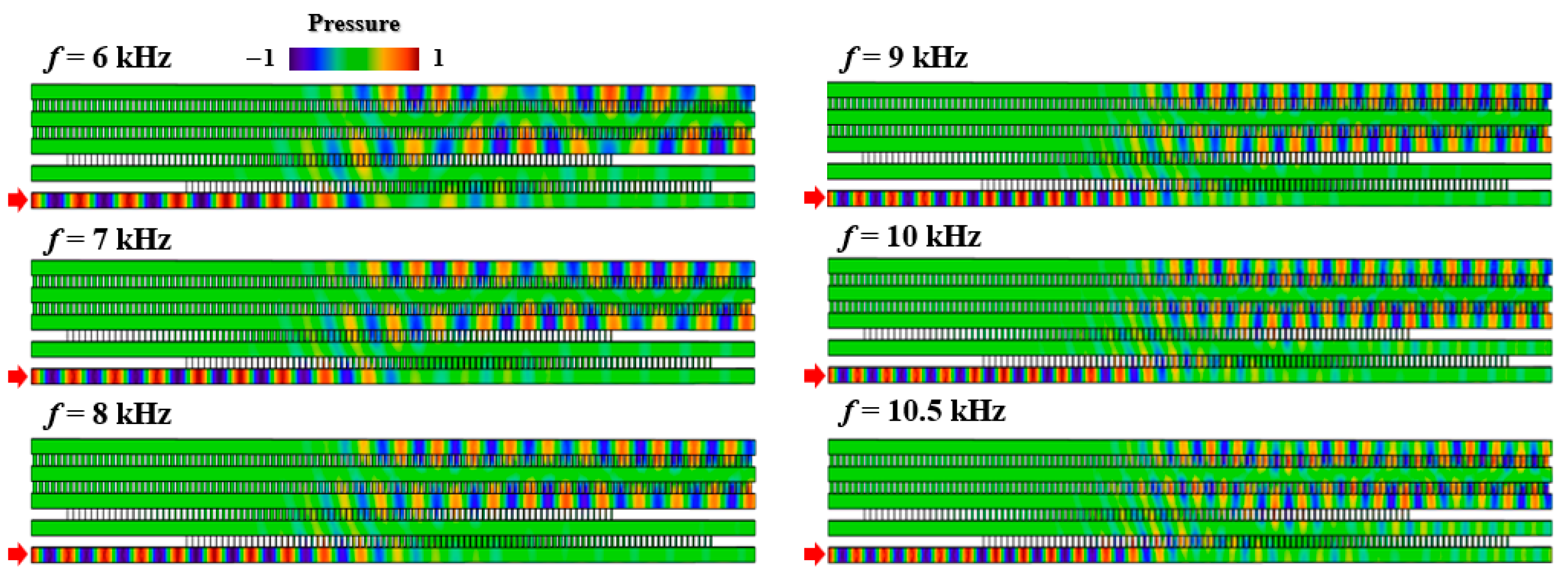
3. Results and Discussions
- I.
- Place the reference microphone (Reference Mic) at a fixed position within the waveguide (e.g., near the sound source or at the waveguide entrance).
- II.
- Move the other probe microphone (Probe Mic) to the target location where we wish to measure the phase.
- III.
- Simultaneously and synchronously record the time-domain signals (time waveforms) received by both microphones.
- IV.
- Perform a Fourier transform (FFT) on both signals to convert them from the time domain to the frequency domain.
- V.
- In the frequency domain, for the specific frequency of interest, extract the complex Fourier coefficients (containing magnitude and phase information) of the signals at both the probe point and the reference point.
- VI.
- Calculate the phase difference between these two complex coefficients, which represents the relative phase of the probe point with respect to the reference point.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Discussions on Adiabatic Passage
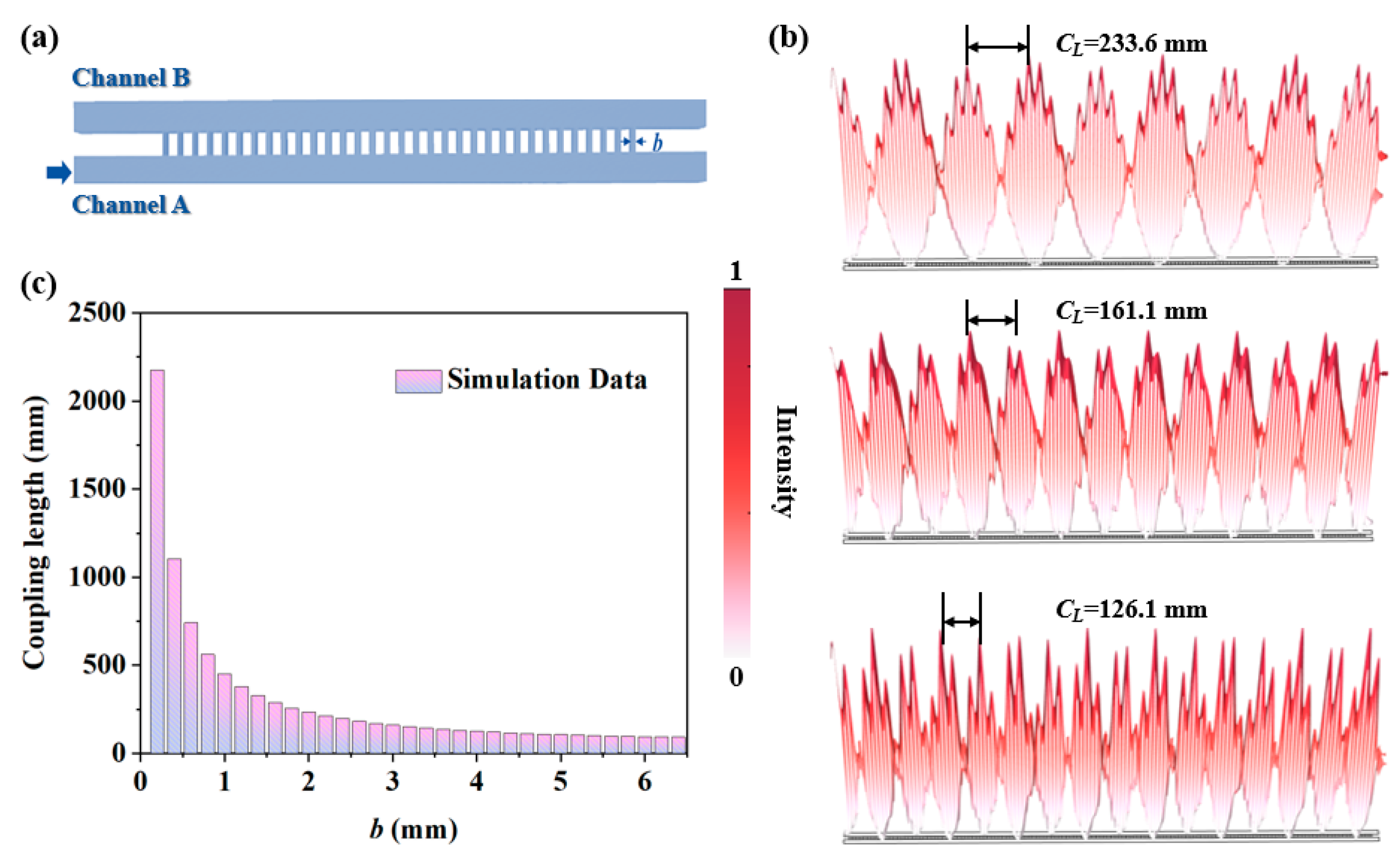
Appendix B. The Relation Between Coupling Strength and Slit Length
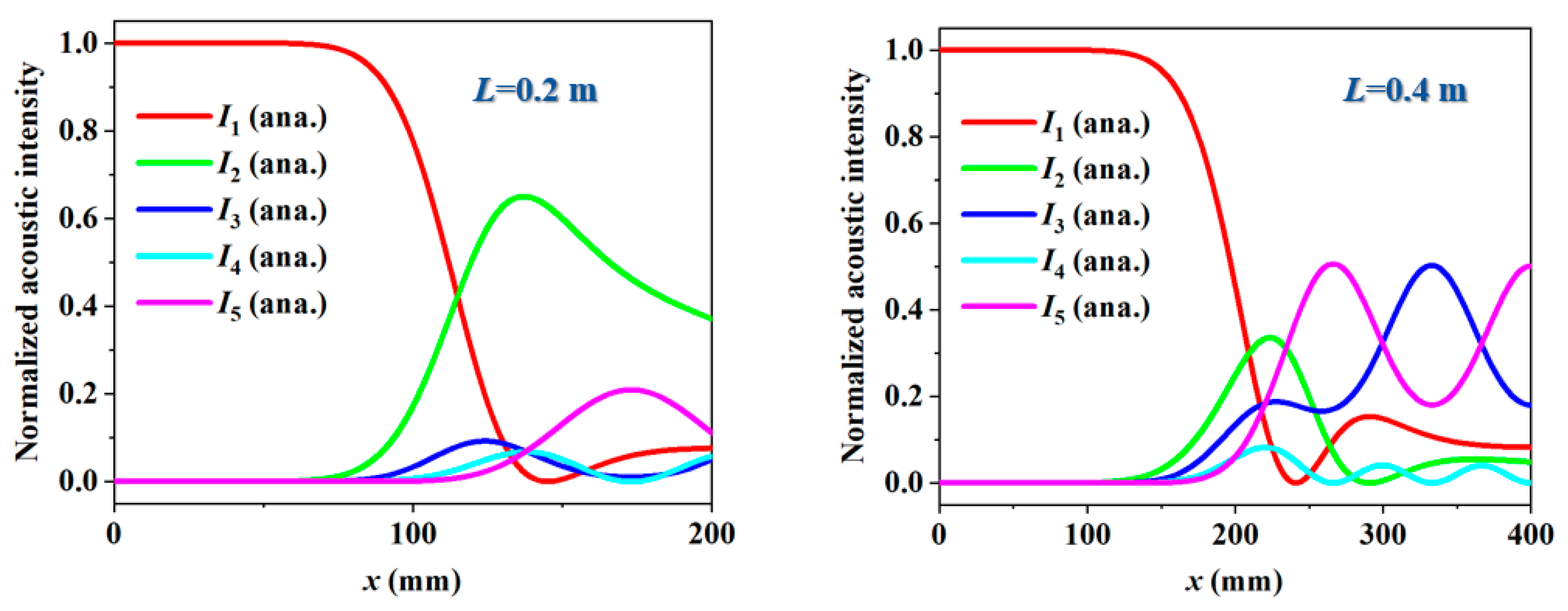
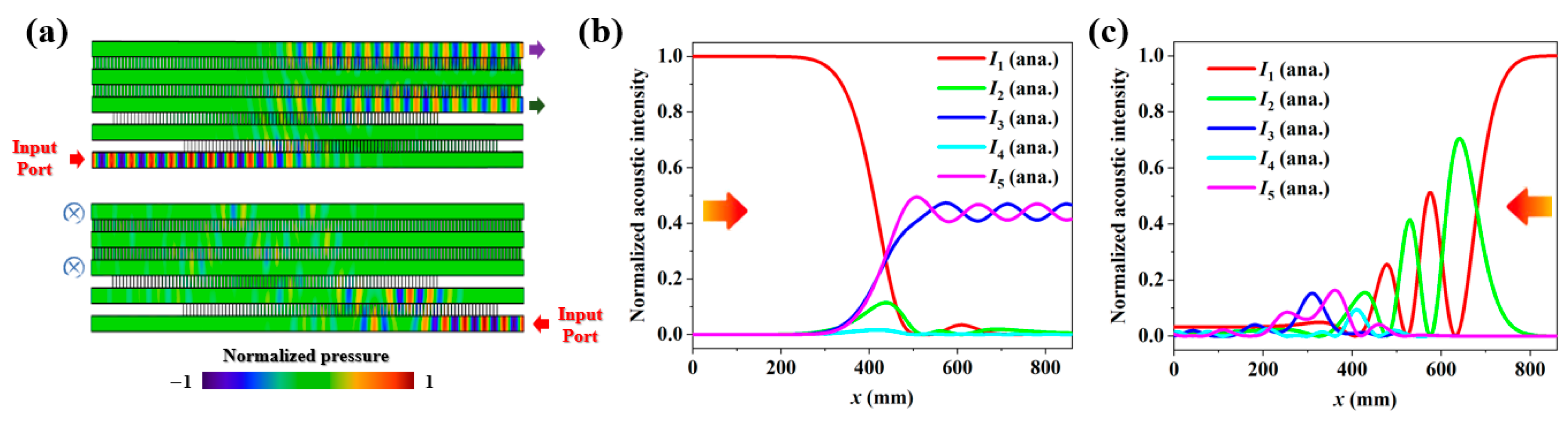
Appendix C. A Discussion of the Five-Channel Acoustic System
References
- Endaylalu, S.A.; Tien, W.-H. A Numerical Investigation of the Mixing Performance in a Y-Junction Microchannel Induced by Acoustic Streaming. Micromachines 2022, 13, 338. [Google Scholar] [CrossRef]
- Lee, H.-J.; Mancini, J.A.; Joshipura, I.; Spadaccini, C.M.; Loh, K.J. Selective Heating Through Y-Junction Waveguide Designed by Acoustic Shape Optimization. Adv. Eng. Mater. 2023, 25, 2200756. [Google Scholar] [CrossRef]
- Endaylalu, S.A.; Tien, W.-H. Mixing enhancement in T-junction microchannel with acoustic streaming induced by triangular structure. Biomicrofluidics 2021, 15, 034102. [Google Scholar] [CrossRef]
- Xu, C.; Huang, S.; Guo, Z.; Jiang, H.; Li, Y.; Wu, Y.; Chen, H. Acoustic Beam Splitting and Cloaking Based on a Compressibility-Near-Zero Medium. Phys. Rev. Appl. 2022, 17, 054025. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, Z.; Liu, Q.; Bi, C. Acoustic beam splitter based on acoustic metamaterial Luneburg lens. Phys. Lett. A 2023, 472, 128815. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, F.; Liu, Y.; Ma, X.; Chen, H.; Chao, K.; Chen, Z.; Wang, J. Electromagnetic-acoustic splitter with a tunable splitting ratio based on copper plates. Opt. Lett. 2023, 48, 3407. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, J.; Duan, G.; Jiang, Z.; Man, X.; Yu, D.; Xia, B. Topological network and valley beam splitter in acoustic biaxially strained moire superlattices. Phys. Rev. B 2022, 105, 184104. [Google Scholar] [CrossRef]
- Ye, L.; Qiu, C.; Lu, J.; Wen, X.; Shen, Y.; Ke, M.; Zhang, F.; Liu, Z. Observation of acoustic valley vortex states and valley-chirality locked beam splitting. Phys. Rev. B 2017, 95, 174106. [Google Scholar] [CrossRef]
- Chen, A.-L.; Wang, Y.-S.; Wang, Y.-F.; Zhou, H.-T.; Yuan, S.-M. Design of Acoustic/Elastic Phase Gradient Metasurfaces: Principles, Functional Elements, Tunability, and Coding. Appl. Mech. Rev. 2022, 74, 020801. [Google Scholar] [CrossRef]
- Quan, J.; Sun, B.; Fu, Y.; Gao, L.; Xu, Y. Acoustic Bilayer Gradient Metasurfaces for Perfect and Asymmetric Beam Splitting. Chin. Phys. Lett. 2024, 41, 014301. [Google Scholar] [CrossRef]
- Liu, T.; Ma, G.; Liang, S.; Gao, H.; Gu, Z.; An, S.; Zhu, J. Single-sided acoustic beam splitting based on parity-time symmetry. Phys. Rev. B 2020, 102, 014306. [Google Scholar] [CrossRef]
- Tang, S.; Lü, C.; Wu, J.-L.; Song, J.; Jiang, Y. Wavelength-selected bifunctional beam shaping for transmitted acoustic waves via coding metasurface. Appl. Acoust. 2022, 194, 108786. [Google Scholar] [CrossRef]
- Krushynska, A.O.; Torrent, D.; Aragón, A.M.; Ardito, R.; Bilal, O.R.; Bonello, B.; Bosia, F.; Chen, Y.; Christensen, J.; Colombi, A.; et al. Emerging topics in nanophononics and elastic, acoustic, and mechanical metamaterials: An overview. Nanophotonics 2023, 12, 659–686. [Google Scholar] [CrossRef]
- Pora, G.; Arie, A. Efficient two-process frequency conversion through a dark intermediate state. J. Opt. Soc. Am. B-Opt. Phys. 2012, 29, 2901. [Google Scholar] [CrossRef]
- Dimova, E.; Rangelov, A.; Kyoseva, E. Broadband and ultra-broadband polarization rotators with adiabatic modular design. J. Opt. 2015, 17, 075605. [Google Scholar] [CrossRef]
- Alrifai, R.; Coda, V.; Peltier, J.; Rangelov, A.A.; Montemezzani, G. Ultrabroadband beam splitting in a dissipative system of three waveguides. Phys. Rev. A 2021, 103, 023527. [Google Scholar] [CrossRef]
- Hristova, H.S.; Rangelov, A.A.; Montemezzani, G.; Vitanov, N.V. Adiabatic three-waveguide coupler. Phys. Rev. A 2016, 93, 033802. [Google Scholar] [CrossRef]
- Chen, J.; Deng, L.; Niu, Y.; Gong, S. Double rapid adiabatic passage in three optical waveguides with longitudinally varying detunings. Phys. Rev. A 2021, 103, 053705. [Google Scholar] [CrossRef]
- Huang, W.; Liang, S.-J.; Kyoseva, E.; Ang, L.K. Adiabatic control of surface plasmon-polaritons in a 3-layers graphene curved configuration. Carbon 2018, 127, 187. [Google Scholar] [CrossRef]
- Huang, W.; Yin, S.; Zhang, W.; Wang, K.; Zhang, Y.; Han, J. Robust and broadband integrated terahertz coupler conducted with adiabatic following. New J. Phys. 2019, 21, 113004. [Google Scholar] [CrossRef]
- Tang, S.; Wu, J.-L.; Lü, C.; Song, J.; Jiang, Y. Functional acoustic metamaterial using shortcut to adiabatic passage in acoustic waveguide couplers. Phys. Rev. Appl. 2022, 18, 014038. [Google Scholar] [CrossRef]
- Shen, Y.-X.; Peng, Y.-G.; Zhao, D.-G.; Chen, X.-C.; Zhu, J.; Zhu, X.-F. One-way Localized Adiabatic Passage in an Acoustic System. Phys. Rev. Lett. 2019, 122, 094501. [Google Scholar] [CrossRef]
- Yao, J.; Tang, S.; Lü, C.; Zhang, J.; Song, J.; Jiang, Y. Fast energy transfer in an acoustic multicavity coupler based on the Su-Schrieffer-Heeger topological model. Phys. Rev. Appl. 2024, 22, 044009. [Google Scholar] [CrossRef]
- Huang, W.; Qu, X.; Yin, S.; Zubair, M.; Yuan, M.; Zhang, W.; Han, J. Quantum engineering enables broadband and robust terahertz surface plasmon-Polaritons coupler. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 8400107. [Google Scholar] [CrossRef]
- Shen, Y.-X.; Zeng, L.-S.; Geng, Z.-G.; Zhao, D.-G.; Peng, Y.-G.; Zhu, J.; Zhu, X.-F. Acoustic topological adiabatic passage via a level crossing. Sci. China Phys. Mech. Astron. 2020, 64, 244302. [Google Scholar] [CrossRef]
- Vitanov, N.V. Adiabatic population transfer by delayed laser pulses in multistate systems. Phys. Rev. A 1998, 58, 2295. [Google Scholar] [CrossRef]
- Ciret, C.; Coda, V.; Rangelov, A.A.; Neshev, D.N.; Montemezzani, G. Planar achromatic multiple beam splitter by adiabatic light transfer. Opt. Lett. 2012, 37, 3789. [Google Scholar] [CrossRef] [PubMed]
- Vitanov, N.V.; Rangelov, A.A.; Shore, B.W.; Bergmann, K. Stimulated Raman adiabatic passage in physics, chemistry, and beyond. Rev. Mod. Phys. 2017, 89, 015006. [Google Scholar] [CrossRef]
- Baksic, A.; Ribeiro, H.; Clerk, A.A. Speeding up Adiabatic Quantum State Transfer by using Dressed States. Phys. Rev. Lett. 2016, 116, 230503. [Google Scholar] [CrossRef]
- Vitanov, N.V.; Suominen, K.A.; Shore, B.W. Creation of coherent atomic superpositions by fractional stimulated Raman adiabatic passage. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 4535. [Google Scholar] [CrossRef]
- Francisco, D.; Ledesma, S. Classical optics analogy of quantum teleportation. J. Opt. Soc. Am. B-Opt. Phys. 2008, 25, 383–390. [Google Scholar] [CrossRef]
- Morris, J.R.; Shore, B.W. Reduction of degenerate two-level excitation to independent two-state systems. Phys. Rev. A 1983, 27, 906. [Google Scholar] [CrossRef]
- Fu, Y.; Tian, Y.; Li, X.; Yang, S.; Liu, Y.; Xu, Y.; Lu, M. Asymmetric Generation of Acoustic Vortex Using Dual-Layer Metasurfaces. Phys. Rev. Lett. 2022, 128, 104501. [Google Scholar] [CrossRef]
- Song, A.; Li, J.; Shen, C.; Peng, X.; Zhu, X.; Chen, T.; Cummer, S.A. Broadband high-index prism for asymmetric acoustic transmission. Appl. Phys. Lett. 2019, 114, 121902. [Google Scholar] [CrossRef]
- Xu, S.-T.; Fan, J.; Xue, Z.; Sun, T.; Li, G.; Li, J.; Lu, D.; Cong, L. Active control of terahertz quasi-BIC and asymmetric transmission in a liquid-crystal-integrated metasurface. Photonics Res. 2024, 12, 2207–2213. [Google Scholar] [CrossRef]
- Fu, Y.; Shen, C.; Cao, Y.; Gao, L.; Chen, H.; Chan, C.T.; Cummer, S.A.; Xu, Y. Reversal of transmission and reflection based on acoustic metagratings with integer parity design. Nat. Commun. 2019, 10, 2326. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.-Y.; Tao, J.-Q.; Song, A.-L.; Liu, Y.-W.; Xu, Y.-D. Controllably asymmetric beam splitting via gap-induced diffraction channel transition in dual-layer binary metagratings. Front. Phys. 2020, 15, 52502. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Xu, Z.; Tang, S.; Zhang, W.; Hou, J.; Cui, H.; Liu, Y. The Realization of One-to-Two-Port Beam Division in a Five-Channel Acoustic System. Entropy 2025, 27, 949. https://doi.org/10.3390/e27090949
Wang R, Xu Z, Tang S, Zhang W, Hou J, Cui H, Liu Y. The Realization of One-to-Two-Port Beam Division in a Five-Channel Acoustic System. Entropy. 2025; 27(9):949. https://doi.org/10.3390/e27090949
Chicago/Turabian StyleWang, Rui, Zhicheng Xu, Shuai Tang, Wencong Zhang, Jiabin Hou, Haipeng Cui, and Yang Liu. 2025. "The Realization of One-to-Two-Port Beam Division in a Five-Channel Acoustic System" Entropy 27, no. 9: 949. https://doi.org/10.3390/e27090949
APA StyleWang, R., Xu, Z., Tang, S., Zhang, W., Hou, J., Cui, H., & Liu, Y. (2025). The Realization of One-to-Two-Port Beam Division in a Five-Channel Acoustic System. Entropy, 27(9), 949. https://doi.org/10.3390/e27090949




