Identifying Network Propagation Sources Using Advanced Centrality Measures
Abstract
1. Introduction and Research Motivation
- A thorough analysis of advanced centrality measures for identifying the source of network propagation.
- For each simulation model, 96 unique propagation schemes were generated. Combining the two simulation models (SIR and IC) produced 192 propagation graphs. When these were paired with 25 tested methods, the total reached 4800 experiments.
- Evaluating source detection effectiveness through centrality measures, enhanced by including suspected sets within one- and two-hop neighborhoods, illustrates the potential of centrality for pinpointing areas suitable for more focused source detection.
- Experiments conducted on networks with various topologies confirmed the methods regarding both computational efficiency and detection performance.
2. Social Networks, Propagation, Source Identification, and Centrality Measures
3. Research Background
- Precision (PPV)
- Recall (TPR)
- F1
- Global Average Distance Error (GADE, hops)—the average shortest distance between a real source(s), , and the estimated ones, .
- Average Detection Error (ADE)—the average ratio of the difference between the number of detected sources and the number of true sources.
4. A Review of Centrality Metrics Used in the Research
- Algebraic centrality [40] measures the absolute and relative changes in a graph’s algebraic connectivity when a vertex is deleted.
- Average distance [41] centrality refers to the average length of the shortest paths from node u to all other nodes in the network. It represents the inverse of closeness centrality.
- Barycenter [42] quantifies a node’s centrality by the inverse of the total distance from that node to all others in the network. This measure identifies nodes centrally located in terms of overall network distance, reflecting their accessibility.
- Betweenness [43] measures the importance of a node by calculating the ratio of the shortest paths that pass through the node to the total number of shortest paths between all pairs of nodes in a network. It highlights nodes that frequently act as bridges along the shortest paths between other nodes, indicating their crucial role in the network’s connectivity.
- Closeness [44] measures how quickly a node can access all other nodes in a network, calculated as the inverse of the total distance from a node to all other nodes. This centrality metric often determines how rapidly information can spread from a given node to the entire network, highlighting strategically positioned nodes for efficient communication.
- ClusterRank [45] is a local ranking algorithm that evaluates a node’s influence by considering its direct connections, neighbors’ influence, and clustering coefficient. This approach enhances the evaluation by incorporating how closely interconnected a node’s neighborhood is. This can significantly improve the assessment of a node’s strategic importance in undirected networks compared to simple degree centrality or k-core decomposition methods.
- Coreness centrality [46], based on the k-shell indices of a node’s neighbors, is a powerful indicator of a node’s ability to disseminate information across a network. This metric evaluates a node’s connections to central or core network members, reflecting its potential influence more effectively.
- Current-flow betweenness [47] is the average amount of current flowing through a specific vertex, calculated across all possible pairs of source and target nodes within the network. This centrality measure averages the current flow for each node, indicating how much a node acts as a conduit for the flow between various pairs in the network. It is shown to be the same as random-walk betweenness [48,49].
- Current-flow closeness [47] transforms the traditional closeness index into a measure based on electrical current. This alternative approach calculates the distance between vertices in a network by assessing the difference in their electrical potentials. This method provides a distinctive perspective on node centrality, reflecting the ease with which current flows through different network parts. It is equivalent to information centrality [50].
- Decay [49,51] is a centrality measure that quantifies the importance of a vertex in a network based on its proximity to all other vertices, adjusted by a decay factor. Specifically, the decay centrality of a chosen vertex in a graph is calculated by weighting the closeness of this vertex to every other vertex by a decay factor, which diminishes the influence of distance.
- Degree measures the number of direct connections a node has in a network, indicating its importance based on how many neighbors it is directly linked to. A node with a higher degree of centrality is often more influential, as it interacts with other nodes directly [52].
- Diffusion degree [53] identifies the most influential nodes in a network by considering their direct connections and their ability to spread influence to neighbors. This measure captures the cumulative impact of a node and its neighbors during the diffusion process, reaching its maximum when all neighbors are successfully activated.
- Eigenvector [54] measures the influence of a node in a network by considering not only its direct connections but also the importance of the nodes it is connected to. It is computed using the principal eigenvector of the adjacency matrix, where the largest eigenvalue provides the desired centrality measure, ensuring that all entries in the eigenvector are positive.
- Geodesic K-path [27] measures the importance of a node by counting its neighbors within a geodesic path length of less than “k”.
- Harmonic [55] is a variation of closeness centrality that handles disconnected networks using the harmonic mean of distances, which performs better than the arithmetic mean when infinite distances are present. It calculates the importance of a node as the denormalized inverse of the harmonic mean of all distances to other nodes, making it more suitable for disconnected or sparse networks.
- Heatmap [56] combines local and global network information by comparing a node’s farness to the average farness of its neighboring nodes. A node with a smaller farness than its neighbors is considered more influential, as information is more likely to pass through it than through adjacent nodes. This makes heatmap centrality effective in identifying super-spreader nodes that control information flow within a network.
- Leverage [57] measures a node’s influence by comparing its degree to the degrees of its neighbors, averaging the differences. A node with negative leverage centrality is influenced by its neighbors, as they are more connected. In contrast, a node with positive leverage centrality has more influence over its neighbors, who have fewer connections.
- Lin [58] adjusts the concept of closeness by considering the average distance and the number of coreachable nodes. It is calculated by multiplying the inverse of the average distance by the square of the number of coreachable nodes, giving more importance to nodes that can reach a larger portion of the network. This modification ensures that nodes with larger coreachable sets are deemed more central, while nodes with no coreachable set have a centrality of 1 by definition.
- Load [59] measures the significance of a node by determining the fraction of all shortest paths in the network that go through it. This reflects the node’s ability to manage flow within the network. Unlike betweenness centrality, load centrality evenly distributes flow among neighboring nodes at the shortest distance to the target. This makes it especially valuable for analyzing flow structures operating below their capacity limits.
- MNC [60] evaluates the importance of a node by assessing the size of the largest connected group within its immediate neighbors, excluding the node itself. It measures how well-connected a node’s neighbors are, indicating the node’s influence based on the cohesion of its surrounding network.
- PageRank [61] evaluates the relative importance of nodes in a network by analyzing the number and quality of incoming links. It is based on a modified random walk, where there is a probability of jumping to any node, ensuring the scores are distributed more evenly across the network. Nodes with more links from highly ranked nodes are considered more important, making PageRank an effective way to measure influence within a network.
- Percolation [62] measures the importance of a node in spreading information or processes in dynamic networks, where nodes can transition between different states (e.g., infected or not). It calculates the proportion of shortest paths that pass through a node, considering its percolation state over time, making it useful for understanding the influence of spreading phenomena, such as diseases or information.
- Radiality [63] measures how close a node is to all other nodes in the network relative to the network’s diameter. A node with high radiality centrality is generally closer to other nodes, indicating a more central position, while a low radiality suggests the node is more peripheral in the network.
- Subgraph [64] measures how much a node participates in all the network subgraphs, accounting for all closed walks of various lengths that start and end at the node. It assigns a higher weight to shorter walks, meaning nodes involved in more local, tightly knit structures receive higher centrality. This centrality is calculated using the eigenvalues and eigenvectors of the network’s adjacency matrix.
- Topological [65] evaluates how much a node shares its neighbors with other nodes in the network. It calculates the ratio of shared neighbors between a node and its connected nodes, plus one if they have a direct connection, divided by the total number of neighbors of the node. Nodes with few or no neighbors receive a coefficient of zero, indicating minimal shared connections.
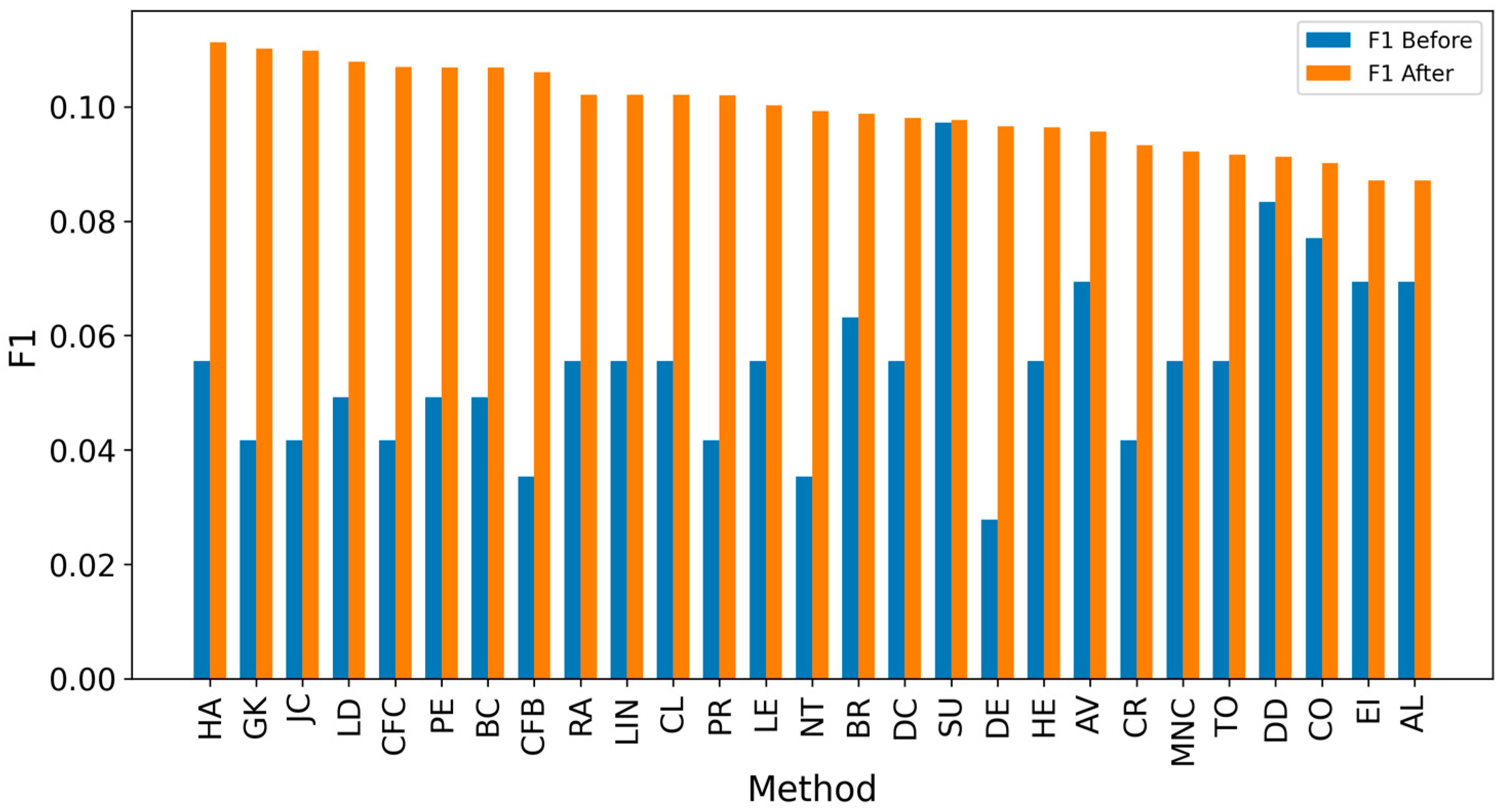
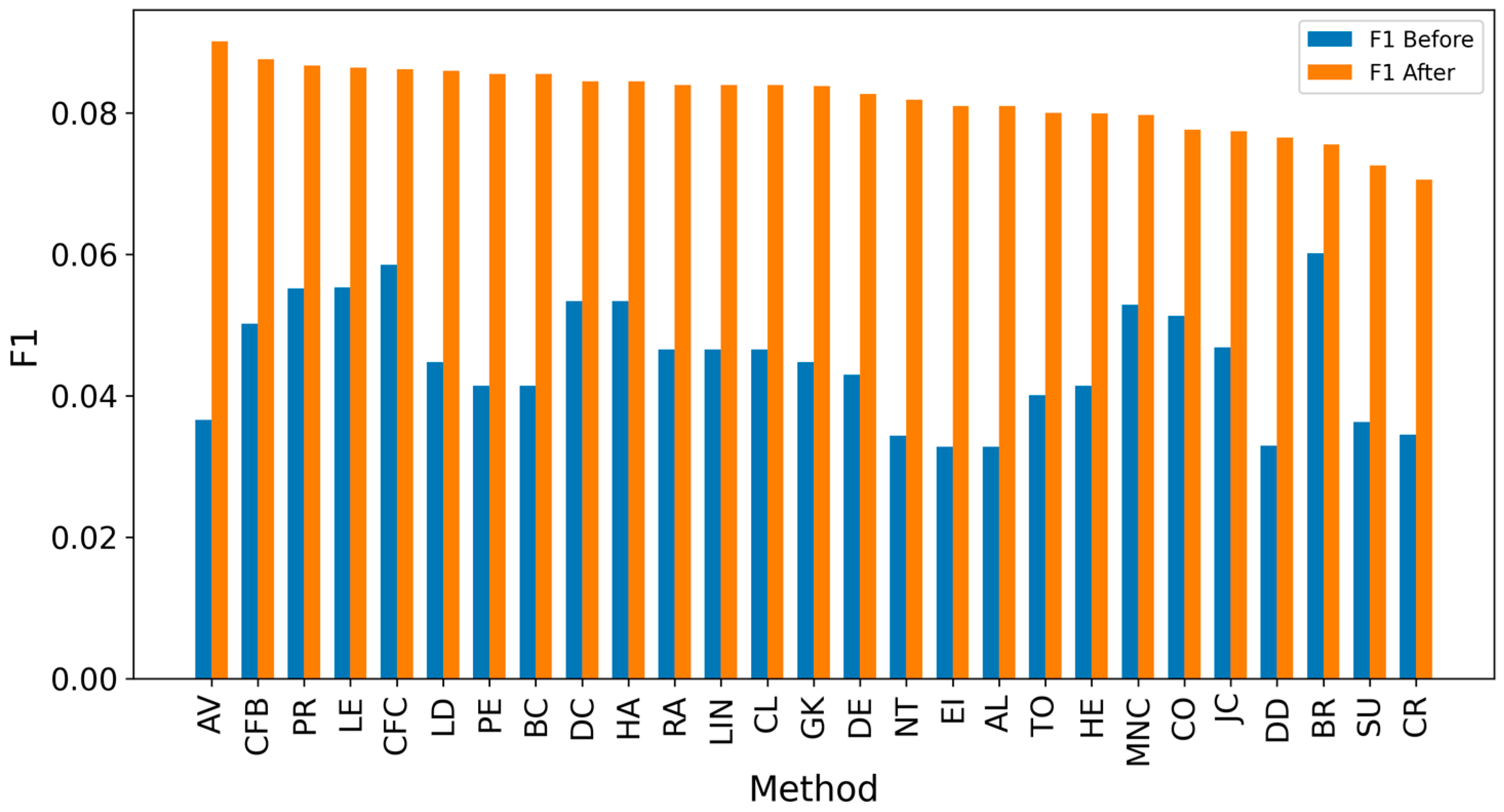
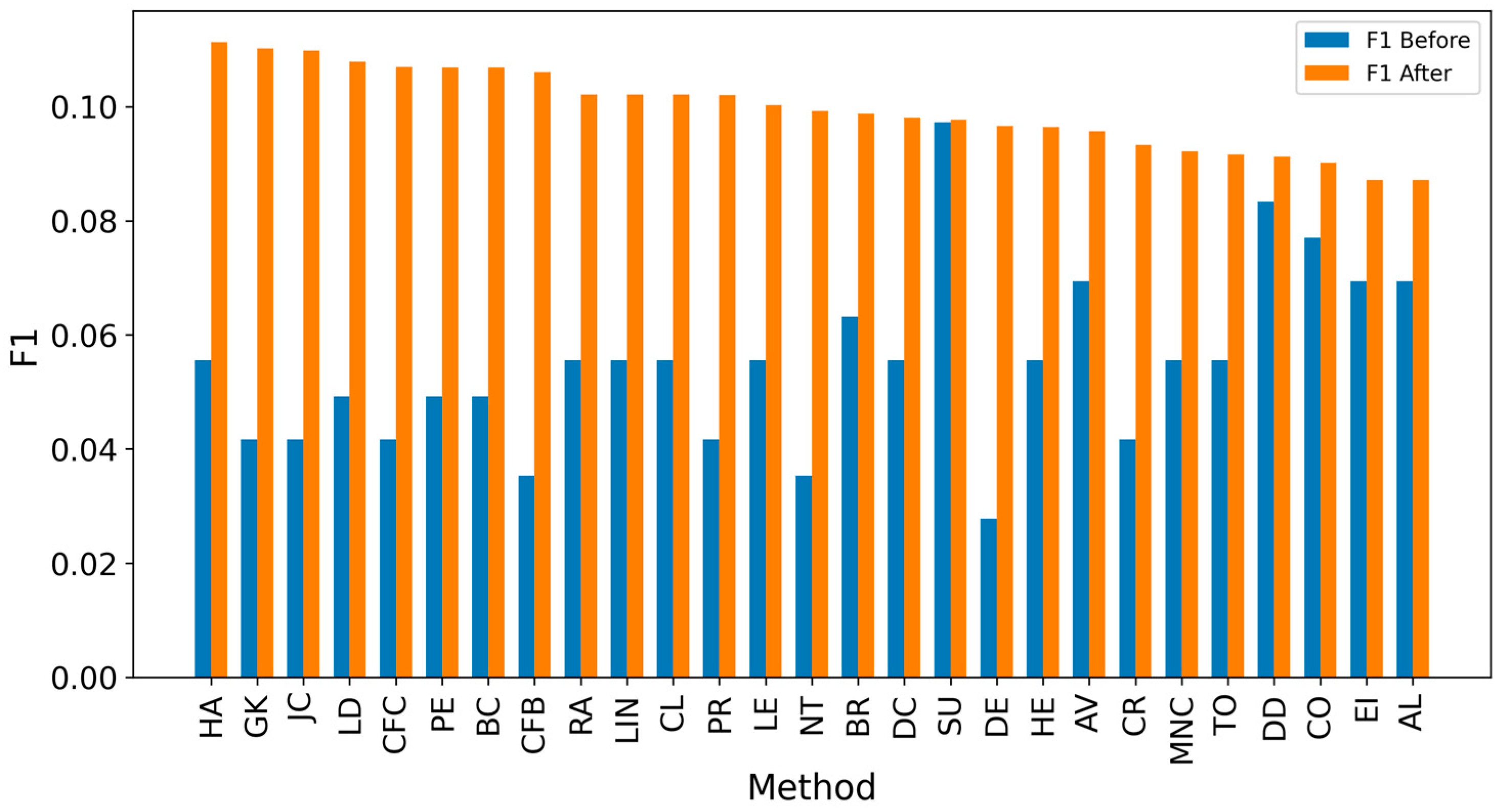
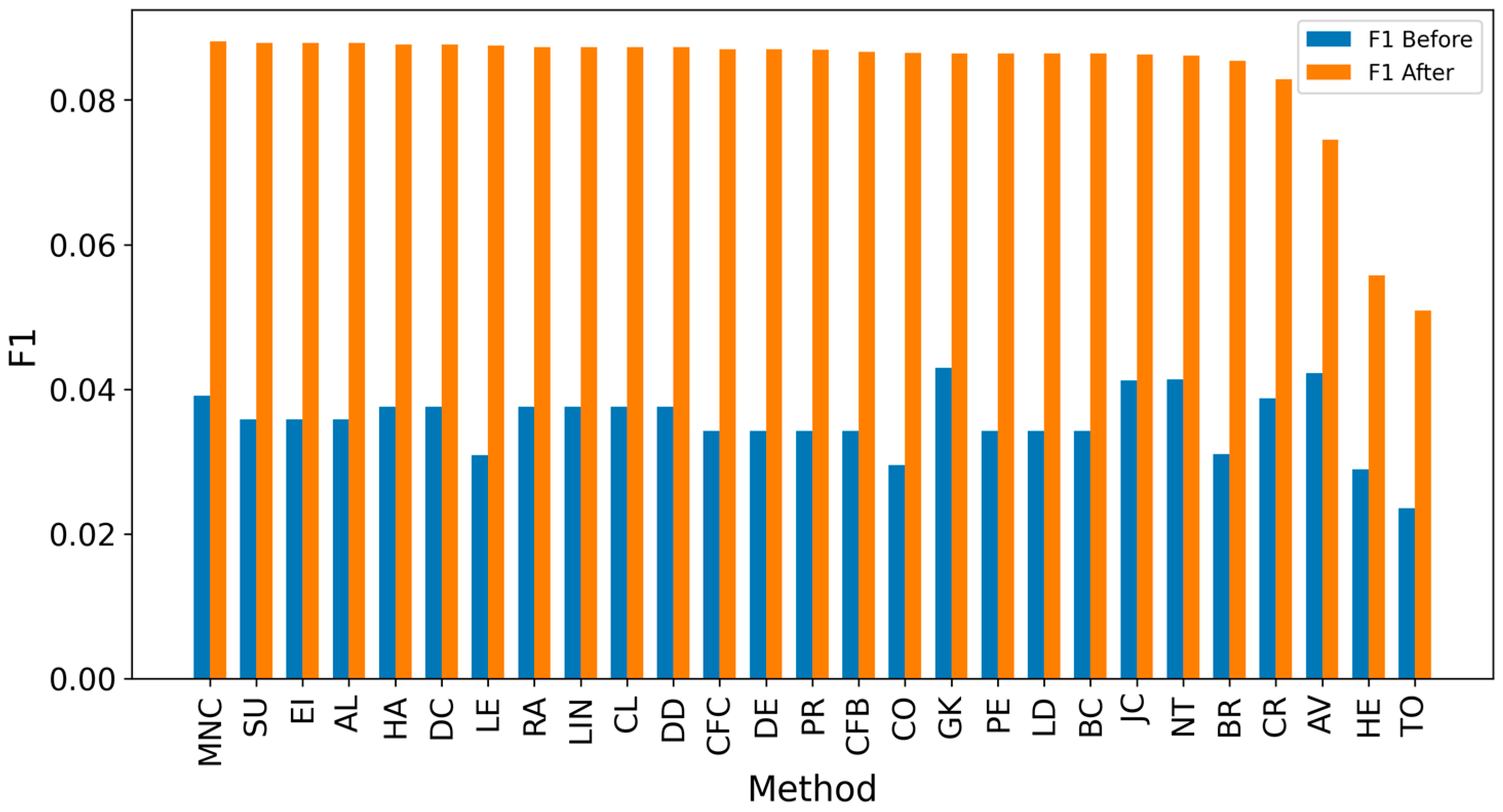
5. Results and Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Results for SIR-Based Simulation


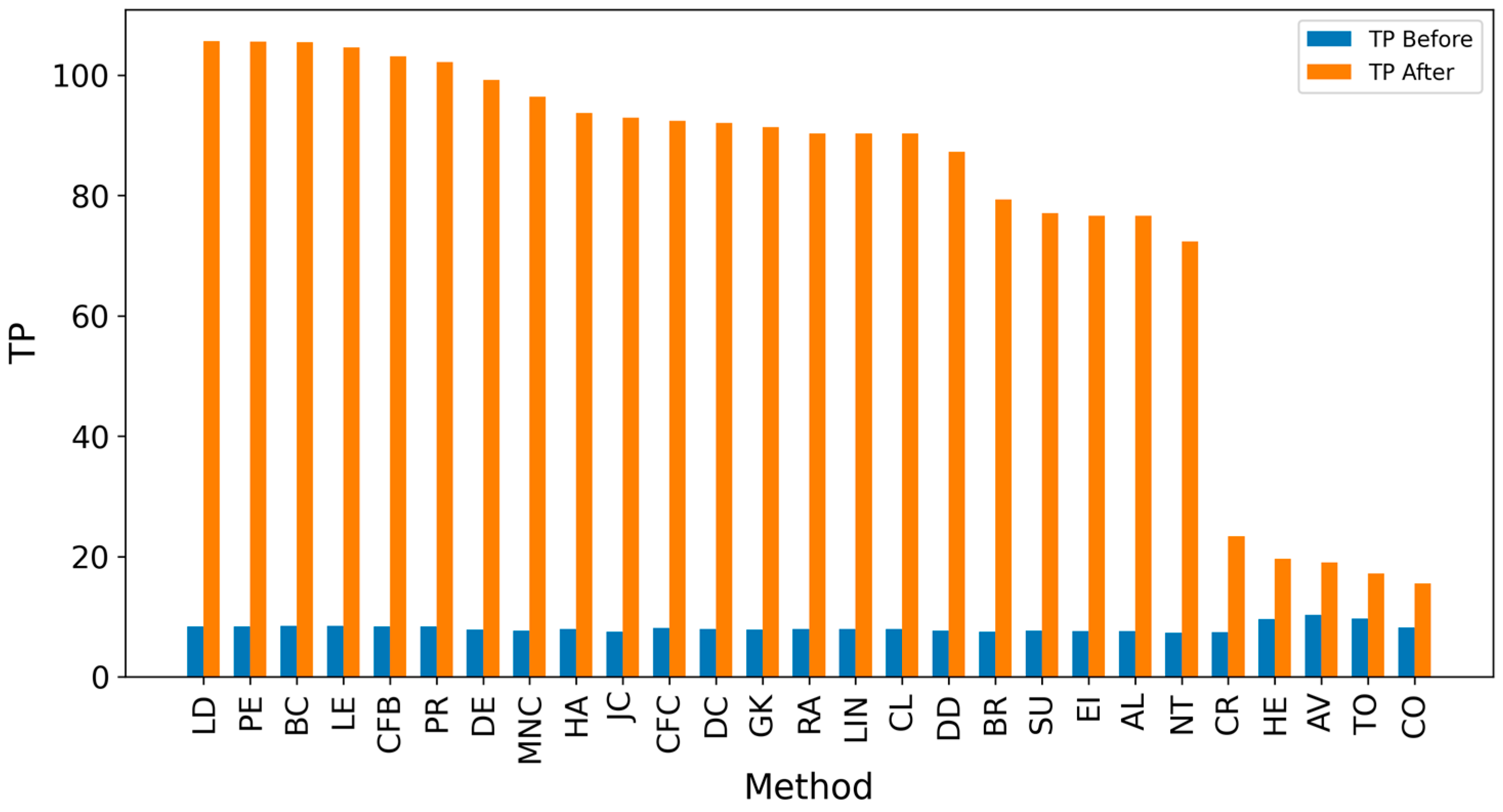
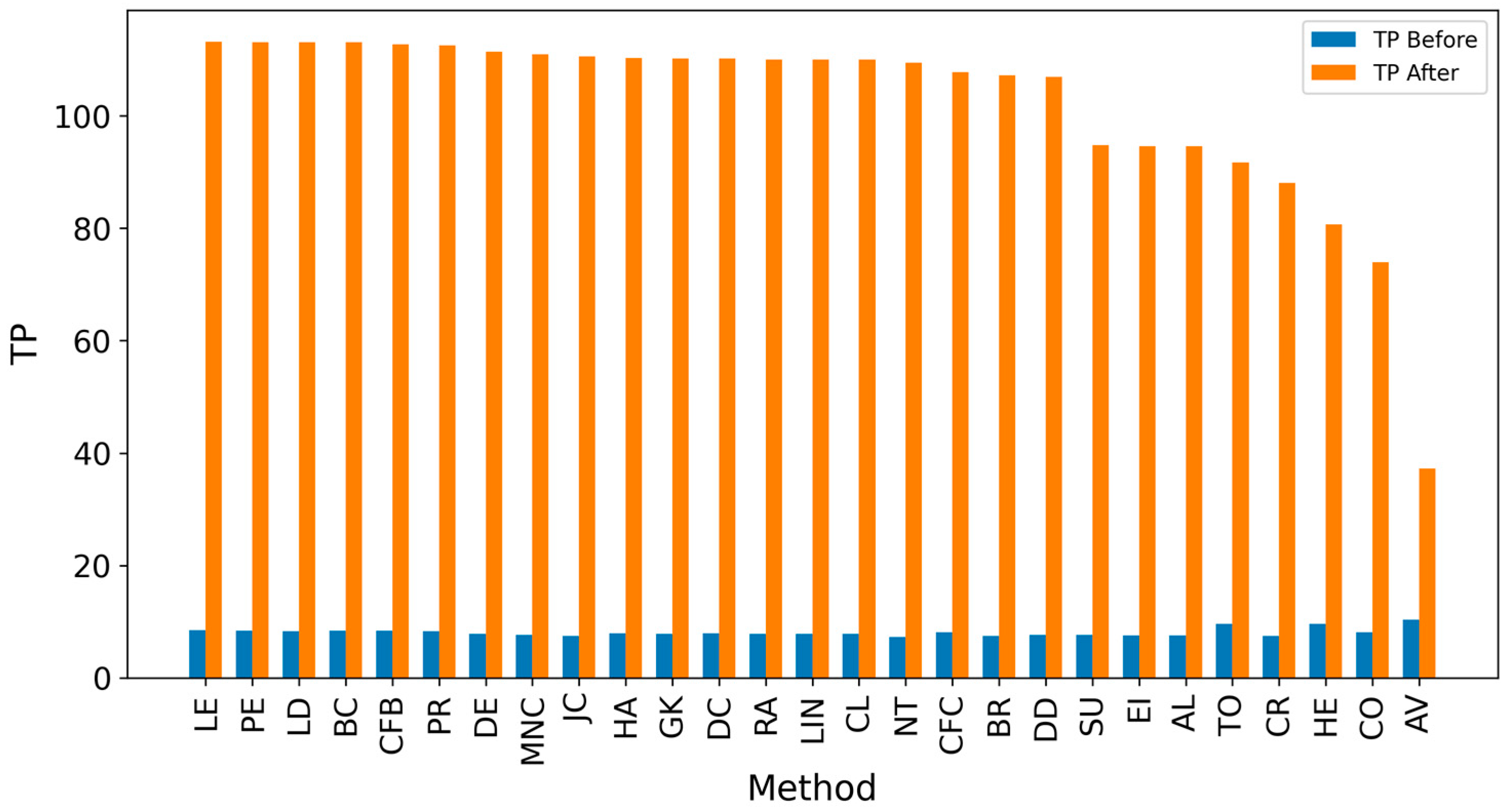
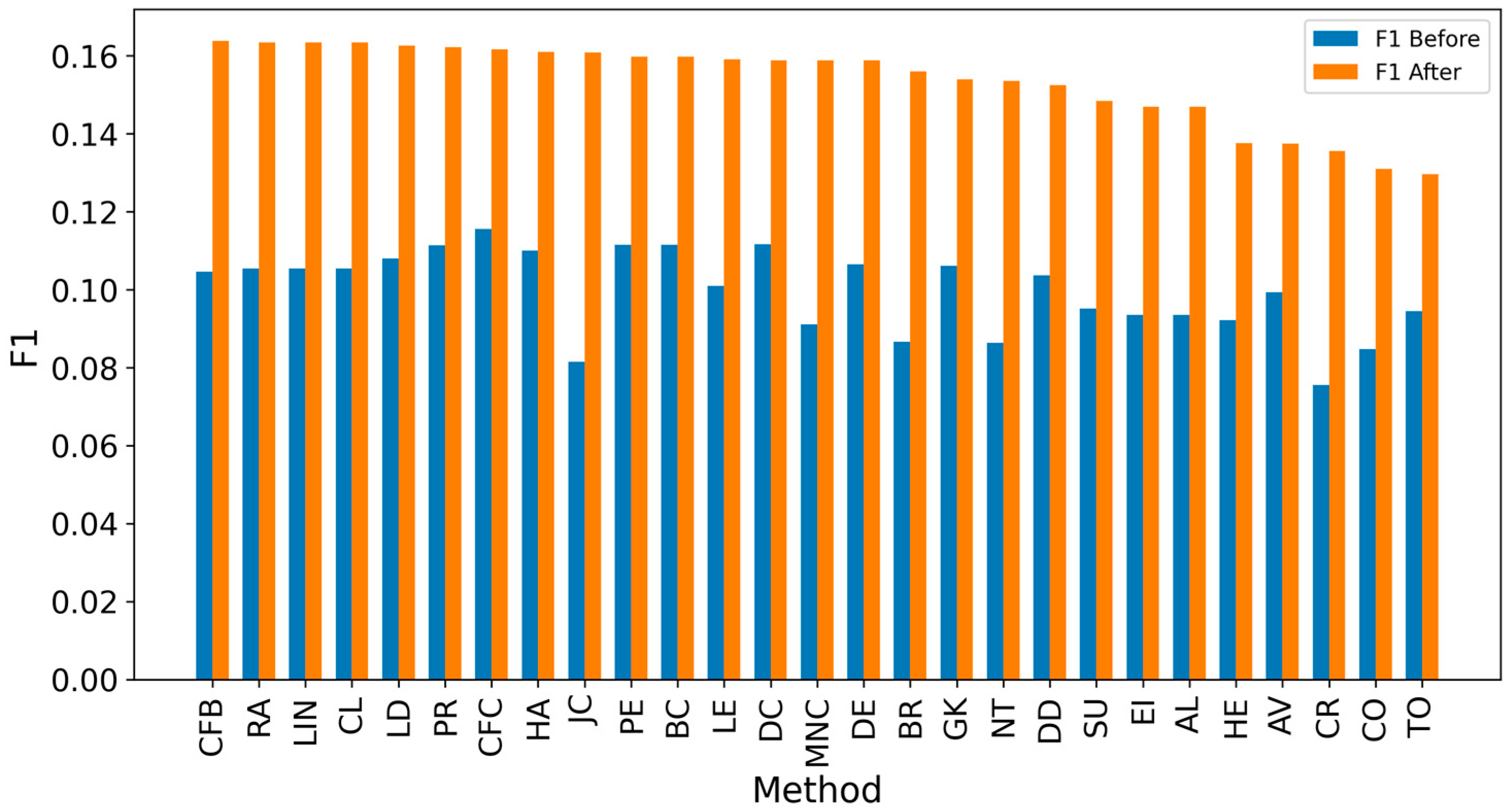



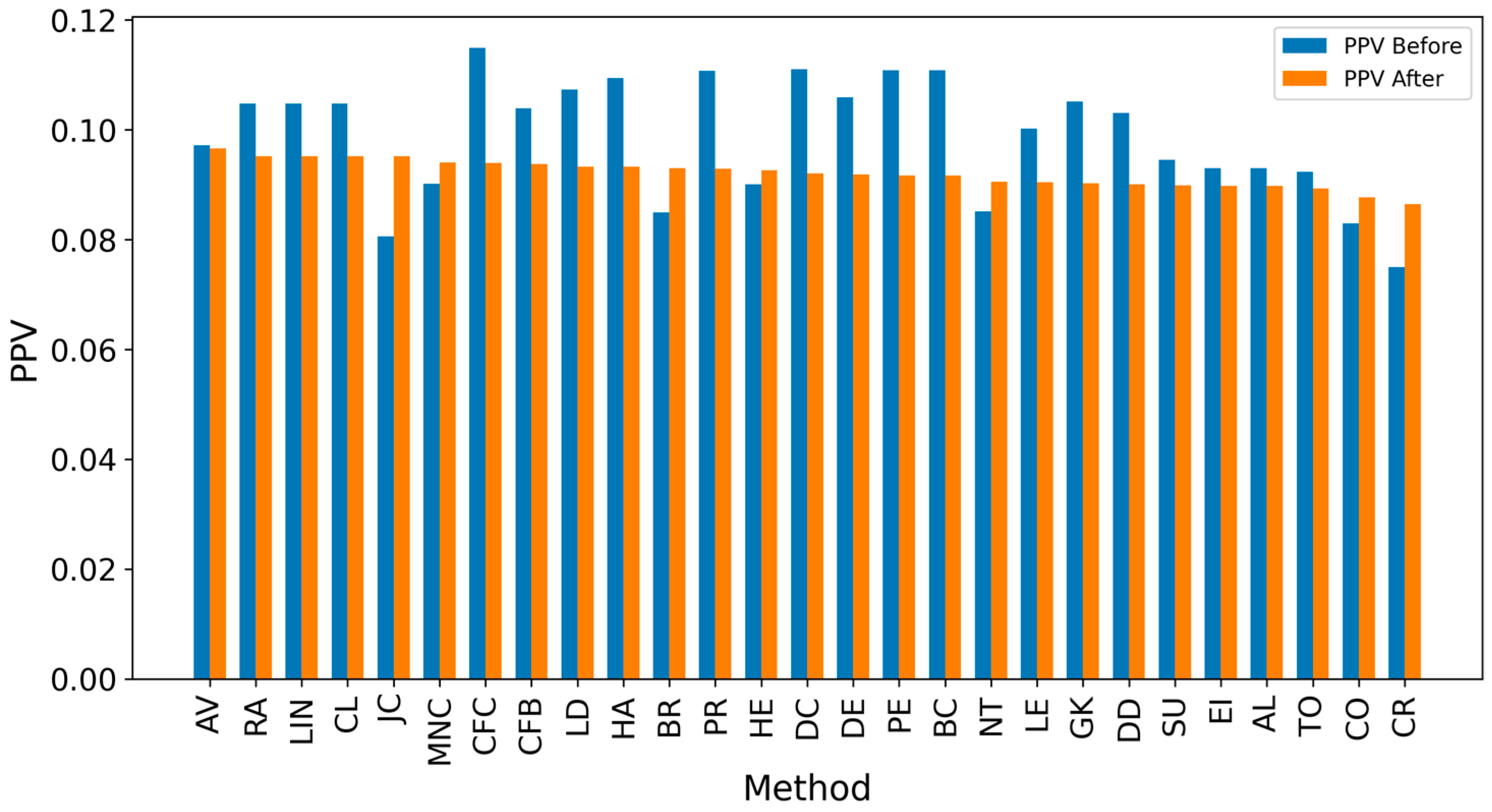









Appendix B. Results for IC-Based Simulation


















References
- Xiao, H.-B.; Hu, F.; Li, P.-Y.; Song, Y.-R.; Zhang, Z.-K. Information Propagation in Hypergraph-Based Social Networks. Entropy 2024, 26, 957. [Google Scholar] [CrossRef]
- Dey, P.; Bhattacharya, S.; Roy, S. A Survey on the Role of Centrality as Seed Nodes for Information Propagation in Large Scale Network. ACMIMS Trans. Data Sci. 2021, 2, 24. [Google Scholar] [CrossRef]
- Frąszczak, D. Information Propagation in Online Social Networks—A Simulation Case Study. In Proceedings of the 38th International Business Information Management Association (IBIMA), Seville, Spain, 23–24 November 2021; International Business Information Management: King of Prussia, PA, USA, 2021. [Google Scholar] [CrossRef]
- Jiang, J.; Wen, S.; Yu, S.; Xiang, Y.; Zhou, W. Identifying Propagation Sources in Networks: State-of-the-Art and Comparative Studies. IEEE Commun. Surv. Tutor. 2017, 19, 465–481. [Google Scholar] [CrossRef]
- Meel, P.; Vishwakarma, D.K. Fake news, rumor, information pollution in social media and web: A contemporary survey of state-of-the-arts, challenges and opportunities. Expert. Syst. Appl. 2020, 153, 112986. [Google Scholar] [CrossRef]
- Frąszczak, D. Fake News Source Detection—The State of The Art Survey for Current Problems and Research. In Proceedings of the 37th International Business Information Management Association (IBIMA), Cordoba, Spain, 30–31 May 2021; International Business Information Management: King of Prussia, PA, USA, 2021. [Google Scholar] [CrossRef]
- Zehmakan, A.N.; Out, C.; Khelejan, S.H. Why Rumors Spread Fast in Social Networks, and How to Stop It. arXiv 2023, arXiv:2305.08558. [Google Scholar] [CrossRef]
- Jin, R.; Wu, W. Schemes of Propagation Models and Source Estimators for Rumor Source Detection in Online Social Networks: A Short Survey of a Decade of Research. Discret. Math. Algorithms Appl. 2021, 12, 2130002. [Google Scholar] [CrossRef]
- Yu, Z.; Lu, S.; Wang, D.; Li, Z. Modeling and analysis of rumor propagation in social networks. Inf. Sci. 2021, 580, 857–873. [Google Scholar] [CrossRef]
- Shelke, S.; Attar, V. Source detection of rumor in social network—A review. Online Soc. Netw. Media 2019, 9, 30–42. [Google Scholar] [CrossRef]
- Liu, Y.; Shen, H.; Shi, L. A review of rumor detection techniques in social networks. J. Intell. Fuzzy Syst. 2022, 44, 3561–3578. [Google Scholar] [CrossRef]
- Aïmeur, E.; Amri, S.; Brassard, G. Fake news, disinformation and misinformation in social media: A review. Soc. Netw. Anal. Min. 2023, 13, 30. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, R.; Sun, J.; Wang, Y.; You, H.; Zhang, Y.; Localization, R. Detection and Prediction in Social Network. IEEE Trans. Comput. Soc. Syst. 2022, 11, 3168–3178. [Google Scholar] [CrossRef]
- Frąszczak, D. Detecting rumor outbreaks in online social networks. Soc. Netw. Anal. Min. 2023, 13, 91. [Google Scholar] [CrossRef] [PubMed]
- Ali, S.S.; Anwar, T.; Rizvi, S.A.M. A Revisit to the Infection Source Identification Problem under Classical Graph Centrality Measures. Online Soc. Netw. Media 2020, 17, 100061. [Google Scholar] [CrossRef]
- Das, A.; Biswas, A. Rumor Source Identification on Social Networks: A Combined Network Centrality Approach. In Progress in Advanced Computing and Intelligent Engineering; Advances in Intelligent Systems and Computing; Panigrahi, C.R., Pati, B., Pattanayak, B.K., Amic, S., Li, K.-C., Eds.; Springer: Singapore, 2021; Volume 1299, pp. 269–280. [Google Scholar] [CrossRef]
- Das, K.; Sinha, S.K. Centrality measure based approach for detection of malicious nodes in twitter social network. Int. J. Eng. Technol. 2018, 7, 518. [Google Scholar] [CrossRef]
- Britt, B.C.; Hayes, J.L.; Musaev, A.; Sheinidashtegol, P.; Parrott, S.; Albright, D.L. Using targeted betweenness centrality to identify bridges to neglected users in the Twitter conversation on veteran suicide. Soc. Netw. Anal. Min. 2021, 11, 40. [Google Scholar] [CrossRef]
- Shah, D.; Zaman, T. Detecting sources of computer viruses in networks: Theory and experiment. In Proceedings of the ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems—SIGMETRICS ’10, New York, NY, USA, 14–18 June 2010; ACM Press: New York, NY, USA, 2010; p. 203. [Google Scholar] [CrossRef]
- Comin, C.H.; Costa, L.d.F. Identifying the starting point of a spreading process in complex networks. Phys. Rev. E 2011, 84, 056105. [Google Scholar] [CrossRef]
- Du, Y.; Gao, C.; Chen, X.; Hu, Y.; Sadiq, R.; Deng, Y. A new closeness centrality measure via effective distance in complex networks. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 033112. [Google Scholar] [CrossRef]
- Shah, D.; Zaman, T. Rumors in a Network: Who’s the Culprit? IEEE Trans. Inf. Theory 2011, 57, 5163–5181. [Google Scholar] [CrossRef]
- Prakash, B.A.; Vreeken, J.; Faloutsos, C. Spotting Culprits in Epidemics: How Many and Which Ones? In Proceedings of the 2012 IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 11–20. [Google Scholar] [CrossRef]
- Ying, L.; Zhu, K. Diffusion Source Localization in Large Networks. In Synthesis Lectures on Learning, Networks, and Algorithms; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Frąszczak, D.; Frąszczak, E. NSDLib: A comprehensive python library for network source detection and evaluation. SoftwareX 2024, 28, 101950. [Google Scholar] [CrossRef]
- Frąszczak, D.; Frąszczak, E. NetCenLib: A comprehensive python library for network centrality analysis and evaluation. SoftwareX 2024, 26, 101699. [Google Scholar] [CrossRef]
- Borgatti, S.P.; Everett, M.G. A Graph-theoretic perspective on centrality. Soc. Netw. 2006, 28, 466–484. [Google Scholar] [CrossRef]
- Das, K.; Samanta, S.; Pal, M. Study on centrality measures in social networks: A survey. Soc. Netw. Anal. Min. 2018, 8, 13. [Google Scholar] [CrossRef]
- Cui, L.; Lee, D. CoAID: COVID-19 Healthcare Misinformation Dataset. arXiv 2020, arXiv:2006.00885. [Google Scholar] [CrossRef]
- Kochkina, E.; Liakata, M.; Zubiaga, A. PHEME dataset for Rumour Detection and Veracity Classification’. Figshare. Dataset 2018, 10, 46531457. [Google Scholar] [CrossRef]
- Shu, K.; Mahudeswaran, D.; Wang, S.; Lee, D.; Liu, H. FakeNewsNet: A Data Repository with News Content, Social Context and Spatialtemporal Information for Studying Fake News on Social Media. Big Data 2021, 8, 171–188. [Google Scholar] [CrossRef]
- Shakarian, P.; Bhatnagar, A.; Aleali, A.; Shaabani, E.; Guo, R. The Independent Cascade and Linear Threshold Models. In Diffusion in Social Networks; Springer Briefs in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; pp. 35–48. [Google Scholar] [CrossRef]
- Peralta, A.F.; Kertész, J.; Iñiguez, G. Opinion dynamics in social networks: From models to data. arXiv 2022, arXiv:2201.01322. [Google Scholar] [CrossRef]
- Gray, C.; Mitchell, L.; Roughan, M. Bayesian inference of network structure from information cascades. arXiv 2019, arXiv:1908.03318. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Q.; Si, L.; Liu, Y. Rumor Detection on Social Media: Datasets, Methods and Opportunities. In Proceedings of the Second Workshop on Natural Language Processing for Internet Freedom: Censorship, Disinformation, and Propaganda, Hong Kong, China, 4 November 2019; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 66–75. [Google Scholar] [CrossRef]
- Murayama, T. Dataset of Fake News Detection and Fact Verification: A Survey. arXiv 2021, arXiv:2111.03299. [Google Scholar] [CrossRef]
- Ju, C.; Jiang, Y.; Bao, F.; Zou, B.; Xu, C. Online Rumor Diffusion Model Based on Variation and Silence Phenomenon in the Context of COVID-19. Front. Public Health 2022, 9, 788475. [Google Scholar] [CrossRef]
- Frąszczak, D. RPaSDT—Rumor Propagation and Source Detection Toolkit. SoftwareX 2022, 17, 100988. [Google Scholar] [CrossRef]
- Rossetti, G.; Milli, L.; Rinzivillo, S.; Sîrbu, A.; Pedreschi, D.; Giannotti, F. NDlib: A python library to model and analyze diffusion processes over complex networks. Int. J. Data Sci. Anal. 2018, 5, 61–79. [Google Scholar] [CrossRef]
- Kirkland, S. Algebraic connectivity for vertex-deleted subgraphs, and a notion of vertex centrality. Discret. Math. 2010, 310, 911–921. [Google Scholar] [CrossRef]
- Del Rio, G.; Koschützki, D.; Coello, G. How to identify essential genes from molecular networks? BMC Syst. Biol. 2009, 3, 102. [Google Scholar] [CrossRef]
- Viswanath, M. Ontology-Based Automatic Text Summarization. Master’s Thesis, University of Georgia, Athens, GA, USA, 2009. [Google Scholar]
- Brandes, U. A faster algorithm for betweenness centrality*. J. Math. Sociol. 2001, 25, 163–177. [Google Scholar] [CrossRef]
- Latora, V.; Marchiori, M. Efficient Behavior of Small-World Networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef]
- Chen, D.-B.; Gao, H.; Lü, L.; Zhou, T. Identifying Influential Nodes in Large-Scale Directed Networks: The Role of Clustering. PLoS ONE 2013, 8, e77455. [Google Scholar] [CrossRef]
- Bae, J.; Kim, S. Identifying and ranking influential spreaders in complex networks by neighborhood coreness. Phys. Stat. Mech. Its Appl. 2014, 395, 549–559. [Google Scholar] [CrossRef]
- Brandes, U.; Fleischer, D. Centrality Measures Based on Current Flow. In Annual Symposium on Theoretical Aspects of Computer Science; Lecture Notes in Computer Science; Diekert, V., Durand, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3404, pp. 533–544. [Google Scholar] [CrossRef]
- Newman, M.E.J. A measure of betweenness centrality based on random walks. Soc. Netw. 2005, 27, 39–54. [Google Scholar] [CrossRef]
- Jalili, M.; Salehzadeh-Yazdi, A.; Asgari, Y.; Arab, S.S.; Yaghmaie, M.; Ghavamzadeh, A.; Alimoghaddam, K.; Li, T. CentiServer: A Comprehensive Resource, Web-Based Application and R Package for Centrality Analysis. PLoS ONE 2015, 10, e0143111. [Google Scholar] [CrossRef]
- Stephenson, K.; Zelen, M. Rethinking centrality: Methods and examples. Soc. Netw. 1989, 11, 1–37. [Google Scholar] [CrossRef]
- Jackson, M.O. Social and Economic Networks; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Chebotarev, P.; Gubanov, D. How to choose the most appropriate centrality measure? arXiv 2020, arXiv:2003.01052. [Google Scholar] [CrossRef]
- Kundu, S.; Murthy, C.A.; Pal, S.K. A New Centrality Measure for Influence Maximization in Social Networks. In Pattern Recognition and Machine Intelligence; Lecture Notes in Computer Science; Kuznetsov, S.O., Mandal, D.P., Kundu, M.K., Pal, S.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6744, pp. 242–247. [Google Scholar] [CrossRef]
- Rodriguez, J.A.; Estrada, E.; Gutierrez, A. Functional centrality in graphs. arXiv 2006, arXiv:math/0610141. [Google Scholar] [CrossRef][Green Version]
- Opsahl, T.; Agneessens, F.; Skvoretz, J. Node centrality in weighted networks: Generalizing degree and shortest paths. Soc. Netw. 2010, 32, 245–251. [Google Scholar] [CrossRef]
- Durón, C. Heatmap centrality: A new measure to identify super-spreader nodes in scale-free networks. PLoS ONE 2020, 15, e0235690. [Google Scholar] [CrossRef] [PubMed]
- Joyce, K.E.; Laurienti, P.J.; Burdette, J.H.; Hayasaka, S. A New Measure of Centrality for Brain Networks. PLoS ONE 2010, 5, e12200. [Google Scholar] [CrossRef] [PubMed]
- Lin, N. Foundations of Social Research; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Brandes, U. On variants of shortest-path betweenness centrality and their generic computation. Soc. Netw. 2008, 30, 136–145. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Chin, C.-H.; Wu, H.-H.; Chen, S.-H.; Ho, C.-W.; Ko, M.-T. Hubba: Hub objects analyzer—A framework of interactome hubs identification for network biology. Nucleic Acids Res. 2008, 36 (Suppl. S2), W438–W443. [Google Scholar] [CrossRef]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual Web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Piraveenan, M.; Prokopenko, M.; Hossain, L. Percolation Centrality: Quantifying Graph-Theoretic Impact of Nodes during Percolation in Networks. PLoS ONE 2013, 8, e53095. [Google Scholar] [CrossRef]
- Valente, T.W.; Foreman, R.K. Integration and radiality: Measuring the extent of an individual’s connectedness and reachability in a network. Soc. Netw. 1998, 20, 89–105. [Google Scholar] [CrossRef]
- Estrada, E.; Rodriguez-Velazquez, J.A. Subgraph Centrality in Complex Networks. arXiv 2005, arXiv:cond-mat/0504730v1. [Google Scholar] [CrossRef]
- Assenov, Y.; Ramírez, F.; Schelhorn, S.-E.; Lengauer, T.; Albrecht, M. Computing topological parameters of biological networks. Bioinformatics 2008, 24, 282–284. [Google Scholar] [CrossRef]
- Frąszczak, D. Leadership-oriented community detection: Enhancing accuracy in social network analysis. Inf. Sci. 2025, 718, 122421. [Google Scholar] [CrossRef]
- Held, P.; Krause, B.; Kruse, R. Dynamic Clustering in Social Networks Using Louvain and Infomap Method. In Proceedings of the 2016 Third European Network Intelligence Conference (ENIC), Wroclaw, Poland, 5–7 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 61–68. [Google Scholar] [CrossRef][Green Version]
- Traag, V.; Waltman, L.; van Eck, N.J. From Louvain to Leiden: Guaranteeing well-connected communities. Sci. Rep. 2019, 9, 5233. [Google Scholar] [CrossRef]
- Rajeh, S.; Cherifi, H. Ranking influential nodes in complex networks with community structure. PLoS ONE 2022, 17, e0273610. [Google Scholar] [CrossRef]
- Liu, C.; Zehmakan, A.N.; Zhang, Z. Fast Query of Biharmonic Distance in Networks. arXiv 2024, arXiv:2408.13538. [Google Scholar] [CrossRef]

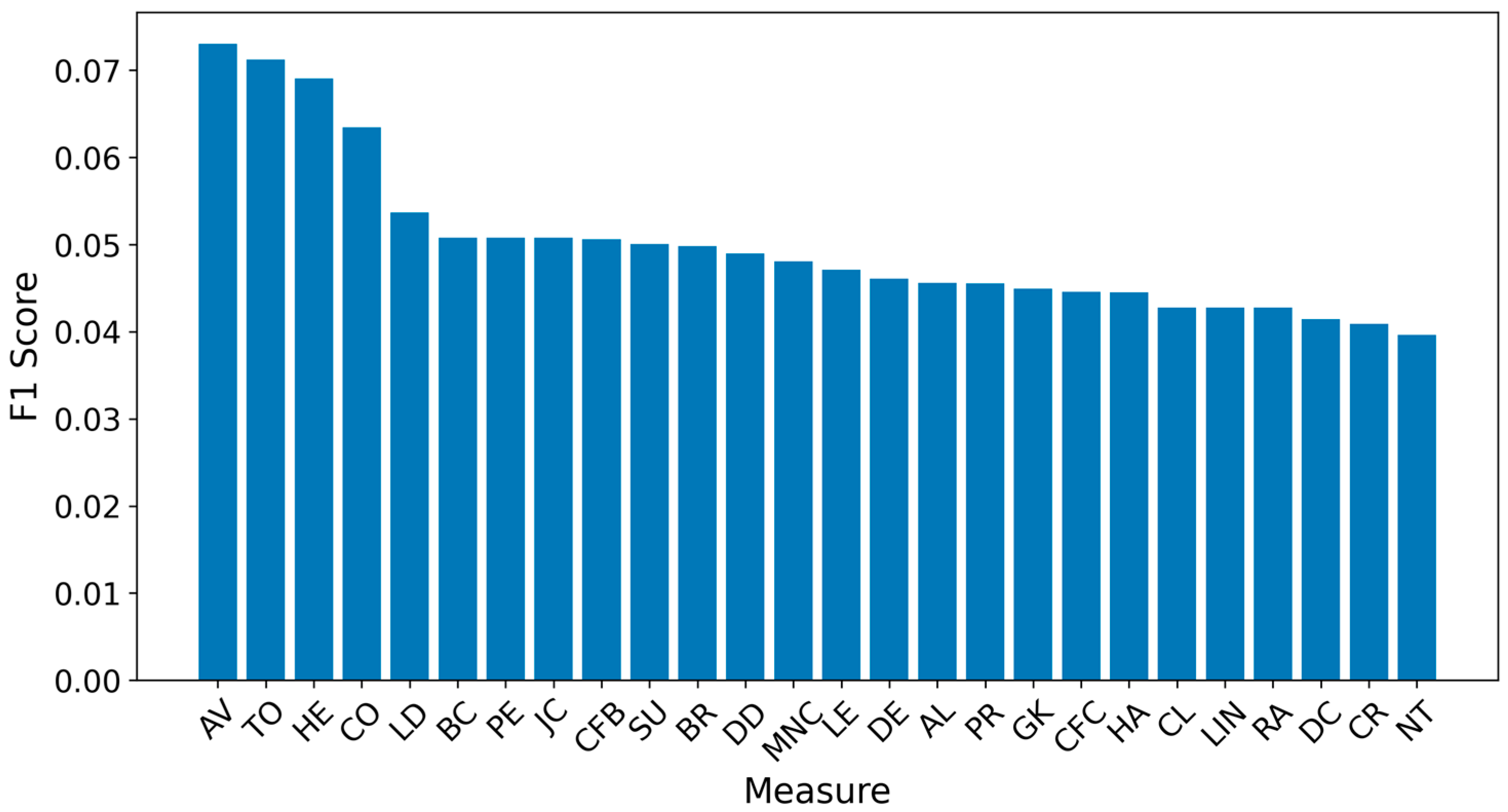
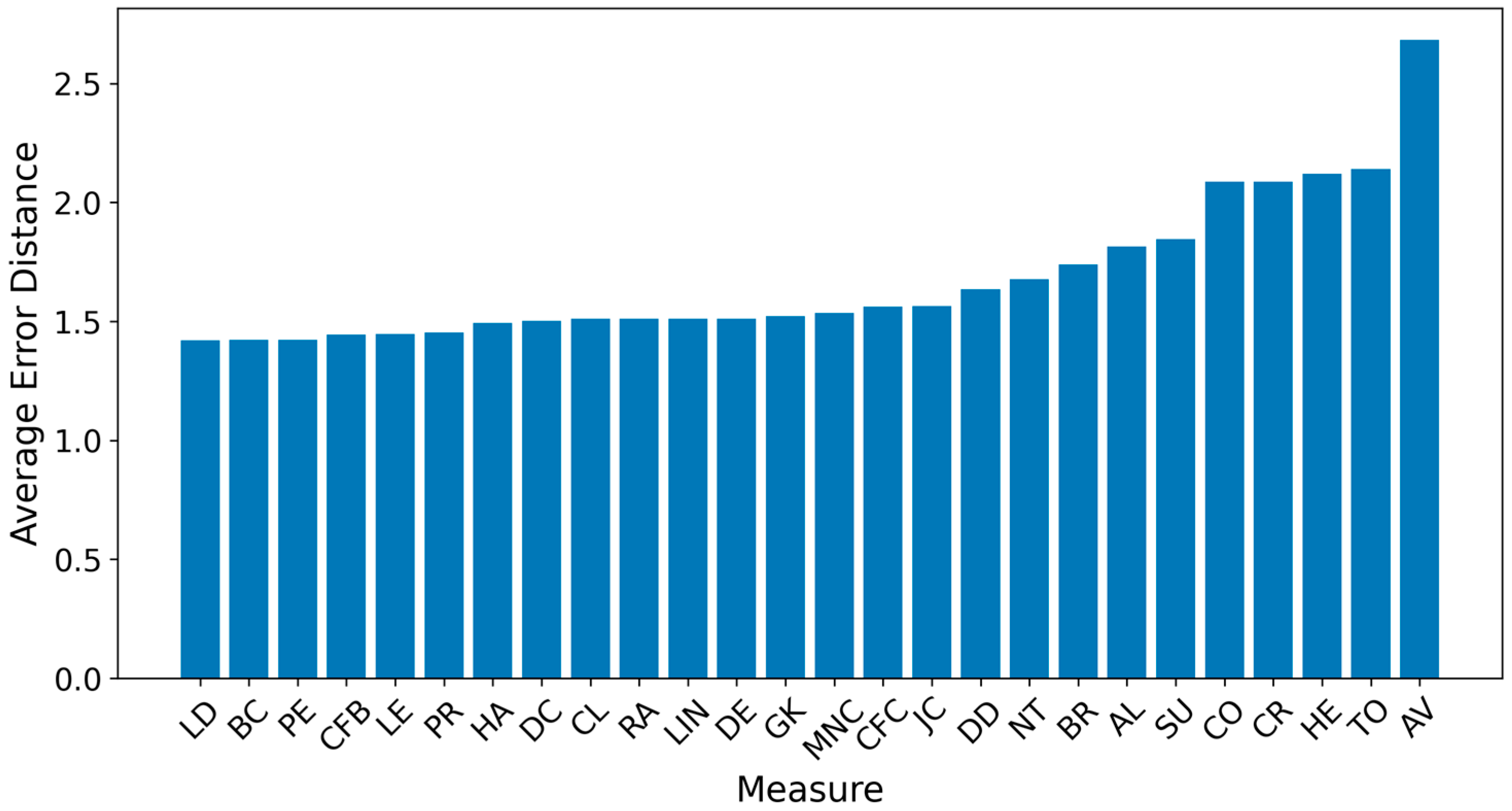
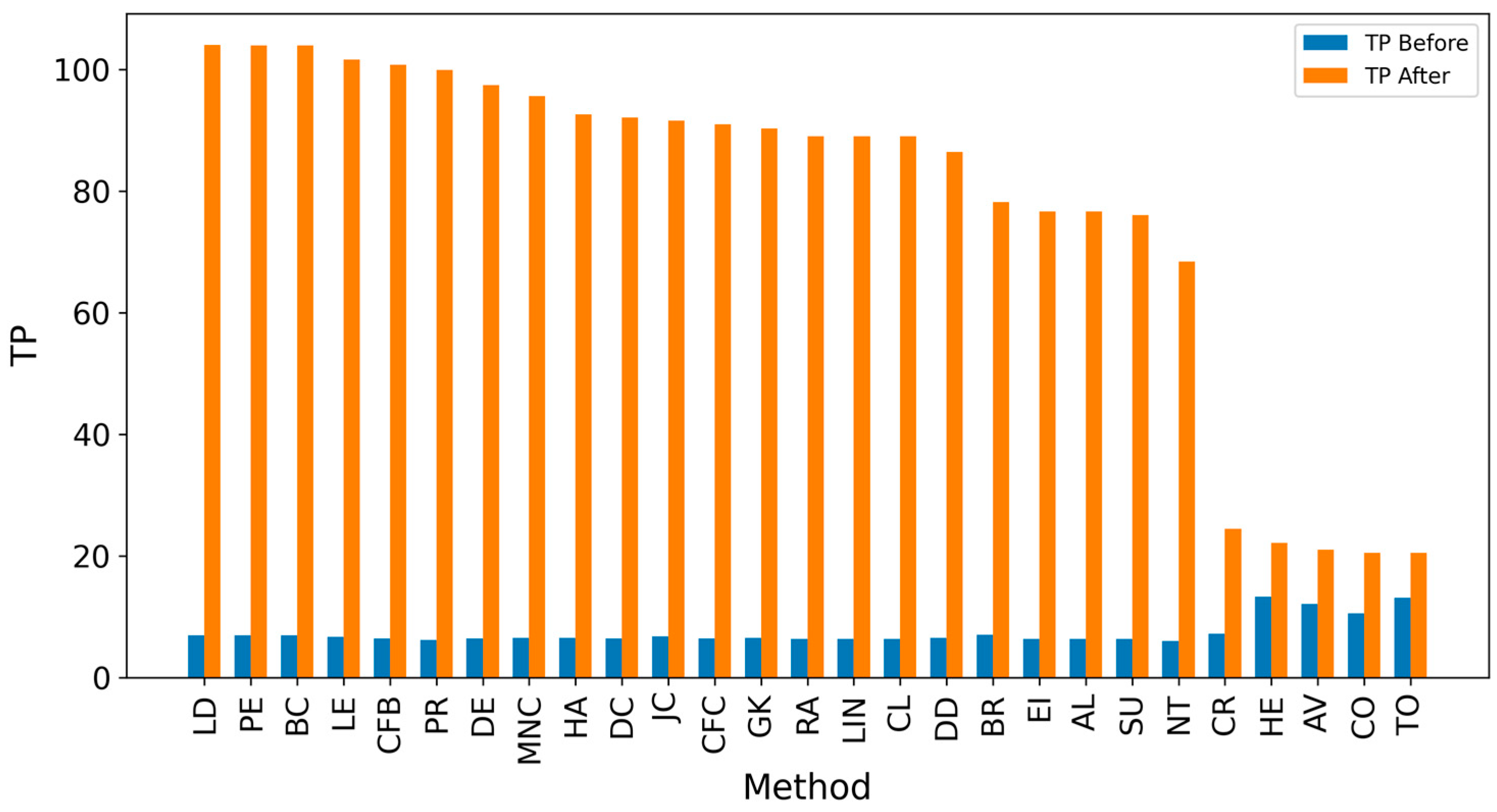
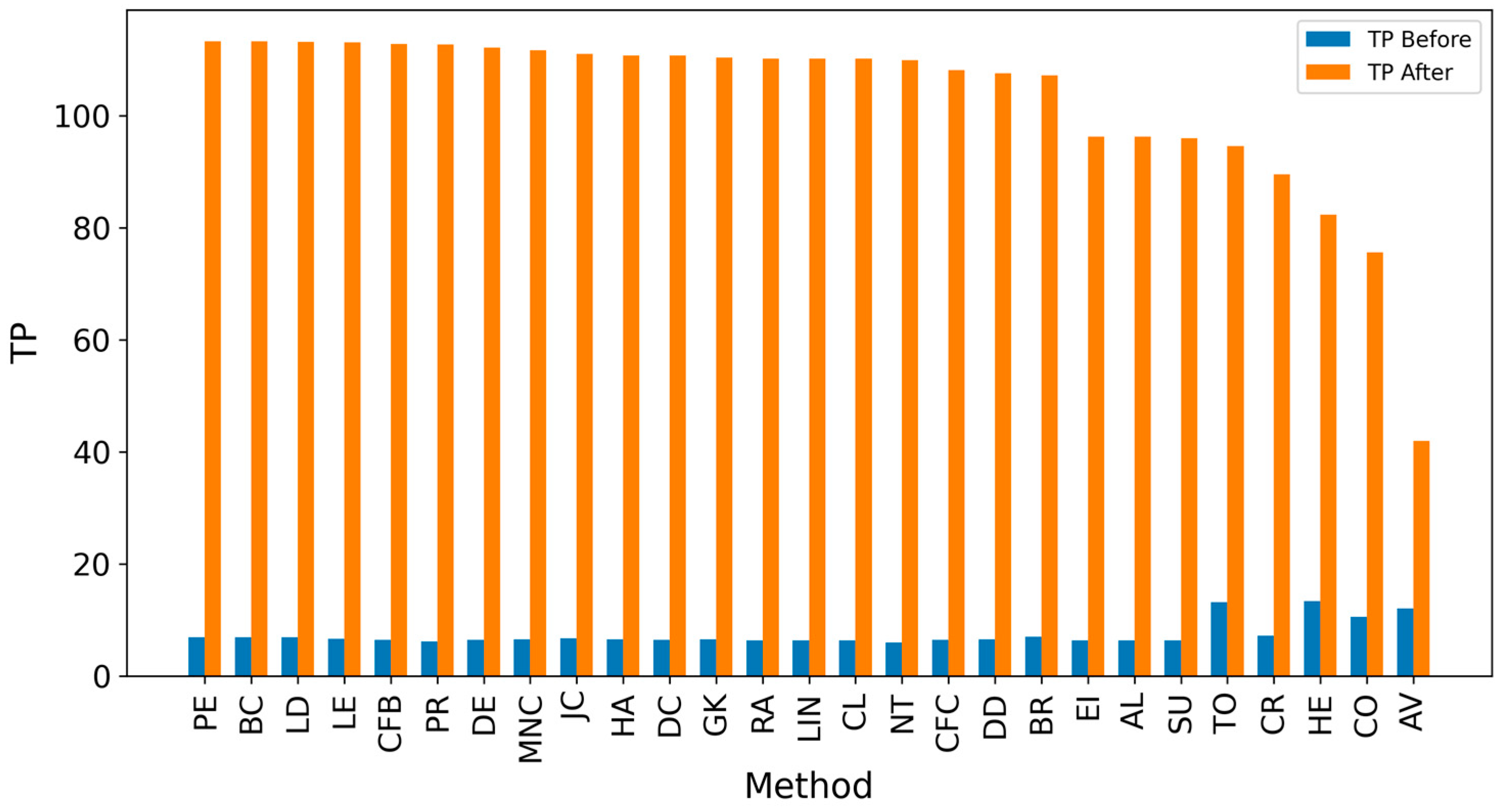
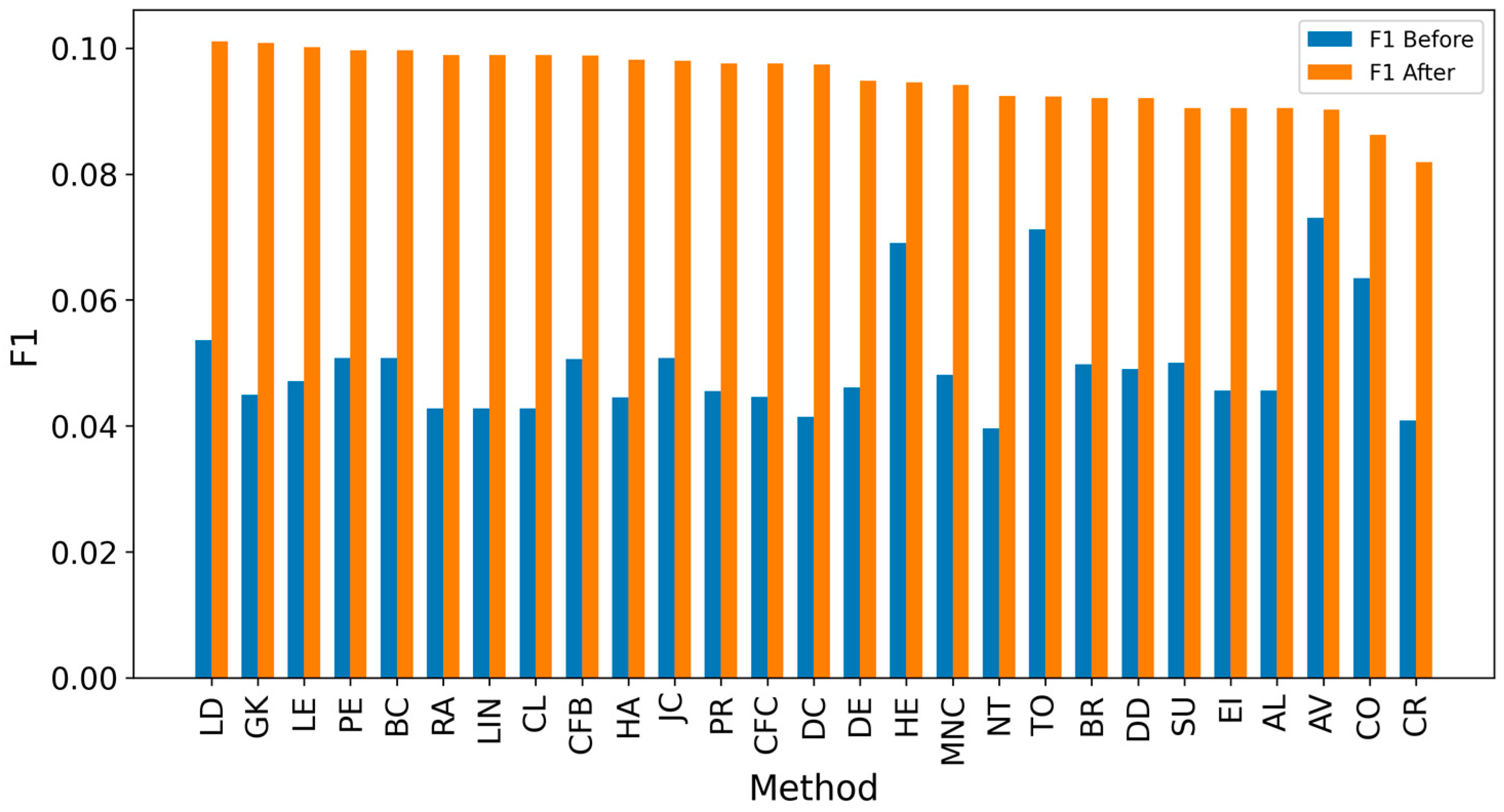

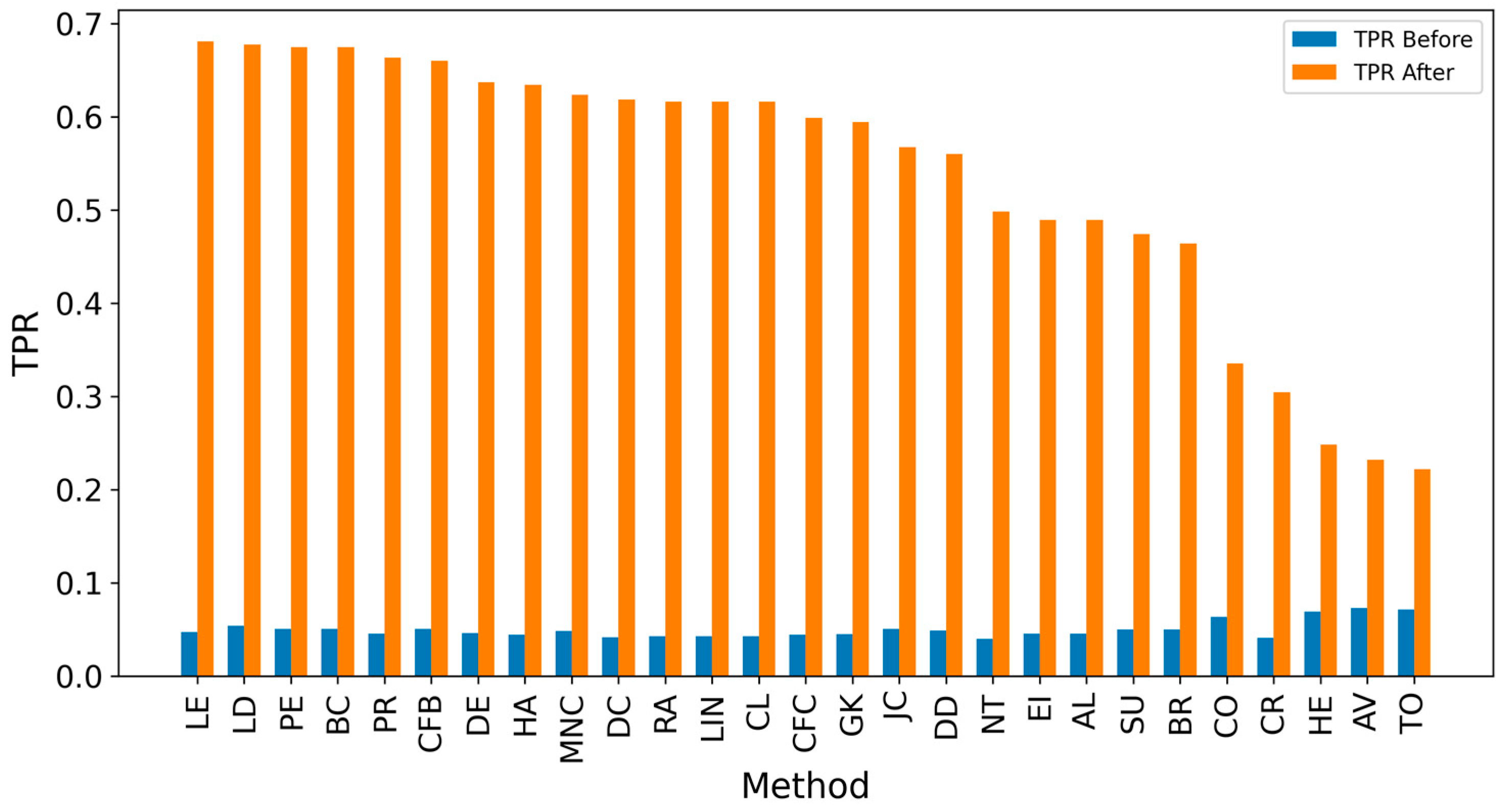
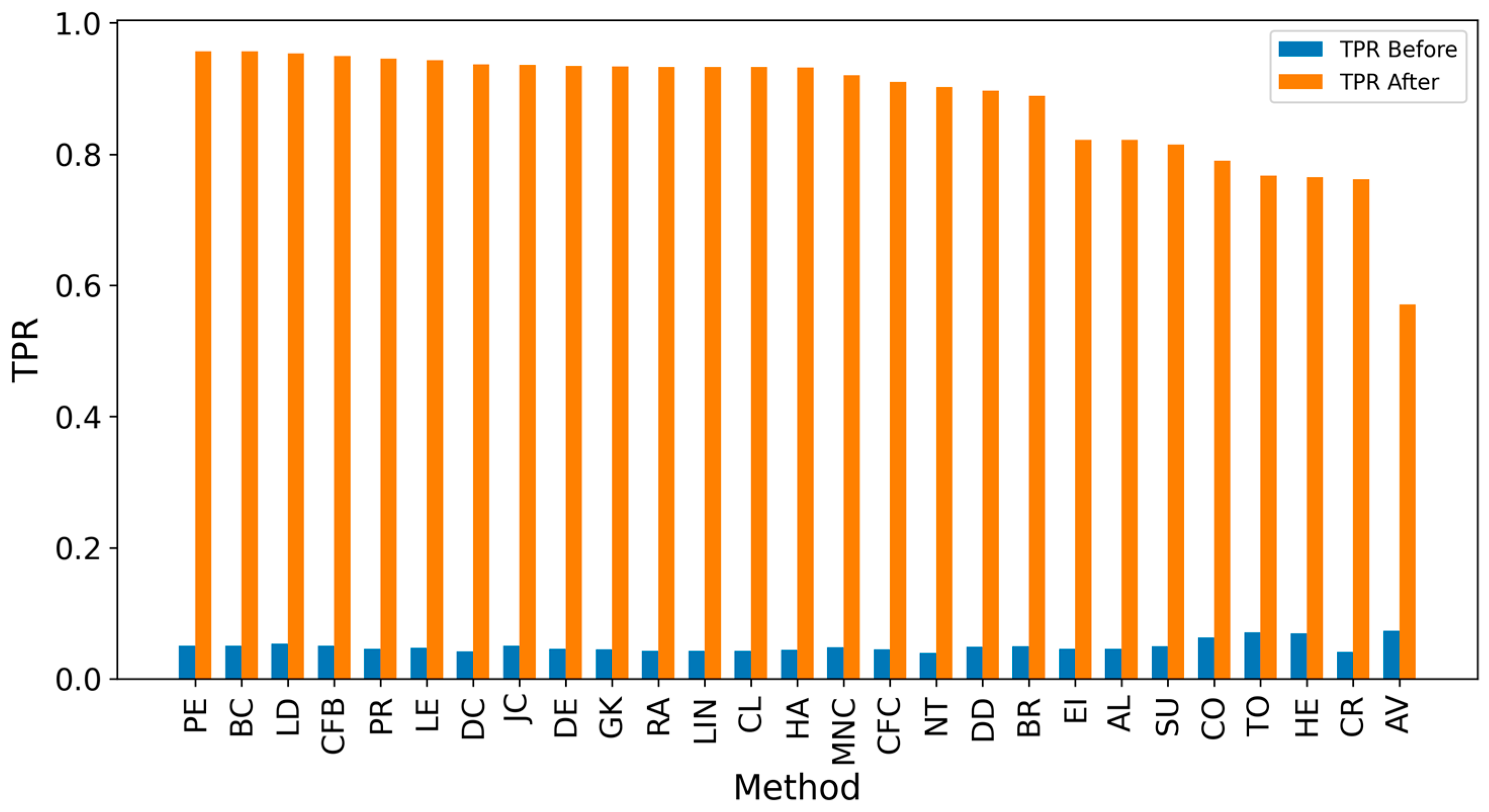
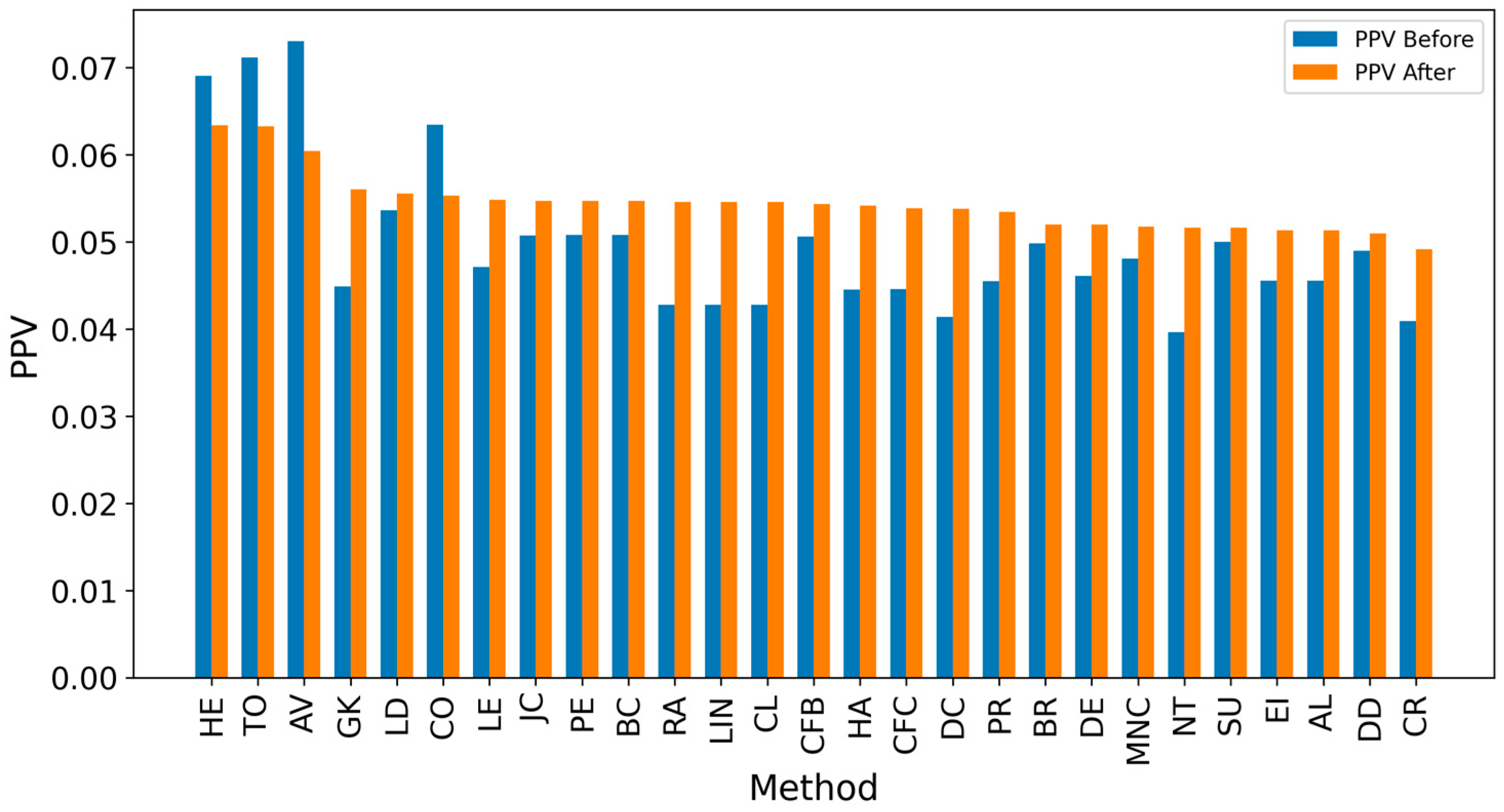


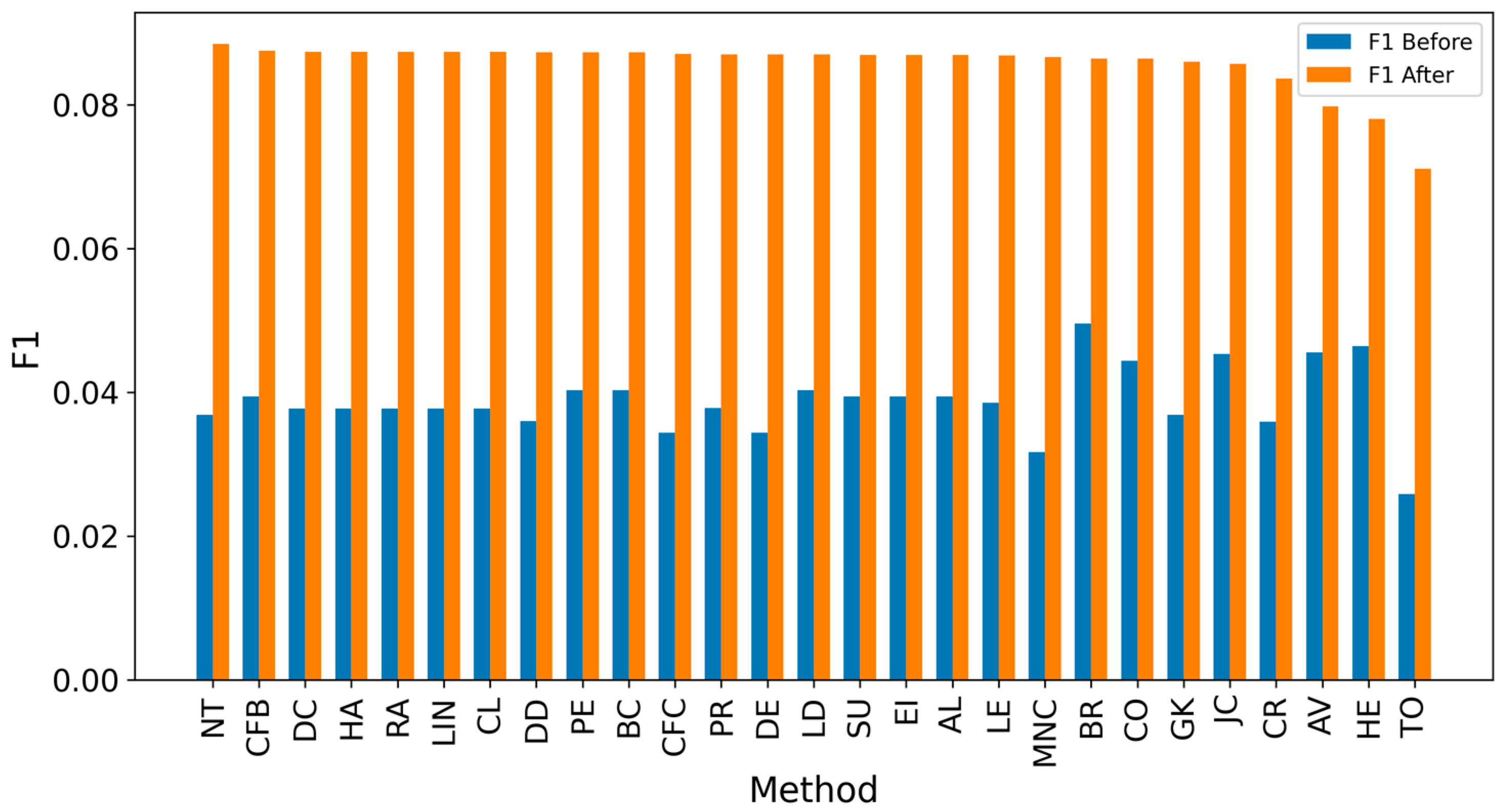
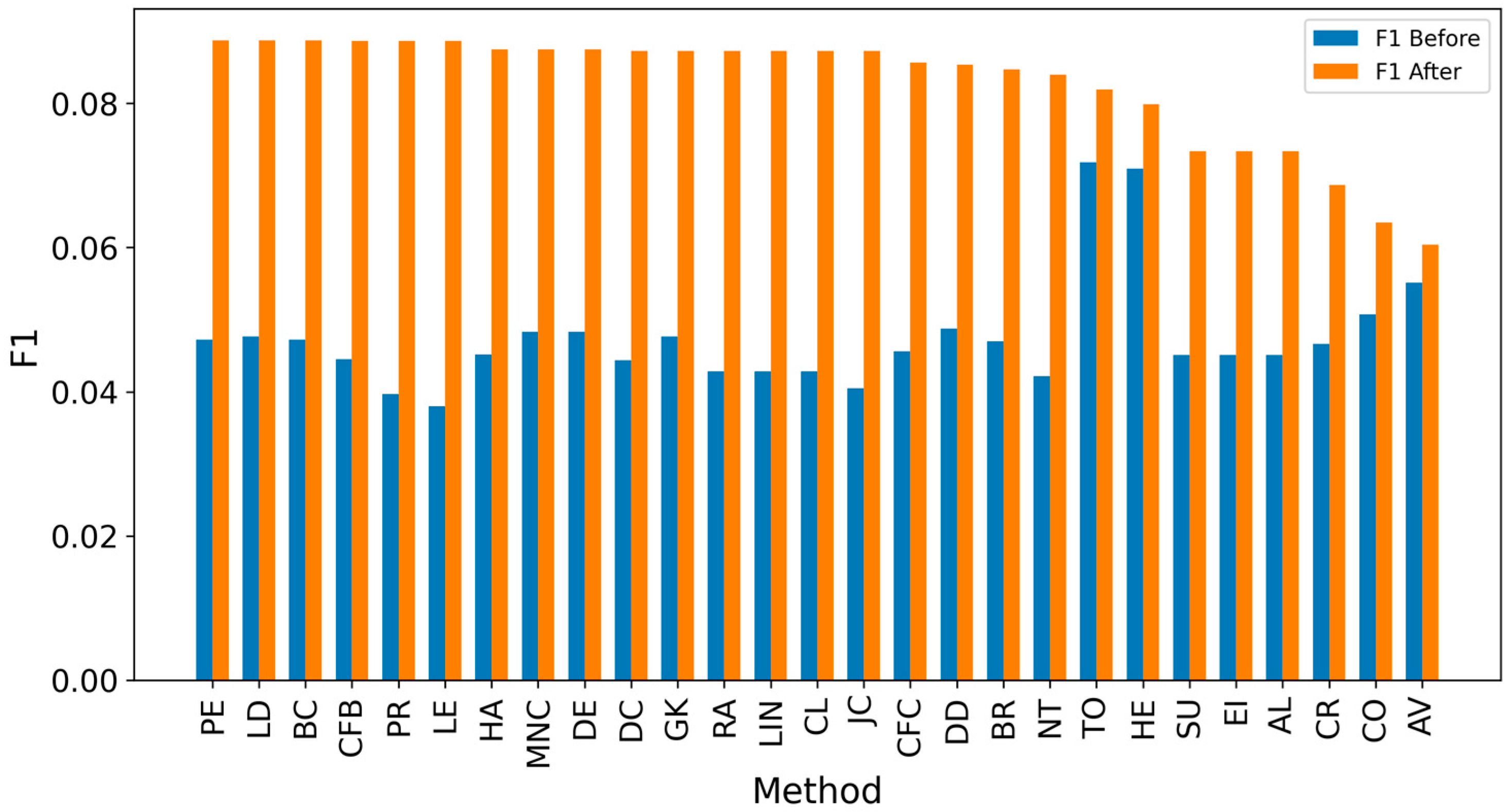
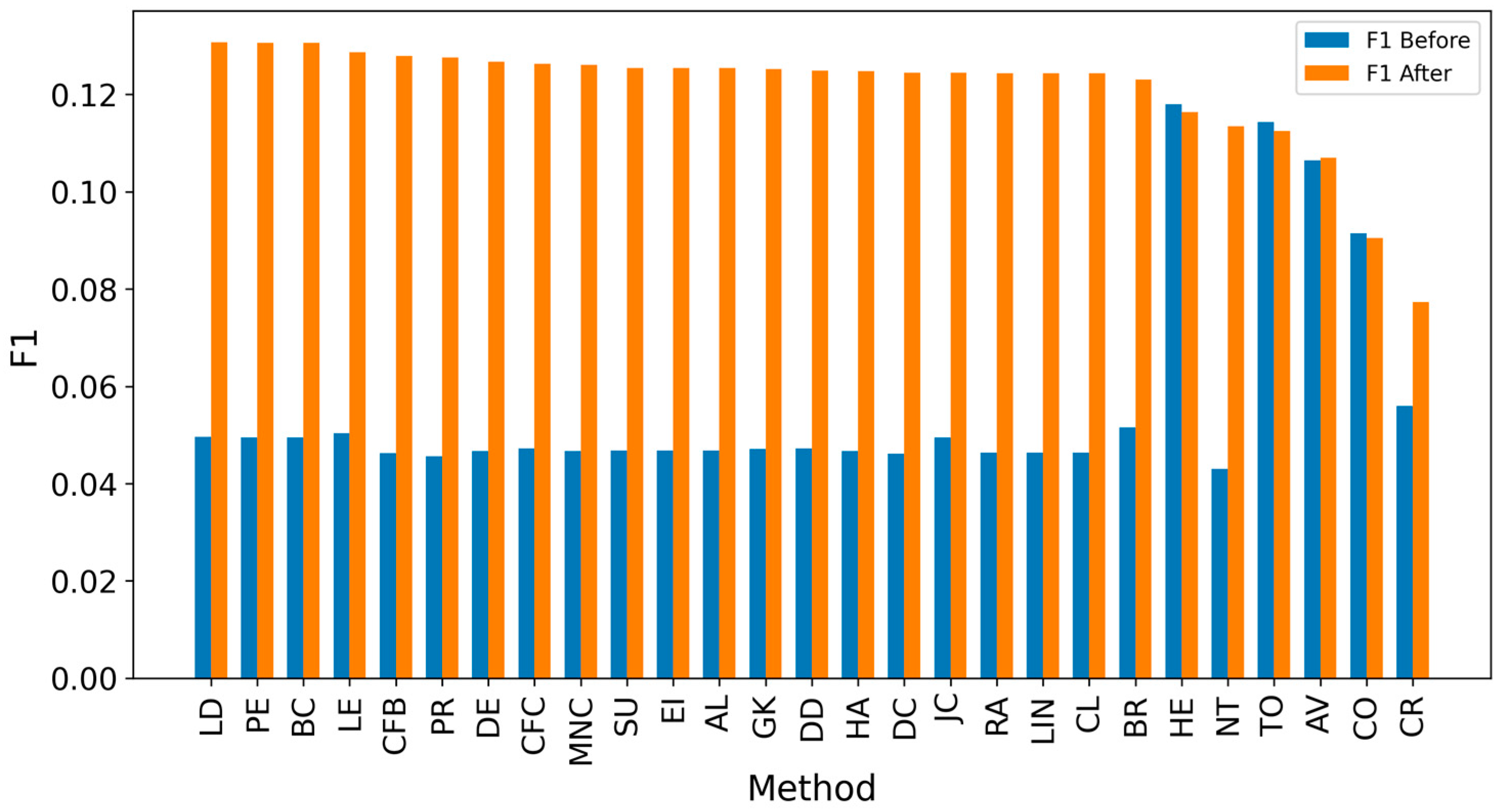
| Network | Nodes | Edges | Density | Assortativity | Avg. Clustering Coefficient | Degree (min/avg./max) |
|---|---|---|---|---|---|---|
| Dolphin | 62 | 159 | 0.0841 | −0.0436 | 0.259 | 1/5.13/12 |
| Football | 115 | 613 | 0.0935 | 0.1624 | 0.4032 | 7/10/12 |
| SF-1 | 500 | 2475 | 0.0198 | −0.0966 | 0.0659 | 5/9.9/69 |
| SW-1 | 500 | 2500 | 0.0200 | −0.0244 | 0.1640 | 5/10.0/16 |
| SF-2 | 1000 | 4975 | 0.0100 | −0.0613 | 0.0423 | 5/9.95/126 |
| SW-2 | 1000 | 5000 | 0.0100 | −0.0061 | 0.1478 | 5/10.0/16 |
| 4039 | 88,234 | 0.0108 | 0.0636 | 0.6055 | 1/44/1045 | |
| Social | 12,600 | 671,000 | 0.0008 | −0.1219 | 0.2275 | 1/10/8700 |
| Predicted Positive | Predicted Negative | |
|---|---|---|
| Actually positive | TP (true positive) | FN (false negative) |
| Actually negative | FP (false positive) | TN (true negative) |
| Centrality Measure | ||
|---|---|---|
| Algebraic [AL] | Decay [DC] | Load [LD] |
| Average distance [AV] | Degree [DE] | MNC [MNC] |
| Barycenter [BR] | Diffusion degree [DD] | PageRank [PR] |
| Betweenness [BC] | Eigenvector [EI] | Percolation [PE] |
| Closeness [CL] | Geodestic k path [GK] | Radiality [RA] |
| Cluster rank [CR] | Harmonic [HA] | Subgraph [SU] |
| Coreness [CO] | Heatmap [HE] | Topological [TO] |
| Current Ffow betweenness (random walk betweenness) [CFB] | Leverage [LE] | |
| Current flow closeness (information centrality) [CFC] | Lin [LIN] | |
| (a) | ||||
|---|---|---|---|---|
| TP | F1 | TPR | PPV | |
| AV | 12.083 | 0.073 | 0.073 | 0.073 |
| TO | 13.146 | 0.071 | 0.071 | 0.071 |
| HE | 13.333 | 0.069 | 0.069 | 0.069 |
| CO | 10.510 | 0.063 | 0.063 | 0.063 |
| LD | 6.927 | 0.054 | 0.054 | 0.054 |
| PE | 6.906 | 0.051 | 0.051 | 0.051 |
| BC | 6,906 | 0.051 | 0.051 | 0.051 |
| JC | 6.760 | 0.051 | 0.051 | 0.051 |
| CFB | 6.406 | 0.051 | 0.051 | 0.051 |
| SU | 6.313 | 0.050 | 0.050 | 0.050 |
| BR | 7.042 | 0.050 | 0.050 | 0.050 |
| DD | 6.521 | 0.049 | 0.049 | 0.049 |
| MNC | 6.500 | 0.048 | 0.048 | 0.048 |
| LE | 6.667 | 0.047 | 0.047 | 0.047 |
| DE | 6.469 | 0.046 | 0.046 | 0.046 |
| AL | 6.333 | 0.046 | 0.046 | 0.046 |
| EI | 6.333 | 0.046 | 0.046 | 0.046 |
| PR | 6.167 | 0.046 | 0.046 | 0.046 |
| GK | 6.552 | 0.045 | 0.045 | 0.045 |
| CFC | 6.427 | 0.045 | 0.045 | 0.045 |
| HA | 6.500 | 0.045 | 0.045 | 0.045 |
| CL | 6.365 | 0.043 | 0.043 | 0.043 |
| LIN | 6.365 | 0.043 | 0.043 | 0.043 |
| RA | 6.365 | 0.043 | 0.043 | 0.043 |
| DC | 6.406 | 0.041 | 0.041 | 0.041 |
| CR | 7.219 | 0.041 | 0.041 | 0.041 |
| NT | 6.021 | 0.040 | 0.040 | 0.040 |
| (b) | ||||
| TP | F1 | TPR | PPV | |
| LD | 103.969 | 0.101 | 0.677 | 0.056 |
| GK | 90.250 | 0.101 | 0.594 | 0.056 |
| LE | 101.635 | 0.100 | 0.681 | 0.055 |
| PE | 103.958 | 0.100 | 0.675 | 0.055 |
| BC | 103.958 | 0.100 | 0.675 | 0.055 |
| LIN | 88.948 | 0.099 | 0.616 | 0.055 |
| RA | 88.948 | 0.099 | 0.616 | 0.055 |
| CL | 88.948 | 0.099 | 0.616 | 0.055 |
| CFB | 100.760 | 0.099 | 0.660 | 0.054 |
| HA | 92.604 | 0.098 | 0.634 | 0.054 |
| JC | 91.521 | 0.098 | 0.568 | 0.055 |
| PR | 99.906 | 0.098 | 0.664 | 0.053 |
| CFC | 90.948 | 0.098 | 0.599 | 0.054 |
| DC | 92.063 | 0.097 | 0.619 | 0.054 |
| DE | 97.427 | 0.095 | 0.637 | 0.052 |
| HE | 22.146 | 0.095 | 0.248 | 0.063 |
| MNC | 95.573 | 0.094 | 0.623 | 0.052 |
| NT | 68.396 | 0.092 | 0.498 | 0.052 |
| TO | 20.500 | 0.092 | 0.222 | 0.063 |
| BR | 78.146 | 0.092 | 0.464 | 0.052 |
| DD | 86.375 | 0.092 | 0.560 | 0.051 |
| SU | 76.010 | 0.090 | 0.474 | 0.052 |
| AL | 76.656 | 0.090 | 0.490 | 0.051 |
| EI | 76.656 | 0.090 | 0.490 | 0.051 |
| AV | 21.031 | 0.090 | 0.232 | 0.060 |
| CO | 20.531 | 0.086 | 0.335 | 0.055 |
| CR | 24.458 | 0.082 | 0.305 | 0.049 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frąszczak, D. Identifying Network Propagation Sources Using Advanced Centrality Measures. Entropy 2025, 27, 948. https://doi.org/10.3390/e27090948
Frąszczak D. Identifying Network Propagation Sources Using Advanced Centrality Measures. Entropy. 2025; 27(9):948. https://doi.org/10.3390/e27090948
Chicago/Turabian StyleFrąszczak, Damian. 2025. "Identifying Network Propagation Sources Using Advanced Centrality Measures" Entropy 27, no. 9: 948. https://doi.org/10.3390/e27090948
APA StyleFrąszczak, D. (2025). Identifying Network Propagation Sources Using Advanced Centrality Measures. Entropy, 27(9), 948. https://doi.org/10.3390/e27090948







