Noise-Robust-Based Clock Parameter Estimation and Low-Overhead Time Synchronization in Time-Sensitive Industrial Internet of Things
Abstract
1. Introduction
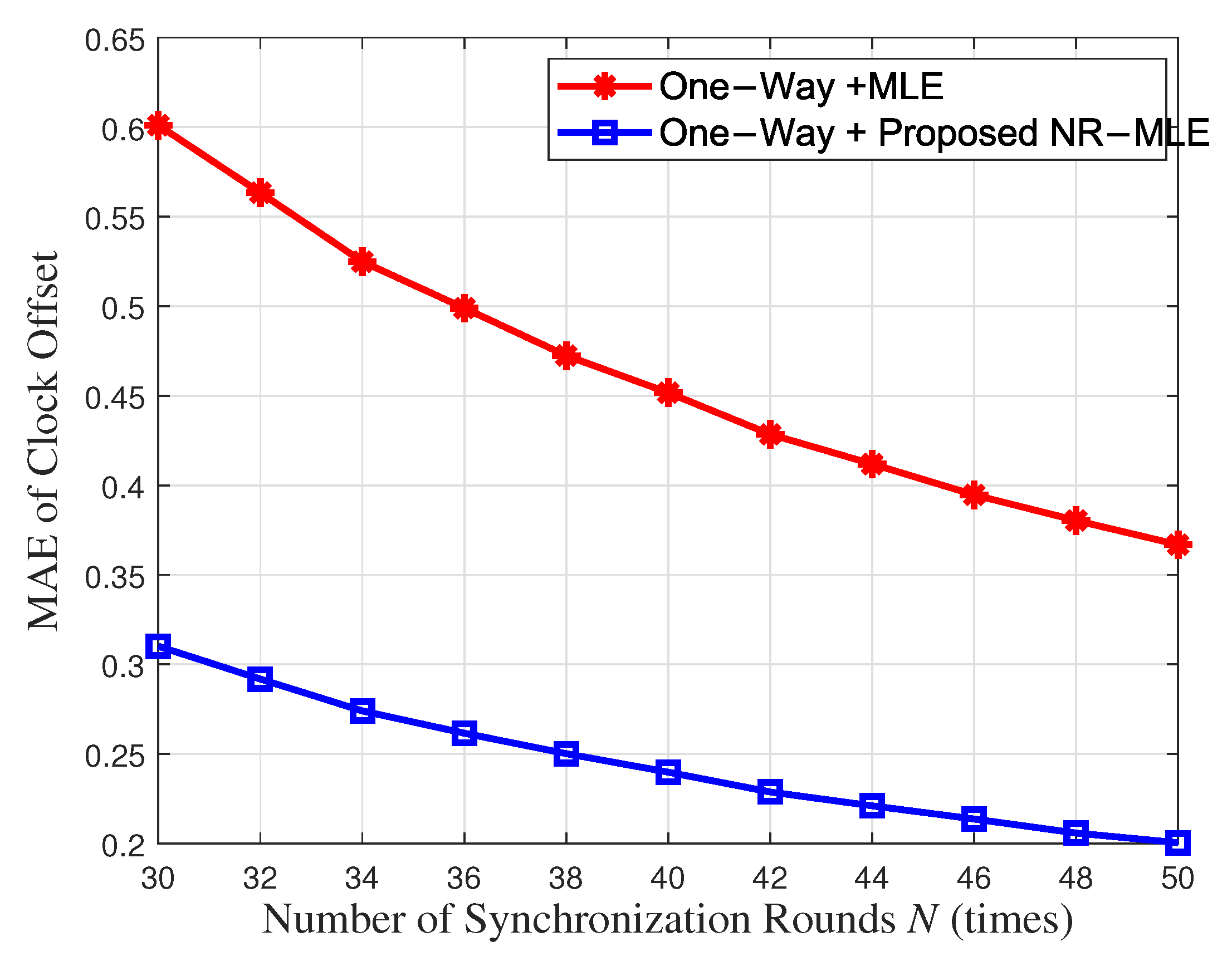
- We propose the noise-robust-based Maximum Likelihood Estimation (NR-MLE) algorithm to address noise-induced performance degradation in time synchronization parameter estimation. Specifically, we decompose the collected timestamp matrix into the product of two low-rank matrices. By employing gradient descent to minimize reconstruction errors and regularization terms, the decomposition approximates the low-rank structure of the true signal, thereby separating noise and yielding a denoised timestamp matrix. This enhances the precision of clock parameter estimation. Furthermore, the denoised timestamps enable the joint estimation of clock skew and offset via MLE. Moreover, we derive the corresponding Cramér–Rao Lower Bounds (CRLBs) to validate the estimation accuracy. The simulation results demonstrate that the proposed NR-MLE algorithm achieves a significant improvement in parameter estimation performance compared to the existing MLE algorithm.
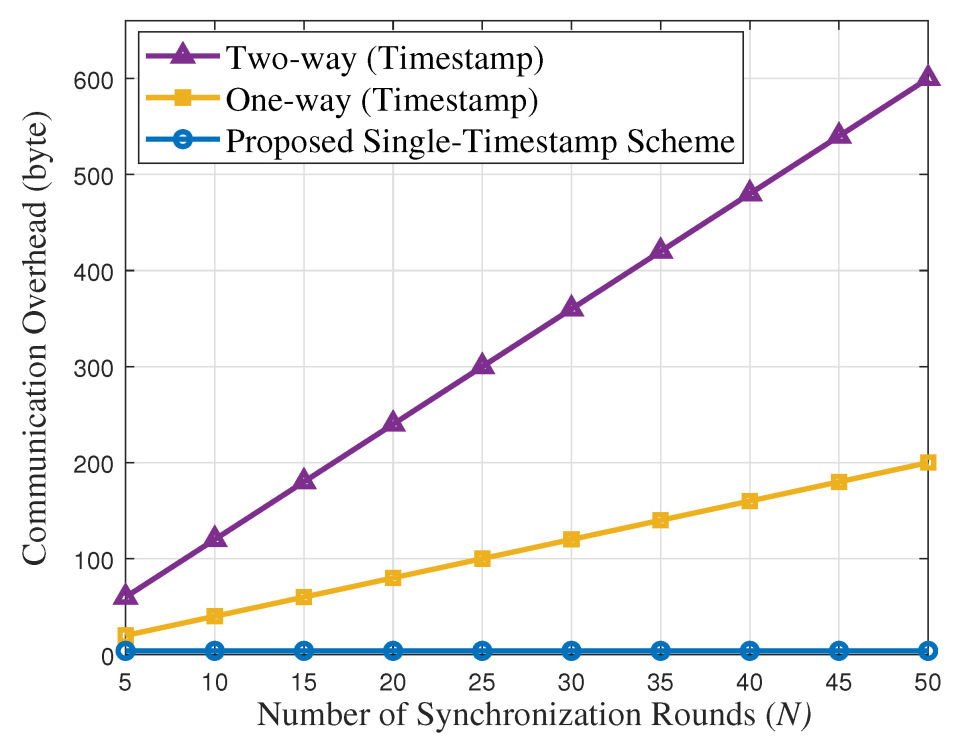
- We propose a single-timestamp time synchronization scheme for IIoT, leveraging one-way message dissemination in sensor networks. The scheme utilizes the existing mechanism, where an access point (AP) periodically collects data from sensor nodes. When synchronization is triggered, the node sends its current timestamp to the AP during the first round. In subsequent rounds, the node omits timestamp transmissions, while the AP records the arrival time of the node’s data packets. Based on the collected timestamps and arrival times, the AP estimates the clock skew and offset between itself and the node, significantly reducing communication overhead.
2. System Model
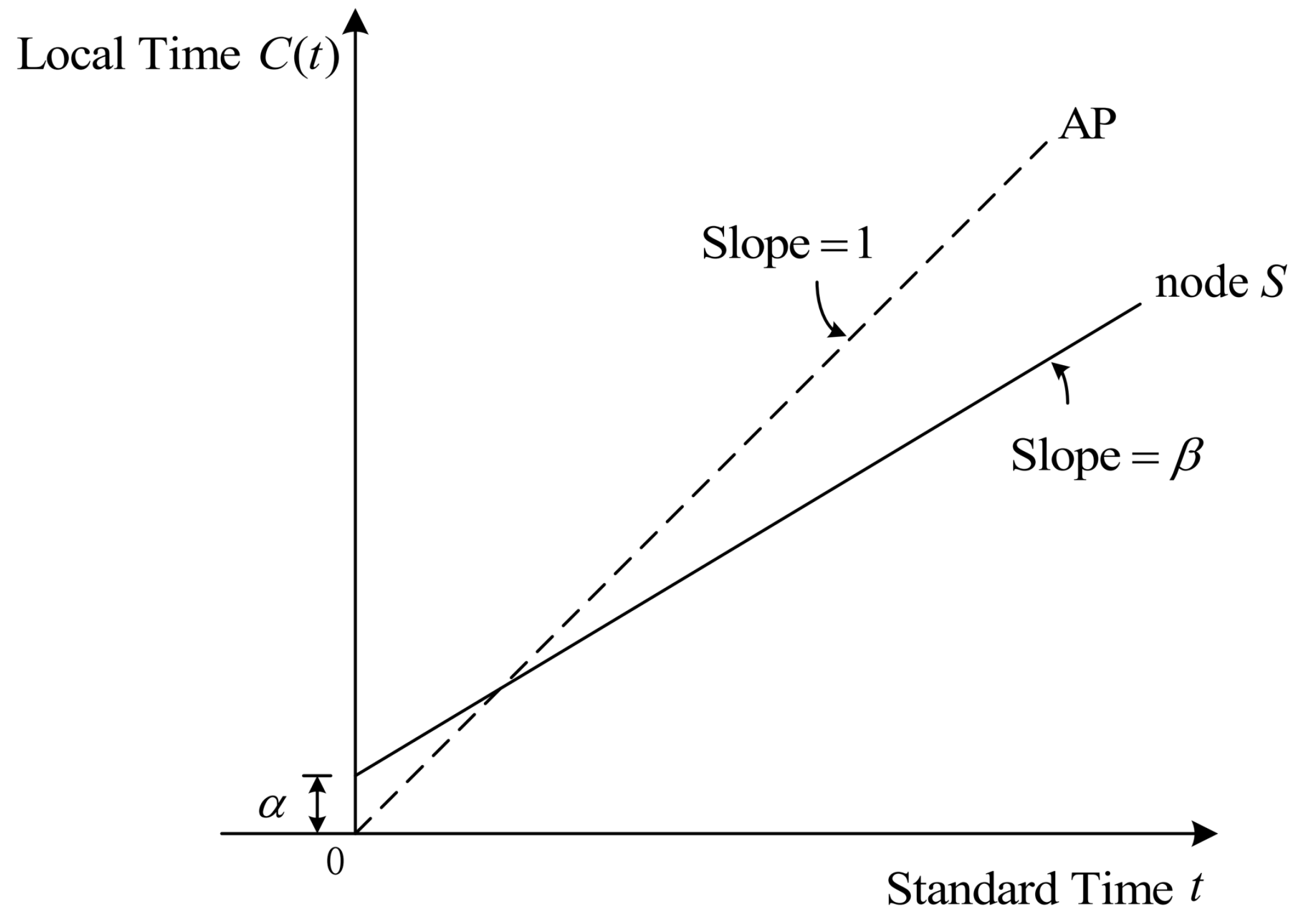
2.1. Clock Model
2.2. Delay Model
2.3. Proposed Single-Timestamp Time Synchronization Model
- First Round ():
- -
- Node S sends a single synchronization timestamp to the AP.
- -
- The AP records its local reception time as .
- Subsequent Rounds ():
- -
- Node S transmits only sensor data (no additional timestamps) to the AP every time units.
- -
- The AP records each reception time .
- Final Steps
- -
- After N rounds of synchronization, the AP obtains a set of timestamp information , which is used to estimate the clock skew and offset relative to node S. Then, they are sent to node S to adjust their own clock parameters, ultimately achieving time synchronization.

3. Noise-Robust-Based Clock Parameter Estimation
3.1. Problem Formulation
- is the ideal rank-1 matrix, which has not been contaminated by random delay noise.
- is the noise matrix with .
3.2. Optimization Objectives
3.2.1. Objective Function Design and Motivation
- Faithful Data Reconstruction: The first term ensures the factorized product closely approximates the observed data. The Frobenius norm is particularly suitable for this purpose [25,26] due to the following reasons:
- -
- It provides a smooth, differentiable measure of the total reconstruction error;
- -
- It corresponds to the Maximum Likelihood Estimator under Gaussian noise assumptions;
- -
- Its quadratic nature leads to computationally efficient optimization;
- -
- It equally weights all matrix elements, making it appropriate when errors are uniformly distributed across observations.
- Effective Noise Suppression: The regularization terms play several crucial roles in denoising [27,28], as follows:
- -
- They prevent overfitting to noise by penalizing large values in the factor matrices;
- -
- They impose implicit rank constraints by shrinking smaller singular values more aggressively (as can be seen through the lens of singular value shrinkage);
- -
- They improve numerical stability during optimization.
3.2.2. Gradient Computation
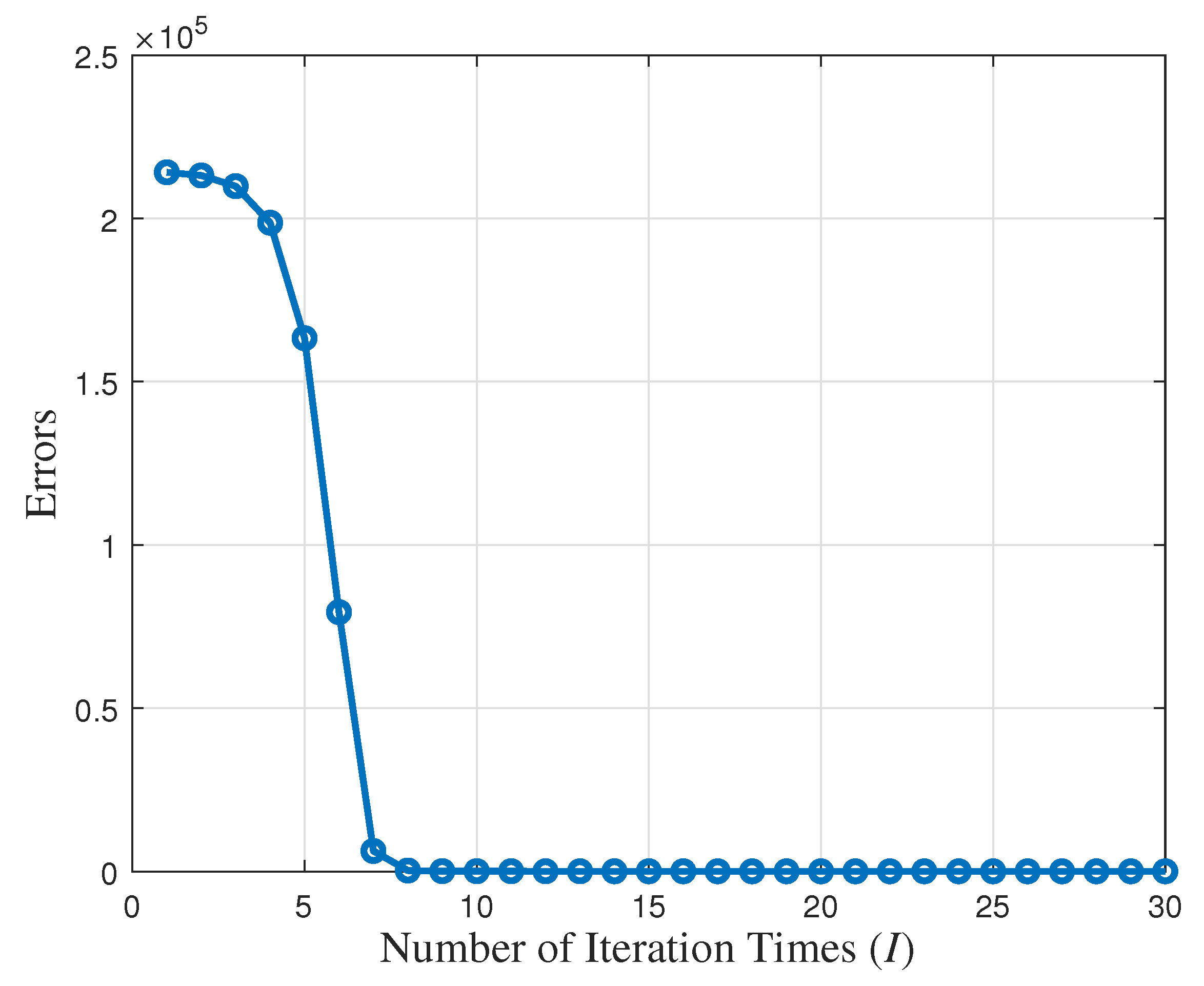
3.2.3. Convergence Analysis
- Primary Stopping Criterion: The relative change in normalized reconstruction error, as follows:where ; t denotes the t-th iteration; and is typically set between and for high-precision applications.
- Convergence Guarantees
- -
- The objective function is guaranteed to decrease monotonically;
- -
- Convergence to a local minimum is assured due to the convexity of subproblems;
- -
- The alternating minimization strategy avoids poor local minima, which are common in joint optimization.
3.3. Joint Clock Parameter Estimation
| Algorithm 1 Proposed NR-MLE algorithm. |
Require: Reducing the noise of the collected timestamp matrix and estimating clock parameters and .
|
3.4. CRLB for Clock Offset and Skew
4. Simulation Results and Analyses
4.1. Parameter Settings
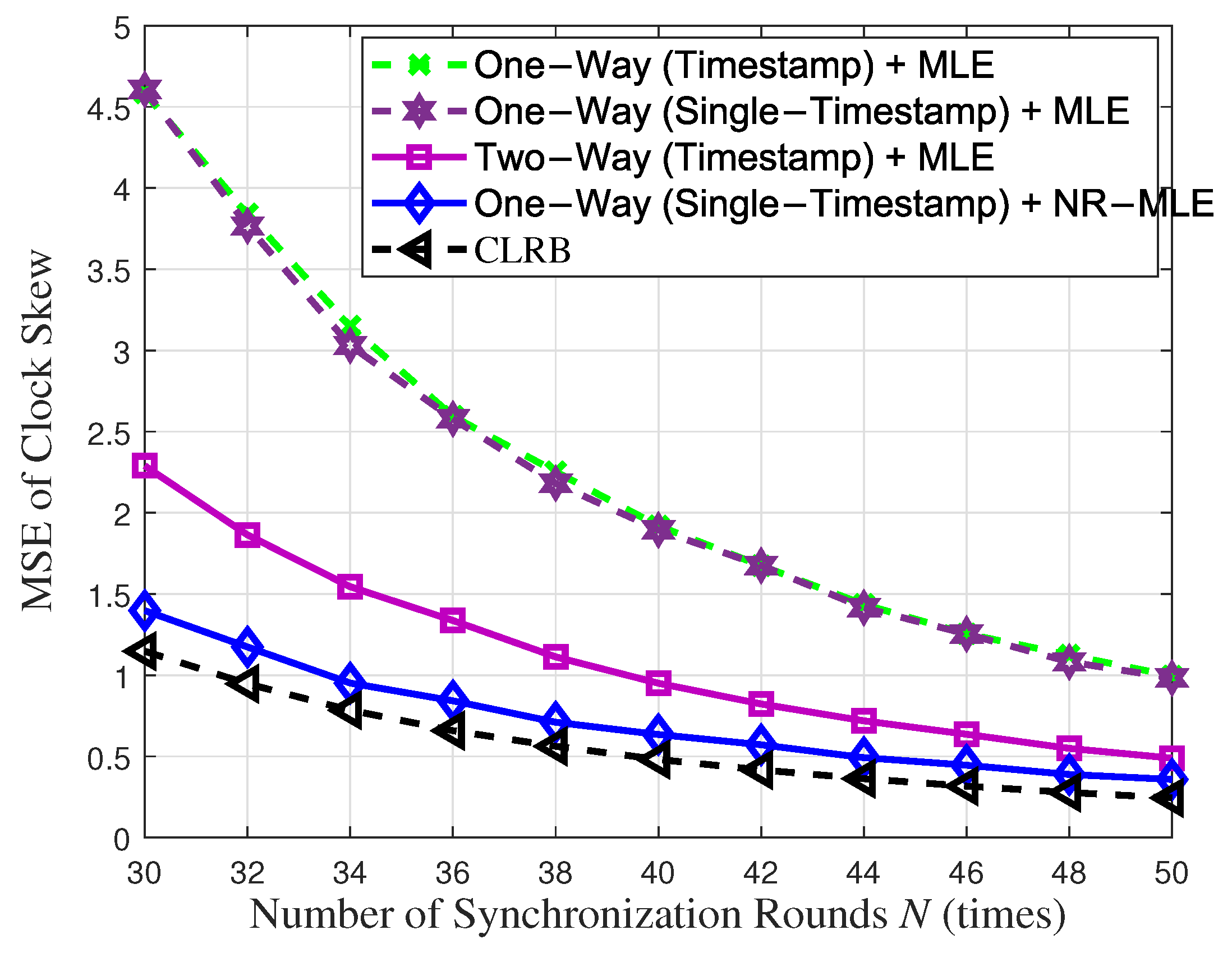
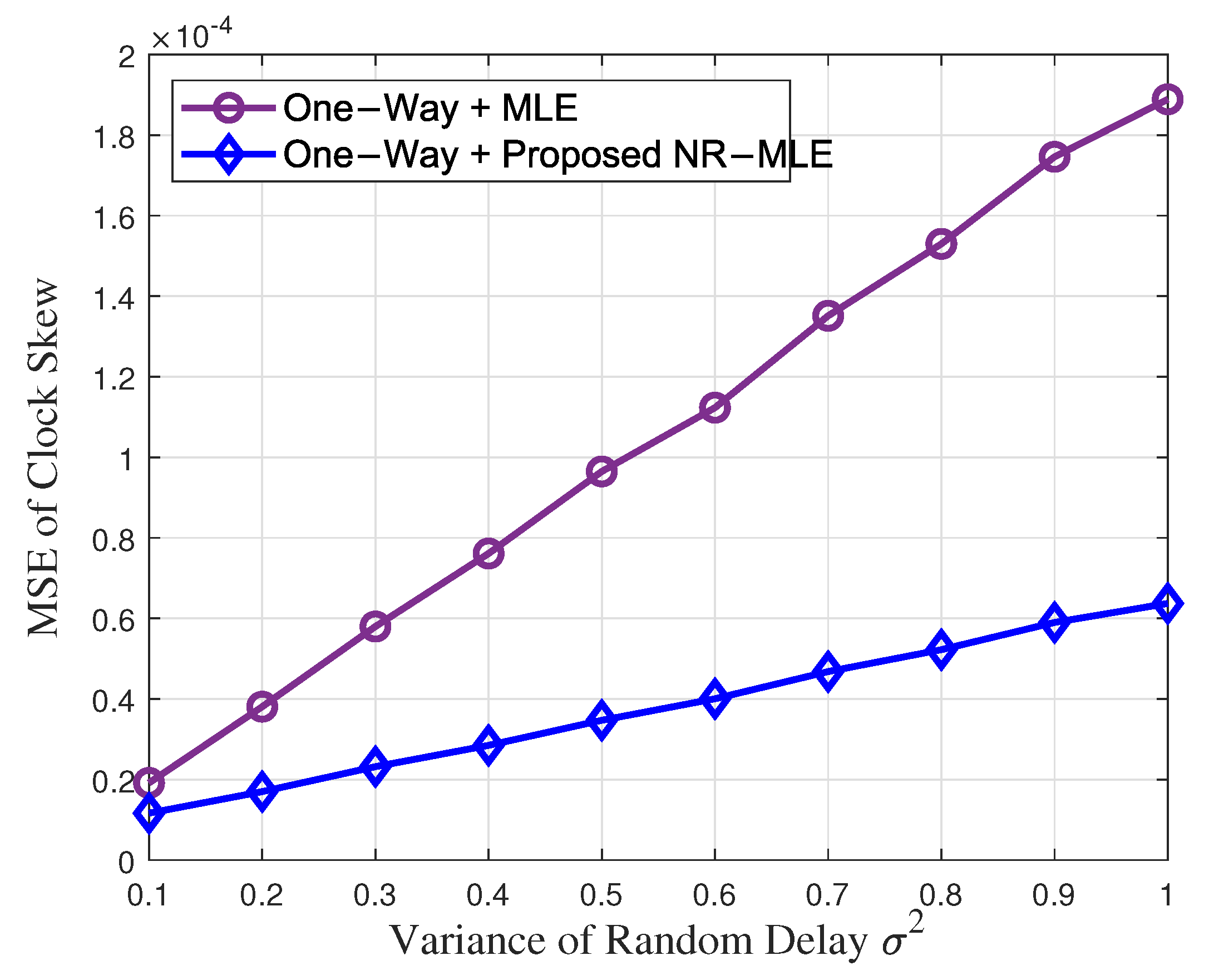
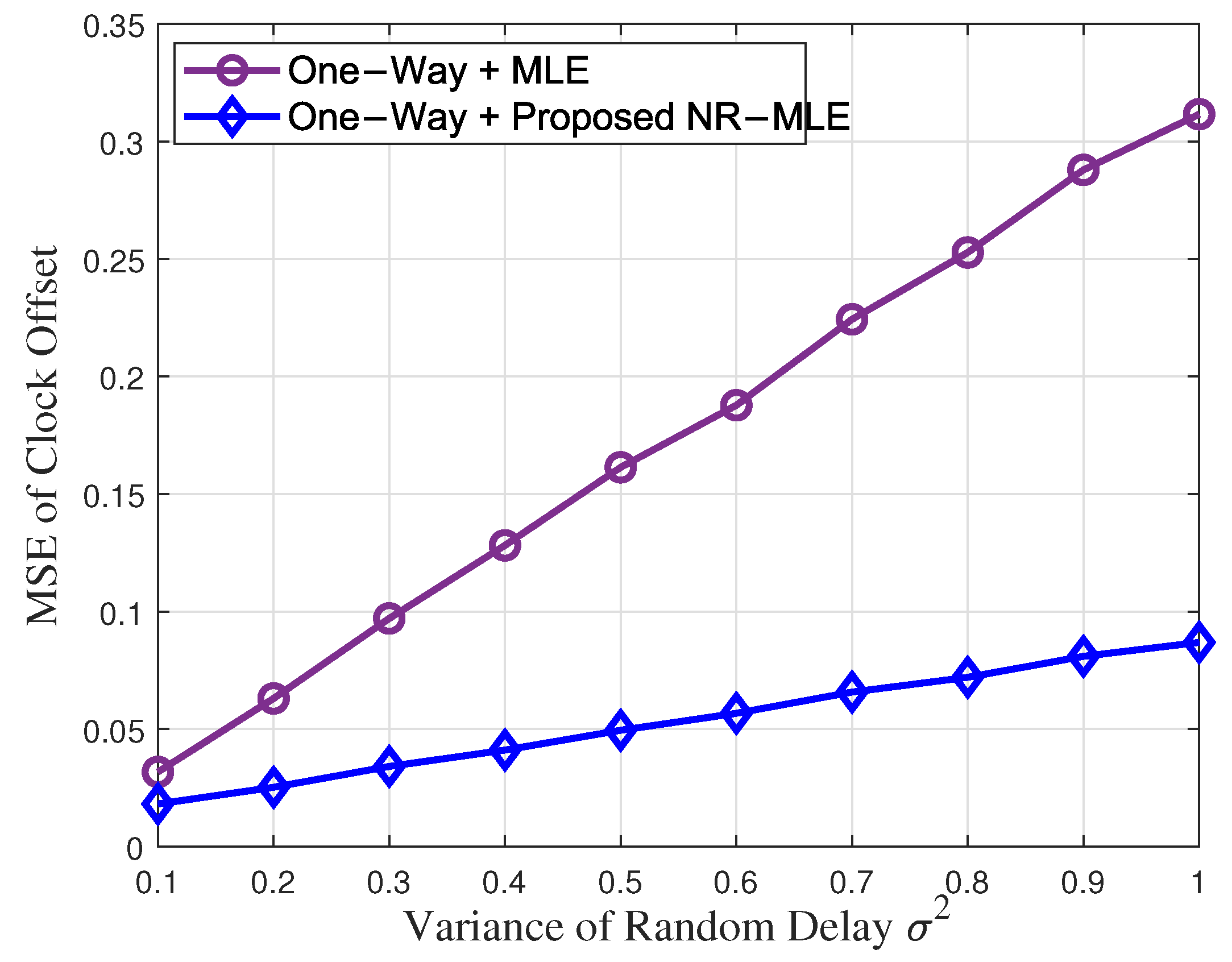
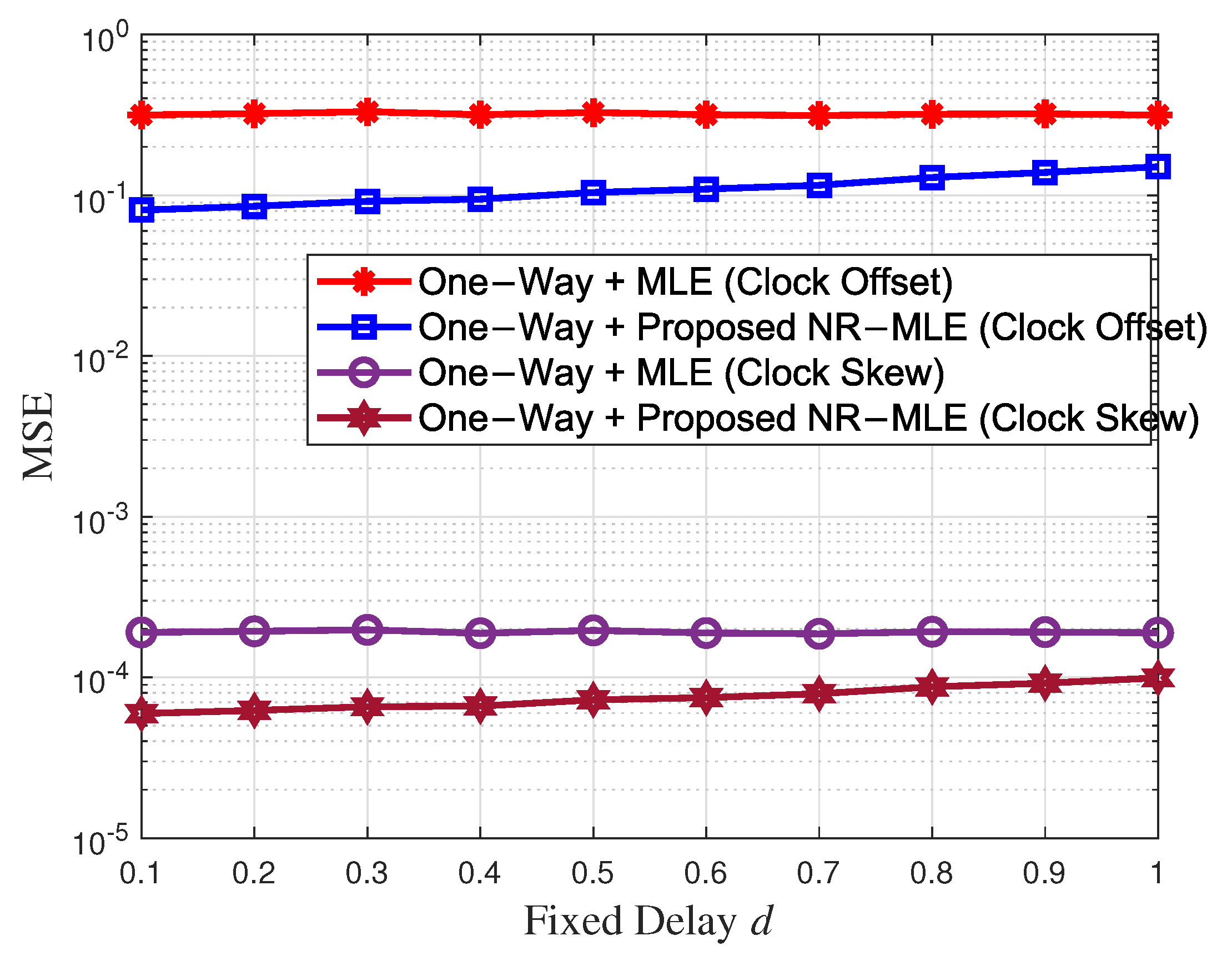
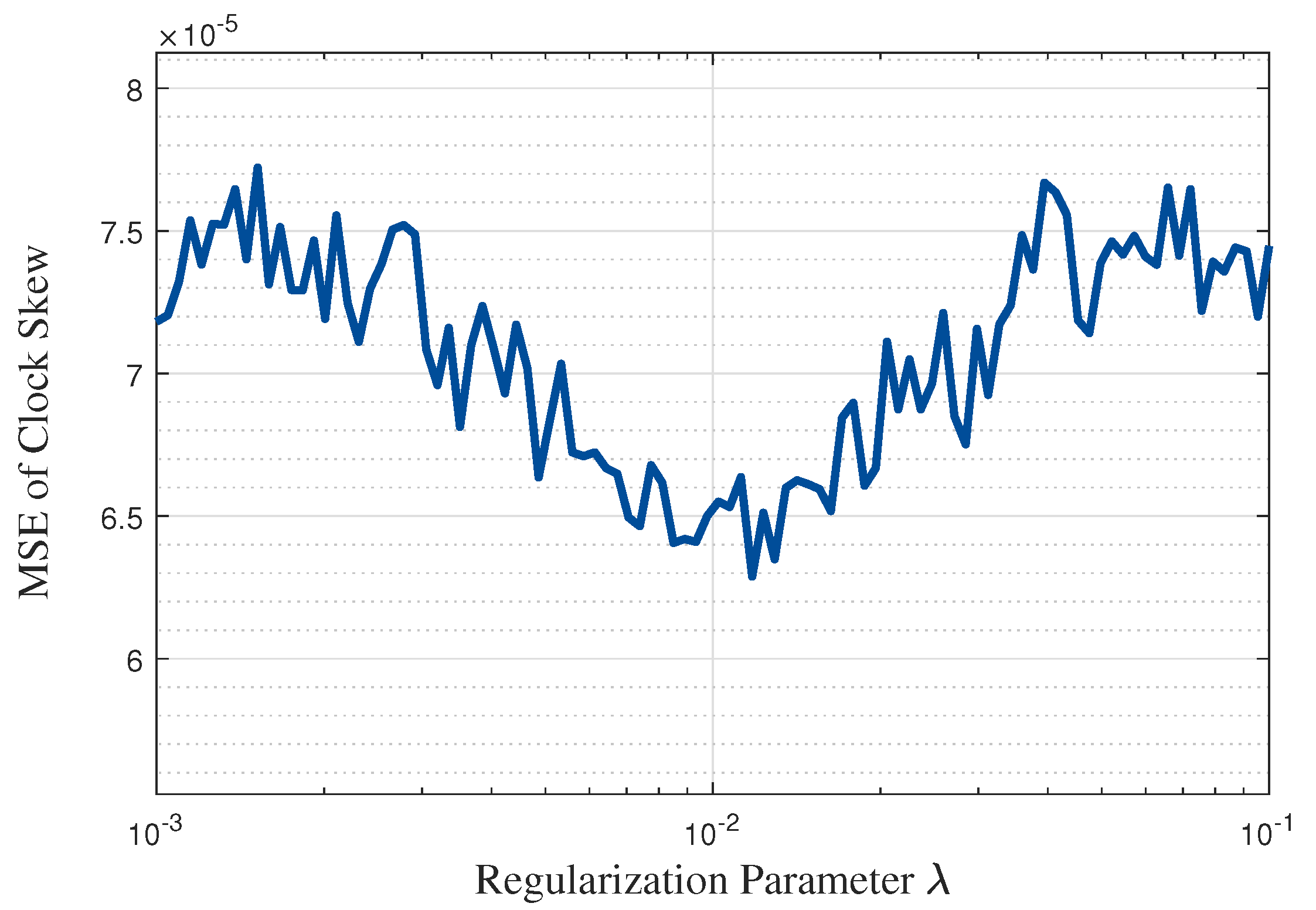
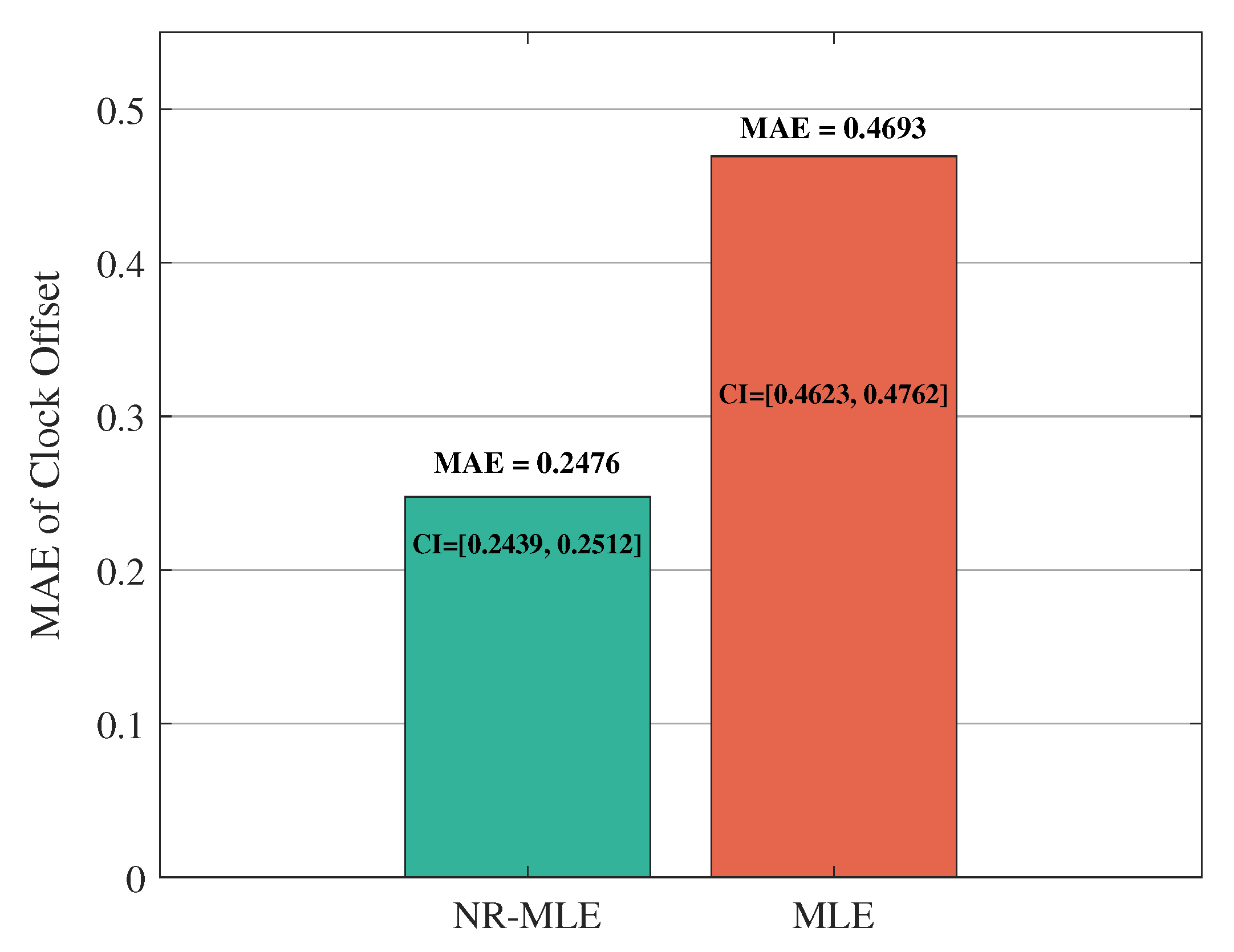
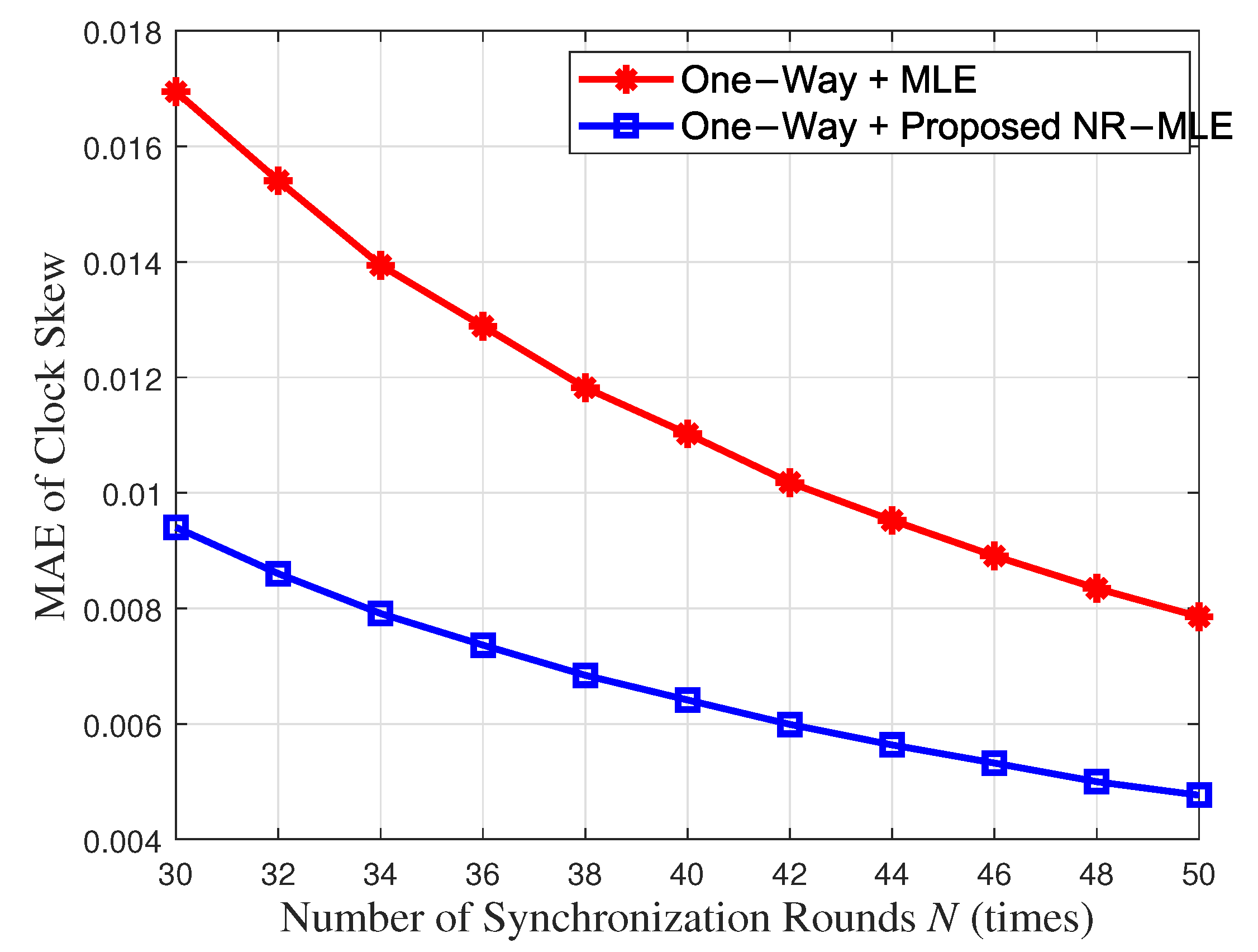
4.2. Simulation Results
4.3. Computational Complexity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Sheng, C.; Zhou, W.; Han, Q.L.; Ma, W.; Zhu, X.; Wen, S.; Xiang, Y. Network traffic fingerprinting for IIoT device identification: A survey. IEEE Trans. Ind. Inf. 2025, 21, 3541–3554. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H. Robust clock parameters tracking for IEEE 1588 with asymmetric packet delays in industrial networks. IEEE Trans. Commun. 2025, 73, 1248–1261. [Google Scholar] [CrossRef]
- Wang, H.; Chen, L.; Gong, P.; Li, M. Skew estimation based on weighted median for average consensus time synchronization in the presence of communication delays. IEEE Wirel. Commun. Lett. 2020, 9, 1384–1388. [Google Scholar] [CrossRef]
- Dang, F.; Sun, X.-K.; Liu, K.-B.; Xu, Y.-F.; Liu, Y.-H. A survey on clock synchronization in the industrial internet. J. Comput. Sci. Technol. 2023, 38, 146–165. [Google Scholar] [CrossRef]
- Qiu, T.; Zheng, K.; Song, H.; Han, M.; Burak, K. A local-optimization emergency scheduling scheme with self-recovery for smart grid. IEEE Trans. Ind. Inf. 2017, 13, 3195–3205. [Google Scholar] [CrossRef]
- Shi, F.; Tuo, X.; Ran, L.; Ren, Z.; Yang, S.X. Fast convergence time synchronization in wireless sensor networks based on average consensus. IEEE Trans. Ind. Inf. 2020, 16, 1120–1129. [Google Scholar] [CrossRef]
- Huan, X.; Kim, K.S. Per-hop delay compensation in time synchronization for multi-hop wireless sensor networks based on packet-relaying gateways. IEEE Commun. Lett. 2020, 24, 2300–2304. [Google Scholar] [CrossRef]
- Huan, X.; Chen, W.; Wang, T.; Hu, H.; Zheng, Y. A one-way time synchronization scheme for practical energy-efficient LoRa network based on reverse asymmetric framework. IEEE Trans. Commun. 2023, 71, 6468–6481. [Google Scholar] [CrossRef]
- Huan, X.; Chen, W.; Wang, T.; Hu, H. A microsecond energy-efficient LoRa time synchronization based on low-layer timestamping and asymmetric time translation. IEEE Trans. Veh. Technol. 2024, 73, 7328–7332. [Google Scholar] [CrossRef]
- Wang, H.; Lu, R.; Peng, Z.; Li, M. Timestamp-free clock parameters tracking using extended Kalman filtering in wireless sensor networks. IEEE Trans. Commun. 2021, 69, 6926–6938. [Google Scholar] [CrossRef]
- Huan, X.; Kim, K.S.; Lee, S.; Lim, E.G.; Marshall, A. A beaconless asymmetric energy-efficient time synchronization scheme for resource constrained multi-hop wireless sensor networks. IEEE Trans. Commun. 2020, 68, 1716–1730. [Google Scholar] [CrossRef]
- Wu, Y.; Chaudhari, Q.; Serpedin, E. Clock synchronization of wireless sensor networks. IEEE Signal Process. Mag. 2011, 28, 124–138. [Google Scholar] [CrossRef]
- Gong, F.; Sichitiu, M.L. On the accuracy of pairwise time synchronization. IEEE Trans. Commun. 2017, 16, 2664–2677. [Google Scholar] [CrossRef]
- Elnahas, O.; Ma, Y.; Jiang, Y.; Quan, Z. Clock synchronization in wireless networks using matrix completion-based maximum likelihood estimation. IEEE Trans. Wirel. Commun. 2020, 19, 8220–8231. [Google Scholar] [CrossRef]
- Wang, H.; Gong, P.; Yu, F.; Li, M. Clock offset and skew estimation using hybrid one-way message dissemination and two-way timestamp free synchronization in wireless sensor networks. IEEE Commun. Lett. 2020, 24, 2893–2897. [Google Scholar] [CrossRef]
- Leng, M.; Wu, Y. Low-complexity maximum-likelihood estimator for clock synchronization of wireless sensor nodes under exponential delays. IEEE Trans. Signal Process. 2011, 59, 4860–4870. [Google Scholar] [CrossRef]
- Liu, G.; Yan, S.; Mao, L. Receiver-only-based time synchronization under exponential delays in underwater wireless sensor networks. IEEE Internet Things J. 2020, 7, 9995–10009. [Google Scholar] [CrossRef]
- Ahmad, A.; Noor, A.; Serpedin, E.; Nounou, H.; Nounou, M. On clock offset estimation in wireless sensor networks with Weibull distributed network delays. In Proceedings of the 2010 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010; pp. 2322–2325. [Google Scholar]
- Elson, J.; Girod, L.; Estrin, D. Fine-grained network time synchronization using reference broadcasts. ACM SIGOPS Oper. Syst. Rev. 2002, 36, 147–163. [Google Scholar] [CrossRef]
- Li, B.; Zeng, H.; Zhu, X.; Jiang, Y.; Wang, Y. Cooperative time synchronization and robust clock parameters estimation for time-sensitive cell-free massive MIMO systems. IEEE Trans. Wirel. Commun. 2024, 23, 11552–11566. [Google Scholar] [CrossRef]
- Wang, H.; Yu, F.; Li, M.; Zhong, Y. Clock skew estimation for timestamp-free synchronization in industrial wireless sensor networks. IEEE Trans. Ind. Inform. 2020, 17, 90–99. [Google Scholar] [CrossRef]
- Leng, M.; Wu, Y.-C. On clock synchronization algorithms for wireless sensor networks under unknown delay. IEEE Trans. Veh. Technol. 2010, 59, 182–190. [Google Scholar] [CrossRef]
- Shrestha, D.; Pang, Z.; Dzung, D. Precise clock synchronization in high performance wireless communication for time sensitive networking. IEEE Access 2018, 6, 8944–8953. [Google Scholar] [CrossRef]
- Puttnies, H.; Schweissguth, E.; Timmermann, D.; Schacht, J. Clock synchronization using linear programming, multicasts, and temperature compensation. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Keshavan, R.H.; Montanari, A.; Oh, S. Matrix completion from noisy entries. J. Mach. Learn. Res. 2010, 11, 2057–2078. [Google Scholar]
- Candès, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2013, 9, 717–772. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical Learning with Sparsity: The Lasso and Generalizations; Chapter 5: Matrix Decompositions; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- De la Torre, F. A least-squares framework for component analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 34, 1041–1055. [Google Scholar] [CrossRef] [PubMed]
- Obozinski, G.; Taskar, B.; Jordan, M.I. Joint covariate selection and joint subspace selection for multiple classification problems. Stat. Comput. 2011, 20, 231–252. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing, Vol I: Estimation Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Hero, A.; Messer, H.; Goldberg, J.; Thomson, D.J.; Amin, M.G.; Giannakis, G.; Swami, A.; Tugnait, J.K.; Nehorai, A.; Swindlehurst, A.L.; et al. Highlights of statistical signal and array processing. IEEE Signal Process. Mag. 1998, 15, 21–64. [Google Scholar] [CrossRef]
- Maróti, M.; Kusy, B.; Simon, G.; Ledeczi, A. The flooding time synchronization protocol. In Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems, New York, NY, USA, 3–5 November 2004; pp. 39–49. [Google Scholar]
- IEC/IEEE 60802; TSN Profile for Industrial Automation. IEC: Geneva, Switzerland; IEEE: Piscataway, NJ, USA, 2023.
- Pottie, G.J.; Kaiser, W.J. Wireless integrated network sensors. Commun. ACM 2000, 43, 51–58. [Google Scholar] [CrossRef]




| Notation | Description | Value |
|---|---|---|
| Relative clock skew | [0.99, 1.01] | |
| Relative clock offset | [−0.02, 0.02] ms | |
| d | Fixed delay | [0, 0.2] ms |
| Variance of random delay | [0.1, 1] | |
| p | Target rank | 1 |
| Regularization coefficient | [0.001, 0.1] | |
| N | Synchronization rounds | 30:5:50 |
| Fixed interval | 1 ms | |
| Simulation times | 10,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Li, F.; Yu, Z.; Zeng, H. Noise-Robust-Based Clock Parameter Estimation and Low-Overhead Time Synchronization in Time-Sensitive Industrial Internet of Things. Entropy 2025, 27, 927. https://doi.org/10.3390/e27090927
Tang L, Li F, Yu Z, Zeng H. Noise-Robust-Based Clock Parameter Estimation and Low-Overhead Time Synchronization in Time-Sensitive Industrial Internet of Things. Entropy. 2025; 27(9):927. https://doi.org/10.3390/e27090927
Chicago/Turabian StyleTang, Long, Fangyan Li, Zichao Yu, and Haiyong Zeng. 2025. "Noise-Robust-Based Clock Parameter Estimation and Low-Overhead Time Synchronization in Time-Sensitive Industrial Internet of Things" Entropy 27, no. 9: 927. https://doi.org/10.3390/e27090927
APA StyleTang, L., Li, F., Yu, Z., & Zeng, H. (2025). Noise-Robust-Based Clock Parameter Estimation and Low-Overhead Time Synchronization in Time-Sensitive Industrial Internet of Things. Entropy, 27(9), 927. https://doi.org/10.3390/e27090927





