Fixed-Time Active Disturbance Rejection Temperature–Pressure Decoupling Control for a High-Flow Air Intake System
Abstract
1. Introduction
- We introduce a static decoupling method to remove the IESS’s static coupling. By defining virtual control inputs, the system is split into pressure and temperature loops, each equipped with a dedicated fixed-time sliding-mode controller (FT-SMC) and super-twisting fixed-time ESO (ST-FT-ESO) to achieve high-quality decoupling under high airflow.
- We employ ST-FT-ESO for rapid and precise estimation of dynamic coupling and other disturbances and FT-SMC as the core controller to reject the total disturbance. Lyapunov analysis shows that the ST-FT-ESO converges in a fixed time and, together with the FT-SMC law, guarantees fixed-time stability of the entire closed-loop system.
- We implement FT-ADRCDC on a hardware-in-the-loop (HIL) simulation platform for the IESS and compare it with LADRC, demonstrating faster response and superior stability in rapid transient tests.
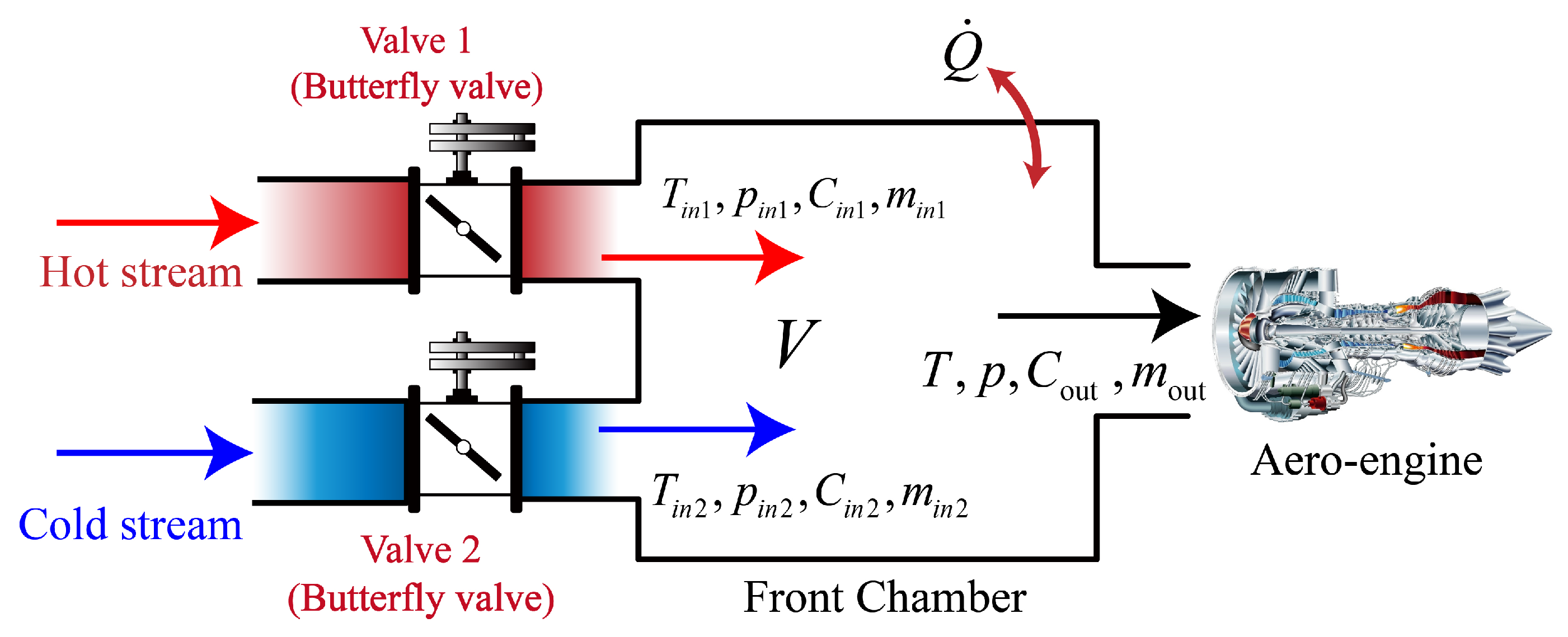
2. Intake Environment Simulation System
2.1. Front-Chamber Cavity Model
2.2. Motion and Flow Characteristics of the Control Valve
2.3. Airflow Model of the Aeroengine
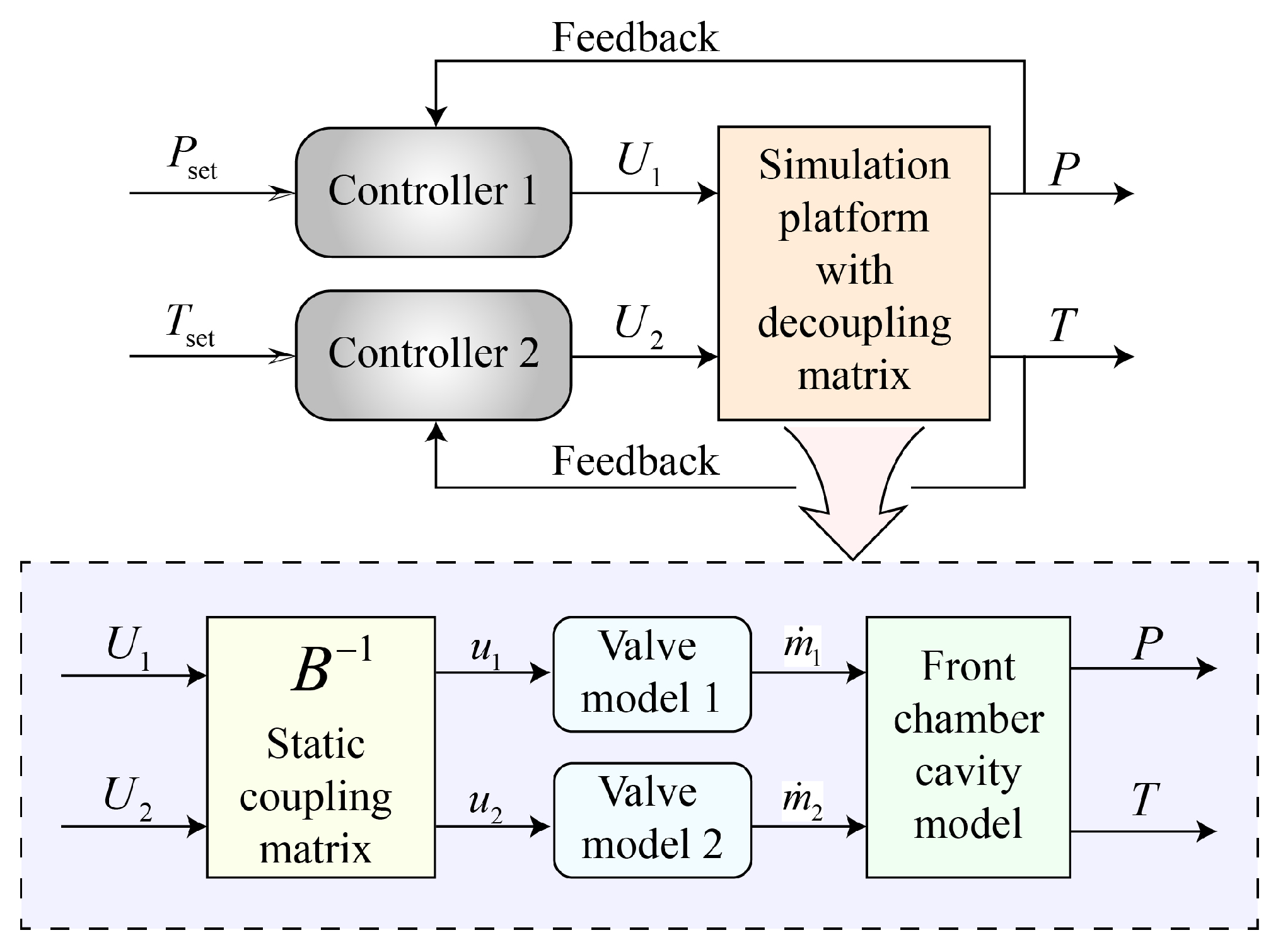
3. Pressure and Temperature Decoupling Design of the IESS
3.1. Decoupling Design
3.1.1. Affine Model of the IESS
3.1.2. Decoupling Design of Valve Control Quantity and System Output
3.2. Static Coupling Matrix Reversibility Analysis
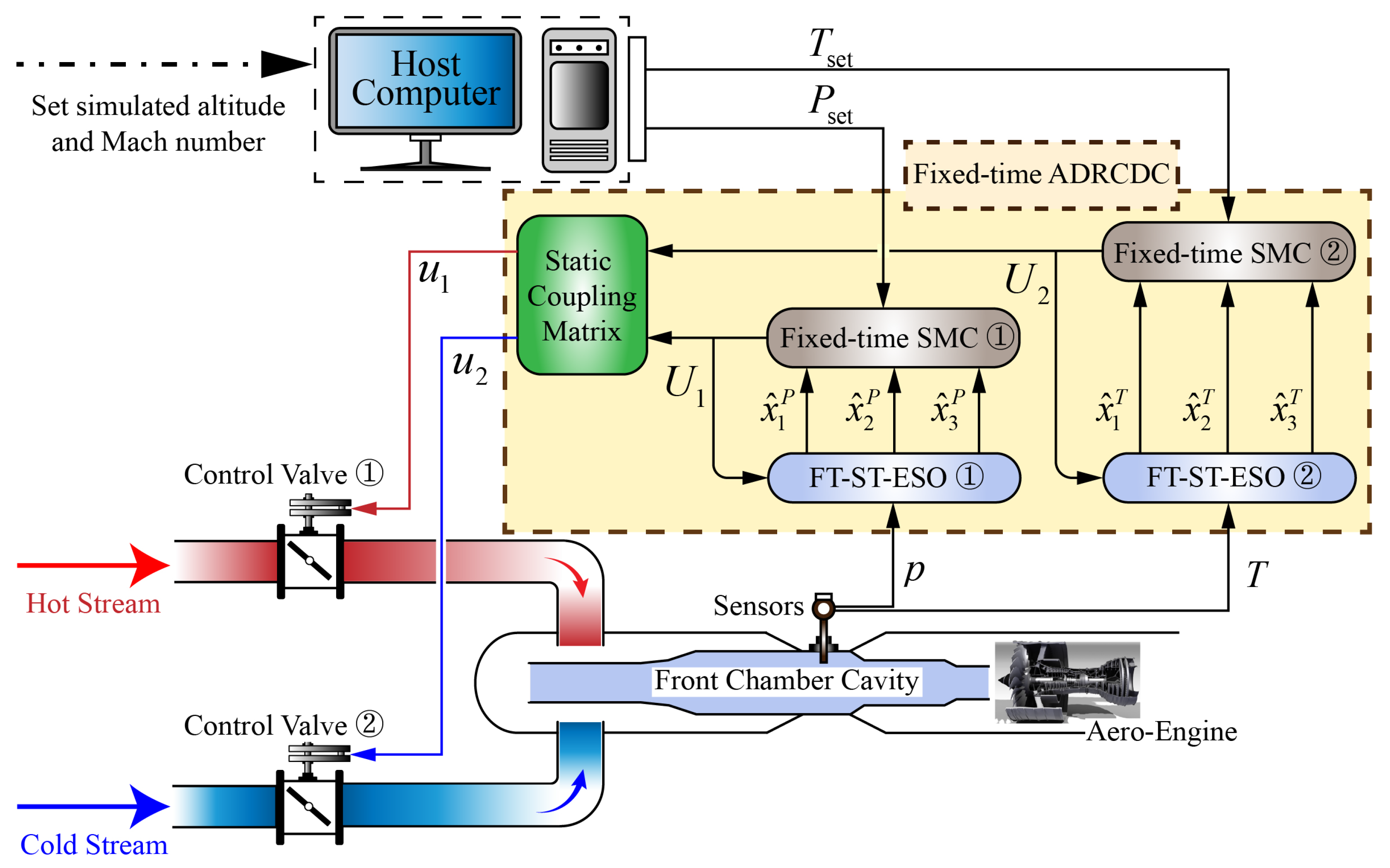
4. Design of Fixed-Time Active Disturbance Rejection Decoupling Controller
4.1. Pressure and Temperature Decoupling Control Structure
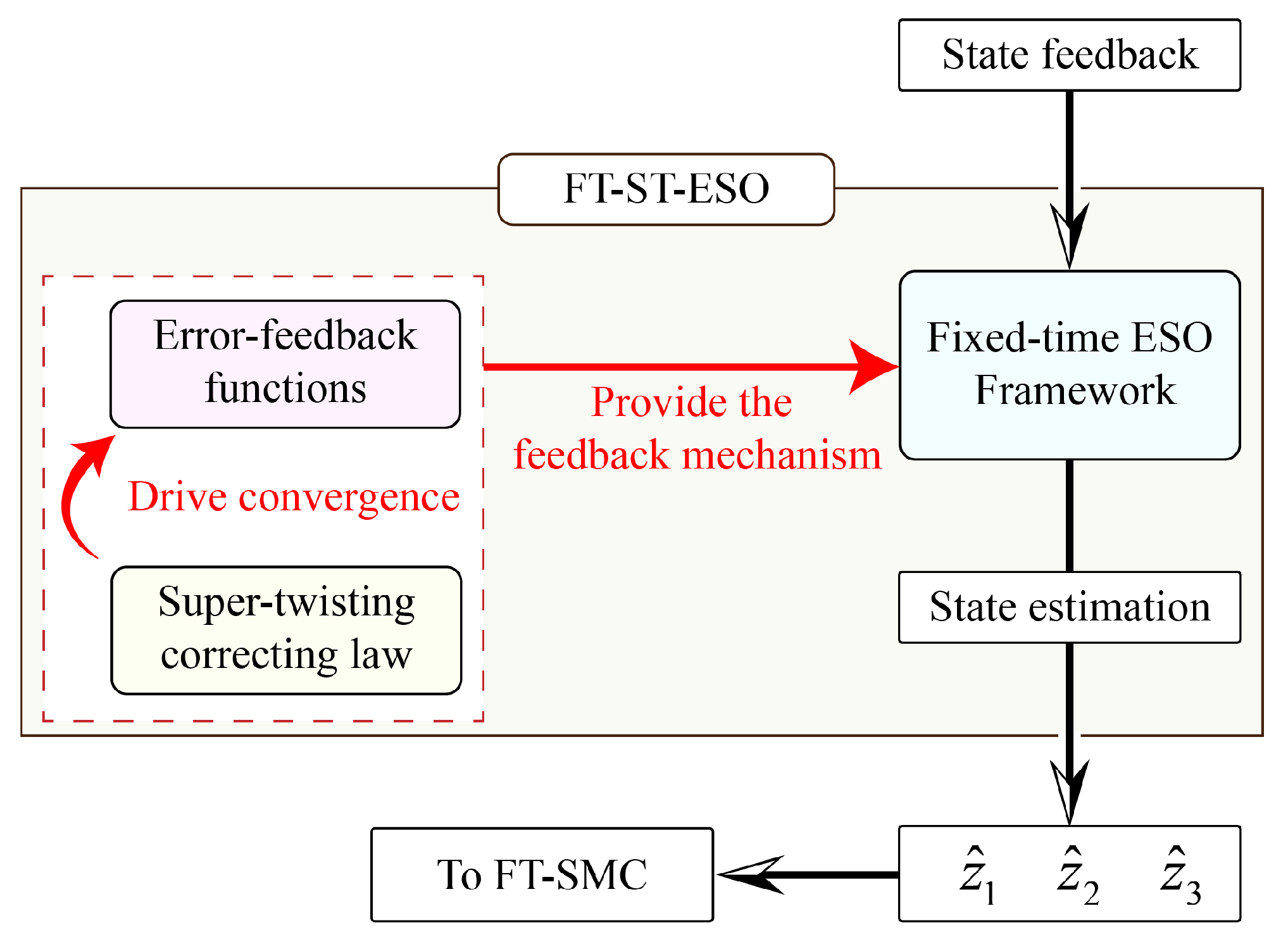
4.2. Design of ST-FT-ESO
- Super-twisting correcting law:
- Error feedback functions:
- The FT-ST-ESO dynamics (pressure loop) are as follows:
4.3. Design of the FT-SMC
5. System Stability Analysis
5.1. Stability of the ST-FT-ESO
- (1)
- Homogeneity property
- (2)
- Fixed-time convergence of the ESO
5.2. Stability of the Closed-Loop IESS
- (1)
- Sliding-surface reachability
- (2)
- Vanishing of the position error
- (3)
- Closed-loop fixed-time stability
6. Experimental Simulation and Validation Analysis
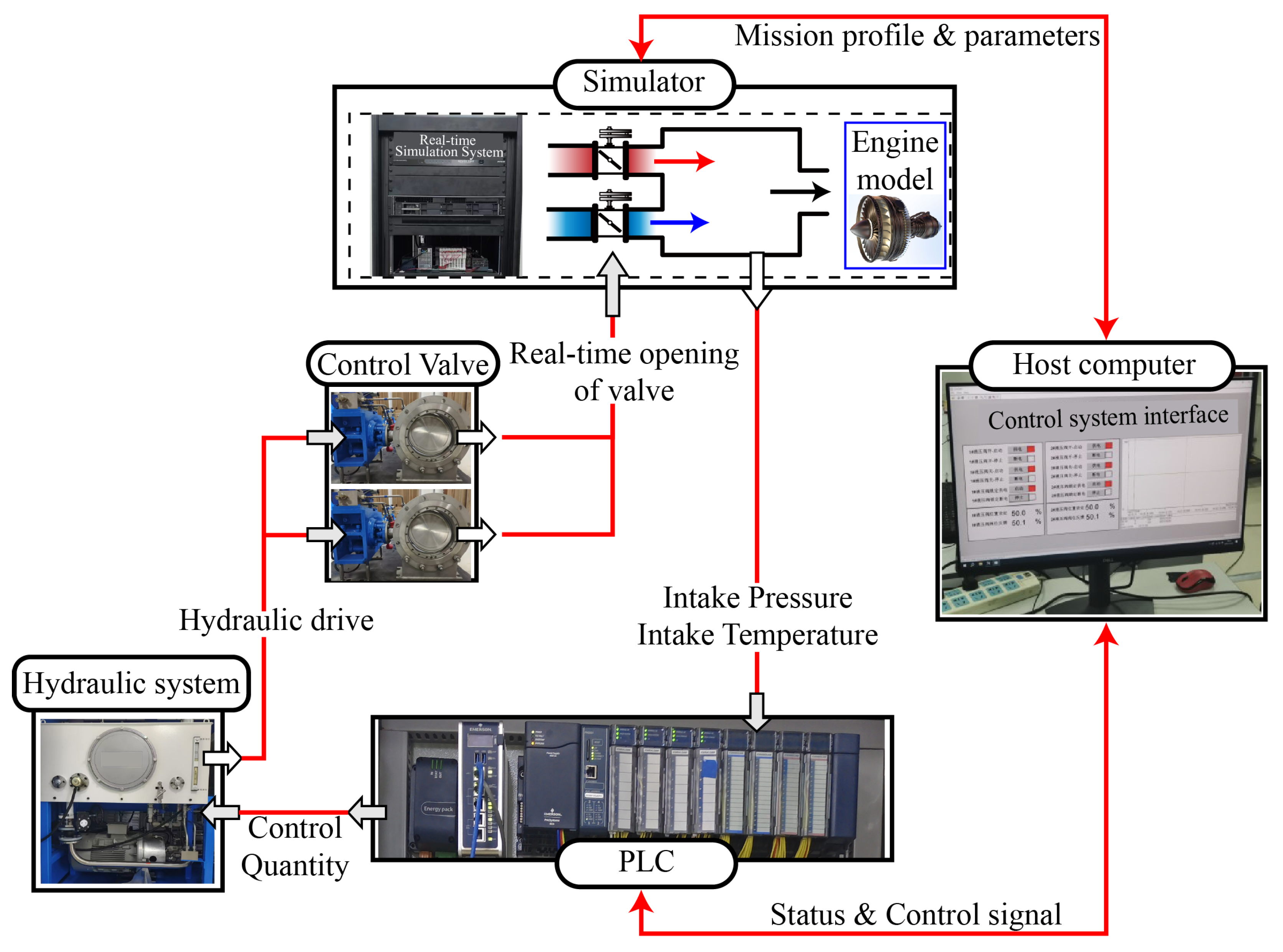
6.1. Simulation Verification Platform Setup
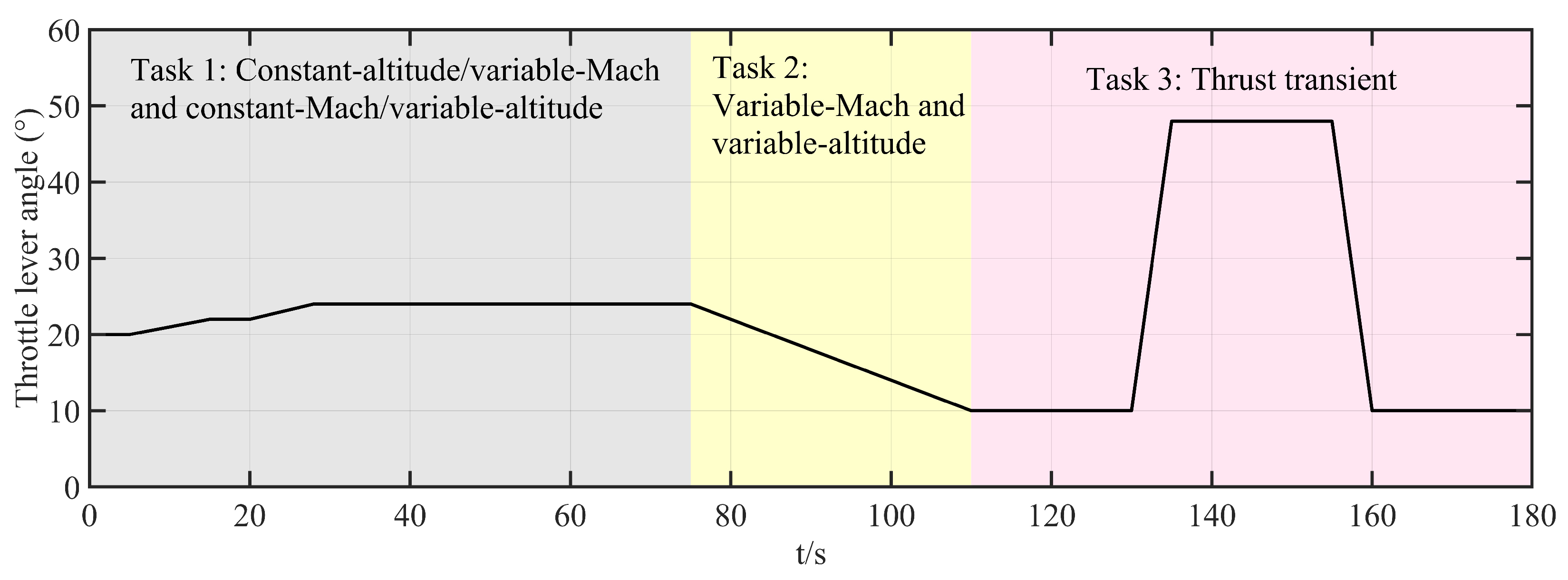
- Task 1:
- Constant-altitude ascent/descent and level-flight acceleration.
- Task 2:
- Simultaneous variation in Mach number and altitude.
- Task 3:
- Thrust transient: sudden engine flow change under constant altitude and Mach number.
6.2. Real-Time Implementation of Control Algorithm
6.3. Experimental Task Setup
- Task 1:
- This test evaluates the control system’s simulation performance under level-flight acceleration and constant-Mach-number ascent/descent conditions.
- 0–30 s (level-flight acceleration) at fixed altitude of 8 km:
- –
- 0–5 s: Mach number, 0.5; throttle, 20°.
- –
- 5–15 s: uniform acceleration to Mach number of 0.75 (hold to 20 s) and throttle of 22°.
- –
- 20–28 s: uniform acceleration to Mach number of 0.9 (hold to 30 s) and throttle of 24°.
- 30–75 s (constant-Mach-number ascent/descent) at Mach number of 0.9 and throttle of 24°:
- –
- 30–38 s: climb from 8 km to 10 km (hold to 43 s).
- –
- 43–53 s: climb from 10 km to 12 km (hold to 58 s).
- –
- 58–63 s: descend from 12 km to 11 km.
- Task 2:
- This test evaluates performance under simultaneous variation in Mach number and altitude (75–110 s):
- Altitude: 11 km → 5 km (uniform descent).
- Mach number: 0.9 → 0.5 (uniform deceleration).
- Throttle: 24° → 10° (uniform decrease).
- Task 3:
- This test evaluates the control system’s response to a thrust transient (110–180 s):
- Altitude: hold at 5 km; Mach number: hold at 0.5.
- 110–130 s: hold throttle at 10°.
- 130–135 s: increase throttle to 48°; hold to 155 s.
- 155–160 s: decrease throttle back to 10°; hold to 180 s.
6.4. Simulation Conditions and Control Parameters
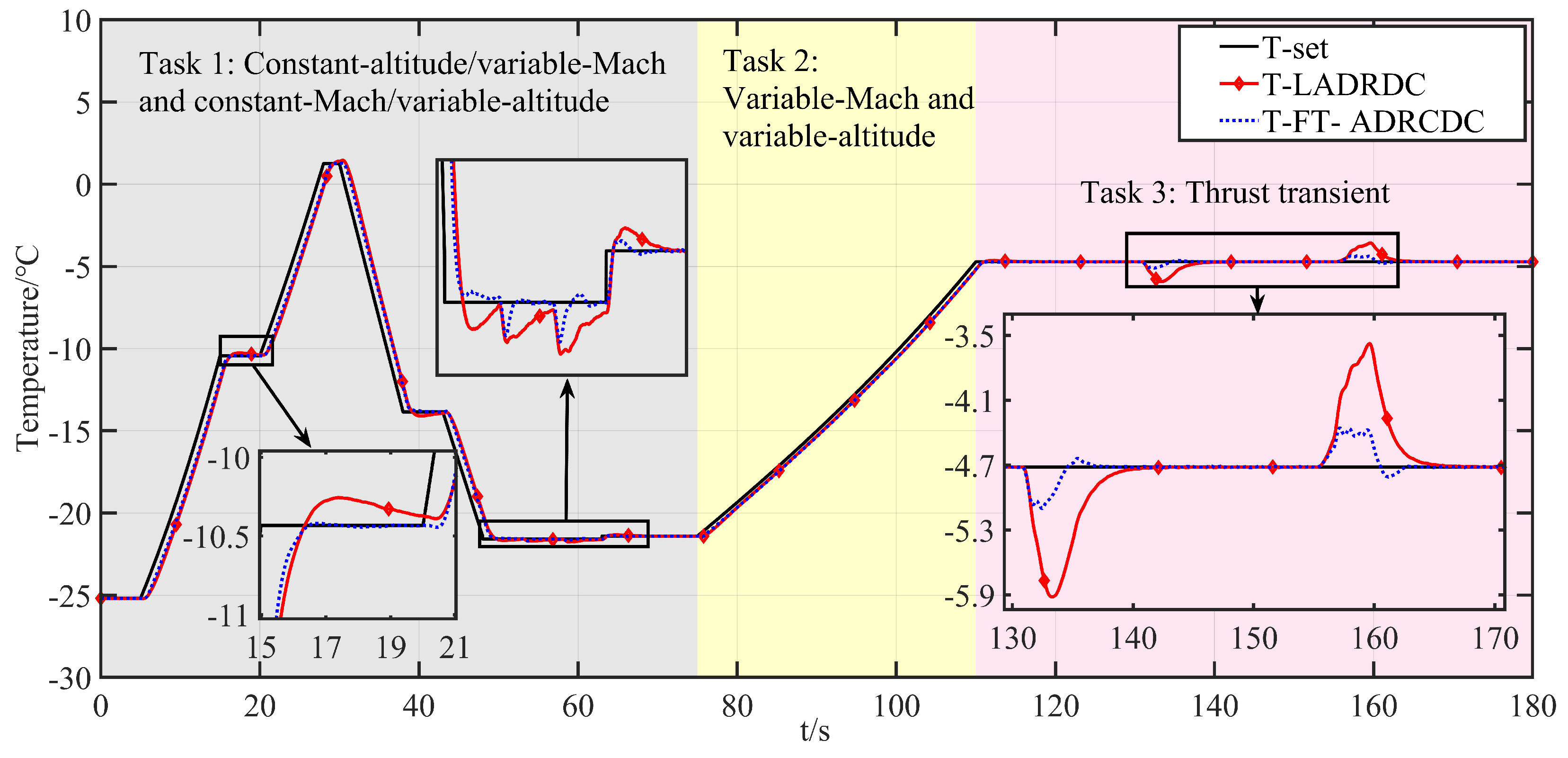
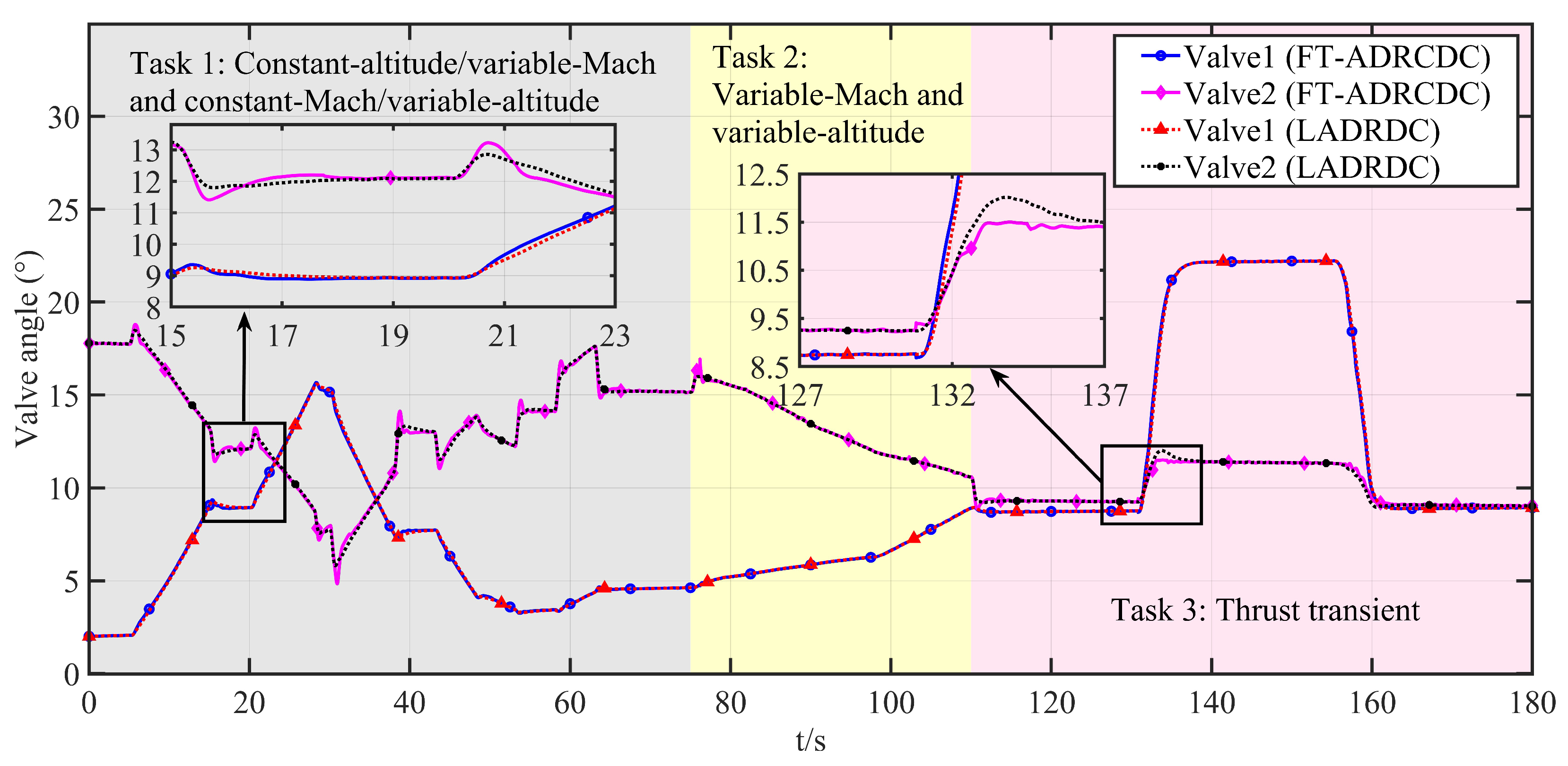
6.5. Results Analysis
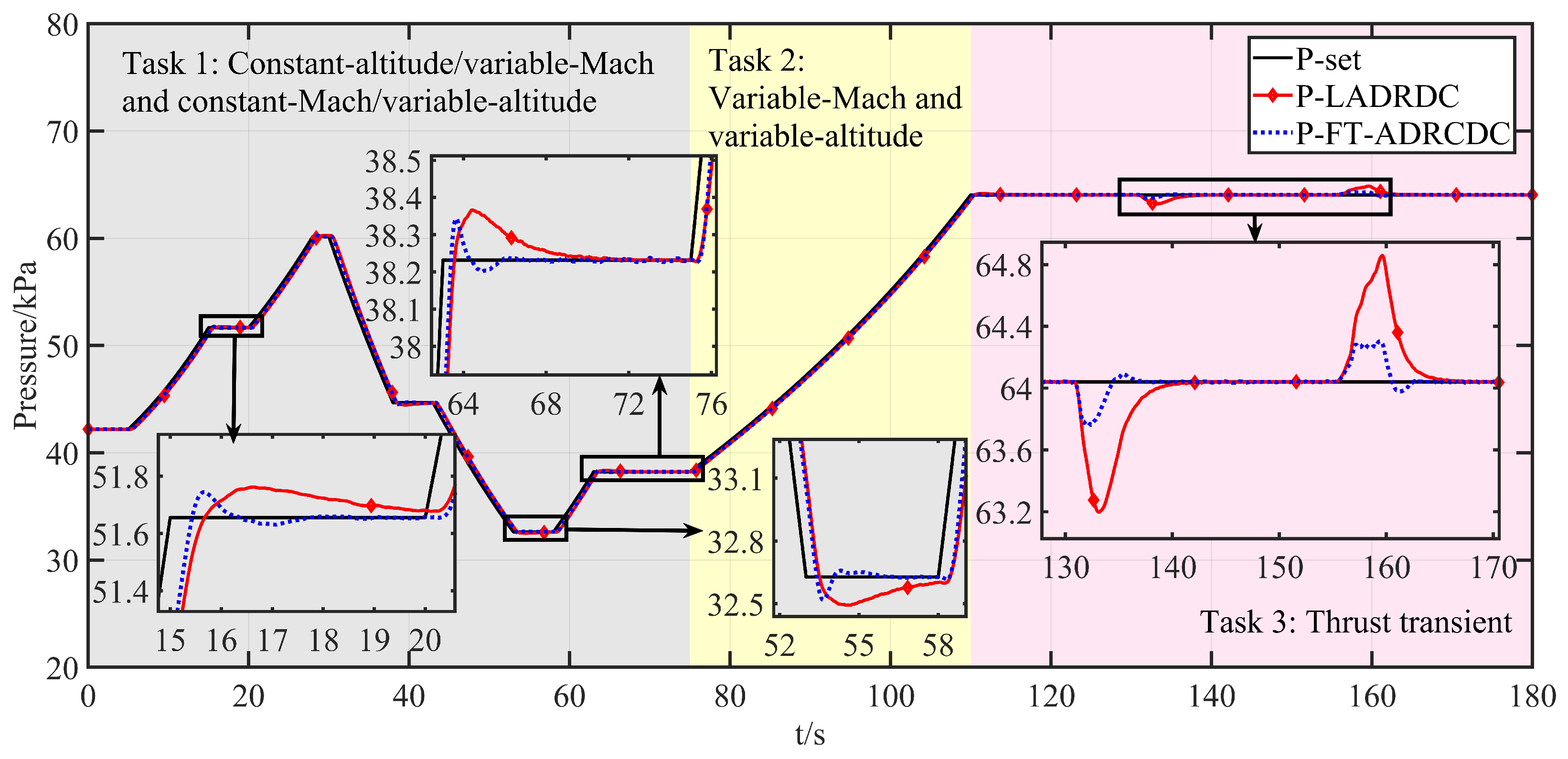
- Comparison of Collaborative Decoupling Control Performance for Dual-Variable Temperature–Pressure Tracking
- 2.
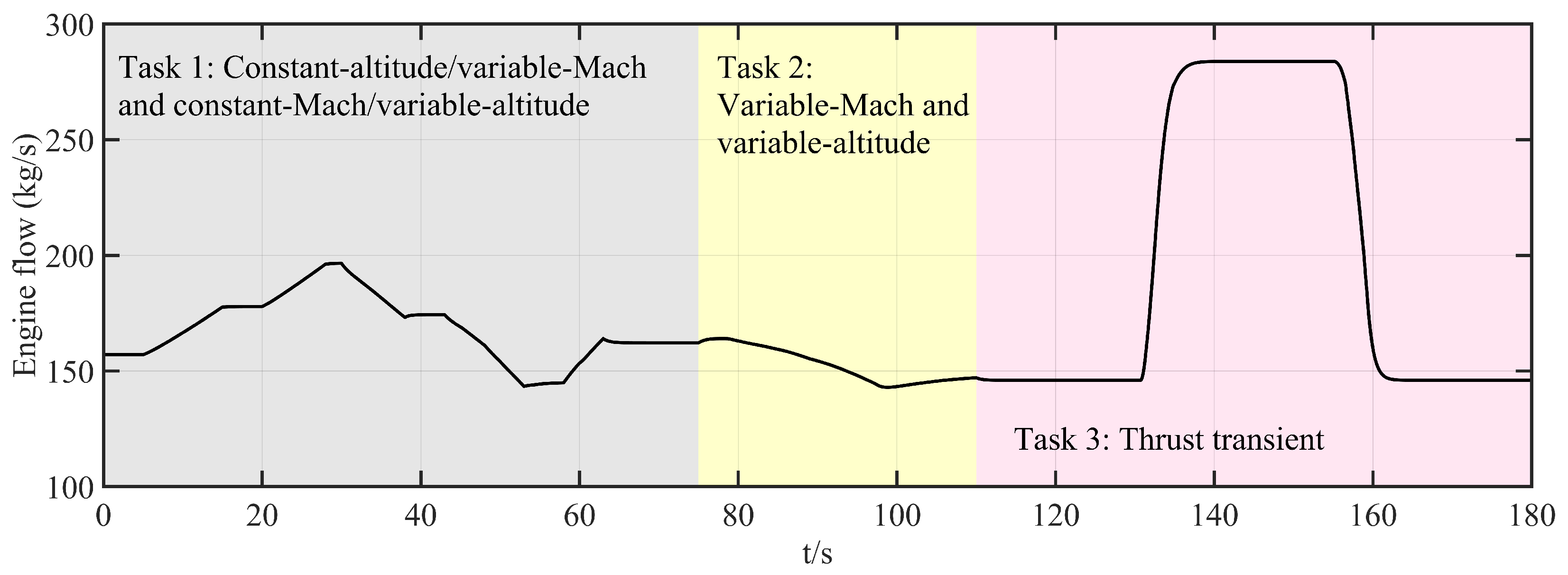
- Comparison of anti-disturbance abilities under changing flow rates of aeroengine
- 3.
- Comparison of convergence rates of FT-ADRDC and LADRDC.
- 4.
- Discussion on algorithmic differences and open issues.
- (i)
- Convergence mechanism: FT-ADRDC adopts a fixed-time sliding-mode law whose settling time is upper-bounded and independent of the initial error, whereas the linear feedback in LADRDC converges proportionally to both the initial error and the ESO bandwidth.
- (ii)
- Observer bandwidth: The super-twisting fixed-time ESO (ST-FT-ESO) in FT-ADRDC permits a higher effective bandwidth without noise, enabling disturbance estimation roughly one sampling period earlier and thereby suppressing the temperature spike at t = 48–53 s in Figure 11.
- (i)
- The fixed-time gains , , and are tuned for flows below ; robustness at higher rates remains to be verified. Adaptive scheduling or data-driven tuning merits investigation.
- (ii)
- Actuator saturation and dead-zone effects are currently only handled implicitly, which may degrade performance under extreme throttle commands. A structured anti-windup design could mitigate this issue.
- (iii)
- The current model neglects distributed duct losses and measurement uncertainty; these factors become important in larger, more complex piping networks.
7. Conclusions
- The algorithm achieves fixed-time convergence by introducing virtual control variables that decouple the intake environment simulation system (IESS) into two single-input, single-output loops. This decoupling mitigates the static coupling between pressure and temperature. The ST-FT-ESO provides rapid, noise-free estimation of the system states and total disturbances. These disturbances are then compensated for in real time by the FT-SMC, enhancing control robustness.
- Compared with the linear ADRDC (LADRDC) baseline, the proposed FT-ADRCDC achieves significantly better performance across the full simulation window (–180 s). Specifically, the absolute integral error (AIE) for pressure tracking is reduced by 71.9%, and for temperature tracking, it is reduced by 77.9%. The corresponding reductions in the mean-squared error (MSE) are 46.0% and 41.3%, respectively. Moreover, the FT-ADRCDC maintains settling times within 1–2 s, compared to 5 s or more under LADRDC. These results validate the fixed-time design and demonstrate improved anti-disturbance capability and tracking accuracy.
- The proposed controller structure is compact, requires moderate parameter tuning, and is compatible with real-time industrial PLC deployment. These properties make FT-ADRCDC a promising solution for high-speed, high-accuracy intake environment control in high-altitude test facilities. Future work will investigate its scalability to more complex multivariable test systems and its robustness under actuator constraints and sensor noise.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Eight-Coefficient Polynomials for Dry Air
| 0.992313 | 0.236688 | 6.083152 | 7.097112 | 0.794571 |
References
- Hou, M.J. High-Altitude Simulation Testing Technology; Aviation Industry Press: Beijing, China, 2014. [Google Scholar]
- Davis, M.; Montgomery, P. A flight-simulation vision for aeropropulsion altitude ground test facilities. J. Eng. Gas Turbines Power 2005, 127, 8–17. [Google Scholar] [CrossRef]
- Walker, S.; Tang, M.; Mamplata, C. TBCC propulsion for a Mach 6 hypersonic airplane. In Proceedings of the 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Bremen, Germany, 16–20 October 2013; p. 7238. [Google Scholar]
- Pei, X.; Wang, X.; Liu, J.; Zhu, M.; Dan, Z.; He, A.; Miao, K.; Xu, Z. A review of modeling, simulation and control technologies of altitude ground test facilities for control application. Chin. J. Aeronaut. 2023, 36, 38–62. [Google Scholar] [CrossRef]
- Lu, L.; Tian, S.; Xue, D.; Zhang, T.; Chen, Y.; Zhang, S. A review of industrial MIMO decoupling control. Int. J. Control Autom. Syst. 2019, 17, 1246–1254. [Google Scholar] [CrossRef]
- Guan, J.C.; Ren, H.W.; Tan, G.L. Distributed dynamic event-triggered control to leader-following consensus of nonlinear multi-agent systems with directed graphs. Entropy 2024, 26, 113. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Wang, D.; Shi, G.; Liu, D.; Li, Y. Decentralized control for large-scale nonlinear systems with unknown mismatched interconnections via policy iteration. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1725–1735. [Google Scholar] [CrossRef]
- Garrido, J.; Vázquez, F.; Morilla, F. Inverted-decoupling internal-model control for square stable multivariable time-delay systems. J. Process Control 2014, 24, 1710–1719. [Google Scholar] [CrossRef]
- Chekari, T.; Mansouri, R.; Bettayeb, M. IMC–PID fractional-order filter multi-loop controller design for multivariable systems based on a two-degree-of-freedom control scheme. Int. J. Control Autom. Syst. 2018, 16, 689–701. [Google Scholar] [CrossRef]
- Gouta, H.; Saïd, S.H.; Barhoumi, N.; M’Sahli, F. Generalized predictive control for a coupled four-tank MIMO system using a continuous–discrete-time observer. ISA Trans. 2017, 67, 280–292. [Google Scholar] [CrossRef] [PubMed]
- Noshadi, A.; Shi, J.; Lee, W.S.; Shi, P.; Kalam, A. System identification and robust control of multi-input multi-output active-magnetic-bearing systems. IEEE Trans. Control Syst. Technol. 2016, 24, 1227–1239. [Google Scholar] [CrossRef]
- Huang, X.; Song, Y. Distributed and performance-guaranteed robust control for uncertain MIMO nonlinear systems with controllability relaxation. IEEE Trans. Autom. Control 2023, 68, 2460–2467. [Google Scholar] [CrossRef]
- Wang, H.; Yang, C.; Liu, X.; Zhou, L. Neural-network-based adaptive control of uncertain MIMO singularly perturbed systems with full-state constraints. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3764–3774. [Google Scholar] [CrossRef] [PubMed]
- Garrard, D.; Vaughn, D.; Milhoan, A.; Williams, S.; Choi, S. Checkout testing of the new basic process-control system at the aerodynamic and propulsion test unit. In Proceedings of the 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference, Tours, France, 24–28 September 2012; p. 5969. [Google Scholar]
- Garrard, G.D. Hypersonic test capabilities at AEDC’s aerodynamic and propulsion test unit. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1784. [Google Scholar]
- Bierkamp, J.; Köcke, S.; Staudacher, S.; Fiola, R. Influence of ATF dynamics and controls on jet-engine performance. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea and Air, Montreal, QC, Canada, 14–17 May 2007; pp. 105–113. [Google Scholar]
- Weisser, M.; Bolk, S.; Staudacher, S. Hardware-in-the-Loop Simulation of a Feedforward Multivariable Controller for the Altitude Test Facility at the University of Stuttgart; DGLR: Bonn, Germany, 2013. [Google Scholar]
- Dan, Z.; Zhang, S.; Bai, K.; Qian, Q.; Pei, X.; Wang, X. Air-intake environment simulation of an altitude-test facility control based on an extended-state observer. J. Propuls. Technol. 2021, 42, 2119–2128. [Google Scholar]
- Lun, Y.; Wang, H.; Zhang, S.; Dan, Z.; Qian, Q.; Pei, X.; Yang, Z. Continuous-state control of a flight-environment testbed based on state feedback and LPV. In Proceedings of the International Conference on Autonomous Unmanned Systems, Beijing, China, 14–16 June 2021; pp. 1055–1063. [Google Scholar]
- Zhu, M.; Wang, X.; Yang, S.; Chen, H.; Miao, K.; Gu, N. Two-degree-of-freedom μ-synthesis control with a Kalman filter for flight-environment simulation volume with sensor uncertainty. In Proceedings of the ASME Turbo Expo 2019: Power for Land, Sea and Air, Phoenix, AZ, USA, 17–21 June 2019; p. V006T05A002. [Google Scholar]
- Han, J. From PID technique to active-disturbance-rejection control technique. Control Eng. China 2002, 9, 13–18. (In Chinese) [Google Scholar]
- Han, J. Active-disturbance-rejection control technique—The technique for estimating and compensating the uncertainties. In Active Disturbance-Rejection Control Technique; National Defense Industry Press: Beijing, China, 2008; pp. 197–270. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterisation-based controller tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Zhang, Z.; Cheng, J.; Guo, Y. PD-based optimal ADRC with an improved linear extended-state observer. Entropy 2021, 23, 888. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.; Wang, M.; Li, Z.; Zhao, X. Improved super-twisting sliding-mode control for single-phase T-type three-level converters based on a fixed-time extended-state observer. IEEE Trans. Transp. Electrific. 2023, in press. [Google Scholar] [CrossRef]
- Cui, L.; Jin, N.; Chang, S.; Zuo, Z.; Zhao, Z. Fixed-time ESO-based fixed-time integral terminal sliding-mode controller design for a missile. ISA Trans. 2022, 125, 237–251. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.; Wang, Y.; Zuo, Z. Fixed-time active-disturbance-rejection control and its application to wheeled mobile robots. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7120–7130. [Google Scholar] [CrossRef]
- Boylston, B.M. Quasi-One-Dimensional Flow for Use in Real-Time Facility Simulations. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2011. [Google Scholar]
- McBride, B.J.; Zehe, M.J.; Gordon, S. NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species. NASA TP-2002-211556, 1 September 2002. Available online: https://ntrs.nasa.gov/citations/20020085330 (accessed on 17 August 2025).
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]


| Method | Core Controller | ESO |
|---|---|---|
| FT-ADRCDC | ||
| LADRDC |
| Category | Metric | FT-ADRCDC | LADRDC | Unit |
|---|---|---|---|---|
| Pressure tracking | MAR | 0.899 | 1.271 | kPa |
| MSE | 0.0821 | 0.1521 | kPa2 | |
| AIE | 5.122 | 18.206 | kPa·s | |
| Temperature tracking | MAR | 1.137 | 1.655 | °C |
| MSE | 0.267 | 0.456 | °C2 | |
| AIE | 5.013 | 22.689 | °C·s |
| Category | Metric | FT-ADRCDC | LADRDC | Unit |
|---|---|---|---|---|
| Pressure tracking | MAR | 0.899 | 1.271 | kPa |
| MSE | 0.109 | 0.213 | kPa2 | |
| AIE | 2.965 | 10.015 | kPa·s | |
| Temperature tracking | MAR | 1.137 | 1.655 | °C |
| MSE | 0.497 | 0.666 | °C2 | |
| AIE | 3.851 | 13.332 | °C·s |
| Category | Metric | FT-ADRCDC | LADRDC | Unit |
|---|---|---|---|---|
| Pressure tracking | MAR | 0.372 | 0.843 | kPa |
| MSE | 0.005 | 0.051 | kPa2 | |
| AIE | 2.019 | 6.381 | kPa·s | |
| Temperature tracking | MAR | 0.489 | 1.203 | °C |
| MSE | 0.009 | 0.101 | °C2 | |
| AIE | 2.625 | 8.435 | °C·s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, H.; Shi, D.; Dan, Z.; Wang, X.; Zhai, C.; Xiao, G.; Xu, Z. Fixed-Time Active Disturbance Rejection Temperature–Pressure Decoupling Control for a High-Flow Air Intake System. Entropy 2025, 27, 880. https://doi.org/10.3390/e27080880
Zhang L, Zhang H, Shi D, Dan Z, Wang X, Zhai C, Xiao G, Xu Z. Fixed-Time Active Disturbance Rejection Temperature–Pressure Decoupling Control for a High-Flow Air Intake System. Entropy. 2025; 27(8):880. https://doi.org/10.3390/e27080880
Chicago/Turabian StyleZhang, Louyue, Hehong Zhang, Duoqi Shi, Zhihong Dan, Xi Wang, Chao Zhai, Gaoxi Xiao, and Zhouzhe Xu. 2025. "Fixed-Time Active Disturbance Rejection Temperature–Pressure Decoupling Control for a High-Flow Air Intake System" Entropy 27, no. 8: 880. https://doi.org/10.3390/e27080880
APA StyleZhang, L., Zhang, H., Shi, D., Dan, Z., Wang, X., Zhai, C., Xiao, G., & Xu, Z. (2025). Fixed-Time Active Disturbance Rejection Temperature–Pressure Decoupling Control for a High-Flow Air Intake System. Entropy, 27(8), 880. https://doi.org/10.3390/e27080880






