Time-Marching Quantum Algorithm for Simulation of Nonlinear Lorenz Dynamics
Abstract
1. Introduction
2. The Lorenz Model
Selection of the Time-Marching Scheme
3. The Quantum Algorithm
3.1. Preparation of the Nonlinear States
3.1.1. The Hadamard Product
3.1.2. Implementing the Lorenz Nonlinear States
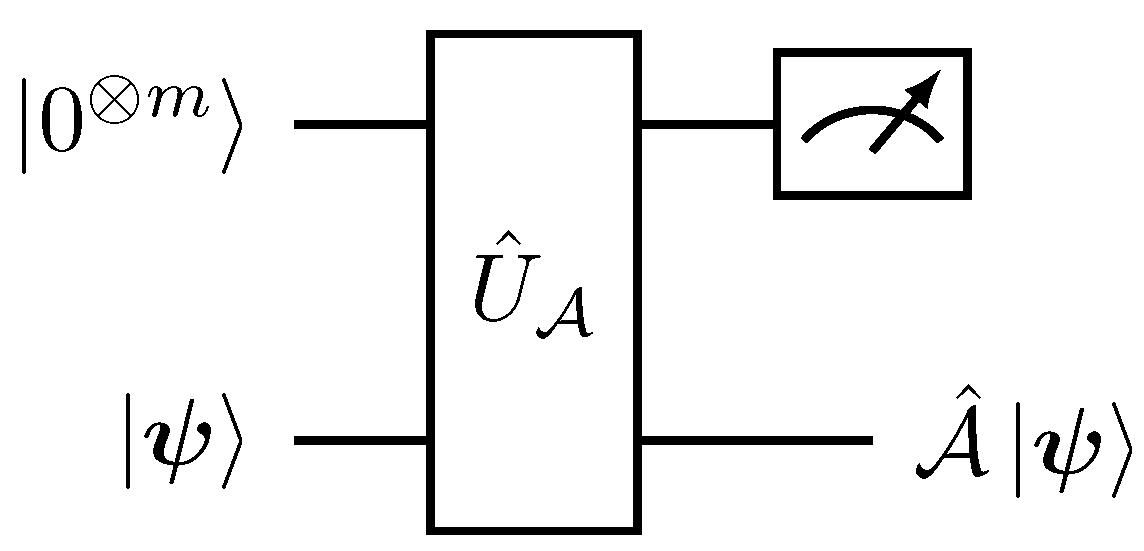
3.2. Block Encoding of Non-Unitary Matrix
3.3. Quantum Circuit Implementation of the Second-Order Time-Marching Scheme for the Lorenz Equations
- The nonlinear state in Equation (13) consists of polynomial terms up to third degree in the amplitudes . Subsequently, as discussed in Section 3.1.2, implementing requires a sum of Hadamard products between three copies of interleaved with amplitude alternating gates,The operators are tensor-fold gates acting on the 12-qubit composite space of the states, with .
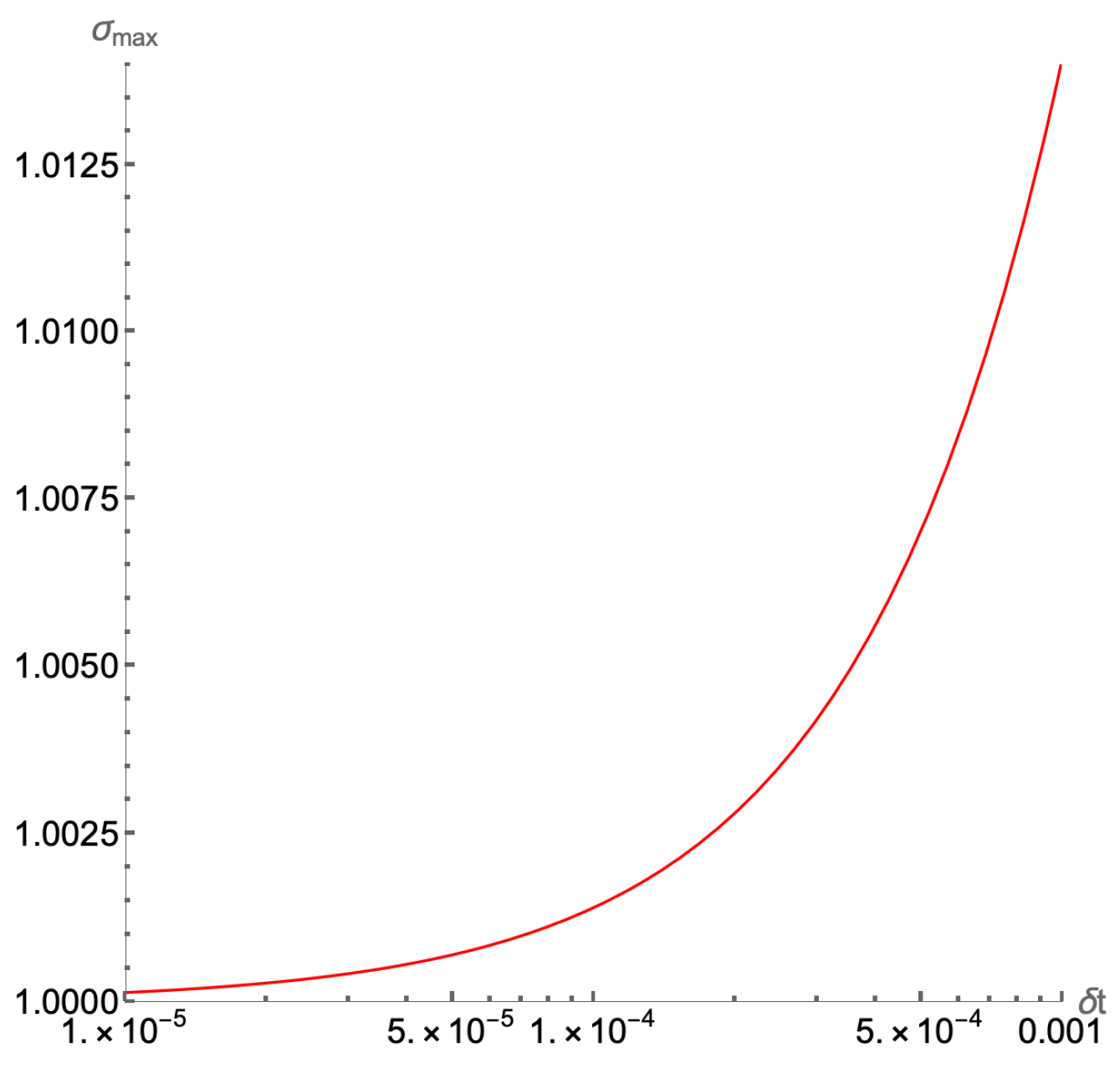
3.4. Complexity Considerations and Discussion
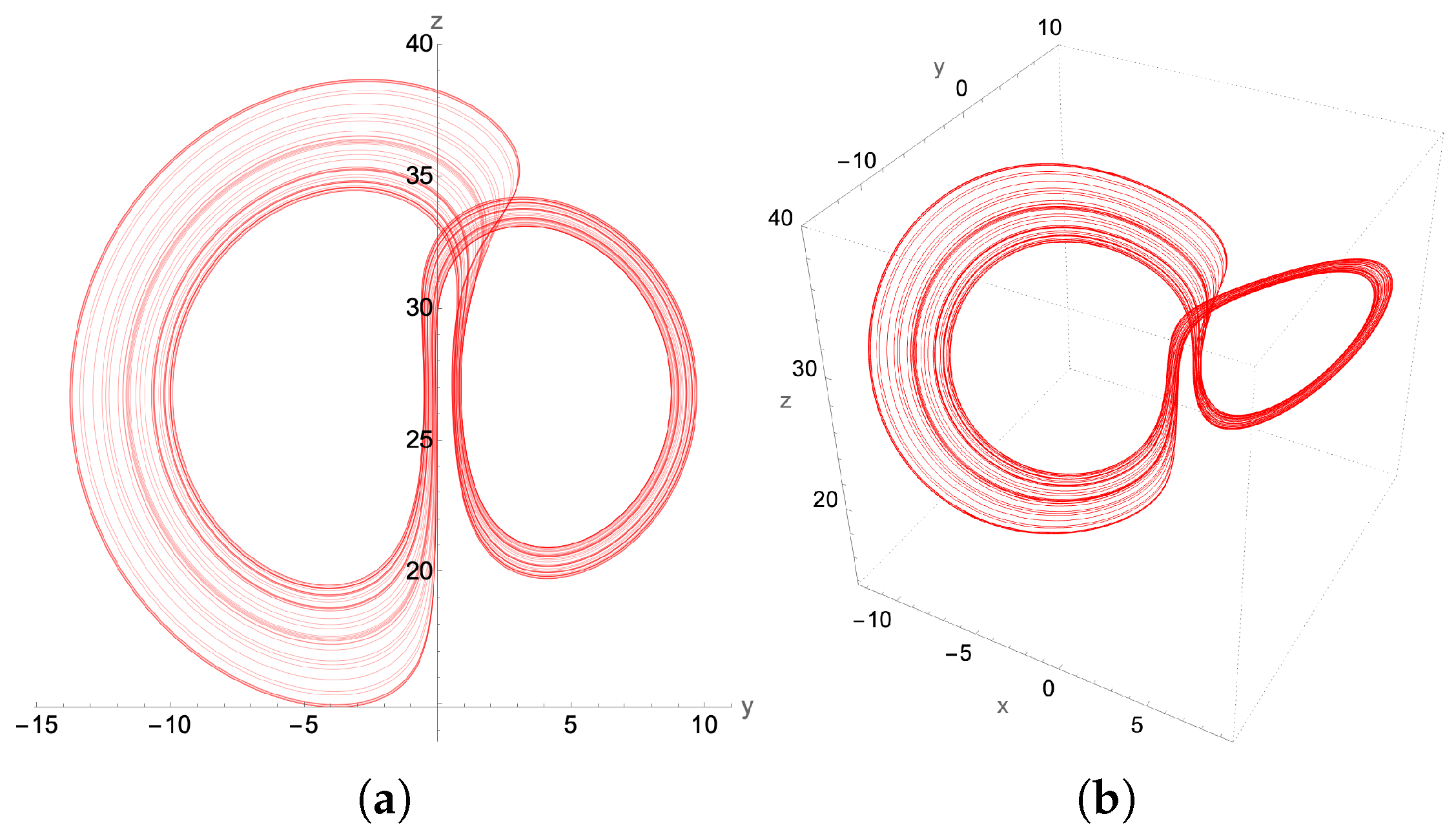
4. Numerical Demonstrations
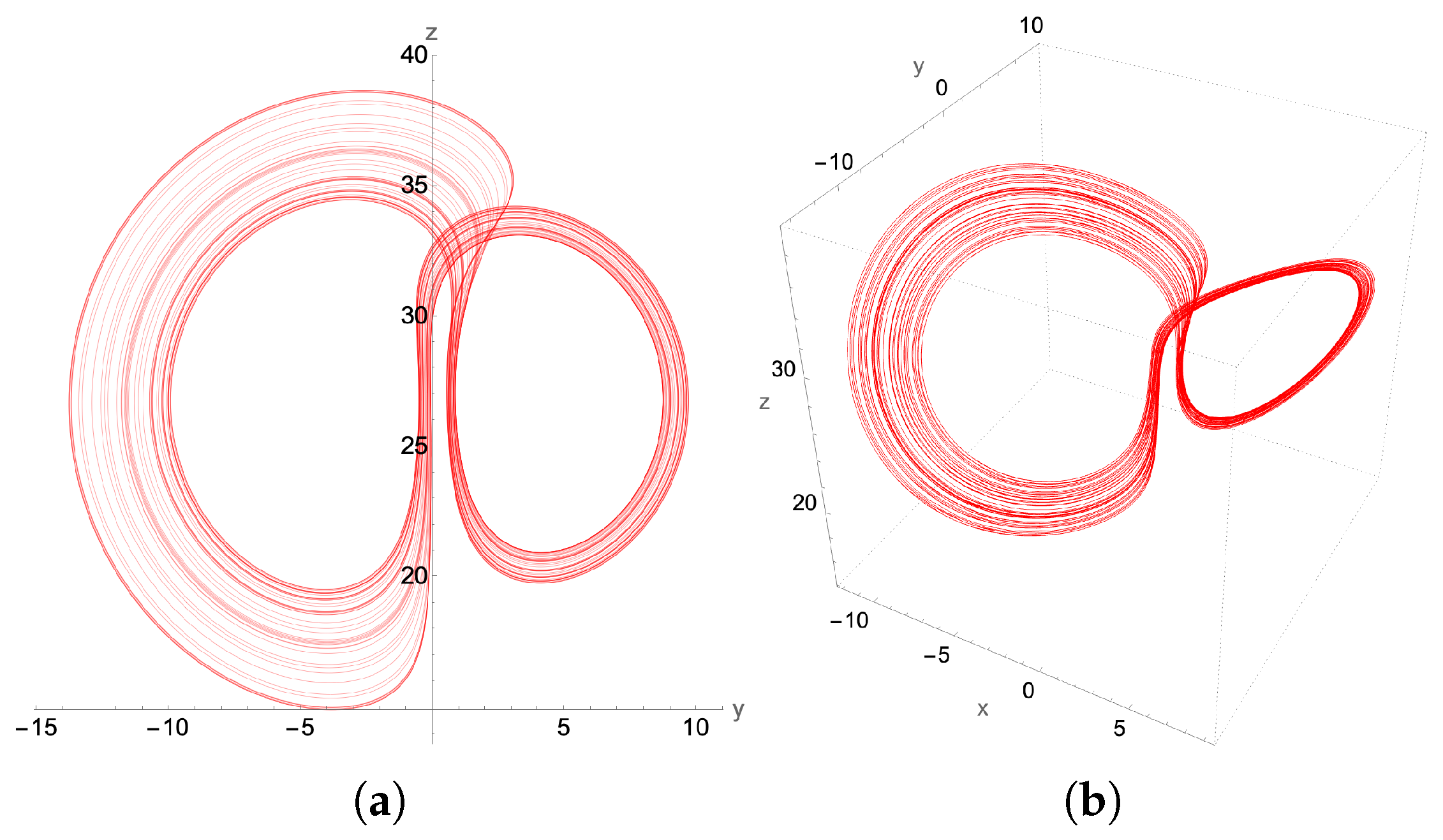
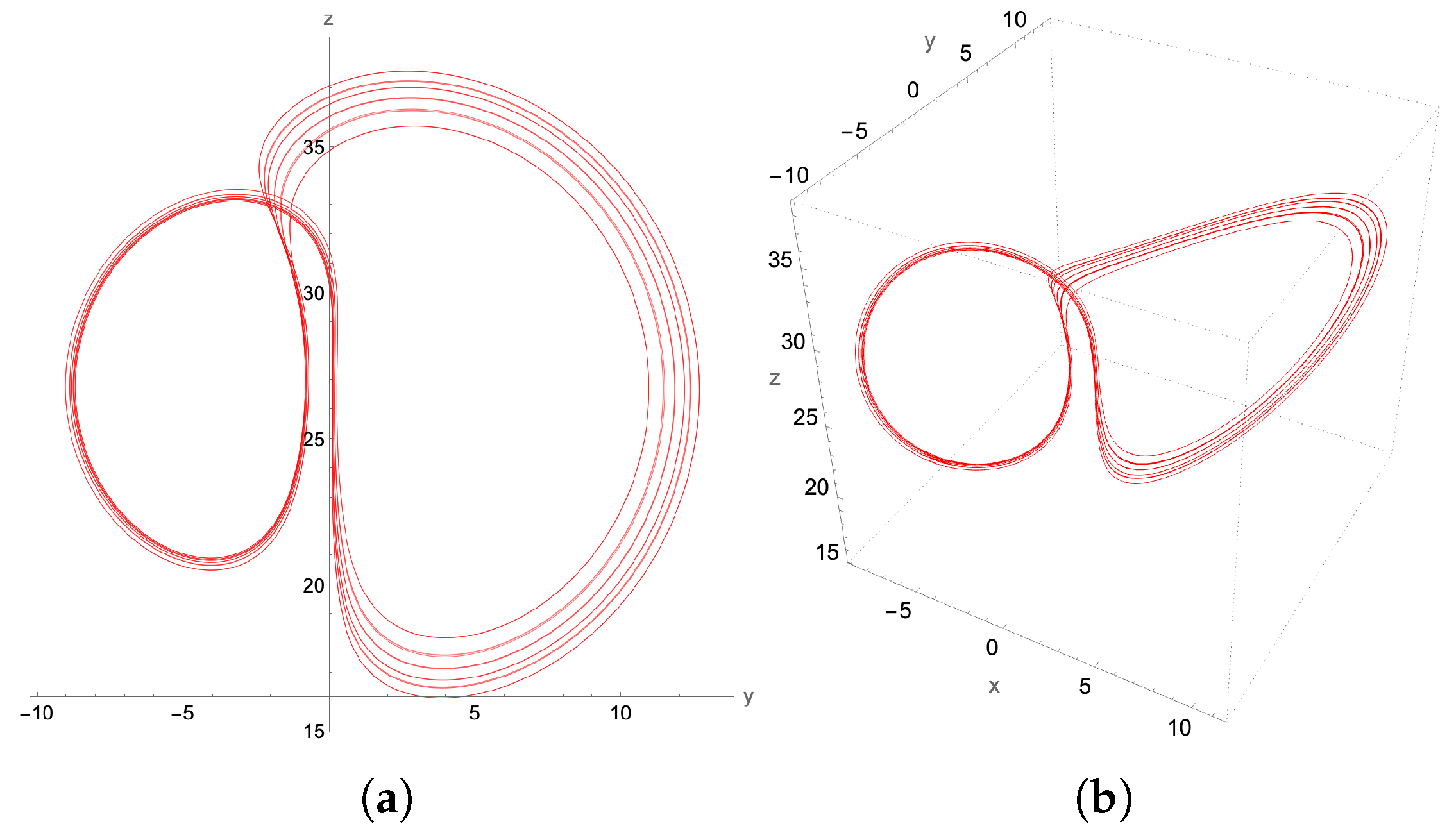
4.1. Chaotic Attractor:
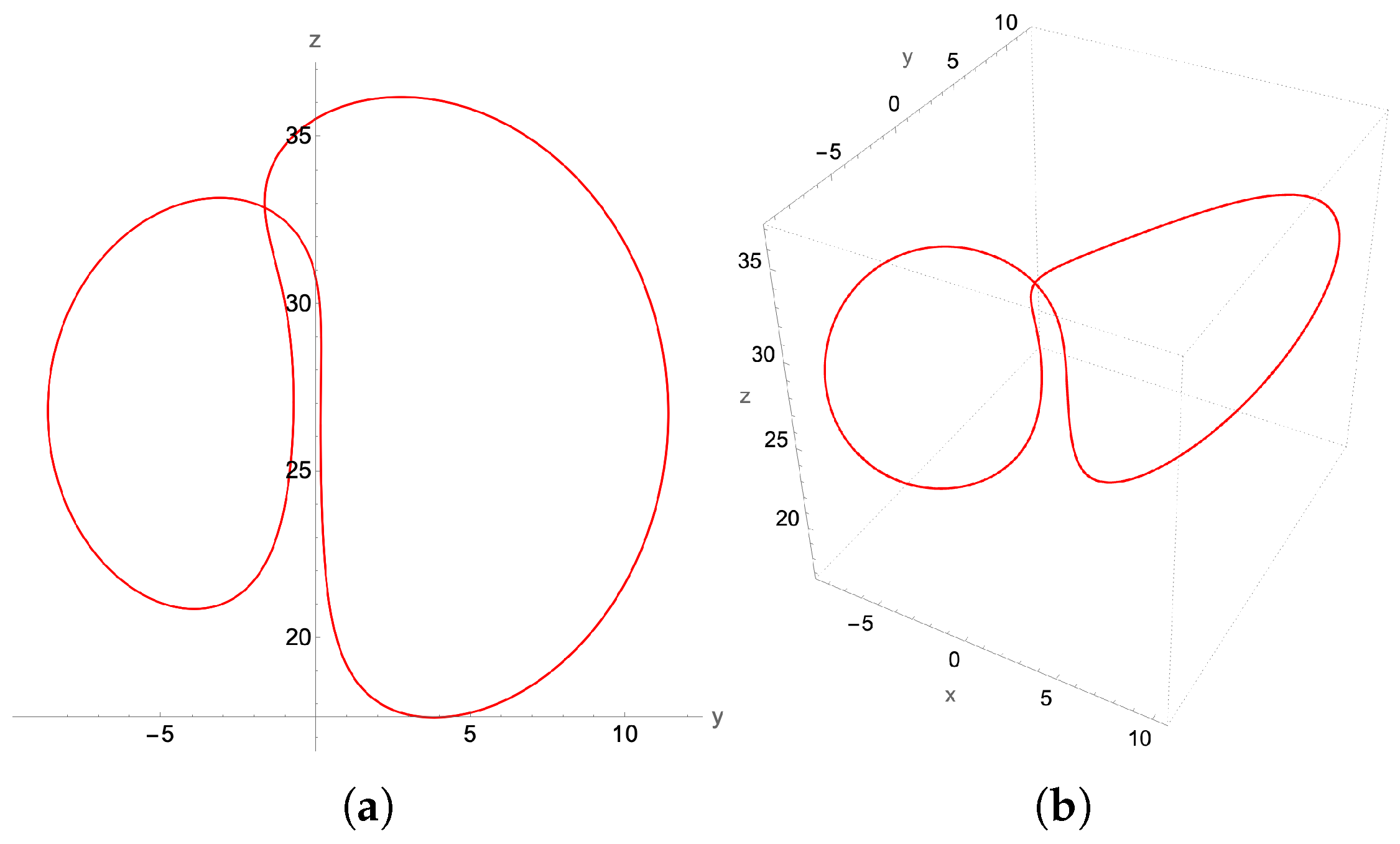
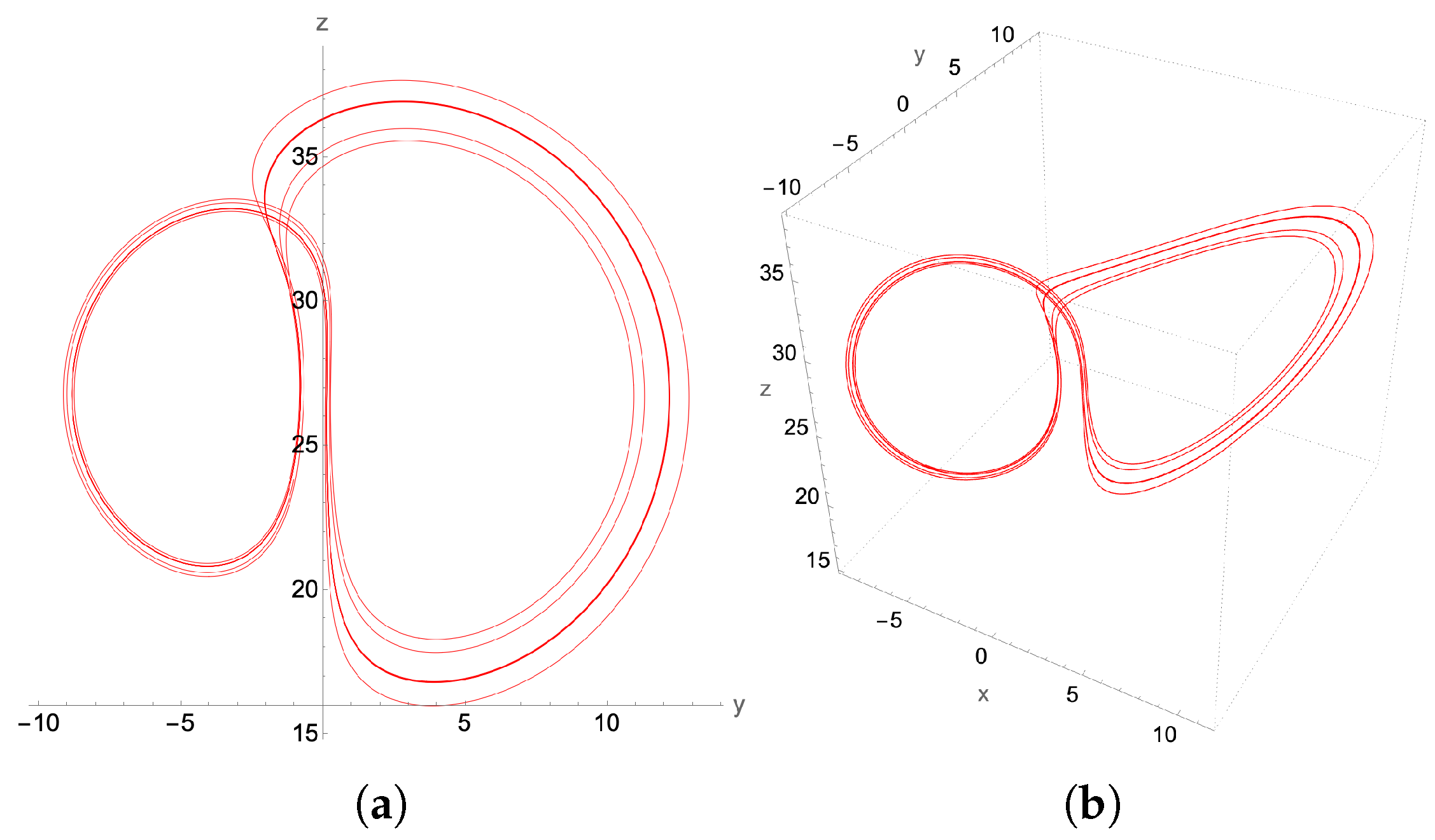
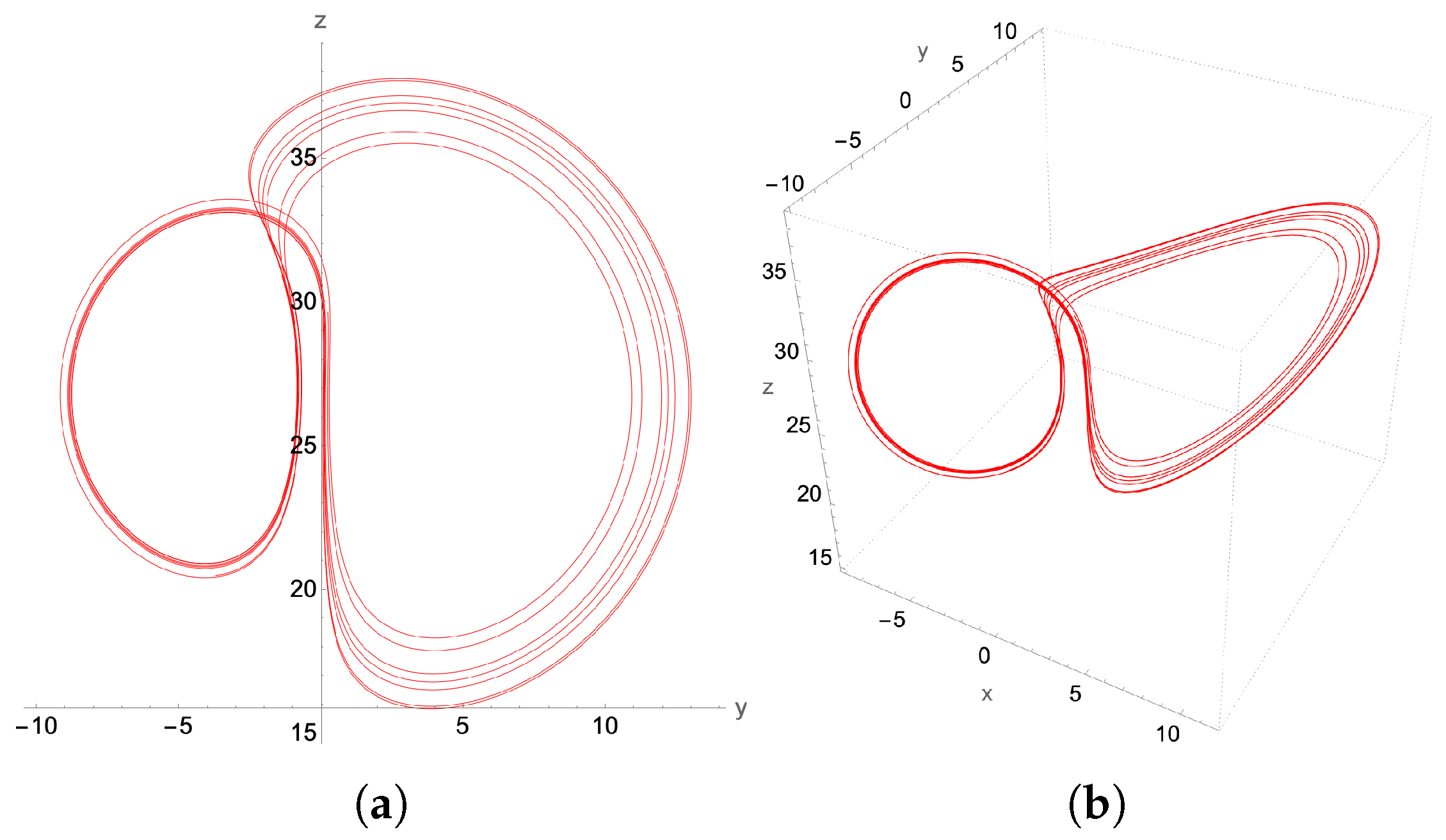
4.2. Limit Cycles
4.2.1. P1-Limit Cycle:
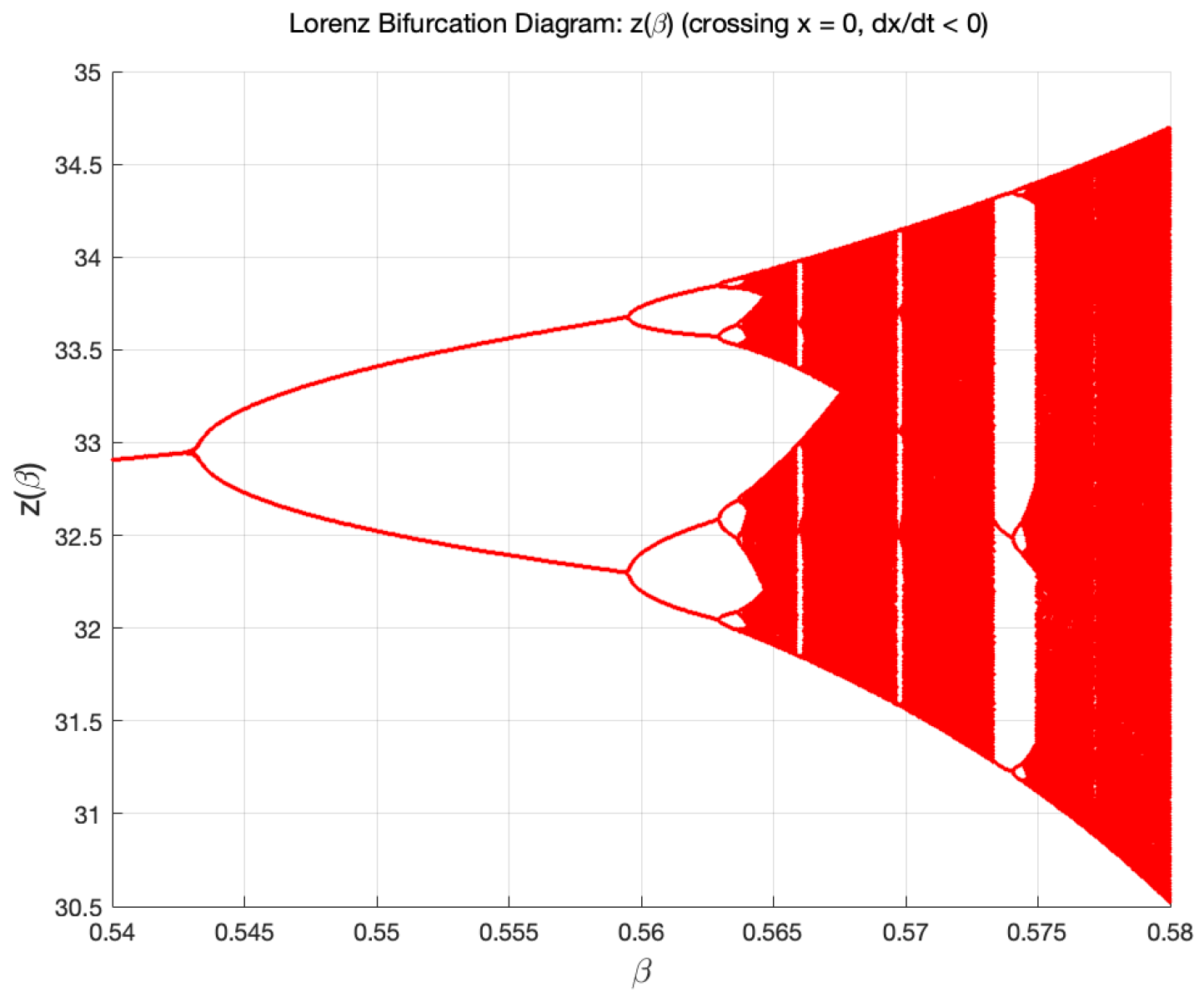
4.2.2. Period Doubling Limit Cycles
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| KvN | Koopman von Neumann |
| CNOT | Controlled-NOT |
| LCU | Linear Combination of Unitaries |
| SVD | Singular Value Decomposition |
| ODE | Ordinary differential equation |
| NISQ | Noisy Intermediate-Scale Quantum |
| PDE | Partial differential equation |
| QLA | Qubit Lattice Algorithm |
References
- Tennie, F.; Laizet, S.; Lloyd, S.; Magri, L. Quantum computing for nonlinear differential equations and turbulence. Nat. Rev. Phys. 2025, 7, 220–230. [Google Scholar] [CrossRef]
- Liu, J.P.; Kolden, H.O.; Krovi, H.K.; Loureiro, N.F.; Trivisa, K.; Childs, A.M. Efficient quantum algorithm for dissipative nonlinear differential equations. Proc. Natl. Acad. Sci. USA 2021, 118, e2026805118. [Google Scholar] [CrossRef]
- Krovi, H. Improved quantum algorithms for linear and nonlinear differential equations. Quantum 2023, 7, 913. [Google Scholar] [CrossRef]
- Sanavio, C.; Scatamacchia, R.; de Falco, C.; Succi, S. Three Carleman routes to the quantum simulation of classical fluids. Phys. Fluids 2024, 36, 057143. [Google Scholar] [CrossRef]
- Wu, H.C.; Wang, J.; Li, X. Quantum Algorithms for Nonlinear Dynamics: Revisiting Carleman Linearization with No Dissipative Conditions. SIAM J. Sci. Comput. 2025, 47, A943–A970. [Google Scholar] [CrossRef]
- Joseph, I. Koopman–von Neumann approach to quantum simulation of nonlinear classical dynamics. Phys. Rev. Res. 2020, 2, 043102. [Google Scholar] [CrossRef]
- Novikau, I.; Joseph, I. Quantum algorithm for the advection-diffusion equation and the Koopman-von Neumann approach to nonlinear dynamical systems. Comput. Phys. Commun. 2025, 309, 109498. [Google Scholar] [CrossRef]
- Shi, Y.; Castelli, A.R.; Wu, X.; Joseph, I.; Geyko, V.; Graziani, F.R.; Libby, S.B.; Parker, J.B.; Rosen, Y.J.; Martinez, L.A.; et al. Simulating non-native cubic interactions on noisy quantum machines. Phys. Rev. A 2021, 103, 062608. [Google Scholar] [CrossRef]
- May, M.Q.; Qin, H. Nonlinear solution of classical three-wave interaction via finite-dimensional quantum model. J. Plasma Phys. 2024, 90, 805900302. [Google Scholar] [CrossRef]
- Shi, Y.; Evert, B.; Brown, A.F.; Tripathi, V.; Sete, E.A.; Geyko, V.; Cho, Y.; DuBois, J.L.; Lidar, D.; Joseph, I.; et al. Simulating nonlinear optical processes on a superconducting quantum device. J. Plasma Phys. 2024, 90, 805900602. [Google Scholar] [CrossRef]
- Andress, J.; Engel, A.; Shi, Y.; Parker, S. Quantum simulation of nonlinear dynamical systems using repeated measurement. J. Plasma Phys. 2025, 91, E55. [Google Scholar] [CrossRef]
- Lubasch, M.; Joo, J.; Moinier, P.; Kiffner, M.; Jaksch, D. Variational quantum algorithms for nonlinear problems. Phys. Rev. A 2020, 101, 010301. [Google Scholar] [CrossRef]
- Pool, A.J.; Somoza, A.D.; Mc Keever, C.; Lubasch, M.; Horstmann, B. Nonlinear dynamics as a ground-state solution on quantum computers. Phys. Rev. Res. 2024, 6, 033257. [Google Scholar] [CrossRef]
- Fathi Hafshejani, S.; Gaur, D.; Dasgupta, A.; Benkoczi, R.; Gosala, N.R.; Iorio, A. A Hybrid Quantum Solver for the Lorenz System. Entropy 2024, 26, 1009. [Google Scholar] [CrossRef] [PubMed]
- Leyton, S.K.; Osborne, T.J. A quantum algorithm to solve nonlinear differential equations. arXiv 2008, arXiv:0812.4423. [Google Scholar] [CrossRef]
- Lloyd, S.; Palma, G.D.; Gokler, C.; Kiani, B.; Liu, Z.W.; Marvian, M.; Tennie, F.; Palmer, T. Quantum algorithm for nonlinear differential equations. arXiv 2020, arXiv:2011.06571. [Google Scholar] [CrossRef]
- Gaitan, F. Finding flows of a Navier-Stokes fluid through quantum computing. NPJ Quantum Inf. 2020, 6, 61. [Google Scholar] [CrossRef]
- Tennie, F.; Palmer, T.N. Quantum Computers for Weather and Climate Prediction: The Good, the Bad, and the Noisy. Bull. Am. Meteorol. Soc. 2023, 104, E488–E500. [Google Scholar] [CrossRef]
- Esmaeilifar, E.; Ahn, D.; Myong, R.S. Quantum algorithm for nonlinear Burgers’ equation for high-speed compressible flows. Phys. Fluids 2024, 36, 106110. [Google Scholar] [CrossRef]
- Andrade, R.; Rauh, A. The Lorenz model and the method of Carleman embedding. Phys. Lett. A 1981, 82, 276–278. [Google Scholar] [CrossRef]
- Lewis, D.; Eidenbenz, S.; Nadiga, B.; Subaşı, Y. Limitations for Quantum Algorithms to Solve Turbulent and Chaotic Systems. Quantum 2024, 8, 1509. [Google Scholar] [CrossRef]
- Lin, Y.T.; Lowrie, R.B.; Aslangil, D.; Subaşı, Y.; Sornborger, A.T. Challenges for quantum computation of nonlinear dynamical systems using linear representations. arXiv 2024, arXiv:2202.02188. [Google Scholar]
- Engel, A.; Smith, G.; Parker, S.E. Linear embedding of nonlinear dynamical systems and prospects for efficient quantum algorithms. Phys. Plasmas 2021, 28, 062305. [Google Scholar] [CrossRef]
- Weiss, J.; Tabor, M.; Carnevale, G. The Painleve property for partial differential equations. J. Math. Phys. 1983, 24, 522–526. [Google Scholar] [CrossRef]
- Nandy, P.; Matsoukas-Roubeas, A.S.; Martinez-Azcona, P.; Dymarsky, A.; del Campo, A. Quantum dynamics in Krylov space: Methods and applications. Phys. Rep. 2025, 1125–1128, 1–82. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Yao, L.S. Computed chaos or numerical errors. Nonlinear Anal. Model. Control 2010, 15, 109–126. [Google Scholar] [CrossRef]
- Süli, E.; Mayers, D.F. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Bechmann-Pasquinucci, H.; Huttner, B.; Gisin, N. Non-linear quantum state transformation of spin-12. Phys. Lett. A 1998, 242, 198–204. [Google Scholar] [CrossRef]
- Möttönen, M.; Vartiainen, J.J.; Bergholm, V.; Salomaa, M.M. Quantum Circuits for General Multiqubit Gates. Phys. Rev. Lett. 2004, 93, 130502. [Google Scholar] [CrossRef]
- Bergholm, V.; Vartiainen, J.J.; Möttönen, M.; Salomaa, M.M. Quantum circuits with uniformly controlled one-qubit gates. Phys. Rev. A 2005, 71, 052330. [Google Scholar] [CrossRef]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457–3467. [Google Scholar] [CrossRef]
- Plesch, M.; Brukner, I.C.V. Quantum-state preparation with universal gate decompositions. Phys. Rev. A 2011, 83, 032302. [Google Scholar] [CrossRef]
- Long, G.L. General Quantum Interference Principle and Duality Computer. Commun. Theor. Phys. 2006, 45, 825. [Google Scholar] [CrossRef]
- Holmes, Z.; Coble, N.J.; Sornborger, A.T.; Subaşı, Y. Nonlinear transformations in quantum computation. Phys. Rev. Res. 2023, 5, 013105. [Google Scholar] [CrossRef]
- Childs, A.M.; Wiebe, N. Hamiltonian simulation using linear combinations of unitary operations. Quantum Inf. Comput. 2012, 12, 901–924. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Schlimgen, A.W.; Head-Marsden, K.; Sager, L.M.; Narang, P.; Mazziotti, D.A. Quantum Simulation of Open Quantum Systems Using a Unitary Decomposition of Operators. Phys. Rev. Lett. 2021, 127, 270503. [Google Scholar] [CrossRef]
- Schlimgen, A.W.; Head-Marsden, K.; Sager-Smith, L.M.; Narang, P.; Mazziotti, D.A. Quantum state preparation and nonunitary evolution with diagonal operators. Phys. Rev. A 2022, 106, 022414. [Google Scholar] [CrossRef]
- Jin, S.; Liu, N.; Yu, Y. Quantum simulation of partial differential equations: Applications and detailed analysis. Phys. Rev. A 2023, 108, 032603. [Google Scholar] [CrossRef]
- Koukoutsis, E.; Hizanidis, K.; Ram, A.K.; Vahala, G. Quantum simulation of dissipation for Maxwell equations in dispersive media. Future Gener. Comput. Syst. 2024, 159, 221–229. [Google Scholar] [CrossRef]
- Koukoutsis, E.; Papagiannis, P.; Hizanidis, K.; Ram, A.K.; Vahala, G.; Amaro, Ó.; Gamiz, L.I.I.; Vallis, D. Quantum Implementation of Non-unitary Operations with Biorthogonal Representations. Quantum Inf. Comput. 2025, 25, 141–155. [Google Scholar] [CrossRef]
- Brustle, N.; Wiebe, N. Quantum and classical algorithms for nonlinear unitary dynamics. Quantum 2025, 9, 1741. [Google Scholar] [CrossRef]
- Pouly, A.; Graça, D.S. Computational complexity of solving polynomial differential equations over unbounded domains. Theor. Comput. Sci. 2016, 626, 67–82. [Google Scholar] [CrossRef]
- Low, G.H.; Wiebe, N. Hamiltonian Simulation in the Interaction Picture. arXiv 2019, arXiv:1805.00675. [Google Scholar] [CrossRef]
- Fang, D.; Lin, L.; Tong, Y. Time-marching based quantum solvers for time-dependent linear differential equations. Quantum 2023, 7, 955. [Google Scholar] [CrossRef]
- Brassard, G.; Høyer, P.; Mosca, M.; Tapp, A. Quantum amplitude amplification and estimation. In Quantum Computation and Information; American Mathematical Society: Providence, RI, USA, 2002; pp. 53–74. [Google Scholar] [CrossRef]
- Zecchi, A.A.; Sanavio, C.; Perotto, S.; Succi, S. Improved amplitude amplification strategies for the quantum simulation of classical transport problems. Quantum Sci. Technol. 2025, 10, 035039. [Google Scholar] [CrossRef]
- Das, S.; Green, J.R. Density matrix formulation of dynamical systems. Phys. Rev. E 2022, 106, 054135. [Google Scholar] [CrossRef]
- Frontin, C.V.; Darmofal, D.L. Output error behavior for discretizations of ergodic, chaotic systems of ordinary differential equations. Phys. Fluids 2022, 34, 105136. [Google Scholar] [CrossRef]
- Kiani, B.T.; De Palma, G.; Englund, D.; Kaminsky, W.; Marvian, M.; Lloyd, S. Quantum advantage for differential equation analysis. Phys. Rev. A 2022, 105, 022415. [Google Scholar] [CrossRef]
- Moysis, L.; Lawnik, M.; Baptista, M.S.; Volos, C.; Fragulis, G.F. A review of chaotification techniques for discrete-time systems. Nonlinear Dyn. 2025, 113, 14103–14119. [Google Scholar] [CrossRef]
- Bao, N.; Suer, G. Exploiting recursive structures for the design of novel quantum primitives. arXiv 2024, arXiv:2410.13927. [Google Scholar] [CrossRef]
- Vahala, G.; Koukoutsis, E.; Soe, M.; Hizanidis, K.; Vahala, L.; Ram, A.K. Qubit lattice algorithms. Rad. Eff. Def. Solids 2023, 178, 1350–1356. [Google Scholar] [CrossRef]
- Koukoutsis, E.; Hizanidis, K.; Vahala, G.; Tsironis, C.; Ram, A.K.; Soe, M.; Vahala, L. A Quantum Walk Inspired Qubit Lattice Algorithm for Simulating Electromagnetic Wave Propagation and Scattering in Conservative and Dissipative Magnetized Plasmas. arXiv 2025, arXiv:2503.24211. [Google Scholar] [CrossRef]
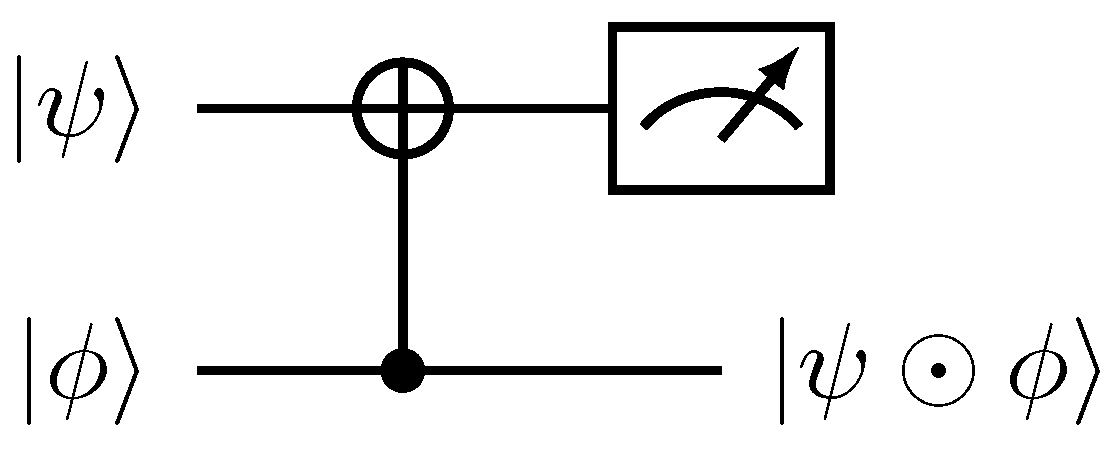
 denotes a uniform quantum multiplex gate [30,31]. (b) Quantum circuit implementation of the operation acting on the |k〉 basis expressed in its binary form, . The gate is the Pauli-x matrix.
denotes a uniform quantum multiplex gate [30,31]. (b) Quantum circuit implementation of the operation acting on the |k〉 basis expressed in its binary form, . The gate is the Pauli-x matrix.
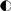 denotes a uniform quantum multiplex gate [30,31]. (b) Quantum circuit implementation of the operation acting on the |k〉 basis expressed in its binary form, . The gate is the Pauli-x matrix.
denotes a uniform quantum multiplex gate [30,31]. (b) Quantum circuit implementation of the operation acting on the |k〉 basis expressed in its binary form, . The gate is the Pauli-x matrix.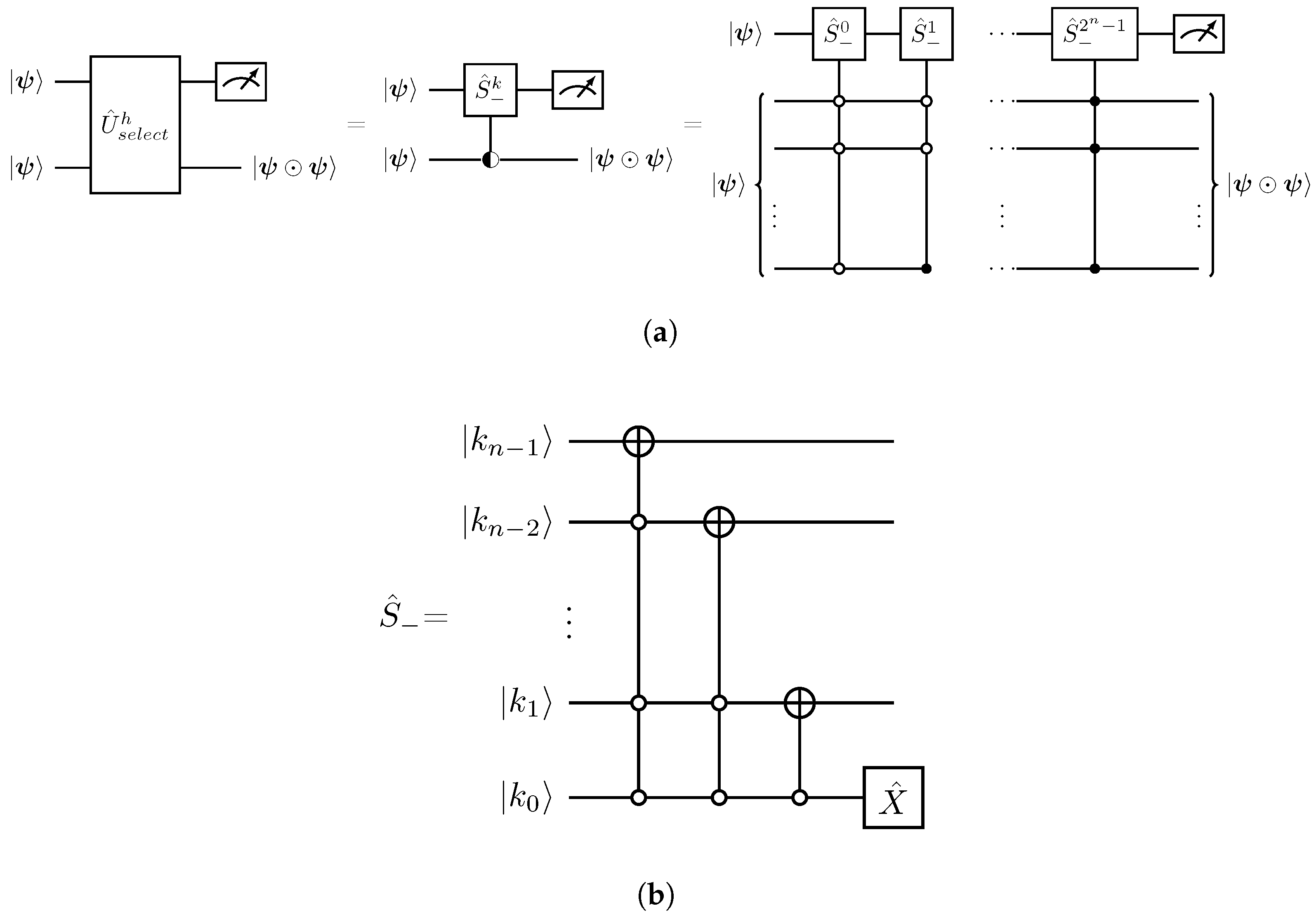
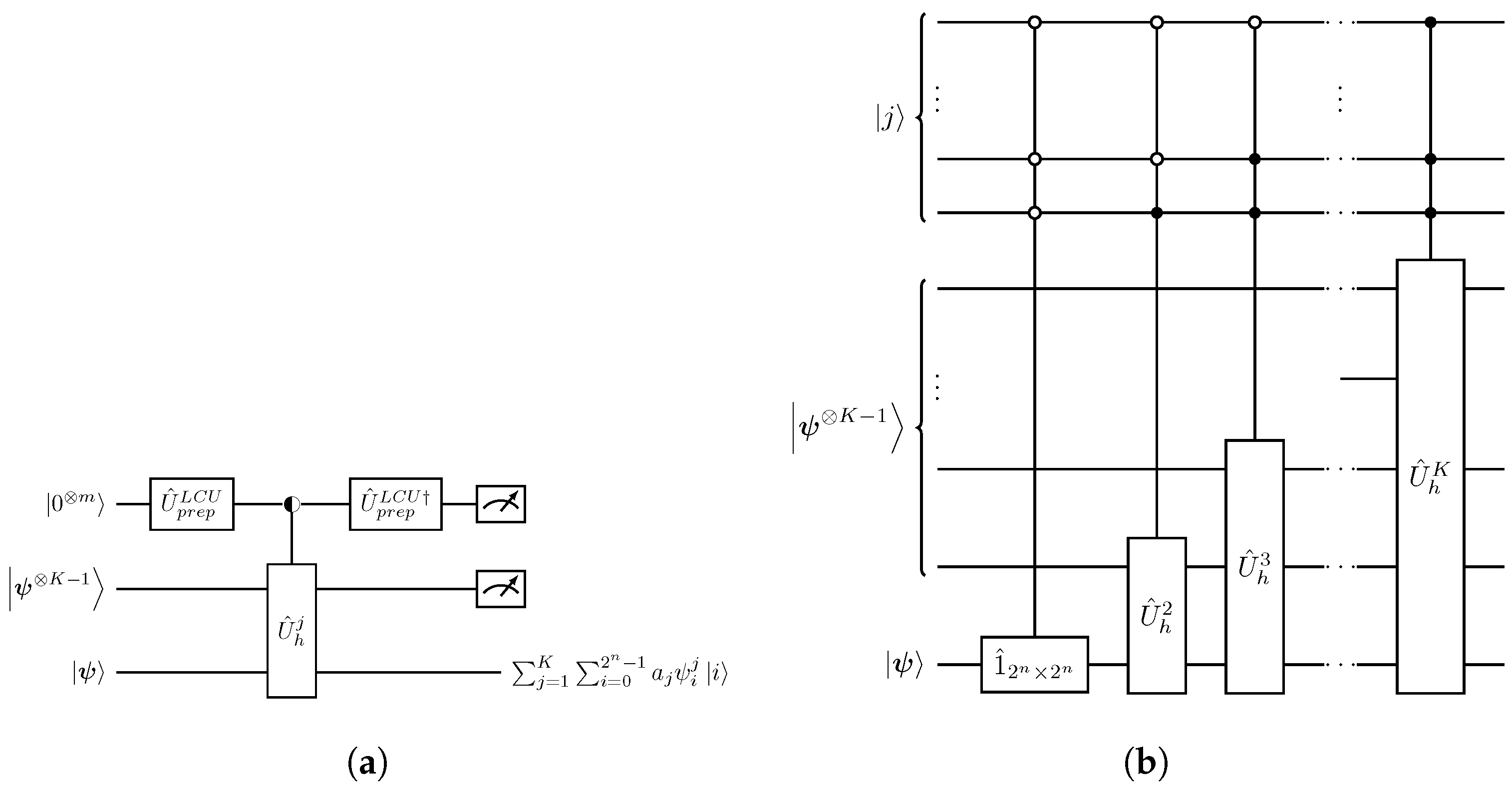
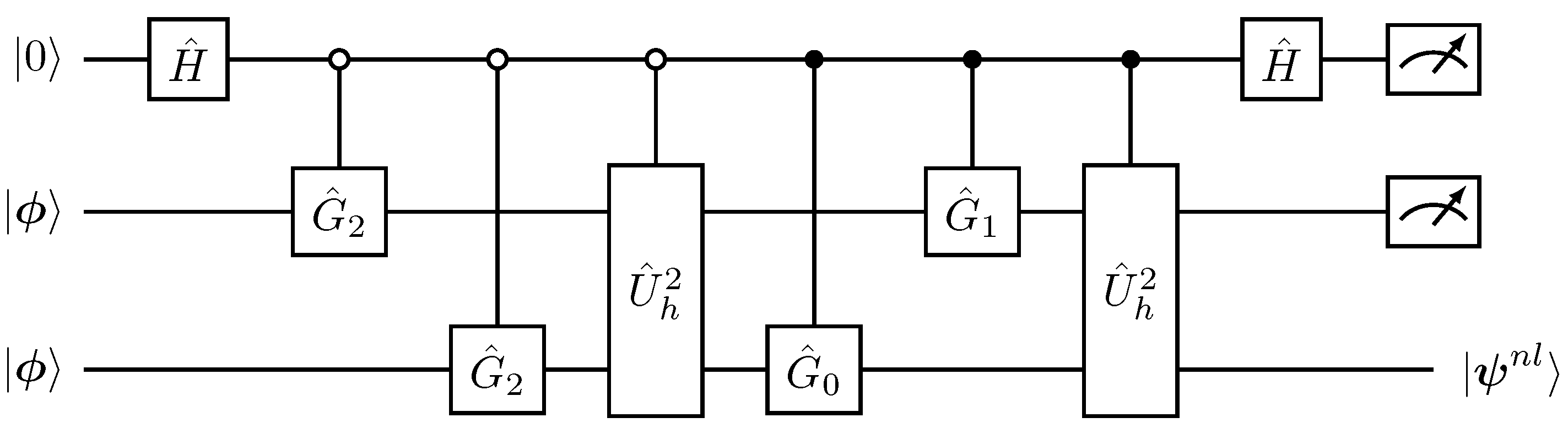

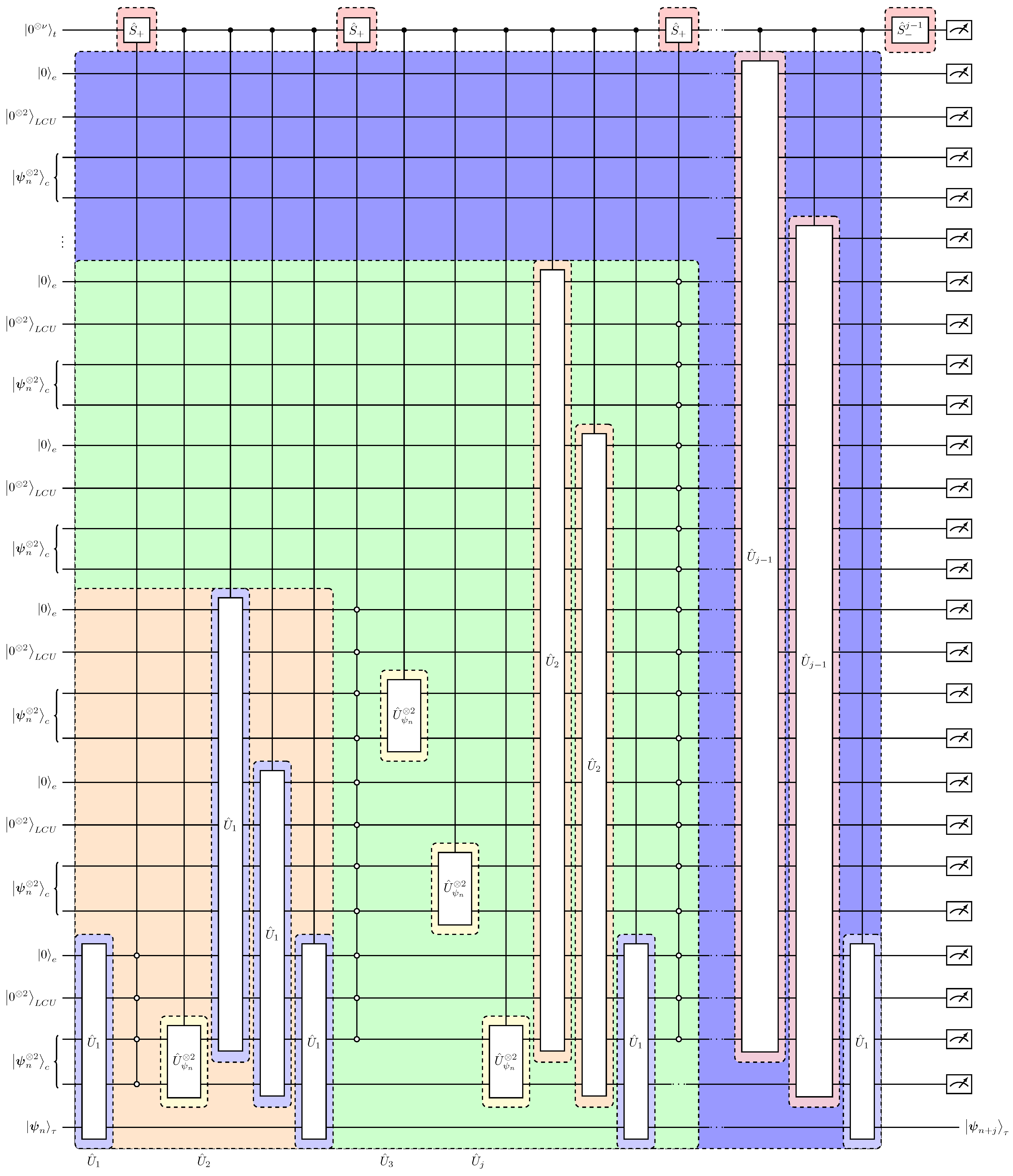

| Single-Step Evolution . |
|---|
| 1. Initial state ← |
| 2. Preparation of the nonlinear state , |
| 3. Evolution with the time-advancement matrix , |
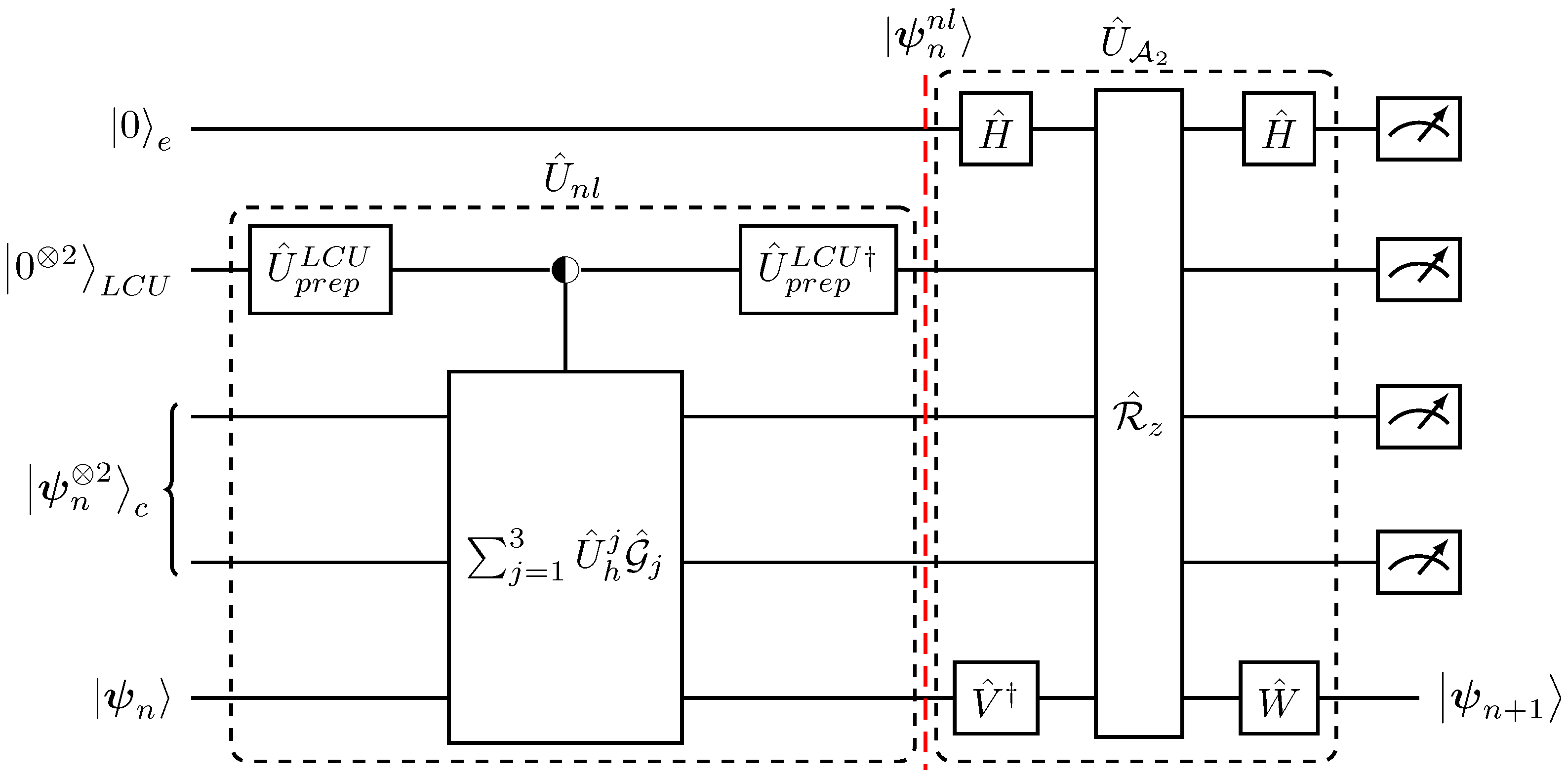
| Time-Marching Evolution . |
|---|
| 1. Initial target state ← . |
| 2. Prepare a clock-time register ← with and copies of the , and registers ← . The target state is chosen to be the least significant. |
| 3. Evolve the target state by acting with the single-step evolution operator using the least significant of the ,,-registers as dictated in Equation (45), . |
| 4. Update the clock register, to keep track of the time advancement of the target state controlled by the 0-bits in the previously used least significant, of the ,,-registers. |
| 5. Replenish the states in the register with a control operator with respect to the 1-bit state in the register with . |
| 6. Recursively repeat times the steps 3, 4 and 5, using in Equation (50) and ancillary registers for each iteration. |
| 7. Initialize the clock register to the state and measure all registers in respect to the 0-bit states to obtain . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koukoutsis, E.; Vahala, G.; Soe, M.; Hizanidis, K.; Vahala, L.; Ram, A.K. Time-Marching Quantum Algorithm for Simulation of Nonlinear Lorenz Dynamics. Entropy 2025, 27, 871. https://doi.org/10.3390/e27080871
Koukoutsis E, Vahala G, Soe M, Hizanidis K, Vahala L, Ram AK. Time-Marching Quantum Algorithm for Simulation of Nonlinear Lorenz Dynamics. Entropy. 2025; 27(8):871. https://doi.org/10.3390/e27080871
Chicago/Turabian StyleKoukoutsis, Efstratios, George Vahala, Min Soe, Kyriakos Hizanidis, Linda Vahala, and Abhay K. Ram. 2025. "Time-Marching Quantum Algorithm for Simulation of Nonlinear Lorenz Dynamics" Entropy 27, no. 8: 871. https://doi.org/10.3390/e27080871
APA StyleKoukoutsis, E., Vahala, G., Soe, M., Hizanidis, K., Vahala, L., & Ram, A. K. (2025). Time-Marching Quantum Algorithm for Simulation of Nonlinear Lorenz Dynamics. Entropy, 27(8), 871. https://doi.org/10.3390/e27080871







