CViT Weakly Supervised Network Fusing Dual-Branch Local-Global Features for Hyperspectral Image Classification
Abstract
1. Introduction
- (1)
- In this paper, we propose a CWSN that integrates a lightweight dual-branch feature enhancement module and a CNN-Vision Transformer, while organically integrating deep semantic feature extraction and noisy sample processing into a deep learning framework.
- (2)
- A Dual-Branch Local Induction Module (DBLIM) is designed, which has a simple architecture, a small number of parameters, and a high generalization capacity. This module can enhance the discriminative and divisible nature of different classes of feature information, and mitigate the gradient vanishing of the depth model.
- (3)
- Local and global deep semantic features are generalized and characterized using CViT, together with Noise Suppression Loss (NSL), which enhances the robustness of the model and makes it stable in the face of both clean and noisy training sets.
2. Related Work
2.1. HSI Supervised Classification
2.2. HSI Weakly Supervised Classification
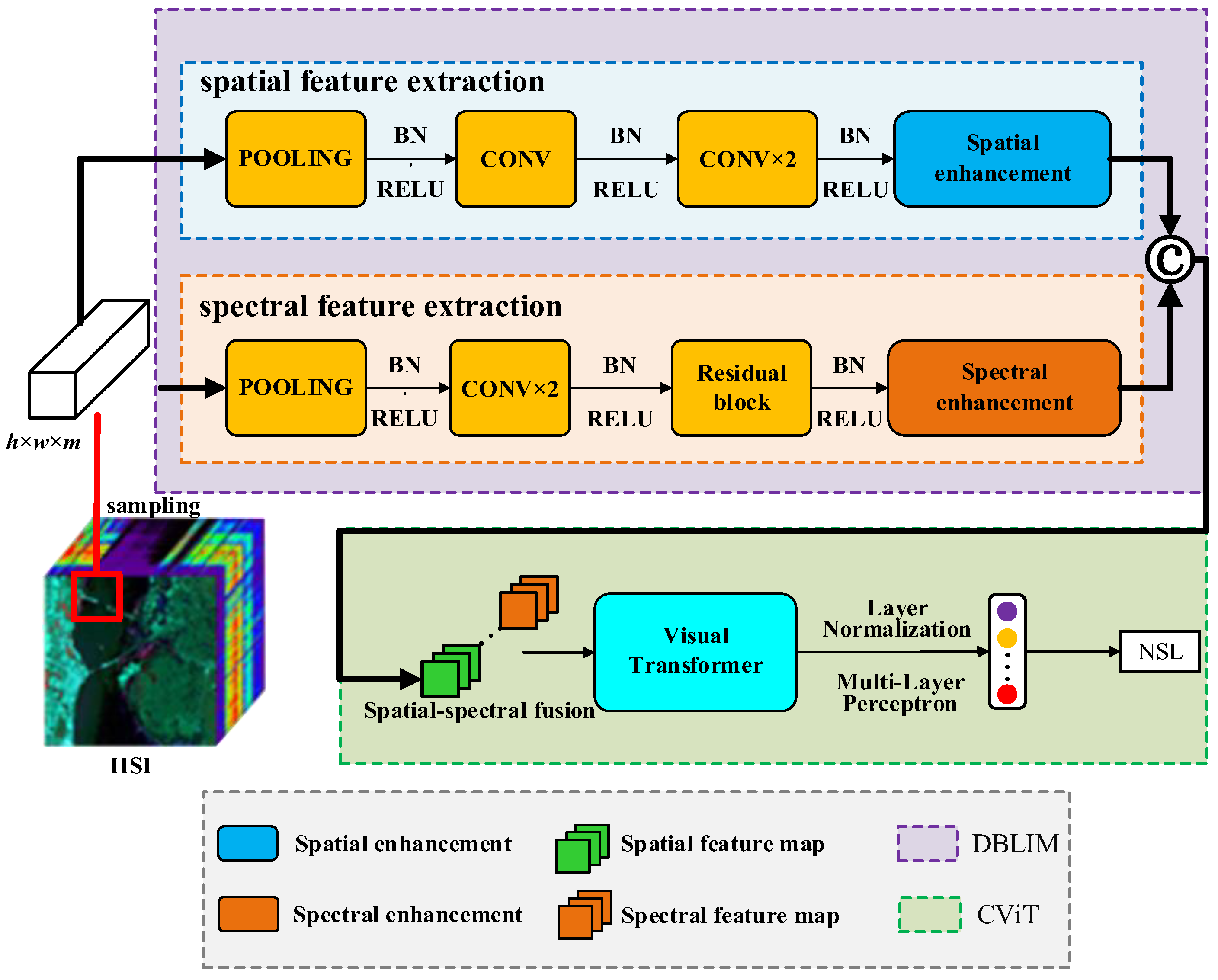
3. Proposed Model
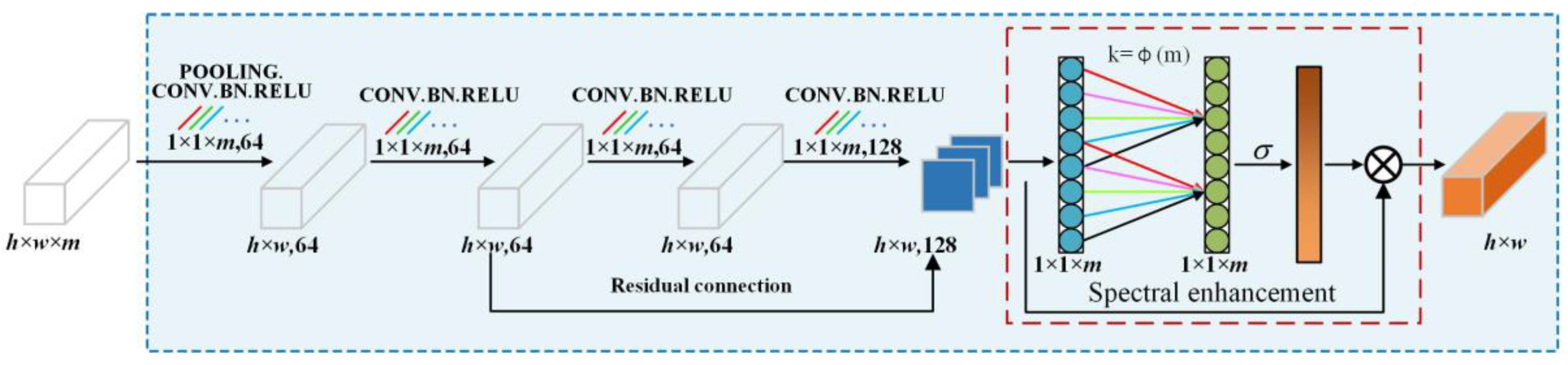
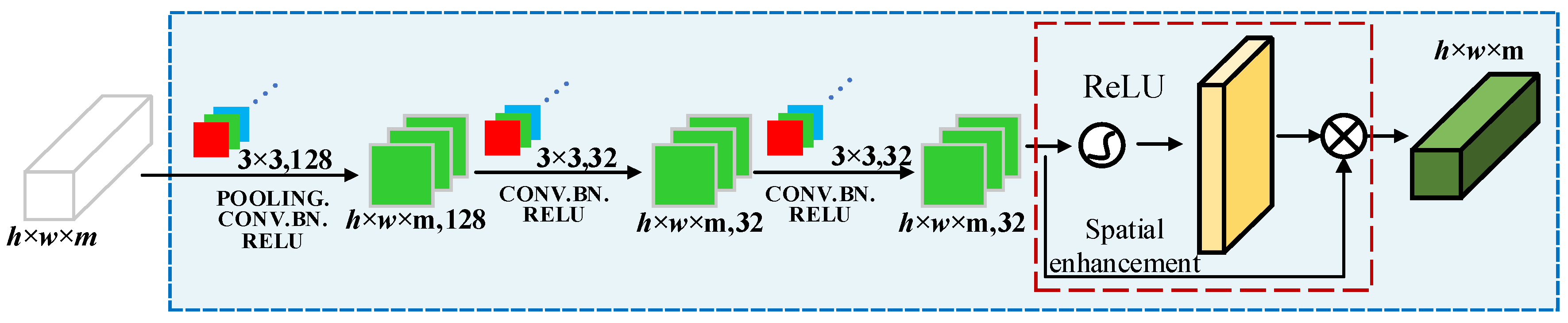
3.1. Dual-Branch Local Induction Module
3.1.1. Spectral Feature Extraction Channel
3.1.2. Spatial Feature Extraction Channel
3.2. CViT Hybrid Structure
3.2.1. CViT
3.2.2. NSL Function
4. Experiments and Analysis of Results
4.1. Datasets and Experimental Setup
4.1.1. Experimental Datasets
- (1)
- University of Pavia (UP): The ROSIS 03 sensor collected data from the University of Pavia campus in Italy. The spatial resolution is 1.3 m, with a spectral coverage of 0.43–0.86 μm. Nine classes of ground cover are included in the datasets.
- (2)
- Washington DC (WDC): The Washington DC dataset was collected using the Hyperspectral Digital Imaging Experiment sensor over Washington DC. Seventy-eight spectral bands were selected from the 400–1000 nm spectral range to form the HSI, and the corresponding RGB images were acquired using a Sentinel-2 SRF. The dataset contains 480 scan lines with 307 pixels on each scan line.
- (3)
- Salinas Valley (SV): The Salinas Valley dataset was collected by the Airborne Visible Infrared Imaging Spectrometer (AVIRIS), a sensor imaging the Salinas Valley region of California, USA. The spatial resolution is 3.7 m, and the number of bands is 224, covering an area with an image size of 512 rows and 217 columns, containing 16 object classes. Twenty water vapor absorption and noise bands (numbers 108–112, 145–167, and 224) have been removed from the data, leaving 204 active bands.
- (4)
- Kennedy Space Centre (KSC): The Kennedy Space Centre dataset was collected by the AVIRIS instrument during an overflight of the Kennedy Space Centre in the USA, although with a low spatial resolution of 18 m. These data include raw spatial dimensions of 512 × 614 pixels, with 48 bands removed due to absorption and low signal-to-noise ratios, and 176 spectral bands used for analysis. It contains 13 classes representing different object classes.
4.1.2. Experimental Settings
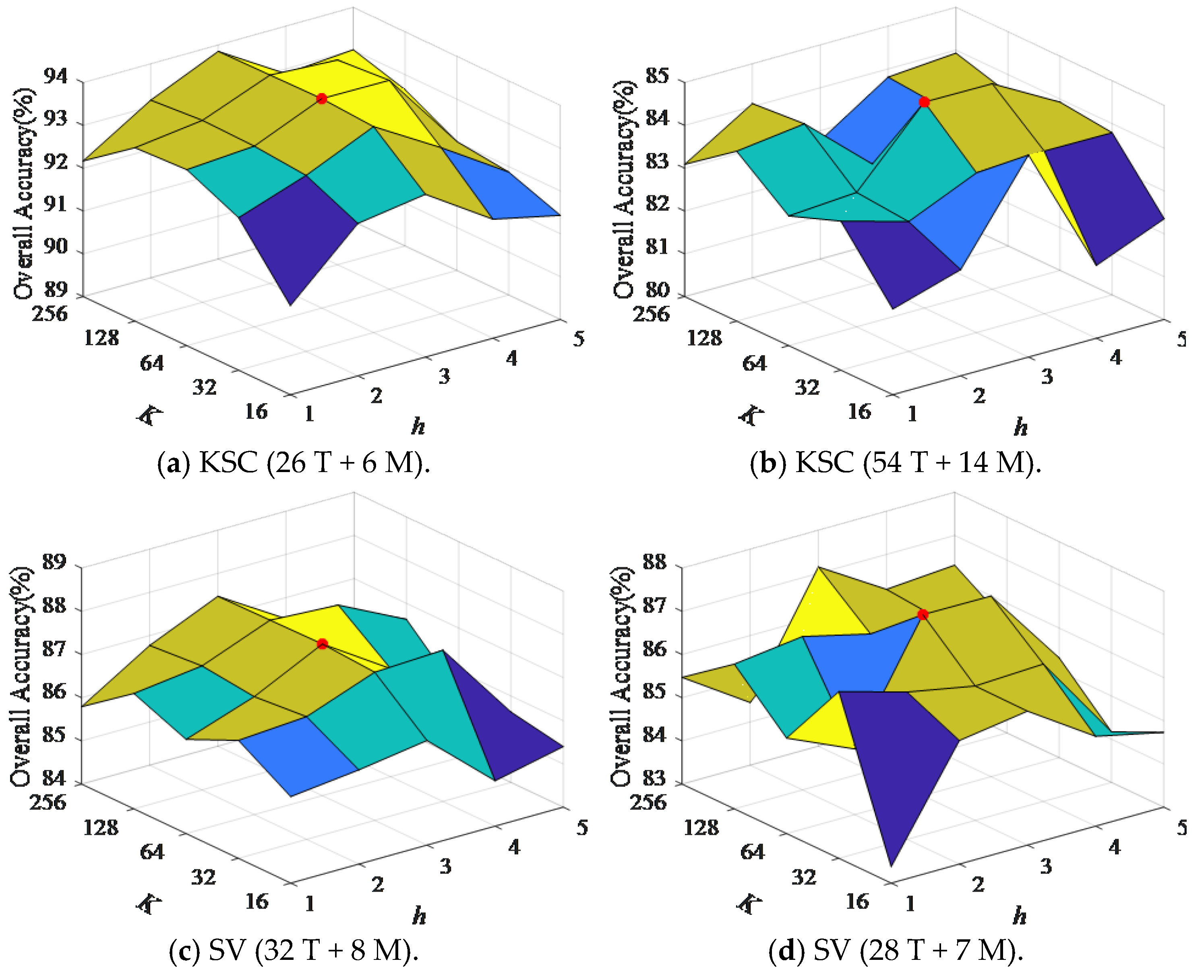
4.2. Parameter Sensitivity Analysis
4.3. Ablation Analysis
4.4. Analysis of Anti-Noise Strategies
4.5. Computational Efficiency Analysis
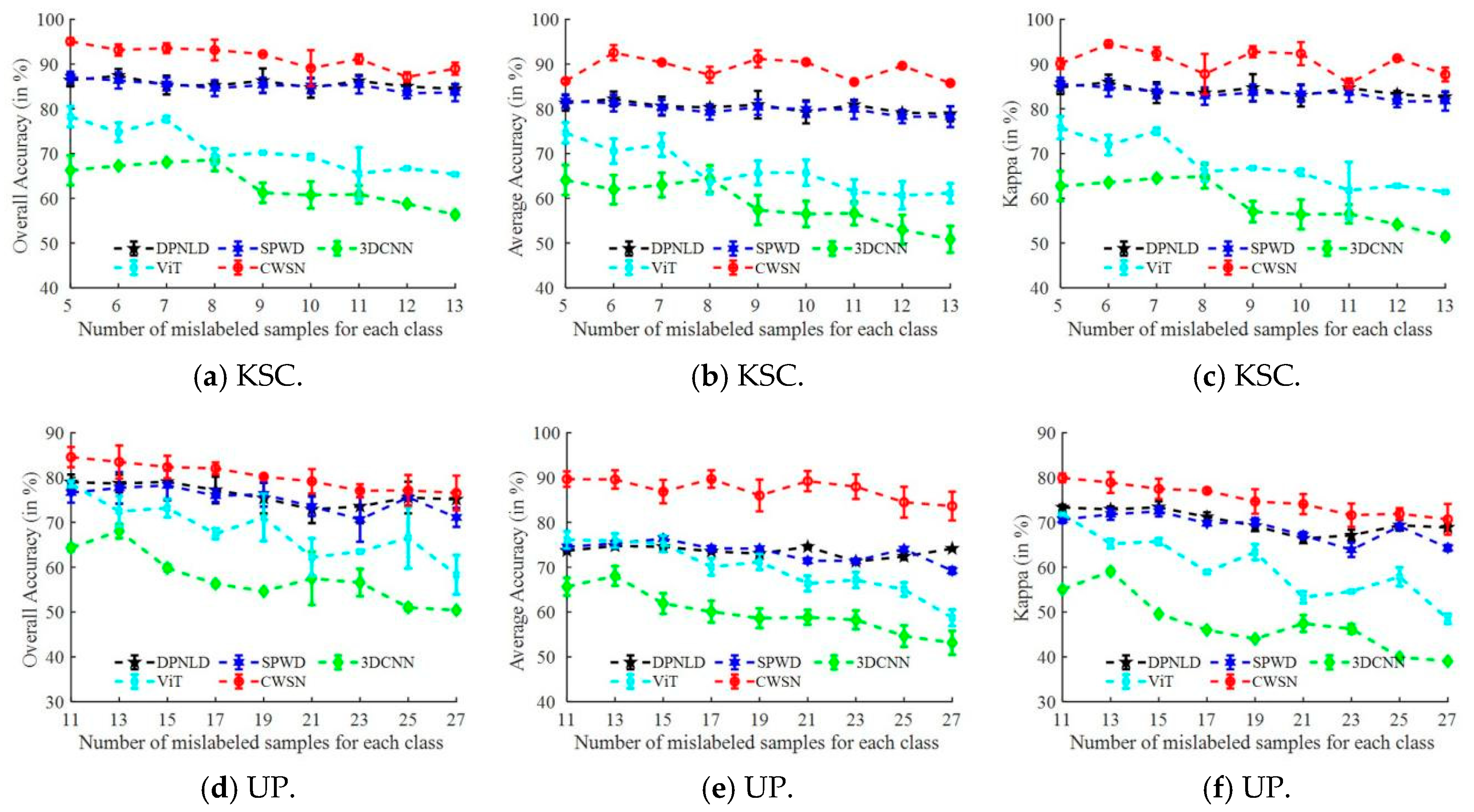
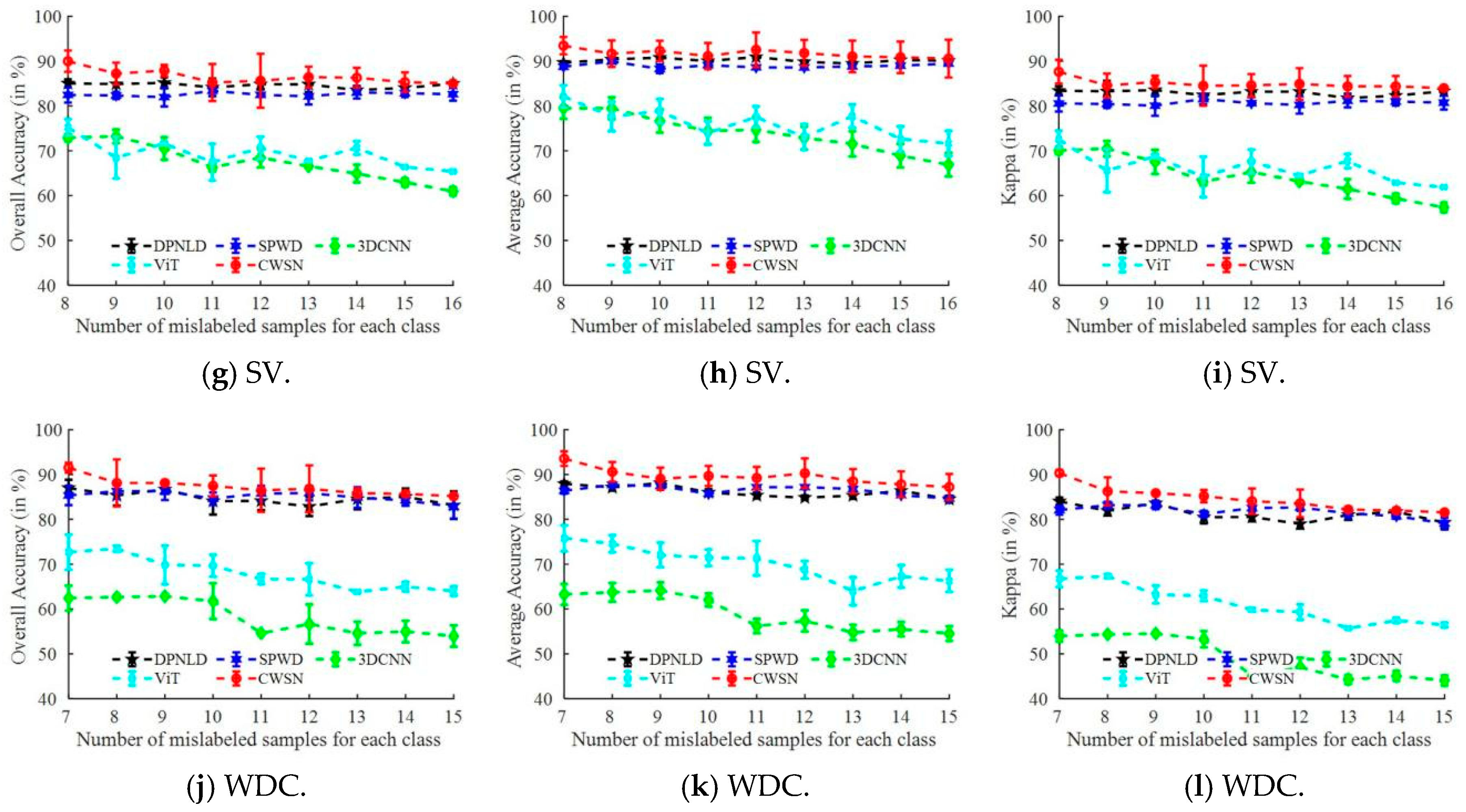
4.6. Comparison of Classification Performance with Low-Confidence Samples
4.7. Comparison of Classification Performance with High-Confidence Samples
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, W.D.; Li, Z.X.; Li, G.H.; Zhuang, P.X.; Hou, G.J.; Zhang, Q.; Li, C.Y. GACNet: Generate Adversarial-Driven Cross-Aware Network for Hyperspectral Wheat Variety Identification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3347745. [Google Scholar] [CrossRef]
- Fang, L.Y.; Li, S.T.; Duan, W.H.; Ren, J.C.; Benediktsson, J.A. Classification of Hyperspectral Images by Exploiting Spectral-Spatial Information of Superpixel via Multiple Kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6674. [Google Scholar] [CrossRef]
- Meyer, J.M.; Kokaly, R.F.; Holley, E. Hyperspectral remote sensing of white mica: A review of imaging and point-based spectrometer studies for mineral resources, with spectrometer design considerations. Remote Sens. Environ. 2022, 275, 113000. [Google Scholar] [CrossRef]
- Siebels, K.; Goïta, K.; Germain, M. Estimation of Mineral Abundance from Hyperspectral Data Using a New Supervised Neighbor-Band Ratio Unmixing Approach. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6754–6766. [Google Scholar] [CrossRef]
- Cao, Q.; Yu, G.L.; Sun, S.J.; Dou, Y.; Li, H.; Qiao, Z.Y. Monitoring Water Quality of the Haihe River Based on Ground-Based Hyperspectral Remote Sensing. Water 2022, 14, 22. [Google Scholar] [CrossRef]
- Liu, C.; Xing, C.Z.; Hu, Q.H.; Wang, S.S.; Zhao, S.H.; Gao, M. Stereoscopic hyperspectral remote sensing of the atmospheric environment: Innovation and prospects. Earth-Sci. Rev. 2022, 226, 103958. [Google Scholar] [CrossRef]
- Pal, M. Deep learning algorithms for hyperspectral remote sensing classifications: An applied review. Int. J. Remote Sens. 2024, 45, 451–491. [Google Scholar] [CrossRef]
- Fang, C.H.; Zhang, G.F.; Li, J.; Li, X.P.; Chen, T.F.; Zhao, L. Intelligent agent for hyperspectral image classification with noisy labels: A deep reinforcement learning framework. Int. J. Remote Sens. 2024, 45, 2939–2964. [Google Scholar] [CrossRef]
- Pour, A.B.; Guha, A.; Crispini, L.; Chatterjee, S. Editorial for the Special Issue Entitled Hyperspectral Remote Sensing from Spaceborne and Low-Altitude Aerial/Drone-Based Platforms—Differences in Approaches, Data Processing Methods, and Applications. Remote Sens. 2023, 15, 5119. [Google Scholar] [CrossRef]
- Datta, D.; Mallick, P.K.; Bhoi, A.K.; Ijaz, M.F.; Shafi, J.; Choi, J. Hyperspectral Image Classification: Potentials, Challenges, and Future Directions. Comput. Intell. Neurosci. 2022, 2022, 3854635. [Google Scholar] [CrossRef]
- Kumar, B.; Dikshit, O.; Gupta, A.; Singh, M.K. Feature extraction for hyperspectral image classification: A review. Int. J. Remote Sens. 2020, 41, 6248–6287. [Google Scholar] [CrossRef]
- Sawant, S.S.; Manoharan, P.; Loganathan, A. Band selection strategies for hyperspectral image classification based on machine learning and artificial intelligent techniques–Survey. Arab. J. Geosci. 2021, 14, 646. [Google Scholar] [CrossRef]
- Gaetano, R.; Scarpa, G.; Poggi, G. Hierarchical Texture-Based Segmentation of Multiresolution Remote-Sensing Images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2129–2141. [Google Scholar] [CrossRef]
- Yuan, J.Y.; Wang, D.L.; Li, R.X. Remote Sensing Image Segmentation by Combining Spectral and Texture Features. IEEE Trans. Geosci. Remote Sens. 2014, 52, 16–24. [Google Scholar] [CrossRef]
- Aptoula, E. Remote Sensing Image Retrieval with Global Morphological Texture Descriptors. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3023–3034. [Google Scholar] [CrossRef]
- Wu, W.; Yang, Q.P.; Lv, J.K.; Li, A.D.; Liu, H.B. Investigation of Remote Sensing Imageries for Identifying Soil Texture Classes Using Classification Methods. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1653–1663. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.Y.; Li, S.T. Recent Advances on Spectral-Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Peng, Y.S.; Zhang, Y.W.; Tu, B.; Li, Q.M.; Li, W.J. Spatial-Spectral Transformer with Cross-Attention for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5537415. [Google Scholar] [CrossRef]
- Li, C.H.; Kuo, B.C.; Lin, C.T.; Huang, C.S. A Spatial-Contextual Support Vector Machine for Remotely Sensed Image Classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 784–799. [Google Scholar] [CrossRef]
- Maurya, K.; Mahajan, S.; Chaube, N. Decision tree (DT) and stacked vegetation indices based mangrove and non-mangrove discrimination using AVIRIS-NG hyperspectral data: A study at Marine National Park (MNP) Jamnagar, Gulf of Kutch. Wetl. Ecol. Manag. 2023, 31, 805–823. [Google Scholar] [CrossRef]
- Feng, J.F.; Wang, D.N.; Gu, Z.J. Bidirectional Flow Decision Tree for Reliable Remote Sensing Image Scene Classification. Remote Sens. 2022, 14, 3943. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Gu, Y.F.; Wang, C.; You, D.; Zhang, Y.H.; Wang, S.Z.; Zhang, Y. Representative Multiple Kernel Learning for Classification in Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2852–2865. [Google Scholar] [CrossRef]
- Xue, Z.H.; Nie, X.Y.; Zhang, M.X. Incremental Dictionary Learning-Driven Tensor Low-Rank and Sparse Representation for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5544019. [Google Scholar] [CrossRef]
- Tang, Y.Y.; Yuan, H.L.; Li, L.Q. Manifold-Based Sparse Representation for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7606–7618. [Google Scholar] [CrossRef]
- Tan, Q.; Guo, B.; Hu, J.; Dong, X.; Hu, J. Object-oriented remote sensing image information extraction method based on multi-classifier combination and deep learning algorithm. Pattern Recognit. Lett. 2021, 141, 32–36. [Google Scholar] [CrossRef]
- Yang, J.M.; Kuo, B.C.; Yu, P.T.; Chuang, C.H. A Dynamic Subspace Method for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2840–2853. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, R.; Rambabu, M.; Dua, Y. Deep learning for hyperspectral image classification: A survey. Comput. Sci. Rev. 2024, 53, 100658. [Google Scholar] [CrossRef]
- Li, S.T.; Song, W.W.; Fang, L.Y.; Chen, Y.S.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Li, X.T.; Ding, H.H.; Yuan, H.B.; Zhang, W.W.; Pang, J.M.; Cheng, G.L.; Chen, K.; Liu, Z.W.; Loy, C.C. Transformer-Based Visual Segmentation: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 10138–10163. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Ermon, S.; Kim, D.; Zhang, L.P.; Zhong, Y.F. Changen2: Multi-Temporal Remote Sensing Generative Change Foundation Model. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 725–741. [Google Scholar] [CrossRef] [PubMed]
- Thoreau, R.; Achard, V.; Risser, L.; Berthelot, B.; Briottet, X. Active Learning for Hyperspectral Image Classification: A Comparative Review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 256–278. [Google Scholar] [CrossRef]
- Chen, L.; He, J.F.; Shi, H.; Yang, J.Y.; Li, W. SWDiff: Stage-Wise Hyperspectral Diffusion Model for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3485483. [Google Scholar] [CrossRef]
- Li, H.F.; Dou, X.; Tao, C.; Wu, Z.X.; Chen, J.; Peng, J.; Deng, M.; Zhao, L. RSI-CB: A Large-Scale Remote Sensing Image Classification Benchmark Using Crowdsourced Data. Sensors 2020, 20, 1594. [Google Scholar] [CrossRef]
- Trias-Sanz, R.; Stamon, G.; Louchet, J. Using colour, texture, and hierarchial segmentation for high-resolution remote sensing. ISPRS J. Photogramm. Remote Sens. 2008, 63, 156–168. [Google Scholar] [CrossRef]
- Xia, J.S.; Falco, N.; Benediktsson, J.A.; Du, P.J.; Chanussot, J. Hyperspectral Image Classification with Rotation Random Forest Via KPCA. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1601–1609. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.R.; Zheng, Y.H.; Wu, Z.B. SpectralSpatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522214. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.S.; Lin, Z.H. Spatial-Spectral Transformer for Hyperspectral Image Classification. Remote Sens. 2021, 13, 498. [Google Scholar] [CrossRef]
- Kang, X.D.; Duan, P.H.; Xiang, X.L.; Li, S.T.; Benediktsson, J.A. Detection and Correction of Mislabeled Training Samples for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5673–5686. [Google Scholar] [CrossRef]
- Li, Z.N.; Yang, X.R.; Meng, D.Y.; Cao, X.Y. An Adaptive Noisy Label-Correction Method Based on Selective Loss for Hyperspectral Image-Classification Problem. Remote Sens. 2024, 16, 2499. [Google Scholar] [CrossRef]
- Leng, Q.M.; Yang, H.O.; Jiang, J.J. Label Noise Cleansing with Sparse Graph for Hyperspectral Image Classification. Remote Sens. 2019, 11, 1116. [Google Scholar] [CrossRef]
- Tu, B.; Zhang, X.F.; Kang, X.D.; Zhang, G.Y.; Li, S.T. Density Peak-Based Noisy Label Detection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1573–1584. [Google Scholar] [CrossRef]
- Tu, B.; Zhou, C.L.; He, D.B.; Huang, S.Y.; Plaza, A. Hyperspectral Classification with Noisy Label Detection via Superpixel-to-Pixel Weighting Distance. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4116–4131. [Google Scholar] [CrossRef]
- Ghaderizadeh, S.; Abbasi-Moghadam, D.; Sharifi, A.; Zhao, N.; Tariq, A. Hyperspectral Image Classification Using a Hybrid 3D-2D Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7570–7588. [Google Scholar] [CrossRef]
- Wang, L.Q.; Zhu, T.C.; Kumar, N.; Li, Z.W.; Wu, C.L.; Zhang, P.Y. Attentive-Adaptive Network for Hyperspectral Images Classification with Noisy Labels. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5505514. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yang, S.Y.; Feng, Z.X.; Song, L.L.; Wei, Y.T.; Jiao, L.C. Triple Contrastive Representation Learning for Hyperspectral Image Classification with Noisy Labels. IEEE Trans. Geosci. Remote Sens. 2023, 61, 500116. [Google Scholar] [CrossRef]
- Yue, X.; Liu, A.; Chen, N.; Xia, S.; Yue, J.; Fang, L. Hypermll: Toward robust hyperspectral image classification with multi-source label learning. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3441095. [Google Scholar] [CrossRef]
- Bazi, Y.; Bashmal, L.; Al Rahhal, M.M.; Al Dayil, R.; Al Ajlan, N. Vision Transformers for Remote Sensing Image Classification. Remote Sens. 2021, 13, 516. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.K.; Shen, Q. Spectral-Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]

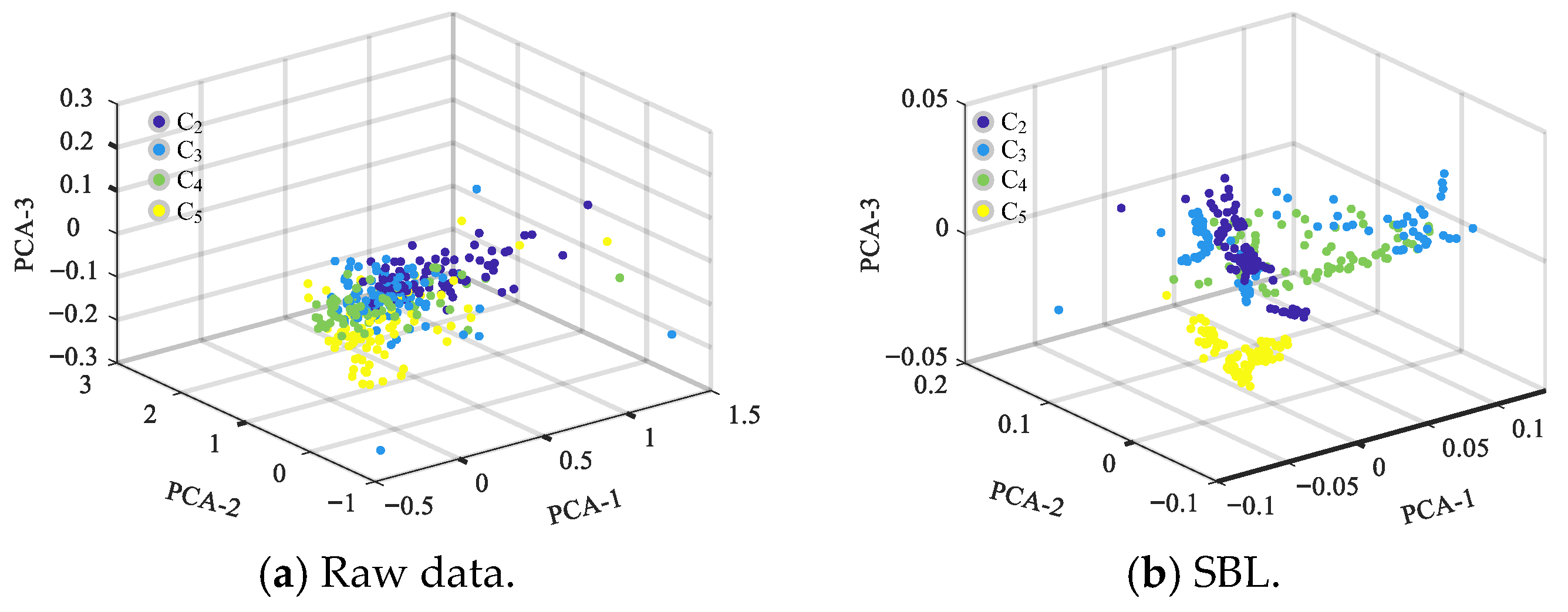
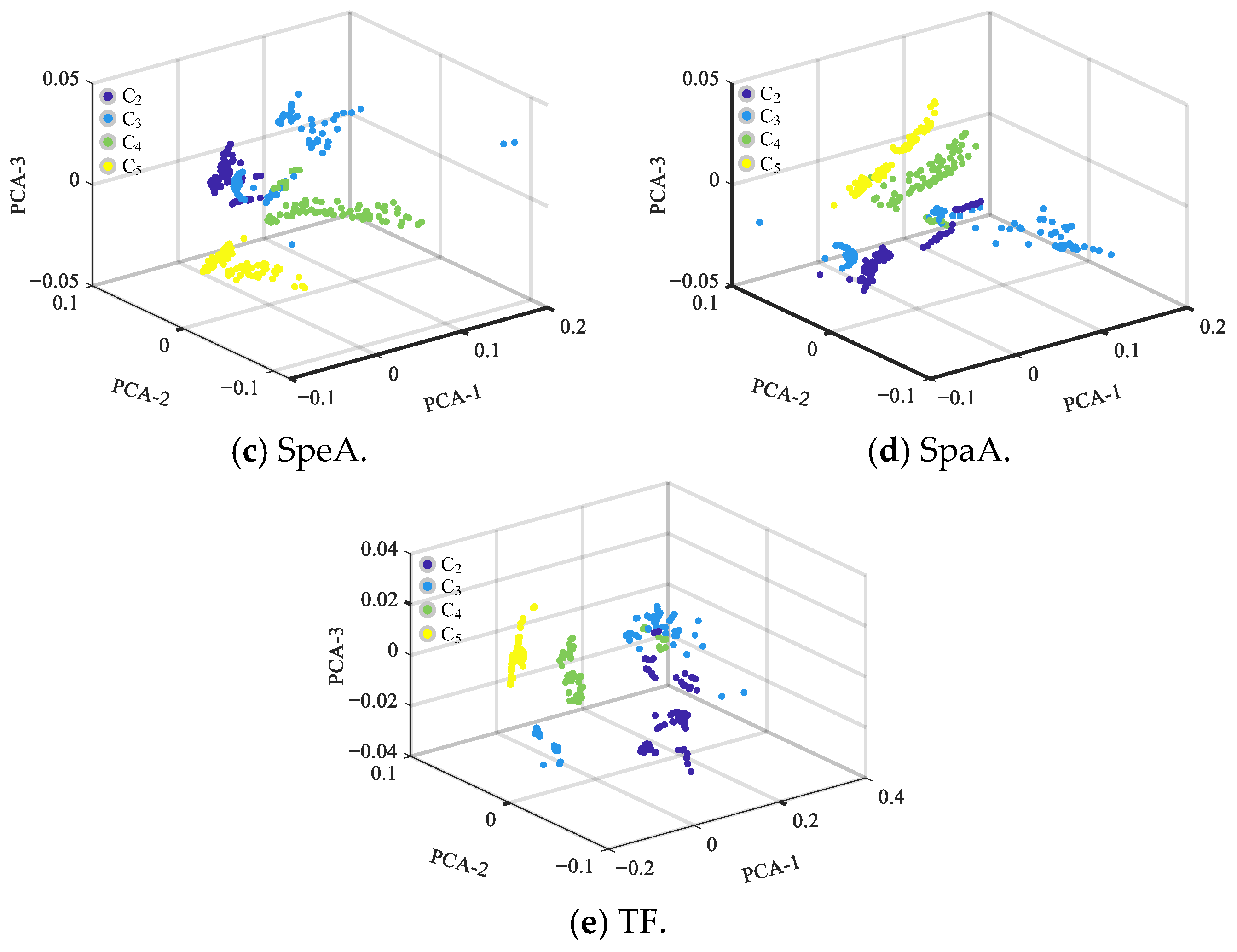
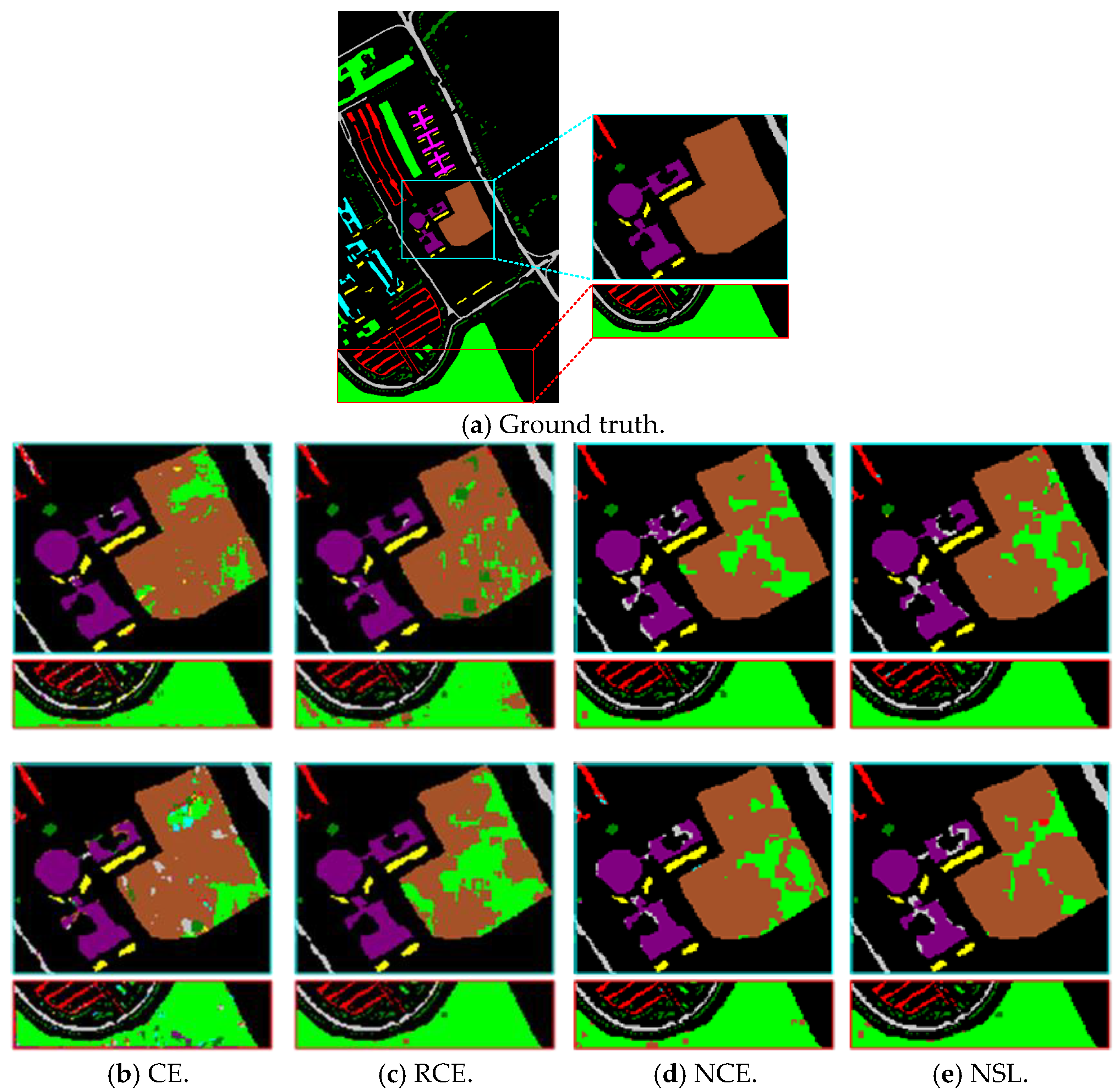

| Dataset | KSC | UP | SV | WDC | ||||
|---|---|---|---|---|---|---|---|---|
| Number of classes | 13 | 9 | 16 | 6 | ||||
| Sample setting | Setting 1 | Setting 2 | Setting 1 | Setting 2 | Setting 1 | Setting 2 | Setting 1 | Setting 2 |
| 26 + 6 | 26 + 13 | 54 + 14 | 54 + 27 | 32 + 8 | 32 + 16 | 28 + 7 | 28 + 14 | |
| Total number of samples | 338 + 78 | 338 + 169 | 486 + 126 | 486 + 243 | 512 + 128 | 512 + 256 | 168 + 42 | 168 + 84 |
| Class | 26 T + 6 M | 26 T + 13 M | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SBL | SpeA | SpaA | TF | CWSN | SBL | SpeA | SpaA | TF | CWSN | |
| C1 | 98.26 | 95.34 | 90.82 | 91.73 | 94.54 | 87.89 | 89.89 | 91.69 | 90.58 | 94.60 |
| C2 | 97.62 | 87.18 | 95.96 | 88.99 | 96.38 | 92.54 | 89.44 | 82.57 | 86.48 | 93.03 |
| C3 | 93.57 | 83.61 | 95.76 | 99.12 | 92.23 | 96.46 | 88.62 | 95.23 | 95.54 | 95.54 |
| C4 | 82.22 | 74.27 | 54.93 | 69.77 | 69.22 | 76.73 | 62.79 | 64.71 | 64.01 | 86.22 |
| C5 | 91.14 | 83.30 | 88.59 | 98.98 | 93.00 | 75.28 | 77.03 | 82.73 | 80.23 | 76.61 |
| C6 | 78.43 | 78.63 | 84.20 | 80.08 | 95.46 | 63.81 | 88.55 | 71.43 | 82.57 | 84.50 |
| C7 | 97.10 | 95.71 | 89.32 | 100.00 | 95.53 | 96.28 | 91.35 | 100.00 | 100.00 | 84.12 |
| C8 | 96.40 | 93.34 | 94.75 | 93.53 | 97.66 | 91.50 | 82.48 | 73.71 | 93.79 | 84.48 |
| C9 | 99.18 | 95.40 | 97.04 | 100.00 | 97.28 | 100.00 | 100.00 | 92.67 | 95.96 | 100.00 |
| C10 | 97.74 | 97.56 | 97.46 | 99.91 | 93.98 | 99.37 | 94.85 | 95.34 | 95.08 | 95.63 |
| C11 | 100.00 | 96.44 | 97.14 | 99.83 | 97.23 | 99.65 | 95.69 | 100.00 | 93.52 | 96.10 |
| C12 | 96.81 | 85.50 | 81.84 | 91.58 | 95.41 | 74.93 | 89.66 | 92.09 | 92.43 | 91.59 |
| C13 | 64.14 | 96.14 | 83.40 | 100.00 | 100.00 | 98.53 | 93.97 | 93.28 | 100.00 | 100.00 |
| OA | 87.76 | 91.73 | 89.99 | 92.60 | 94.93 | 87.91 | 90.15 | 89.47 | 92.19 | 92.73 |
| AA | 89.57 | 89.42 | 90.55 | 91.35 | 93.69 | 85.69 | 88.02 | 87.34 | 90.01 | 90.96 |
| Kappa | 84.68 | 90.98 | 87.98 | 91.97 | 94.56 | 86.84 | 89.34 | 89.56 | 91.61 | 92.22 |
| Class | 54 T + 14 M | 54 T + 27 M | ||||||
|---|---|---|---|---|---|---|---|---|
| CE | RCE | NCE | NSL | CE | RCE | NCE | NSL | |
| C1 | 88.03 | 84.18 | 91.64 | 86.49 | 79.09 | 90.09 | 90.60 | 89.75 |
| C2 | 69.69 | 76.69 | 79.79 | 86.25 | 87.68 | 85.58 | 83.15 | 75.66 |
| C3 | 59.27 | 85.85 | 98.42 | 88.98 | 70.81 | 90.28 | 87.07 | 91.61 |
| C4 | 96.77 | 97.05 | 93.33 | 94.38 | 89.76 | 95.76 | 90.31 | 94.62 |
| C5 | 99.97 | 99.97 | 99.79 | 99.79 | 95.65 | 99.97 | 100.00 | 100.00 |
| C6 | 84.48 | 74.25 | 73.58 | 70.56 | 63.03 | 62.40 | 74.38 | 83.54 |
| C7 | 93.60 | 97.20 | 96.91 | 96.96 | 86.16 | 94.26 | 97.74 | 95.42 |
| C8 | 93.39 | 93.23 | 47.60 | 73.48 | 80.14 | 90.89 | 88.01 | 84.31 |
| C9 | 97.81 | 99.89 | 99.51 | 87.21 | 96.33 | 99.38 | 99.92 | 99.96 |
| OA | 79.96 | 82.68 | 81.54 | 84.81 | 82.51 | 82.94 | 82.67 | 83.46 |
| AA | 87.00 | 89.81 | 86.73 | 87.12 | 83.18 | 89.85 | 90.13 | 90.54 |
| Kappa | 74.91 | 77.83 | 76.34 | 80.07 | 77.13 | 78.96 | 81.36 | 81.53 |
| Method | KSC | UP | SV | WDC | ||||
|---|---|---|---|---|---|---|---|---|
| 26 T+ 6 M | 26 T+ 13 M | 54 T+ 14 M | 54 T+ 27 M | 32 T + 8 M | 32 T+ 16 M | 28 T+ 7 M | 28 T + 14 M | |
| DPNLD | 14.19 | 19.30 | 29.09 | 25.73 | 31.05 | 75.36 | 2.26 | 9.49 |
| SPWD | 19.11 | 26.16 | 33.48 | 21.60 | 43.72 | 84.80 | 3.33 | 4.51 |
| 3DCNN | 856.82 | 796.04 | 4014.01 | 3663.19 | 6429.89 | 6152.87 | 533.75 | 520.64 |
| ViT | 1825.77 | 1952.51 | 5439.61 | 4814.67 | 8369.64 | 8979.92 | 1105.73 | 1087.98 |
| CWSN | 3472.07 | 3040.37 | 8155.47 | 8943.99 | 11,816.94 | 11,597.85 | 1865.95 | 1982.46 |
| Dataset | KSC | UP | ||||
| 3DCNN | ViT | CWSN | 3DCNN | ViT | CWSN | |
| OA | 91.79 | 91.66 | 95.43 | 86.07 | 90.57 | 91.75 |
| AA | 89.30 | 89.14 | 93.37 | 88.62 | 90.91 | 92.48 |
| Kappa | 90.84 | 90.69 | 94.90 | 81.92 | 87.53 | 90.10 |
| Dataset | SV | WDC | ||||
| 3DCNN | ViT | CWSN | 3DCNN | ViT | CWSN | |
| OA | 88.15 | 84.46 | 86.72 | 85.47 | 88.96 | 89.60 |
| AA | 93.98 | 92.27 | 93.22 | 86.93 | 91.38 | 92.01 |
| Kappa | 86.81 | 82.73 | 85.24 | 82.08 | 86.41 | 87.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, W.; Sun, X.; Zhang, X.; Ji, Y.; Zhang, J. CViT Weakly Supervised Network Fusing Dual-Branch Local-Global Features for Hyperspectral Image Classification. Entropy 2025, 27, 869. https://doi.org/10.3390/e27080869
Fu W, Sun X, Zhang X, Ji Y, Zhang J. CViT Weakly Supervised Network Fusing Dual-Branch Local-Global Features for Hyperspectral Image Classification. Entropy. 2025; 27(8):869. https://doi.org/10.3390/e27080869
Chicago/Turabian StyleFu, Wentao, Xiyan Sun, Xiuhua Zhang, Yuanfa Ji, and Jiayuan Zhang. 2025. "CViT Weakly Supervised Network Fusing Dual-Branch Local-Global Features for Hyperspectral Image Classification" Entropy 27, no. 8: 869. https://doi.org/10.3390/e27080869
APA StyleFu, W., Sun, X., Zhang, X., Ji, Y., & Zhang, J. (2025). CViT Weakly Supervised Network Fusing Dual-Branch Local-Global Features for Hyperspectral Image Classification. Entropy, 27(8), 869. https://doi.org/10.3390/e27080869








