Fault Diagnosis Method of Planetary Gearboxes Based on Multi-Scale Wavelet Packet Energy Entropy and Extreme Learning Machine
Abstract
1. Introduction
- (1)
- A fault diagnosis approach utilizing multi-scale wavelet packet energy entropy is proposed. The wavelet packet algorithm is employed to decompose and reconstruct vibration signals at multiple scales and directions. The wavelet packet energy entropy of nodes with different scale factors under various operating conditions is calculated to form the signal’s feature vector, thereby accurately extracting the fault characteristics of vibration signals corresponding to different tooth fractures of the sun gear.
- (2)
- A gear fault diagnosis method with high computational efficiency and accurate diagnostic results is proposed by combining the multi-scale wavelet packet energy entropy feature extraction method with the ELM(MSWPEE-ELM) diagnosis model. The diagnostic results validate the practicality and high efficiency of the method.
- (3)
- The MSWPEE-ELM fault diagnosis is compared with other methods to verify the superiority and feasibility of the proposed scheme. The results show that this method has high accuracy and prove the efficiency of the proposed method in the fault diagnosis of different degrees of broken teeth of the solar gear.
2. Basic Theory
2.1. Wavelet Packet Theory
- (1)
- Initial condition
- (2)
- Decomposition at the first layer
- (3)
- Decomposition at the j-th layer
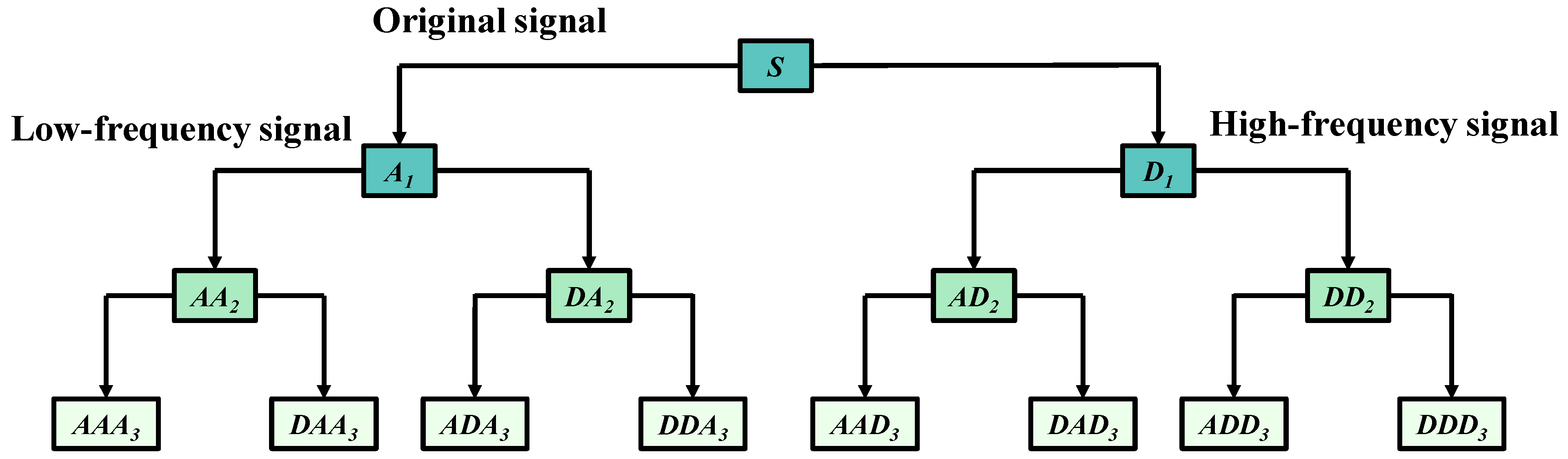
2.2. Multi-Scale Wavelet Packet Energy Entropy
- (1)
- Suppose the signal sequence to be analyzed has a length of . Under different scale factors, a new coarse-grained sequence is established:
- (2)
- The signal is split into the -layer wavelet packet. After the wavelet packet decomposition, sub-signals of different frequency bands are obtained.
- (3)
- The wavelet packet reconstruction is performed on each frequency band of the decomposed sub-signals, and the reconstruction coefficient is represented as .
- (4)
- Calculate the energy value of each frequency band:
- (5)
- Calculate the total energy value :
- (6)
- Calculate the proportion of the energy of each child node to the total energy:
- (7)
- Calculate the energy entropy value of the wavelet packet in the layer after signal decomposition:
2.3. Extreme Learning Machine
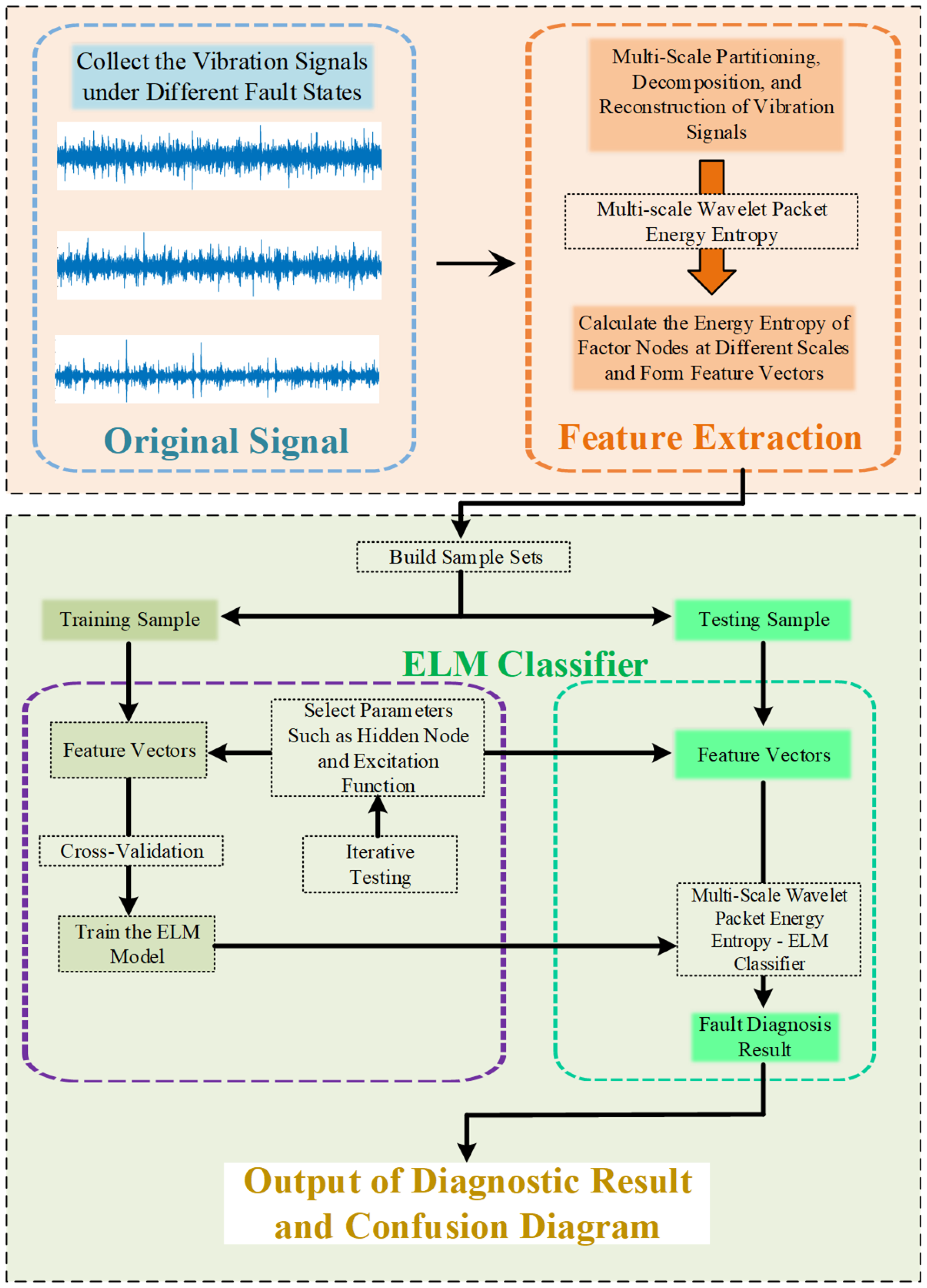
3. Fault Diagnosis Methods
3.1. Fault Diagnosis Method Process
3.2. Experimental Setup
4. Experimental Simulation and Data Analysis
4.1. Fault Feature Extraction
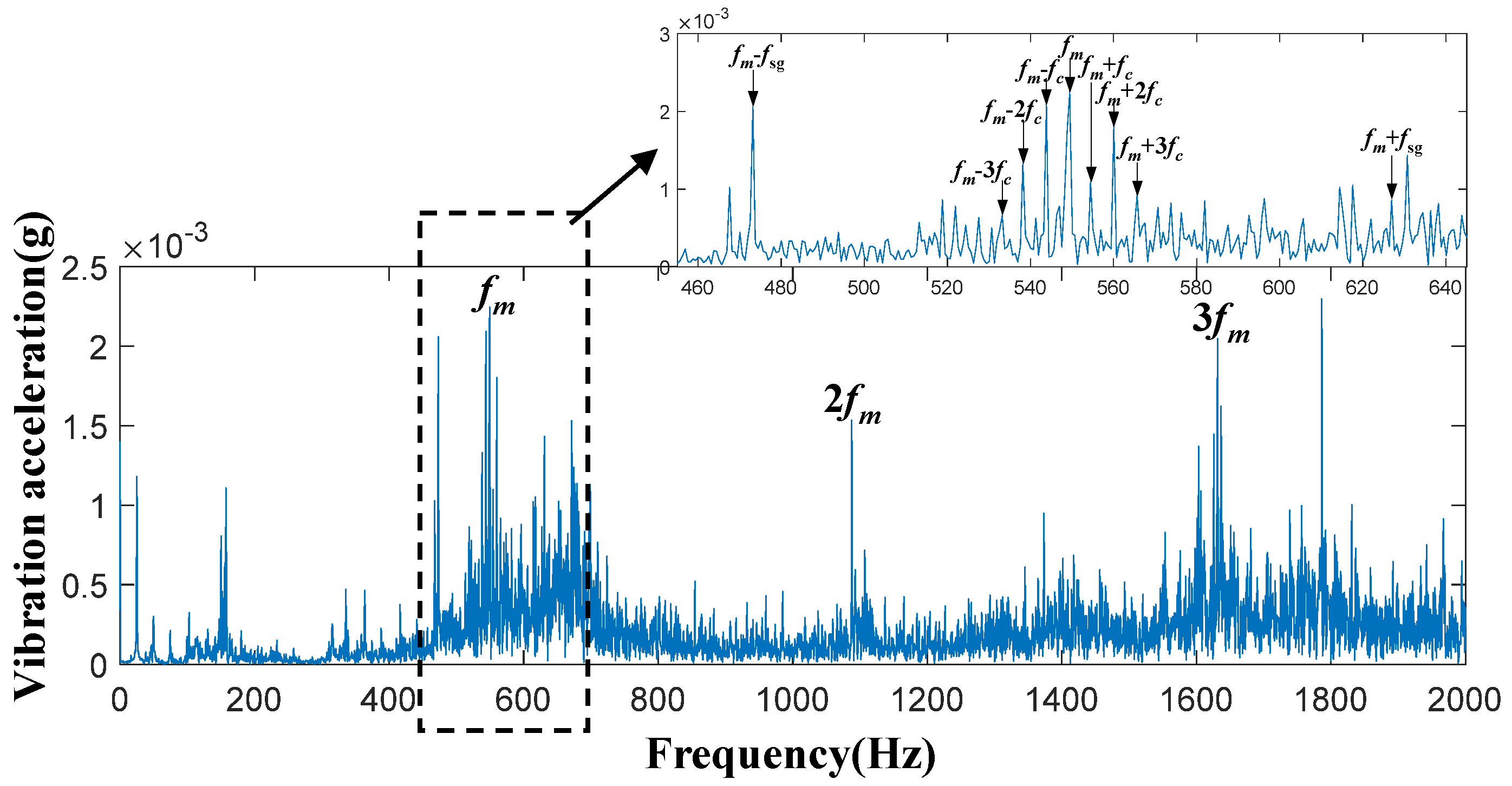
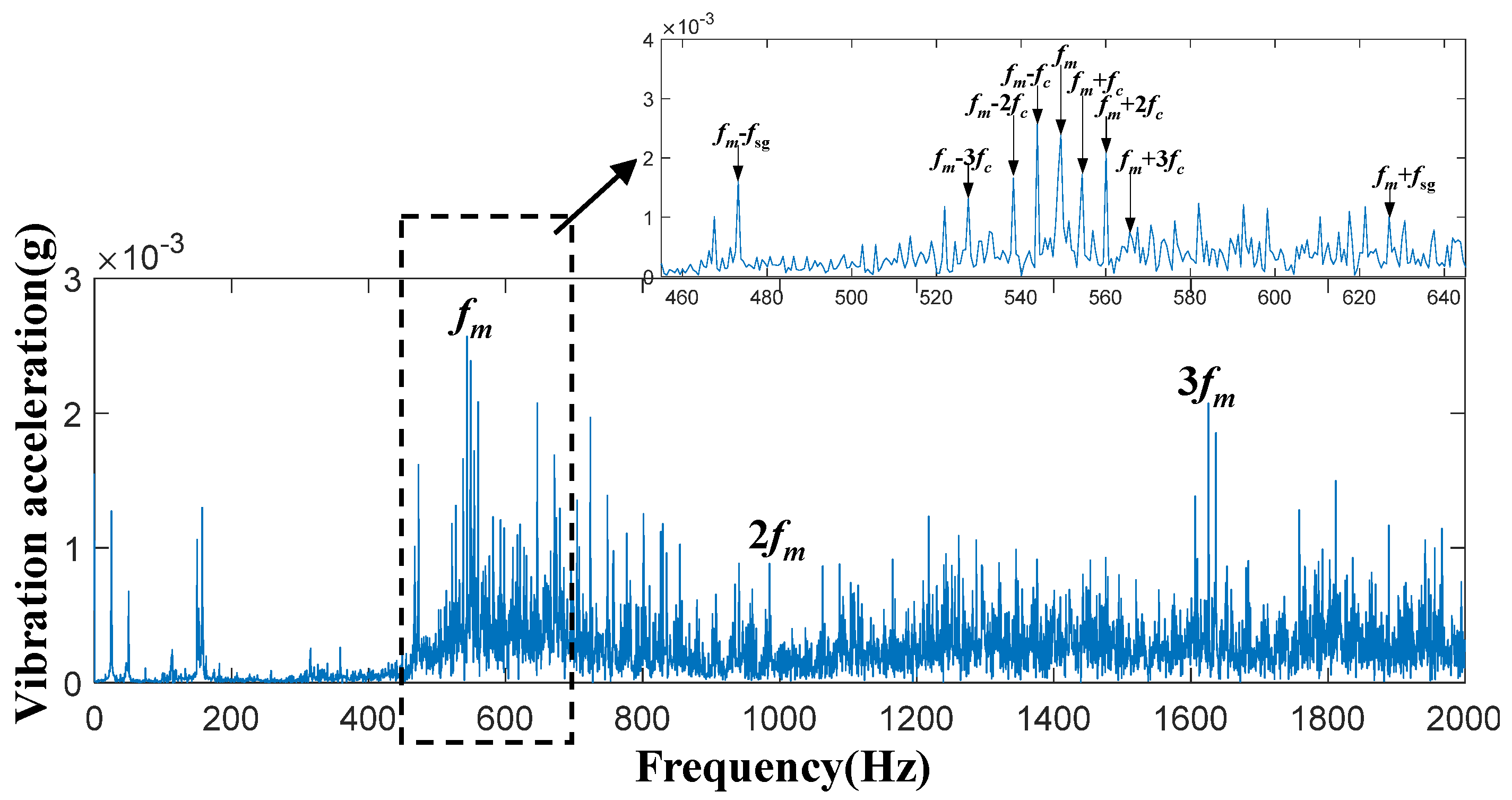
4.1.1. Experimental Signal Acquisition and Analysis
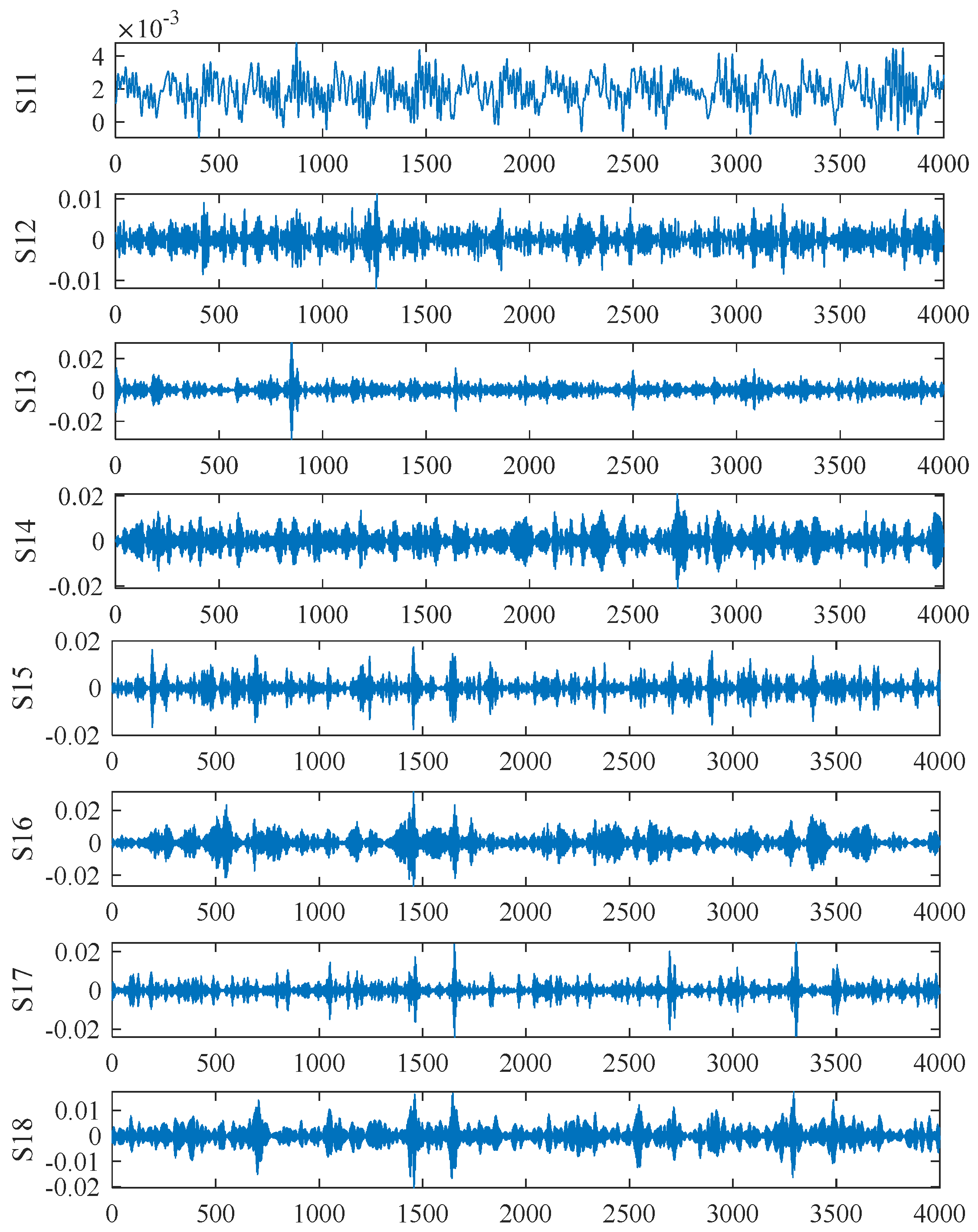
4.1.2. Multi-Scale Division of Experimental Signals
4.1.3. Wavelet Packet Decomposition of the Experimental Signal
4.1.4. Feature Vector Calculation
4.2. Fault Diagnosis and Comparison Verification
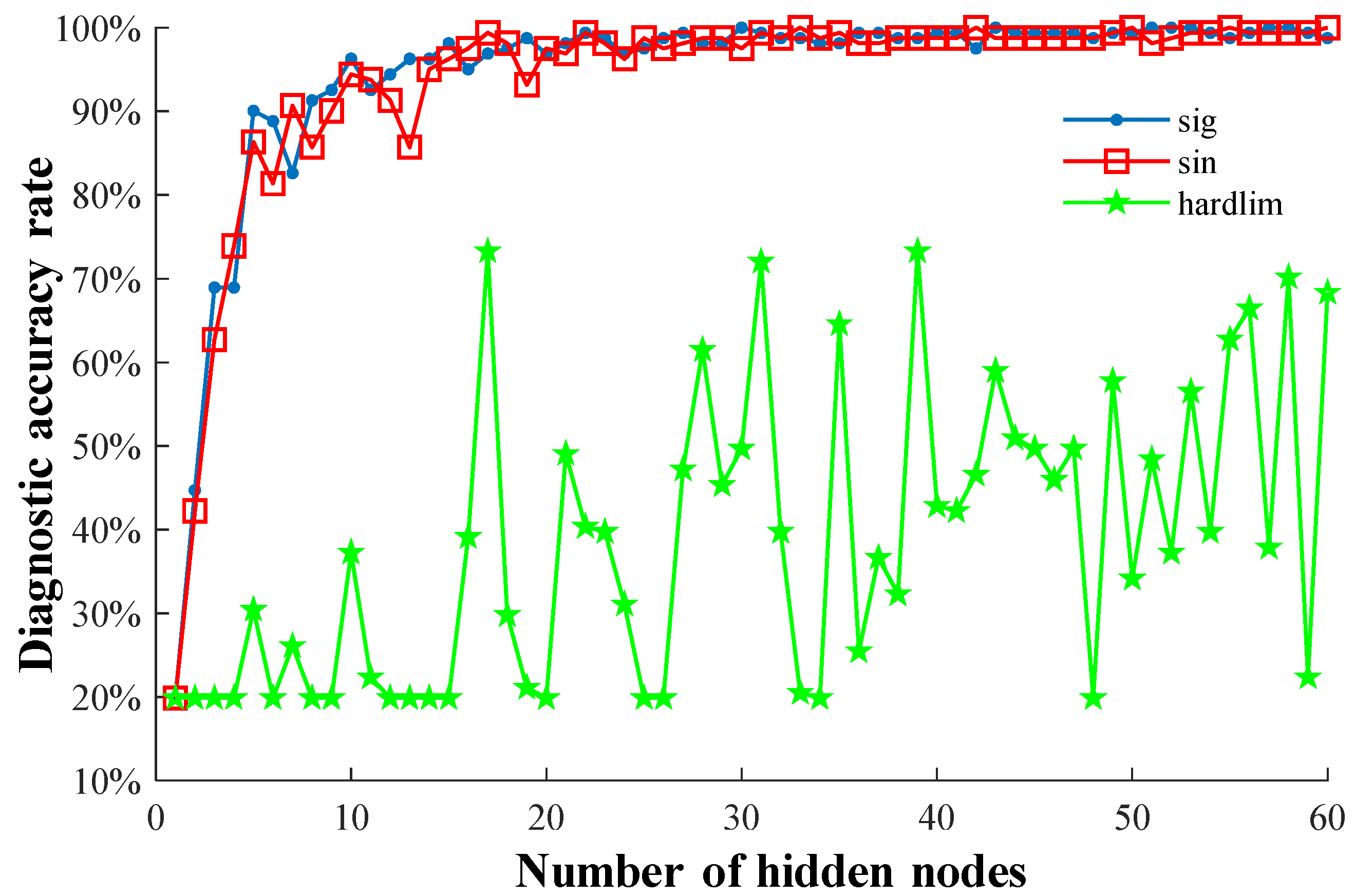
4.2.1. ELM Parameter Selection
4.2.2. Fault Identification
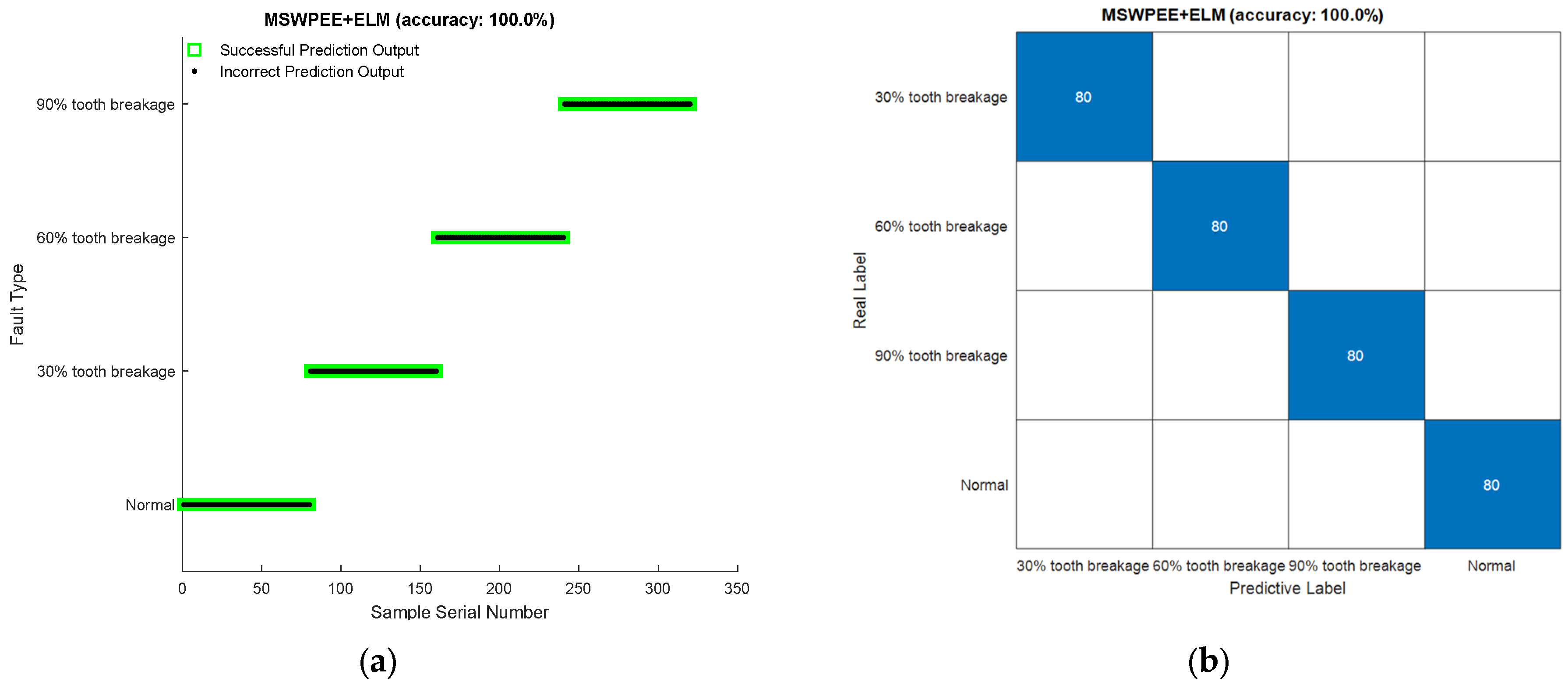
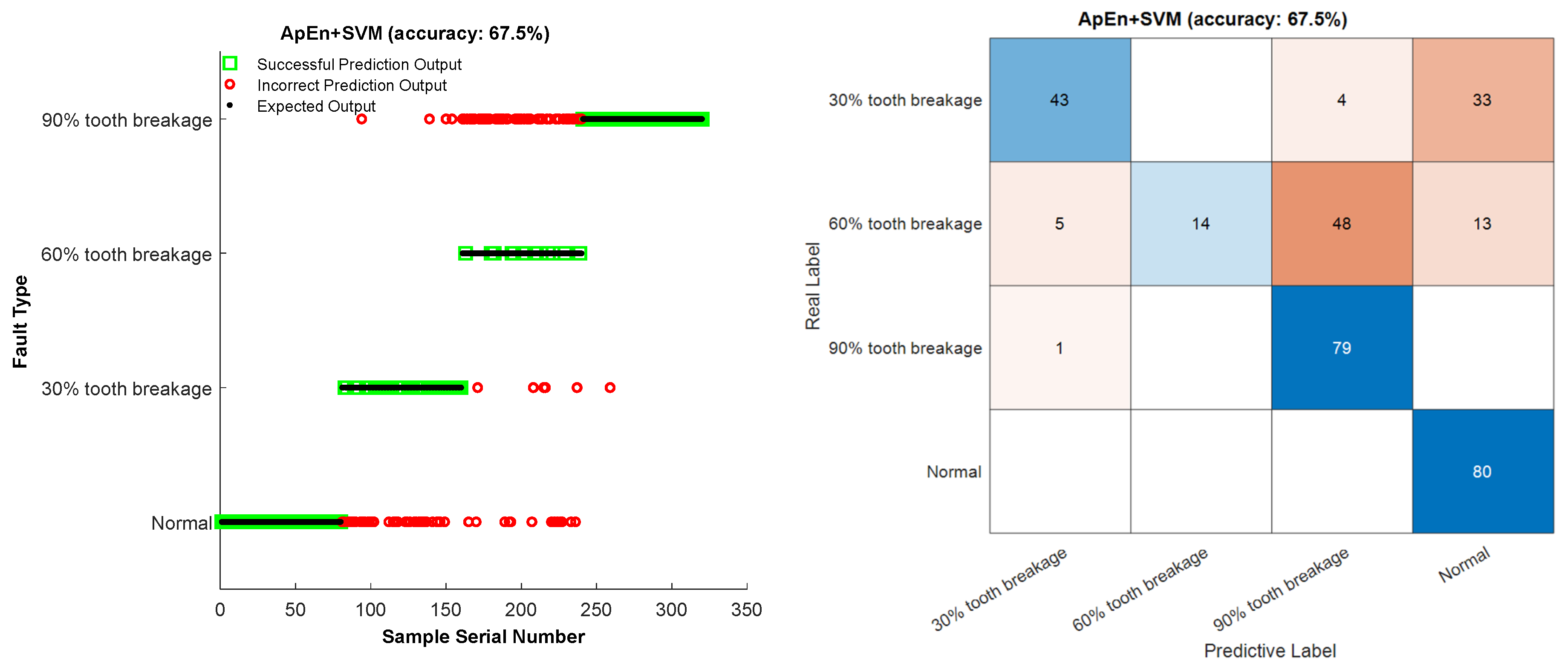
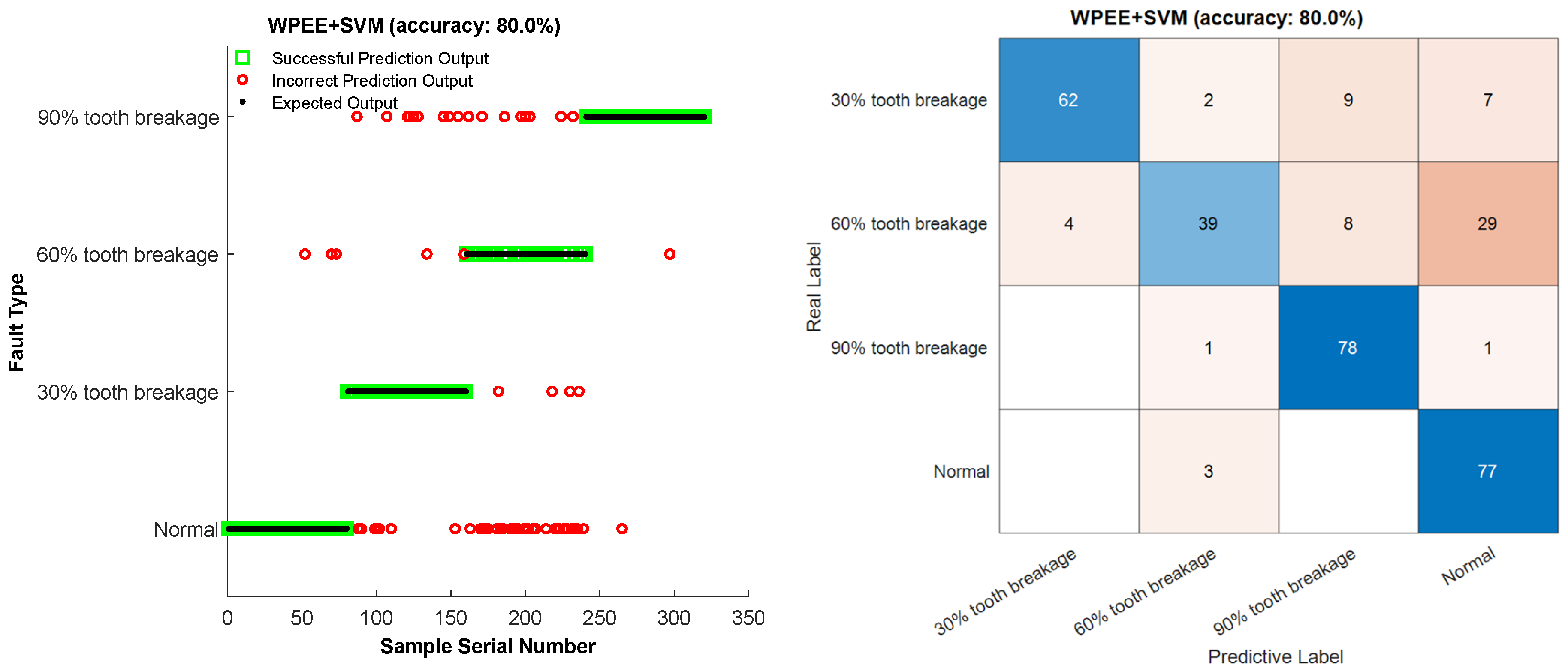
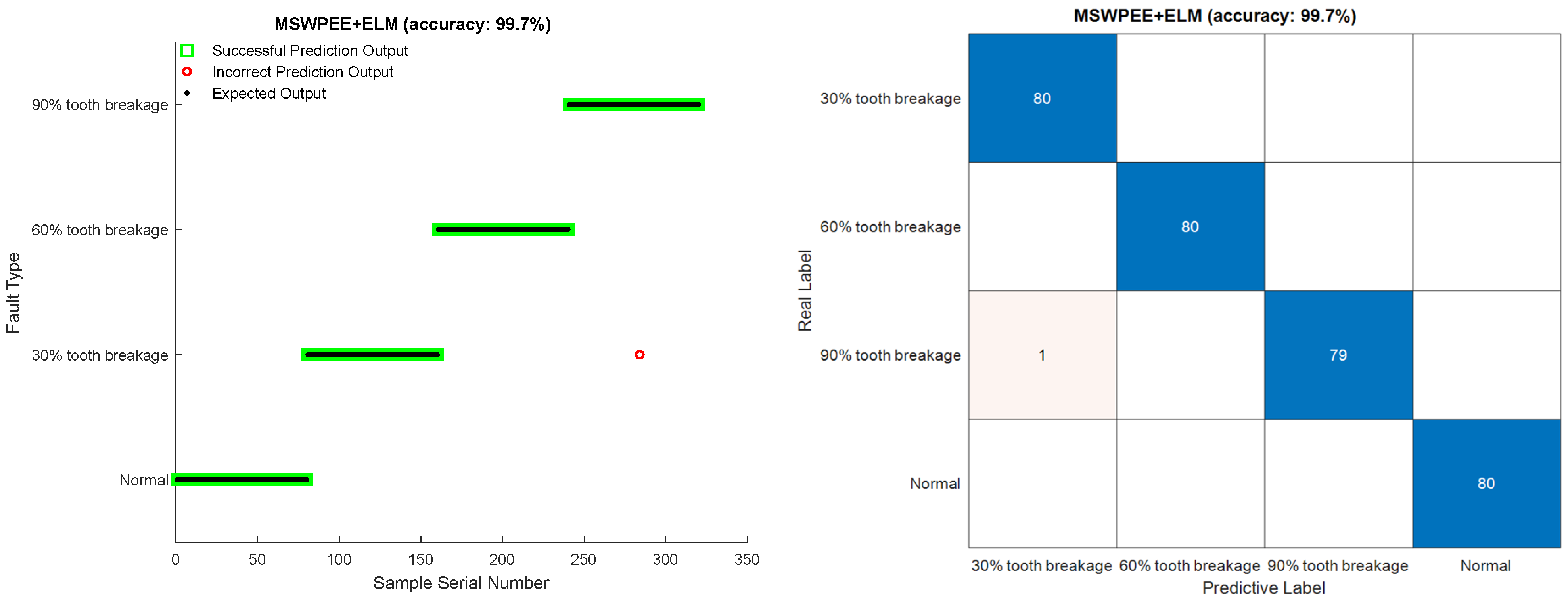
4.3. Comparison of Different Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Liu, X.; Yang, Y.; Zhang, J. Resultant vibration signal model based fault diagnosis of a single stage planetary gear train with an incipient tooth crack on the sun gear. Renew. Energy 2018, 122, 65–79. [Google Scholar] [CrossRef]
- Zheng, H.; Deng, W.; Song, W.; Cheng, W.; Cattani, P.; Villecco, F. Remaining Useful Life Prediction of a Planetary Gearbox Based on Meta Representation Learning and Adaptive Fractional Generalized Pareto Motion. Fractal Fract. 2023, 8, 14. [Google Scholar] [CrossRef]
- Shao, Z.; Hai, S.; Tian, W. Gearbox localized fault detection based on meshing frequency modulation analysis. Appl. Acoust. 2024, 219, 109943. [Google Scholar] [CrossRef]
- Cheng, W.; Li, Y.; Hao, W.; Bao, Z.; Hua, L. Fault modulation mechanism and kinematic modeling of planetary gear with local fault. J. Sound Vib. 2024, 590, 118572. [Google Scholar] [CrossRef]
- Xia, X.; Wang, X.; Chen, W. Fault Diagnosis of Wind Turbine Gearbox Based on Improved Multivariate Variational Mode Decomposition and Ensemble Refined Composite Multivariate Multiscale Dispersion Entropy. Entropy 2025, 27, 192. [Google Scholar] [CrossRef]
- Wang, X.; Lu, Z.; Wei, J.; Zhang, Y. Fault Diagnosis for Rail Vehicle Axle-Box Bearings Based on Energy Feature Reconstruction and Composite Multiscale Permutation Entropy. Entropy 2019, 21, 865. [Google Scholar] [CrossRef]
- Wang, X.; Du, Y. Fault Diagnosis Method for Wind Turbine Gearbox Based on Ensemble-Refined Composite Multiscale Fluctuation-Based Reverse Dispersion Entropy. Entropy 2024, 26, 705. [Google Scholar] [CrossRef]
- Amin, J.; Sharif, M.; Raza, M.; Saba, T.; Anjum, M.A. Brain tumor detection using statistical and machine learning method. Comput. Methods Prog. Biomed. 2019, 177, 69–79. [Google Scholar] [CrossRef]
- Fan, W.; Zhou, Q.; Li, J.; Zhu, Z. A wavelet-based statistical approach for monitoring and diagnosis of compound faults with application to rolling bearings. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1563–1572. [Google Scholar] [CrossRef]
- Bin, G.F.; Gao, J.J.; Li, X.J.; Dhillon, B.S. Early fault diagnosis of rotating machinery based on wavelet packets-Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Wang, C.; Gan, M.; Zhu, C.A. Fault feature extraction of rolling element bearings based on wavelet packet transform and sparse representation theory. J. Intell. Manuf. 2018, 29, 937–951. [Google Scholar] [CrossRef]
- Wan, S.T.; Zhang, X.; Dou, L.J. Shannon entropy of binary wavelet packet subbands and its application in bearing fault extraction. Entropy 2018, 20, 260. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, T.; Luo, Z.; Sun, K. A Novel Rolling Bearing Fault Diagnosis and Severity Analysis Method. Appl. Sci. 2019, 9, 2356. [Google Scholar] [CrossRef]
- Zhang, W.B.; Zhou, J.Z. Fault diagnosis for rolling element bearings based on feature space reconstruction and multiscale permutation entropy. Entropy 2019, 21, 519. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, J.; Tang, H.; Liu, X.; Zhong, Y. Minimum entropy deconvolution based on simulation-determined band pass filter to detect faults in axial piston pump bearings. ISA Trans. 2018, 88, 186–198. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, H. Gearbox Fault Diagnosis Based on Refined Time-Shift Multiscale Reverse Dispersion Entropy and Optimised Support Vector Machine. Machines 2023, 11, 646. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. Approximate entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 824–839. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhuang, J.; Yu, W. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Application of EEMD and improved frequency band entropy in bearing fault feature extraction. ISA Trans. 2019, 88, 170–185. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.B.; Feng, K.; Liang, X.H.; Zuo, M.J. A fault diagnosis method for planetary gearboxes under non-stationary working conditions using improved Vold-Kalman filter and multi-scale sample entropy. J. Sound Vib. 2019, 439, 271–286. [Google Scholar] [CrossRef]
- Zheng, J.D.; Jiang, Z.W.; Pan, H.Y. Sigmoid-based refined composite multiscale fuzzy entropy and t-SNE based fault diagnosis approach for rolling bearing. Measurement 2018, 129, 332–342. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, Y.; Li, P. Contactless Fault Diagnosis for Railway Point Machines Based on Multi-Scale Fractional Wavelet Packet Energy Entropy and Synchronous Optimization Strategy. IEEE Trans. Veh. Technol. 2022, 71, 5906–5914. [Google Scholar] [CrossRef]
- Rodriguez, N.; Alvarez, P.; Barba, L.; Cabrera-Guerrero, G. Combining Multi-Scale Wavelet Entropy and Kernelized Classification for Bearing Multi-Fault Diagnosis. Entropy 2019, 21, 152. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- He, J.; Huang, W.; Liu, Y.; Qian, C.; Ma, C.; Gao, W.; Jin, X. Data imbalance fault diagnosis method based on an ensemble multi-scale convolutional attention network. Mech. Syst. Signal Process. 2025, 236, 112934. [Google Scholar] [CrossRef]
- Zhu, D.; Song, X.; Yang, J.; Cong, Y.; Wang, L. A Bearing Fault Diagnosis Method Based on L1 Regularization Transfer Learning and LSTM Deep Learning. In Proceedings of the 2021 IEEE International Conference on Information Communication and Software Engineering (ICICSE), Chengdu, China, 19–21 March 2021; pp. 308–312. [Google Scholar]
- Chen, Y.; Yuan, Z.; Chen, J.; Sun, K. A Novel Fault Diagnosis Method for Rolling Bearing Based on Hierarchical Refined Composite Multiscale Fluctuation-Based Dispersion Entropy and PSO-ELM. Entropy 2022, 24, 1517. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, J.; Lu, C.; Wang, Z. Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine. Mech. Mach. Theory 2015, 90, 175–186. [Google Scholar] [CrossRef]
- Mao, W.; He, L.; Yan, Y.; Wang, J. Online sequential prediction of bearings imbalanced fault diagnosis by extreme learning machine. Mech. Syst. Signal Process. 2017, 83, 450–473. [Google Scholar] [CrossRef]
- He, C.; Wu, T.; Gu, R.; Jin, Z.; Ma, R.; Qu, H. Rolling bearing fault diagnosis based on composite multiscale permutation entropy and reverse cog-nitive fruit fly optimization algorithm–extreme learning machine. Measurement 2021, 173, 108636. [Google Scholar] [CrossRef]
- Yu, R.; Xiang, R.; Yao, S.W. Extreme learning machine for fault diagnosis of rotating machinery. Adv. Mater. Res. 2014, 960–961, 1400–1403. [Google Scholar] [CrossRef]
- Shu, Z.; Liang, X.; Wang, L. A fault diagnosis method for analog circuits based on EEMD-PSO-SVM. Heliyon 2024, 10, e38064. [Google Scholar] [CrossRef]
- Pang, L.; Zhang, T.; Wang, X.; Zhang, K.; Liu, L. Parameter identification of key components of thyristor converter valve based on wavelet packet key feature extraction and Elman neural network. IET Gener. Transm. Distrib. 2023, 17, 947–961. [Google Scholar] [CrossRef]
- Wan, S.; Zhang, X. Teager energy entropy ratio of wavelet packet transform and its application in bearing fault diagnosis. Entropy 2018, 20, 388. [Google Scholar] [CrossRef] [PubMed]
- Mallat, S. Wavelet Packet and Local Cosine Bases. In A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999; pp. 377–434. [Google Scholar]
- Vetterli, M.; Herley, C. Wavelets and filter banks: Theory and design. IEEE Trans. Signal Process. 1992, 40, 2207–2232. [Google Scholar] [CrossRef]
- Lin, D.; Dong, Z.; Sun, J.; Xu, W.; Chen, X.; Liu, S.; Jiang, Y.; Jiao, W. MSE-NERSPPNet: A Multi-Channel Framework for Bearing Fault Diagnosis in the Presence of Imbalanced Samples. Res. Sq. 2025, 10, 21203. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy to distinguish physiologic and synthetic RR time series. In Proceedings of the Computers in Cardiology, Memphis, TN, USA, 22–25 September 2002; pp. 137–140. [Google Scholar]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait dynamics. Phys. A Stat. Mech. Its Appl. 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]
- Zhang, L.; Xiong, G.; Liu, H.; Zou, H.; Guo, W. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference. Expert Syst. Appl. 2010, 37, 6077–6085. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Q.; Wang, D.; Li, Q. Research on the Harmonic Prediction Method of a PV Plant Based on an Improved Kernel Extreme Learning Machine Model. Electronics 2023, 13, 32. [Google Scholar] [CrossRef]
- Yuan, X.; Fan, Y.; Zhou, C.; Wang, X.; Zhang, G. Research on Twin Extreme Learning Fault Diagnosis Method Based on Multi-Scale Weighted Permutation Entropy. Entropy 2022, 24, 1181. [Google Scholar] [CrossRef]


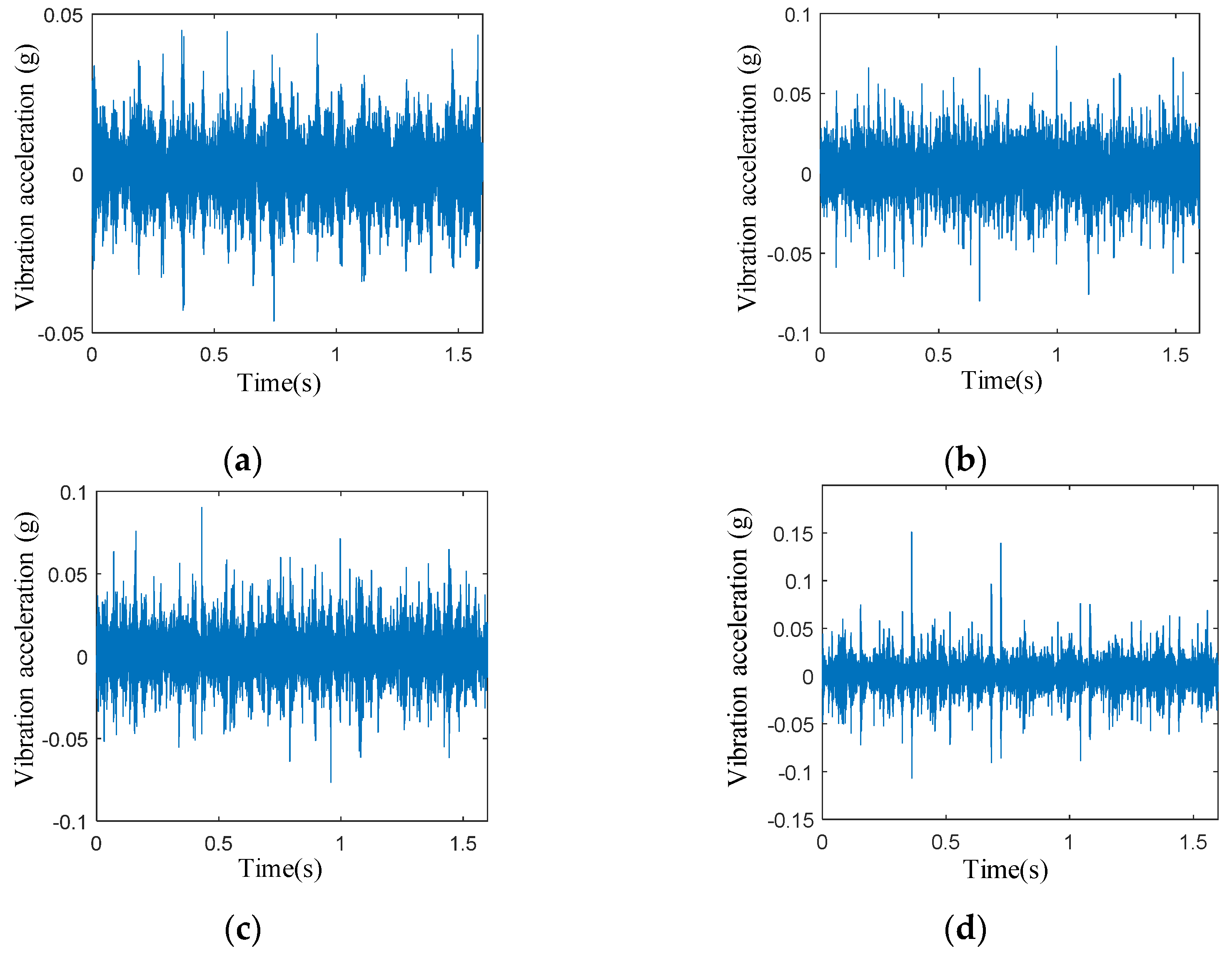




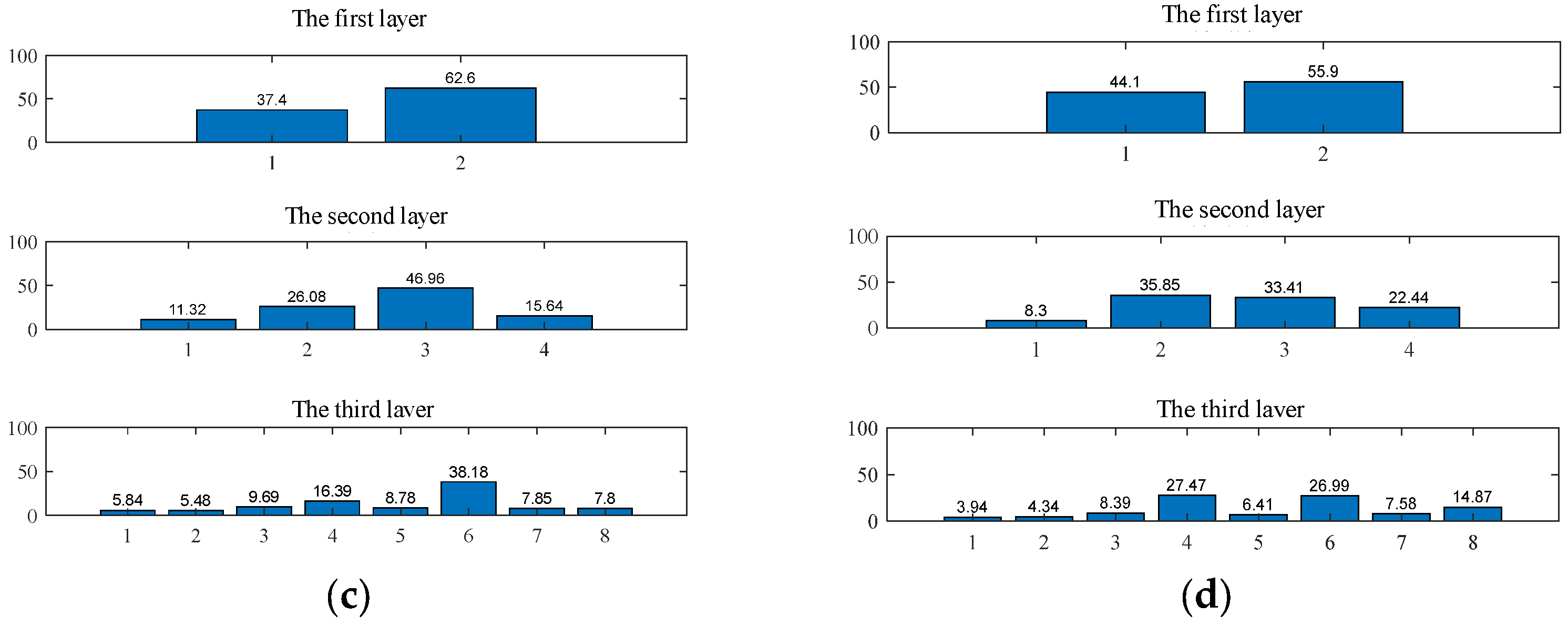

| 0 | 30 | 60 | 90 | |
|---|---|---|---|---|
| Maximum amplitude of vibration (g) | 0.04486 | 0.0795 | 0.09027 | 0.1511 |
| Gear Operating Condition | Scale Factor | S11 | S12 | S13 | S14 | S15 | S16 | S17 | S18 |
|---|---|---|---|---|---|---|---|---|---|
| Normal | 1 | 0.27 | 0.27 | 0.28 | 0.23 | 0.17 | 0.27 | 0.30 | 0.20 |
| 2 | 0.34 | 0.12 | 0.15 | 0.31 | 0.26 | 0.31 | 0.25 | 0.15 | |
| 3 | 0.36 | 0.05 | 0.13 | 0.14 | 0.17 | 0.35 | 0.23 | 0.27 | |
| 30% tooth breakage | 1 | 0.13 | 0.17 | 0.30 | 0.23 | 0.22 | 0.26 | 0.34 | 0.26 |
| 2 | 0.23 | 0.06 | 0.18 | 0.24 | 0.32 | 0.33 | 0.26 | 0.27 | |
| 3 | 0.30 | 0.04 | 0.07 | 0.16 | 0.24 | 0.32 | 0.28 | 0.35 | |
| 60% tooth breakage | 1 | 0.16 | 0.15 | 0.29 | 0.22 | 0.19 | 0.19 | 0.36 | 0.21 |
| 2 | 0.24 | 0.13 | 0.23 | 0.21 | 0.31 | 0.33 | 0.28 | 0.24 | |
| 3 | 0.30 | 0.04 | 0.21 | 0.19 | 0.25 | 0.30 | 0.26 | 0.33 | |
| 90% tooth breakage | 1 | 0.12 | 0.13 | 0.35 | 0.20 | 0.19 | 0.28 | 0.35 | 0.17 |
| 2 | 0.20 | 0.04 | 0.14 | 0.20 | 0.33 | 0.36 | 0.24 | 0.21 | |
| 3 | 0.28 | 0.04 | 0.08 | 0.14 | 0.21 | 0.24 | 0.29 | 0.36 |
| Gear Operating Condition | S11 | S12 | S13 | S14 | S15 | S16 | S17 | S18 |
|---|---|---|---|---|---|---|---|---|
| Normal | 0.27 | 0.27 | 0.28 | 0.23 | 0.17 | 0.27 | 0.30 | 0.20 |
| 30% tooth breakage | 0.13 | 0.17 | 0.30 | 0.23 | 0.22 | 0.26 | 0.34 | 0.26 |
| 60% tooth breakage | 0.16 | 0.15 | 0.29 | 0.22 | 0.19 | 0.19 | 0.36 | 0.21 |
| 90% tooth breakage | 0.12 | 0.13 | 0.35 | 0.20 | 0.19 | 0.28 | 0.35 | 0.17 |
| Methods | Accuracy of Correctly Identified Samples (%) | Fault Identification Time(s) | Average Accuracy (%) | |||
|---|---|---|---|---|---|---|
| Category 1 | Category 2 | Category 3 | Category 4 | |||
| ApEn-SVM | 98.875 | 52 | 78 | 98.875 | 0.51165 | 67.94 |
| WPEE-SVM | 95.625 | 79.5 | 49.375 | 97.5 | 0.51711 | 80.25 |
| MSWPEE-SVM | 100 | 86.125 | 72.875 | 100 | 0.54475 | 89.75 |
| MSWPEE-ELM | 100 | 98.5 | 99.125 | 99.875 | 0.02237 | 99.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, R.; Zhang, J.; Chen, M.; Chen, L. Fault Diagnosis Method of Planetary Gearboxes Based on Multi-Scale Wavelet Packet Energy Entropy and Extreme Learning Machine. Entropy 2025, 27, 782. https://doi.org/10.3390/e27080782
Meng R, Zhang J, Chen M, Chen L. Fault Diagnosis Method of Planetary Gearboxes Based on Multi-Scale Wavelet Packet Energy Entropy and Extreme Learning Machine. Entropy. 2025; 27(8):782. https://doi.org/10.3390/e27080782
Chicago/Turabian StyleMeng, Rui, Junpeng Zhang, Ming Chen, and Liangliang Chen. 2025. "Fault Diagnosis Method of Planetary Gearboxes Based on Multi-Scale Wavelet Packet Energy Entropy and Extreme Learning Machine" Entropy 27, no. 8: 782. https://doi.org/10.3390/e27080782
APA StyleMeng, R., Zhang, J., Chen, M., & Chen, L. (2025). Fault Diagnosis Method of Planetary Gearboxes Based on Multi-Scale Wavelet Packet Energy Entropy and Extreme Learning Machine. Entropy, 27(8), 782. https://doi.org/10.3390/e27080782






