Dynamic Balance: A Thermodynamic Principle for the Emergence of the Golden Ratio in Open Non-Equilibrium Steady States
Abstract
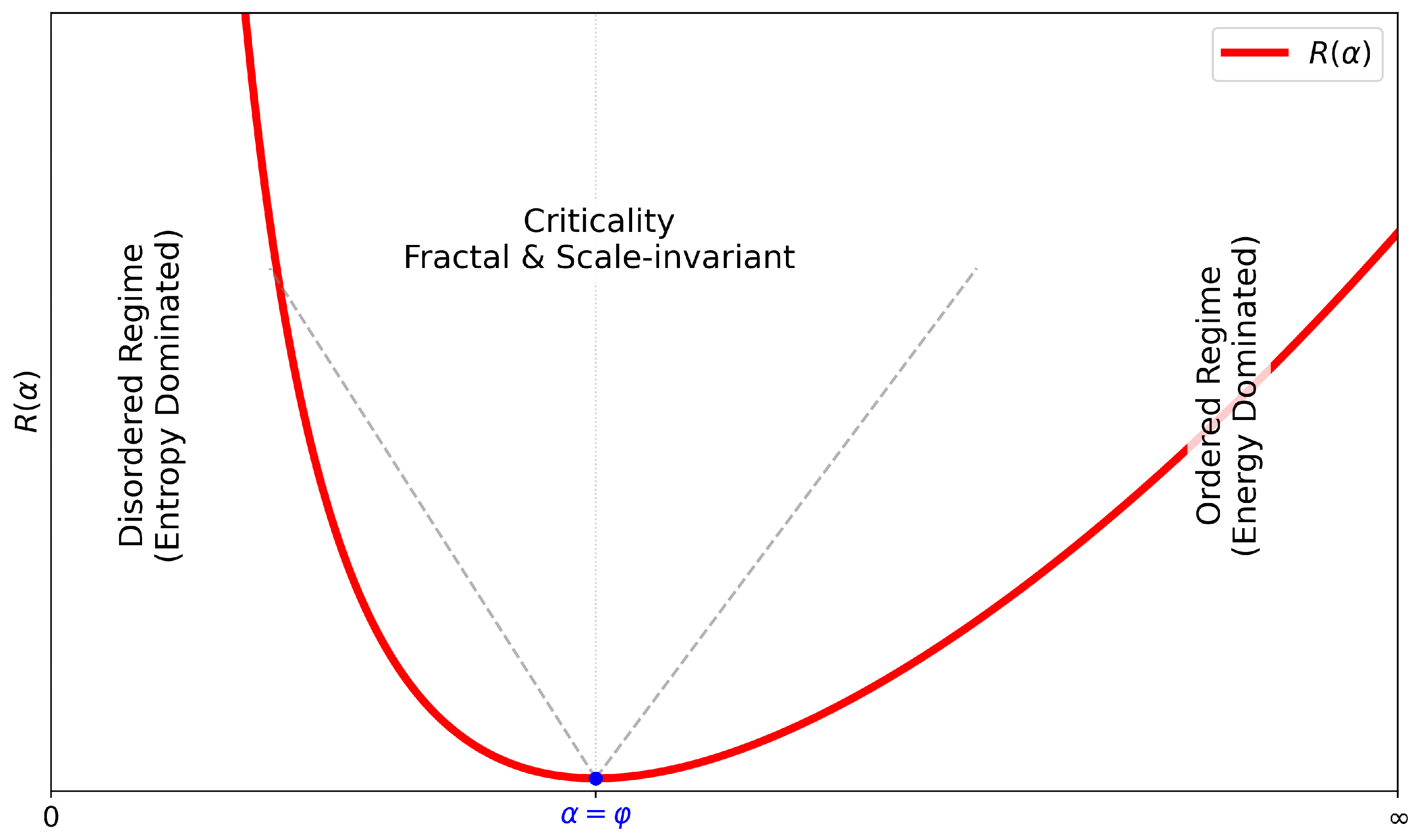
1. Introduction
2. Mathematical Framework
- antisymmetric Onsager exchange
- cross–correlated noise source source
- (a)
- Any minimizer satisfies .
- (b)
- Combining the two fixed-point equations gives and .
- (c)
- Therefore, .
2.1. Coarse-Grained Energy and Entropy Fluxes
2.2. Energy–Entropy Flux Ratio
2.3. Modular Symmetry and Convex Geometry
2.4. Microscopic Origin of the Möbius Involution : Onsager Antisymmetric Reactive Exchange
2.5. Microscopic Origin of the Self-Similar Shift : Cross-Correlated Noise
2.6. Convex Lyapunov Functional Invariant Under
2.7. Common Fixed Point and Identification of
- (i)
- Two irreducible power channels forming the entropy flux field ;
- (ii)
- Möbius inversion symmetry ;
- (iii)
- Self-similar translation symmetry ;
- (iv)
- A strictly convex Casimir functional diverging at .
3. Thermodynamic Cost Function and Relaxation Dynamics
Parameter-Free Experimental Invariants

- About 61.8% of energy is thermal entropy ().
- About 38.2% of energy is effective free energy ().
4. Discrete Markov Realization of the Flux–Ratio Dynamics
- (i)
- Slow drive (energy input): at constant rate .
- (ii)
- Avalanche relaxation (entropy release): for any and : at rate , where is the probability per unit time of a downward jump of size m. Reflecting boundary imposed .
4.1. Continuum Limit and Fokker–Planck Correspondence
4.2. Parameter Dictionary

5. Modular Symmetry and Non-Equilibrium Field Theory
5.1. Stochastic Dynamic-Balance Equation
5.2. MSRJD Path Integral Formalism
5.3. Modular Symmetries and Ward Identities
5.4. Quadratic Theory and Diffusive Pole

Interpretation of : A Modular Einstein Relation
5.5. Dynamical-Exponent Landscape
- Full modular symmetry ( and preserved; Onsager matrix antisymmetric):The nonlinearity couples left- and right-moving modes through dual Möbius rotations. The retarded self-energy inherits the golden eigen-angle, and the dispersion becomes , i.e., . This is the fully symmetry-protected golden dynamic exponent, characteristic of balanced, -stabilized flows.
- Self-dual line ( preserved, broken): One modular charge is violated. The resulting loop integral resembles the modified KPZ class with [62]. This phase retains -inversion symmetry but lacks self-similarity, leading to intermediate roughening.
6. Discussion
6.1. Two-Fluid Decomposition and Quantum-Critical Universality
- on thermodynamic fluxes ();
- on RG couplings .
6.2. Dynamic Balance in Gravity and Cosmology
- Drives the Universe to a de-Sitter vacuum with equation of state ;
- Predicts the dark-energy fraction ;
- Reproduces the cosmic web’s spiral structure and fractal dimension ;
- Links directly to AdS2 modular dualities through the same Möbius involution.
7. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DB | Dynamic Balance |
| NESS | Non-Equilibrium Steady-State |
| PDE | Partial Differential Equation |
| ODE | Ordinary Differential Equation |
| PGL | Projective General Linear |
| RG | Renormalization Group |
| SOC | Self-Organized Criticality |
| CFC | Cross-Frequency Couplings |
| FLRW | Friedmann–Lemaître–Robertson–Walker metric |
| QCP | Quantum Critical Point |
Appendix A. Two–Fluid Decomposition
Appendix A.1. Quantum First-Law Split at T→0
- is the power delivered through coherent, phase-locked drive fields (laser, microwave, synaptic network, etc.). This is the “work channel” A.
- counts the incoherent quanta (photons, phonons, and quasiparticles) irreversibly emitted to the environment during the interval ; each carries energy . This constitutes the “entropy channel” B.
Appendix A.2. Emergent Flip Sφ
Appendix B. Quantum-Critical Two-Fluid RG
- (a)
- A slow, coherent set of conserved hydrodynamic fields (momentum, charge, spin);
- (b)
- A fast, incoherent set (entropy, heat, or gauge-flux currents).
- are bare diffusion constants of the two fluids.
- The antisymmetric Onsager coupling encodes the modular “flip” that mixes the currents ().
- Noise correlators follow from the quadratic term with amplitudes .
- Setting and collapses the matrix to a single-field critical action, Equation (33) in the main text.
Appendix B.1. One-Loop Self Energy
Appendix B.2. Dimensionless Couplings and β-Functions
- Equation (A13) shows and as symmetry-protected subspaces.
- Equation (A11) implies a non-trivial only if .
- (i)
- Golden manifold : ; modular symmetry intact.
- (ii)
- Self-dual line: ; möbius shift preserved, flip broken.
- (iii)
- Gaussian: (unstable).
Appendix B.3. Extracting the Dynamic Exponent
- Strange metals: (universal Hall angle).
- Cuprate : Specific-heat jump gains a prefactor .
Appendix B.4. Summary
- One-loop RG shows the modular flip and shift restricts the flow to a one-parameter line.
- Full symmetry → golden exponent .
- Breaking but keeping the flip → square-root exponent .
- Gaussian or generic symmetry-broken theories revert to .
Appendix C. Golden Möbius Flip as a Weyl Reflection Inside E8
Appendix C.1. Embedding H2 Inside the E8 Root Lattice
Appendix C.2. Coxeter Phases and the Golden Casimir
Appendix C.3. Link to the 1-D Ising E8 Spectrum
| Closed Form | ||
| 1 | 1 | 1 |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
Appendix C.4. Beyond the Ising Chain: Other Materials Sharing the Discrete Symmetry
- Kagome AV3Sb5 “strange metals”. Non-symmorphic phonons in the kagome layer furnish a two-dimensional representation isomorphic to an sublattice. Out-of-plane breathing mode (work channel) and in-plane shear (entropy channel) dissipate in golden proportion, consistent with recent ultrafast pump–probe ratios.
- Fibonacci anyon chains ( FQH plateau). The Read–Rezayi state hosts non-Abelian anyons obeying the fusion rule . Mapping the braid group to identifies the “charge” fusion channel (A) and the “flux” channel (B) as the dynamic-balance pair. Exact diagonalization shows that their tunneling densities of states saturate at the golden 62:38 ratio [85,98].
- Fractional quantum Hall () edge state. The bosonic quantum Hall edge realises an WZW theory. Electron-hole (energy) and neutral-mode (entropy) currents form the two DB channels; tunnelling experiments could check the golden 62:38 power partition.
- Kitaev honeycomb spin liquids. At the isotropic point , Majorana fermions (channel A) and vison fluxes (channel B) couple antisymmetrically. The low-energy field theory factors into an lattice where the same reflection acts on the Majorana-vison balance, predicting a golden viscous damping ratio for THz optical conductivity in RuCl3.
- Flux-charge dual Josephson circuits (0– qubit). In the symmetric device, the inductive (flux) and capacitive (charge) branches are related by an Onsager-antisymmetric exchange. Microwave-drive experiments already report a maximal coherence time when the cross-correlated noise between the two branches matches the dissipative variance of the flux port (), exactly the DB condition that produces the Möbius shift [99]. A re-analysis of the published relaxation data gives , squarely within the golden window.
- Non-thermal fixed point in unitary Fermi gases. After a strong quench, the density (channel A) and entropy (channel B) currents of a unitary 6Li gas display an emergent scale invariance. Recent functional RG work finds a discrete pair of Möbius transformations that lock the stationary distribution at , giving a dynamic exponent [55]. Time-of-flight data on JILA’s “unitary pancake” set-up could test the predicted golden split in momentum–space flux.
Appendix C.5. Physical Interpretation
Appendix D. The Brain as an Open NESS
- Dendritic and vascular fractal dimension [104].
Appendix D.1. Thermodynamic Wilson–Cowan Field
Linear Decay Rate
Appendix D.2. Critical Scaling and Avalanche Cut-Off
Appendix D.3. Multi-Scale Ramifications
- (i)
- Travelling-split waves. For (myelinated axons), a solitary E-pulse with receives a DB “kick”, splitting its crest amplitude by . Repetition yields a wavelet cascade of box-counting dimension , matching optical VSD data in mouse.
- (ii)
- Dendritic and vascular trees. Interpreting E as elongation drive and I as nutrient supply, growth stops when ; the tip bifurcates into two branches, each scaled by . Iteration produces a binary tree with , matching Purkinje and cortical microvasculature.
- (iii)
- Cross-frequency coupling (CFC). Near a double-Hopf point amplitude, equations gain an extra damping with . Rational ratios damp fastest; the most robust phase-amplitude locking is , as observed for theta–gamma nesting.
Appendix D.4. Metabolic 60:40 Partition
Appendix D.5. Pathology and Intervention
| Deviation | Physiological Meaning | Clinical Correlate |
|---|---|---|
| hyper-inhibition, energy crisis | deep anaesthesia, coma | |
| runaway excitation | epilepsy, excitotoxicity | |
| patchy | local imbalance | perilesional tissue |
Appendix D.6. Take-Aways for Neuroscience
- (a)
- The golden Lyapunov term substitutes ad-hoc saturation, ensuring self-regulation toward .
- (b)
- Avalanche scaling, CFC peaks, and fractal dendrites all descend from the three DB invariants .
- (c)
- Pathologies map to breaches of Lyapunov walls; therapies can be viewed as flux-balancing manoeuvres restoring the golden partition.
Appendix E. Dynamic Balance in Gravity and Cosmology
- Black-hole horizon thermodynamics via the bathtub analogy;
- A semi-classical gravity action with a “golden” cost potential;
- The emergence of a de-Sitter attractor () and a small effective cosmological constant;
- A universal golden split of dark-energy vs. matter;
- The golden-spiral fractal dimension of the cosmic web.
Appendix E.1. Black-Hole Horizon as a Two-Channel Bathtub
- (1)
- (2)
- Flux–ratio field. Define a scalar on the “stretched membrane” that measures the bulk-to-surface balance.
- (3)
- Bathtub analogy. Continuous infall (“tap”) and Hawking dissipation (“drain”) map exactly onto our two-channel OU model with antisymmetric coupling and cross-correlated noise, producing the Möbius involution
Appendix E.2. Semi-Classical Gravity Action with Golden Cost
- is the Ricci scalar, and the boundary term is the usual Gibbons–Hawking surface action.
- The non-minimal coupling enforces the exchange at the level of the action.
- provides gradient stiffness (horizon elasticity).
- The cost potential is the unique smooth, strictly convex DB invariant under ,with an arbitrary mass scale that drops out of the fixed-point condition.
Appendix E.3. Field Equations and de-Sitter Attractor
Appendix E.4. Golden Dark-Energy Partition
Appendix E.5. Connection to Unified-Gravity Approaches
Appendix E.6. Predictions and Observational Tests
- , vs. Planck 2020: 0.6847(6)—within once baryons and radiation are accounted for.
- Horizon-entropy flux ratio , testable in analogue gravity experiments [106].
- Cosmic-web fractal dimension on 5–100 Mpc scales [94].
References
- Jean, R.V. Phyllotaxis: A Systemic Study in Plant Morphogenesis; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar] [CrossRef]
- Adler, I. A model of contact pressure in phyllotaxis. J. Theor. Biol. 1974, 45, 1–79. [Google Scholar] [CrossRef] [PubMed]
- Mitchison, G. Phyllotaxis and the Fibonacci series. Sci. Prog. 1977, 64, 469–486. [Google Scholar] [CrossRef] [PubMed]
- Douady, S.; Couder, Y. Phyllotaxis as a physical self-organization process. Phys. Rev. Lett. 1992, 68, 2098–2101. [Google Scholar] [CrossRef] [PubMed]
- Seigar, M.S. Galactic spiral arms, dark matter, and black holes: The observational case. Mon. Not. R. Astron. Soc. 2005, 361, 311–322. [Google Scholar] [CrossRef]
- Anthes, R.A. Tropical Cyclones: Their Evolution, Structure, and Effects; American Meteorological Society, Meteorological Monographs: Boston, MA, USA, 1982; Volume 19. [Google Scholar] [CrossRef]
- Bartello, P.; Warn, T. Self-similarity of decaying two-dimensional turbulence. J. Fluid Mech. 1996, 326, 357–372. [Google Scholar] [CrossRef]
- Fernando, H.J.S. Turbulence in Stratified Fluids. In Environmental Stratified Flows; Grimshaw, R., Ed.; Springer: Boston, MA, USA, 2002; pp. 161–189. [Google Scholar] [CrossRef]
- Mininni, P.D.; Pouquet, A.G.; Montgomery, D.C. Small-Scale Structures in Three-Dimensional Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2006, 97, 244503. [Google Scholar] [CrossRef]
- Alexakis, A.; Doering, C.R. Bounds on Dissipation in Rotating and Stratified Turbulence. J. Fluid Mech. 2022, 940, A46. [Google Scholar] [CrossRef]
- Gardner, M. Extraordinary nonperiodic tiling that enriches the theory of tiles. Sci. Am. 1977, 236, 110–119. [Google Scholar] [CrossRef]
- Penrose, R. The Role of Aesthetics in Pure and Applied Mathematical Research. Bull. Inst. Math. Its Appl. 1974, 10, 266. [Google Scholar]
- He, A.-L.; Ding, L.-R.; Zhou, Y.; Wang, Y.-F.; Gong, C.-D. Quasicrystal Chern Insulators. Phys. Rev. B 2019, 100, 214109. [Google Scholar] [CrossRef]
- Zamolodchikov, A. Integrable field theory from conformal field theory. In Advanced Studies in Pure Mathematics; Mathematical Society of Japan: Tokyo, Japan, 1989; Volume 19, pp. 641–674. [Google Scholar] [CrossRef]
- Coldea, R.; Tennant, D.; Wheeler, E.; Wawrzynska, E.; Prabhakaran, D.; Telling, M.; Habicht, K.; Smeibidl, P.; Kiefer, K. Quantum criticality in an Ising chain: Experimental evidence for E8 symmetry. Science 2010, 327, 177–180. [Google Scholar] [CrossRef] [PubMed]
- Bistritzer, R.; MacDonald, A. Moiré bands in twisted double-layer graphene. Proc. Natl. Acad. Sci. USA 2011, 108, 12233–12237. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Fatemi, V.; Demir, A.; Fang, S.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional Superconductivity in Magic-Angle Graphene Superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Nuckolls, K.P.; Scheer, M.G.; Wong, D.; Oh, M.; Lee, R.L.; Herzog-Arbeitman, J.; Watanabe, K.; Taniguchi, T.; Lian, B.; Yazdani, A. Spectroscopy of the fractal Hofstadter energy spectrum. Nature 2025, 639, 60–66. [Google Scholar] [CrossRef]
- Freedman, M.; Kitaev, A.; Larsen, M.; Wang, Z. Topological quantum computation. Bull. Am. Math. Soc. 2002, 40, 31–38. [Google Scholar] [CrossRef]
- Shew, W.L.; Plenz, D. The functional benefits of criticality in the cortex. Neuroscientist 2013, 17, 88–100. [Google Scholar] [CrossRef]
- Ribeiro, T.L.; Copelli, M.; Caixeta, F.; Belchior, H.; Chialvo, D.R.; Nicolelis, M.A.L.; Nicolelis, S.T. Spike avalanches exhibit universal dynamics across the sleep–wake cycle. PLoS ONE 2010, 5, e14129. [Google Scholar] [CrossRef]
- Beggs, J.M.; Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 2003, 23, 11167–11177. [Google Scholar] [CrossRef]
- Prigogine, I.; Rysselberghe, P.V. Introduction to Thermodynamics of Irreversible Processes. J. Electrochem. Soc. 1963, 110, 97C. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Cross, M.C.; Hohenberg, P.C. Pattern formation out of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef]
- Tracy, C. Universality class of a Fibonacci Ising model. J. Stat. Phys. 1988, 51, 481–490. [Google Scholar] [CrossRef]
- Xiong, D. Observing golden-mean universality class in the scaling of thermal transport. Phys. Rev. E 2018, 97, 022116. [Google Scholar] [CrossRef] [PubMed]
- Popkov, V.; Schadschneider, A.; Schmidt, J.; Schütz, G.M. Fibonacci family of dynamical universality classes. Proc. Natl. Acad. Sci. USA 2015, 112, 12645–12650. [Google Scholar] [CrossRef] [PubMed]
- Rizzo, A. The Golden Ratio Theorem: A Framework for Interchangeability and Self-Similarity in Complex Systems. Adv. Pure Math. 2023, 13, 559–596. [Google Scholar] [CrossRef]
- Popkov, V.; Schütz, G.M. Quest for the golden ratio universality class. Phys. Rev. E 2024, 109, 044111. [Google Scholar] [CrossRef]
- de Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; North-Holland Publishing Company: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Budyko, M.I. The Effect of Solar Radiation Variations on the Climate of the Earth. Tellus 1969, 21, 611–619. [Google Scholar] [CrossRef]
- Rolfe, D.F.S.; Brown, G.C. Cellular energy utilization and the molecular origin of standard metabolic rate in mammals. Physiol. Rev. 1997, 77, 731–758. [Google Scholar] [CrossRef]
- Wigner, E.P. Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra; Academic Press: Cambridge, MA, USA, 1959. [Google Scholar]
- Dresselhaus, M.S.; Dresselhaus, G.; Jorio, A. Group Theory: Application to the Physics of Condensed Matter; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On Onsager’s Principle of Microscopic Reversibility. Rev. Mod. Phys. 1945, 17, 343–350. [Google Scholar] [CrossRef]
- Potanina, E.; Flindt, C.; Moskalets, M.; Brandner, K. Thermodynamic bounds on coherent transport in periodically driven conductors. Phys. Rev. X 2021, 11, 021013. [Google Scholar] [CrossRef]
- Fodor, É.; Guo, M.; Gov, N.S.; Visco, P.; Weitz, D.A.; van Wijland, F. Activity-Driven Fluctuations in Living Cells. EPL 2015, 110, 48005. [Google Scholar] [CrossRef]
- Agren, J. The Onsager Reciprocity Relations Revisited. J. Phase Equilib. Diffus. 2022, 43, 640–647. [Google Scholar] [CrossRef]
- Otto, F. The geometry of dissipative evolution equations: The porous medium equation. Commun. Partial Differ. Equ. 2001, 26, 101–174. [Google Scholar] [CrossRef]
- Herbert, D. Some principles of continuous culture. J. Gen. Microbiol. 1956, 14, 601–622. [Google Scholar] [CrossRef] [PubMed]
- Pirt, S.J. The maintenance energy concept in microbial growth. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1965, 163, 224–231. [Google Scholar] [CrossRef]
- Pirt, S.J. Principles of Microbe and Cell Cultivation; Wiley: London, UK, 1975. [Google Scholar]
- Clarke, A.; Portner, H.O. Temperature, metabolic power and the evolution of endothermy. Biol. Rev. 2010, 85, 703–727. [Google Scholar] [CrossRef]
- Amthor, J.S. Respiration and Crop Productivity; Springer: New York, NY, USA, 1989. [Google Scholar]
- Gifford, R.M. Plant respiration in productivity models: Conceptualisation, representation and issues for global terrestrial carbon-cycle research. Funct. Plant Biol. 2003, 30, 171–186. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef]
- Mahieu, S.; Ruelle, P. Scaling fields in the two-dimensional Abelian sandpile model. Phys. Rev. E 2001, 64, 066130. [Google Scholar] [CrossRef]
- van Kampen, N.G. Stochastic Processes in Physics and Chemistry, 3rd ed.; North-Holland Personal Library, Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Tadić, B.; Shapoval, A.; Shnirman, M. Signatures of self-organized dynamics in rapidly driven critical sandpiles. Phys. Rev. E 2024, 110, 054203. [Google Scholar] [CrossRef]
- Christensen, K.; Corral, Á.; Frette, V.; Feder, J.; Jøssang, T. Tracer Dispersion in a Self-Organized Critical Pile. Phys. Rev. Lett. 1992, 69, 609–612. [Google Scholar] [CrossRef]
- Dickman, R.; Muñoz, M.A.; Vespignani, A.; Zapperi, S. Avalanche exponents and scaling in driven dissipative systems. Phys. Rev. E 1998, 57, 5095–5105. [Google Scholar] [CrossRef]
- Eyink, G.; Lebowitz, J.; Spohn, H. Hydrodynamics of stationary nonequilibrium states for some lattice gas models. J. Stat. Phys. 1996, 83, 385–472. [Google Scholar] [CrossRef]
- Kamenev, A.; Meerson, B. Ensuring detailed balance in nonequilibrium field theories. Phys. Rev. Lett. 2022, 128, 120601. [Google Scholar] [CrossRef]
- Medina, E.; Hwa, T.; Kardar, M.; Zhang, Y. Burgers Equation with Correlated Noise: Renormalization-Group Analysis and Applications to Directed Polymers and Interface Growth. Phys. Rev. A 1989, 39, 3053–3075. [Google Scholar] [CrossRef]
- Täuber, U.C. Critical Dynamics: A Field Theory Approach to Equilibrium and Non-Equilibrium Scaling Behavior; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Dominicis, C.d. Technics of field renormalization and dynamics of critical phenomena. J. Phys. Colloq. 1976. [Google Scholar]
- Janssen, H. On a Lagrangian for classical field dynamics and renormalization group calculations of dynamical critical properties. Z. Phys. B 1976, 23, 377–380. [Google Scholar] [CrossRef]
- Seiberg, N.; Witten, E. Electric–Magnetic Duality, Monopole Condensation, and Confinement in N = 2 Supersymmetric Yang–Mills Theory. Nucl. Phys. B 1994, 426, 19–52, Erratum in Nucl. Phys. B 1994, 430, 485–486. [Google Scholar] [CrossRef]
- Cardy, J. Scaling and Renormalization in Statistical Physics; Cambridge Lecture Notes in Physics, Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Halpin-Healy, T.; Zhang, Y.C. Kinetic Roughening Phenomena, Stochastic Growth, Directed Polymers and All That. Phys. Rep. 1995, 254, 215–414. [Google Scholar] [CrossRef]
- Kardar, M.; Parisi, G.; Zhang, Y.C. Dynamic Scaling of Growing Interfaces. Phys. Rev. Lett. 1986, 56, 889–892. [Google Scholar] [CrossRef]
- Sinai, Y. The Limiting Behavior of a One-Dimensional Random Walk in a Random Medium. Theory Probab. Its Appl. 1983, 27, 256–268. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Attwell, D.; Laughlin, S.B. An Energy Budget for Signalling in the Grey Matter of the Brain. J. Cereb. Blood Flow Metab. 2001, 21, 1133–1145. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- Kubo, R.; Toda, M.; Hashitsume, N. Statistical Physics II: Nonequilibrium Statistical Mechanics; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 1991; Volume 31. [Google Scholar]
- Frisch, U. Turbulence: The Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Davidson, P. Turbulence: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2004. [Google Scholar] [CrossRef]
- Emanuel, K. Divine Wind: The History and Science of Hurricanes; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Grand, R.J.J.; Kawata, D.; Cropper, M. The dynamics of stars around spiral arms. Mon. Not. R. Astron. Soc. 2012, 421, 1529–1538. [Google Scholar] [CrossRef]
- Rivera, M.K.; Aluie, H.; Ecke, R.E. The direct enstrophy cascade of two-dimensional soap film flows. Phys. Fluids 2014, 26, 055105. [Google Scholar] [CrossRef]
- Sethna, J.P. Statistical Mechanics: Entropy, Order Parameters, and Complexity; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Zaanen, J. Why the temperature is high. Nat. Phys. 2004, 430, 512–513. [Google Scholar] [CrossRef]
- Hollands, S.; Wald, R.M. Quantum fields in curved spacetime. Phys. Rep. 2015, 574, 1–35. [Google Scholar] [CrossRef]
- Hartnoll, S.A.; Mackenzie, A.P. Colloquium: Planckian dissipation in metals. Rev. Mod. Phys. 2022, 94, 041002. [Google Scholar] [CrossRef]
- Lucas, A. Hydrodynamic transport in strongly coupled disordered quantum field theories. New J. Phys. 2015, 17, 113007. [Google Scholar] [CrossRef]
- Lucas, A.; Fong, K.C. Hydrodynamics of Electrons in Graphene. J. Phys. Condens. Matter 2018, 30, 053001. [Google Scholar] [CrossRef] [PubMed]
- Orenstein, J. Ultrafast Spectroscopy of Quantum Materials. Phys. Today 2012, 65, 44–50. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum Phase Transitions, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Kitaev, A. Anyons in an Exactly Solved Model and Beyond. Ann. Phys. 2006, 321, 2–111. [Google Scholar] [CrossRef]
- Zschocke, F.; Vojta, M. Physical Properties of the Kitaev Model: Bond Disorder, Spin Excitations, and Spin Dynamics. Phys. Rev. B 2015, 92, 014403. [Google Scholar] [CrossRef]
- Xu, S.; Sun, Z.-Z.; Wang, K.; Li, H.; Zhu, Z.; Dong, H.; Deng, J.; Zhang, X.; Chen, J.; Wu, Y.; et al. Non-Abelian braiding of Fibonacci anyons with a superconducting processor. Nat. Phys. 2024, 20, 1469–1475. [Google Scholar] [CrossRef]
- Fendley, P. Free fermions in disguise. J. Phys. A 2014, 47, 075001. [Google Scholar] [CrossRef]
- Takayanagi, T. Modular Invariance of Strings on PP-Waves with RR-flux. J. High Energy Phys. 2003, 2002, 022. [Google Scholar] [CrossRef]
- Sandberg, A.; Awoga, O.A.; Black-Schaffer, A.M.; Holmvall, P. Josephson effect in a Fibonacci quasicrystal. Phys. Rev. B 2024, 110, 104513. [Google Scholar] [CrossRef]
- Sen, A. Dyon-Monopole Bound States, Self-Duality and Duality Symmetry. Phys. Rev. B 1994, 73, 3297–3300. [Google Scholar] [CrossRef][Green Version]
- Hartman, T.; Strominger, A. Central Charge for AdS2 Quantum Gravity. J. High Energy Phys. 2009, 2009, 026. [Google Scholar] [CrossRef]
- Bousso, R. The Holographic Principle. Rev. Mod. Phys. 2002, 74, 825–874. [Google Scholar] [CrossRef]
- Padmanabhan, T.; Paranjape, A. Entropy of null surfaces and dynamics of spacetime. Phys. Rev. D 2007, 75, 064004. [Google Scholar] [CrossRef]
- Bianconi, G. Gravity from entropy. Phys. Rev. D 2025, 111, 066001. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Einasto, J.; Hütsi, G.; Kuutma, T.; Einasto, M. Correlation function: Biasing and fractal properties of the cosmic web. Astron. Astrophys. 2020, 640, A47. [Google Scholar] [CrossRef]
- Sachdev, S. Strange Metals and Black Holes: Insights From the Sachdev-Ye-Kitaev Model. Oxf. Res. Encycl. Phys. 2025. [CrossRef]
- Meschke, K.; Guichard, W.; Pekola, J.P. Single-Mode Heat Conduction by Photons. Nature 2006, 444, 187–190. [Google Scholar] [CrossRef]
- Carter, R.W. Conjugacy classes in the weyl group. Compos. Math. 1972, 25, 1–59. [Google Scholar]
- Freedman, M.; Nayak, C.; Shtengel, K. A Route to a Non-Abelian Topological Phase. Phys. Rev. Lett. 2005, 94, 066401. [Google Scholar] [CrossRef]
- Niu, M.Y.; Chuang, I.L.; Shapiro, J.H. Hardware-efficient bosonic quantum error correction Based on Symmetry Operators. Phys. Rev. A. 2018, 97, 032323. [Google Scholar] [CrossRef]
- Raichle, M.E.; Gusnard, D.A. Appraising the brain’s energy budget. Proc. Natl. Acad. Sci. USA 2002, 99, 10237–10239. [Google Scholar] [CrossRef] [PubMed]
- Harris, J.J.; Jolivet, R.; Attwell, D. Synaptic energy use and supply. Neuron 2012, 75, 762–777. [Google Scholar] [CrossRef] [PubMed]
- Roopun, A.K.; Kramer, M.A.; Carracedo, L.M.; Kaiser, M.; Davies, C.H.; Traub, R.D.; Kopell, N.J.; Whittington, M.A. Temporal Interactions between Cortical Rhythms. Front. Neurosci. 2008, 2, 145–154. [Google Scholar] [CrossRef] [PubMed]
- Pletzer, B.; Kerschbaum, H.; Klimesch, W. When frequencies never synchronize: The golden mean and the resting EEG. Brain Res. 2010, 1335, 91–102. [Google Scholar] [CrossRef]
- Smith, T.G.J.; Lange, G.D.; Marks, W.B. Fractal methods and results in cellular morphology—Dimensions, lacunarity and multifractals. J. Neurosci. Methods 1996, 69, 123–136. [Google Scholar] [CrossRef]
- Partanen, M.; Tulkki, J. Gravity generated by four one-dimensional unitary gauge symmetries and the Standard Model. Rep. Prog. Phys. 2025, 88, 057802. [Google Scholar] [CrossRef]
- Unruh, W.G. Experimental black-hole evaporation? Phys. Rev. Lett. 1981, 46, 1351–1353. [Google Scholar] [CrossRef]
| Coxeter Class | Onsager | ||||
|---|---|---|---|---|---|
| (Lorentzian) | ✓ | × | symm. (decoupled) | 1 | |
| (self-dual line) | ✓ | × | antisymm. | ||
| (Golden Point) | ✓ | ✓ | antisymm. | ||
| (self-dual line) | ✓ | × | antisymm. | ||
| (Gaussian–diff.) | ✓ | × | symmetric | 2 | |
| KPZ/Lévy (nonlinear) | × | × | symmetric | − | |
| Sinai creep (1D, quenched) | × | × | non-modular | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz, A. Dynamic Balance: A Thermodynamic Principle for the Emergence of the Golden Ratio in Open Non-Equilibrium Steady States. Entropy 2025, 27, 745. https://doi.org/10.3390/e27070745
Ruiz A. Dynamic Balance: A Thermodynamic Principle for the Emergence of the Golden Ratio in Open Non-Equilibrium Steady States. Entropy. 2025; 27(7):745. https://doi.org/10.3390/e27070745
Chicago/Turabian StyleRuiz, Alejandro. 2025. "Dynamic Balance: A Thermodynamic Principle for the Emergence of the Golden Ratio in Open Non-Equilibrium Steady States" Entropy 27, no. 7: 745. https://doi.org/10.3390/e27070745
APA StyleRuiz, A. (2025). Dynamic Balance: A Thermodynamic Principle for the Emergence of the Golden Ratio in Open Non-Equilibrium Steady States. Entropy, 27(7), 745. https://doi.org/10.3390/e27070745






