Abstract
Photonic quantum metrology has emerged as a leading platform for quantum-enhanced precision measurements. By taking advantage of quantum resources such as entanglement, quantum metrology enables parameter estimation with sensitivities surpassing classical limits. In this review, we describe the basic tools and recent experimental progress in the determination of an optical phase with a precision that may exceed the shot-noise limit, enabled by the use of nonclassical states of light. We review the state of the art and discuss the challenges and trends in the field.
1. Introduction
Quantum mechanics has transformed our understanding of nature, introducing counterintuitive phenomena such as superposition and entanglement. These quantum features offer opportunities not only for foundational science but also for practical applications. Among these, quantum metrology has emerged as a powerful approach to achieving precision measurements that outperform classical strategies. In recent years, quantum technologies have reached an unprecedented pace of development, with quantum metrology playing a central role in this revolution. By designing protocols that exploit nonclassical resources, quantum metrology enables enhanced estimation of physical parameters, pushing measurement sensitivity beyond the classical bounds.
The applications of quantum metrology are vast and diverse, ranging from gravitational-wave detection [1,2] to quantum imaging of biological samples [3,4,5,6,7,8,9,10]. A particularly promising platform for implementing these advancements is photonic quantum metrology, which harnesses quantum states of light to probe physical systems [11,12,13,14]. Photons are ideal carriers of quantum information: they are robust, easily manipulated, and can be generated and detected with high precision using current technologies.
At the heart of quantum metrology lies the task of parameter estimation, where an unknown physical quantity is encoded into a quantum probe and then inferred from measurements on the output state [15]. Within this framework, phase estimation stands out as one of the most relevant problems [16]. The measurement of an optical phase is fundamental, as it can be directly related to various experimental quantities, such as distance, birefringence, angle, or sample concentration [1,2,17,18,19,20,21,22,23]. To detect a phase shift, optical interferometers are essential. The parameter is encoded during the evolution of the probe, and the information is extracted through appropriate measurements at the output.
Evaluating the uncertainty associated with parameter estimation is a central issue. The variance of an estimator quantifies the sensitivity of the measurement protocol. According to the Central Limit Theorem (CLT), repeating a measurement M times results in a variance scaling as defining the bound for classical strategies, known as the shot-noise limit (SNL). However, quantum resources such as entanglement and squeezing enable more precise estimations. Quantum metrology can reach the Heisenberg limit (HL), the ultimate bound set by quantum mechanics, with a variance scaling as [24,25].
Traditional phase estimation techniques rely on interferometers such as the Mach–Zehnder or Michelson interferometers fed by classical states of light, such as coherent states, which are limited by the SNL. Quantum-enhanced approaches use resources like N00N states [24,25], which offer superior phase sensitivity. Notably, recent experimental breakthroughs have demonstrated that quantum advantages can still be realized in the presence of realistic imperfections, such as photon loss or partial distinguishability [13]. This progress highlights the practical viability of quantum metrology and its transition from idealized theoretical models to robust, real-world applications.
As research advances, photonic quantum metrology is evolving from a proof-of-principle domain into a versatile tool for ultra-precise sensing, laying the groundwork for next-generation technologies in quantum communication and quantum imaging [6,7,26,27].
In this review, we explore the fundamental concepts of photonic quantum metrology, with a particular emphasis on phase estimation. Rather than attempting to provide an exhaustive overview of the entire research field, our goal is to offer a clear and accessible introduction to the core theoretical tools and experimental techniques that support this area. We focus specifically on implementations using photonic systems, which are among the most mature and versatile platforms for quantum-enhanced precision measurements. By highlighting essential principles and representative experiments, we aim to provide readers, especially those new to the field, with a solid foundation for understanding how quantum resources can be harnessed to surpass classical limits in optical metrology. For those interested in a deeper understanding, a wide collection of reviews is available in the field of photonic quantum metrology [6,12,13,14,28,29], interferometry [30,31,32] and quantum information [33,34,35], to name a few.
This review is organized as follows: in Section 2, we present the general framework for quantum parameter estimation, addressing the key concepts to evaluate the precision in the estimation process: the Cramér–Rao bound and the Fisher information, both in a classical and in a quantum scenario. We then focus on the particular problem of phase estimation in Section 3. In Section 4, we go through the current state of the art and trends in photonic implementations for phase estimation. Finally, in Section 5, we analyze the open problems and perspectives in the field.
2. Theoretical Tools for Parameter Estimation
The main goal of an estimation process is to obtain a numerical value (an estimate) of an unknown parameter from a set of measurement outcomes. In a general scheme, the parameter is encoded in a probe state, and information about it is retrieved after performing a measurement. We will restrict our description to quantum systems, where probe states are described by density matrices, and the encoding of the parameter is realized by a quantum operation. The general procedure for quantum parameter estimation can be described following four basic steps (sketched in Figure 1) [13]:

Figure 1.
Quantum estimation process. An initial probe state is prepared and sent to interact with a quantum operation that encodes the parameter to be estimated. Measurements are then performed on the output state, and an estimator is inferred from the measured probability distributions.
- (i)
- preparation of an initial quantum state , the so-called probe state;
- (ii)
- encoding of the parameter to be estimated into a quantum state by means of a quantum operation applied to the initial state;
- (iii)
- performing a measurement on the final state that is, in general, given by a positive-operator valued measure (POVM) with possible outcomes ;
- (iv)
- obtaining an estimator from the probabilities of the outcomes that are, according to the Born rule, .
An estimator is, therefore, a function of the observations, which are random variables. Different methods can be used to find an estimator, according to two fundamentally different approaches: frequentist vs. Bayesian [36]. In the frequentist approach, probabilities are viewed as the long-run frequency of events. Parameters are considered fixed but unknown quantities, and inference is based on the sampling distribution of the estimator [37]. In the Bayesian approach, probabilities are viewed as a measure of knowledge about an event. Parameters are treated as random variables with prior distributions that represent prior knowledge about the parameter. These distributions are updated with the observations to form posterior distributions, reflecting the updated knowledge [38].
We will focus particularly on maximum likelihood estimation (MLE), which is a fundamental frequentist method used to estimate the parameters of a model by maximizing the likelihood function. This approach involves identifying the values of the parameters that make the observed data more probable under the assumed model.
2.1. Maximum Likelihood Estimation
The likelihood function (LF) of N independent measurements , for a given parameter is defined as
where is the conditional probability of obtaining the measurement , given . The LF, therefore, represents the joint conditional probability of obtaining outcomes , given the parameter . The ML estimator is given by the parameter value that maximizes the likelihood function, obtained by evaluating the first and second derivatives with respect to (if is twice differentiable):
It is often convenient to work with the log-likelihood function, given that both and its logarithm attain their maxima for the same parameter value, such that
Estimators are evaluated based on several properties to ensure that they provide reliable and accurate estimates. The MLE procedure provides good estimators in the sense that these satisfy key properties:
- Consistency: the estimator converges (in probability) to the true value of the parameter;
- Unbiasedness: the mean value of the estimator’s distribution is equal to the true value of the parameter;
- Efficiency: the estimator has the smallest possible variance among all unbiased estimators.
As the sample size increases, the distribution of the ML estimators approaches a normal distribution, with a mean equal to the true parameter value. Given the efficiency condition, MLEs achieve the lowest possible variance among all unbiased estimators. However, there is a fundamental limit given by the Cramér–Rao bound (CRB), which provides a lower bound on the variance [39,40]. In what follows, we will first focus on the classical description of the CRB and then extend it to the quantum framework.
2.2. Cramér–Rao Bound and Fisher Information
The Cramér–Rao bound sets a lower bound to the variance of any estimator, given by the following fundamental inequality:
with the Fisher information (FI) given by
For unbiased estimators, where , the CRB reduces to the inverse of the Fisher information. In addition, an estimator that saturates the CRB is said to be efficient. In the limit of a large number of measurements, the MLE produces an efficient estimator whenever there is one.
We will derive the inequality in Equation (4) following a few simple steps. We start from the definition of the mean value of the estimator, given by
Let us now calculate the partial derivative of this expression with respect to the parameter :
the range of x is independent of , such that .
On the other hand, given that , when calculating the partial derivative of this expression with respect to , we obtain
Finally, we take the square of this expression and apply the Cauchy–Schwartz inequality, such that
After rearranging the terms and identifying the variance and the FI, this expression is exactly Equation (4).
2.3. Quantum Cramér–Rao Bound and Quantum Fisher Information
From the description of parameter estimation given at the beginning of Section 2, the variance of the estimator depends on the chosen probe state, the quantum operation that encodes the parameter, and the performed measurement. For fixed probe states, quantum mechanics sets an upper bound to the CRB by maximizing the Fisher information over all possible measurements. The quantum Fisher information (QFI) is then defined as
which, in turn, defines the quantum Cramér–Rao bound (QCRB) such that for unbiased estimators, the following inequality holds
The QFI, therefore, sets the ultimate limit on precision [41,42]. To find this bound, let us express Equation (5) using the Born rule for the probabilities and assume a single repetition such that . Then,
where we have used the Symmetric Logarithmic Derivative (SLD) Hermitian operator for the last step, defined as the solution to the equation
The expression in Equation (13) can be upper-bounded using the following inequalities:
- , where the equality holds if and only if is a real number :
- where we used the Cauchy–Schwarz inequality , taking and . The equality holds if and only if
Combining the above expressions with Equation (13), we obtain
where, by definition, the QFI does not depend on the POVM. For the equality to hold, conditions expressed in Equations (15) and (16) must be fulfilled for a given POVM. It can be shown that an optimal measurement exists, built from the eigenstates of [34,43].
For the particular case of unitary transformations such that (where H is a Hermitian operator), the QFI does not depend on the parameter to be estimated. Moreover, for initial pure sates , it has a simple expression:
with . A complete and detailed description of QFI and its explicit forms can be found in [33,34,35].
Essentially, for a given probe state, quantum metrology defines the ultimate limit in precision, and the goal is to determine the measurement such that . This involves finding the POVM that ensures that the FI of the process matches the QFI associated with the given probe state.
3. Phase Estimation
The phase of an electromagnetic field is a relative quantity that describes the relationship between different points in the wave. A phase shift expresses the relative displacement between a reference and the position within the cycle of the wave. Quantum mechanics does not account for an interferometric phase Hermitian operator; hence, the task of experimentally obtaining a reliable value for the phase at the quantum level is hard and indirect and relies on estimations rather than on measurements [16,34,44]. The estimation method consists of decoding the phase from the quantum measurement of a relevant observable in a suitable setup. The quintessential experimental arrangement for this estimation is an interferometer, where the (optical or atomic) phase is encoded into a probe state, which traverses the apparatus via two or more alternate modes or paths. Upon the coherent recombination of these modes, the phase can be estimated from the measurement of the interference pattern present in the selected observable. An efficient interferometry protocol for phase estimation requires an adequate choice of several instances: the input probe state; the transformation suffered within the interferometer, the specific observable that is measured, and the estimator that, given the available resources, allows inferring the phase shift with the minimum attainable uncertainty (Figure 2). In a classical scenario, where the apparatus is probed with uncorrelated photons, this uncertainty is bounded by the SNL: , where is the number of independent (identical) measurements and n is the mean photon number of the input state on each measurement.
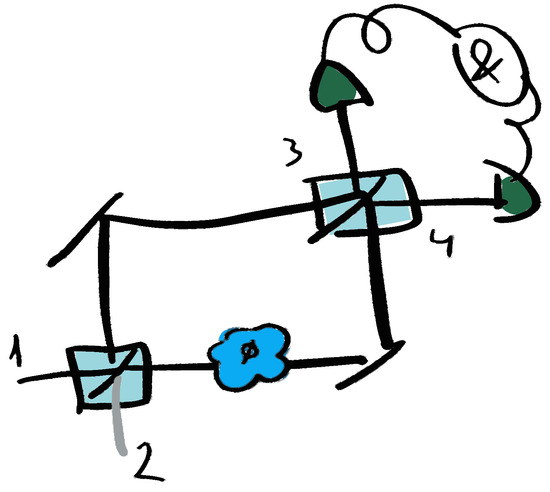
Figure 2.
A schematic representation of a Mach–Zehnder interferometer for phase estimation in a classic framework. A probe state is sent to the apparatus through inputs 1 and 2, where a two-mode superposition state is created at the first beamsplitter. This state interacts with a phase encoding mechanism. The phase can be estimated from measurements of a specific observable at outputs 3 and 4 after the coherent recombination of the two modes at the output beamsplitter.
The SNL on the phase sensitivity of a single-port interferometer is actually a quantum limit imposed by fluctuations of the vacuum state present at the unused port of the input beamsplitter. In fact, the source of such fluctuations “has nothing to do with fluctuations in [the input photon state]; rather, it is an intrinsic property of a standard interferometer” [45]: the same limit applies to Fock states, which have zero photon number dispersion. However, the idle port of the interferometer can be transformed from foe to friend through the proper selection of the photon state injected into it: with a smart selection of both input states, the so-called Heisenberg limit can be reached. Such a limit requires the engineering of nonclassical states, as originally suggested by Caves [46], and bounds the phase fluctuations by .
3.1. Interferometric Setups
The Mach–Zehnder interferometer (MZI) represents the prototype two-mode interferometer. It is composed of two balanced beam splitters (equal transmission and reflection coefficients) and two mirrors arranged in such a way that a single light source is split into two coherent beams that travel different paths before being recombined (as shown in Figure 2). A phase shift may occur between the two arms, resulting in an interference pattern that depends on the relative phase difference between the two paths.
The unitary map describing the phase encoding by an MZI with input modes a and b [47,48,49,50] is given by
with . The annihilation and creation operators , and satisfy the usual bosonic commutation relations .
The ubiquitous Michelson interferometer has a comparable behavior; its double-pass configuration and particular geometry have rendered it especially suitable for implementing sophisticated experiments in high-sensitivity phase estimation, as required for gravitational wave detection [1,2,46]. Also, common-path interferometers such as the displaced Sagnac, taking advantage of its intrinsic stability, have been used to achieve high-visibility interference fringes with multi-photon states [51].
3.2. Optimized Probe States
Clearly, at the core of the strategy behind overcoming the SNL is the preparation of specific input states that could lead to a quantum advantage in the phase estimation task. It must be kept in mind that it is fairly easy to scale up the photon number (intensity) for a classical coherent state: in the Advanced Laser Interferometer Gravitational-wave Observatory (Advanced LIGO, [1]), the optical power inside the interferometer is increased above 100 kW, which corresponds to roughly photons per second. At the shot noise limit, this implies a phase dispersion for a classical photonic state as small as . Nevertheless, many applications where low light levels are mandatory, such as phase imaging of fragile biological samples and living organisms or inspection of photosensitive surfaces, can fully exploit the quantum advantage obtained by working at or close to the Heisenberg limit.
An additional word of attention is required here regarding the losses in real experimental conditions, a point that cannot be neglected when the goal is to push the precision limits of parameter estimation in phase estimation: Davidovich et al. demonstrated that, independently of the initial state of the probe, the phase uncertainty scales as (Heisenberg limit) as long as the losses within the interferometer are kept below ; for larger loss, the scaling of the uncertainty recovers the law [52]. In other words, on average, the total loss must not exceed one photon, regardless of the total photon number of the input state. Again, this condition favors the quantum phase estimation approach in applications where weak light levels are required.
3.2.1. Coherent States
The classical interferometry experiment that leads to the SNL precision corresponds to a coherent state of light entering through one port of the input beamsplitter in an MZI, whereas vacuum fluctuations are present at the other port. Coherent states are defined as eigenstates of the annihilation operator with eigenvalue : . The mean value and variance of the photon number operator are given by . Then, for the input state , the phase uncertainty scales as the SNL: [13].
3.2.2. Squeezed States
Several engineered (i.e., nonclassical) input states have been used to obtain a quantum advantage in the bibliography. As a natural choice, a zero dispersion state may be used instead of a coherent state, that is, an n-photon Fock state: . However, as Caves demonstrated in [45], such an input state gives no quantum advantage since it is still affected by the vacuum state fluctuations that are present at the unused input. Indeed, in [46], he showed that a reduction in the phase dispersion could be obtained if a “squeezed vacuum” state was used at the second input: , where S is the squeeze operator and the complex squeeze parameter [53]. This is an improvement with respect to the SNL, although dispersion still scales with the inverse of the square root of n: Precision on the phase determination is bounded by . By using squeezed states as input on large Michelson interferometers, gravitational wave detectors such as LIGO, VIRGO, and GEO demonstrated the best sensitivity ever achieved, showing an improvement factor of up to 10 better than the initial classical laser-interferometer observatory [18,54,55]. Further enhancement could be observed [56] by using frequency-dependent squeezing [57,58,59,60,61].
3.2.3. Twin Fock States
The class of so-called twin Fock states can be used to obtain precision approaching the Heisenberg limit: these are non-entangled product states of two Fock states, one on each input of the interferometer. When the two-photon states are indistinguishable, modal entanglement is obtained with the input beamsplitter. In particular, for the symmetric state, (even total photon number ) and the “almost symmetrical” state (odd total photon number ), the precision on the phase estimation is bounded by and , respectively [62]. Symmetric twin Fock states have been extensively investigated and experimentally implemented to obtain a quantum advantage in the phase determination, showing the above asymptotic scaling on the precision [48,63,64,65,66,67].
3.2.4. N00N States
Of special interest is the particular case of a family of states that can be engineered by exploiting photon indistinguishability: these are the so-called N00N states, prepared not as input states but as path-entangled states inside the Mach–Zehnder interferometer:
For n = 2, this state can be obtained in a deterministic and straightforward manner as the result of a Hong–Ou–Mandel (HOM) interference between two indistinguishable single photons entering separate input ports of a 50:50 beamsplitter [68]. When two identical photons enter different input ports of a balanced beamsplitter, they exit together through the same output port, canceling the coincidence probability (that is, the probability of finding a photon at each output arm), creating a bunching effect, as shown schematically in Figure 3.
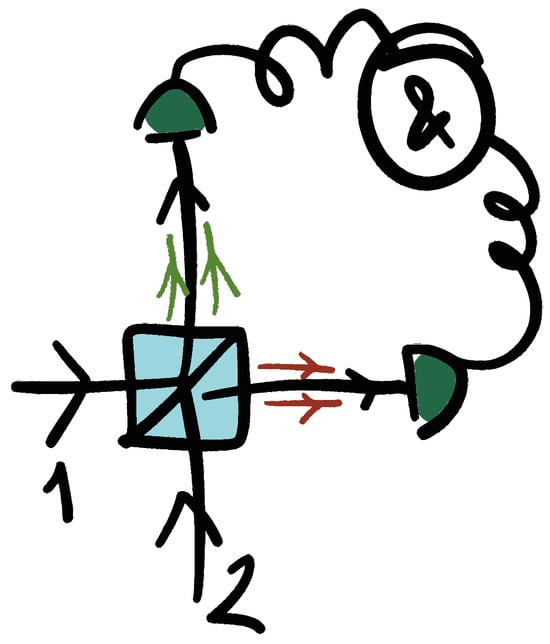
Figure 3.
Scheme for HOM interference. Two identical single photons enter ports 1 and 2 of a beamsplitter and exit bunched together through one or the other output port, illustrated by the double green and red arrows.
For larger photon numbers, however, preparation is not trivial, and experimental results with such states have been obtained using post-selection at the output [22,51,69,70,71,72,73,74]. Up to date, deterministic generation of N00N states with photon number remains an open challenge. When used as a probe for phase estimation, N00N states allow us to obtain a precision strictly limited by the Heisenberg bound: [75]. However, the quantum advantage in precision achievable with multi-photon N00N states is extremely sensitive to photon losses [76]. Another drawback to the use of N00N states is the requirement of photon-number-resolving detectors. Current trends in the field show a preference for alternative probing schemes to achieve metrological advantage [77,78].
4. Photonic Schemes for Phase Estimation: State of the Art
Traditional approaches often struggle with scalability and sensitivity to noise. In recent years, efforts have been made to design probe states to improve precision even in the presence of noise, going beyond N00N states, whose practical use is hindered by difficulties in generation and extreme sensitivity to losses [79]. Many theoretical scenarios have been studied in which quantum strategies can exceed classical limits despite noise [80,81,82,83]. These theoretical foundations and the technological advances in photon detectors [84] have enabled experiments to go beyond the SNL.
The work of Slussarenko et al. in [85] marks a pivotal advance in quantum metrology. This work presents the first experimental demonstration surpassing the shot-noise limit using photonic quantum states without any post-selection or correction for losses and inefficiencies. Previous experiments achieved sub-SNL sensitivity by correcting for system losses or discarding imperfect data. Slussarenko et al. overcame this by employing ultra-efficient photon sources and superconducting nanowire single-photon detectors (SNSPDs), enabling genuine quantum-enhanced measurements without post-processing adjustments.
In [77] the authors build upon Slussarenko et al.’s work by combining nonlinear interferometry with stimulated emission of squeezed light. They report a 5.8-fold enhancement over the SNL, surpassing ideal five-photon N00N state precision, and emphasize scalability and robustness in their approach.
The use of two-mode squeezed vacuum states [13,86] and multi-photon-subtracted twin beams [87] has also been shown to outperform traditional N00N state-based schemes. A deterministic phase estimation scheme based on a source of Gaussian squeezed vacuum states and high-efficiency homodyne detection has also been shown to overcome the performance of a pure N00N state protocol [78]. This scheme significantly surpasses the shot noise limit and even beats the conventional Heisenberg limit by a constant factor, given by the use of squeezed states without a definite number of photons.
In theory, perfect photon indistinguishability is essential for quantum-enhanced measurements. Challenging this notion, sources of partially distinguishable photons can still achieve sensitivities beyond the classical shot-noise limit (SNL) [88,89,90]. Other works have explored non-Markovian environments to preserve quantum advantages in metrology [91], using multi-photon states and multiple passes through the system under test to demonstrate scalability and robustness in quantum sensing [92], and generating entanglement with ancillary qubits to enhance the precision in phase estimation [93,94]. A recent review discusses the potential of vortex beams—beams carrying orbital angular momentum (OAM)—in quantum metrology, suggesting that their integration could lead to reduced noise and improved precision in measurements [95].
An alternative type of interferometer, theoretically introduced by Yurke et al. in 1986 as a promise for obtaining a similar performance to that of the traditional interferometers with fewer optical elements [47], replaces the passive beamsplitters with nonlinear optical devices (parametric amplifiers) which act as two-mode squeezers. These interferometers are called SU(1,1), while the standard instruments belong to the SU(2) category. The nomenclature corresponds to the names of the Special Unitary (SU) groups that mathematically describe each interferometer family. By using SU(1,1) interferometers, one can usually obtain a gain in the signal-to-noise ratio amplification, which leads to improved precision. Such an effect is accomplished via the three main characteristics of SU(1,1) interferometers that distinguish them from traditional interferometers, which are (i) the exclusive type of coherent superpositions of waves that are only allowed by second- and higher-order wave mixing in nonlinear optical devices, (ii) the ability to generate quantum entanglement—and consequently, correlations in quantum noise—that can be canceled depending on the selected interference conditions, and (iii) the immunity to losses that is guaranteed by the amplified noise levels that exceed the quantum noise level in parametric processes. The review of this class of interferometers is beyond the scope of this work, although it is worth noticing that the advent of such accessible improvement in sensitivity has led to a substantial amount of work in the last quindecennium, both from the theoretical [96,97,98,99,100,101,102,103,104,105,106,107,108,109] and the experimental [110,111,112,113,114,115,116,117,118,119,120] points of view.
The problem of phase estimation inside an optical interferometer can be mapped to a quantum circuit [121]. This approach offers high versatility, allowing the exploration of different input probe states and detection schemes. In a recent work [122] an unknown phase shift in the presence of photon loss was simulated in a quantum circuit for four different definite photon-number states of light, each containing six photons, and using photon-number-resolving detectors. This scheme relies on a Bayesian approach, as described in [123].
Given that optical sensors based on quantum states of light are susceptible to noise and imperfections that affect their performance, the estimation of multiple parameters is relevant for a wide range of sensors. The simultaneous estimation of several parameters in a single experiment opens the door to more complex measurement devices, which aim to estimate multiple parameters related to the object or sample of interest [29,124,125,126,127,128,129,130]. The optimal strategy entails a trade-off between the achievable precisions of the various parameters. This trade-off requires an optimization strategy to determine both the best quantum state and the optimal measurement that allows reaching the ultimate precision limit in multiparameter quantum metrology.
Recently, in the Noisy Intermediate-Scale Quantum (NISQ) era of quantum computing [131], variational quantum algorithms (VQAs) [132] have emerged as a promising solution to noise sensitivity, offering flexibility and adaptability in optimizing quantum circuits for specific tasks. For the case of single-parameter metrology, VQAs have been used to optimize quantum probes [133,134,135]. Meyer et al. [136] introduced a variational toolbox for quantum multiparameter estimation, laying the theoretical foundation for the application of VQAs in metrology. Recent works have explored deep reinforcement learning for quantum multiparameter estimation, highlighting the potential of machine learning techniques to optimize quantum sensors [137]. Hybrid quantum-classical frameworks have also been introduced [138], as well as protocols combining quantum optical nonlinearities with VQAs [139], aimed at enhancing multiparameter quantum metrology and integrating variational quantum algorithms with photonic systems.
5. Conclusions and Perspectives
The recent experimental advances in photonic quantum metrology highlight both the maturity of current photonic platforms and the growing feasibility of real-world quantum sensors.
Despite these advances, several limitations remain that must be addressed before photonic quantum metrology can be widely used in practical technologies. A primary challenge is scalability: generating and maintaining highly entangled multi-photon states remains technically demanding, particularly as the photon number increases [140]. Photon loss, mode mismatch, and detector inefficiencies continue to affect performance in larger-scale implementations. Moreover, many protocols still rely on post-selection or operate under idealized assumptions that limit their applicability in noisy environments. Recently, the emerging field of non-Hermitian quantum metrology has achieved promising progress in realizing non-Hermitian systems at the quantum level for metrology and quantum estimation tasks [141,142,143,144].
Another challenge lies in the robustness and adaptability of quantum metrological schemes. While quantum advantage has been shown in specific, controlled settings, generalizing these results to multiparameter estimation, real-time sensing, or distributed quantum networks remains an open problem. Additionally, quantum resource quantification and the identification of the optimal trade-off between metrological precision and experimental complexity are still active areas of research.
Advances in integrated photonics and detector technologies [145,146,147] and in machine-learning-assisted protocols [136,148,149,150] are likely to mitigate many current limitations. In the near term, we can expect improvements in the implementation of quantum-enhanced metrological protocols using imperfect but realistic resources. Photonic quantum metrology will continue to contribute to the development of quantum technologies, with increasing applications to quantum communication, computation, and precision navigation. The integration of metrology with emerging quantum networks and the transition toward fully autonomous, adaptive quantum sensors represent exciting directions for future research and development.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Aasi, J.; Abbott, B.; Abbott, R.; Abbott, T.; Abernathy, M.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. Advanced ligo. Class. Quantum Gravity 2015, 32, 074001. [Google Scholar]
- Abadie, J.; Abbott, B.; Abbott, R.; Abbott, T.; Abernathy, M.; Adams, C.; Adhikari, R.; Affeldt, C.; Allen, B.; Allen, G.; et al. A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 2011, 7, 962–965. [Google Scholar]
- Cox, G. Optical Imaging Techniques in Cell Biology; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Taylor, M.A.; Bowen, W.P. Quantum metrology and its application in biology. Phys. Rep. 2016, 615, 1–59. [Google Scholar] [CrossRef]
- Mauranyapin, N.; Madsen, L.; Taylor, M.; Waleed, M.; Bowen, W. Evanescent single-molecule biosensing with quantum-limited precision. Nat. Photonics 2017, 11, 477–481. [Google Scholar] [CrossRef]
- Defienne, H.; Bowen, W.P.; Chekhova, M.; Lemos, G.B.; Oron, D.; Ramelow, S.; Treps, N.; Faccio, D. Advances in quantum imaging. Nat. Photonics 2024, 18, 1024–1036. [Google Scholar] [CrossRef]
- Genovese, M. Real applications of quantum imaging. J. Opt. 2016, 18, 073002. [Google Scholar] [CrossRef]
- Ortolano, G.; Paniate, A.; Boucher, P.; Napoli, C.; Soman, S.; Pereira, S.F.; Ruo-Berchera, I.; Genovese, M. Quantum enhanced non-interferometric quantitative phase imaging. Light Sci. Appl. 2023, 12, 171. [Google Scholar] [CrossRef] [PubMed]
- Couteau, C.; Barz, S.; Durt, T.; Gerrits, T.; Huwer, J.; Prevedel, R.; Rarity, J.; Shields, A.; Weihs, G. Applications of single photons in quantum metrology, biology and the foundations of quantum physics. Nat. Rev. Phys. 2023, 5, 354–363. [Google Scholar] [CrossRef]
- Schirhagl, R.; Chang, K.; Loretz, M.; Degen, C.L. Nitrogen-vacancy centers in diamond: Nanoscale sensors for physics and biology. Annu. Rev. Phys. Chem. 2014, 65, 83–105. [Google Scholar] [CrossRef]
- Dowling, J.P.; Seshadreesan, K.P. Quantum optical technologies for metrology, sensing, and imaging. J. Light. Technol. 2015, 33, 2359–2370. [Google Scholar] [CrossRef]
- Pirandola, S.; Bardhan, B.R.; Gehring, T.; Weedbrook, C.; Lloyd, S. Advances in photonic quantum sensing. Nat. Photonics 2018, 12, 724–733. [Google Scholar] [CrossRef]
- Polino, E.; Valeri, M.; Spagnolo, N.; Sciarrino, F. Photonic quantum metrology. AVS Quantum Sci. 2020, 2, 024703. [Google Scholar]
- Barbieri, M. Optical quantum metrology. PRX Quantum 2022, 3, 010202. [Google Scholar] [CrossRef]
- Helstrom, C.W. Quantum detection and estimation theory. J. Stat. Phys. 1969, 1, 231–252. [Google Scholar] [CrossRef]
- Barnett, S.M.; Pegg, D.T. Phase in quantum optics. J. Phys. A Math. Gen. 1986, 19, 3849. [Google Scholar] [CrossRef]
- Sahota, J.; Quesada, N.; James, D.F. Physical resources for optical phase estimation. Phys. Rev. A 2016, 94, 033817. [Google Scholar] [CrossRef]
- Grote, H.; Danzmann, K.; Dooley, K.L.; Schnabel, R.; Slutsky, J.; Vahlbruch, H. First long-term application of squeezed states of light in a gravitational-wave observatory. Phys. Rev. Lett. 2013, 110, 181101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quantum Gravity 2014, 32, 024001. [Google Scholar] [CrossRef]
- Aso, Y.; Michimura, Y.; Somiya, K.; Ando, M.; Miyakawa, O.; Sekiguchi, T.; Tatsumi, D.; Yamamoto, H.; Collaboration), K. Interferometer design of the KAGRA gravitational wave detector. Phys. Rev. D Part. Fields Gravit. Cosmol. 2013, 88, 043007. [Google Scholar] [CrossRef]
- Rozema, L.A.; Bateman, J.D.; Mahler, D.H.; Okamoto, R.; Feizpour, A.; Hayat, A.; Steinberg, A.M. Scalable spatial superresolution using entangled photons. Phys. Rev. Lett. 2014, 112, 223602. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Bromley, T.R.; Huang, Y.F.; Cao, H.; Lv, W.M.; Liu, B.H.; Li, C.F.; Guo, G.C.; Cianciaruso, M.; Adesso, G. Demonstrating quantum coherence and metrology that is resilient to transversal noise. Phys. Rev. Lett. 2019, 123, 180504. [Google Scholar] [CrossRef] [PubMed]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-enhanced measurements: Beating the standard quantum limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef] [PubMed]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Moreau, P.A.; Toninelli, E.; Gregory, T.; Padgett, M.J. Imaging with quantum states of light. Nat. Rev. Phys. 2019, 1, 367–380. [Google Scholar] [CrossRef]
- Slussarenko, S.; Pryde, G.J. Photonic quantum information processing: A concise review. Appl. Phys. Rev. 2019, 6, 041303. [Google Scholar]
- Berchera, I.R.; Degiovanni, I.P. Quantum imaging with sub-Poissonian light: Challenges and perspectives in optical metrology. Metrologia 2019, 56, 024001. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzański, R.; Jarzyna, M.; Kołodyński, J. Quantum limits in optical interferometry. Prog. Opt. 2015, 60, 345–435. [Google Scholar]
- Genovese, M. Experimental quantum enhanced optical interferometry. AVS Quantum Sci. 2021, 3, 044702. [Google Scholar] [CrossRef]
- Jin, R.B.; Zeng, Z.Q.; You, C.; Yuan, C. Quantum interferometers: Principles and applications. Prog. Quantum Electron. 2024, 96, 100519. [Google Scholar]
- Paris, M.G. Quantum estimation for quantum technology. Int. J. Quantum Inf. 2009, 7, 125–137. [Google Scholar] [CrossRef]
- Pezze, L.; Smerzi, A. Quantum theory of phase estimation. In Atom Interferometry; IOS Press: Amsterdam, The Netherlands, 2014; pp. 691–741. [Google Scholar]
- Tóth, G.; Apellaniz, I. Quantum metrology from a quantum information science perspective. J. Phys. A Math. Theor. 2014, 47, 424006. [Google Scholar] [CrossRef]
- Li, Y.; Pezzè, L.; Gessner, M.; Ren, Z.; Li, W.; Smerzi, A. Frequentist and Bayesian quantum phase estimation. Entropy 2018, 20, 628. [Google Scholar] [CrossRef] [PubMed]
- Lane, A.S.; Braunstein, S.L.; Caves, C.M. Maximum-likelihood statistics of multiple quantum phase measurements. Phys. Rev. A 1993, 47, 1667. [Google Scholar] [CrossRef] [PubMed]
- Kramer, S.C.; Sorenson, H.W. Bayesian parameter estimation. IEEE Trans. Autom. Control 1988, 33, 217–222. [Google Scholar] [CrossRef]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1922, 222, 309–368. [Google Scholar]
- Rao, C.R. Information and the accuracy attainable in the estimation of statistical parameters. In Breakthroughs in Statistics: Foundations and Basic Theory; Springer: New York, NY, USA, 1992; pp. 235–247. [Google Scholar]
- Helstrom, C.W. Minimum mean-squared error of estimates in quantum statistics. Phys. Lett. A 1967, 25, 101–102. [Google Scholar] [CrossRef]
- Holevo, A.S. Probabilistic and Statistical Aspects of Quantum Theory; Springer Science & Business Media: Berlin, Germany, 2011; Volume 1. [Google Scholar]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439. [Google Scholar] [CrossRef]
- Lynch, R. The quantum phase problem: A critical review. Phys. Rep. 1995, 256, 367–436. [Google Scholar] [CrossRef]
- Caves, C.M. Quantum-mechanical radiation-pressure fluctuations in an interferometer. Phys. Rev. Lett. 1980, 45, 75. [Google Scholar] [CrossRef]
- Caves, C.M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693. [Google Scholar] [CrossRef]
- Yurke, B.; McCall, S.L.; Klauder, J.R. SU (2) and SU (1, 1) interferometers. Phys. Rev. A 1986, 33, 4033. [Google Scholar] [CrossRef]
- Kim, T.; Pfister, O.; Holland, M.J.; Noh, J.; Hall, J.L. Influence of decorrelation on Heisenberg-limited interferometry with quantum correlated photons. Phys. Rev. A 1998, 57, 4004. [Google Scholar] [CrossRef]
- Sanders, B.; Milburn, G. Optimal quantum measurements for phase estimation. Phys. Rev. Lett. 1995, 75, 2944. [Google Scholar] [CrossRef] [PubMed]
- Pezzé, L.; Smerzi, A. Phase sensitivity of a Mach-Zehnder interferometer. Phys. Rev. A At. Mol. Opt. Phys. 2006, 73, 011801. [Google Scholar] [CrossRef]
- Nagata, T.; Okamoto, R.; O’brien, J.L.; Sasaki, K.; Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 2007, 316, 726–729. [Google Scholar] [CrossRef]
- Escher, B.M.; de Matos Filho, R.L.; Davidovich, L. General framework for estimating the ultimate precision limit in noisy quantum-enhanced metrology. Nat. Phys. 2011, 7, 406–411. [Google Scholar] [CrossRef]
- Loudon, R. The Quantum Theory of Light; OUP Oxford: Oxford, UK, 2000. [Google Scholar]
- Tse, M.; Yu, H.; Kijbunchoo, N.; Fernandez-Galiana, A.; Dupej, P.; Barsotti, L.; Blair, C.; Brown, D.; Dwyer, S.e.; Effler, A.; et al. Quantum-enhanced advanced LIGO detectors in the era of gravitational-wave astronomy. Phys. Rev. Lett. 2019, 123, 231107. [Google Scholar] [CrossRef] [PubMed]
- Acernese, F.; Agathos, M.; Aiello, L.; Allocca, A.; Amato, A.; Ansoldi, S.; Antier, S.; Arène, M.; Arnaud, N.; Ascenzi, S.; et al. Increasing the astrophysical reach of the advanced virgo detector via the application of squeezed vacuum states of light. Phys. Rev. Lett. 2019, 123, 231108. [Google Scholar]
- Capote, E.; Jia, W.; Aritomi, N.; Nakano, M.; Xu, V.; Abbott, R.; Abouelfettouh, I.; Adhikari, R.; Ananyeva, A.; Appert, S.; et al. Advanced LIGO detector performance in the fourth observing run. Phys. Rev. D 2025, 111, 062002. [Google Scholar]
- Evans, M.; Barsotti, L.; Kwee, P.; Harms, J.; Miao, H. Realistic filter cavities for advanced gravitational wave detectors. Phys. Rev. D Part. Fields Gravit. Cosmol. 2013, 88, 022002. [Google Scholar] [CrossRef]
- McCuller, L.; Whittle, C.; Ganapathy, D.; Komori, K.; Tse, M.; Fernandez-Galiana, A.; Barsotti, L.; Fritschel, P.; MacInnis, M.; Matichard, F.; et al. Frequency-dependent squeezing for advanced LIGO. Phys. Rev. Lett. 2020, 124, 171102. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Aritomi, N.; Capocasa, E.; Leonardi, M.; Eisenmann, M.; Guo, Y.; Polini, E.; Tomura, A.; Arai, K.; Aso, Y.; et al. Frequency-dependent squeezed vacuum source for broadband quantum noise reduction in advanced gravitational-wave detectors. Phys. Rev. Lett. 2020, 124, 171101. [Google Scholar] [CrossRef]
- Polini, E. Broadband quantum noise reduction via frequency dependent squeezing for Advanced Virgo Plus. Phys. Scr. 2021, 96, 084003. [Google Scholar] [CrossRef]
- Ganapathy, D.; Jia, W.; Nakano, M.; Xu, V.; Aritomi, N.; Cullen, T.; Kijbunchoo, N.; Dwyer, S.; Mullavey, A.; McCuller, L.; et al. Broadband quantum enhancement of the LIGO detectors with frequency-dependent squeezing. Phys. Rev. X 2023, 13, 041021. [Google Scholar] [CrossRef]
- Lang, M.D.; Caves, C.M. Optimal quantum-enhanced interferometry. Phys. Rev. A 2014, 90, 025802. [Google Scholar] [CrossRef]
- Campos, R.; Gerry, C.C.; Benmoussa, A. Optical interferometry at the Heisenberg limit with twin Fock states and parity measurements. Phys. Rev. A 2003, 68, 023810. [Google Scholar] [CrossRef]
- Sun, F.; Liu, B.; Gong, Y.; Huang, Y.; Ou, Z.; Guo, G. Experimental demonstration of phase measurement precision beating standard quantum limit by projection measurement. Europhys. Lett. 2008, 82, 24001. [Google Scholar] [CrossRef]
- Meiser, D.; Holland, M. Robustness of Heisenberg-limited interferometry with balanced Fock states. New J. Phys. 2009, 11, 033002. [Google Scholar] [CrossRef]
- Hou, L.L.; Wang, S.; Xu, X.F. Optical enhanced interferometry with two-mode squeezed twin-Fock states and parity detection. Chin. Phys. B 2020, 29, 034203. [Google Scholar] [CrossRef]
- Volkoff, T.J.; Ryu, C. Globally optimal interferometry with lossy twin Fock probes. Front. Phys. 2024, 12, 1369786. [Google Scholar] [CrossRef]
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044. [Google Scholar] [CrossRef]
- Kok, P.; Lee, H.; Dowling, J.P. Creation of large-photon-number path entanglement conditioned on photodetection. Phys. Rev. A 2002, 65, 052104. [Google Scholar] [CrossRef]
- Walther, P.; Pan, J.W.; Aspelmeyer, M.; Ursin, R.; Gasparoni, S.; Zeilinger, A. De Broglie wavelength of a non-local four-photon state. Nature 2004, 429, 158–161. [Google Scholar] [CrossRef]
- Cable, H.; Dowling, J.P. Efficient Generation of Large Number-Path Entanglement Using Only Linear Optics and Feed-Forward. Phys. Rev. Lett. 2007, 99, 163604. [Google Scholar] [CrossRef] [PubMed]
- Afek, I.; Ambar, O.; Silberberg, Y. High-NOON states by mixing quantum and classical light. Science 2010, 328, 879–881. [Google Scholar] [CrossRef]
- Wang, X.L.; Chen, L.K.; Li, W.; Huang, H.L.; Liu, C.; Chen, C.; Luo, Y.H.; Su, Z.E.; Wu, D.; Li, Z.D.; et al. Experimental ten-photon entanglement. Phys. Rev. Lett. 2016, 117, 210502. [Google Scholar] [CrossRef]
- Thekkadath, G.; Mycroft, M.; Bell, B.; Wade, C.; Eckstein, A.; Phillips, D.; Patel, R.; Buraczewski, A.; Lita, A.; Gerrits, T.; et al. Quantum-enhanced interferometry with large heralded photon-number states. NPJ Quantum Inf. 2020, 6, 89. [Google Scholar] [CrossRef]
- Yurke, B. Input states for enhancement of fermion interferometer sensitivity. Phys. Rev. Lett. 1986, 56, 1515. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzanski, R.; Dorner, U.; Smith, B.; Lundeen, J.; Wasilewski, W.; Banaszek, K.; Walmsley, I. Quantum phase estimation with lossy interferometers. Phys. Rev. A At. Mol. Opt. Phys. 2009, 80, 013825. [Google Scholar] [CrossRef]
- Qin, J.; Deng, Y.H.; Zhong, H.S.; Peng, L.C.; Su, H.; Luo, Y.H.; Xu, J.M.; Wu, D.; Gong, S.Q.; Liu, H.L.; et al. Unconditional and robust quantum metrological advantage beyond N00N states. Phys. Rev. Lett. 2023, 130, 070801. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, J.A.; Neergaard-Nielsen, J.S.; Gehring, T.; Andersen, U.L. Deterministic quantum phase estimation beyond N00N states. Phys. Rev. Lett. 2023, 130, 123603. [Google Scholar] [CrossRef]
- Dowling, J.P. Quantum optical metrology–the lowdown on high-N00N states. Contemp. Phys. 2008, 49, 125–143. [Google Scholar] [CrossRef]
- Chaves, R.; Brask, J.; Markiewicz, M.; Kołodyński, J.; Acín, A. Noisy metrology beyond the standard quantum limit. Phys. Rev. Lett. 2013, 111, 120401. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzański, R.; Maccone, L. Using entanglement against noise in quantum metrology. Phys. Rev. Lett. 2014, 113, 250801. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Zhang, M.; Preskill, J.; Jiang, L. Achieving the Heisenberg limit in quantum metrology using quantum error correction. Nat. Commun. 2018, 9, 78. [Google Scholar] [CrossRef]
- Albarelli, F.; Rossi, M.A.; Tamascelli, D.; Genoni, M.G. Restoring Heisenberg scaling in noisy quantum metrology by monitoring the environment. Quantum 2018, 2, 110. [Google Scholar] [CrossRef]
- Marsili, F.; Verma, V.B.; Stern, J.A.; Harrington, S.; Lita, A.E.; Gerrits, T.; Vayshenker, I.; Baek, B.; Shaw, M.D.; Mirin, R.P.; et al. Detecting single infrared photons with 93% system efficiency. Nat. Photonics 2013, 7, 210–214. [Google Scholar] [CrossRef]
- Slussarenko, S.; Weston, M.M.; Chrzanowski, H.M.; Shalm, L.K.; Verma, V.B.; Nam, S.W.; Pryde, G.J. Unconditional violation of the shot-noise limit in photonic quantum metrology. Nat. Photonics 2017, 11, 700–703. [Google Scholar] [CrossRef]
- You, C.; Hong, M.; Bierhorst, P.; Lita, A.E.; Glancy, S.; Kolthammer, S.; Knill, E.; Nam, S.W.; Mirin, R.P.; Magaña-Loaiza, O.S.; et al. Scalable multiphoton quantum metrology with neither pre-nor post-selected measurements. Appl. Phys. Rev. 2021, 8, 041406. [Google Scholar] [CrossRef]
- Eaton, M.; Nehra, R.; Win, A.; Pfister, O. Heisenberg-limited quantum interferometry with multiphoton-subtracted twin beams. Phys. Rev. A 2021, 103, 013726. [Google Scholar] [CrossRef]
- Birchall, P.M.; Sabines-Chesterking, J.; O’Brien, J.L.; Cable, H.; Matthews, J.C. Beating the shot-noise limit with sources of partially-distinguishable photons. arXiv 2016, arXiv:1603.00686. [Google Scholar]
- Knoll, L.T.; Bosyk, G.M.; López Grande, I.H.; Larotonda, M.A. Role of indistinguishability in interferometric phase estimation. Phys. Rev. A 2019, 100, 062125. [Google Scholar] [CrossRef]
- Knoll, L.T.; Bosyk, G.M. Simultaneous quantum estimation of phase and indistinguishability in a two-photon interferometer. J. Opt. Soc. Am. B 2023, 40, C67–C72. [Google Scholar] [CrossRef]
- Bai, K.; Peng, Z.; Luo, H.G.; An, J.H. Retrieving ideal precision in noisy quantum optical metrology. Phys. Rev. Lett. 2019, 123, 040402. [Google Scholar] [CrossRef]
- Liu, L.Z.; Zhang, Y.Z.; Li, Z.D.; Zhang, R.; Yin, X.F.; Fei, Y.Y.; Li, L.; Liu, N.L.; Xu, F.; Chen, Y.A.; et al. Distributed quantum phase estimation with entangled photons. Nat. Photonics 2021, 15, 137–142. [Google Scholar] [CrossRef]
- Wang, K.; Wang, X.; Zhan, X.; Bian, Z.; Li, J.; Sanders, B.C.; Xue, P. Entanglement-enhanced quantum metrology in a noisy environment. Phys. Rev. A 2018, 97, 042112. [Google Scholar] [CrossRef]
- Sbroscia, M.; Gianani, I.; Mancino, L.; Roccia, E.; Huang, Z.; Maccone, L.; Macchiavello, C.; Barbieri, M. Experimental ancilla-assisted phase estimation in a noisy channel. Phys. Rev. A 2018, 97, 032305. [Google Scholar] [CrossRef]
- Cheng, M.; Jiang, W.; Guo, L.; Li, J.; Forbes, A. Metrology with a twist: Probing and sensing with vortex light. Light Sci. Appl. 2025, 14, 4. [Google Scholar]
- Plick, W.N.; Dowling, J.P.; Agarwal, G.S. Coherent-light-boosted, sub-shot noise, quantum interferometry. New J. Phys. 2010, 12, 083014. [Google Scholar] [CrossRef]
- Ou, Z. Enhancement of the phase-measurement sensitivity beyond the standard quantum limit by a nonlinear interferometer. Phys. Rev. A At. Mol. Opt. Phys. 2012, 85, 023815. [Google Scholar] [CrossRef]
- Marino, A.M.; Corzo Trejo, N.; Lett, P.D. Effect of losses on the performance of an SU (1, 1) interferometer. Phys. Rev. A At. Mol. Opt. Phys. 2012, 86, 023844. [Google Scholar] [CrossRef]
- Li, D.; Yuan, C.H.; Ou, Z.; Zhang, W. The phase sensitivity of an SU (1, 1) interferometer with coherent and squeezed-vacuum light. New J. Phys. 2014, 16, 073020. [Google Scholar] [CrossRef]
- Sparaciari, C.; Olivares, S.; Paris, M.G. Gaussian-state interferometry with passive and active elements. Phys. Rev. A 2016, 93, 023810. [Google Scholar] [CrossRef]
- Li, D.; Gard, B.T.; Gao, Y.; Yuan, C.H.; Zhang, W.; Lee, H.; Dowling, J.P. Phase sensitivity at the Heisenberg limit in an SU (1, 1) interferometer via parity detection. Phys. Rev. A 2016, 94, 063840. [Google Scholar] [CrossRef]
- Gong, Q.K.; Hu, X.L.; Li, D.; Yuan, C.H.; Ou, Z.; Zhang, W. Intramode-correlation-enhanced phase sensitivities in an SU (1, 1) interferometer. Phys. Rev. A 2017, 96, 033809. [Google Scholar] [CrossRef]
- Guo, L.L.; Yu, Y.F.; Zhang, Z.M. Improving the phase sensitivity of an SU (1, 1) interferometer with photon-added squeezed vacuum light. Opt. Express 2018, 26, 29099–29109. [Google Scholar] [CrossRef]
- Ou, Z.; Li, X. Quantum SU (1, 1) interferometers: Basic principles and applications. APL Photonics 2020, 5, 080902. [Google Scholar] [CrossRef]
- Salykina, D.; Khalili, F. Sensitivity of quantum-enhanced interferometers. Symmetry 2023, 15, 774. [Google Scholar] [CrossRef]
- Santandrea, M.; Luo, K.H.; Stefszky, M.; Sperling, J.; Herrmann, H.; Brecht, B.; Silberhorn, C. Lossy SU (1, 1) interferometers in the single-photon-pair regime. Quantum Sci. Technol. 2023, 8, 025020. [Google Scholar] [CrossRef]
- Kang, Q.; Zhao, Z.; Zhao, T.; Liu, C.; Hu, L. Phase estimation via a number-conserving operation inside a SU (1, 1) interferometer. Phys. Rev. A 2024, 110, 022432. [Google Scholar] [CrossRef]
- Ferreri, A.; Wang, H.; Nori, F.; Wilhelm, F.K.; Bruschi, D.E. Quantum heat engine based on quantum interferometry: The SU (1, 1) Otto cycle. Phys. Rev. Res. 2025, 7, 013284. [Google Scholar] [CrossRef]
- Jiang, T.; Zhao, Z.; Kang, Q.; Zhao, T.; Zhou, N.; Liu, C.; Hu, L. Phase sensitivity for an SU (1, 1) interferometer via multiphoton subtraction at the output port. Opt. Express 2025, 33, 19191–19204. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Liu, C.; Zhou, Z.; Ou, Z.; Zhang, W. Realization of a nonlinear interferometer with parametric amplifiers. Appl. Phys. Lett. 2011, 99, 011110. [Google Scholar] [CrossRef]
- Hudelist, F.; Kong, J.; Liu, C.; Jing, J.; Ou, Z.; Zhang, W. Quantum metrology with parametric amplifier-based photon correlation interferometers. Nat. Commun. 2014, 5, 3049. [Google Scholar] [CrossRef] [PubMed]
- Linnemann, D.; Strobel, H.; Muessel, W.; Schulz, J.; Lewis-Swan, R.J.; Kheruntsyan, K.V.; Oberthaler, M.K. Quantum-enhanced sensing based on time reversal of nonlinear dynamics. Phys. Rev. Lett. 2016, 117, 013001. [Google Scholar] [CrossRef] [PubMed]
- Lemieux, S.; Manceau, M.; Sharapova, P.R.; Tikhonova, O.V.; Boyd, R.W.; Leuchs, G.; Chekhova, M.V. Engineering the frequency spectrum of bright squeezed vacuum via group velocity dispersion in an SU (1, 1) interferometer. Phys. Rev. Lett. 2016, 117, 183601. [Google Scholar] [CrossRef]
- Manceau, M.; Leuchs, G.; Khalili, F.; Chekhova, M. Detection loss tolerant supersensitive phase measurement with an SU (1, 1) interferometer. Phys. Rev. Lett. 2017, 119, 223604. [Google Scholar] [CrossRef]
- Anderson, B.E.; Gupta, P.; Schmittberger, B.L.; Horrom, T.; Hermann-Avigliano, C.; Jones, K.M.; Lett, P.D. Phase sensing beyond the standard quantum limit with a variation on the SU (1, 1) interferometer. Optica 2017, 4, 752–756. [Google Scholar] [CrossRef]
- Gupta, P.; Schmittberger, B.L.; Anderson, B.E.; Jones, K.M.; Lett, P.D. Optimized phase sensing in a truncated SU (1, 1) interferometer. Opt. Express 2018, 26, 391–401. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Jia, J.; Chen, J.; Ou, Z.; Zhang, W. Absolute sensitivity of phase measurement in an SU (1, 1) type interferometer. Opt. Lett. 2018, 43, 1051–1054. [Google Scholar] [CrossRef]
- Frascella, G.; Mikhailov, E.; Takanashi, N.; Zakharov, R.; Tikhonova, O.; Chekhova, M. Wide-field SU (1, 1) interferometer. Optica 2019, 6, 1233–1236. [Google Scholar] [CrossRef]
- Du, W.; Kong, J.; Bao, G.; Yang, P.; Jia, J.; Ming, S.; Yuan, C.H.; Chen, J.; Ou, Z.; Mitchell, M.W.; et al. SU (2)-in-SU (1, 1) nested interferometer for high sensitivity, loss-tolerant quantum metrology. Phys. Rev. Lett. 2022, 128, 033601. [Google Scholar] [CrossRef] [PubMed]
- Huo, N.; Cui, L.; Zhang, Y.; Zhao, W.; Guo, X.; Ou, Z.; Li, X. Measurement-dependent erasure of distinguishability for the observation of interference in an unbalanced SU (1, 1) interferometer. PRX Quantum 2022, 3, 020313. [Google Scholar] [CrossRef]
- Lee, H.; Kok, P.; Dowling, J.P. A quantum Rosetta stone for interferometry. J. Mod. Opt. 2002, 49, 2325–2338. [Google Scholar] [CrossRef]
- Najafi, P.; Naeimi, G.; Saeidian, S. Phase estimation of definite photon number states by using quantum circuits. Sci. Rep. 2023, 13, 15268. [Google Scholar] [CrossRef]
- Zhou, B.; Guha, S.; Gagatsos, C.N. Bayesian quantum phase estimation with fixed photon states. Quantum Inf. Process. 2024, 23, 366. [Google Scholar] [CrossRef]
- Roccia, E.; Cimini, V.; Sbroscia, M.; Gianani, I.; Ruggiero, L.; Mancino, L.; Genoni, M.G.; Ricci, M.A.; Barbieri, M. Multiparameter approach to quantum phase estimation with limited visibility. Optica 2018, 5, 1171–1176. [Google Scholar] [CrossRef]
- Crowley, P.J.; Datta, A.; Barbieri, M.; Walmsley, I.A. Tradeoff in simultaneous quantum-limited phase and loss estimation in interferometry. Phys. Rev. A 2014, 89, 023845. [Google Scholar] [CrossRef]
- Birchall, P.M.; Allen, E.J.; Stace, T.M.; O’Brien, J.L.; Matthews, J.C.; Cable, H. Quantum Optical Metrology of Correlated Phase and Loss. Phys. Rev. Lett. 2020, 124, 140501. [Google Scholar] [CrossRef] [PubMed]
- Vidrighin, M.D.; Donati, G.; Genoni, M.G.; Jin, X.M.; Kolthammer, W.S.; Kim, M.S.; Datta, A.; Barbieri, M.; Walmsley, I.A. Joint estimation of phase and phase diffusion for quantum metrology. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Albarelli, F.; Barbieri, M.; Genoni, M.G.; Gianani, I. A perspective on multiparameter quantum metrology: From theoretical tools to applications in quantum imaging. Phys. Lett. A 2020, 384, 126311. [Google Scholar]
- Markiewicz, M.; Pandit, M.; Laskowski, W. Simultaneous estimation of multiple phases in generalised Mach–Zehnder interferometer. Sci. Rep. 2021, 11, 15669. [Google Scholar] [CrossRef]
- Szczykulska, M.; Baumgratz, T.; Datta, A. Multi-parameter quantum metrology. Adv. Phys. X 2016, 1, 621–639. [Google Scholar] [CrossRef]
- Brooks, M. Beyond quantum supremacy: The hunt for useful quantum computers. Nature 2019, 574, 19–22. [Google Scholar] [CrossRef]
- McClean, J.R.; Romero, J.; Babbush, R.; Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 2016, 18, 023023. [Google Scholar] [CrossRef]
- Kaubruegger, R.; Silvi, P.; Kokail, C.; van Bijnen, R.; Rey, A.M.; Ye, J.; Kaufman, A.M.; Zoller, P. Variational spin-squeezing algorithms on programmable quantum sensors. Phys. Rev. Lett. 2019, 123, 260505. [Google Scholar] [CrossRef]
- Koczor, B.; Endo, S.; Jones, T.; Matsuzaki, Y.; Benjamin, S.C. Variational-state quantum metrology. New J. Phys. 2020, 22, 083038. [Google Scholar] [CrossRef]
- Yang, X.; Thompson, J.; Wu, Z.; Gu, M.; Peng, X.; Du, J. Probe optimization for quantum metrology via closed-loop learning control. npj Quantum Inf. 2020, 6, 62. [Google Scholar] [CrossRef]
- Meyer, J.J.; Borregaard, J.; Eisert, J. A variational toolbox for quantum multi-parameter estimation. npj Quantum Inf. 2021, 7, 89. [Google Scholar] [CrossRef]
- Cimini, V.; Valeri, M.; Polino, E.; Piacentini, S.; Ceccarelli, F.; Corrielli, G.; Spagnolo, N.; Osellame, R.; Sciarrino, F. Deep reinforcement learning for quantum multiparameter estimation. Adv. Photonics 2023, 5, 016005. [Google Scholar] [CrossRef]
- Cimini, V.; Valeri, M.; Piacentini, S.; Ceccarelli, F.; Corrielli, G.; Osellame, R.; Spagnolo, N.; Sciarrino, F. Variational quantum algorithm for experimental photonic multiparameter estimation. npj Quantum Inf. 2024, 10, 26. [Google Scholar] [CrossRef]
- Muñoz de las Heras, A.; Tabares, C.; Schneider, J.T.; Tagliacozzo, L.; Porras, D.; González-Tudela, A. Photonic quantum metrology with variational quantum optical nonlinearities. Phys. Rev. Res. 2024, 6, 013299. [Google Scholar] [CrossRef]
- Chu, Y.; Li, X.; Cai, J. Strong quantum metrological limit from many-body physics. Phys. Rev. Lett. 2023, 130, 170801. [Google Scholar] [CrossRef]
- Lau, H.K.; Clerk, A.A. Fundamental limits and non-reciprocal approaches in non-Hermitian quantum sensing. Nat. Commun. 2018, 9, 4320. [Google Scholar] [CrossRef]
- Zhang, M.; Sweeney, W.; Hsu, C.W.; Yang, L.; Stone, A.; Jiang, L. Quantum noise theory of exceptional point amplifying sensors. Phys. Rev. Lett. 2019, 123, 180501. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Meng, Y.; Tang, J.S.; Xu, X.Y.; Wang, Y.T.; Yin, P.; Ke, Z.J.; Liu, W.; Li, Z.P.; Yang, Y.Z.; et al. Experimental investigation of quantum PT-enhanced sensor. Phys. Rev. Lett. 2020, 125, 240506. [Google Scholar] [CrossRef]
- Yu, X.; Zhao, X.; Li, L.; Hu, X.M.; Duan, X.; Yuan, H.; Zhang, C. Toward Heisenberg scaling in non-Hermitian metrology at the quantum regime. Sci. Adv. 2024, 10, eadk7616. [Google Scholar] [CrossRef]
- Esmaeil Zadeh, I.; Chang, J.; Los, J.W.; Gyger, S.; Elshaari, A.W.; Steinhauer, S.; Dorenbos, S.N.; Zwiller, V. Superconducting nanowire single-photon detectors: A perspective on evolution, state-of-the-art, future developments, and applications. Appl. Phys. Lett. 2021, 118, 190502. [Google Scholar] [CrossRef]
- Becher, C.; Gao, W.; Kar, S.; Marciniak, C.D.; Monz, T.; Bartholomew, J.G.; Goldner, P.; Loh, H.; Marcellina, E.; Goh, K.E.J.; et al. 2023 roadmap for materials for quantum technologies. Mater. Quantum Technol. 2023, 3, 012501. [Google Scholar] [CrossRef]
- Labonté, L.; Alibart, O.; D’Auria, V.; Doutre, F.; Etesse, J.; Sauder, G.; Martin, A.; Picholle, É.; Tanzilli, S. Integrated photonics for quantum communications and metrology. PRX Quantum 2024, 5, 010101. [Google Scholar] [CrossRef]
- Lumino, A.; Polino, E.; Rab, A.S.; Milani, G.; Spagnolo, N.; Wiebe, N.; Sciarrino, F. Experimental phase estimation enhanced by machine learning. Phys. Rev. Appl. 2018, 10, 044033. [Google Scholar] [CrossRef]
- Huang, J.; Zhuang, M.; Zhou, J.; Shen, Y.; Lee, C. Quantum metrology assisted by machine learning. Adv. Quantum Technol. 2025, 8, 2300329. [Google Scholar] [CrossRef]
- Xu, H.; Xiao, T.; Huang, J.; He, M.; Fan, J.; Zeng, G. Toward Heisenberg Limit without Critical Slowing Down via Quantum Reinforcement Learning. Phys. Rev. Lett. 2025, 134, 120803. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).