Abstract
We consider Onsager’s non-equilibrium thermodynamics from the perspective of the gradient flow in information geometry. Assuming Onsager’s reciprocal relations, we can regard his phenomenological equations as gradient-flow equations and develop two different gradient-flow models. We consider their features and their relations. Both models are applied to the ideal gas and van der Waals gas.
1. Introduction
In a closed thermal system evolving from a non-equilibrium state that is not far from the equilibrium state, the thermodynamic entropic function can be expanded around the equilibrium state as
where each is an extensive variable, and then, we introduce the Ruppeiner metric [1]:
The components are positive definite and symmetric , if the is a smooth concave function, i.e., is convex. The entropy production rate can be described by
where
are the (conjugate) intensive variables, and are the thermodynamic fluxes of the variable . Onsager [2,3] expands the fluxes as the linear combinations of the thermodynamic forces:
which are known as Onsager’s phenomenological equations (OPE), the linear constitutive equations relating the fluxes and the forces with the condition that all when all . He assumes the coefficients to be symmetric, i.e.,
whose symmetry is known as the reciprocal relations. Several studies have been performed concerning the OPE, e.g., Doi [4,5] extensively studied Onsager’s variational principle in soft matter.
Our previous studies on the gradient flow [6,7,8] in information geometry (IG) [9] showed some relations to different fields such as thermodynamics [10], geometric optics [10,11], analytical mechanics, and general relativity [12,13]. Among them, we pointed out [13] that Equation (5) can be regarded as the gradient-flow equation:
with respect to the -potential function in IG, if we make the correspondence
where denotes the components of the Fisher matrix, and and are mutually dual affine coordinates in IG (see Appendix A for the details). In this correspondence, Onsager’s reciprocal relations (6) can be understood in IG as the symmetry of the metric , which is due to integrability.
Research focusing on the mathematical scientific structures common to different fields is at the heart of SUURI engineering. SUURI is a Japanese word, which consists of the two Kanji characters: SUU (numbers, or mathematical things) and RI (reason, theory, or laws). SUURI is often translated as mathematics or applied physics, but they are not appropriate, and there is no direct counterpart in other languages. It treats natural and social phenomena as SUURI phenomena and deals with theorems and laws, theorizing and applying them. We explore this type of research on Onsager’s phenomenological equations from the perspective of the gradient-flow equations in IG.
The rest of the paper is organized as follows. In Section 2, we first consider the simple extension of OPE (5) based on our studies on the gradient-flow equations in IG. In this simple model, which we call the natural gradient-flow model, Onsager’s phenomenological coefficients are replaced with the Hessian of the negative thermodynamic entropic function . In Section 3, we adopt the components of the inverse of the metric G on a space spanned by the thermodynamic extensive variables . We call this model the G-gradient-flow model. Section 4 applies these two models to the ideal gas and van der Waals gas. The final section is devoted to our conclusions. The basics of IG and the gradient flow in IG are summarized in Appendix A. Appendix B explains the connection to the cotangent bundle. This connection relates the flow in the tangent space to the flow in the cotangent space . Appendix C shows the expression of the Levi–Civita connection of a metric G obtained from Jacobi matrix J. Throughout the paper, we use Einstein’s summation convention for a repeated index.
2. Natural Gradient-Flow Model
Here, we extend OPE (5) based on our studies [10,11,12,13] of the gradient-flow equations in IG. We apply the methods for deriving some important relations in IG to Onsager’s non-equilibrium thermodynamics. From the correspondence (8), as our first model, we introduce the coefficients as
It is worth noting that the coefficients depend on X in general, whereas the coefficients in OPE (5) are independent. One readily confirms the reciprocal relations as follows.
Note that (9) means that the matrix is simultaneously a Jacobi matrix whose components are and a Hessian matrix of , similar to the distinct feature of the Fisher matrix g in IG (cf. (A4)).
We can introduce the total Legendre transform of the thermodynamic entropic function , i.e.,
Then, as the dual relation to (9), we have
Note that since the extensive variables and the intensive variables are related through (11), the coefficient can be regarded as a function of , i.e., . With the coefficients , as the gradient-flow equations corresponding to (A10) in IG, we propose
where denotes the thermodynamic force at a thermal state X. We assume that has a non-zero value in general, whereas in OPE (5), is assumed to be zero. Since in the fields of optimization and IG, the operator is called the natural gradient [8,14], we call this model characterized by (13) the natural gradient-flow model.
Next, by using (9) and (13), we have
Consequently, it follows the linearized differential equations:
which are the dual equations to (13). Note that, whereas the original Equation (13) is nonlinear in general, the linearized Equation (15) is readily solved. As is clear from the above derivation process, the key point is that the coefficients are the components of the Jacobi matrix.
By using (13), the entropy production rate (3) can be expressed as
where we introduced the dissipation function:
It is convenient to introduce the function :
which corresponds to (A13b) in IG.
The relation between the gradient flow in IG and Hamilton flow were pointed out in [6,7]. Boumuki and Noda [15] studied this relationship from the perspective of symplectic geometry. Chirco et al. [16] discussed Lagrangian and Hamiltonian dynamics in their non-parametric formalism. In our previous studies [11,13], we proposed the special type of Hamiltonian, which describes the gradient flow in IG. Based on the results, Equation (A12b) of the Hamilton flow in IG, we can construct the Hamiltonian:
whose Hamilton flow is equivalent to the natural gradient flow (13) and its dual (15). Indeed, Hamilton’s equations of motion are
The first equations are equivalent to (13). For the second equations, from (18), we have
Substituting this relation into the right-hand side in (20b), we obtain the linearized Equation (15).
One may wonder why the Hamiltonian (19) describes simultaneously the natural gradient-flow and its dual flow . In Appendix B, we explain the connection with the cotangent bundle. The connection relates the flow in the tangent space to the flow in the cotangent space. The Hamiltonian (19) is constant along all horizontal curves and satisfies the distinctive relation (A40), from which the flow in tangent space and the flow in cotangent space are related, as shown (A42), by the transport Equation (A17). Actually, the natural gradient flow Equation (13) and the dual linearized Equation (15) are related by
3. -Gradient-Flow Model
In the natural gradient-flow model, the coefficients are important ingredients and equivalent to the Hessian of , and also to the Ruppeiner metric [1]. However, in order to obtain the coefficients in (9), it requires an expression of the thermodynamic entropic function as a function of the extensive variables . It is difficult to determine an explicit expression of the thermodynamic entropy, in general. Thermodynamic systems are often characterized by a set of equations of thermodynamic state, which are experimentally determined. Vaz [17] provided the method for obtaining the metric G in the space spanned by the extensive variables from a set of equations of thermodynamic state. Here, we propose another model (G-gradient-flow equations) based on Vaz’s method.
Let us consider the coordinate transformation from to a function of X,
where are the components of the Jacobi matrix J. The meaning of each function is shown in (30). Similarly, the inverse relations are given by
The following relations are satisfied.
Thus, (23) describes the transformation rule from the frame consisting of the coordinate basis to the frame consisting of the basis . Their dual bases are and , respectively, and they satisfy
In general, equilibrium thermodynamic systems with n-independent macroscopic variables are completely described by the n-independent equations of state, which, in some cases, can be cast into the following form [10,17],
where is given in (4), and each is an independent constant. We can assign as the components in an orthogonal basis with the invertible constant diagonal matrix . In other words, the frame consisting of the orthogonal basis is Cartan’s moving frame. In general, the frame is non-orthogonal and is characterized by a metric tensor G, whose components are related by
The Jacobi matrix J relates the non-orthogonal frame with the local orthogonal frame as shown in (27).
Next, by inverting (27), we have
which implies that the entropic function is expressed in the form:
except for the constant of integration. In this way, when the thermodynamic equations of state are cast into the form (27), the thermodynamic entropic function is decomposed in the form (30), which consists of the sum of the product of a constant and a function .
The inner product in the orthogonal frame with a diagonal metric tensor and that in the non-orthogonal frame with a metric tensor G are related by
We can regard this relation as the generalized eikonal equation [10] (or Hamilton–Jacobi equation):
where
is a positive constant. From Equations (27) and (31), it follows that
It is worth noting that a Jacobi matrix is determined by components, whereas a Riemann metric has components. Consequently, the metric is obtained from a given Jacobi matrix as (28) and (34), whereas the converse is not possible in general, since for .
Now, we introduce the G-gradient-flow model as follows.
Note that, since is a diagonal matrix, is symmetric under exchanging of indices, i.e, the reciprocal relations are satisfied. Since the coefficient comprises the components of the metric , we call this model the G-gradient-flow model.
The entropic rate in this model is
From (29), we obtain the dual equations with respect to (35) as follows.
Combining (35) and (37), we have
which are the transport equations in (A17). As explained in Appendix B, the connection to the cotangent bundle relates the flow in the tangent space to the flow in the cotangent space . Hence, we find that plays a role of the connection to a cotangent bundle.
This relation () can be confirmed as follows. As shown in Appendix C, the coefficients of the Levi–Civita connection with respect to G are obtained in (A47), i.e.,
Then, the associated linear connection in (A25) becomes
4. Applications
Here, we apply the natural- and G-gradient-flow models to ideal gas and van der Waals gas.
4.1. Ideal Gas
Ideal gas is a simple model for a dilute gas, which is characterized by the following equations of state:
where u denotes the molar internal energy, v the molar volume, T the absolute temperature, P the pressure, R the gas constant, and the molar heat capacity at constant volume.
Now, the extensive variables are , and Equation (41) can be cast into the form (27):
where
where we set the conserved quantity and . From the definition of , the components are related by
from which we obtain
Then, from (30), the thermodynamic entropic function of the ideal gas model is expressed as
Setting and , we have
and
The matrix of the ideal gas model is
which is same as the metric in (47). Hence, there is no difference between the natural gradient-flow equations and G-gradient-flow equations for the ideal gas model. This is because this model is too simple. In contrast, as we show in the next subsection for van der Waals gas that both gradient-flow equations are different.
Now, we consider the gradient-flow Equation (13) for the ideal gas model.
Instead of solving these nonlinear differential equations, it is easier to solve their dual linear Equation (15):
where and are the equilibrium temperature and pressure, respectively. The solutions are
where and are the initial temperature and pressure, respectively. From the explicit expression of the entropic function in (46), we obtain
From these relations, we obtain . The relations between the extensive variables and the intensive variables are simple and separated. Consequently, we can readily obtain the solutions of the gradient-flow Equation (50) as
4.2. van der Waals Gas
Here, we consider the natural- and G-gradient-flow of the van der Waals gas model, which is characterized by the following equations of state:
where and are the real parameters. The first equation of (55) states the equipartition theorem, and the second equation states the equation of state by van der Waals [18]. The term accounts for the long-range attractive forces that increase the pressure, and the term accounts for the short-range repulsive forces that decrease the volume available to molecules. In the limit of , the van der Waals gas model reduces to the ideal gas model.
Now, we have the extensive variables , and the equations in (55) are cast into the form (27):
where
The components are
where
The thermodynamic entropic function can be obtained as
Setting and , we have
and
The non-zero elements of the Levi–Civita connection are
The straightforward calculations lead to all components of Riemann curvature tensor being zero; hence, the scalar curvature of the G-gradient-flow model is zero.
The dual linear Equation (15) for the van der Waals gas model is the same as that (51) for the ideal gas model. From the explicit expression (60) of the entropic function, we obtain
from which we obtain
Next, we consider the G-gradient-flow model. From (35) and (66), after straightforward but tedious calculations, we have
The dual Equation (37) for the van der Waals gas model is obtained by using
so that
In contrast to the case of the natural gradient-flow model, the second differential equation is nonlinear.
We performed a numerical analysis and obtained the numerical solutions. Figure 1 shows the contour plot of the entropic function (60) and the trajectories of the natural- and G-gradient flow starting from to the equilibrium state at . For the same parameters and the initial and final (equilibrium) states, the trajectories on of both models are plotted in Figure 2.
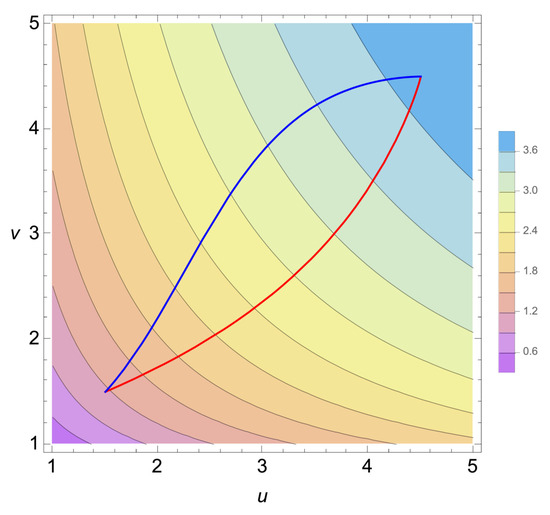
Figure 1.
The contour plot of the entropic function (60). The trajectories of the natural gradient flow (blue curve) and G-gradient flow (red curve) are also plotted. We set (a monoatomic gas), .
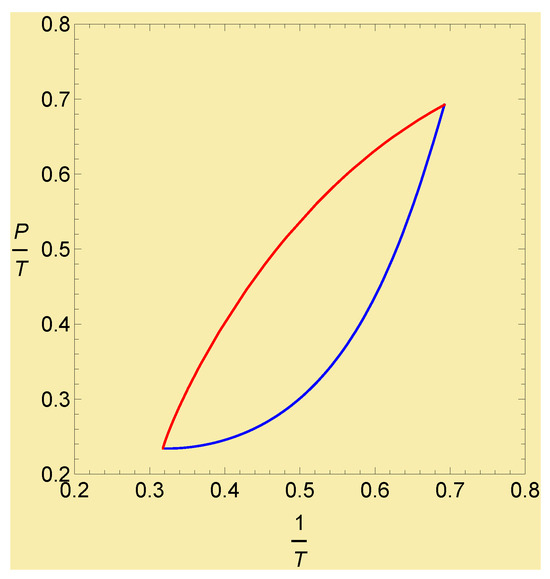
Figure 2.
The trajectories of the natural gradient flow (blue curve) and G-gradient flow (red curve). The parameters and the initial and final values of are same as in Figure 1.
5. Conclusions
We reconsidered Onsager’s non-equilibrium thermodynamics from the perspective of our previous studies [10,11,12,13] on the gradient flow in IG. As extensions of the OPE, we proposed the two different gradient-flow equations by replacing Onsager’s phenomenological coefficients with the Hessian of or with the inverse of the metric G in the space spanned by the thermodynamic extensive variables X. We call the former the natural gradient-flow model and the latter G-gradient-flow model. We considered both gradient-flow models and their relations. In a similar way to how IG works, where the natural gradient-flow equations are nonlinear in the extensive variables in general, the dual equations are linear in the intensive variables . We considered the relationship between both models and showed that the coefficients in the natural gradient-flow model are the (negative of) the connection coefficient in the cotangent bundle. For both models, the flow in tangent space and the flow in cotangent space are related by the transport equations as shown in (22) and in (38). We applied both models to the ideal gas and the van der Waals gas models. Since the ideal gas model is too simple, both models for the ideal gas are the same. In contrast, for the van der Waals gas model, both models are different. We performed numerical analysis and obtained the numerical solutions for the natural- and G-gradient flow equations. Their trajectories are clearly different as shown in Figure 1 and Figure 2; hence, they describe different thermodynamic processes.
Recently, Bravetti et al. [19] studied asymmetric relaxations within the context of IG. In order to obtain a gradient-flow equation within the context of IG, they used the gradient of the internal energy of a system, whereas in this work, the gradient of the entropic function of a system is used as well as IG. Thus, it should be interesting to extend our method to a gradient flow with respect to an internal energy or free energy.
Author Contributions
Conceptualization, T.W. and A.M.S.; methodology, T.W.; validation, T.W. and A.M.S.; formal analysis, T.W.; investigation, T.W. and A.M.S.; resources, T.W.; data curation, T.W.; writing—original draft preparation, T.W.; writing—review and editing, T.W. and A.M.S.; visualization, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
The first named author (T.W.) was partially supported by the Japan Society for the Promotion of Science (JSPS) Grants-in-aid for Scientific Research (KaKENHI) Grant Number 22K03431 and 25K0710.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Basics of Information Geometry and the Gradient Flow
Historically, IG [9] was developed by considering a parametrized statistical model, which is called an exponential probability distribution function (pdf):
Here, is determined from the normalization of as , and its (Legendre) dual potential function is
where is the entropic function with respect to .
However, such an exponential pdf is not necessarily needed if one would like to construct the dually flat structure in IG. For a given convex function , one can readily construct its dual convex function and the associated dual affine coordinates and as follows.
The positive definite matrices and are obtained from the Hessian matrices of the convex function and as
respectively. These matrices satisfy the relation , where denotes Kronecker’s delta. As is clear from (A4), these matrices are also Jacobian matrices, e.g., . In this way, the matrices and the inverse are simultaneously Jacobi and Hessian matrices, which are distinctive in the dually flat structure of IG.
Since the connection coefficients are not tensors, there exists a coordinate system in which all connection coefficients become zero, and such a coordinate system is called affine. The -connection [9], which is a one-parameter extension of Levi–Civita’s connection , and its dual are defined by their coefficients as
respectively. Among the -connections, plays a central role [9]. One readily sees, from (A5), that the connection coefficients of ( of ) vanish, and hence, the -coordinates (-coordinates) are affine for the connection ().
A divergence of a set of two states p and r is a non-negative function providing a measure of how much they differ. We can regard r as a reference state. A well-known example of the divergence is relative entropy (or Kullback–Leibler divergence). In IG, the - and -divergence functions are
respectively. Here, the (or ) denotes the - (or -) vector of a reference state. When , the -divergence vanishes, and similarly, the -divergence vanishes when .
Having described the basics of IG, we briefly explain the gradient-flow equations [6,7] in IG. The gradient-flow equations with respect to the -divergence function with a given fixed are
in the -coordinate system. By using the properties (A3) and (A4), the left-hand side of (A7) is rewritten by
and applying (A3) to the right-hand side of (A7) leads to . Consequently, the gradient-flow Equation (A7) in the -coordinate system is equivalent to the linear differential equations
in the -coordinate system. This linearization is one of the merits of the dually flat structure [9] in IG.
The other set (or the dual) of the gradient-flow equations are given by
in the -coordinate system. Similarly, they are equivalent to the linear differential equations
in the -coordinate system.
The gradient flow (A7) and (A10) can be related to the Hamilton flow characterized by the following Hamiltonians
respectively. Here, and are given by
respectively. Note also that and are related through the canonical transformation to [12].
It is worth noting that the scalar field characterizes the rate of the -potential, since it is related to the -potential function as follows.
where the relations (A3) and (A7) are used. Similarly, the scalar field characterizes the rate of the -potential as
Since is the entropy in (A2), the scalar field characterizes the rate of the entropy in the gradient flows.
Appendix B. Connections to Cotangent Bundles
Here, we review the connections to cotangent bundles, according to Ref. [20]. In order to retain the consistency of the notations in the text, we use X for the local coordinates and for the canonical coordinates. The local coordinates on a smooth manifold generate natural canonical coordinates on the cotangent bundle and fibered coordinates on the tangent of the cotangent bundle . A connection on can be represented by three different methods:
- (1)
- By the differential equationswhich are called the transport equations;
- (2)
- By generators given by
- (3)
- By the characteristic forms
where are coefficients of the connection . Be carful not to confuse the connection with a connection ∇ on a Riemann manifold. As can be seen from the transport Equation (A17), the connection relates with . We denote the coefficients of a connection ∇ as , whereas those of are . The horizontal lift of the vector fields Y on the base manifold is defined by
which states that the horizontal lift of on is the generator
The difference
is a vertical field. Here, denotes the Lie bracket of the vector fields . The bilinear mapping from vector fields to vertical fields is the curvature of the connection. Since , we have
with
which are the curvature coefficients of the connection .
A connection is called linear if the parallel transport is linear. In this case, the connection coefficients are linear in a, i.e.,
as well as the curvature coefficients
where
It is well-known that when the integrability conditions , are satisfied, there exists a potential function such that
Then, taking the derivative of both sides with respect to the parameter t, we have
Comparing this relation with (A17), it follows that
which states that the connection is symmetric (or torsion-free). Similarly, we see that
Next, we introduce the dual potential function as the Legendre transform of ,
We then see that
which implies the integrability conditions . Now, since
we see that
are the inverse matrix elements of , i.e., . Taking a partial derivative of both sides, we obtain
By multiplying , we have
We also see that
Then, from (A37), we have
Thus, it follows that
Therefore, the system is completely integrable if , i.e., the connection is flat.
A smooth function , which is constant along all the horizontal curves (i.e., constant on the parallel covectors), is said to be an invariant function of . This is equivalent to , i.e.,
On a cotangent bundle, a Hamilton function generates a Hamilton vector field . In canonical coordinates , the first-order equations of are Hamilton’s equations
The value of the Hamiltonian is a first integral of , i.e., a constant along the integral curves of .
Appendix C. Levi–Civita Connection and Jacobi Matrix
References
- Ruppeiner, G. Riemannian geometry in thermodynamic fluctuation theory. Rev. Mod. Phys. 1995, 67, 605. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. II. Phys. Rev. 1931, 38, 2265. [Google Scholar] [CrossRef]
- Doi, M. Onsager’s variational principle in soft matter. J. Phys. Condens. Matter 2011, 23, 284118. [Google Scholar] [CrossRef] [PubMed]
- Doi, M. Onsager principle as a tool for approximation. Chin. Phys. B 2015, 24, 020505. [Google Scholar] [CrossRef]
- Nakamura, Y. Gradient systems associated with probability distributions. Jpn. J. Ind. Appl. Math. 1994, 11, 21–30. [Google Scholar] [CrossRef]
- Fujiwara, A.; Amari, S.-I. Gradient systems in view of information geometry. Physica D 1995, 80, 317. [Google Scholar] [CrossRef]
- Malagó, L.; Pistone, G. Natural Gradient Flow in the Mixture Geometry of a Discrete Exponential Family. Entropy 2015, 17, 4215–4254. [Google Scholar] [CrossRef]
- Amari, S.-I. Information Geometry and Its Applications; Springer: Tokyo, Japan, 2016; Volume 194. [Google Scholar]
- Wada, T.; Scarfone, A.M.; Matsuzoe, H. An eikonal equation approach to thermodynamics and the gradient flows in information geometry. Physica A 2021, 570, 125820. [Google Scholar] [CrossRef]
- Wada, T.; Scarfone, A.M.; Matsuzoe, H. Huygens’ equations and the gradient-flow equations in information geometry. Int. J. Geom. Methods Mod. Phys. 2023, 20, 2450012. [Google Scholar] [CrossRef]
- Chanda, S.; Wada, T. Mechanics of geodesics in information geometry and black hole thermodynamics. Int. J. Geom. Methods Mod. Phys. 2024, 21, 2450098. [Google Scholar] [CrossRef]
- Wada, T.; Scarfone, A.M. A Hamiltonian approach to the gradient-flow equations in information geometry. Eur. Phys. J. B 2024, 97, 103. [Google Scholar] [CrossRef]
- Amari, S.-I. Natural gradient works efficiently in learning. Neural Comput. 1998, 10, 251–276. [Google Scholar] [CrossRef]
- Boumuki, N.; Noda, T. On gradient and Hamiltonian flows on even dimensional dually flat spaces. Fundam. J. Math. Math. Sci. 2016, 6, 51–66. [Google Scholar]
- Chirco, G.; Malagó, L.; Pistone, G. Lagrangian and Hamiltonian Mechanics for Probabilities on the Statistical Manifold. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250214. [Google Scholar] [CrossRef]
- Vaz, C. A Lagrangian description of thermodynamics. arXiv 2011, arXiv:1110.6152. [Google Scholar]
- MLA Style: J., D. van der Waals—Nobel Lecture. NobelPrize.org. Nobel Media AB 2018. Mon. 10 December 2018. Available online: https://www.nobelprize.org/prizes/physics/1910/waals/lecture/ (accessed on 20 April 2025).
- Bravetti, A.; Arzia, M.A.G.; Padilla, P. Asymmetric relaxations through the lens of information geometry. J. Phys. A Math. Theor. 2025, 58, 125004. [Google Scholar] [CrossRef]
- Benenti, S.; Connections and Hamilton Mechanics. Proc. Int. Conferencein in honour of A. Lichnerowicz in Gravitation Electromagnetism and Geometrical Structures edited by Ferrarese, G. 1996. Pitagora Editrice Bologna. pp. 185–206. Available online: http://www.sergiobenenti.it/cp/61.pdf (accessed on 20 April 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).