Inferring Cinematic Aesthetic Biases from the Statistics of Early Movies
Abstract
1. Introduction
2. Methods
2.1. Movie Clips
2.2. Processing the Movie Clips Before Analysis
2.3. Candidate Cinematic Aesthetic Variables
2.4. Temporal Smoothness, Roughness, and Complexity
2.5. Statistical Analyses
3. Results
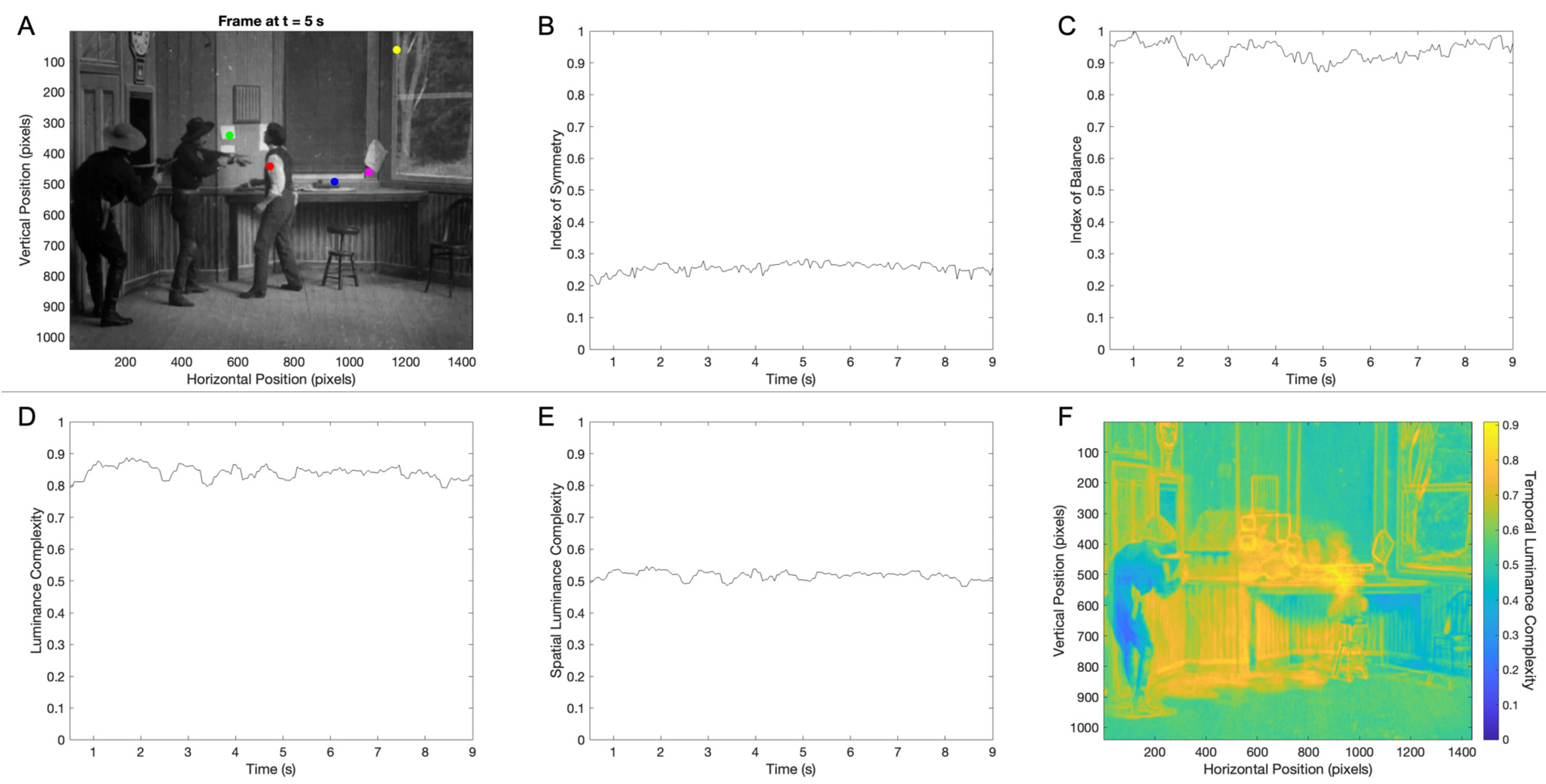
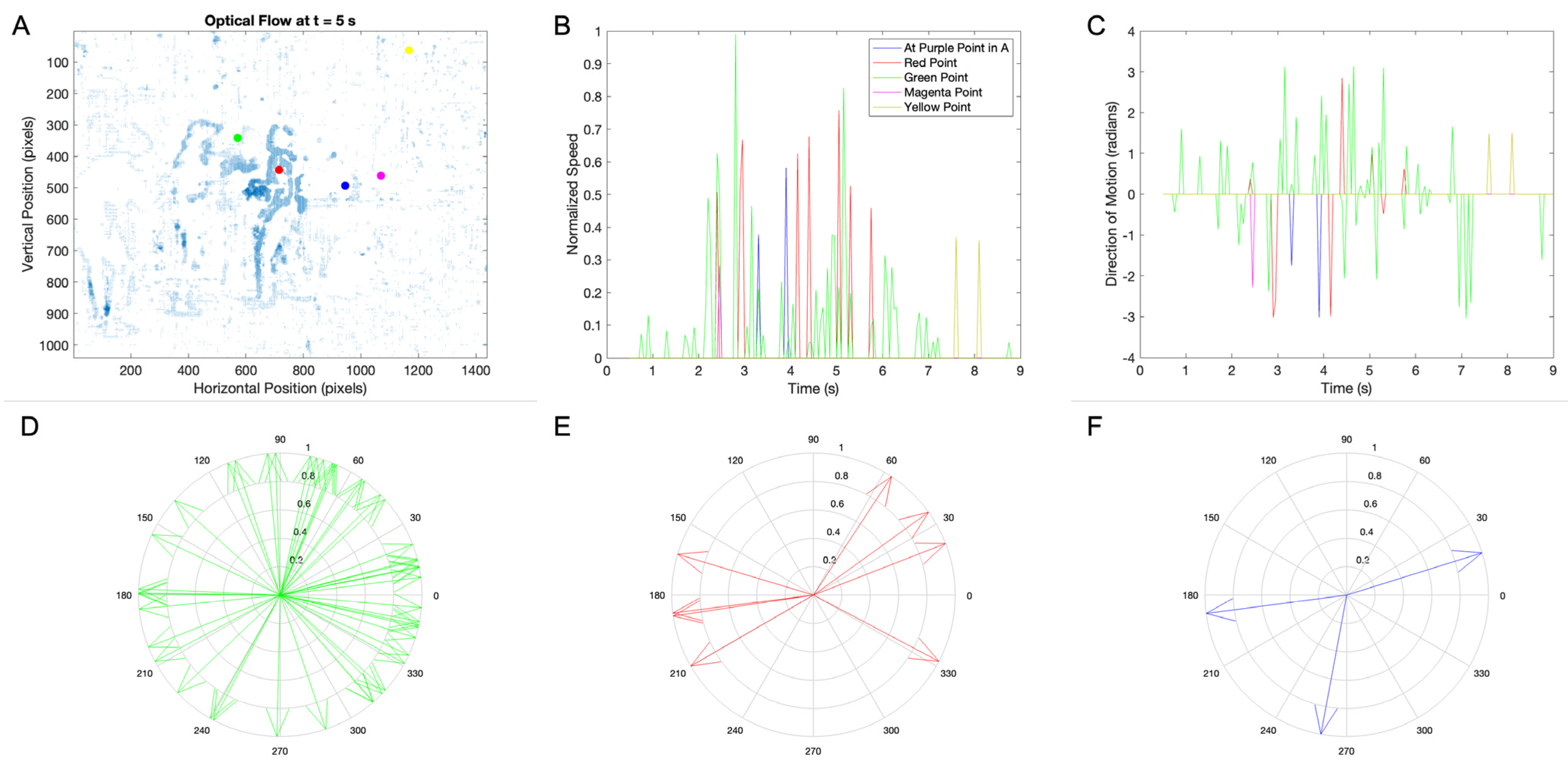
3.1. Temporal Dynamics of Individual-Frame Aesthetic Variables in a Movie Clip
3.2. Mitigating the Problem of False Positives in the Measurement Motion
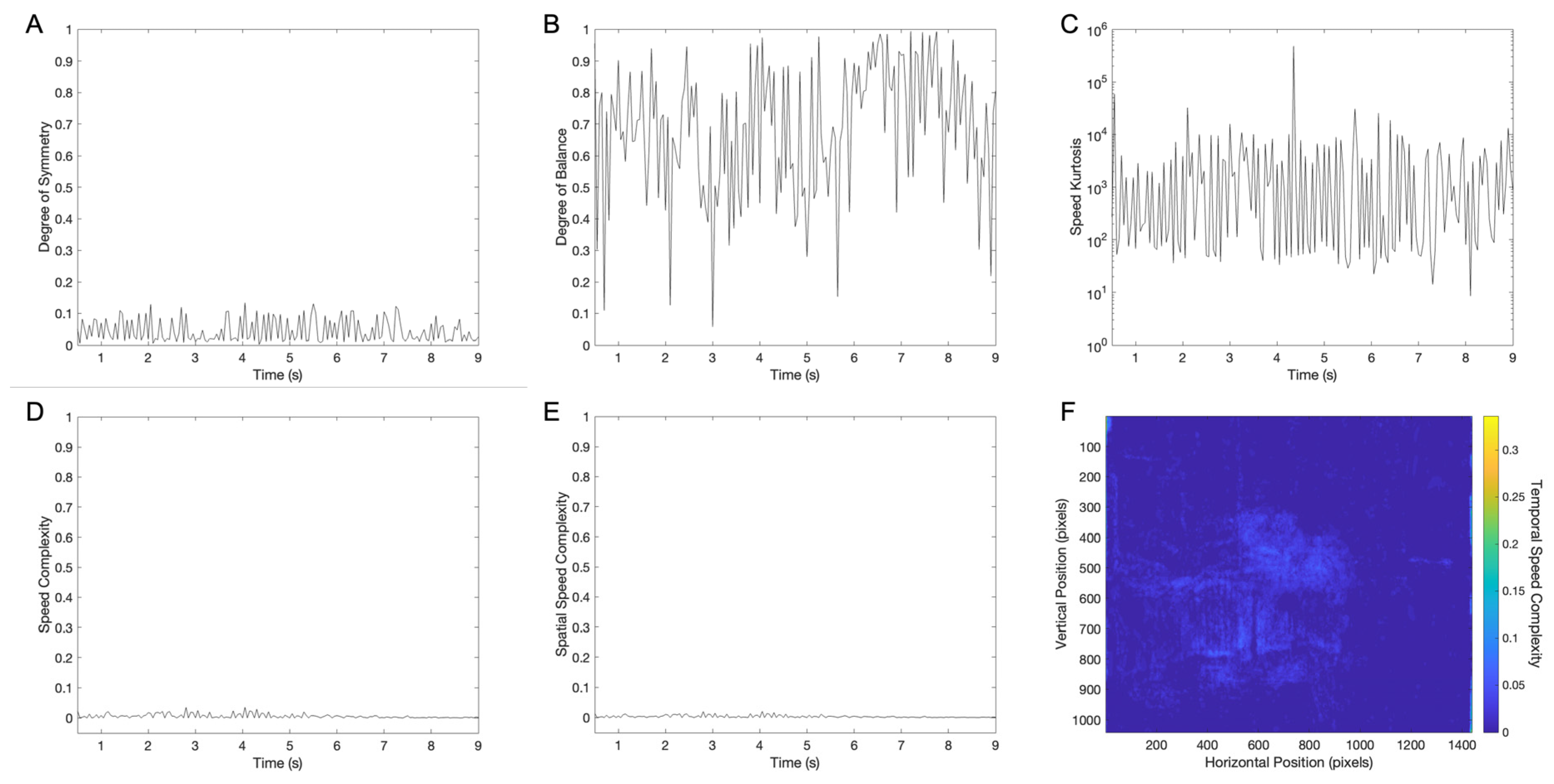
3.3. Temporal Dynamics of Between-Frame Aesthetic Variables in a Movie Clip
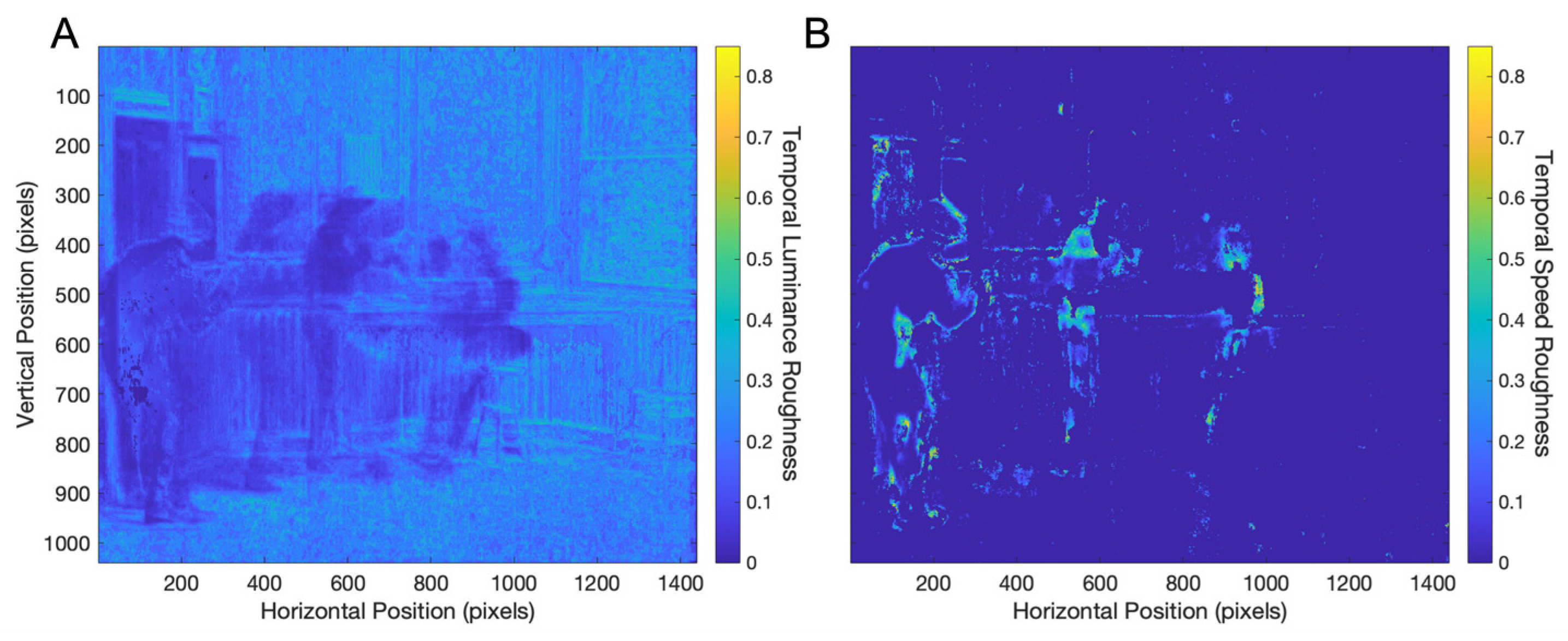
3.4. Temporal Smoothness and Temporal Roughness in a Movie Clip
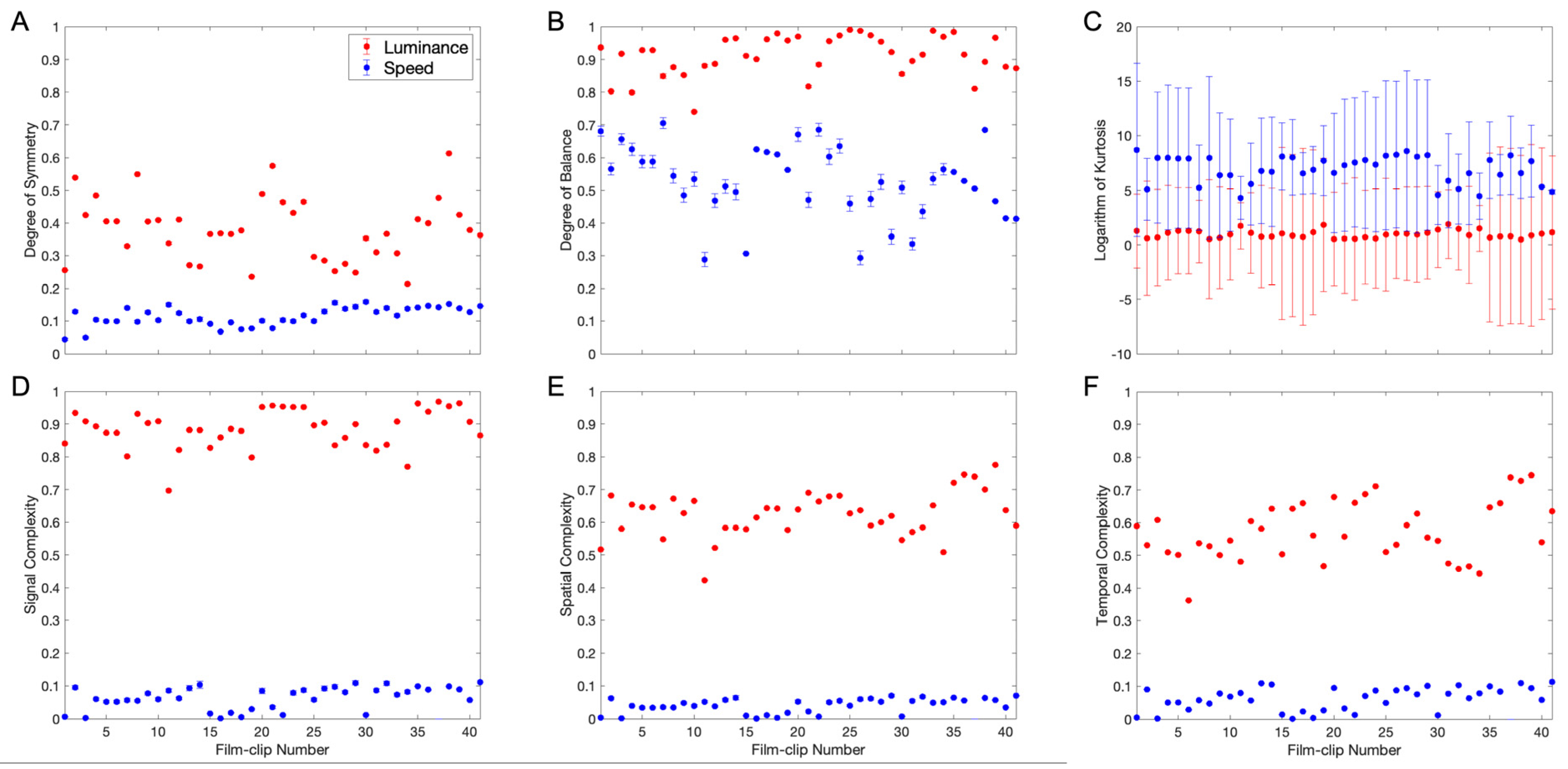
3.5. Statistics of Aesthetic Variables Across Early Movie Clips
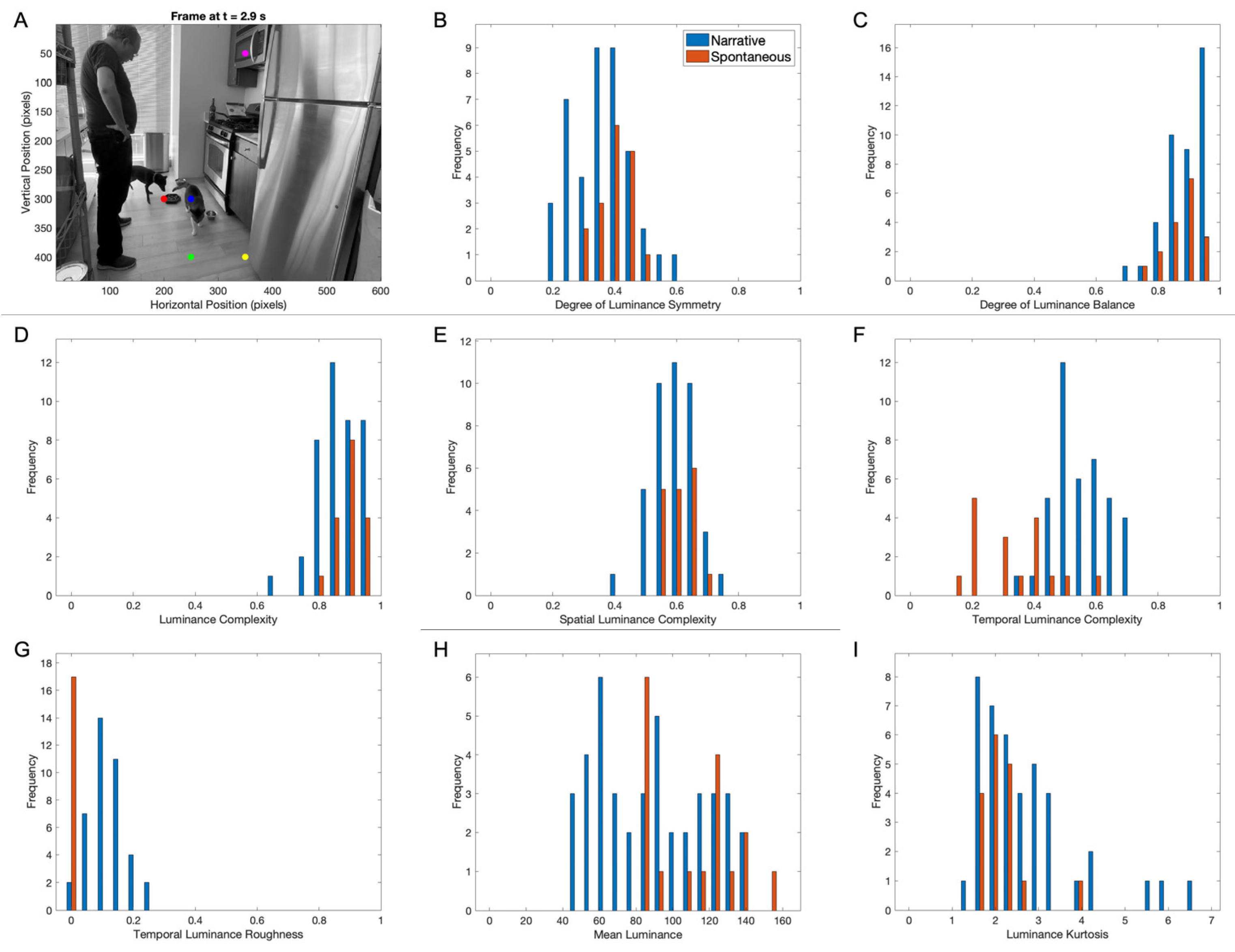
3.6. Comparing Luminance Aesthetic Variables in Early and Spontaneous Movie Clips
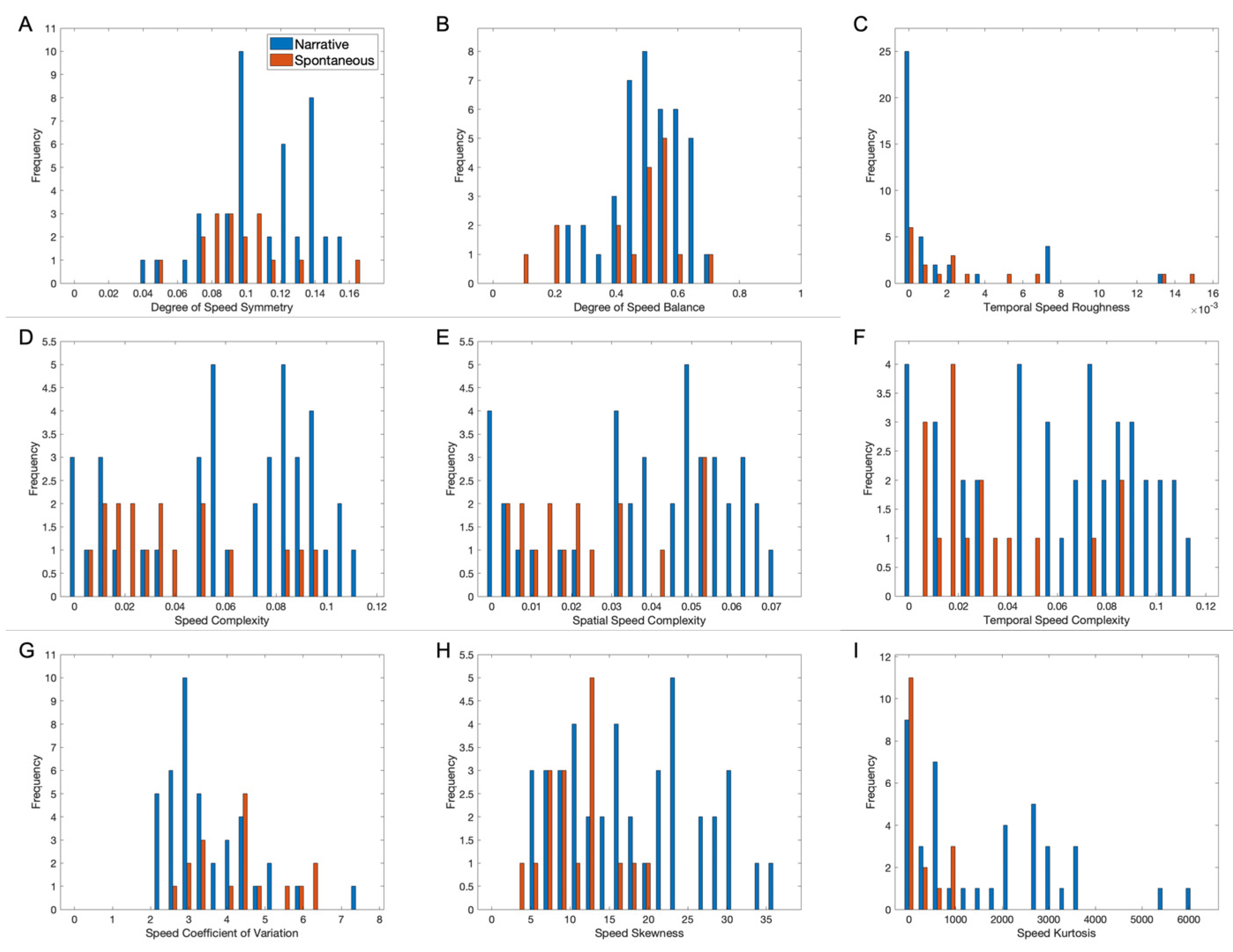
3.7. Comparing Speed Aesthetic Variables in Early and Spontaneous Movie Clips
4. Discussion
4.1. A Study of Statistics Guiding Aesthetics Research
4.2. Limitations
4.3. Are Painting Aesthetic Values Applicable to Movies?
4.4. Is Optical Flow Spatial Smoothness a Cinematic Aesthetic Variable?
4.5. Is Temporal Smoothness a Cinematic Aesthetic Variable?
4.6. Is Either Temporal or Spatial Complexity a Cinematic Aesthetic Variable?
4.7. Is Surprise a Cinematic Aesthetic Variable?
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Basten, U.; Biele, G.; Heekeren, H.R.; Fiebach, C.J. How the brain integrates costs and benefits during decision making. Proc. Natl. Acad. Sci. USA 2010, 107, 21767–21772. [Google Scholar] [CrossRef] [PubMed]
- Glimcher, P.W. Neuroeconomics: Decision Making and the Brain; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Ruff, C.C.; Fehr, E. The neurobiology of rewards and values in social decision making. Nat. Rev. Neurosci. 2014, 15, 549–562. [Google Scholar] [CrossRef]
- Entwistle, J. The aesthetic economy: The production of value in the field of fashion modelling. J. Consum. Cult. 2002, 2, 317–339. [Google Scholar] [CrossRef]
- Schummer, J.; MacLennan, B.; Taylor, N. Aesthetic values in technology and engineering design. In Philosophy of Technology and Engineering Sciences; Elsevier: Amsterdam, The Netherlands, 2009; pp. 1031–1068. [Google Scholar]
- Grzywacz, N.M.; Correa, C.M.; Correa-Herran, I. Domain-specific aesthetic values: A comparison of paintings and architecture. Psychol. Aesthet. Creat. Arts 2024, 18. [Google Scholar] [CrossRef]
- Darwin, C. The Descent of Man, and Selection in Relation to Sex; John Murray: London, UK, 2008. [Google Scholar]
- Bignardi, G.; Chamberlain, R.; Kevenaar, S.T.; Tamimy, Z.; Boomsma, D.I. On the etiology of aesthetic chills: A behavioral genetic study. Sci. Rep. 2022, 12, 3247. [Google Scholar] [CrossRef] [PubMed]
- Bignardi, G.; Wesseldijk, L.W.; Mas-Herrero, E.; Zatorre, R.J.; Ullén, F.; Fisher, S.E.; Mosing, M.A. Distinct genetic pathways to music enjoyment. bioRxiv 2024, bioRxiv:2024.04.04.588094. [Google Scholar]
- Bignardi, G.; Smit, D.J.; Vessel, E.A.; Trupp, M.D.; Ticini, L.F.; Fisher, S.E.; Polderman, T.J. Genetic effects on variability in visual aesthetic evaluations are partially shared across visual domains. Commun. Biol. 2024, 7, 55. [Google Scholar] [CrossRef]
- Bartra, O.; McGuire, J.T.; Kable, J.W. The valuation system: A coordinate-based meta-analysis of BOLD fMRI experiments examining neural correlates of subjective value. Neuroimage 2013, 76, 412–427. [Google Scholar] [CrossRef]
- Vessel, E.A.; Starr, G.G.; Rubin, N. Art reaches within: Aesthetic experience, the self and the default mode network. Front. Neurosci. 2013, 7, 258. [Google Scholar] [CrossRef]
- Chatterjee, A.; Vartanian, O. Neuroaesthetics. Trends Cogn. Sci. 2014, 18, 370–375. [Google Scholar] [CrossRef]
- Nadal, M. The experience of art: Insights from neuroimaging. Prog. Brain Res. 2013, 204, 135–158. [Google Scholar] [PubMed]
- Brown, S.; Gao, X.; Tisdelle, L.; Eickhoff, S.B.; Liotti, M. Naturalizing aesthetics: Brain areas for aesthetic appraisal across sensory modalities. Neuroimage 2011, 58, 250–258. [Google Scholar] [CrossRef] [PubMed]
- Grzywacz, N.M. Stochasticity, nonlinear value functions, and update rules in learning aesthetic biases. Front. Hum. Neurosci. 2021, 15, 639081. [Google Scholar] [CrossRef]
- Aleem, H.; Correa-Herran, I.; Grzywacz, N.M. A Theoretical Framework for How We Learn Aesthetic Values. Front. Hum. Neurosci. 2020, 14, 345. [Google Scholar] [CrossRef]
- Correa-Herran, I.; Aleem, H.; Grzywacz, N.M. Evolution of Neuroaesthetic Variables in Portraits Paintings Throughout the Renaissance. Entropy 2020, 22, 146. [Google Scholar] [CrossRef] [PubMed]
- McManus, I.C. Symmetry and asymmetry in aesthetics and the arts. Eur. Rev. 2005, 13, 157–180. [Google Scholar] [CrossRef]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Locher, P.J. How does a visual artist create an artwork. In The Cambridge Handbook of Creativity; Cambridge University Press: Cambridge, UK, 2010; pp. 131–144. [Google Scholar]
- Arnheim, R. Art and Visual Perception: A Psychology of the Creative Eye; University of California Press: Berkeley, CA, USA, 1972. [Google Scholar]
- Huron, D. Sweet Anticipation: Music and the Psychology of Expectation; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Meyer, L.B. Meaning in music and information theory. J. Aesthet. Art Crit. 1957, 15, 412–424. [Google Scholar] [CrossRef]
- Meyer, L.B. Emotion and Meaning in Music; University of Chicago Press: Chicago, IL, USA, 2008. [Google Scholar]
- Miles, S.A.; Rosen, D.S.; Grzywacz, N.M. A statistical analysis of the relationship between harmonic surprise and preference in popular music. Front. Hum. Neurosci. 2017, 11, 263. [Google Scholar] [CrossRef]
- Miles, S.A.; Rosen, D.S.; Grzywacz, N.M. Behavioral evidence of a harmonic surprise effect on preference in popular music. Curr. Res. Behav. Sci. 2022, 3, 100080. [Google Scholar] [CrossRef]
- Schmidhuber, J. Low-complexity art. Leonardo 1997, 30, 97–103. [Google Scholar] [CrossRef]
- Sigaki, H.Y.; Perc, M.; Ribeiro, H.V. History of art paintings through the lens of entropy and complexity. Proc. Natl. Acad. Sci. USA 2018, 115, E8585–E8594. [Google Scholar] [CrossRef]
- Marin, M.M.; Leder, H. Examining complexity across domains: Relating subjective and objective measures of affective environmental scenes, paintings and music. PLoS ONE 2013, 8, e72412. [Google Scholar] [CrossRef]
- Pearson, R. Early cinema. In The Oxford History of World Cinema; Oxford University Press: Oxford, UK, 1996; pp. 32–48. [Google Scholar]
- Pearson, R. Transitional cinema. In The Oxford History of World Cinema; Oxford University Press: Oxford, UK, 1996; pp. 48–69. [Google Scholar]
- Auerbach, J. Chasing film narrative: Repetition, recursion, and the body in early cinema. Crit. Inq. 2000, 26, 798–820. [Google Scholar] [CrossRef]
- Auerbach, J. Body Shots: Early Cinema’s Incarnations; University of California Press: Berkeley, CA, USA, 2007. [Google Scholar]
- Brewster, B.; Jacobs, L. Theatre to Cinema: Stage Pictorialism and the Early Feature Film; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Hansen, M. Early cinema, late cinema: Permutations of the public sphere. Screen 1993, 34, 197–210. [Google Scholar] [CrossRef]
- Pierce, J. The Basic Visual Aesthetics of the Silent Era pt. 1: Ortho Film and Color. Available online: https://silentcinemastump.com/the-basic-aesthetics-of-the-silent-era-pt-1/ (accessed on 19 June 2025).
- Brown, B. Motion Picture and Video Lighting; Routledge: Oxfordshire, UK, 2023. [Google Scholar]
- Gunning, T. The cinema of attraction[s]: Early film, its spectator and the avant-garde. Theater Film A Comp. Anthol. 1986, 39, 63–70. [Google Scholar]
- Blom, I.L. Quo vadis? From Painting to Cinema and everything in between. In La Decima Musa: Il Cinema e le Altre Arti: Atti Del VI Convegno DOMITOR, VII Convegno Internazionale di Studi Sul Cinema: Udine, Gemona del Friuli; 21–25 marzo 2000; Forum: Deerfield Beach, FL, USA, 2000; pp. 281–296. [Google Scholar]
- Simmon, S. The Films of DW Griffith; CUP Archive: Cambridge, UK, 1993. [Google Scholar]
- Bellour, R. The Analysis of Film; Indiana University Press: Bloomington, IN, USA, 2000. [Google Scholar]
- Wolf, W. Key Frame Selection by Motion Analysis. In Proceedings of the 1996 IEEE International Conference on Acoustics, Speech, and Signal Processing Conference Proceedings, Atlanta, GA, USA, 7–10 May 1996; IEEE: Piscataway, NJ, USA, 1996; pp. 1228–1231. [Google Scholar]
- Jahn, M. A guide to narratological film analysis. In Poems, Plays, and Prose: A Guide to the Theory of Literary Genres; Taylor & Francis: Oxfordshire, UK, 2003; Volume 2. [Google Scholar]
- Van Geert, E.; Wagemans, J. Order, complexity, and aesthetic appreciation. Psychol. Aesthet. Creat. Arts 2020, 14, 135. [Google Scholar] [CrossRef]
- Berlyne, D.E. Aesthetics and psychobiology. J. Aesthet. Art Crit. 1973, 31, 553. [Google Scholar]
- Munsinger, H.; Kessen, W. Uncertainty, structure, and preference. Psychol. Monogr. Gen. Appl. 1964, 78, 1. [Google Scholar] [CrossRef]
- Grzywacz, N.M. Perceptual Complexity as Normalized Shannon Entropy. Entropy 2025, 27, 166. [Google Scholar] [CrossRef]
- Berquet, S.; Aleem, H.; Grzywacz, N.M. A Fisher information theory of aesthetic preference for complexity. Entropy 2024, 26, 901. [Google Scholar] [CrossRef]
- Grzywacz, N.M.; Aleem, H. Does amount of information support aesthetic values? Front. Neurosci. 2022, 16, 805658. [Google Scholar] [CrossRef] [PubMed]
- Tarozo, M.M.; Pessa, A.A.; Zunino, L.; Rosso, O.A.; Perc, M.; Ribeiro, H.V. Two-by-two ordinal patterns in art paintings. PNAS Nexus 2025, 4, pgaf092. [Google Scholar] [CrossRef]
- Lee, B.; Seo, M.K.; Kim, D.; Shin, I.-s.; Schich, M.; Jeong, H.; Han, S.K. Dissecting landscape art history with information theory. Proc. Natl. Acad. Sci. USA 2020, 117, 26580–26590. [Google Scholar] [CrossRef]
- Horn, B.K.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the IJCAI’81: 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; pp. 674–679. [Google Scholar]
- Farneback, G. Very high accuracy velocity estimation using orientation tensors, parametric motion, and simultaneous segmentation of the motion field. In Proceedings of the Eighth IEEE International Conference on Computer Vision. ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 171–177. [Google Scholar]
- Barraza, J.F.; Grzywacz, N.M. Measurement of angular velocity in the perception of rotation. Vis. Res. 2002, 42, 2457–2462. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Warren, W.H.; Morris, M.W.; Kalish, M. Perception of translational heading from optical flow. J. Exp. Psychol. Hum. Percept. Perform. 1988, 14, 646. [Google Scholar] [CrossRef]
- Koenderink, J.J. Optic flow. Vis. Res. 1986, 26, 161–179. [Google Scholar] [CrossRef]
- Reber, R.; Schwarz, N.; Winkielman, P. Processing fluency and aesthetic pleasure: Is beauty in the perceiver’s processing experience? Personal. Soc. Psychol. Rev. 2004, 8, 364–382. [Google Scholar] [CrossRef]
- Vaina, L.M.; Grzywacz, N.M.; Kikinis, R. Segregation of computations underlying perception of motion discontinuity and coherence. NeuroReport 1994, 5, 2289–2294. [Google Scholar] [CrossRef]
- Yuille, A.L.; Grzywacz, N.M. A Theoretical Framework for Visual Motion. MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Adelson, E.H.; Movshon, J.A. Phenomenal coherence of moving visual patterns. Nature 1982, 300, 523–525. [Google Scholar] [CrossRef]
- Movshon, J.A.; Newsome, W.T. Visual response properties of striate cortical neurons projecting to area MT in macaque monkeys. J. Neurosci. 1996, 16, 7733–7741. [Google Scholar] [CrossRef] [PubMed]
- Rust, N.C.; Mante, V.; Simoncelli, E.P.; Movshon, J.A. How MT cells analyze the motion of visual patterns. Nat. Neurosci. 2006, 9, 1421–1431. [Google Scholar] [CrossRef]
- Bertero, M.; Poggio, T.A.; Torre, V. Ill-posed problems in early vision. Proc. IEEE 1988, 76, 869–889. [Google Scholar] [CrossRef]
- Poggio, T.; Torre, V. Ill-posed problems and regularization analysis in early vision. Artif. Intell. Lab. Memo 1984, 773. Available online: http://hdl.handle.net/1721.1/6402 (accessed on 29 June 2025).
- Nesi, P. Variational approach to optical flow estimation managing discontinuities. Image Vis. Comput. 1993, 11, 419–439. [Google Scholar] [CrossRef]
- Grzywacz, N.M.; Smith, J.A.; Yuille, A.L. A Common Theoretical Framework for Visual Motion’s Spatial and Temporal Coherence. In Proceedings of the Workshop on Visual Motion, Irvine, CA, USA, 20–22 March 1989; IEEE Computer Society: Washington, DC, USA, 1989; pp. 148–155. [Google Scholar]
- Piana, S.; Alborno, P.; Niewiadomski, R.; Mancini, M.; Volpe, G.; Camurri, A. Movement Fluidity Analysis Based on Performance and Perception, Proceedings of the 2016 CHI Conference Extended Abstracts on Human Factors in Computing Systems, San Jose, CA, USA, 7–12 May 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1629–1636. [Google Scholar]
- Alborno, P.; Cera, A.; Piana, S.; Mancini, M.; Niewiadomski, R.; Canepa, C.; Volpe, G.; Camurri, A. Interactive sonification of movement qualities–A case study on fluidity. Proc. ISon 2016, 35. [Google Scholar]
- Slepian, M.L.; Weisbuch, M.; Pauker, K.; Bastian, B.; Ambady, N. Fluid movement and fluid social cognition: Bodily movement influences essentialist thought. Personal. Soc. Psychol. Bull. 2014, 40, 111–120. [Google Scholar] [CrossRef]
- Aleem, H.; Correa-Herran, I.; Grzywacz, N.M. Inferring Master Painters’ Esthetic Biases from the Statistics of Portraits. Front. Hum. Neurosci. 2017, 11, 94. [Google Scholar] [CrossRef]
- Chatterjee, A.; Vartanian, O. Neuroscience of aesthetics. Ann. N. Y. Acad. Sci. 2016, 1369, 172–194. [Google Scholar] [CrossRef]
- Isik, A.I.; Vessel, E.A. From visual perception to aesthetic appeal: Brain responses to aesthetically appealing natural landscape movies. Front. Hum. Neurosci. 2021, 15, 676032. [Google Scholar] [CrossRef]
- Clemente, A.; Pearce, M.T.; Skov, M.; Nadal, M. Evaluative judgment across domains: Liking balance, contour, symmetry and complexity in melodies and visual designs. Brain Cogn. 2021, 151, 105729. [Google Scholar] [CrossRef] [PubMed]
- Trost, W.; Ethofer, T.; Zentner, M.; Vuilleumier, P. Mapping aesthetic musical emotions in the brain. Cereb. Cortex 2012, 22, 2769–2783. [Google Scholar] [CrossRef] [PubMed]
- Rapela, J.; Mendel, J.M.; Grzywacz, N.M. Estimating nonlinear receptive fields from natural images. J. Vis. 2006, 6, 11. [Google Scholar] [CrossRef] [PubMed]
- Field, D.J. Relations between the statistics of natural images and the response properties of cortical cells. J. Opt. Soc. Am. A 1987, 4, 2379–2394. [Google Scholar] [CrossRef]
- Simoncelli, E.P.; Olshausen, B.A. Natural image statistics and neural representation. Annu. Rev. Neurosci. 2001, 24, 1193–1216. [Google Scholar] [CrossRef]
- Kay, K.N.; Naselaris, T.; Prenger, R.J.; Gallant, J.L. Identifying natural images from human brain activity. Nature 2008, 452, 352–355. [Google Scholar] [CrossRef]
- Geisler, W.S. Visual perception and the statistical properties of natural scenes. Annu. Rev. Psychol. 2008, 59, 167–192. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: Oxfordshire, UK, 2013. [Google Scholar]
- Kattelle, A.D. The evolution of amateur motion picture equipment 1895–1965. J. Film Video 1986, 38, 47–57. [Google Scholar]
- Turquety, B. Inventing Cinema: Machines, Gestures and Media History; Amsterdam University Press: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Manley, B. Moving pictures: The history of early cinema. ProQuest Discov. Guides 2011, 1. Available online: https://www.lkouniv.ac.in/site/writereaddata/siteContent/202004260643328777nishi_films.pdf (accessed on 8 May 2025).
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef]
- Schroeder, R.G.; Linderman, K.; Liedtke, C.; Choo, A.S. Six Sigma: Definition and underlying theory. J. Oper. Manag. 2008, 26, 536–554. [Google Scholar] [CrossRef]
- Yang, K.; Basem, S.; El-Haik, B. Design for Six Sigma; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Moganti, M.; Ercal, F.; Dagli, C.H.; Tsunekawa, S. Automatic PCB inspection algorithms: A survey. Comput. Vis. Image Underst. 1996, 63, 287–313. [Google Scholar] [CrossRef]
- Barney, M. Six Sigma. Ind. Organ. Psychol. 2002, 39, 104–107. [Google Scholar]
- DeCarlo, L.T. On the meaning and use of kurtosis. Psychol. Methods 1997, 2, 292. [Google Scholar] [CrossRef]
- Kim, T.-H.; White, H. On more robust estimation of skewness and kurtosis. Financ. Res. Lett. 2004, 1, 56–73. [Google Scholar] [CrossRef]
- Brys, G.; Hubert, M.; Struyf, A. A robust measure of skewness. J. Comput. Graph. Stat. 2004, 13, 996–1017. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Entropy, relative entropy and mutual information. Elem. Inf. Theory 1991, 2, 12–13. [Google Scholar]
- Donald, M.J. On the relative entropy. Commun. Math. Phys. 1986, 105, 13–34. [Google Scholar] [CrossRef]
- Smeeton, N.; Spencer, N.; Sprent, P. Applied Nonparametric Statistical Methods; CRC Press: Boca Raton, FL, USA, 2025. [Google Scholar]
- Ruppert, D.; Matteson, D.S. Statistics and Data Analysis for Financial Engineering; Springer: Berlin/Heidelberg, Germany, 2011; Volume 13. [Google Scholar]
- Hinton, P.R. Statistics Explained; Routledge: Oxfordshire, UK, 2024. [Google Scholar]
- Armstrong, R.A. When to use the Bonferroni correction. Ophthalmic Physiol. Opt. 2014, 34, 502–508. [Google Scholar] [CrossRef]
- Lakens, D. Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Front. Psychol. 2013, 4, 863. [Google Scholar] [CrossRef]
- Flueckiger, B. Color and subjectivity in film. In Subjectivity Across Media; Routledge: Oxfordshire, UK, 2016; pp. 145–161. [Google Scholar]
- Fu, X. Horror Movie Aesthetics: How Color, Time, Space and Sound Elicit Fear in an Audience; Northeastern University: Boston, MA, USA, 2016. [Google Scholar]
- Grzywacz, N.M.; de Juan, J. Sensory adaptation as Kalman filtering: Theory and illustration with contrast adaptation. Netw. Comput. Neural Syst. 2003, 14, 465. [Google Scholar] [CrossRef]
- Wark, B.; Lundstrom, B.N.; Fairhall, A. Sensory adaptation. Curr. Opin. Neurobiol. 2007, 17, 423–429. [Google Scholar] [CrossRef]
- Ji, Y.; Zhu, C.L.; Grzywacz, N.M.; Lee, E.J. Rearrangement of the cone mosaic in the retina of the rat model of retinitis pigmentosa. J. Comp. Neurol. 2012, 520, 874–888. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.L.; Ji, Y.; Lee, E.-J.; Grzywacz, N.M. Spatiotemporal pattern of rod degeneration in the S334ter-line-3 rat model of retinitis pigmentosa. Cell Tissue Res. 2013, 351, 29–40. [Google Scholar] [CrossRef]
- Norrix, L.W.; Velenovsky, D.S. Auditory neuropathy spectrum disorder: A review. J. Speech Lang. Hear. Res. 2014, 57, 1564–1576. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.J.; Gibo, T.L.; Grzywacz, N.M. Dark-rearing-induced reduction of GABA and GAD and prevention of the effect by BDNF in the mouse retina. Eur. J. Neurosci. 2006, 24, 2118–2134. [Google Scholar] [CrossRef]
- Yu, W.-Q.; Grzywacz, N.M.; Lee, E.-J.; Field, G.D. Cell type-specific changes in retinal ganglion cell function induced by rod death and cone reorganization in rats. J. Neurophysiol. 2017, 118, 434–454. [Google Scholar] [CrossRef]
- Kendall, R. Degas and the contingency of vision. Burlingt. Mag. 1988, 130, 180–216. [Google Scholar]
- Marmor, M.F. Vision, eye disease, and art: 2015 Keeler Lecture. Eye 2016, 30, 287–303. [Google Scholar] [CrossRef][Green Version]
- Knittel, K.M. Wagner, deafness, and the reception of Beethoven’s late style. J. Am. Musicol. Soc. 1998, 51, 49–82. [Google Scholar] [CrossRef]
- Stevens, M.H.; Jacobsen, T.; Crofts, A.K. Lead and the deafness of Ludwig van Beethoven. Laryngoscope 2013, 123, 2854–2858. [Google Scholar] [CrossRef] [PubMed]
- Marmor, M.F. Ophthalmology and art: Simulation of Monet’s cataracts and Degas’ retinal disease. Arch. Ophthalmol. 2006, 124, 1764–1769. [Google Scholar] [CrossRef][Green Version]
- Ravin, J.G. Monet’s cataracts. JAMA 1985, 254, 394–399. [Google Scholar] [CrossRef] [PubMed]
- Dieguez, S.; Assal, G.; Bogousslavsky, J. Visconti and Fellini: From left social neorealism to right-hemisphere stroke. Front. Neurol. Neurosci. 2007, 22, 44. [Google Scholar]
- Comte, J.A.; de Foville, J.; Dezarrois, A. La Revue de l’art Ancien et Modern; Imprimerie Georges Petit: Paris, France, 1927; Volume 52. [Google Scholar]
- Ma, Y. A Brief Analysis on the Use of Color in Film Scenes Taking the Grand Budapest Hotel as an Example. In Proceedings of the 5th International Conference on Arts, Design and Contemporary Education (ICADCE 2019), Moscow, Russia, 14–16 May 2019; Atlantis Press: Dordrecht, The Netherlands, 2019; pp. 328–330. [Google Scholar]
- Galt, R. Pretty: Film and the Decorative Image; Columbia University Press: New York, NY, USA, 2011. [Google Scholar]
- Kinder, M.; Almodóvar, P. Pleasure and the New Spanish mentality: A conversation with Pedro Almodóvar. Film Q. 1987, 33–44. Available online: https://www.enotes.com/topics/pedro-almodovar/criticism/criticism/pedro-almodovar-with-marsha-kinder-interview-date (accessed on 20 May 2025).
- Bartram, L.; Nakatani, A. What Makes Motion Meaningful? Affective Properties of Abstract Motion. In Proceedings of the 2010 Fourth Pacific-Rim Symposium on Image and Video Technology, Singapore, 14–17 November 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 468–474. [Google Scholar]
- Schonig, J. The Shape of Motion: Cinema and the Aesthetics of Movement; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Ricotta, C.; Szeidl, L. Towards a unifying approach to diversity measures: Bridging the gap between the Shannon entropy and Rao’s quadratic index. Theor. Popul. Biol. 2006, 70, 237–243. [Google Scholar] [CrossRef]
- Zillmann, D.; Hay, T.A.; Bryant, J. The effect of suspense and its resolution on the appreciation of dramatic presentations. J. Res. Personal. 1975, 9, 307–323. [Google Scholar] [CrossRef]
- Reisenzein, R. Exploring the strength of association between the components of emotion syndromes: The case of surprise. Cogn. Emot. 2000, 14, 1–38. [Google Scholar] [CrossRef]
- Lehne, M.; Koelsch, S. Toward a general psychological model of tension and suspense. Front. Psychol. 2015, 6, 79. [Google Scholar] [CrossRef]
- Itti, L.; Baldi, P. Bayesian surprise attracts human attention. Vis. Res. 2009, 49, 1295–1306. [Google Scholar] [CrossRef] [PubMed]
- Baldi, P.; Itti, L. Of bits and wows: A Bayesian theory of surprise with applications to attention. Neural Netw. 2010, 23, 649–666. [Google Scholar] [CrossRef]
- Meyer, W.-U.; Niepel, M.; Rudolph, U.; Schützwohl, A. An experimental analysis of surprise. Cogn. Emot. 1991, 5, 295–311. [Google Scholar] [CrossRef]
- Orpen, V. Film Editing: The Art of the Expressive; Wallflower Press: New York, NY, USA, 2003; Volume 16. [Google Scholar]
- Marcus, L. “A new form of true beauty”: Aesthetics and Early Film Criticism. Mod. Mod. 2006, 13, 267–289. [Google Scholar] [CrossRef]
- Wiegand, D. Tableaux Vivants, Early Cinema and “Beauty-as-Attraction”. Acta Univ. Sapientiae Film Media Stud. 2018, 15, 9–32. [Google Scholar] [CrossRef]
- De Kuyper, E. Anyone for an Aesthetic of Film History? Film Hist. 1994, 6, 100–109. [Google Scholar]
- Dmytryk, E.; Lund, A.; Hurbis-Cherrier, M. On Film Editing: An Introduction to the Art of Film Construction; Routledge: Oxfordshire, UK, 2018. [Google Scholar]
- Isenhour, J.P. The effects of context and order in film editing. AV Commun. Rev. 1975, 23, 69–80. [Google Scholar] [CrossRef]
- Lütticken, S. Suspense and surprise. New Left Rev. 2006, 40, 95–109. [Google Scholar]
- Available online: https://www.instagram.com/reel/DIe1xIjMv_Z/?utm_source=ig_web_copy_link (accessed on 8 May 2025).
Disclaimer/Publisher’s Note: The statements, opinions, and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions, or products referred to in the content. |

| Movie | Director | Year | # Clips |
|---|---|---|---|
| The Great Train Robbery | Edwin Stanton Porter | 1903 | 1 |
| Jupiter’s Thunderballs | Georges Méliès | 1903 | 2 |
| Le Diable Noir | Georges Méliès | 1905 | 5 |
| Rescued by Rover | Cecil Milton Hepworth | 1905 | 1 |
| Les Résultats du Féminisme | Alice Guy | 1906 | 5 |
| L’Assassinat du Duc de Guise | André Calmettes | 1908 | 5 |
| The Electric Hotel | Víctor Aurelio Chomón y Ruiz | 1908 | 1 |
| La Battaglia del Grano | D. W. Griffith | 1909 | 4 |
| The Invisible Thief | Ferdinand Zecca | 1909 | 3 |
| The Panicky Picnic | Camille de Morlhon | 1909 | 2 |
| Frankenstein | J. Searle Dawley | 1910 | 4 |
| L’Inferno | Francesco Bertolini, Adolfo Padovan, Giuseppe De Liguoro | 1911 | 5 |
| Falling Leaves | Alice Guy Blaché | 1912 | 3 |
| Name | Definition |
|---|---|
| Degree of Luminance Symmetry | Index of symmetry in Reference [72] |
| Degree of Speed Symmetry | Same as last row but for optical flow speeds |
| Degree of Luminance Balance | Index of balance in Reference [72] |
| Degree of Speed Balance | Same as last row but for optical flow speeds |
| Luminance Complexity | Complexity of Order 1 in References [48,72] |
| Speed Complexity | Same as last row but for optical flow speeds |
| Luminance Spatial Complexity | Complexity of Order 2 in References [48,72] |
| Speed Spatial Complexity | Same as last row but for optical flow speeds |
| Luminance Temporal Complexity | Equations (3) and (4) applied to luminance |
| Speed Temporal Complexity | Equations (3) and (4) applied to speed |
| Luminance Temporal Roughness | Equations (5) and (6) applied to luminance |
| Speed Temporal Roughness | Equations (5) and (6) applied to luminance |
| Mean Luminance | Mean across positions and times |
| Luminance Standard Deviation | Time average of spatial standard deviation |
| Luminance Coefficient of Variation | Ratio of last two rows |
| Speed Coefficient of Variation | Same as last row but for optical flow speeds |
| Luminance Skewness | Time average of spatial skewness |
| Speed Skewness | Same as last row but for optical flow speeds |
| Luminance Kurtosis | Time average of spatial kurtosis [91] |
| Speed Kurtosis | Same as last row but for optical flow speeds |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grzywacz, D.M.; Grzywacz, N.M. Inferring Cinematic Aesthetic Biases from the Statistics of Early Movies. Entropy 2025, 27, 707. https://doi.org/10.3390/e27070707
Grzywacz DM, Grzywacz NM. Inferring Cinematic Aesthetic Biases from the Statistics of Early Movies. Entropy. 2025; 27(7):707. https://doi.org/10.3390/e27070707
Chicago/Turabian StyleGrzywacz, Daniel M., and Norberto M. Grzywacz. 2025. "Inferring Cinematic Aesthetic Biases from the Statistics of Early Movies" Entropy 27, no. 7: 707. https://doi.org/10.3390/e27070707
APA StyleGrzywacz, D. M., & Grzywacz, N. M. (2025). Inferring Cinematic Aesthetic Biases from the Statistics of Early Movies. Entropy, 27(7), 707. https://doi.org/10.3390/e27070707







