A Hybrid Framework Integrating Traditional Models and Deep Learning for Multi-Scale Time Series Forecasting
Abstract
1. Introduction
2. Related Work
2.1. Traditional Time Series Models
2.2. Deep Learning Methods for Time Series
2.3. Hybrid Approaches
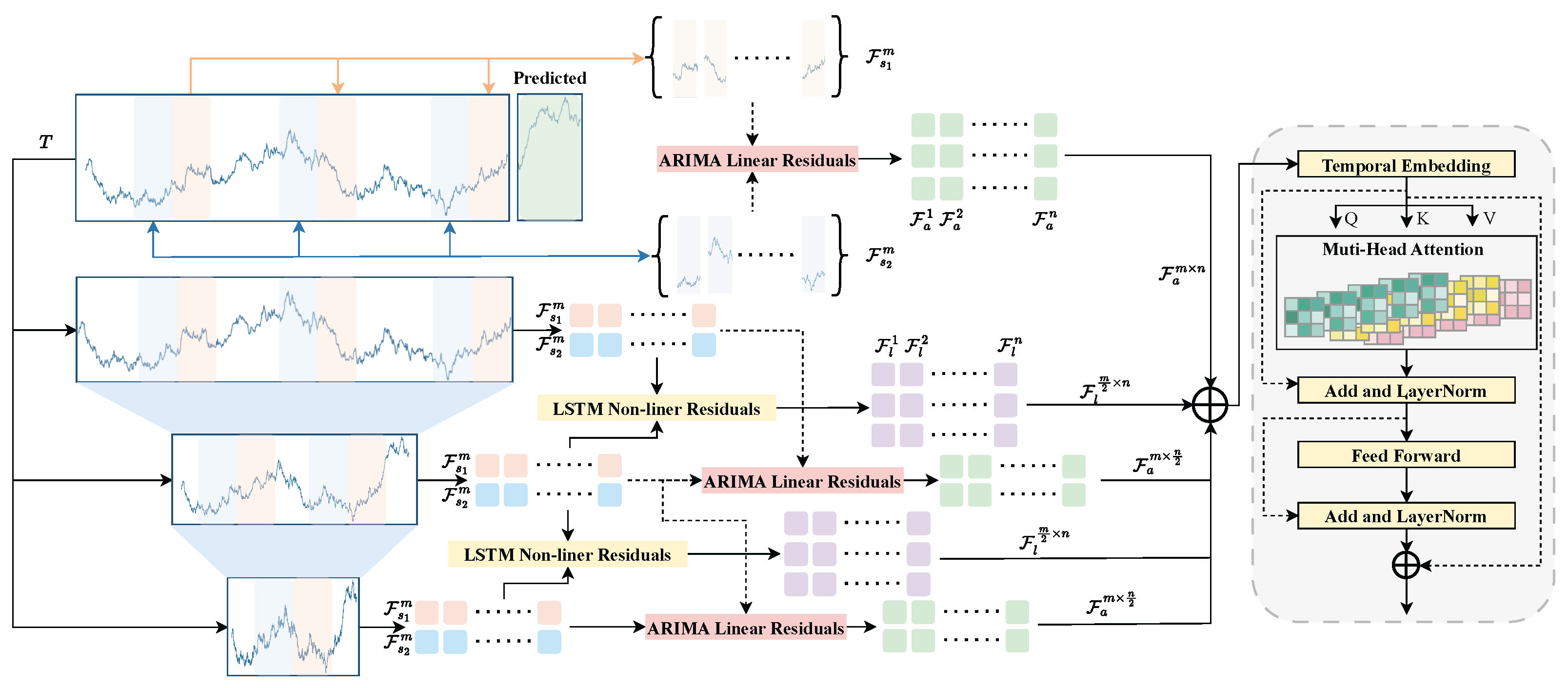
3. Method
3.1. Notation and Problem Formulation
3.2. ARIMA Linear Module
3.3. Deep Residual Forecasting Module
3.4. Hybrid Forecast Fusion Strategy
3.5. Training Objective and Computational Pipeline
3.6. Uncertainty Quantification Extension
- The proportion of true values falling within predicted intervals;
- The average interval width normalized by the data range.
4. Experiments
4.1. Datasets and Experimental Setup
4.2. Deep Learning Architecture Configuration and Hyperparameter Settings
4.3. Data Splitting and Normalization
4.4. Experimental Environment and Training Configuration
4.5. Evaluation Metrics
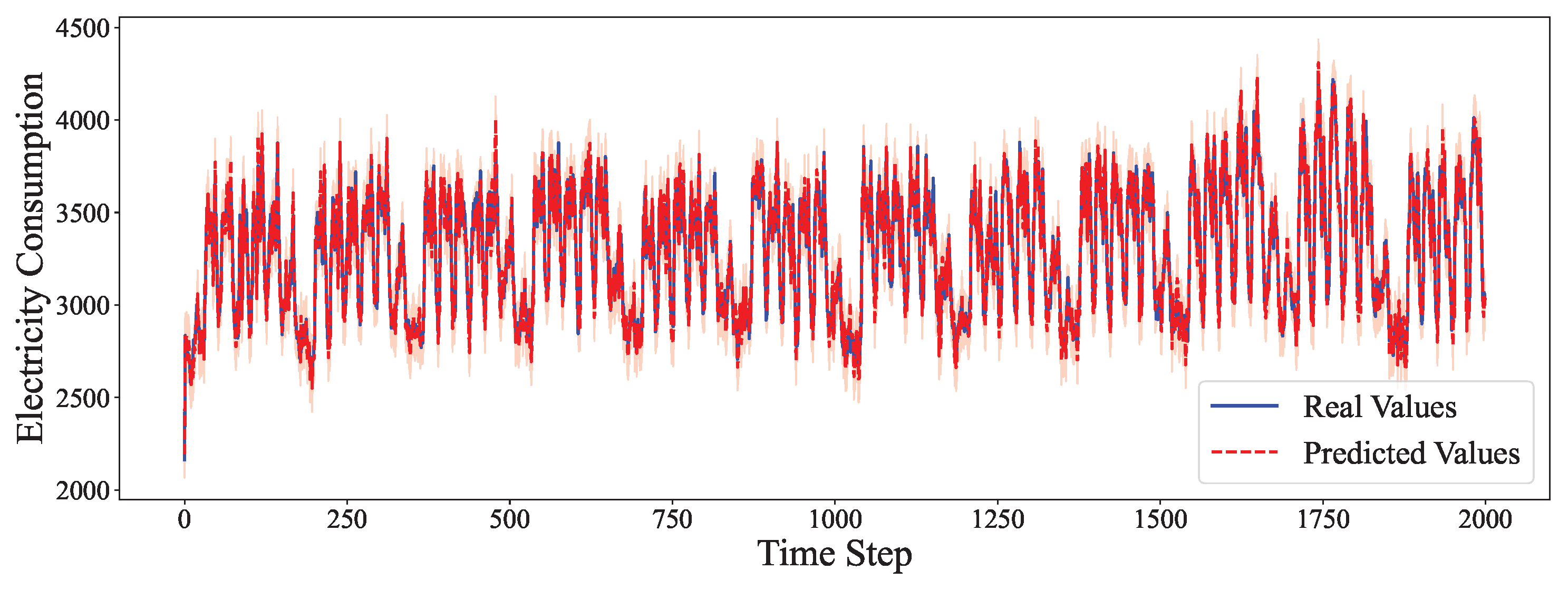
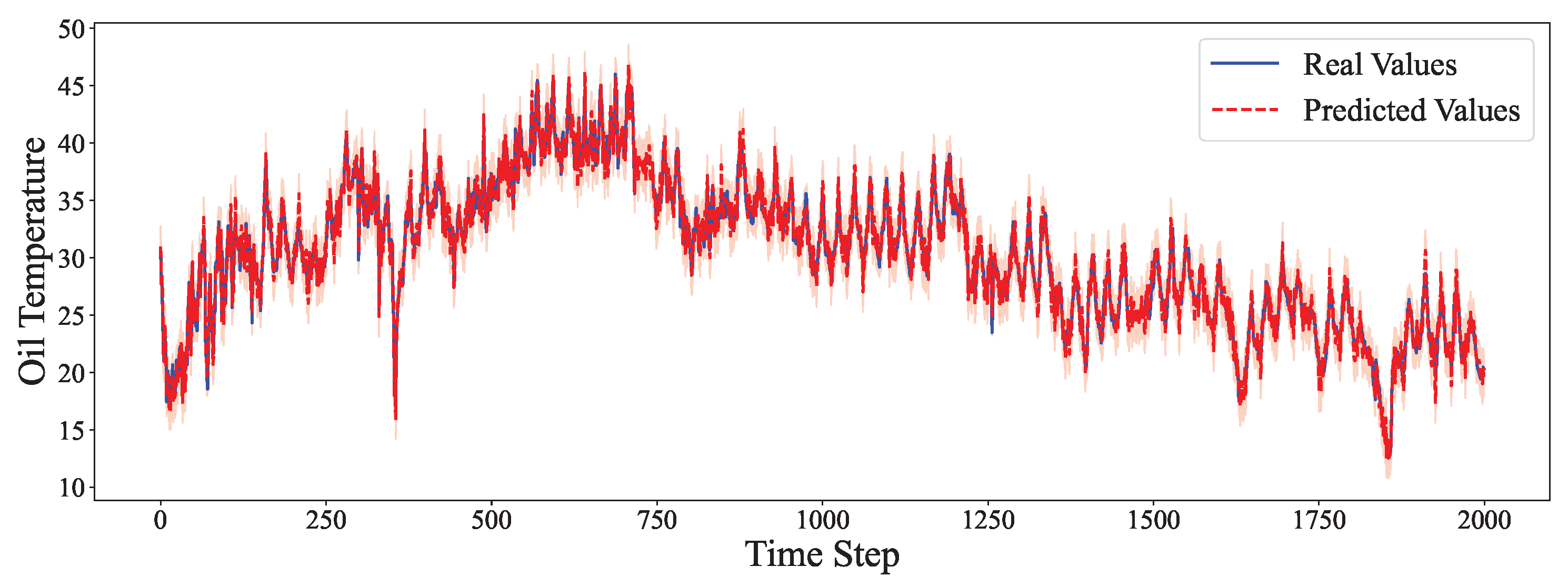
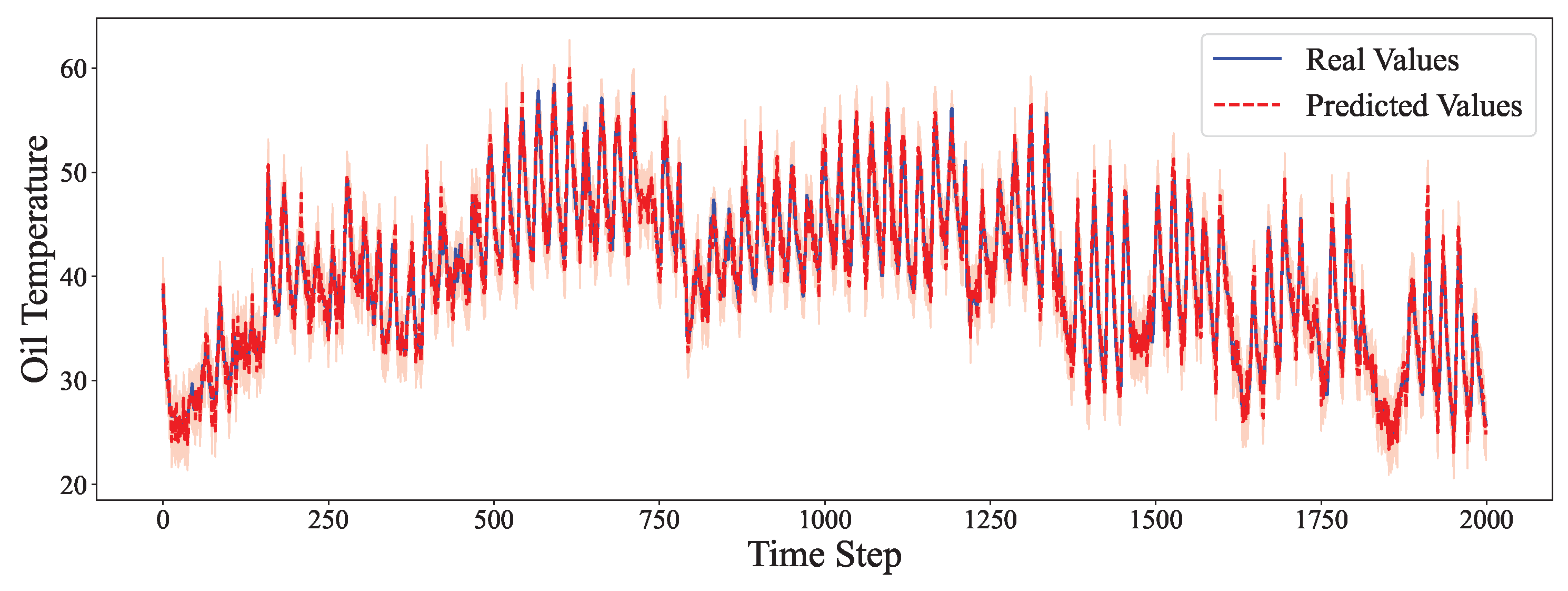
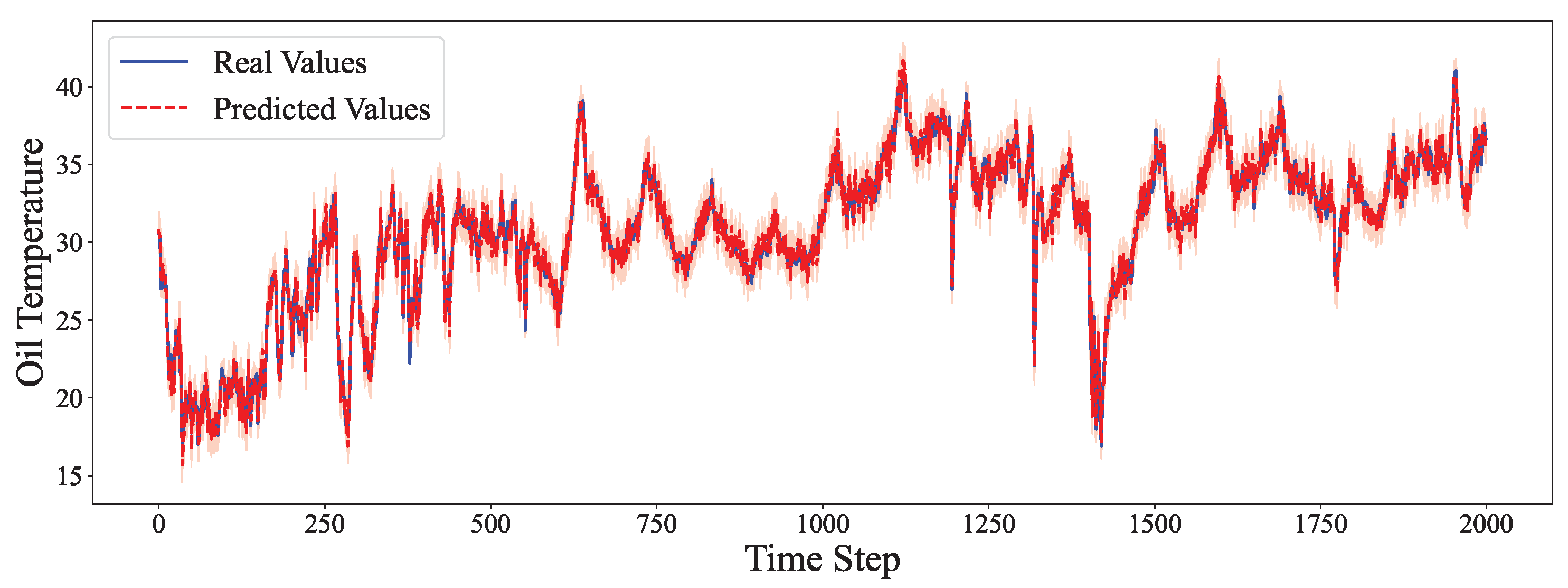
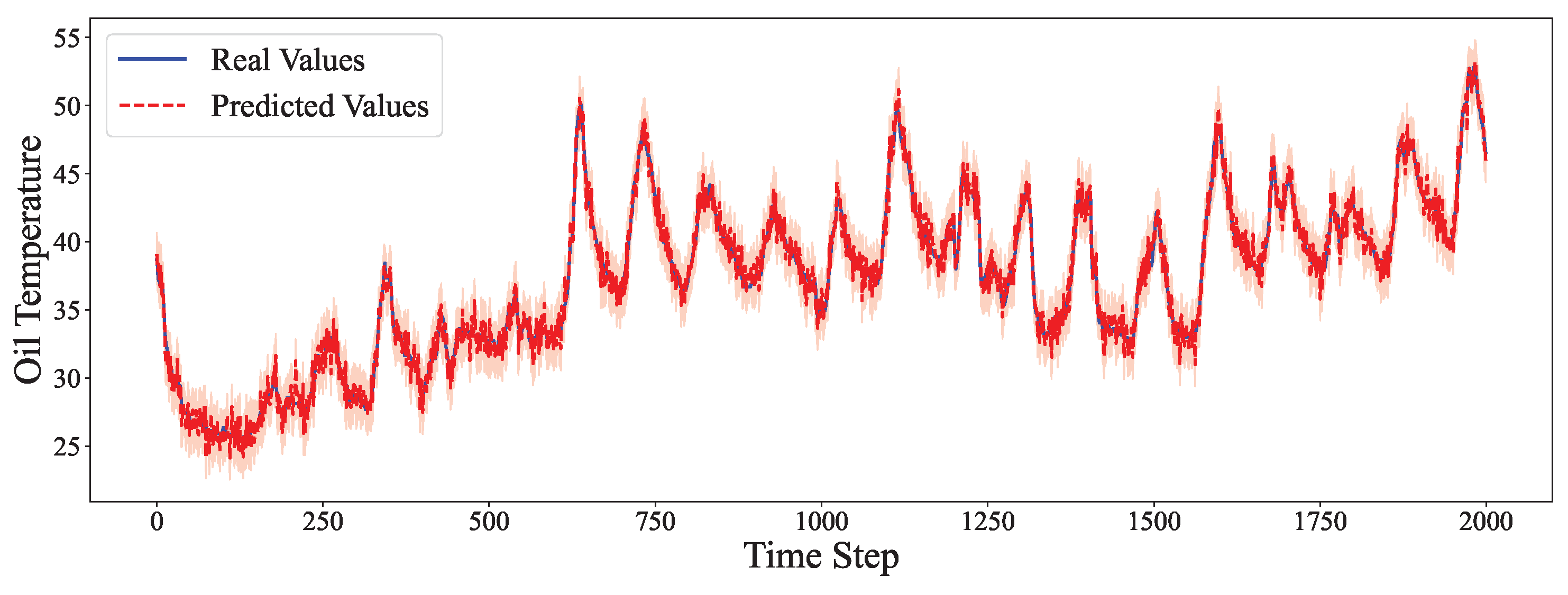
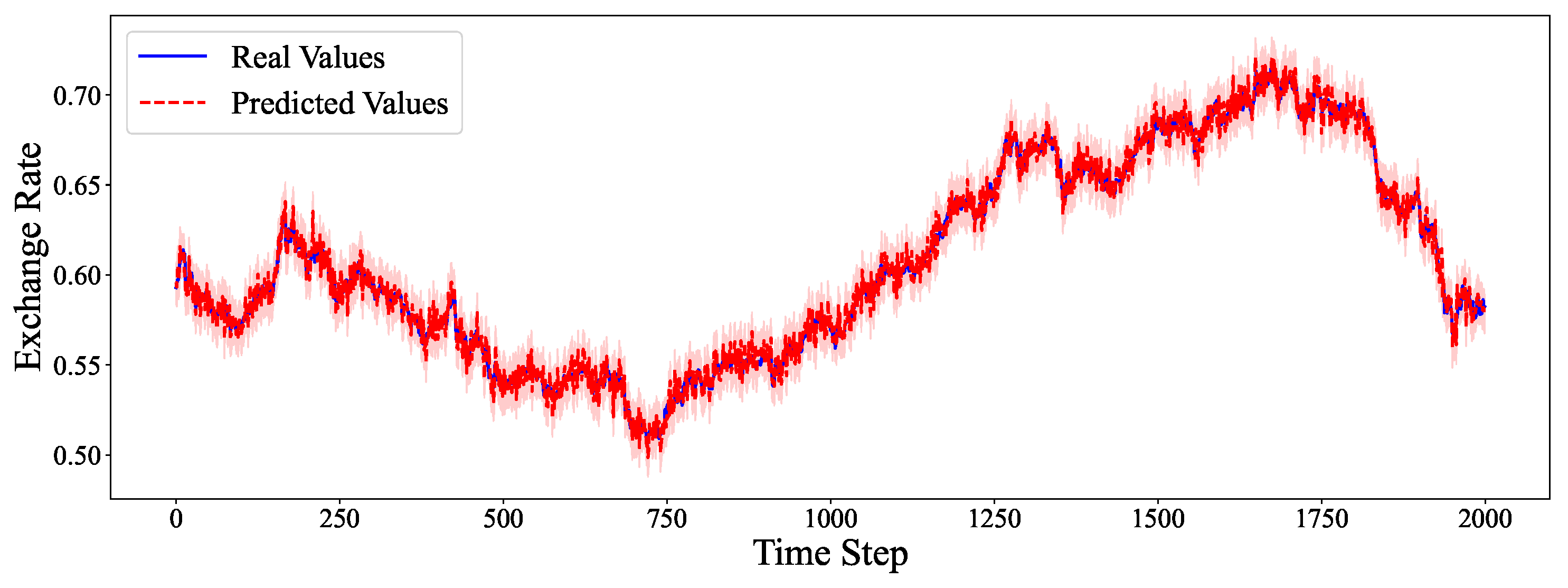
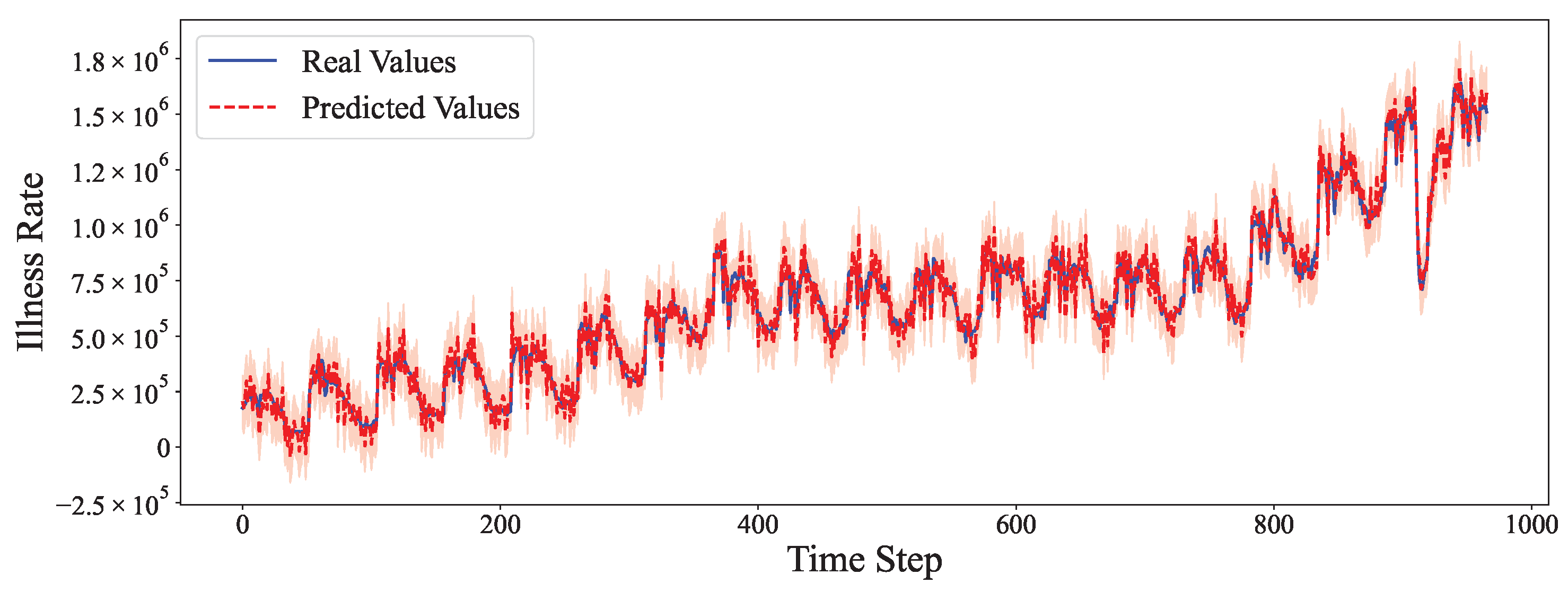
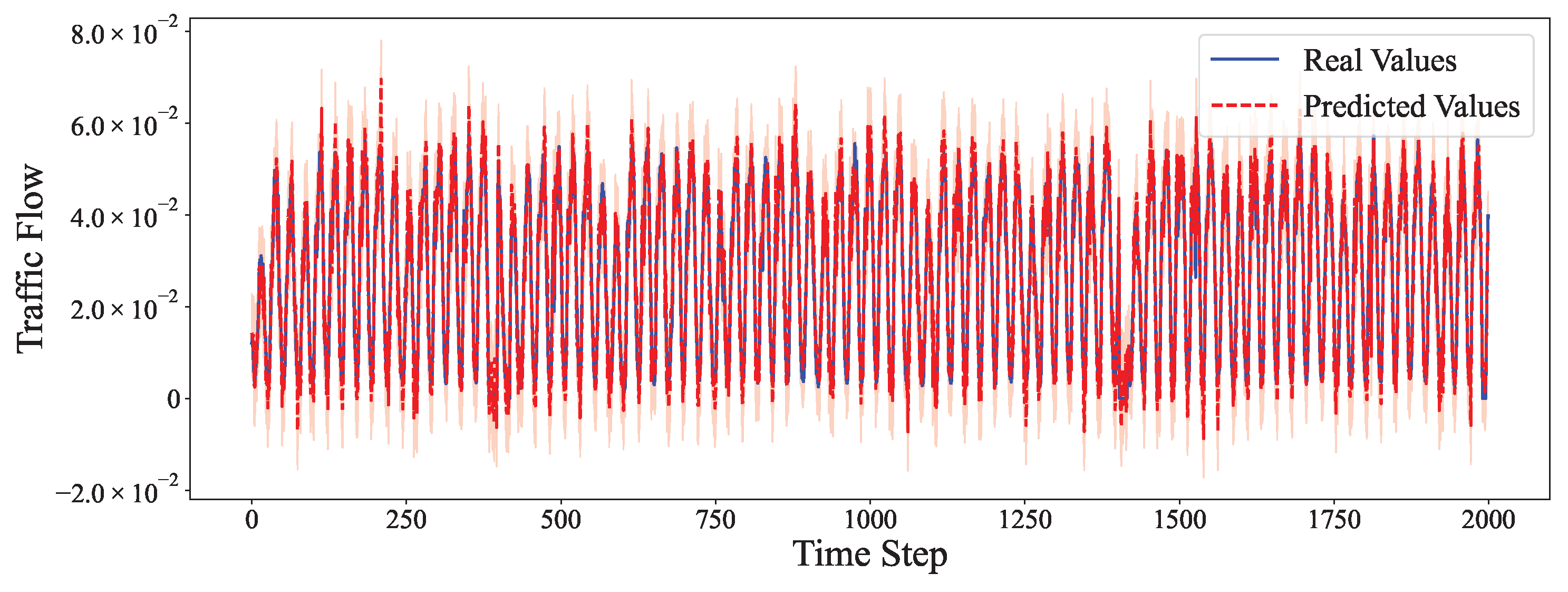
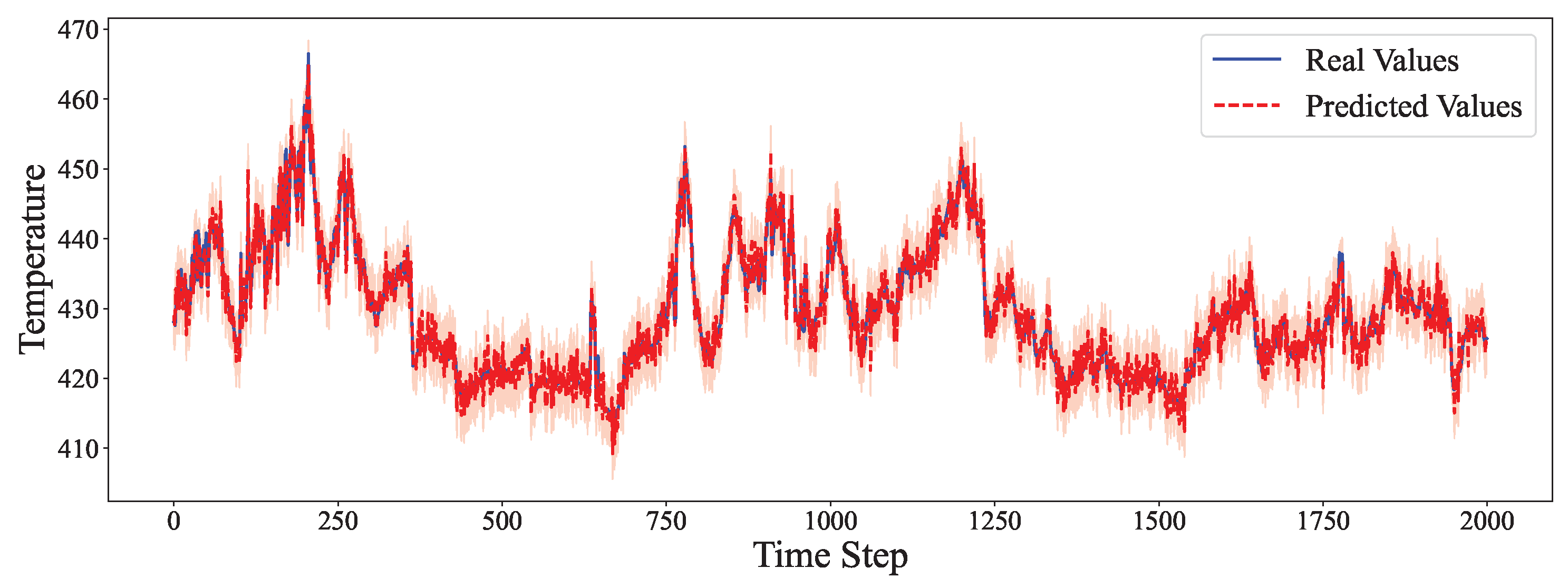
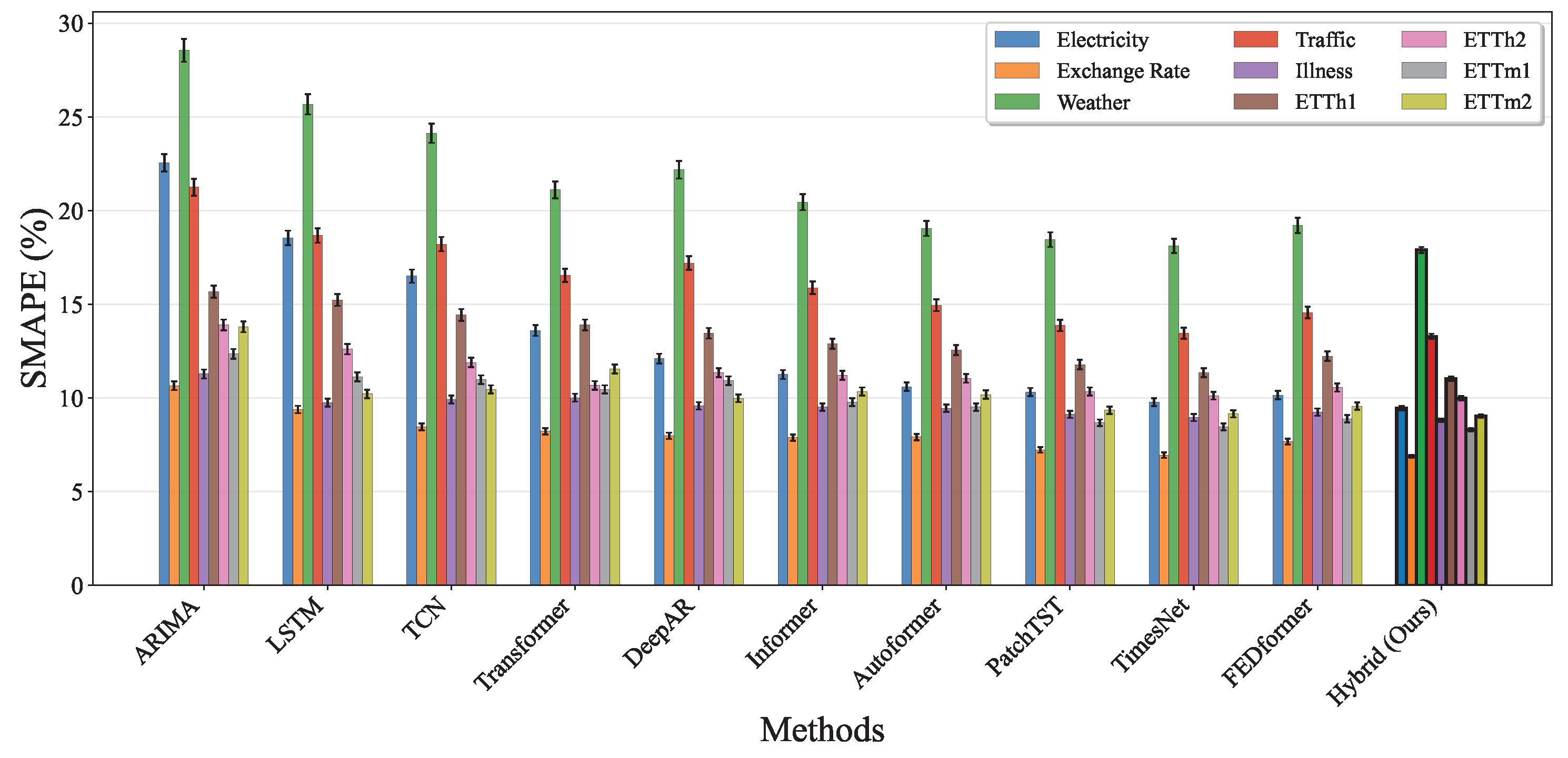
4.6. Comparative Experiment
- On periodic datasets like Electricity and Traffic, our model achieves the lowest MSE and SMAPE by effectively modeling both the linear seasonal component via ARIMA and the nonlinear residuals via the neural network.
- For Exchange Rate, a dataset known for weak seasonality and high stochasticity, our hybrid model outperforms both ARIMA and deep learning models by capturing subtle mean-reverting trends.
- For Weather forecasting, where complex inter-variable dependencies exist, our model leverages the ARIMA module for short-term local trends and the deep component for long-range interactions, resulting in notable error reductions.
- On datasets with strong yearly seasonality, like Illness, our hybrid model surpasses traditional seasonal ARIMA and Transformer variants, especially in longer horizons where extrapolation is more challenging.
- Even in multivariate high-frequency scenarios, like ETTm1 and ETTm2, the hybrid model delivers the most stable and accurate predictions.
5. Ablation Experiment
- No ARIMA: The hybrid model without the ARIMA component, i.e., only the deep residual module is used;
- No Deep: The hybrid model without the deep learning module, equivalent to using only the ARIMA forecast;
- No Adaptive Fusion: Instead of learned fusion weights, a simple static average is used to combine ARIMA and deep model outputs.
- Removing the ARIMA module leads to significant degradation in performance, particularly on datasets with clear periodic structures, such as Electricity, Traffic, and Illness. This highlights the importance of linear modeling for short-term trends and seasonality.
- Excluding the deep component also results in larger errors, especially on datasets where residual nonlinear patterns exist (e.g., Weather, ETTm1, and Exchange Rate). This confirms the benefit of deep networks in capturing complex dynamics beyond the capacity of ARIMA.
- The No Adaptive Fusion variant performs better than the two single-component models but worse than the full hybrid. This suggests that learned fusion weights provide a performance advantage over naive averaging, allowing the model to emphasize the more reliable prediction source under different scenarios.
Short-Term vs. Long-Term Forecasting Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.; Hu, S.; Wang, J.; Deng, Y.; Chen, X.; Fang, Y. Prioritized Information Bottleneck Theoretic Framework With Distributed Online Learning for Edge Video Analytics. IEEE Trans. Netw. 2025, 33, 1203–1219. [Google Scholar] [CrossRef]
- Jain, S.; Agrawal, S.; Mohapatra, E.; Srinivasan, K. A novel ensemble ARIMA-LSTM approach for evaluating COVID-19 cases and future outbreak preparedness. Health Care Sci. 2024, 3, 409–425. [Google Scholar] [CrossRef]
- Lea, C.; Flynn, M.D.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal convolutional networks for action segmentation and detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 156–165. [Google Scholar]
- Lea, C.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal convolutional networks: A unified approach to action segmentation. In Proceedings of the Computer Vision—ECCV 2016 Workshops, Amsterdam, The Netherlands, 8–10 and 15–16 October 2016; Part III 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 47–54. [Google Scholar]
- He, Y.; Zhao, J. Temporal convolutional networks for anomaly detection in time series. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1213, p. 042050. [Google Scholar]
- Wu, B.; Huang, J.; Duan, Q. Real-time Intelligent Healthcare Enabled by Federated Digital Twins with AoI Optimization. IEEE Netw. 2025, in press. [Google Scholar] [CrossRef]
- Wu, B.; Wu, W. Model-Free Cooperative Optimal Output Regulation for Linear Discrete-Time Multi-Agent Systems Using Reinforcement Learning. Math. Probl. Eng. 2023, 2023, 6350647. [Google Scholar] [CrossRef]
- Barrenetxea, M.; Lopez Erauskin, R. Comparison between the ETT and LTT Technologies for Electronic OLTC Transformer Applications. In Proceedings of the 2023 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023. [Google Scholar]
- Huang, J.; Wu, B.; Duan, Q.; Dong, L.; Yu, S. A Fast UAV Trajectory Planning Framework in RIS-assisted Communication Systems with Accelerated Learning via Multithreading and Federating. IEEE Trans. Mob. Comput. 2025, in press. [Google Scholar] [CrossRef]
- Berkowitz, J.; Giorgianni, L. Long-horizon exchange rate predictability? Rev. Econ. Stat. 2001, 83, 81–91. [Google Scholar] [CrossRef]
- Qin, L.; Shanks, K.; Phillips, G.A.; Bernard, D. The impact of lengths of time series on the accuracy of the ARIMA forecasting. Int. Res. High. Educ. 2019, 4, 58–68. [Google Scholar] [CrossRef]
- Redd, A.; Khin, K.; Marini, A. Fast es-rnn: A gpu implementation of the es-rnn algorithm. arXiv 2019, arXiv:1907.03329. [Google Scholar]
- Wu, B.; Cai, Z.; Wu, W.; Yin, X. AoI-aware resource management for smart health via deep reinforcement learning. IEEE Access 2023, 11, 81180–81195. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Ma, Y.; Tao, Y.; Deng, Y.; Chen, X.; Fang, Y. R-ACP: Real-Time Adaptive Collaborative Perception Leveraging Robust Task-Oriented Communications. arXiv 2025, arXiv:2410.04168. [Google Scholar]
- Li, H.; Chen, J.; Zheng, A.; Wu, Y.; Luo, Y. Day-Night Cross-domain Vehicle Re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 12626–12635. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Wu, B.; Huang, J.; Duan, Q. FedTD3: An Accelerated Learning Approach for UAV Trajectory Planning. In Proceedings of the International Conference on Wireless Artificial Intelligent Computing Systems and Applications (WASA), Tokyo, Japan, 24–26 June 2025. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 27268–27286. [Google Scholar]
- Zhu, Q.; Han, J.; Chai, K.; Zhao, C. Time series analysis based on informer algorithms: A survey. Symmetry 2023, 15, 951. [Google Scholar] [CrossRef]
- Pan, D.; Wu, B.N.; Sun, Y.L.; Xu, Y.P. A fault-tolerant and energy-efficient design of a network switch based on a quantum-based nano-communication technique. Sustain. Comput. Inform. Syst. 2023, 37, 100827. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, H.; Wang, H. Data-driven wind-induced response prediction for slender civil infrastructure: Progress, challenges and opportunities. Structures 2025, 74, 108650. [Google Scholar] [CrossRef]
- Sina, L.B.; Secco, C.A.; Blazevic, M.; Nazemi, K. Hybrid Forecasting Methods—A Systematic Review. Electronics 2023, 12, 2019. [Google Scholar] [CrossRef]
- Amreen, S.; Panigrahi, R.; Patne, N.R. Solar Power Forecasting Using Hybrid Model. In Proceedings of the 2023 5th International Conference on Energy, Power and Environment: Towards Flexible Green Energy Technologies (ICEPE), Shillong, India, 15–17 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Benjamin, D.M.; Morstatter, F.; Abbas, A.; Abeliuk, A.; Atanasov, P.; Bennett, S.T.; Beger, A.; Birari, S.; Budescu, D.; Catasta, M.; et al. Hybrid forecasting of geopolitical events. AI Mag. 2023, 44, 112–128. [Google Scholar] [CrossRef]
- Li, L.; Wang, L.; Su, J.Y.; Zou, H.; Chaudhry, S.S. An ARIMA-ANN Hybrid Model for Time Series Forecasting. Syst. Res. Behav. Sci. 2013, 30, 244–259. [Google Scholar] [CrossRef]
- Gasmi, L.; Kabou, S.; Laiche, N.; Nichani, R. Time series forecasting using deep learning hybrid model (ARIMA-LSTM). Stud. Eng. Exact Sci. 2024, 5, e6976. [Google Scholar] [CrossRef]
- Souto, H.G.; Moradi, A. Can Transformers Transform Financial Forecasting? SSRN Electron. J. 2024. [Google Scholar] [CrossRef]
- Zuo, C.; Deng, S.; Wang, J.; Liu, M.; Wang, Q. An Ensemble Framework for Short-Term Load Forecasting Based on TimesNet and TCN. Energies 2023, 16, 5330. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2023, arXiv:1706.03762. [Google Scholar]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]


| Dataset | Horizon | Model | MSE | MAE | SMAPE (%) |
|---|---|---|---|---|---|
| Electricity | 96 | ARIMA | 0.2287 | 0.2266 | 22.55 |
| LSTM | 0.1816 | 0.1783 | 18.54 | ||
| TCN | 0.1638 | 0.1605 | 16.50 | ||
| Transformer | 0.1302 | 0.1281 | 13.60 | ||
| DeepAR | 0.1165 | 0.1133 | 12.10 | ||
| Informer | 0.1072 | 0.1034 | 11.25 | ||
| Autoformer | 0.0987 | 0.0945 | 10.60 | ||
| PatchTST | 0.0963 | 0.0952 | 10.31 | ||
| TimesNet | 0.0889 | 0.0867 | 9.78 | ||
| FEDformer | 0.0976 | 0.0941 | 10.15 | ||
| Hybrid (Ours) | 0.0861 | 0.0840 | 9.45 | ||
| Exchange Rate | 96 | ARIMA | 0.2603 | 0.2433 | 10.65 |
| LSTM | 0.2024 | 0.1985 | 9.38 | ||
| TCN | 0.1923 | 0.1869 | 8.45 | ||
| Transformer | 0.1896 | 0.1811 | 8.22 | ||
| DeepAR | 0.1734 | 0.1687 | 7.98 | ||
| Informer | 0.1698 | 0.1634 | 7.88 | ||
| Autoformer | 0.1645 | 0.1552 | 7.91 | ||
| PatchTST | 0.1537 | 0.1468 | 7.23 | ||
| TimesNet | 0.1478 | 0.1412 | 6.95 | ||
| FEDformer | 0.1612 | 0.1534 | 7.67 | ||
| Hybrid (Ours) | 0.1444 | 0.1382 | 6.89 | ||
| Weather | 192 | ARIMA | 0.3465 | 0.3288 | 28.55 |
| LSTM | 0.2934 | 0.2745 | 25.67 | ||
| TCN | 0.2783 | 0.2602 | 24.13 | ||
| Transformer | 0.2433 | 0.2209 | 21.11 | ||
| DeepAR | 0.2456 | 0.2387 | 22.18 | ||
| Informer | 0.2298 | 0.2145 | 20.45 | ||
| Autoformer | 0.2123 | 0.1984 | 19.05 | ||
| PatchTST | 0.2065 | 0.1943 | 18.45 | ||
| TimesNet | 0.1978 | 0.1856 | 18.12 | ||
| FEDformer | 0.2134 | 0.2007 | 19.21 | ||
| Hybrid (Ours) | 0.1941 | 0.1827 | 17.90 | ||
| Traffic | 336 | ARIMA | 0.4427 | 0.4226 | 21.25 |
| LSTM | 0.3245 | 0.3089 | 18.67 | ||
| TCN | 0.3134 | 0.2976 | 18.21 | ||
| Transformer | 0.2745 | 0.2634 | 16.54 | ||
| DeepAR | 0.2984 | 0.2861 | 17.20 | ||
| Informer | 0.2567 | 0.2411 | 15.88 | ||
| Autoformer | 0.2311 | 0.2202 | 14.95 | ||
| PatchTST | 0.2156 | 0.2054 | 13.87 | ||
| TimesNet | 0.2034 | 0.1923 | 13.45 | ||
| FEDformer | 0.2267 | 0.2143 | 14.56 | ||
| Hybrid (Ours) | 0.1998 | 0.1893 | 13.28 | ||
| Illness | 36 | ARIMA | 0.1444 | 0.1235 | 11.28 |
| LSTM | 0.1156 | 0.1054 | 9.75 | ||
| TCN | 0.1189 | 0.1078 | 9.92 | ||
| Transformer | 0.1203 | 0.1086 | 10.01 | ||
| DeepAR | 0.1134 | 0.1033 | 9.58 | ||
| Informer | 0.1098 | 0.1019 | 9.51 | ||
| Autoformer | 0.1091 | 0.1011 | 9.45 | ||
| PatchTST | 0.1054 | 0.0976 | 9.12 | ||
| TimesNet | 0.1021 | 0.0952 | 8.95 | ||
| FEDformer | 0.1067 | 0.0989 | 9.24 | ||
| Hybrid (Ours) | 0.0995 | 0.0933 | 8.81 | ||
| ETTh1 | 720 | ARIMA | 0.3211 | 0.3065 | 15.67 |
| LSTM | 0.3089 | 0.2934 | 15.23 | ||
| TCN | 0.2899 | 0.2715 | 14.43 | ||
| Transformer | 0.2678 | 0.2534 | 13.89 | ||
| DeepAR | 0.2567 | 0.2423 | 13.45 | ||
| Informer | 0.2445 | 0.2298 | 12.89 | ||
| Autoformer | 0.2366 | 0.2208 | 12.55 | ||
| PatchTST | 0.2187 | 0.2067 | 11.78 | ||
| TimesNet | 0.2134 | 0.1987 | 11.34 | ||
| FEDformer | 0.2298 | 0.2156 | 12.23 | ||
| Hybrid (Ours) | 0.2089 | 0.1943 | 11.02 | ||
| ETTh2 | 336 | ARIMA | 0.2843 | 0.2631 | 13.89 |
| LSTM | 0.2483 | 0.2331 | 12.60 | ||
| TCN | 0.2298 | 0.2156 | 11.89 | ||
| Transformer | 0.2067 | 0.1954 | 10.67 | ||
| DeepAR | 0.2201 | 0.2089 | 11.34 | ||
| Informer | 0.2189 | 0.2034 | 11.21 | ||
| Autoformer | 0.2155 | 0.2007 | 11.04 | ||
| PatchTST | 0.1967 | 0.1856 | 10.34 | ||
| TimesNet | 0.1923 | 0.1801 | 10.12 | ||
| FEDformer | 0.2012 | 0.1889 | 10.56 | ||
| Hybrid (Ours) | 0.1888 | 0.1772 | 9.99 | ||
| ETTm1 | 96 | ARIMA | 0.2384 | 0.2234 | 12.35 |
| LSTM | 0.1934 | 0.1823 | 11.12 | ||
| TCN | 0.1887 | 0.1789 | 10.98 | ||
| Transformer | 0.1756 | 0.1634 | 10.45 | ||
| DeepAR | 0.1865 | 0.1746 | 10.92 | ||
| Informer | 0.1634 | 0.1523 | 9.78 | ||
| Autoformer | 0.1517 | 0.1432 | 9.51 | ||
| PatchTST | 0.1398 | 0.1312 | 8.67 | ||
| TimesNet | 0.1354 | 0.1278 | 8.45 | ||
| FEDformer | 0.1456 | 0.1367 | 8.89 | ||
| Hybrid (Ours) | 0.1326 | 0.1244 | 8.30 | ||
| ETTm2 | 192 | ARIMA | 0.2564 | 0.2431 | 13.80 |
| LSTM | 0.1889 | 0.1771 | 10.21 | ||
| TCN | 0.1945 | 0.1823 | 10.45 | ||
| Transformer | 0.2105 | 0.1983 | 11.54 | ||
| DeepAR | 0.1834 | 0.1724 | 9.98 | ||
| Informer | 0.1923 | 0.1789 | 10.34 | ||
| Autoformer | 0.1879 | 0.1750 | 10.18 | ||
| PatchTST | 0.1689 | 0.1578 | 9.34 | ||
| TimesNet | 0.1634 | 0.1523 | 9.15 | ||
| FEDformer | 0.1756 | 0.1645 | 9.56 | ||
| Hybrid (Ours) | 0.1602 | 0.1493 | 9.02 |
| Dataset | Horizon | Variant | MSE | MAE | SMAPE (%) | PICP (%) |
|---|---|---|---|---|---|---|
| Electricity | 96 | Full Hybrid | 0.0861 | 0.0840 | 9.45 | 94.2 |
| No ARIMA | 0.1140 | 0.1102 | 11.38 | 91.8 | ||
| No Deep | 0.1685 | 0.1592 | 15.81 | 96.4 | ||
| No Adaptive Fusion | 0.0982 | 0.0935 | 10.37 | 89.3 | ||
| No Uncertainty | 0.0861 | 0.0840 | 9.45 | – | ||
| Exchange Rate | 96 | Full Hybrid | 0.1444 | 0.1382 | 6.89 | 93.7 |
| No ARIMA | 0.1732 | 0.1594 | 8.01 | 89.5 | ||
| No Deep | 0.1901 | 0.1767 | 8.48 | 95.8 | ||
| No Adaptive Fusion | 0.1583 | 0.1453 | 7.42 | 87.9 | ||
| No Uncertainty | 0.1444 | 0.1382 | 6.89 | – | ||
| Weather | 192 | Full Hybrid | 0.1941 | 0.1827 | 17.90 | 94.8 |
| No ARIMA | 0.2210 | 0.2015 | 19.55 | 92.1 | ||
| No Deep | 0.3025 | 0.2807 | 26.24 | 96.2 | ||
| No Adaptive Fusion | 0.2088 | 0.1962 | 18.73 | 88.6 | ||
| No Uncertainty | 0.1941 | 0.1827 | 17.90 | – | ||
| Traffic | 336 | Full Hybrid | 0.1998 | 0.1893 | 13.28 | 93.9 |
| No ARIMA | 0.2635 | 0.2488 | 17.10 | 90.3 | ||
| No Deep | 0.3160 | 0.2912 | 19.92 | 95.7 | ||
| No Adaptive Fusion | 0.2217 | 0.2054 | 14.72 | 86.4 | ||
| No Uncertainty | 0.1998 | 0.1893 | 13.28 | – | ||
| Illness | 36 | Full Hybrid | 0.0995 | 0.0933 | 8.81 | 94.6 |
| No ARIMA | 0.1238 | 0.1122 | 10.43 | 91.2 | ||
| No Deep | 0.1327 | 0.1191 | 10.95 | 96.1 | ||
| No Adaptive Fusion | 0.1075 | 0.0998 | 9.14 | 88.1 | ||
| No Uncertainty | 0.0995 | 0.0933 | 8.81 | – | ||
| ETTh1 | 720 | Full Hybrid | 0.2089 | 0.1943 | 11.02 | 93.8 |
| No ARIMA | 0.2481 | 0.2304 | 13.24 | 89.9 | ||
| No Deep | 0.2846 | 0.2602 | 14.70 | 95.4 | ||
| No Adaptive Fusion | 0.2223 | 0.2067 | 11.90 | 85.7 | ||
| No Uncertainty | 0.2089 | 0.1943 | 11.02 | – | ||
| ETTh2 | 336 | Full Hybrid | 0.1888 | 0.1772 | 9.99 | 94.1 |
| No ARIMA | 0.2134 | 0.1988 | 11.45 | 91.7 | ||
| No Deep | 0.2509 | 0.2305 | 12.64 | 95.9 | ||
| No Adaptive Fusion | 0.2013 | 0.1899 | 10.42 | 87.2 | ||
| No Uncertainty | 0.1888 | 0.1772 | 9.99 | – | ||
| ETTm1 | 96 | Full Hybrid | 0.1326 | 0.1244 | 8.30 | 94.4 |
| No ARIMA | 0.1578 | 0.1451 | 9.81 | 90.8 | ||
| No Deep | 0.1823 | 0.1705 | 10.82 | 96.3 | ||
| No Adaptive Fusion | 0.1445 | 0.1347 | 8.95 | 86.9 | ||
| No Uncertainty | 0.1326 | 0.1244 | 8.30 | – | ||
| ETTm2 | 192 | Full Hybrid | 0.1602 | 0.1493 | 9.02 | 93.5 |
| No ARIMA | 0.1807 | 0.1669 | 10.12 | 90.1 | ||
| No Deep | 0.2016 | 0.1865 | 11.54 | 95.6 | ||
| No Adaptive Fusion | 0.1729 | 0.1604 | 9.48 | 87.8 | ||
| No Uncertainty | 0.1602 | 0.1493 | 9.02 | – |
| Dataset | Horizon Range | Optimal | MSE | MAE | SMAPE (%) |
|---|---|---|---|---|---|
| Electricity | Short (≤96) | 0.8 | 0.0861 | 0.0840 | 9.45 |
| Medium (97–336) | 0.6 | 0.0945 | 0.0923 | 10.12 | |
| Long (>336) | 0.4 | 0.1124 | 0.1089 | 11.78 | |
| Exchange Rate | Short (≤96) | 0.7 | 0.1444 | 0.1382 | 6.89 |
| Medium (97–336) | 0.4 | 0.1687 | 0.1598 | 7.92 | |
| Long (>336) | 0.3 | 0.1923 | 0.1812 | 8.84 | |
| Traffic | Short (≤96) | 0.8 | 0.1756 | 0.1689 | 11.23 |
| Medium (97–336) | 0.6 | 0.1998 | 0.1893 | 13.28 | |
| Long (>336) | 0.5 | 0.2234 | 0.2156 | 14.67 | |
| Weather | Short (≤96) | 0.7 | 0.1678 | 0.1589 | 15.34 |
| Medium (97–336) | 0.5 | 0.1941 | 0.1827 | 17.90 | |
| Long (>336) | 0.3 | 0.2187 | 0.2034 | 19.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, Z.; Zhang, W. A Hybrid Framework Integrating Traditional Models and Deep Learning for Multi-Scale Time Series Forecasting. Entropy 2025, 27, 695. https://doi.org/10.3390/e27070695
Liu Z, Zhang Z, Zhang W. A Hybrid Framework Integrating Traditional Models and Deep Learning for Multi-Scale Time Series Forecasting. Entropy. 2025; 27(7):695. https://doi.org/10.3390/e27070695
Chicago/Turabian StyleLiu, Zihan, Zijia Zhang, and Weizhe Zhang. 2025. "A Hybrid Framework Integrating Traditional Models and Deep Learning for Multi-Scale Time Series Forecasting" Entropy 27, no. 7: 695. https://doi.org/10.3390/e27070695
APA StyleLiu, Z., Zhang, Z., & Zhang, W. (2025). A Hybrid Framework Integrating Traditional Models and Deep Learning for Multi-Scale Time Series Forecasting. Entropy, 27(7), 695. https://doi.org/10.3390/e27070695






