Transverse Self-Propulsion Enhances the Aggregation of Active Dumbbells
Abstract
1. Introduction
2. Model and Numerical Methods
3. Results
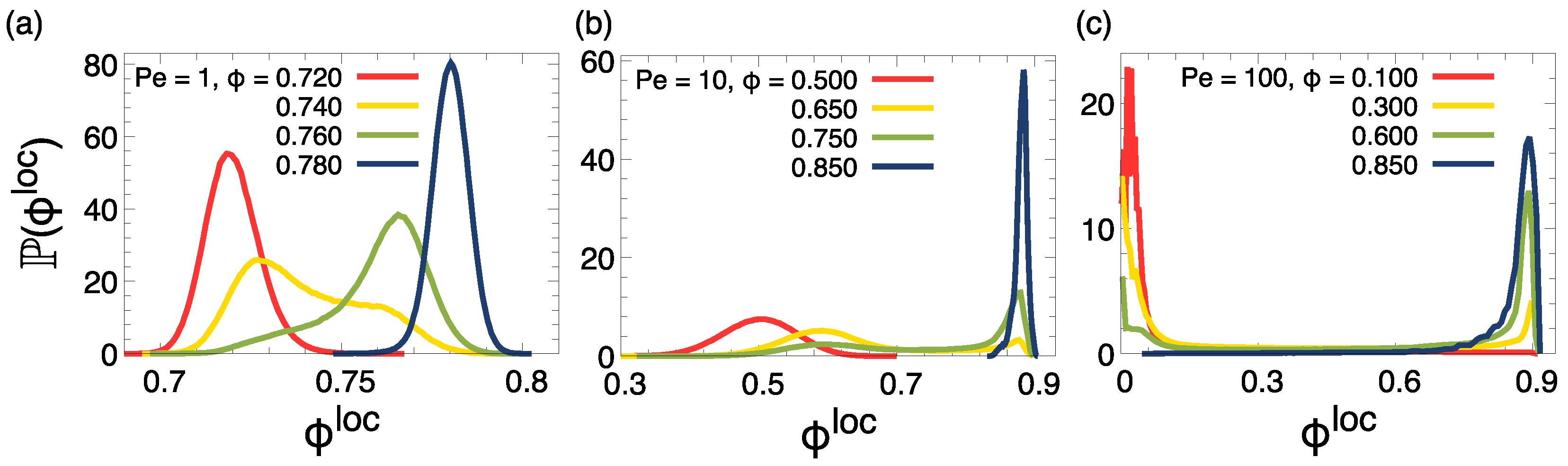
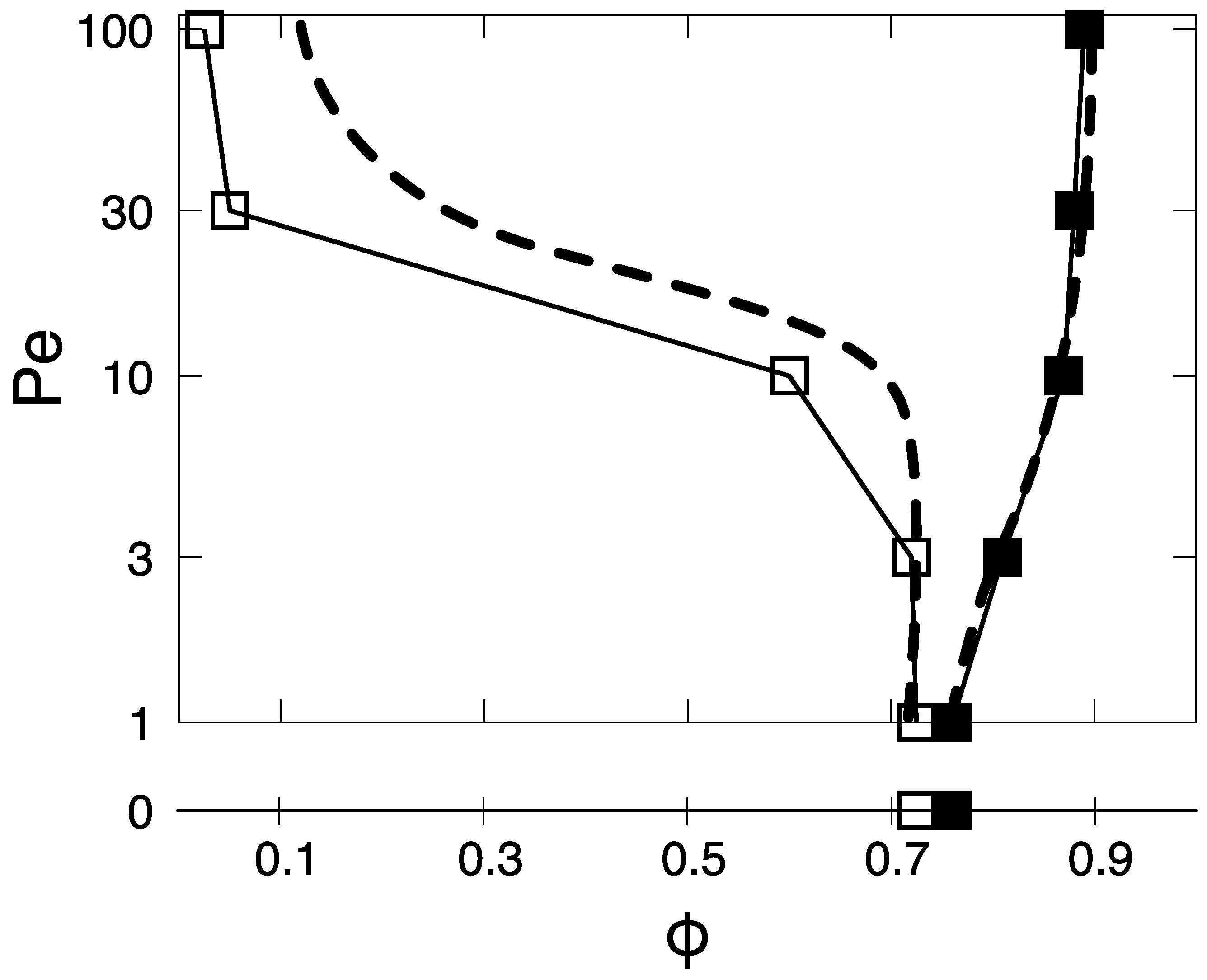
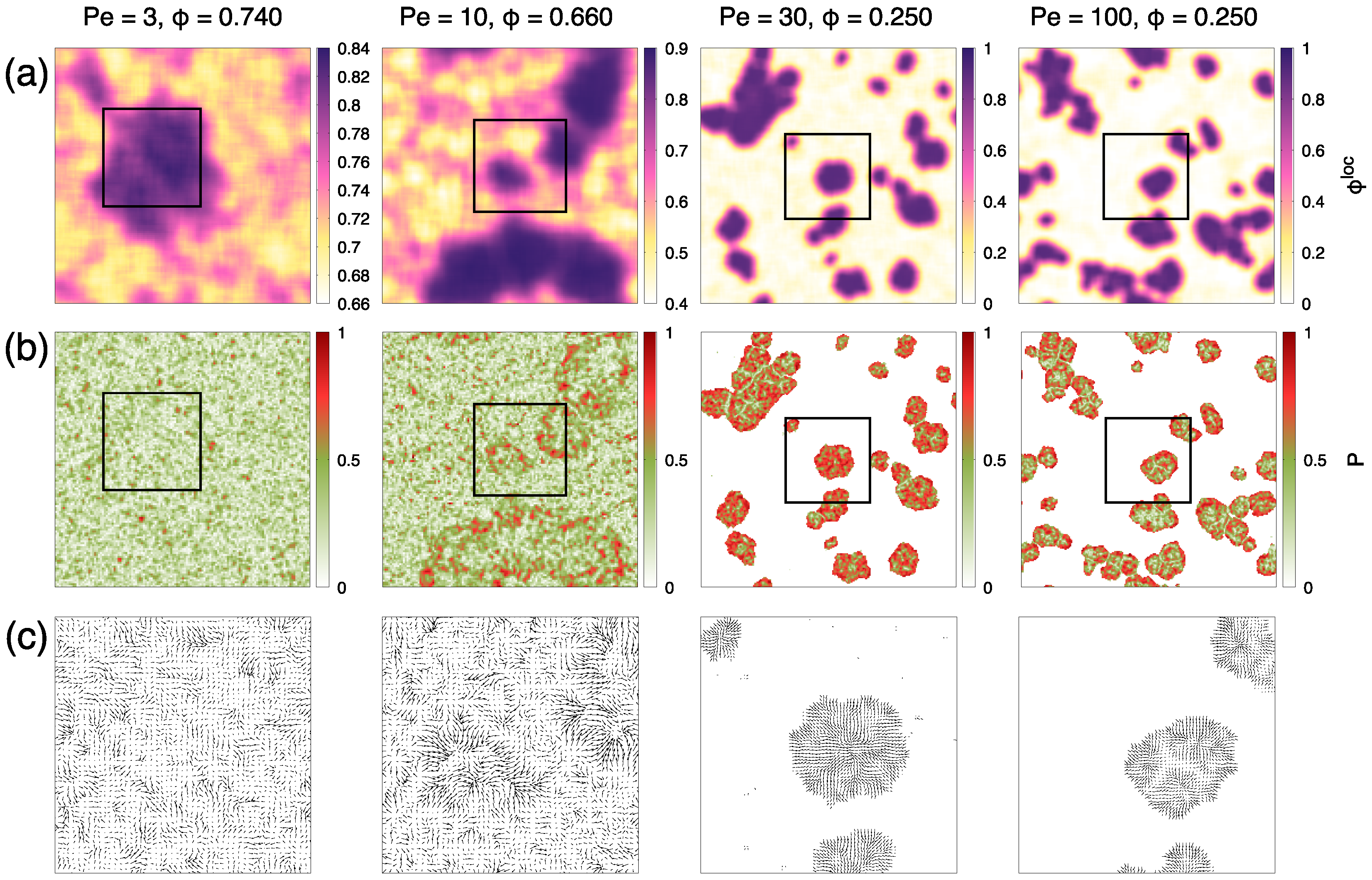
3.1. Phase Diagram
3.2. Comparison Between Transverse and Axially Driven Dumbbells and Aggregation Mechanisms
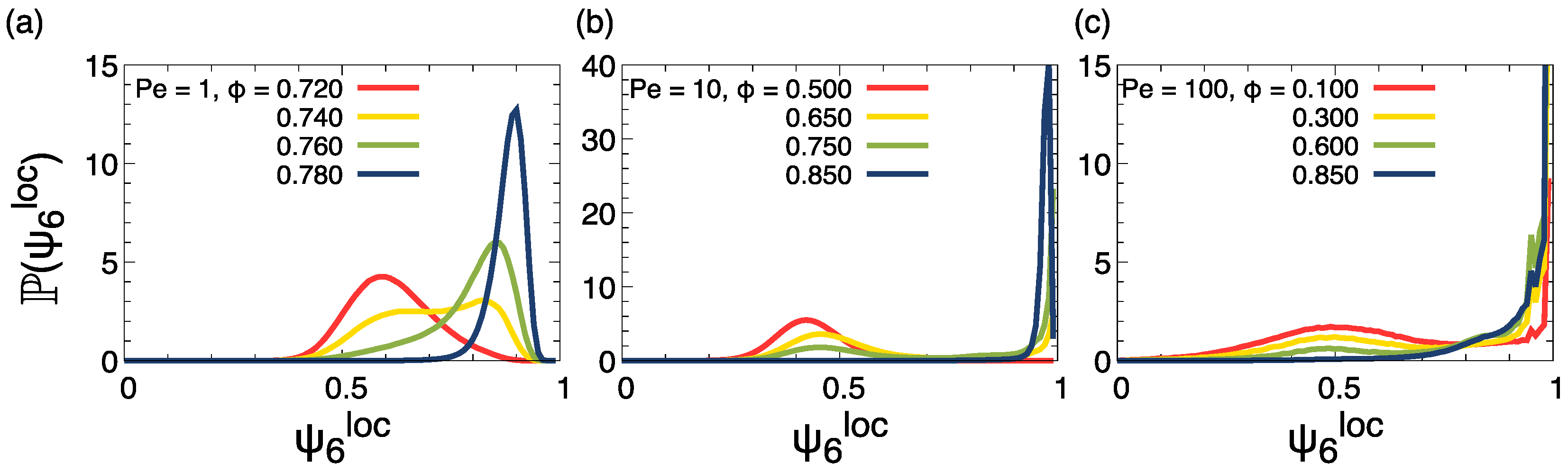
3.3. Hexatic Ordering of the Dense Phase
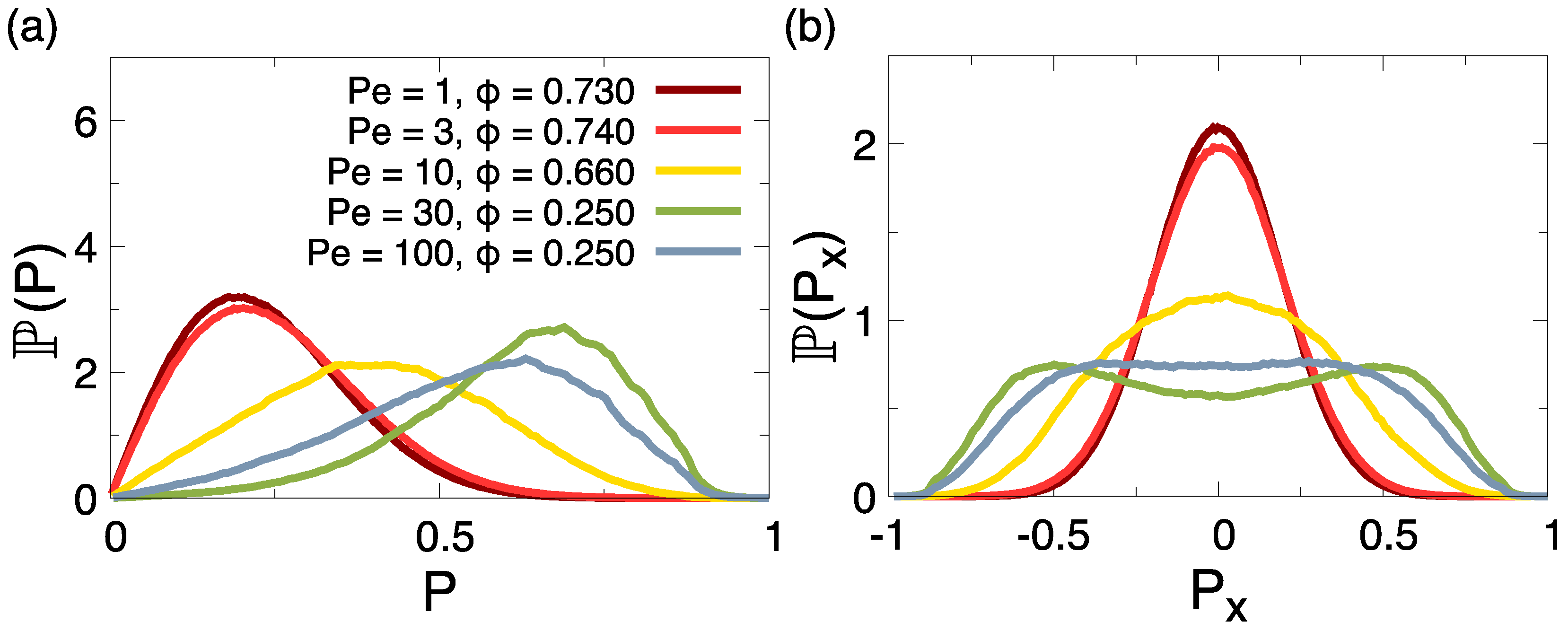
3.4. Polarization of Dense Phase
3.5. Rotational Properties of Clusters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bechinger, C.; Leonardo, R.D.; Löwen, H.; Reichhardt, C.; Volpe, G.; Volpe, G. Active particles in complex and crowded environments. Rev. Mod. Phys. 2016, 88, 045006. [Google Scholar] [CrossRef]
- Ramaswamy, S. The mechanics and statistics of active matter. Annu. Rev. Cond. Matt. Phys. 2010, 1, 323. [Google Scholar] [CrossRef]
- Vicsek, T.; Zafeiris, A. Collective motion. Phys. Rep. 2012, 517, 71. [Google Scholar] [CrossRef]
- Marchetti, M.C.; Joanny, J.F.; Ramaswamy, S.; Liverpool, T.B.; Prost, J.; Rao, M.; Simha, R.A. Hydrodynamics of soft active matter. Rev. Mod. Phys. 2013, 85, 1143. [Google Scholar] [CrossRef]
- Elgeti, J.; Winkler, R.; Gompper, G. Physics of Microswimmers—Single Particle Motion and Collective Behavior. Rep. Prog. Phys. 2015, 78, 056601. [Google Scholar] [CrossRef]
- Te Vrugt, M.; Wittkowski, R. Metareview: A survey of active matter reviews. Eur. Phys. J. E 2025, 48, 12. [Google Scholar] [CrossRef]
- Sanchez, T.; Chen, D.; DeCamp, S.; Heymann, M.; Dogic, Z. Spontaneous motion in hierarchically assembled active matter. Nature 2012, 491, 431–434. [Google Scholar] [CrossRef]
- De Magistris, G.; Marenduzzo, D. An introduction to the physics of active matter. Phys. A 2015, 418, 65–77. [Google Scholar] [CrossRef]
- Kumar, N.; Zhang, R.; de Pablo, J.; Gardel, M.L. Tunable structure and dynamics of active liquid crystals. Sci. Adv. 2018, 4, eaat7779. [Google Scholar] [CrossRef]
- Doostmohammadi, A.; Ignés-Mullol, J.; Yeomans, J.; Sagués, F. Active nematics. Nat. Commun. 2018, 9, 3246. [Google Scholar] [CrossRef]
- Saintillan, D. Rheology of Active Fluids. Annu. Rev. Fluid Mech. 2018, 50, 563–592. [Google Scholar] [CrossRef]
- Giordano, M.G.; Bonelli, F.; Carenza, L.N.; Gonnella, G.; Negro, G. Activity-induced isotropic-polar transition in active liquid crystals. Europhys. Lett. 2021, 133, 58004. [Google Scholar] [CrossRef]
- Zhang, Y.; Fodor, E. Pulsating active matter. Phys. Rev. Lett. 2023, 131, 238302. [Google Scholar] [CrossRef]
- Hernández-López, C.; Baconnier, P.; Coulais, C.; Dauchot, O.; Düring, G. Model of Active Solids: Rigid Body Motion and Shape-Changing Mechanisms. Phys. Rev. Lett. 2024, 132, 238303. [Google Scholar] [CrossRef]
- Wiese, R.; Kroy, K.; Levis, D. Fluid-Glass-Jamming Rheology of Soft Active Brownian Particles. Phys. Rev. Lett. 2023, 131, 178302. [Google Scholar] [CrossRef]
- Caprini, L.; Löwen, H. Flocking without alignment interactions in attractive active Brownian particles. Phys. Rev. Lett. 2023, 130, 148202. [Google Scholar] [CrossRef]
- Favuzzi, I.; Carenza, L.; Corberi, F.; Gonnella, G.; Lamura, A.; Negro, G. Rheology of active emulsions with negative effective viscosity. Soft Mater. 2021, 19, 334–345. [Google Scholar] [CrossRef]
- Bayram, A.G.; Schwarzendahl, F.J.; Löwen, H.; Biancofiore, L. Motility-induced shear thickening in dense colloidal suspensions. Soft Matter 2023, 19, 4571. [Google Scholar] [CrossRef]
- Caprini, L.; Cecconi, F.; Maggi, C.; Marini Bettolo Marconi, U. Activity-controlled clogging and unclogging of microchannels. Phys. Rev. Res. 2020, 2, 043359. [Google Scholar] [CrossRef]
- Digregorio, P.; Levis, D.; Suma, A.; Cugliandolo, L.F.; Gonnella, G.; Pagonabarraga, I. Full Phase Diagram of Active Brownian Disks: From Melting to Motility-Induced Phase Separation. Phys. Rev. Lett. 2018, 121, 098003. [Google Scholar] [CrossRef]
- Digregorio, P.; Levis, D.; Suma, A.; Cugliandolo, L.F.; Gonnella, G.; Pagonabarraga, I. 2D melting and motility induced phase separation in Active Brownian Hard Disks and Dumbbells. J. Phys. Conf. Ser. 2019, 1163, 012073. [Google Scholar] [CrossRef]
- Fily, Y.; Marchetti, M.C. Athermal phase separation of self-propelled particles with no alignment. Phys. Rev. Lett. 2012, 108, 235702. [Google Scholar] [CrossRef] [PubMed]
- Redner, G.S.; Hagan, M.F.; Baskaran, A. Structure and dynamics of a phase-separating active colloidal fluid. Phys. Rev. Lett. 2013, 110, 055701. [Google Scholar] [CrossRef] [PubMed]
- Semeraro, M.; Negro, G.; Suma, A.; Corberi, F.; Gonnella, G. Entropy production of active Brownian particles going from liquid to hexatic and solid phases. Europhys. Lett. 2024, 148, 37001. [Google Scholar] [CrossRef]
- Tailleur, J.; Cates, M.E. Statistical mechanics of interacting run-and-tumble bacteria. Phys. Rev. Lett. 2008, 100, 218103. [Google Scholar] [CrossRef]
- Cates, M.E.; Tailleur, J. Motility-Induced Phase Separation. Annu. Rev. Cond. Matt. Phys. 2015, 6, 219. [Google Scholar] [CrossRef]
- Wittkowski, R.; Tiribocchi, A.; Stenhammar, J.; Allen, R.; Marenduzzo, D.; Cates, M. Scalar ϕ4 field theory for active-particle phase separation. Nat. Commun. 2014, 5, 4351. [Google Scholar] [CrossRef]
- Stenhammar, J.; Marenduzzo, D.; Allen, R.J.; Cates, M.E. Phase behaviour of active Brownian particles: The role of dimensionality. Soft Matter 2014, 10, 1489–1499. [Google Scholar] [CrossRef]
- Tjhung, E.; Nardini, C.; Cates, M.E. Cluster Phases and Bubbly Phase Separation in Active Fluids: Reversal of the Ostwald Process. Phys. Rev. X 2018, 8, 031080. [Google Scholar] [CrossRef]
- Moran, S.E.; Bruss, I.R.; Schönhöfer, P.W.A.; Glotzer, S.C. Particle anisotropy tunes emergent behavior in active colloidal systems. Soft Matter 2022, 18, 1044. [Google Scholar] [CrossRef]
- Peruani, F.; Deutsch, A.; Bär, M. Nonequilibrium clustering of self-propelled rods. Phys. Rev. E 2006, 74, 030904(R). [Google Scholar] [CrossRef] [PubMed]
- Ginelli, F.; Peruani, F.; Bär, M.; Chaté, H. Large-scale collective properties of self-propelled rods. Phys. Rev. Lett. 2010, 104, 184502. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Marceau, V.; Gompper, G. Swarm behavior of self-propelled rods and swimming flagella. Phys. Rev. E 2010, 82, 031904. [Google Scholar] [CrossRef]
- van Damme, R.; Rodenburg, J.; van Roij, R.; Dijkstra, M. Interparticle torques suppress motility-induced phase separation for rodlike particles. J. Chem. Phys. 2019, 150, 164501. [Google Scholar] [CrossRef]
- Bär, M.; Grossmann, R.; Heidenreich, S.; Peruani, F. Self-Propelled Rods: Insights and Perspectives for Active Matter. Annu. Rev. Cond. Matt. Phys. 2020, 11, 441. [Google Scholar] [CrossRef]
- Paoluzzi, M.; Levis, D.; Pagonabarraga, I. From flocking to glassiness in dense disordered polar active matter. Commun. Phys. 2024, 7, 57. [Google Scholar] [CrossRef]
- Takatori, S.C.; Yan, W.; Brady, J.F. Swim Pressure: Stress Generation in Active Matter. Phys. Rev. Lett. 2014, 113, 028103. [Google Scholar] [CrossRef]
- Solon, A.P.; Stenhammar, J.; Wittkowski, R.; Kardar, M.; Kafri, Y.; Cates, M.E.; Tailleur, J. Pressure and Phase Equilibria in Interacting Active Brownian Spheres. Phys. Rev. Lett. 2015, 114, 198301. [Google Scholar] [CrossRef]
- Ginot, F.; Theurkauff, I.; Levis, D.; Ybert, C.; Bocquet, L.; Berthier, L.; Cottin-Bizonne, C. Nonequilibrium Equation of State in Suspensions of Active Colloids. Phys. Rev. X 2015, 5, 011004. [Google Scholar] [CrossRef]
- Fily, Y.; Kafri, Y.; Solon, A.P.; Tailleur, J.; Turner, A. Mechanical pressure and momentum conservation in dry active matter. J. Phys. A 2018, 51, 044003. [Google Scholar] [CrossRef]
- Joyeux, M.; Bertin, E. Pressure of a gas of underdamped active dumbbells. Phys. Rev. E 2016, 93, 032605. [Google Scholar] [CrossRef] [PubMed]
- Joyeux, M. Recovery of mechanical pressure in a gas of underdamped active dumbbells with Brownian noise. Phys. Rev. E 2017, 95, 052603. [Google Scholar] [CrossRef]
- Pirhadi, E.; Cheng, X.; Yong, X. Dependency of active pressure and equation of state on stiffness of wall. Sci. Rep. 2021, 11, 22204. [Google Scholar] [CrossRef] [PubMed]
- Suma, A.; Marenduzzo, D.; Gonnella, G.; Orlandini, E. Motility-induced phase separation in an active dumbbell fluid. Europhys. Lett. 2014, 108, 56004. [Google Scholar] [CrossRef]
- Cugliandolo, L.F.; Digregorio, P.; Gonnella, G.; Suma, A. Phase co-existence in bidimensional passive and active dumbbell systems. Phys. Rev. Lett. 2017, 119, 268002. [Google Scholar] [CrossRef]
- Petrelli, I.; Digregorio, P.; Cugliandolo, L.F.; Gonnella, G.; Suma, A. Active dumbbells: Dynamics and morphology in the coexisting region. Eur. Phys. J. E 2018, 41, 128. [Google Scholar] [CrossRef]
- Caporusso, C.B.; Negro, G.; Suma, A.; Digregorio, P.; Carenza, L.N.; Gonnella, G.; Cugliandolo, L.F. Phase behaviour and dynamics of three-dimensional active dumbbell systems. Soft Matter 2024, 20, 923. [Google Scholar] [CrossRef]
- Caporusso, C.B.; Cugliandolo, L.F.; Digregorio, P.; Gonnella, G.; Suma, A. Phase separation kinetics and cluster dynamics in two-dimensional active dumbbell systems. Soft Matter 2024, 20, 4208–4225. [Google Scholar] [CrossRef]
- Cugliandolo, L.F.; Gonnella, G.; Suma, A. Rotational and translational diffusion in an interacting active dumbbell system. Phys. Rev. E 2015, 91, 062124. [Google Scholar] [CrossRef]
- Tung, C.; Harder, J.; Valeriani, C.; Cacciuto, A. Micro-phase separation in two dimensional suspensions of self-propelled spheres and dumbbells. Soft Matter 2016, 12, 555. [Google Scholar] [CrossRef]
- Schwarz-Linek, J.; Valeriani, C.; Cacciuto, A.; Cates, M.; Marenduzzo, D.; Morozov, A.; Poon, W. Phase separation and rotor self-assembly in active particle suspensions. Proc. Natl. Acad. Sci. USA 2012, 109, 4052. [Google Scholar] [CrossRef] [PubMed]
- Siebert, J.T.; Letz, J.; Speck, T.; Virnau, P. Phase behavior of active Brownian disks, spheres, and dumbbells. Soft Matter 2017, 13, 1020. [Google Scholar] [CrossRef] [PubMed]
- Fei, W.; Gu, Y.; Bishop, K.J. Active colloidal particles at fluid-fluid interfaces. Curr. Opin. Colloid Interface Sci. 2017, 32, 57–68. [Google Scholar] [CrossRef]
- Lee, J.G.; Al Harraq, A.; Bishop, K.J.M.; Bharti, B. Fabrication and Electric Field-Driven Active Propulsion of Patchy Microellipsoids. J. Phys. Chem. B 2021, 125, 4232–4240. [Google Scholar] [CrossRef]
- Parisi, D.R.; Cruz Hidalgo, R.; Zuriguel, I. Active particles with desired orientation flowing through a bottleneck. Sci. Rep. 2018, 8, 9133. [Google Scholar] [CrossRef]
- Andersen, H.C. RATTLE: A “Velocity” Version of the SHAKE Algorithm for Molecular Dynamics Calculations. J. Comp. Phys. 1983, 52, 24. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1989; p. 385. [Google Scholar]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996. [Google Scholar]


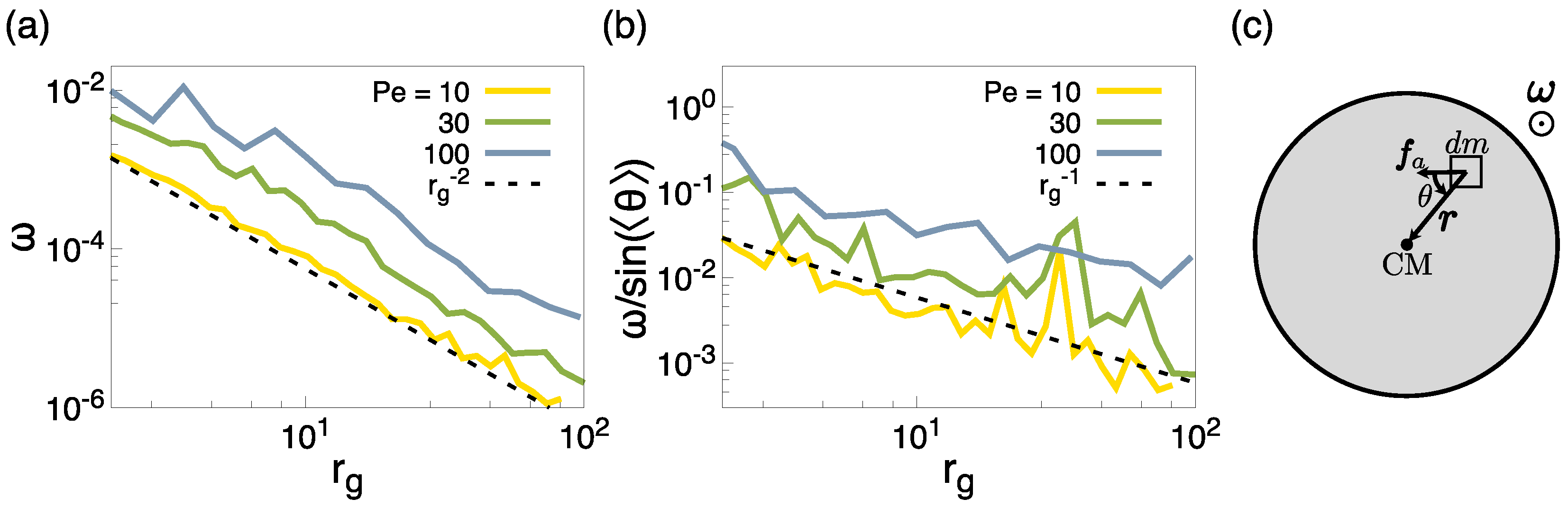
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Digregorio, P.; Caporusso, C.B.; Carenza, L.M.; Gonnella, G.; Moretti, D.; Negro, G.; Semeraro, M.; Suma, A. Transverse Self-Propulsion Enhances the Aggregation of Active Dumbbells. Entropy 2025, 27, 692. https://doi.org/10.3390/e27070692
Digregorio P, Caporusso CB, Carenza LM, Gonnella G, Moretti D, Negro G, Semeraro M, Suma A. Transverse Self-Propulsion Enhances the Aggregation of Active Dumbbells. Entropy. 2025; 27(7):692. https://doi.org/10.3390/e27070692
Chicago/Turabian StyleDigregorio, Pasquale, Claudio Basilio Caporusso, Lucio Mauro Carenza, Giuseppe Gonnella, Daniela Moretti, Giuseppe Negro, Massimiliano Semeraro, and Antonio Suma. 2025. "Transverse Self-Propulsion Enhances the Aggregation of Active Dumbbells" Entropy 27, no. 7: 692. https://doi.org/10.3390/e27070692
APA StyleDigregorio, P., Caporusso, C. B., Carenza, L. M., Gonnella, G., Moretti, D., Negro, G., Semeraro, M., & Suma, A. (2025). Transverse Self-Propulsion Enhances the Aggregation of Active Dumbbells. Entropy, 27(7), 692. https://doi.org/10.3390/e27070692





