Impact of Calcium and Potassium Currents on Spiral Wave Dynamics in the LR1 Model
Abstract
1. Introduction
2. Materials and Methods
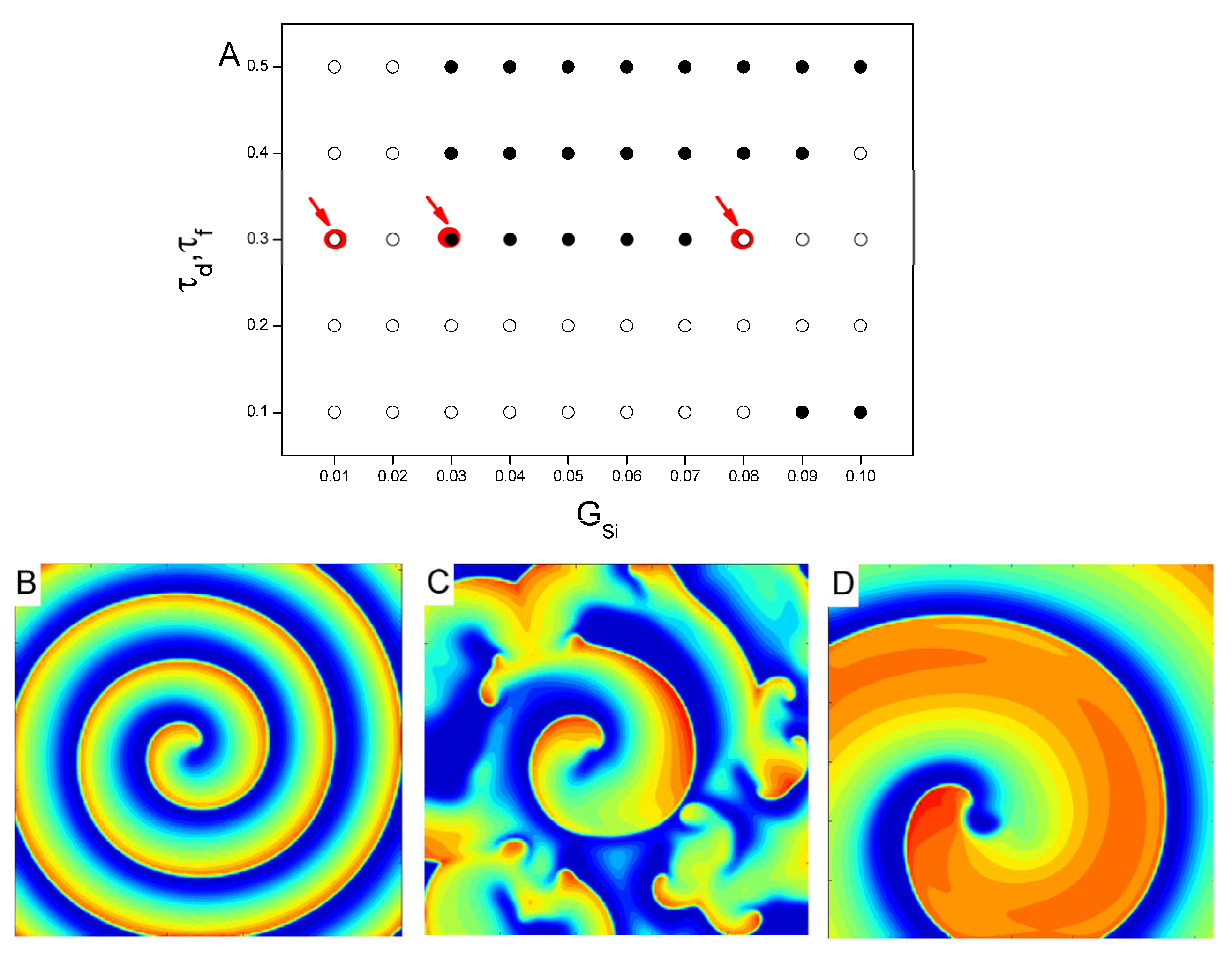
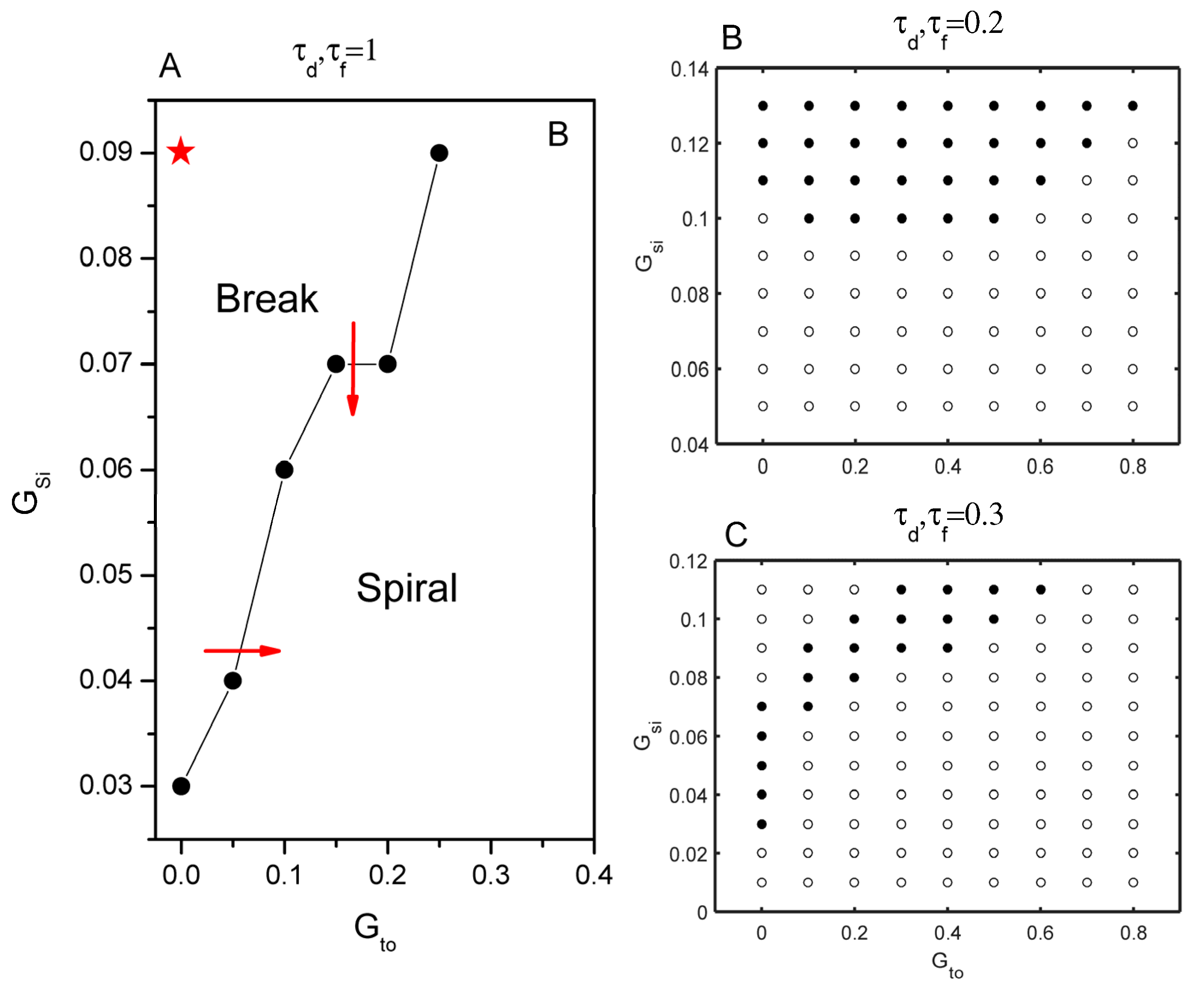
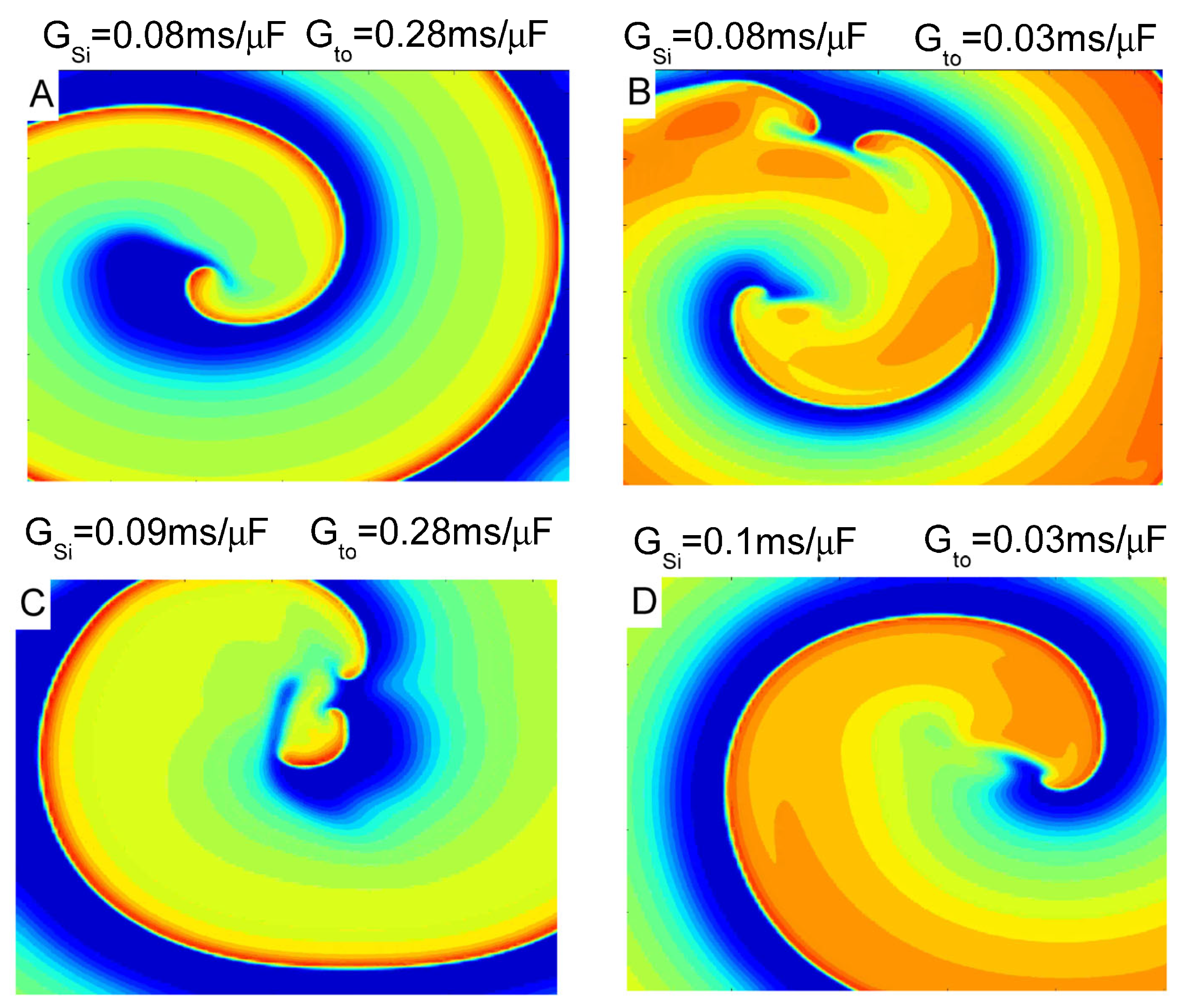
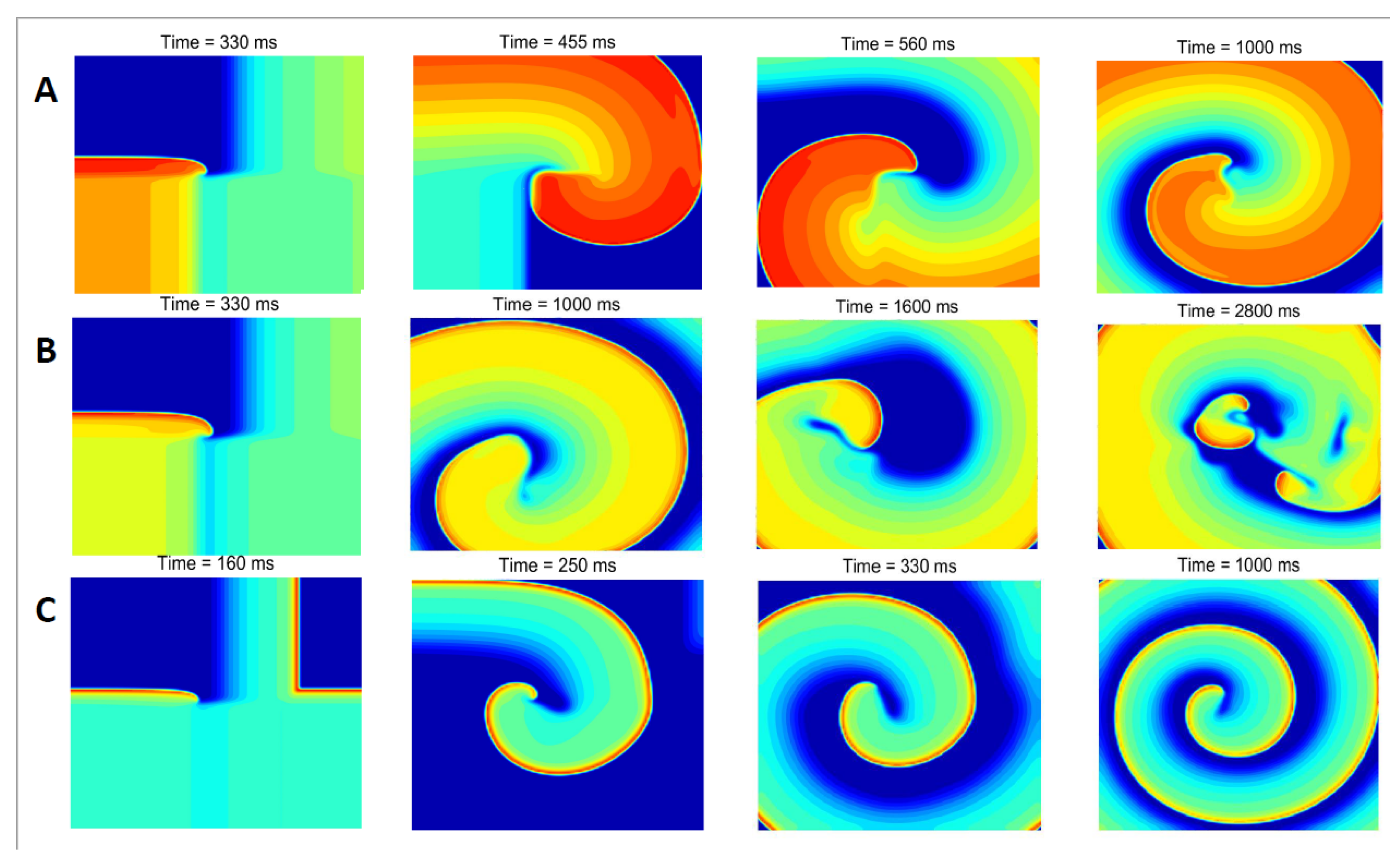
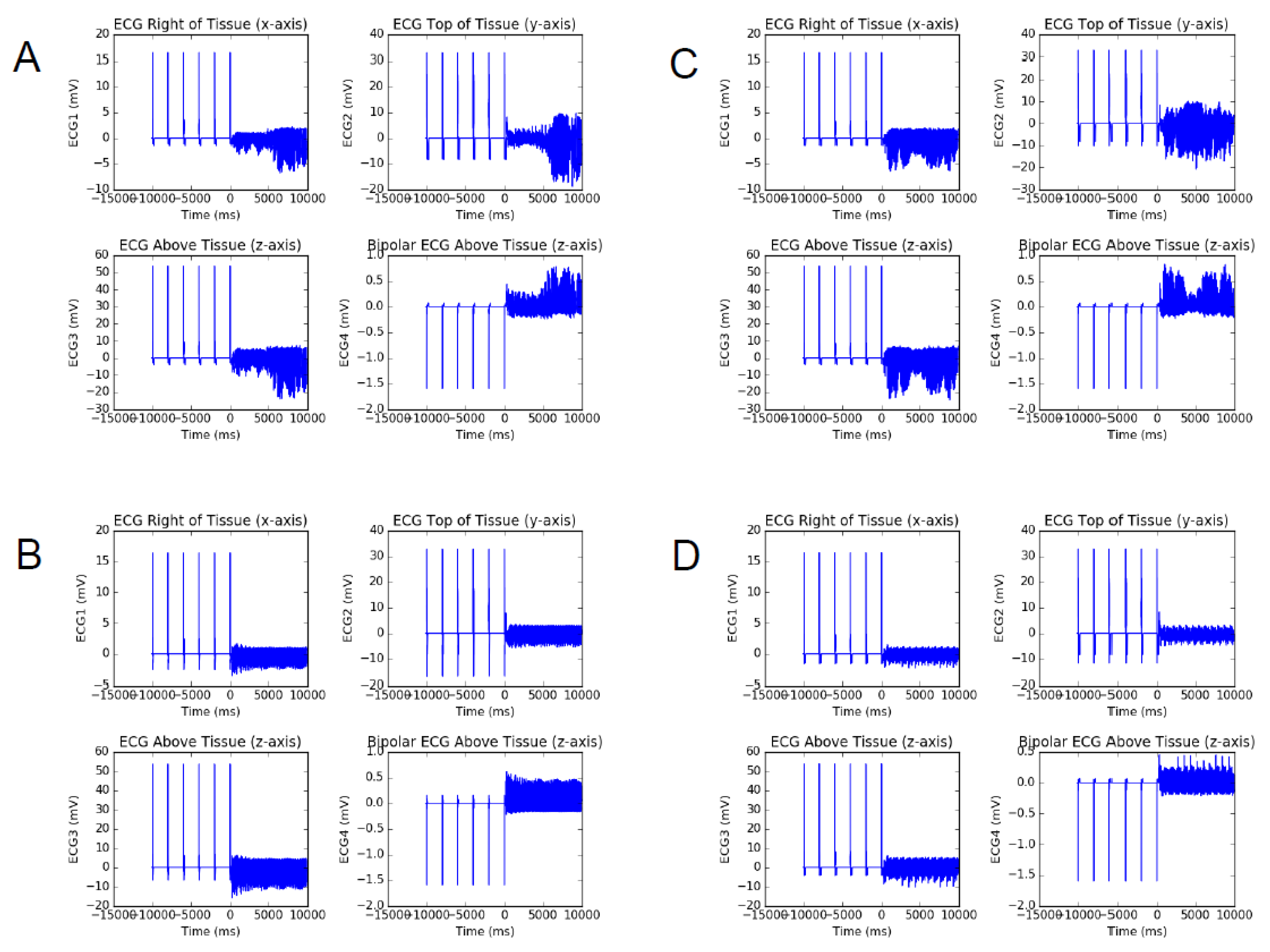
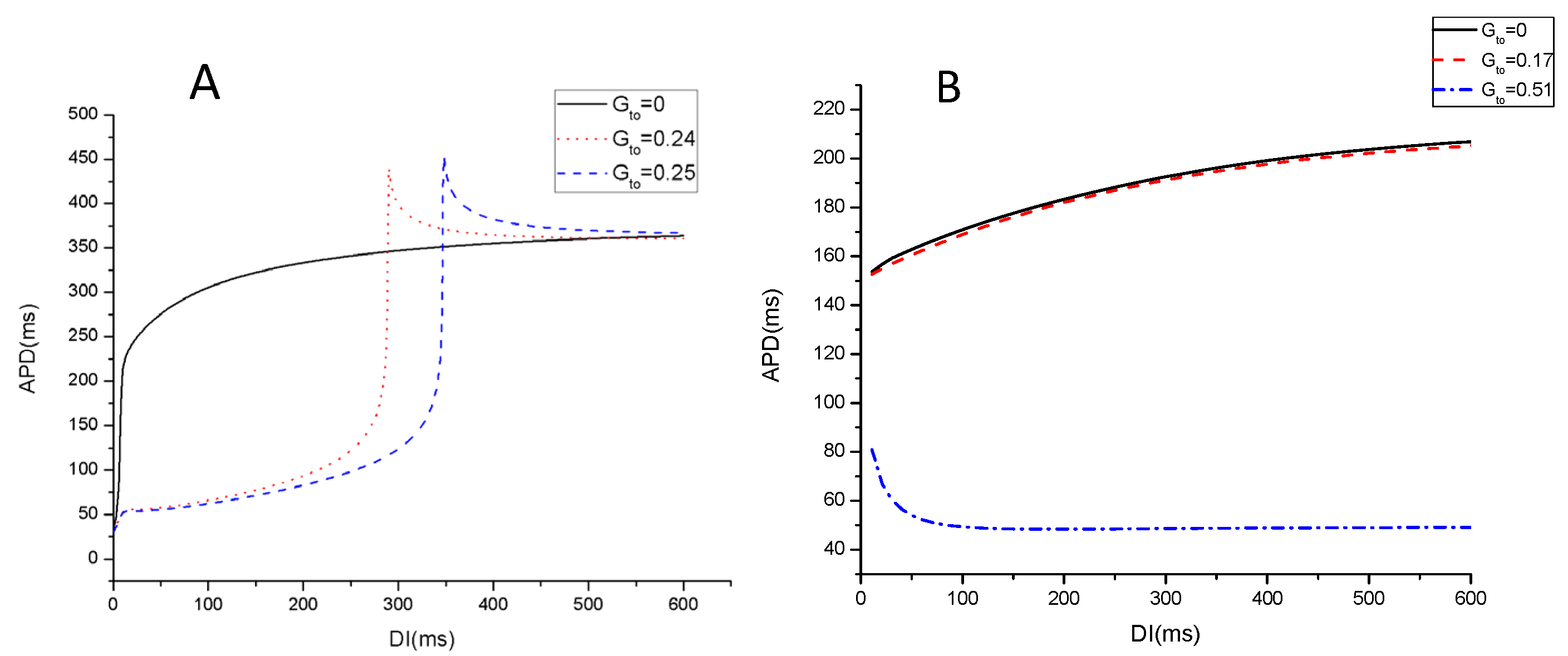
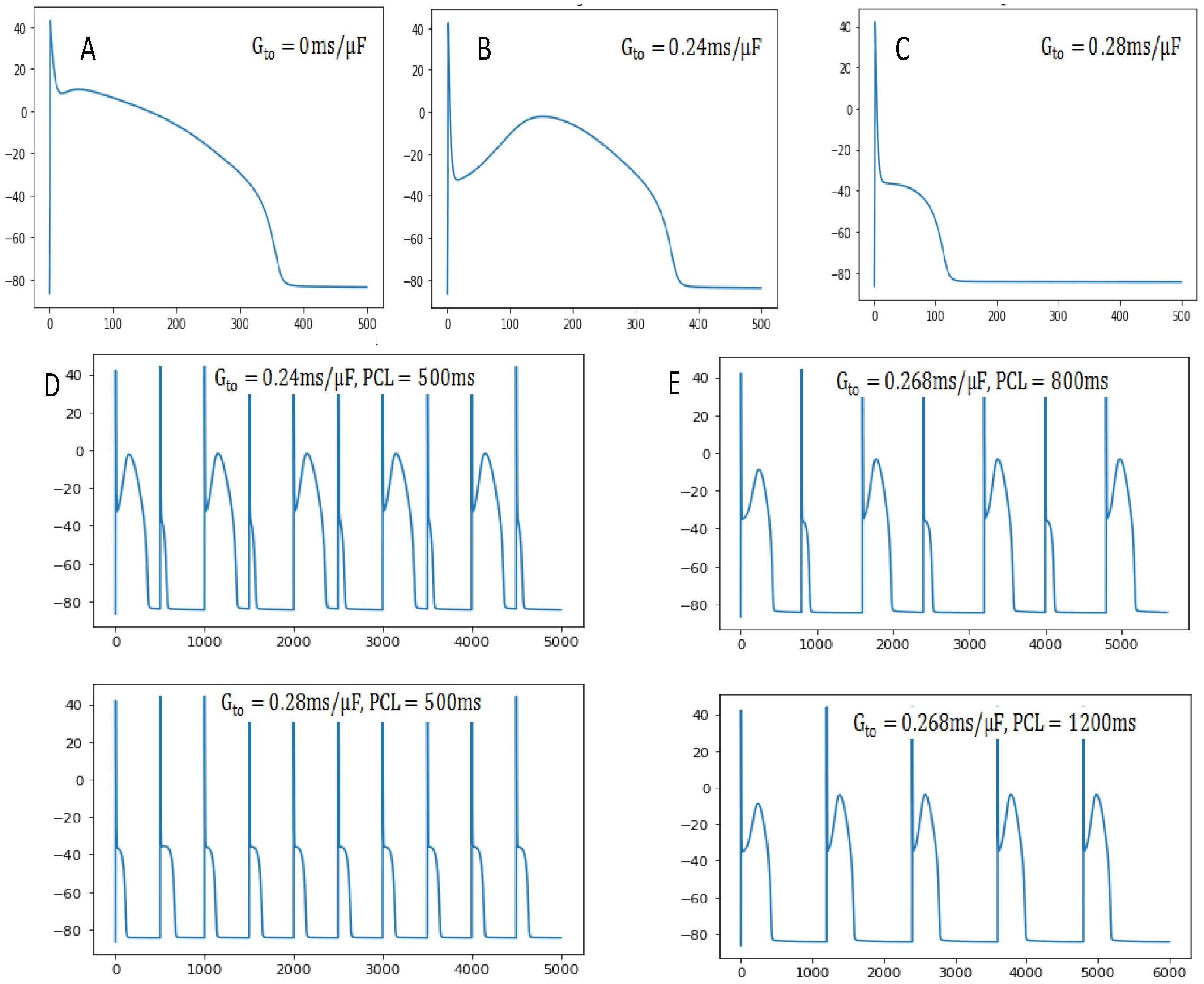
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DI | diastolic interval |
| PCL | pacing cycle length |
| APD | action potential duration |
| ECG | electrocardiogram |
| Ito | transient outward current |
| Isi | slow inward calcium current |
References
- ten Tusscher, K.H.; Panfilov, A.V. Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Heart Circ. Physiol. 2006, 291, H1088–H1100. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z.; Xie, F.; Garfinkel, A.; Weiss, J.N. Origins of spiral wave meander and breakup in a two-dimensional cardiac tissue model. Ann. Biomed. Eng. 2000, 28, 755–771. [Google Scholar] [CrossRef] [PubMed]
- Cherry, E.M.; Fenton, F.H. Visualization of spiral and scroll waves in simulated and experimental cardiac tissue. New J. Phys. 2008, 10, 125016. [Google Scholar] [CrossRef]
- Elshrif, M.M.; Cherry, E.M. A quantitative comparison of the behavior of human ventricular cardiac electrophysiology models in tissue. PLoS ONE 2014, 9, e84401. [Google Scholar] [CrossRef]
- Courtemanche, M.; Winfree, A.T. Re-entrant rotating waves in a Beeler-Reuter based model of two-dimensional cardiac conduction. Int. J. Bifurc. Chaos 1991, 1, 431–444. [Google Scholar] [CrossRef]
- Janse, M.J. Focus, reentry, or “focal” reentry? Am. J. Physiol. Heart Circ. Physiol. 2007, 292, H2561–H2562. [Google Scholar] [CrossRef]
- Qu, Z.; Weiss, J.N.; Garfinkel, A. Cardiac electrical restitution properties and the stability of reentrant spiral waves: A simulation study. Am. J. Physiol. 1999, 276, H269–H283. [Google Scholar] [CrossRef]
- Kong, X.; Ravikumar, V.; Mulpuru, S.K.; Roukoz, H.; Tolkacheva, E.G. A data-driven preprocessing framework for atrialfibrillation intracardiac electrocardiogram analysis. Entropy 2023, 25, 332. [Google Scholar] [CrossRef]
- Bai, J.; Zhang, C.F.; Liang, Y.C.; Tavares, A.; Wang, L.D. Impact of Combined Modulation of Two Potassium Ion Currents on Spiral Waves and Turbulent States in the Heart. Entropy 2024, 26, 446. [Google Scholar] [CrossRef]
- Qu, Z.; Weiss, J.N. Mechanisms of ventricular arrhythmias: From molecular fluctuations to electrical turbulence. Annu. Rev. Physiol. 2015, 77, 29–55. [Google Scholar] [CrossRef]
- Weiss, J.N.; Chen, P.S.; Qu, Z.; Karagueuzian, H.S.; Garfinkel, A. Ventricular fibrillation: How do we stop the waves from breaking? Circ. Res. 2000, 87, 1103–1107. [Google Scholar] [CrossRef] [PubMed]
- Shiferaw, Y.; Sato, D.; Karma, A. Coupled dynamics of voltage and calcium in paced cardiac cells. Phys. Rev. E 2005, 71, 021903. [Google Scholar] [CrossRef] [PubMed]
- Shajahan, T.K.; Nayak, A.R.; Pandit, R. Spiral-wave turbulence and its control in the presence of inhomogeneities in four mathematical models of cardiac tissue. PLoS ONE 2009, 4, e4738. [Google Scholar] [CrossRef]
- Courtemanche, M. Complex spiral wave dynamics in a spatially distributed ionic model of cardiac electrical activity. Chaos 1996, 6, 579–600. [Google Scholar] [CrossRef]
- Huang, C.L.; Song, Z.; Landaw, J.; Qu, Z.L. Spatially Discordant Repolarization Alternans in the Absence of Conduction Velocity Restitution. Biophys. J. 2020, 118, 2574–2587. [Google Scholar] [CrossRef]
- Xie, F.; Qu, Z.; Garfinkel, A.; Weiss, J.N. Electrophysiological heterogeneity and stability of reentry in simulated cardiac tissue. Am. J. Physiol. Heart Circ. Physiol. 2001, 280, H535–H545. [Google Scholar] [CrossRef]
- Huang, C.L.; Song, Z.; Di, Z.R.; Qu, Z.L. Stability of spatially discordant repolarization alternans in cardiac tissue. Chaos 2020, 30, 123141. [Google Scholar] [CrossRef]
- Fenton, F.H.; Cherry, E.M.; Hastings, H.M.; Evans, S.J. Multiple mechanisms of spiral wave breakup in a model of cardiac electrical activity. Chaos 2002, 12, 852–892. [Google Scholar] [CrossRef]
- Rosen, M.R. Mechanisms for arrhythmias. Am. J. Cardiol. 1988, 61, 2A–8A. [Google Scholar] [CrossRef]
- Rosen, M.R.; Binah, O.; Maron, S. Cardiac Memory and Cortical Memory Do Learning Patterns in Neural Networks Impact on Cardiac Arrhythmias? Circulation 2003, 108, 1784. [Google Scholar] [CrossRef]
- Rosenbaum, M.B.; Blanco, H.H.; Elizari, M.V.; Lázzari, O.; Davidenko, J.M. Electrotonic modulation of the T wave and cardiac memory. Am. J. Cardiol 1982, 50, 213–222. [Google Scholar] [CrossRef] [PubMed]
- Lukas, A.; Antzelevitch, C. Differences in the electrophysiological response of canine ventricular epicardium and endocardium to ischemia. Role of the transient outward current. Circulation 1993, 88, 2903–2915. [Google Scholar] [CrossRef] [PubMed]
- Warren, M.; Guha, P.K.; Berenfeld, O.; Zaitsev, A.; Anumonwo, J.M.B.; Dhamoon, A.S.; Bagwe, S.; Taffet, S.M.; Jalife, J. Blockade of the inward rectifying potassium current terminates ventricular fibrillation in the guinea pig heart. J. Cardiovasc. Electrophysiol. 2003, 14, 621–631. [Google Scholar] [CrossRef]
- Jongsma, H.J.; Wilders, R. Gap junctions in cardiovascular disease. Circ. Res. 2000, 86, 1193–1197. [Google Scholar] [CrossRef]
- Cascio, W.E.; Yang, H.; Muller-Borer, B.J.; Johnson, T.A. Ischemia-induced arrhythmia: The role of connexins, gap junctions, and attendant changes in impulse propagation. J. Electrocardiol. 2005, 38, 55–59. [Google Scholar] [CrossRef]
- Kuang, Y.L.; Tang, G.N. Eliminate spiral wave and spatiotemporal chaos by using short-term cardiac memory. Acta Phys. Sin. 2012, 61, 190501. [Google Scholar] [CrossRef]
- Greenstein, J.L.; Wu, R.; Po, S.; Tomaselli, G.F.; Winslow, R.L. Role of the Calcium-Independent Transient Outward Current Ito1 in Shaping Action Potential Morphology and Duration. Circ. Res. 2000, 87, 1026–1033. [Google Scholar] [CrossRef]
- Dong, M.; Sun, X.; Prinz, A.A.; Wang, H.-S. Effect of simulated Ito on guinea pig and canine ventricular action potential morphology. Am. J. Physiol. Heart Circ. Physiol. 2006, 291, H631–H637. [Google Scholar] [CrossRef][Green Version]
- Landaw, J.; Garfinkel, A.; Weiss, J.N.; Qu, Z. Memory-induced chaos in cardiac excitation. Phys. Rev. Lett. 2017, 118, 138101. [Google Scholar] [CrossRef]
- Landaw, J.; Qu, Z.L. Memory-induced nonlinear dynamics of excitation in cardiac diseases. Phys. Rev. E 2018, 97, 042414. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Zhang, Y.H.; Qu, Z.L. Bistable spiral wave dynamics in electrically excitable media. Phys. Rev. E 2023, 108, 064405. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.H.; Rudy, Y.A. Model of the ventricular cardiac action potential: Depolarization, repolarization, and their interaction. Circ. Res. 1991, 68, 1501–1526. [Google Scholar] [CrossRef] [PubMed]
- Mahajan, A.; Shiferaw, Y.; Sato, D.; Baher, A.; Olcese, R.; Xie, L.H.; Yang, M.J.; Chen, P.S.; Restrepo, J.G.; Karma, A.; et al. A rabbit ventricular action potential model replicating cardiac dynamics at rapid heart rates. Biophys. J. 2008, 94, 392–410. [Google Scholar] [CrossRef] [PubMed]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of menbrane current and its application to conduction and excitation in nerve. J. Physiol. Lond. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Li, Y.; Schmid, G.; Hänggi, P.; Schimansky-Geier, L. Spontaneous spiking in an autaptic Hodgkin-Huxley setup. Phys. Rev. E 2010, 82, 061917. [Google Scholar] [CrossRef]
- Luo, C.H.; Rudy, Y.A. Dynamical model of the cardiac ventricular action potential: I. simulations of ionic currents and concentration changes. Circ. Res. 1994, 74, 1071–1096. [Google Scholar] [CrossRef]
- Landaw, J.; Yuan, X.P.; Chen, P.S.; Qu, Z.L. The transient outward potassium current plays a key role in spiral wave breakup in ventricular tissue. Am. J. Physiol. Heart Circ. Physiol. 2021, 320, H826–H837. [Google Scholar] [CrossRef]
- Gima, K.; Rudy, Y. Ionic Current Basis of Electrocardiographic Waveforms: A Model Study. Circ. Res. 2002, 90, 889–896. [Google Scholar] [CrossRef]
- Shannon, T.R.; Wang, F.; Puglisi, J.; Weber, C.; Bers, D.M. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys. J. 2004, 87, 3351–3371. [Google Scholar] [CrossRef]
- Armoundas, A.A.; Tomaselli, G.F.; Esperer, H.D. Pathophysiological basis and clinical application of T-wave alternans. J. Am. Coll. Cardiol. 2002, 40, 207–217. [Google Scholar] [CrossRef]
- Morita, H.; Nagase, S.; Kusano, K.; Ohe, T. Spontaneous T wave alternans and premature ventricular contractions during febrile illness in a patient with Brugada syndrome. J. Cardiovasc. Electrophysiol. 2002, 13, 816–818. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, X.; Zheng, Q. Impact of Calcium and Potassium Currents on Spiral Wave Dynamics in the LR1 Model. Entropy 2025, 27, 690. https://doi.org/10.3390/e27070690
Yuan X, Zheng Q. Impact of Calcium and Potassium Currents on Spiral Wave Dynamics in the LR1 Model. Entropy. 2025; 27(7):690. https://doi.org/10.3390/e27070690
Chicago/Turabian StyleYuan, Xiaoping, and Qianqian Zheng. 2025. "Impact of Calcium and Potassium Currents on Spiral Wave Dynamics in the LR1 Model" Entropy 27, no. 7: 690. https://doi.org/10.3390/e27070690
APA StyleYuan, X., & Zheng, Q. (2025). Impact of Calcium and Potassium Currents on Spiral Wave Dynamics in the LR1 Model. Entropy, 27(7), 690. https://doi.org/10.3390/e27070690




