Manipulating Entanglement Dynamics in Dephased Interacting Qubits Using a Radiation Field
Abstract
1. Introduction
2. Mathematical Formulation
2.1. The Model
2.2. Quantifying Entanglement
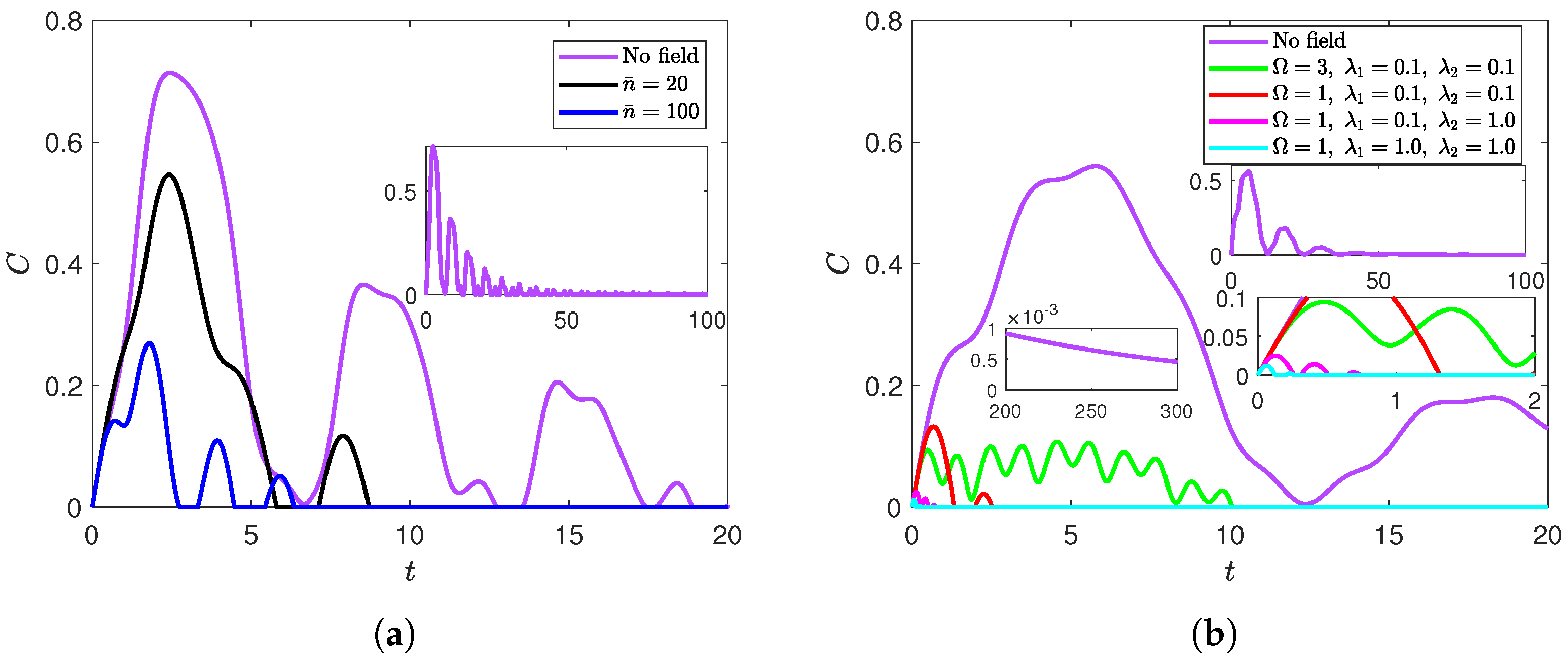
3. Entanglement Death and Revival Variation in the Presence of a Radiation Field
4. Entanglement Dynamics Under Varying Dephasing Rates
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QIP | Quantum Information Processing |
| ESD | Entanglement Sudden Death |
| ESB | Entanglement Sudden Birth |
Appendix A
Appendix A.1


Appendix A.2
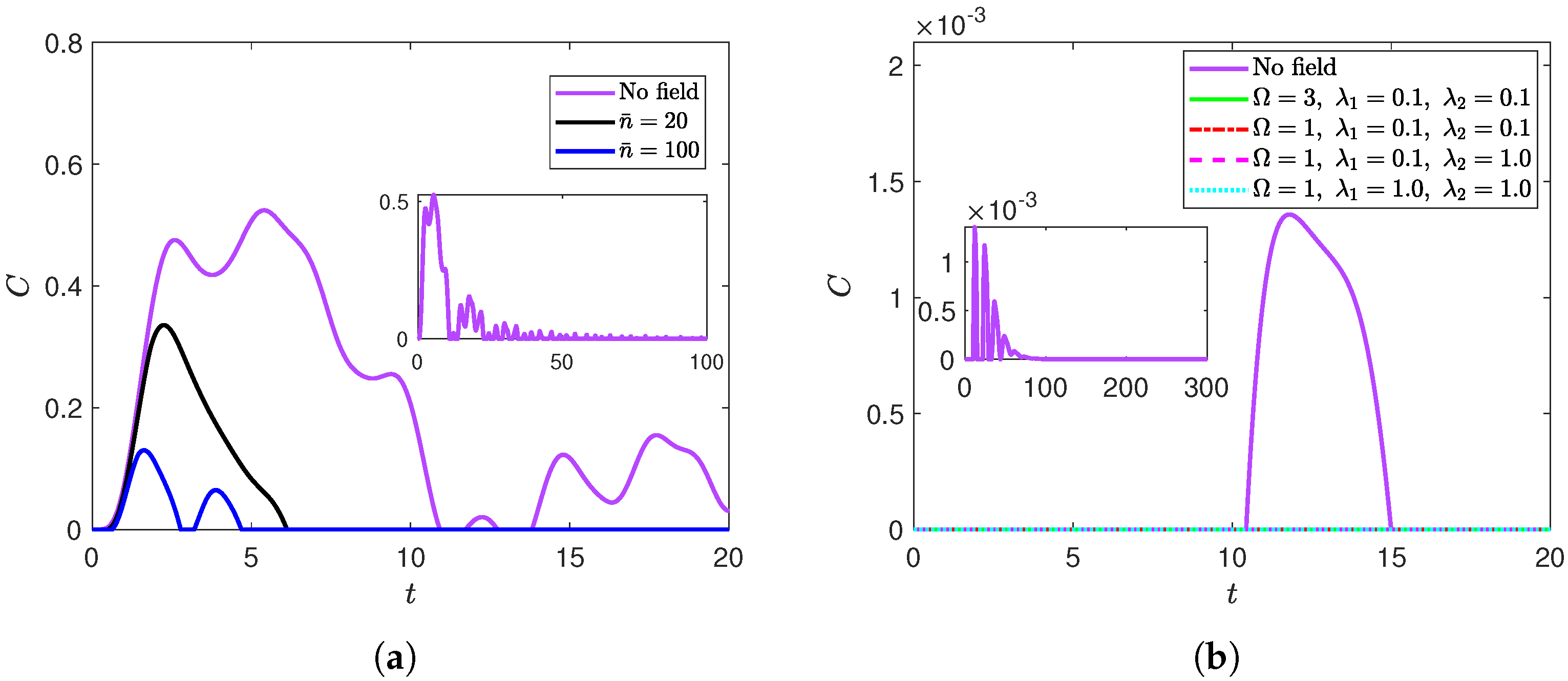

Appendix B
Appendix B.1
Appendix B.1.1
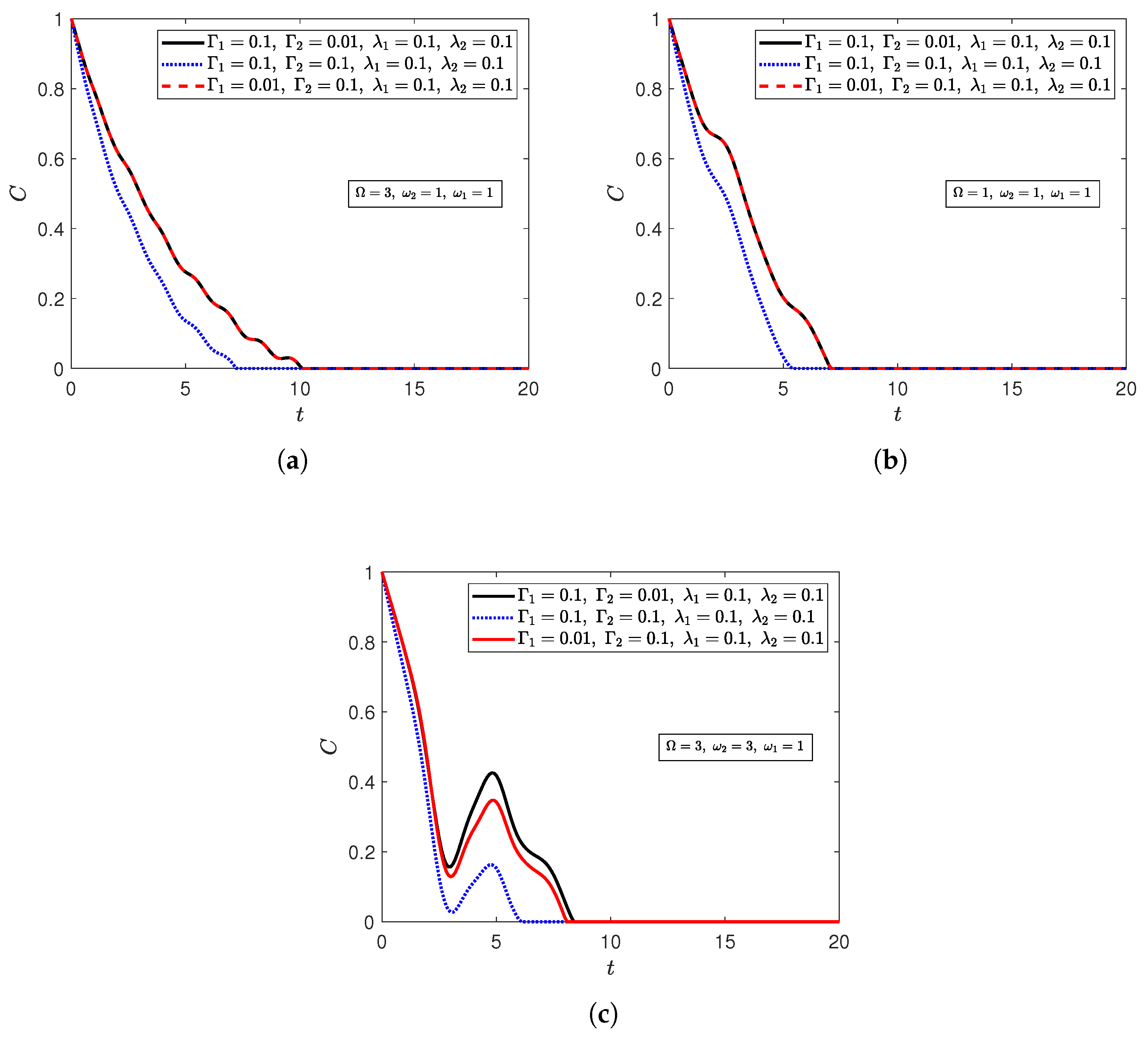
Appendix B.1.2

Appendix B.1.3
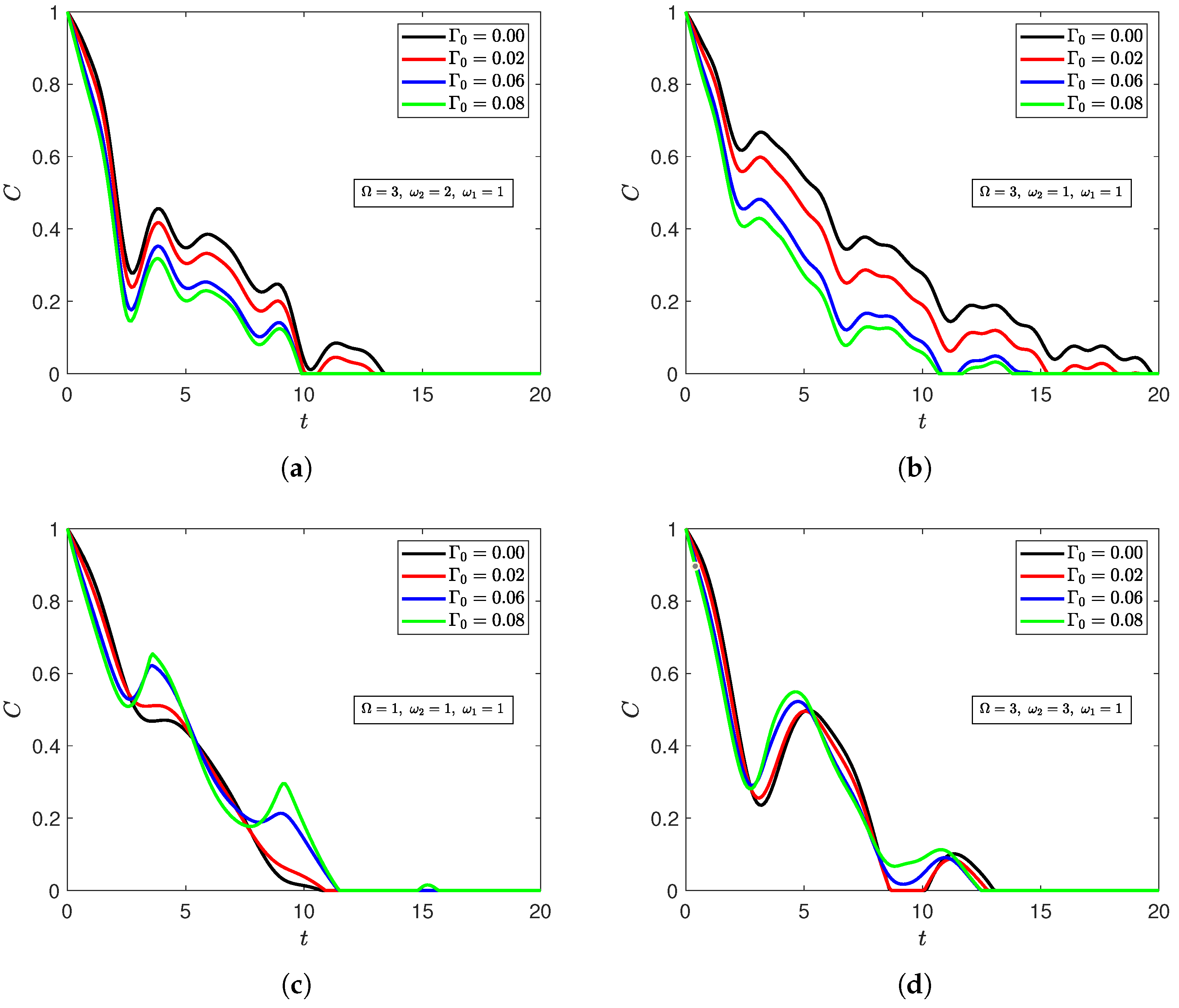
Appendix B.2
Appendix B.2.1
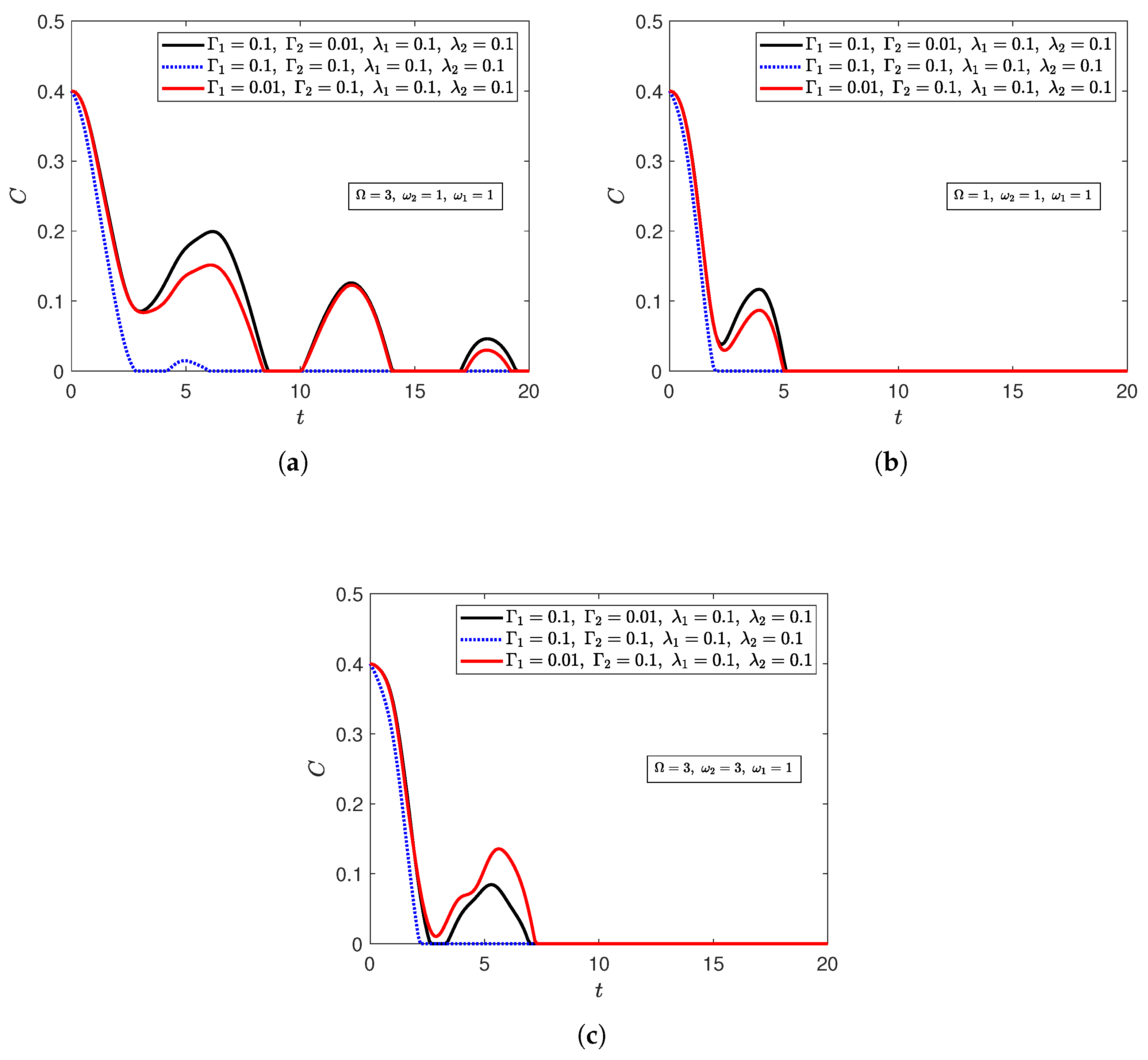
Appendix B.2.2

Appendix B.2.3

References
- Jaynes, E.; Cummings, F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Larson, J.; Mavrogordatos, T. The Jaynes–Cummings Model and Its Descendants: Modern Research Directions; IOP Publishing: Bristol, UK, 2021. [Google Scholar]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Tavis, M.; Cummings, F.W. Exact Solution for an N-Molecule—Radiation-Field Hamiltonian. Phys. Rev. 1968, 170, 379–384. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Finite-Time Disentanglement Via Spontaneous Emission. Phys. Rev. Lett. 2004, 93, 140404. [Google Scholar] [CrossRef] [PubMed]
- Ficek, Z.; Tanaś, R. Delayed sudden birth of entanglement. Phys. Rev. A 2008, 77, 054301. [Google Scholar] [CrossRef]
- Tessier, T.E.; Deutsch, I.H.; Delgado, A.; Fuentes-Guridi, I. Entanglement sharing in the two-atom Tavis-Cummings model. Phys. Rev. A 2003, 68, 062316. [Google Scholar] [CrossRef]
- Oh, S.; Kim, J. Entanglement between qubits induced by a common environment with a gap. Phys. Rev. A 2006, 73, 062306. [Google Scholar] [CrossRef]
- Barker, D.; Lehmann, S.; Namazi, L.; Nilsson, M.; Thelander, C.; Dick, K.A.; Maisi, V.F. Individually addressable double quantum dots formed with nanowire polytypes and identified by epitaxial markers. Appl. Phys. Lett. 2019, 114, 183502. [Google Scholar] [CrossRef]
- Chang, Y.C.; Karimi, B.; Senior, J.; Ronzani, A.; Peltonen, J.T.; Goan, H.S.; Chen, C.D.; Pekola, J.P. Utilization of the superconducting transition for characterizing low-quality-factor superconducting resonators. Appl. Phys. Lett. 2019, 115, 022601. [Google Scholar] [CrossRef]
- B’egoc, B.; Cichelli, G.; Singh, S.P.; Bensch, F.; Amico, V.; Perciavalle, F.; Rossini, D.; Amico, L.; Morsch, O. Controlled dissipation for Rydberg atom experiments. arXiv 2023, arXiv:2310.20687. [Google Scholar]
- Abdelmagid, R.; Alshehhi, K.; Sadiek, G. Entanglement Degradation in Two Interacting Qubits Coupled to Dephasing Environments. Entropy 2023, 25, 1458. [Google Scholar] [CrossRef] [PubMed]
- Kavokin, K.V. Anisotropic exchange interaction of localized conduction-band electrons in semiconductors. Phys. Rev. B 2001, 64, 075305. [Google Scholar] [CrossRef]
- Shim, Y.P.; Oh, S.; Hu, X.; Friesen, M. Controllable Anisotropic Exchange Coupling between Spin Qubits in Quantum Dots. Phys. Rev. Lett. 2011, 106, 180503. [Google Scholar] [CrossRef] [PubMed]
- DiVincenzo, D.P.; Bacon, D.; Kempe, J.; Burkard, G.; Whaley, K.B. Universal quantum computation with the exchange interaction. Nature 2000, 408, 339–342. [Google Scholar] [CrossRef]
- Buluta, I.; Ashhab, S.; Nori, F. Natural and artificial atoms for quantum computation. Rep. Prog. Phys. 2011, 74, 104401. [Google Scholar] [CrossRef]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347–400. [Google Scholar] [CrossRef]
- Xiang, Z.L.; Ashhab, S.; You, J.Q.; Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 2013, 85, 623–653. [Google Scholar] [CrossRef]
- Wendin, G. Quantum information processing with superconducting circuits: A review. Rep. Prog. Phys. 2017, 80, 106001. [Google Scholar] [CrossRef] [PubMed]
- Chan, S.; Reid, M.D.; Ficek, Z. Entanglement evolution of two remote and non-identical Jaynes–Cummings atoms. J. Phys. B 2009, 42, 065507. [Google Scholar] [CrossRef]
- Laha, P. Dynamics of a multipartite hybrid quantum system with beamsplitter, dipole–dipole, and Ising interactions. J. Opt. Soc. Am. B 2023, 40, 1911–1921. [Google Scholar] [CrossRef]
- Hiltunen, T.; Bluhm, H.; Mehl, S.; Harju, A. Charge-noise tolerant exchange gates of singlet-triplet qubits in asymmetric double quantum dots. Phys. Rev. B 2015, 91, 075301. [Google Scholar] [CrossRef]
- Matsuzaki, Y.; Nakano, H. Enhanced energy relaxation process of a quantum memory coupled to a superconducting qubit. Phys. Rev. B 2012, 86, 184501. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, J. Asymmetric steerability of quantum equilibrium and nonequilibrium steady states through entanglement detection. Phys. Rev. A 2021, 104, 042404. [Google Scholar] [CrossRef]
- Spethmann, M.; Bosco, S.; Hofmann, A.; Klinovaja, J.; Loss, D. High-fidelity two-qubit gates of hybrid superconducting-semiconducting singlet-triplet qubits. Phys. Rev. B 2024, 109, 085303. [Google Scholar] [CrossRef]
- Xu, D.; Gu, X.K.; Weng, Y.C.; Li, H.K.; Wang, Y.P.; Zhu, S.Y.; You, J.Q. Macroscopic Bell state between a millimeter-sized spin system and a superconducting qubit. Quantum Sci. Technol. 2024, 9, 035002. [Google Scholar] [CrossRef]
- Fox, M.A.M. Quantum Optics: An Introduction; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Chuan-Jia, S.; Ji-Bing, L.; Wei-Wen, C.; Tang-Kun, L.; Yan-Xia, H.; Hong, L. Entanglement Dynamics of Two-Qubit System in Different Types of Noisy Channels. Commun. Theor. Phys. 2009, 51, 1013. [Google Scholar] [CrossRef]
- Orth, P.P.; Roosen, D.; Hofstetter, W.; Le Hur, K. Dynamics, synchronization, and quantum phase transitions of two dissipative spins. Phys. Rev. B 2010, 82, 144423. [Google Scholar] [CrossRef]
- Jiang, L.N.; Ma, J.; Yu, S.Y.; Tan, L.Y.; Ran, Q.W. Entanglement Evolution of the Extended Werner-like State under the Influence of Different Noisy Channels. Int. J. Theor. Phys. 2015, 54, 440–449. [Google Scholar] [CrossRef]
- Yang, C.; Guo, Y.N.; Peng, H.P.; Lu, Y.B. Dynamics of local quantum uncertainty for a two-qubit system under dephasing noise. Laser Phys. 2019, 30, 015203. [Google Scholar] [CrossRef]
- Yeo, Y.; Kho, Z.W.; Wang, L. Effects of Pauli channels and noisy quantum operations on standard teleportation. Europhys. Lett. 2009, 86, 40009. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, L.N.; Yu, S.Y.; Ran, Q.W.; Tan, L.Y. Entanglement Dynamics of the Mixed Two-qubit System in Different Noisy Channels. Int. J. Theor. Phys. 2014, 53, 3843–3855. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R.; Piani, M. Environment Induced Entanglement in Markovian Dissipative Dynamics. Phys. Rev. Lett. 2003, 91, 070402. [Google Scholar] [CrossRef]
- Caruso, F.; Huelga, S.F.; Plenio, M.B. Noise-Enhanced Classical and Quantum Capacities in Communication Networks. Phys. Rev. Lett. 2010, 105, 190501. [Google Scholar] [CrossRef]
- Kassal, I.; Aspuru-Guzik, A. Environment-assisted quantum transport in ordered systems. New J. Phys. 2012, 14, 053041. [Google Scholar] [CrossRef]
- Mülken, O. Enhanced Quantum Transport in Multiplex Networks. J. Stat. Phys. 2016, 162, 644–651. [Google Scholar] [CrossRef]
- Suzuki, F.; Lemeshko, M.; Zurek, W.H.; Krems, R.V. Anderson Localization of Composite Particles. Phys. Rev. Lett. 2021, 127, 160602. [Google Scholar] [CrossRef]
- Braun, D. Creation of Entanglement by Interaction with a Common Heat Bath. Phys. Rev. Lett. 2002, 89, 277901. [Google Scholar] [CrossRef]
- Gillard, N.; Belin, E.; Chapeau-Blondeau, F. Enhancing qubit information with quantum thermal noise. Phys. A Stat. Mech. Its Appl. 2018, 507, 219–230. [Google Scholar] [CrossRef]
- Das, S.; Agarwal, G.S. Decoherence effects in interacting qubits under the influence of various environments. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 229801. [Google Scholar] [CrossRef]
- Wu, L.A.; Yu, C.X.; Segal, D. Exact dynamics of interacting qubits in a thermal environment: Results beyond the weak coupling limit. New J. Phys. 2013, 15, 023044. [Google Scholar] [CrossRef]
- Li, Z.; Yang, P.; You, W.L.; Wu, N. Dynamics of the homogeneous two-qubit $XXZ$ central spin model with the spin bath prepared in superpositions of symmetric Dicke states. Phys. Rev. A 2020, 102, 032409. [Google Scholar] [CrossRef]
- Vovcenko, I.V.; Shishkov, V.Y.; Andrianov, E.S. Dephasing-assisted entanglement in a system of strongly coupled qubits. Opt. Express 2021, 29, 9685–9698. [Google Scholar] [CrossRef]
- Jerger, M. Experiments on Superconducting Qubits Coupled to Resonators. Ph.D. Thesis, Karlsruher Institut für Technologie (KIT), Oberpfaffenhofen, Germany, 2013. [Google Scholar] [CrossRef]
- Bianchetti, R.A. Control and Readout of a Superconducting Artificial Atom. Doctoral Thesis, ETH Zurich, Zürich, Switzerland, 2010. [Google Scholar] [CrossRef]
- Burd, S.C.; Allcock, D.T.C.; Leinonen, T.; Penttinen, J.P.; Slichter, D.H.; Srinivas, R.; Wilson, A.C.; Jördens, R.; Guina, M.; Leibfried, D.; et al. VECSEL systems for the generation and manipulation of trapped magnesium ions. Opt. Lett. 2016, 3, 1294–1299. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK; New York, NY, USA, 2002. [Google Scholar]
- Sadiek, G.; Almalki, S. Entanglement dynamics in Heisenberg spin chains coupled to a dissipative environment at finite temperature. Phys. Rev. A 2016, 94, 012341. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef]
- Vedral, V.; Plenio, M.B.; Rippin, M.A.; Knight, P.L. Quantifying Entanglement. Phys. Rev. Lett. 1997, 78, 2275–2279. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef]
- Dillenschneider, R. Quantum discord and quantum phase transition in spin chains. Phys. Rev. B 2008, 78, 224413. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef]
- Li, S.P.; Sun, Z.H. Local and intrinsic quantum coherence in critical systems. Phys. Rev. A 2018, 98, 022317. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qisieh, O.; Abdelmagid, R.; Sadiek, G. Manipulating Entanglement Dynamics in Dephased Interacting Qubits Using a Radiation Field. Entropy 2025, 27, 673. https://doi.org/10.3390/e27070673
Qisieh O, Abdelmagid R, Sadiek G. Manipulating Entanglement Dynamics in Dephased Interacting Qubits Using a Radiation Field. Entropy. 2025; 27(7):673. https://doi.org/10.3390/e27070673
Chicago/Turabian StyleQisieh, Omar, Rahma Abdelmagid, and Gehad Sadiek. 2025. "Manipulating Entanglement Dynamics in Dephased Interacting Qubits Using a Radiation Field" Entropy 27, no. 7: 673. https://doi.org/10.3390/e27070673
APA StyleQisieh, O., Abdelmagid, R., & Sadiek, G. (2025). Manipulating Entanglement Dynamics in Dephased Interacting Qubits Using a Radiation Field. Entropy, 27(7), 673. https://doi.org/10.3390/e27070673




