Bayesian Discrepancy Measure: Higher-Order and Skewed Approximations
Abstract
1. Introduction
- Higher-order asymptotic approximations: These offer improved accuracy at minimal additional computational costs compared to first-order approximations, and are applicable to posterior distributions and quantities of interest such as tail probabilities and credible regions (see, e.g., [4], and references therein);
2. Background
2.1. Scalar Case
2.2. Nuisance Parameters
2.3. The Multivariate Case
- It yields a value between 0 and 1;
- if corresponds to the geometric center (or multivariate median) of the distribution (mapped to by );
- increases as moves away from the center toward the “boundary” of the distribution, approaching 1 for points mapped near the surface of the unit ball ;
- It is invariant under suitable classes of transformations (affine transformations if is elliptically contoured, more generally under monotone transformations linked to an optimal transport map construction);
- It naturally reduces to the univariate definition when .
3. Beyond Gaussian I: Higher-Order Asymptotic Approximations
3.1. Scalar Case
3.2. Nuisance Parameters
Approximations with Matching Priors
3.3. Multidimensional Parameters
4. Beyond Gaussian II: Skewed Approximations
4.1. Scalar Case
4.2. Nuisance Parameters
4.3. Multidimensional Parameters
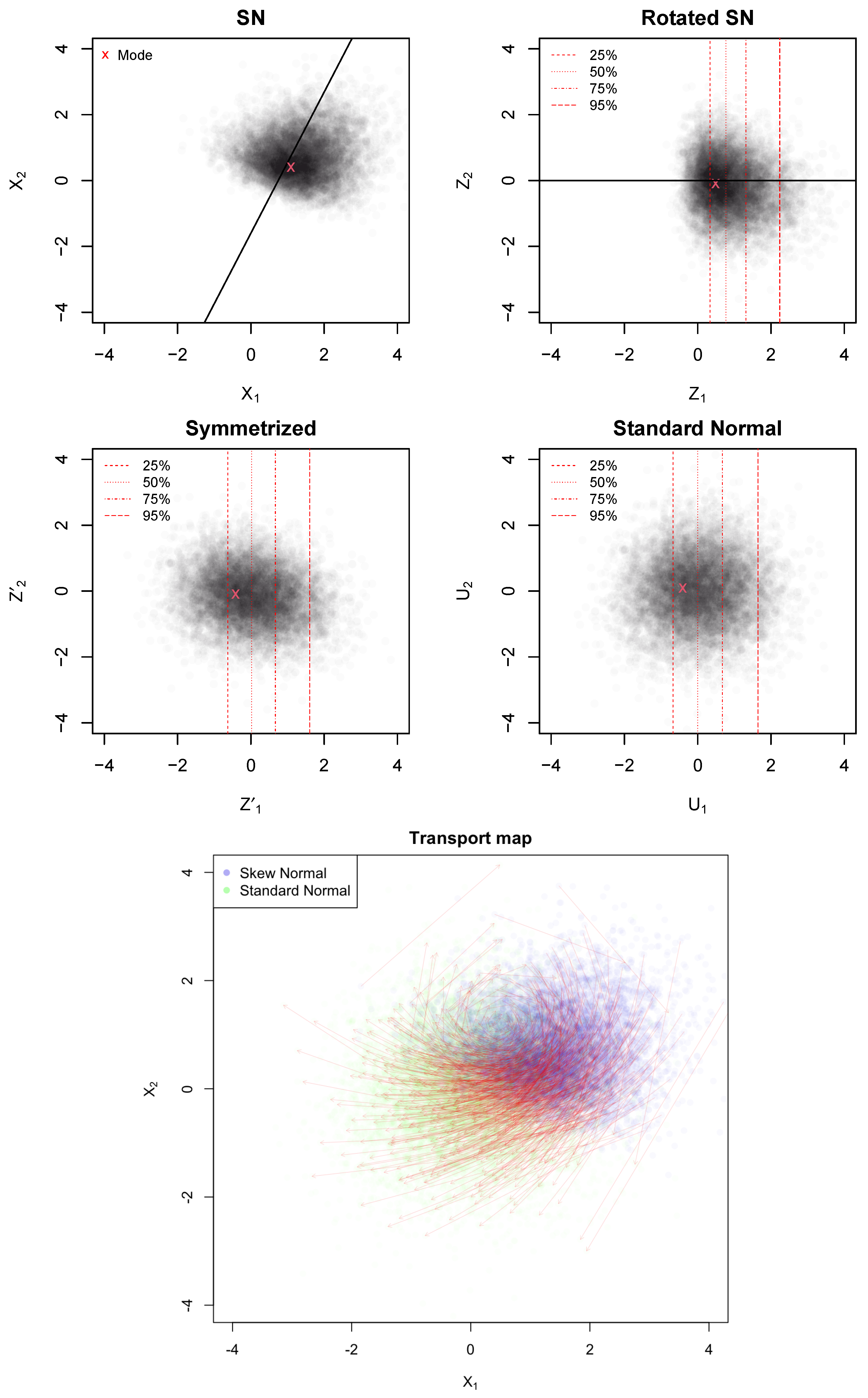
- aligns the skewness with the first coordinate;
- in the rotated space, , with , and are Gaussian.
| Algorithm 1 Optimal transport from to |
|
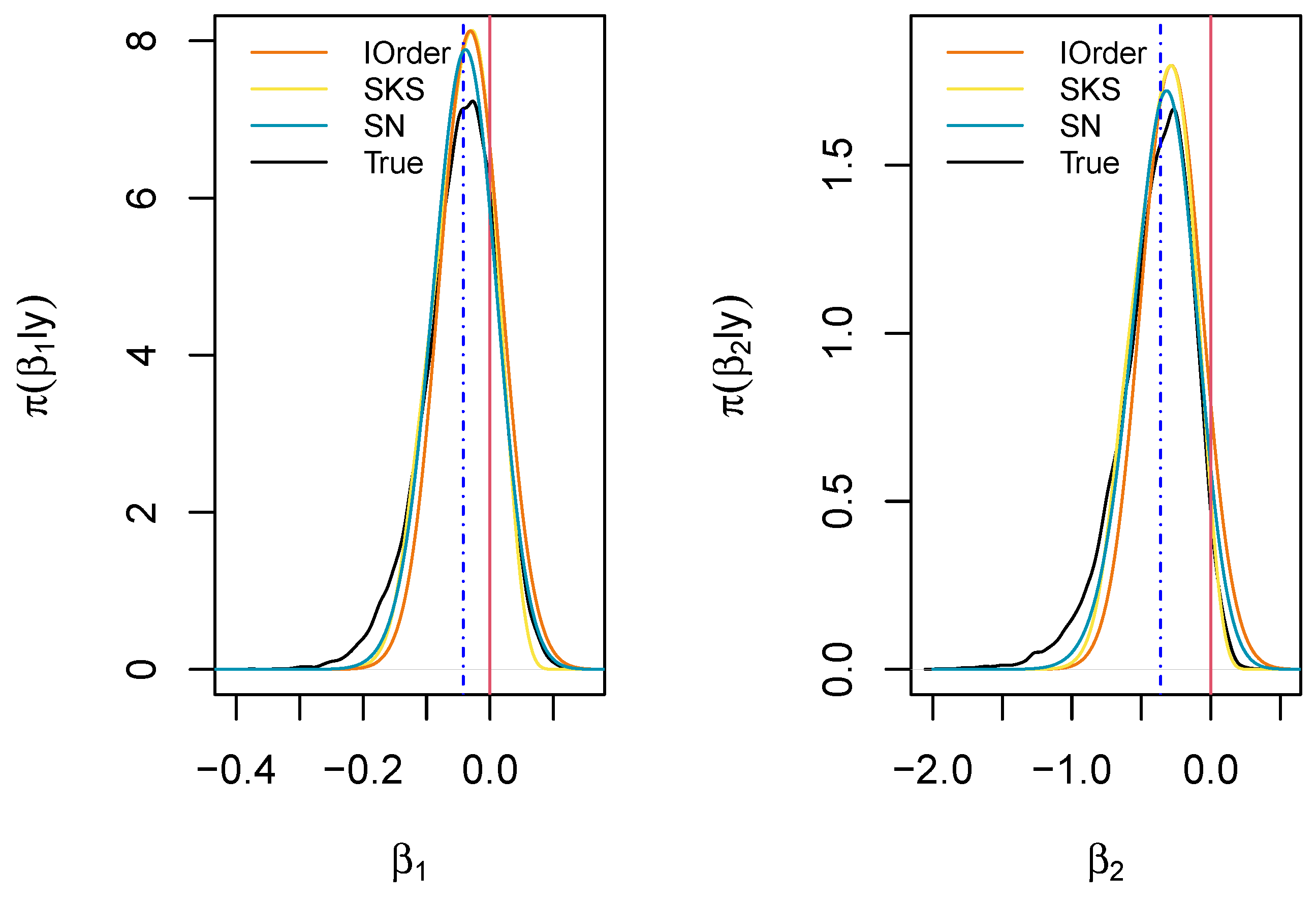
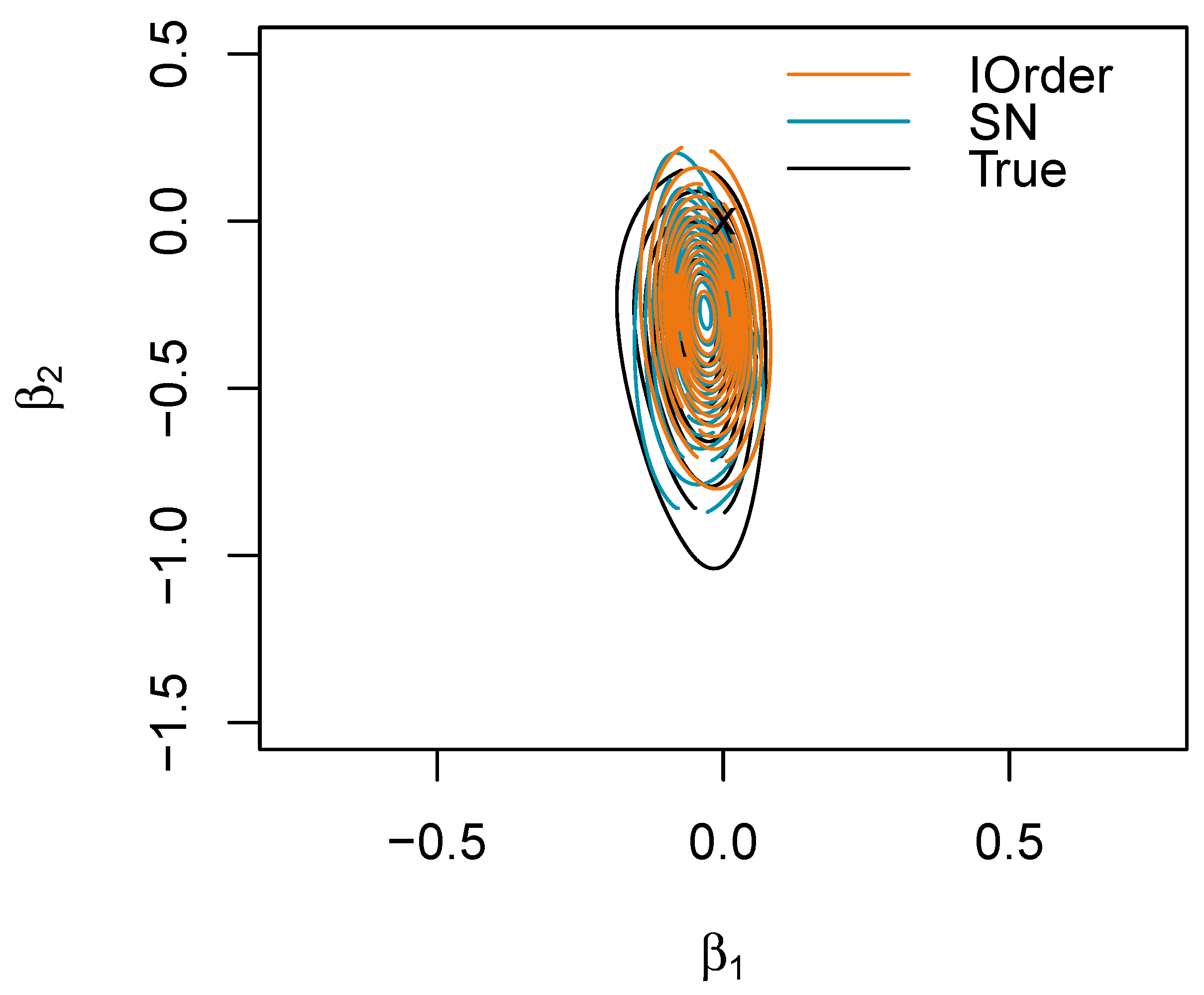
5. Examples of Higher-Order and Skewed Approximations
5.1. Exponential Model
5.2. Logistic Regression Model
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations and Notation Glossary
| Symbol | Meaning/Definition |
| BDM | Bayesian discrepancy measure |
| BF | Bayes factor |
| LR | Log-likelihood ratio |
| MAP | Maximum a posteriori |
| MLE | Maximum likelihood estimate |
| OT | Optimal transport |
| SKS | Skew-symmetric |
| SN | Skew-normal |
| Sharp (precise) null hypothesis | |
| Scalar parameter or parameter vector in the multivariate case | |
| Specific hypothesized value of the parameter under | |
| Scalar parameter of interest | |
| Nuisance parameter (scalar or vector) | |
| y | Observed data |
| d | Dimension of the full parameter vector |
| n | Sample size |
| MLE of | |
| MAP of | |
| Constrained MLE of given | |
| , | Log-likelihood function |
| Profile log-likelihood function for | |
| , | Score function, profile score function |
| , | Observed information matrix, profile observed information |
| Submatrices of for parameter partitions | |
| , | Wald statistic, profile Wald statistic |
| , | Score statistic, profile score statistic |
| Log-likelihood ratio statistic | |
| , | Likelihood root, profile likelihood root |
| , | Prior density of , posterior density of |
| Bayesian discrepancy measure, quantifying evidence against | |
| Bayesian modified likelihood root statistic (scalar, with nuisance parameters) | |
| Standard normal cumulative distribution function | |
| Marginal posterior density of | |
| Center-outward distribution function mapping posterior to the unit ball | |
| Center-outward quantile function (inverse of ) | |
| Uniform distribution on the unit ball | |
| , | Unit ball in , unit sphere in |
| , | Center-outward quantile regions and quantile contours of order |
| Euclidean norm | |
| Approximate equality to first- or third-order (e.g., or accuracy) |
References
- Kass, R.E.; Tierney, L.; Kadane, J. The validity of posterior expansions based on Laplace’s method. In Bayesian and Likelihood Methods in Statistics and Econometrics; Elsevier: Amsterdam, The Netherlands, 1990; pp. 473–488. [Google Scholar]
- Reid, N. Likelihood and Bayesian approximation methods. Bayesian Stat. 1995, 5, 351–368. [Google Scholar]
- Reid, N. The 2000 Wald memorial lectures: Asymptotics and the theory of inference. Ann. Stat. 2003, 31, 1695–1731. [Google Scholar] [CrossRef]
- Ventura, L.; Reid, N. Approximate Bayesian computation with modified log-likelihood ratios. Metron 2014, 7, 231–245. [Google Scholar] [CrossRef]
- Durante, D.; Pozza, F.; Szabo, B. Skewed Bernstein–von Mises theorem and skew-modal approximations. Ann. Stat. 2024, 52, 2714–2737. [Google Scholar] [CrossRef]
- Zhou, J.; Grazian, C.; Ormerod, J.T. Tractable skew-normal approximations via matching. J. Statist. Comput. Simul. 2024, 94, 1016–1034. [Google Scholar] [CrossRef]
- Bertolino, F.; Manca, M.; Musio, M.; Racugno, W.; Ventura, L. A new Bayesian discrepancy measure. Stat. Methods Appl. 2024, 33, 381–405. [Google Scholar] [CrossRef]
- Hallin, M.; Del Barrio, E.; Cuesta-Albertos, J.; Matrán, C. Distribution and quantile functions, ranks and signs in dimension d: A measure transportation approach. Ann. Stat. 2021, 49, 1139–1165. [Google Scholar] [CrossRef]
- Hallin, M.; Konen, D. Multivariate Quantiles: Geometric and Measure-Transportation-Based Contours. In Applications of Optimal Transport to Economics and Related Topics; Springer Nature: Cham, Switzerland, 2024; pp. 61–78. [Google Scholar]
- Madruga, M.; Pereira, C.; Stern, J. Bayesian evidence test for precise hypotheses. J. Stat. Plan. Inf. 2003, 117, 185–198. [Google Scholar] [CrossRef]
- Pereira, C.; Stern, J.M. Evidence and Credibility: Full Bayesian Significance Test for Precise Hypotheses. Entropy 1999, 1, 99–110. [Google Scholar] [CrossRef]
- Pereira, C.; Stern, J.M. The e-value: A fully Bayesian significance measure for precise statistical hypotheses and its research program. Sao Paulo J. Math. Sci. 2022, 16, 566–584. [Google Scholar] [CrossRef]
- Bertolino, F.; Columbu, S.; Manca, M.; Musio, M. Comparison of two coefficients of variation: A new Bayesian approach. Commun. Stat. Simul. Comput. 2024, 53, 6260–6273. [Google Scholar] [CrossRef]
- Ruli, E.; Ventura, L. Can Bayesian, confidence distribution and frequentist inference agree? Stat. Methods Appl. 2021, 30, 359–373. [Google Scholar] [CrossRef]
- Peyré, G.; Cuturi, M. Computational optimal transport: With applications to data science. Found. Trends Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Fraser, D.A.S.; Reid, N. Strong matching of frequentist and Bayesian parametric inference. J. Stat. Plan. Inf. 2002, 103, 263–285. [Google Scholar] [CrossRef]
- Welch, B.L.; Peers, H.W. On formulae for confidence points based on integrals of weighted likelihoods. J. Roy. Statist. Soc. B 1963, 25, 318–329. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Chamberlin, S.R. Stable and invariant adjusted directed likelihoods. Biometrika 1994, 81, 485–499. [Google Scholar] [CrossRef]
- Severini, T.A. Likelihood Methods in Statistics; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Pierce, D.A.; Bellio, R. Modern likelihood-frequentist inference. Int. Stat. Rev. 2017, 85, 519–541. [Google Scholar] [CrossRef]
- Skovgaard, I.M. Likelihood Asymptotics. Scand. J. Stat. 2001, 28, 3–32. [Google Scholar] [CrossRef]
- Ventura, L.; Ruli, E.; Racugno, W. A note on approximate Bayesian credible sets based on modified log-likelihood ratios. Stat. Prob. Lett. 2013, 83, 2467–2472. [Google Scholar] [CrossRef]
- Tan, L.S.; Chen, A. Variational inference based on a subclass of closed skew normals. J. Stat. Comput. Simul. 2024, 34, 1–15. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Statistical applications of the multivariate skew normal distribution. J. R. Stat. Soc. B 1999, 61, 579–602. [Google Scholar] [CrossRef]
- Reid, N.; Sun, Y. Assessing Sensitivity to Priors Using Higher Order Approximations. Commun. Stat. Simul. Comput. 2010, 39, 1373–1386. [Google Scholar] [CrossRef]
- Li, K.; Han, W.; Wang, Y.; Yang, Y. Optimal Transport-Based Generative Models for Bayesian Posterior Sampling. arXiv 2025, arXiv:2504.08214. [Google Scholar]
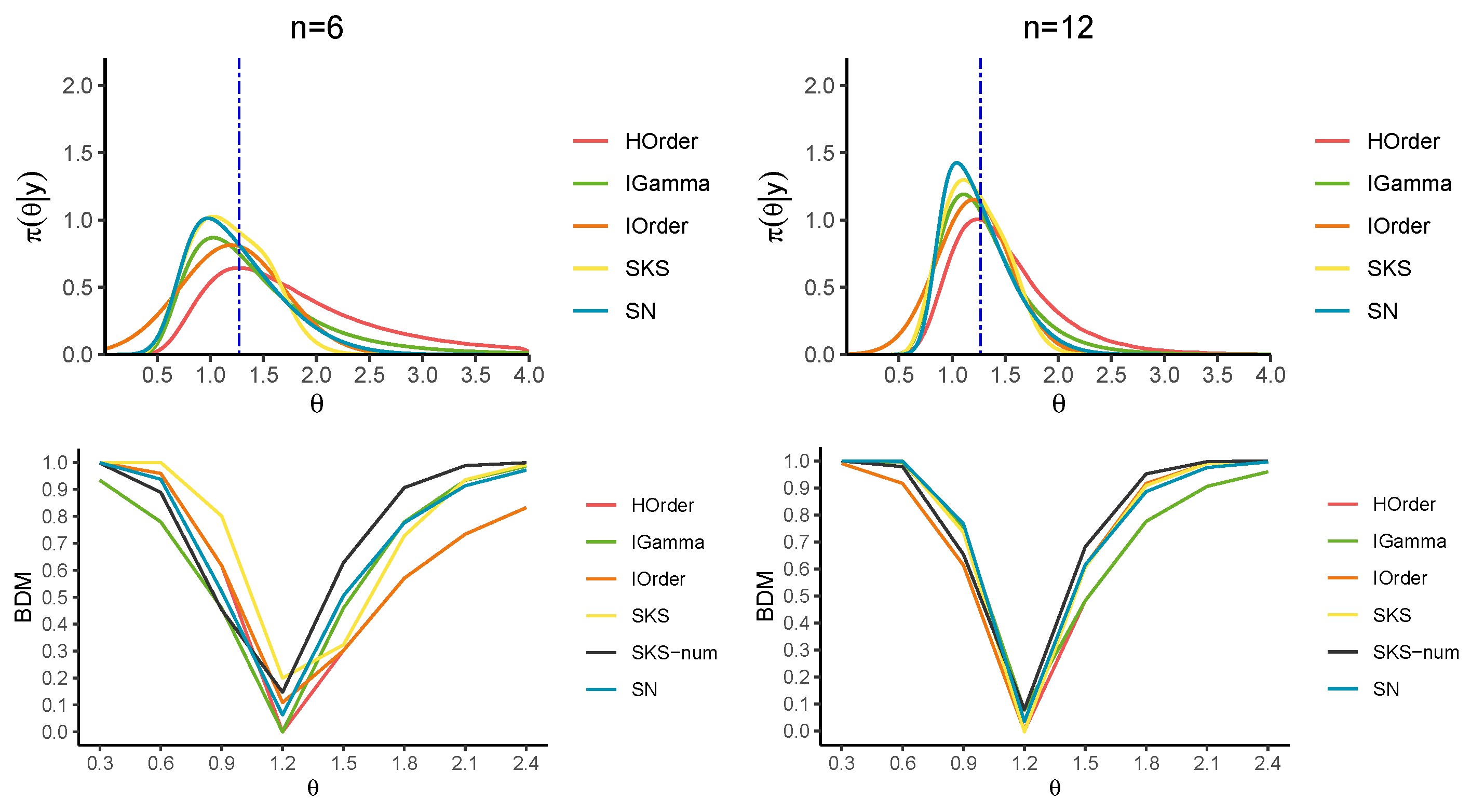

| 0.3 | 0.6 | 0.9 | 1.2 | 1.5 | 1.8 | 2.1 | 2.4 | ||
|---|---|---|---|---|---|---|---|---|---|
| IO | 0.93 | 0.78 | 0.46 | 0.00 | 0.46 | 0.78 | 0.93 | 0.99 | |
| HO | 1.00 | 0.96 | 0.62 | 0.00 | 0.30 | 0.57 | 0.73 | 0.83 | |
| SKS | 1.00 | 1.00 | 0.80 | 0.20 | 0.32 | 0.73 | 0.94 | 0.99 | |
| SKS-num | 1.00 | 0.94 | 0.53 | 0.07 | 0.58 | 0.91 | 0.99 | 1.00 | |
| SN | 1.00 | 0.94 | 0.52 | 0.06 | 0.51 | 0.78 | 0.91 | 0.97 | |
| BDM | 1.00 | 0.96 | 0.62 | 0.11 | 0.30 | 0.57 | 0.73 | 0.83 | |
| IO | 0.99 | 0.92 | 0.61 | 0.00 | 0.61 | 0.92 | 0.99 | 1.00 | |
| HO | 1.00 | 0.99 | 0.75 | 0.00 | 0.48 | 0.78 | 0.91 | 0.96 | |
| SKS | 1.00 | 1.00 | 0.74 | −0.00 | 0.61 | 0.91 | 0.99 | 1.00 | |
| SKS-num | 1.00 | 0.99 | 0.72 | 0.01 | 0.64 | 0.95 | 1.00 | 1.00 | |
| SN | 1.00 | 1.00 | 0.77 | 0.04 | 0.62 | 0.89 | 0.98 | 1.00 | |
| BDM | 1.00 | 0.99 | 0.75 | 0.08 | 0.48 | 0.78 | 0.91 | 0.96 | |
| IO | 1.00 | 0.97 | 0.74 | 0.00 | 0.74 | 0.97 | 1.00 | 1.00 | |
| HO | 1.00 | 1.00 | 0.85 | 0.00 | 0.62 | 0.90 | 0.97 | 0.99 | |
| SKS | 1.00 | 1.00 | 0.91 | 0.08 | 0.66 | 0.96 | 1.00 | 1.00 | |
| SKS-num | 1.00 | 1.00 | 0.84 | 0.02 | 0.73 | 0.98 | 1.00 | 1.00 | |
| SN | 1.00 | 1.00 | 0.94 | 0.02 | 0.72 | 0.95 | 1.00 | 1.00 | |
| BDM | 1.00 | 1.00 | 0.85 | 0.06 | 0.62 | 0.90 | 0.97 | 0.99 | |
| IO | 1.00 | 1.00 | 0.89 | 0.00 | 0.89 | 1.00 | 1.00 | 1.00 | |
| HO | 1.00 | 1.00 | 0.95 | 0.00 | 0.81 | 0.98 | 1.00 | 1.00 | |
| SKS | 1.00 | 1.00 | 0.99 | 0.05 | 0.83 | 1.00 | 1.00 | 1.00 | |
| SKS-num | 1.00 | 1.00 | 0.96 | 0.03 | 0.87 | 1.00 | 1.00 | 1.00 | |
| SN | 1.00 | 1.00 | 1.00 | 0.02 | 0.87 | 0.99 | 1.00 | 1.00 | |
| BDM | 1.00 | 1.00 | 0.95 | 0.04 | 0.81 | 0.98 | 1.00 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bortolato, E.; Bertolino, F.; Musio, M.; Ventura, L. Bayesian Discrepancy Measure: Higher-Order and Skewed Approximations. Entropy 2025, 27, 657. https://doi.org/10.3390/e27070657
Bortolato E, Bertolino F, Musio M, Ventura L. Bayesian Discrepancy Measure: Higher-Order and Skewed Approximations. Entropy. 2025; 27(7):657. https://doi.org/10.3390/e27070657
Chicago/Turabian StyleBortolato, Elena, Francesco Bertolino, Monica Musio, and Laura Ventura. 2025. "Bayesian Discrepancy Measure: Higher-Order and Skewed Approximations" Entropy 27, no. 7: 657. https://doi.org/10.3390/e27070657
APA StyleBortolato, E., Bertolino, F., Musio, M., & Ventura, L. (2025). Bayesian Discrepancy Measure: Higher-Order and Skewed Approximations. Entropy, 27(7), 657. https://doi.org/10.3390/e27070657







