Operational Constraints in Quantum Otto Engines: Energy-Gap Modulation and Majorization
Abstract
1. Introduction
2. Quantum Otto Engine with -Level System
3. Gap Modulation and Majorization in Three-Level System
3.1. Changing the Gaps Vis-à-Vis Probabilities
3.2. Case of a Fixed Gap
3.3. Constraints on the Reservoir Temperatures
3.4. Examples
4. Otto Efficiency
5. Swap Engine with Two Three-Level Systems
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. n-Level System
Appendix A.2. Case (a)
Appendix A.3. Case (b)
Appendix A.4. When One Gap Is Kept Fixed
References
- Scovil, H.E.D.; Schulz-DuBois, E.O. Three-level masers as heat engines. Phys. Rev. Lett. 1959, 2, 262. [Google Scholar] [CrossRef]
- Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A Math. Gen. 1979, 12, L103. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119. [Google Scholar] [CrossRef]
- Sheehan, D.P. Quantum limits to the Second law. In Proceedings of the First International Conference on Quantum Limits to the Second Law, San Diego, CA, USA, 28–31 July 2002. [Google Scholar]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting work from a single heat bath via vanishing quantum coherence. Science 2003, 299, 862. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Balian, R.; Nieuwenhuizen, T.M. Maximal work extraction from finite quantum systems. Europhys. Lett. EPL 2004, 67, 565–571. [Google Scholar] [CrossRef]
- Gemmer, J.; Michel, M.; Mahler, G. Quantum Thermodynamics: Emergence of Thermodynamic Behavior Within Composite Quantum System, 2nd ed.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Johal, R.S.; Mahler, G. Work extremum principle: Structure and function of quantum heat engines. Phys. Rev. E 2008, 77, 041118. [Google Scholar] [CrossRef]
- Quan, H.; Liu, Y.-X.; Sun, C.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef]
- Myers, N.M.; Abah, O.; Deffner, S. Quantum thermodynamic devices: From theoretical proposals to experimental reality. AVS Quantum Sci. 2022, 4, 027101. [Google Scholar] [CrossRef]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545. [Google Scholar] [CrossRef]
- Millen, J.; Xuereb, A. Perspective on quantum thermodynamics. New J. Phys. 2016, 18, 011002. [Google Scholar] [CrossRef]
- Quan, H.T. Quantum thermodynamic cycles and quantum heat engines. II. Phys. Rev. E 2009, 79, 041129. [Google Scholar] [CrossRef] [PubMed]
- Altintas, F.; Hardal, A.U.C.; Müstecaplıog, O.E. Quantum correlated heat engine with spin squeezing. Phys. Rev. E 2014, 90, 032102. [Google Scholar] [CrossRef] [PubMed]
- Barrios, G.A.; Albarrán-Arriagada, F.; Cárdenas-López, F.A.; Romero, G.; Retamal, J.C. Role of quantum correlations in light-matter quantum heat engines. Phys. Rev. A 2017, 96, 052119. [Google Scholar] [CrossRef]
- Um, J.; Dorfman, K.E.; Park, H. Coherence-enhanced quantum-dot heat engine. Phys. Rev. Res. 2022, 4, L032034. [Google Scholar] [CrossRef]
- Camati, P.A.; Santos, J.F.G.; Serra, R.M. Coherence effects in the performance of the quantum Otto heat engine. Phys. Rev. A 2019, 99, 062103. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, W.-T.; Chen, P.-X.; Li, C.-Z. Four-level entangled quantum heat engines. Phys. Rev. A 2007, 75, 062102. [Google Scholar] [CrossRef]
- Niedenzu, W.; Gelbwaser-Klimovsky, D.; Kurizki, G. Performance limits of multilevel and multipartite quantum heat machines. Phys. Rev. E 2015, 92, 042123. [Google Scholar] [CrossRef]
- Kamimura, S.; Hakoshima, H.; Matsuzaki, Y.; Yoshida, K.; Tokura, Y. Quantum-enhanced heat engine based on superabsorption. Phys. Rev. Lett. 2022, 128, 180602. [Google Scholar] [CrossRef]
- Tajima, H.; Funo, K. Superconducting-like Heat Current: Effective Cancellation of Current-Dissipation Trade-Off by Quantum Coherence. Phys. Rev. Lett. 2021, 127, 190604. [Google Scholar] [CrossRef]
- Peterson, J.P.S.; Batalhão, T.B.; Herrera, M.; Souza, A.M.; Sarthour, R.S.; Oliveira, I.S.; Serra, R.M. Experimental characterization of a spin quantum heat engine. Phys. Rev. Lett. 2019, 123, 240601. [Google Scholar] [CrossRef]
- de Assis, R.J.; de Mendonça, T.M.; Villas-Boas, C.J.; de Souza, A.M.; Sarthour, R.S.; Oliveira, I.S.; de Almeida, N.G. Efficiency of a quantum Otto heat engine operating under a reservoir at effective negative temperatures. Phys. Rev. Lett. 2019, 122, 240602. [Google Scholar] [CrossRef] [PubMed]
- Nettersheim, J.; Burgardt, S.; Bouton, Q.; Adam, D.; Lutz, E.; Widera, A. Power of a quasispin quantum otto engine at negative effective spin temperature. PRX Quantum 2022, 3, 040334. [Google Scholar] [CrossRef]
- Abah, O.; Roßnagel, J.; Jacob, G.; Deffner, S.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Single-ion heat engine at maximum power. Phys. Rev. Lett. 2012, 109, 203006. [Google Scholar] [CrossRef]
- Hübner, W.; Lefkidis, G.; Dong, C.; Chaudhuri, D.; Chotorlishvili, L.; Berakdar, J. Spin-dependent Otto quantum heat engine based on a molecular substance. Phys. Rev. B 2014, 90, 024401. [Google Scholar] [CrossRef]
- Solfanelli, A.; Falsetti, M.; Campisi, M. Nonadiabatic single-qubit quantum Otto engine. Phys. Rev. B 2020, 101, 054513. [Google Scholar] [CrossRef]
- Karimi, B.; Pekola, J.P. Otto refrigerator based on a superconducting qubit: Classical and quantum performance. Phys. Rev. B 2016, 94, 184503. [Google Scholar] [CrossRef]
- Thomas, G.; Pekola, J.P. Dynamical phase and quantum heat at fractional frequencies. Phys. Rev. Res. 2023, 5, L022036. [Google Scholar] [CrossRef]
- Ji, W.; Chai, Z.; Wang, M.; Guo, Y.; Rong, X.; Shi, F.; Ren, C.; Wang, Y.; Du, J. Spin quantum heat engine quantified by quantum steering. Phys. Rev. Lett. 2022, 128, 090602. [Google Scholar] [CrossRef]
- Del Grosso, N.F.; Lombardo, F.C.; Mazzitelli, F.D.; Villar, P.I. Quantum Otto cycle in a superconducting cavity in the nonadiabatic regime. Phys. Rev. A 2022, 105, 022202. [Google Scholar] [CrossRef]
- Myers, N.M.; Deffner, S. Thermodynamics of statistical anyons. PRX Quantum 2021, 2, 040312. [Google Scholar] [CrossRef]
- Ono, K.; Shevchenko, S.N.; Mori, T.; Moriyama, S.; Nori, F. Analog of a quantum heat engine using a single-spin qubit. Phys. Rev. Lett. 2020, 125, 166802. [Google Scholar] [CrossRef] [PubMed]
- Klatzow, J.; Becker, J.N.; Ledingham, P.M.; Weinzetl, C.; Kaczmarek, K.T.; Saunders, D.J.; Nunn, J.; Walmsley, I.A.; Uzdin, R.; Poem, E. Experimental demonstration of quantum effects in the operation of microscopic heat engines. Phys. Rev. Lett. 2019, 122, 110601. [Google Scholar] [CrossRef]
- Zou, Y.; Jiang, Y.; Mei, Y.; Guo, X.; Du, S. Quantum heat engine using electromagnetically induced transparency. Phys. Rev. Lett. 2017, 119, 050602. [Google Scholar] [CrossRef]
- von Lindenfels, D.; Gräb, O.; Schmiegelow, C.T.; Kaushal, V.; Schulz, J.; Mitchison, M.T.; Goold, J.; Schmidt-Kaler, F.; Poschinger, U.G. Spin heat engine coupled to a harmonic-oscillator flywheel. Phys. Rev. Lett. 2019, 123, 080602. [Google Scholar] [CrossRef]
- Roßnagel, J.; Dawkins, S.T.; Tolazzi, K.N.; Abah, O.; Lutz, E.; Schmidt-Kaler, F.; Singer, K. A single-atom heat engine. Science 2016, 352, 325. [Google Scholar] [CrossRef] [PubMed]
- Maslennikov, G.; Ding, S.; Hablützel, R.; Gan, J.; Roulet, A.; Nimmrichter, S.; Dai, J.; Scarani, V.; Matsukevich, D. Quantum ab-sorption refrigerator with trapped ions. Nat. Commun. 2019, 10, 202. [Google Scholar] [CrossRef] [PubMed]
- Bouton, Q.; Nettersheim, J.; Burgardt, S.; Adam, D.; Lutz, E.; Widera, A. A quantum heat engine driven by atomic collisions. Nat. Commun. 2021, 12, 2063. [Google Scholar] [CrossRef]
- Beyer, K.; Luoma, K.; Strunz, W.T. Steering heat engines: A truly quantum Maxwell demon. Phys. Rev. Lett. 2019, 123, 250606. [Google Scholar] [CrossRef]
- Altintas, F.; Müstecaplıog, O.E. General formalism of local thermodynamics with an example: Quantum Otto engine with a spin-1/2 coupled to an arbitrary spin. Phys. Rev. E 2015, 92, 022142. [Google Scholar] [CrossRef]
- Thomas, G.; Johal, R.S. Coupled quantum Otto cycle. Phys. Rev. E 2011, 83, 031135. [Google Scholar] [CrossRef]
- Thomas, G.; Johal, R.S. Friction due to inhomogeneous driving of coupled spins in a quantum heat engine. Eur. Phys. J. B 2014, 87, 166. [Google Scholar] [CrossRef]
- Johal, R.S.; Mehta, V. Quantum heat engines with complex working media, complete Otto cycles and heuristics. Entropy 2021, 23, 1149. [Google Scholar] [CrossRef]
- Sonkar, S.; Johal, R.S. Spin-based quantum Otto engines and majorization. Phys. Rev. A 2023, 107, 032220. [Google Scholar] [CrossRef]
- Ivanchenko, E.A. Quantum Otto cycle efficiency on coupled qudits. Phys. Rev. E 2015, 92, 032124. [Google Scholar] [CrossRef]
- Türkpençe, D.; Altintas, F. Coupled quantum Otto heat engine and refrigerator with inner friction. Quantum Inf. Process. 2019, 18, 255. [Google Scholar] [CrossRef]
- Brunner, N.; Huber, M.; Linden, N.; Popescu, S.; Silva, R.; Skrzypczyk, P. Entanglement enhances cooling in microscopic quantum refrigerators. Phys. Rev. E 2014, 89, 032115. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. Optimization performance of quantum Otto heat engines and refrigerators with squeezed thermal reservoirs. Phys. A Stat. Mech. Its Appl. 2020, 559, 125083. [Google Scholar] [CrossRef]
- de Assis, R.J.; Sales, J.S.; Mendes, U.C.; de Almeida, N.G. Two-level quantum Otto heat engine operating with unit efficiency far from the quasi-static regime under a squeezed reservoir. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 095501. [Google Scholar] [CrossRef]
- Singh, V.; Müstecaplıog, O.E. Performance bounds of nonadiabatic quantum harmonic Otto engine and refrigerator under a squeezed thermal reservoir. Phys. Rev. E 2020, 102, 062123. [Google Scholar] [CrossRef]
- Wang, J.; He, J.; Ma, Y. Finite-time performance of a quantum heat engine with a squeezed thermal bath. Phys. Rev. E 2019, 100, 052126. [Google Scholar] [CrossRef]
- Huang, X.L.; Guo, D.Y.; Wu, S.L.; Yi, X.X. Multilevel quantum Otto heat engines with identical particles. Quantum Inf. Process. 2017, 17, 27. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Z.; He, J. Quantum Otto engine of a two-level atom with single-mode fields. Phys. Rev. E 2012, 85, 041148. [Google Scholar] [CrossRef]
- Halpern, N.Y.; White, C.D.; Gopalakrishnan, S.; Refael, G. Quantum engine based on many-body localization. Phys. Rev. B 2019, 99, 024203. [Google Scholar] [CrossRef]
- Izadyari, M.; Naseem, M.T.; Müstecaplıog, O.E. Enantiomer detection via quantum Otto cycle. Phys. Rev. E 2023, 107, L042103. [Google Scholar] [CrossRef] [PubMed]
- Makouri, A.E.; Slaoui, A.; Daoud, M. Enhancing the performance of coupled quantum Otto thermal machines without entan-glement and quantum correlations. J. Phys. B At. Mol. Opt. Phys. 2023, 56, 085501. [Google Scholar] [CrossRef]
- Kaneyasu, M.; Hasecondawa, Y. Quantum Otto cycle under strong coupling. Phys. Rev. E 2023, 107, 044127. [Google Scholar] [CrossRef] [PubMed]
- Piccitto, G.; Campisi, M.; Rossini, D. The Ising critical quantum Otto engine. New J. Phys. 2022, 24, 103023. [Google Scholar] [CrossRef]
- Solfanelli, A.; Giachetti, G.; Campisi, M.; Ruffo, S.; Defenu, N. Quantum heat engine with long-range advantages. New J. Phys. 2023, 25, 033030. [Google Scholar] [CrossRef]
- Ptaszyn, K. Non-markovian thermal operations boosting the performance of quantum heat engines. Phys. Rev. E 2022, 106, 014114. [Google Scholar] [CrossRef]
- Ishizaki, M.; Hatano, N.; Tajima, H. Switching the function of the quantum Otto cycle in non-markovian dynamics: Heat engine, heater, and heat pump. Phys. Rev. Res. 2023, 5, 023066. [Google Scholar] [CrossRef]
- Chakraborty, S.; Das, A.; Chrus, D. Strongly coupled quantum Otto cycle with single qubit bath. Phys. Rev. E 2022, 106, 064133. [Google Scholar] [CrossRef] [PubMed]
- Thomas, G.; Siddharth, N.; Banerjee, S.; Ghosh, S. Thermodynamics of non-markovian reservoirs and heat engines. Phys. Rev. E 2018, 97, 062108. [Google Scholar] [CrossRef]
- Wu, F.; He, J.; Ma, Y.; Wang, J. Efficiency at maximum power of a quantum Otto cycle within finite-time or irreversible thermo-dynamics. Phys. Rev. E 2014, 90, 062134. [Google Scholar] [CrossRef]
- Das, A.; Mukherjee, V. Quantum-enhanced finite-time otto cycle. Phys. Rev. Res. 2020, 2, 033083. [Google Scholar] [CrossRef]
- Chand, S.; Dasgupta, S.; Biswas, A. Finite-time performance of a single-ion quantum otto engine. Phys. Rev. E 2021, 103, 032144. [Google Scholar] [CrossRef]
- Lee, S.; Ha, M.; Park, J.-M.; Jeong, H. Finite-time quantum otto engine: Surpassing the quasistatic efficiency due to friction. Phys. Rev. E 2020, 101, 022127. [Google Scholar] [CrossRef] [PubMed]
- Geva, E.; Kosloff, R. A quantum-mechanical heat engine operating in finite time. a model consisting of spin-1/2 systems as the working fluid. J. Chem. Phys. 1992, 96, 3054. [Google Scholar] [CrossRef]
- Saha, D.; Ghoshal, A.; Sen, U. Temperature- and interaction-tweaked efficiency boost of finite-time robust quantum otto engines. arXiv 2023, arXiv:2309.11483. [Google Scholar]
- Feldmann, T.; Kosloff, R. Performance of discrete heat engines and heat pumps in finite time. Phys. Rev. E 2000, 61, 4774. [Google Scholar] [CrossRef]
- Alicki, R. Quantum thermodynamics: An example of two-level quantum machine. Open Syst. Inf. Dyn. 2014, 21, 1440002. [Google Scholar] [CrossRef]
- Kieu, T.D. The Second law, Maxwell’s demon, and work derivable from quantum heat engines. Phys. Rev. Lett. 2004, 93, 140403. [Google Scholar] [CrossRef] [PubMed]
- Kieu, T.D. Quantum heat engines, the second law and Maxwell’s demon. Eur. Phys. J. D At. Mol. Opt. Plasma Phys. 2006, 39, 115–128. [Google Scholar] [CrossRef]
- Henrich, M.; Rempp, F.; Mahler, G. Quantum thermodynamic Otto machines: A spin-system approach. Eur. Phys. J. Spec. Top. 2007, 151, 157. [Google Scholar] [CrossRef]
- Beretta, G.P. Quantum thermodynamic Carnot and Otto-like cycles for a two-level system. Europhys. Lett. 2012, 99, 20005. [Google Scholar] [CrossRef]
- Ghosh, A.; Gelbwaser-Klimovsky, D.; Niedenzu, W.; Lvovsky, A.I.; Mazets, I.; Scully, M.O.; Kurizki, G. Two-level masers as heat-to-work converters. Proc. Natl. Acad. Sci. USA 2018, 115, 9941–9944. [Google Scholar] [CrossRef]
- Papadatos, N. Quantum Stirling heat engine with squeezed thermal reservoir. Chin. Phys. B 2023, 32, 100702. [Google Scholar] [CrossRef]
- Uzdin, R.; Kosloff, R. The multilevel four-stroke swap engine and its environment. New J. Phys. 2014, 16, 095003. [Google Scholar] [CrossRef]
- de Oliveira, T.R.; Jonathan, D. Efficiency gain and bidirectional operation of quantum engines with decoupled internal levels. Phys. Rev. E 2021, 104, 044133. [Google Scholar] [CrossRef]
- Simmons, E.Q.; Sajjad, R.; Keithley, K.; Mas, H.; Tanlimco, J.L.; Nolasco-Martinez, E.; Bai, Y.; Fredrickson, G.H.; Weld, D.M. Thermodynamic engine with a quantum degenerate working fluid. Phys. Rev. Res. 2023, 5, L042009. [Google Scholar] [CrossRef]
- Jaseem, N.; Vinjanampathy, S.; Mukherjee, V. Quadratic enhancement in the reliability of collective quantum engines. Phys. Rev. A 2023, 107, L040202. [Google Scholar] [CrossRef]
- Williamson, L.A.; Davis, M.J. Many-body enhancement in a spin-chain quantum heat engine. Phys. Rev. B 2024, 109, 024310. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I.; Arnold, B.C. Inequalities: Theory of Majorization and Its Applications; Springer Series in Statistics; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Sagawa, T. Entropy, Divergence, and Majorization in Classical and Quantum Thermodynamics; Springer Briefs in Mathematical Physics; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Bhatia, R. Matrix Analysis; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Buscemi, F.; Gour, G. Quantum relative Lorenz curves. Phys. Rev. A 2017, 95, 012110. [Google Scholar] [CrossRef]
- Joe, H. Majorization and divergence. J. Math. Anal. Appl. 1990, 148, 287. [Google Scholar] [CrossRef]
- Shiraishi, N. Two constructive proofs on d-majorization and thermo-majorization. J. Phys. A Math. Theor. 2020, 53, 425301. [Google Scholar] [CrossRef]
- Egloff, D.; Dahlsten, O.C.O.; Renner, R.; Vedral, V. A measure of majorization emerging from single-shot statistical mechanics. New J. Phys. 2015, 17, 073001. [Google Scholar] [CrossRef]
- Renes, J.M. Relative submajorization and its use in quantum resource theories. J. Math. Phys. 2016, 57, 122202. [Google Scholar] [CrossRef]
- Ruch, E.; Schranner, R.; Seligman, T.H. Generalization of a theorem by Hardy, Littlewood, and Pólya. J. Math. Anal. Appl. 1980, 76, 222–229. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Vidal, G. Majorization and the interconversion of bipartite states. Quantum Info. Comput. 2001, 1, 76–93. [Google Scholar] [CrossRef]
- Nielsen, M.A. Conditions for a class of entanglement transformations. Phys. Rev. Lett. 1999, 83, 436. [Google Scholar] [CrossRef]
- Du, S.; Bai, Z.; Guo, Y. Conditions for coherence transformations under incoherent operations. Phys. Rev. A 2015, 91, 052120. [Google Scholar] [CrossRef]
- Jonathan, D.; Plenio, M.B. Entanglement-assisted local manipulation of pure quantum states. Phys. Rev. Lett. 1999, 83, 3566. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Oppenheim, J. Reversible transformations from pure to mixed states and the unique measure of in-formation. Phys. Rev. A 2003, 67, 062104. [Google Scholar] [CrossRef]
- Singh, U.; Das, S.; Cerf, N.J. Partial order on passive states and Hoffman majorization in quantum thermodynamics. Phys. Rev. Res. 2021, 3, 033091. [Google Scholar] [CrossRef]
- Lostaglio, M.; Korzekwa, K. Continuous thermomajorization and a complete set of laws for markovian thermal processes. Phys. Rev. A 2022, 106, 012426. [Google Scholar] [CrossRef]
- Gour, G.; Jennings, D.; Buscemi, F.; Duan, R.; Marvian, I. Quantum majorization and a complete set of entropic conditions for quantum thermodynamics. Nat. Commun. 2018, 9, 5352. [Google Scholar] [CrossRef]
- Rethinasamy, S.; Wilde, M.M. Relative entropy and catalytic relative majorization. Phys. Rev. Res. 2020, 2, 033455. [Google Scholar] [CrossRef]
- Brandão, F.; Horodecki, M.; Ng, N.; Oppenheim, J.; Wehner, S. The second laws of quantum thermodynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 3275–3279. [Google Scholar] [CrossRef]
- Horodecki, M.; Oppenheim, J. Fundamental limitations for quantum and nanoscale thermodynamics. Nat. Commun. 2013, 4, 2059. [Google Scholar] [CrossRef] [PubMed]
- Junior, A.D.O.; Czartowski, J.; Życzkowski, K.; Korzekwa, K. Geometric structure of thermal cones. Phys. Rev. E 2022, 106, 064109. [Google Scholar] [CrossRef]
- Bosyk, G.M.; Bellomo, G.; Holik, F.; Freytes, H.; Sergioli, G. Optimal common resource in majorization-based resource theories. New J. Phys. 2019, 21, 083028. [Google Scholar] [CrossRef]
- Alimuddin, M.; Guha, T.; Parashar, P. Independence of work and entropy for equal-energetic finite quantum systems: Passive-state energy as an entanglement quantifier. Phys. Rev. E 2020, 102, 012145. [Google Scholar] [CrossRef]
- Alimuddin, M.; Guha, T.; Parashar, P. Bound on ergotropic gap for bipartite separable states. Phys. Rev. A 2019, 99, 052320. [Google Scholar] [CrossRef]
- Joshi, J.; Alimuddin, M.; Mahesh, T.S.; Banik, M. Experimental verification of many-body entanglement using thermodynamic quantities. Phys. Rev. A 2024, 109, L020403. [Google Scholar] [CrossRef]
- Puliyil, S.; Banik, M.; Alimuddin, M. Thermodynamic signatures of genuinely multipartite entanglement. Phys. Rev. Lett. 2022, 129, 070601. [Google Scholar] [CrossRef]
- Mannalath, V.; Pathak, A. Multiparty entanglement routing in quantum networks. Phys. Rev. A 2023, 108, 062614. [Google Scholar] [CrossRef]
- Alimuddin, M.; Guha, T.; Parashar, P. Structure of passive states and its implication in charging quantum batteries. Phys. Rev. E 2020, 102, 022106. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Fock, V. Beweis des Adiabatensatzes. Z. Fur Phys. 1928, 51, 165. [Google Scholar] [CrossRef]
- Anka, M.F.; de Oliveira, T.R.; Jonathan, D. Measurement-based quantum heat engine in a multilevel system. Phys. Rev. E 2021, 104, 054128. [Google Scholar] [CrossRef]
- Bayona-Pena, P.; Takahashi, K. Thermodynamics of a continuous quantum heat engine: Interplay between population and coher-ence. Phys. Rev. A 2021, 104, 042203. [Google Scholar] [CrossRef]
- Boukobza, E.; Tannor, D.J. Three-level systems as amplifiers and attenuators: A thermodynamic analysis. Phys. Rev. Lett. 2007, 98, 240601. [Google Scholar] [CrossRef]
- Linden, N.; Popescu, S.; Skrzypczyk, P. How small can thermal machines be? The smallest possible refrigerator. Phys. Rev. Lett. 2010, 105, 130401. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.; Johal, R.S. Three-level laser heat engine at optimal performance with ecological function. Phys. Rev. E 2019, 100, 012138. [Google Scholar] [CrossRef] [PubMed]
- Macovei, M.A. Performance of the collective three-level quantum thermal engine. Phys. Rev. A 2022, 105, 043708. [Google Scholar] [CrossRef]
- Deng, G.X.; Shao, W.; Liu, Y.; Cui, Z. Continuous three-level quantum heat engine with high performance under medium temperature difference. J. Appl. Phys. 2023, 133, 124903. [Google Scholar] [CrossRef]
- Fedorov, A.; Steffen, L.; Baur, M.; da Silva, M.P.; Wallraff, A. Implementation of a Toffoli gate with superconducting circuits. Nature 2012, 481, 170. [Google Scholar] [CrossRef]
- Yurtalan, M.A.; Shi, J.; Kononenko, M.; Lupascu, A.; Ashhab, S. Implementation of a Walsh-Hadamard gate in a superconducting qutrit. Phys. Rev. Lett. 2020, 125, 180504. [Google Scholar] [CrossRef]
- Morvan, A.; Ramasesh, V.V.; Blok, M.S.; Kreikebaum, J.M.; O’Brien, K.; Chen, L.; Mitchell, B.K.; Naik, R.K.; Santiago, D.I.; Siddiqi, I. Qutrit randomized benchmarking. Phys. Rev. Lett. 2021, 126, 210504. [Google Scholar] [CrossRef]
- Díaz, I.; Sánchez, R. The qutrit as a heat diode and circulator. New J. Phys. 2021, 23, 125006. [Google Scholar] [CrossRef]
- Thomas, G.; Gubaydullin, A.; Golubev, D.S.; Pekola, J.P. Thermally pumped on-chip maser. Phys. Rev. B 2020, 102, 104503. [Google Scholar] [CrossRef]
- Gelbwaser-Klimovsky, D.; Niedenzu, W.; Brumer, P.; Kurizki, G. Power enhancement of heat engines via correlated thermalization in a three-level “working fluid”. Sci. Rep. 2015, 5, 14413. [Google Scholar] [CrossRef]
- Mehta, V.; Johal, R.S. Quantum Otto engine with exchange coupling in the presence of level degeneracy. Phys. Rev. E 2017, 96, 032110. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.T.; Zhang, P.; Sun, C.P. Quantum heat engine with multilevel quantum systems. Phys. Rev. E 2005, 72, 056110. [Google Scholar] [CrossRef] [PubMed]
- Hirotani, T.; Yoshimura, K.G. Relativistic quantum Otto heat engine using a three-level Unruh-DeWitt detector. arXiv 2025, arXiv:2504.01435. [Google Scholar]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Solfanelli, A.; Santini, A.; Campisi, M. Experimental Verification of Fluctuation Relations with a Quantum Computer. PRX Quantum 2021, 2, 030353. [Google Scholar] [CrossRef]
- Sacchi, M.F. Multilevel quantum thermodynamic swap engines. Phys. Rev. A 2021, 104, 012217. [Google Scholar] [CrossRef]
- The Mediant Inequality: For Positive Real Numbers a, b, c, d > 0, the Inequality a/b > c/d implies > > . Available online: https://mathpages.com/home/kmath055/kmath055.htm (accessed on 10 June 2025).


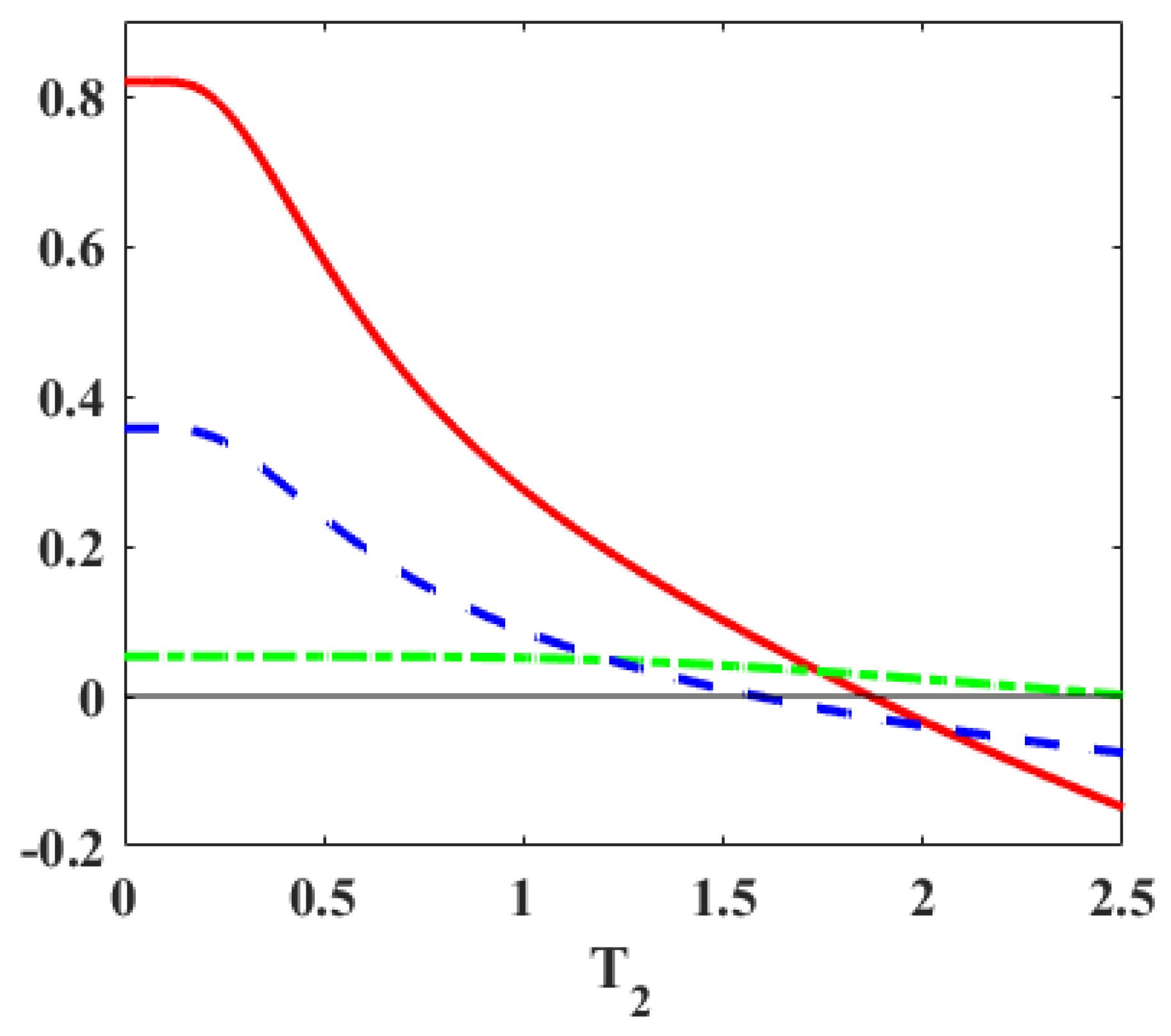
| G-1 | |
| Case (a) | |
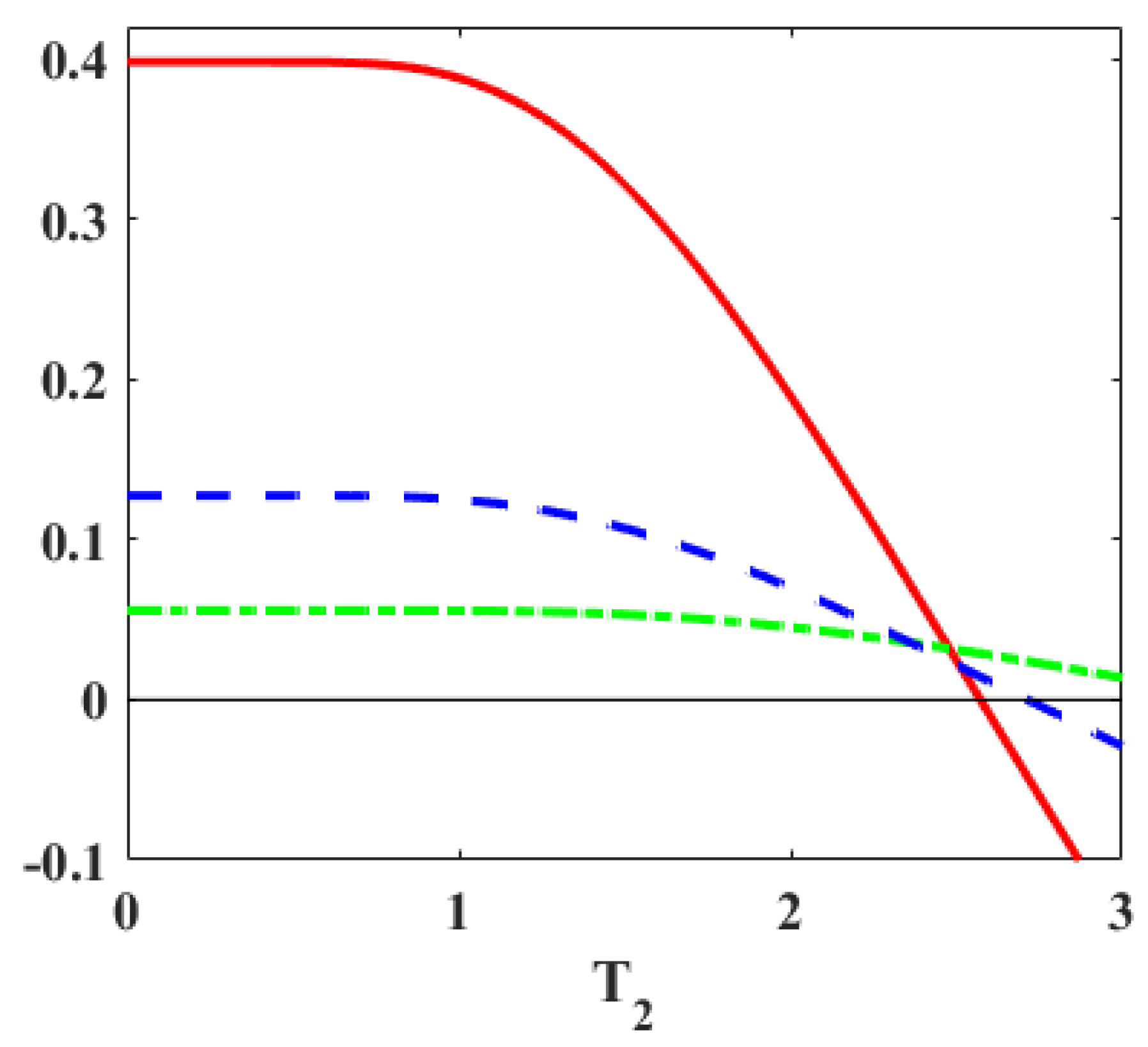
| Case (b) | |
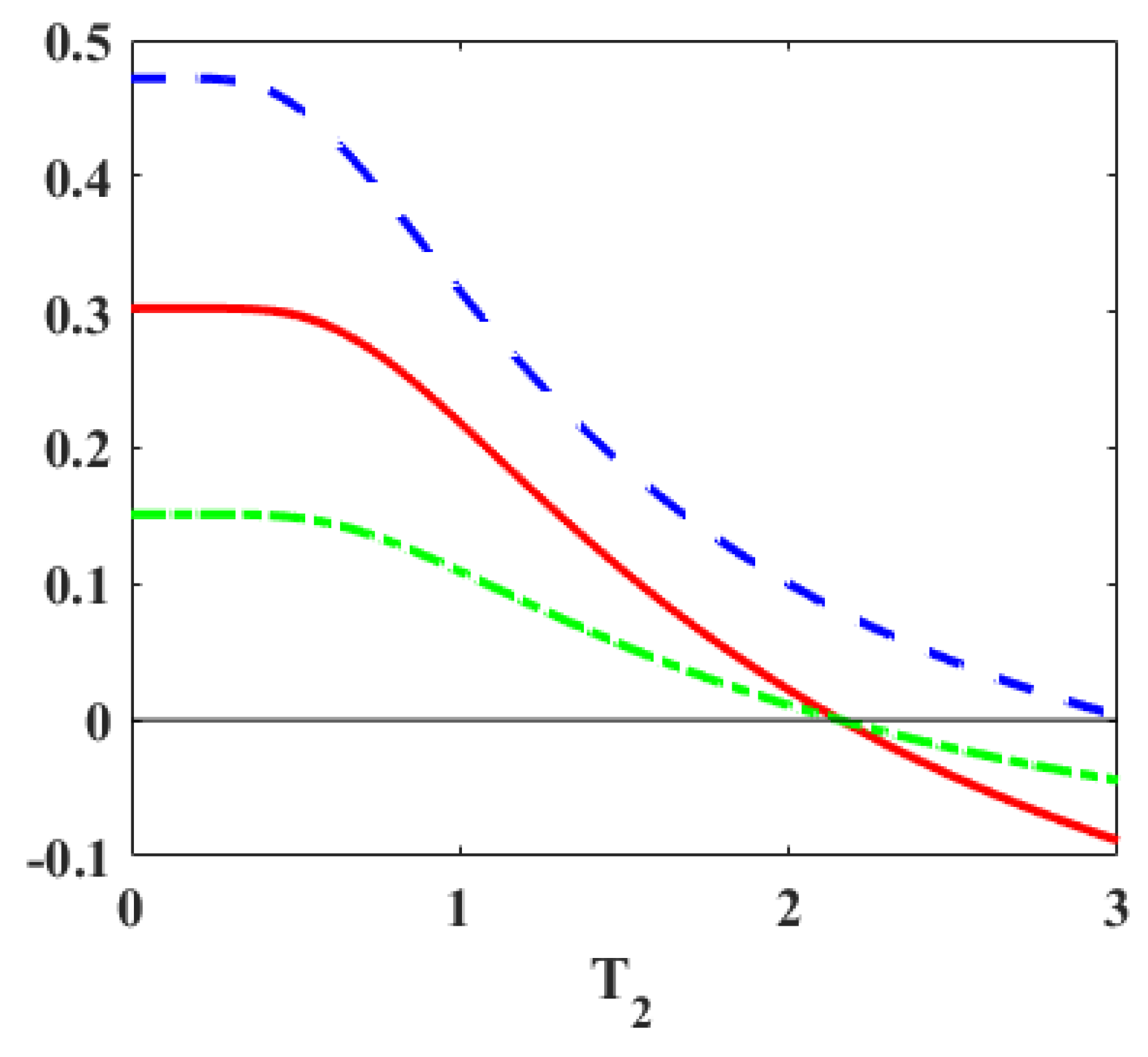
| Case (c) |
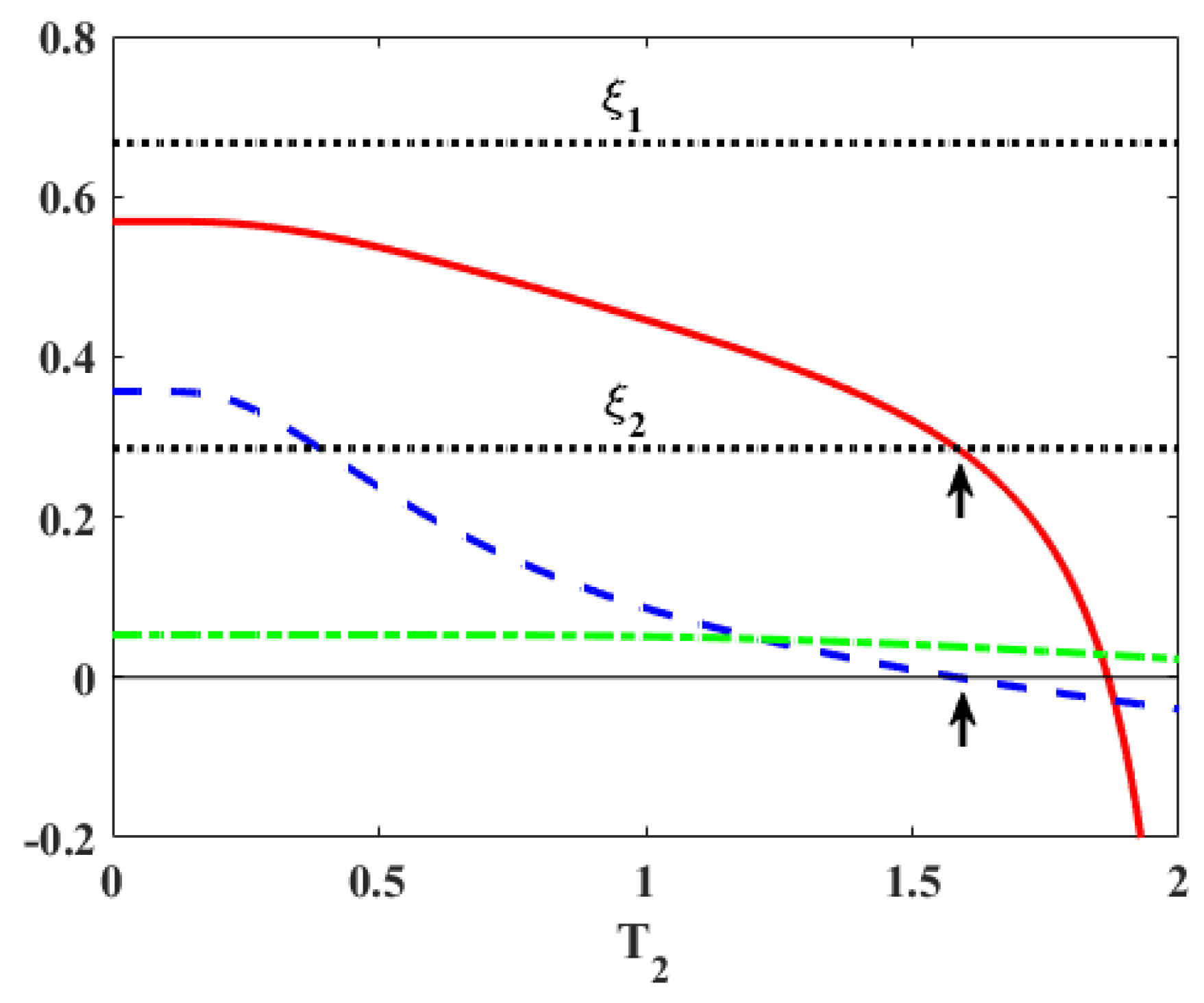
| Case (c) | G-2 | G-3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sonkar, S.; Johal, R.S. Operational Constraints in Quantum Otto Engines: Energy-Gap Modulation and Majorization. Entropy 2025, 27, 625. https://doi.org/10.3390/e27060625
Sonkar S, Johal RS. Operational Constraints in Quantum Otto Engines: Energy-Gap Modulation and Majorization. Entropy. 2025; 27(6):625. https://doi.org/10.3390/e27060625
Chicago/Turabian StyleSonkar, Sachin, and Ramandeep S. Johal. 2025. "Operational Constraints in Quantum Otto Engines: Energy-Gap Modulation and Majorization" Entropy 27, no. 6: 625. https://doi.org/10.3390/e27060625
APA StyleSonkar, S., & Johal, R. S. (2025). Operational Constraints in Quantum Otto Engines: Energy-Gap Modulation and Majorization. Entropy, 27(6), 625. https://doi.org/10.3390/e27060625






