Sic Transit Gloria Mundi: A Mathematical Theory of Popularity Waves Based on a SIIRR Model of Epidemic Spread
Abstract
1. Introduction
2. The SIIRR Model of Spread of Two Viruses in a Population
3. An Exact Solution to Equations Connected to the Model Equations for the SIIRR Model
4. Several Results from the Numerical Study of the Model Equations
4.1.
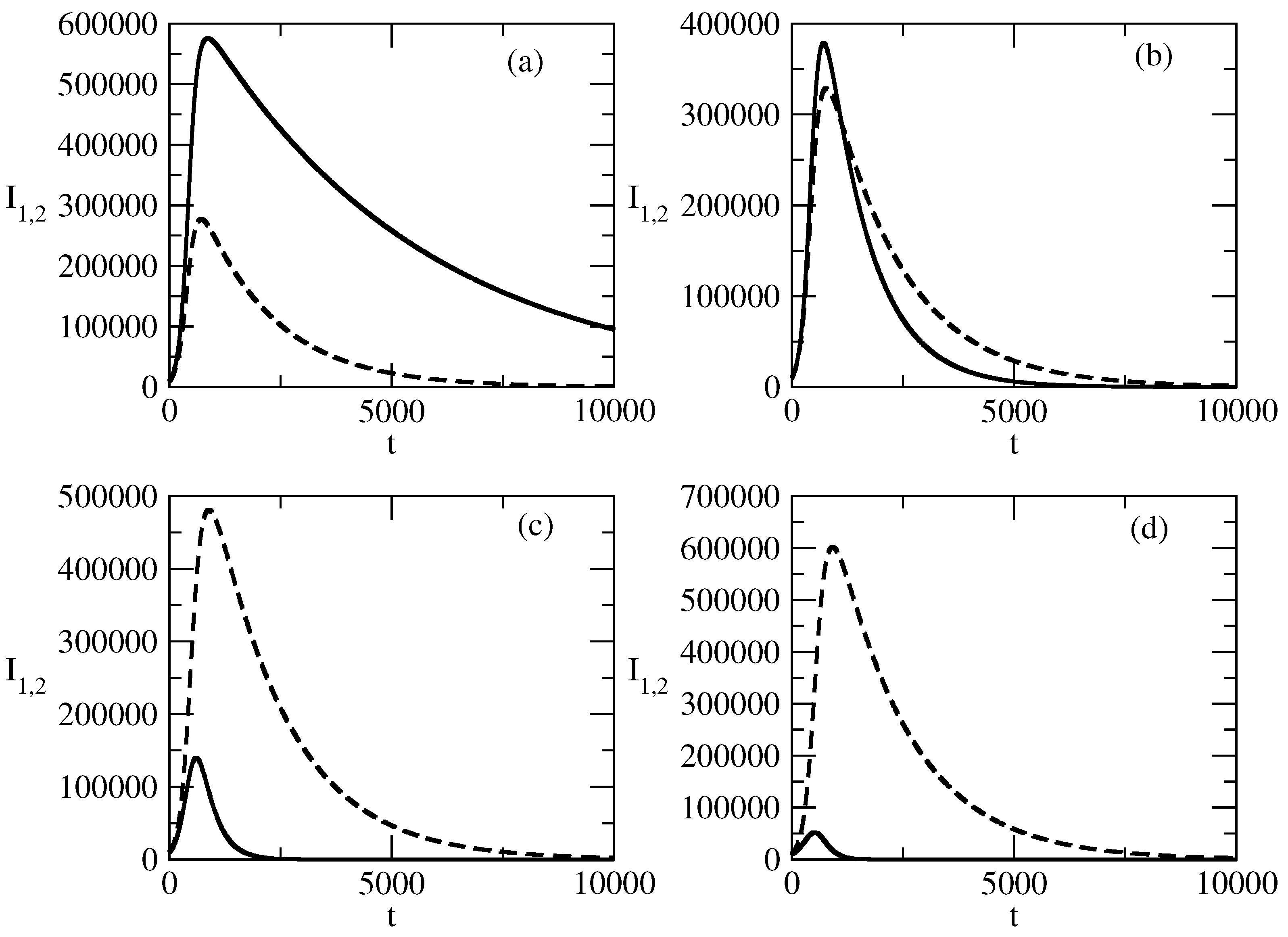
- Suppression of the peak of with an increase in . The peak of may even vanish.
- The smaller peak of occurs faster with an increasing value of .
4.2. and Have the Same Values
5. Discussion of the Obtained Exact Analytical Solutions of the Studied Chain of Equations from the Point of View of Modeling of Waves of Popularity
- We consider the popularity change as a process of infecting individuals of a population with a possibility of a recovery (losing interest in the popular person/idea).
- The popularity of something (person or idea) is measured by the number of infected individuals (individuals who have an opinion about the corresponding person or idea).
- We distinguish between two kinds of popularity:
- (a)
- Positive popularity;
- (b)
- Negative popularity.
In the case of positive popularity, the “infected” have a positive opinion about the person or towards the idea. In the case of negative popularity, the “infected” have a negative opinion about the person or towards the idea. - The positive popularity and the negative popularity coexist. They can be considered as two different infections with a specific feature.
- The specific feature is that if one is infected by positive popularity, this person cannot be infected by negative popularity at the same time.
- Recovering from the infection with positive or negative popularity can also occur. In this case, the corresponding person becomes indifferent to the popular person or the popular idea.
- Thus, in the SIIRR model, we have suspected individuals S which can be infected by the positive or negative popularity of an individual (or group of individuals) or towards an idea (or system of ideas).
- The two kinds of infection are positive popularity ( infected individuals) and negative popularity ( infected individuals).
- There are also two groups of recovered individuals. is the group of individuals who recovered from positive popularity and is the group of individuals who recovered from negative popularity. The assumption is that recovered individuals cannot be infected further: they become indifferent to the person or towards the idea or system of ideas.
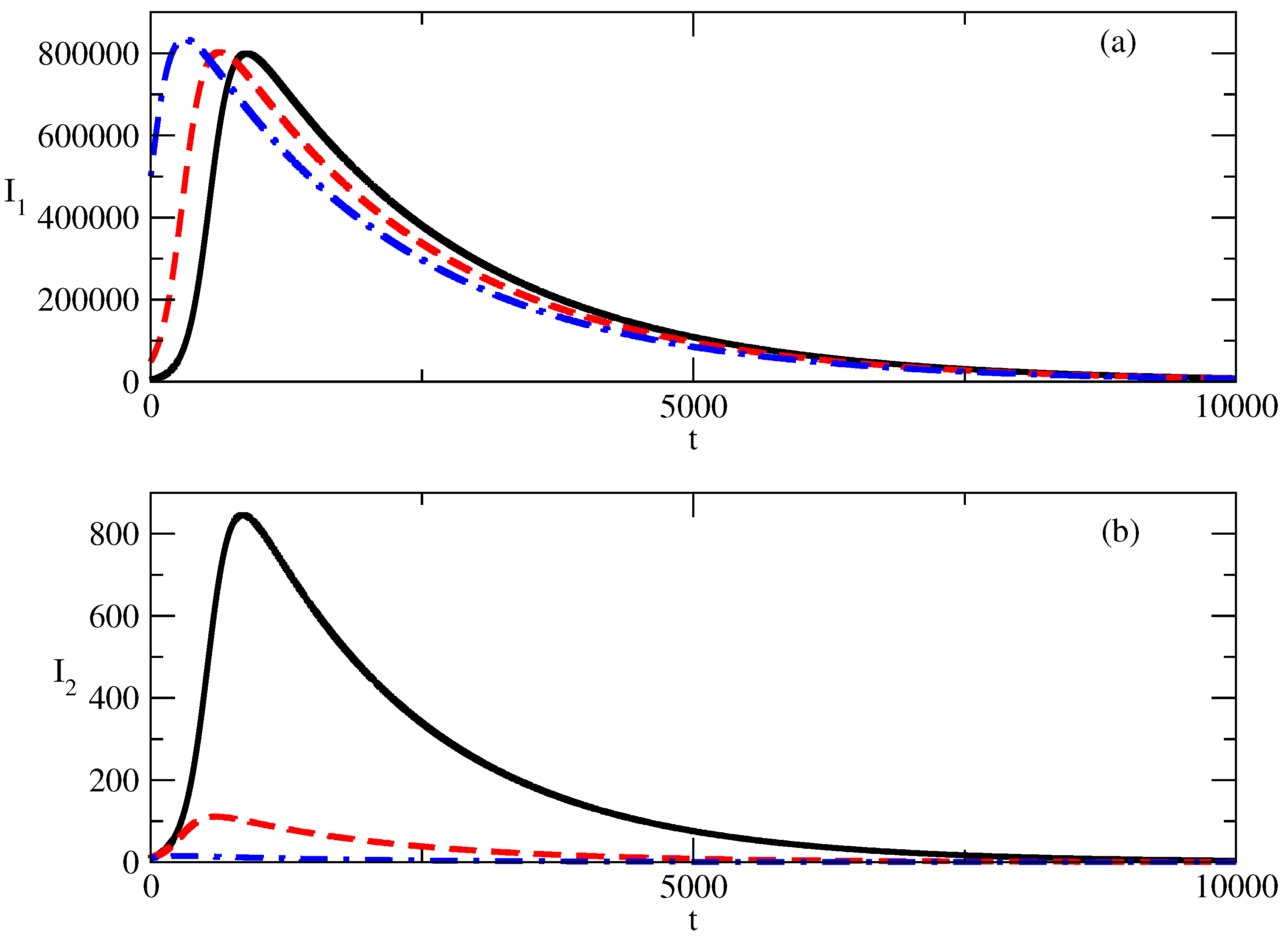
- We associate with positive popularity and with negative popularity. We observe a large wave of positive popularity and a much smaller wave of negative popularity.
- The peak of the wave of negative popularity occurs slightly earlier than the peak of the wave of positive popularity.
- For the discussed specific case, the corresponding person or idea (group of individuals or groups of ideas) is (are) much more popular than unpopular.
- Over the course of time, popularity and unpopularity tend to 0 and the number of indifferent individuals increases to N. The system is ready to deal with the next popular individuals or ideas.
- Thus, popularity occurs, rises, falls, and vanishes.
- For small values of the initial number of the susceptible individuals , the positive and negative popularity of the individual/group of individuals or of the idea/group of ideas decreases monotonically from its initial value at . This means that it is very important to have a much larger number of individuals which can be affected by popularity in comparison to the initial numbers connected to positive and negative popularity. We call this phenomenon “suppression of popularity”.
- If the number of susceptible individuals is large enough, there is a change in the behavior of the system. In this case, classical bell-shaped curves of popularity (positive and negative) occur. One observes an increase and peak of the positive and negative popularity, and then the popularity decreases to 0. This is the “effect of forgetting”: society “forgets” the popular person/group of persons or the popular idea/group of ideas.
- Different times of occurrence of the peaks of positive and negative popularity can be present. We call this the “effect of the delay of a peak”. In the discussed case, the peak of negative popularity occurs earlier. In this case, for some time, the positive popularity increases and the negative popularity decreases. We call this time period the “window of dominance”. Of course, for other values of the parameters, we could have a peak of positive popularity before a peak of negative popularity. Then, we have another “window of dominance”: a time window in which the positive popularity decreases and the negative popularity still increases.
- Finally, in Figure 2b,d, we observe that the positive popularity can peak very fast, but then the decrease is also very fast. In contrast, the negative popularity can peak slowly, but then the decay of this popularity is also very slow. We call this effect “short term win–long term loss”. For other values of the parameters, we could have the opposite situation: short-term win for the negative popularity, which leads to its long-term loss.
- A larger initial value of positive popularity leads to a larger peak.
- In addition, the larger initial value of positive popularity suppresses the negative popularity: the peak value of negative popularity decreases and occurs earlier in time.
- Thus, the goal of an image-maker can be to increase the initial positive popularity of the corresponding individual/group of individuals or idea/group of ideas. In such a way, the coexisting wave of negative popularity will be suppressed.
- But this has a price: the peak of positive popularity will occur earlier and then one will observe a faster decrease in this popularity.
- The increase in the initial value of the negative popularity leads to a sharp decrease in the positive popularity, as can be seen in Figure 4a.
- At the same time, the larger initial value of negative popularity can lead to a large increase in this popularity—Figure 4b.
- Thus, we have an important mechanism for the control of positive popularity: we just need to have a large enough value of the corresponding negative popularity.
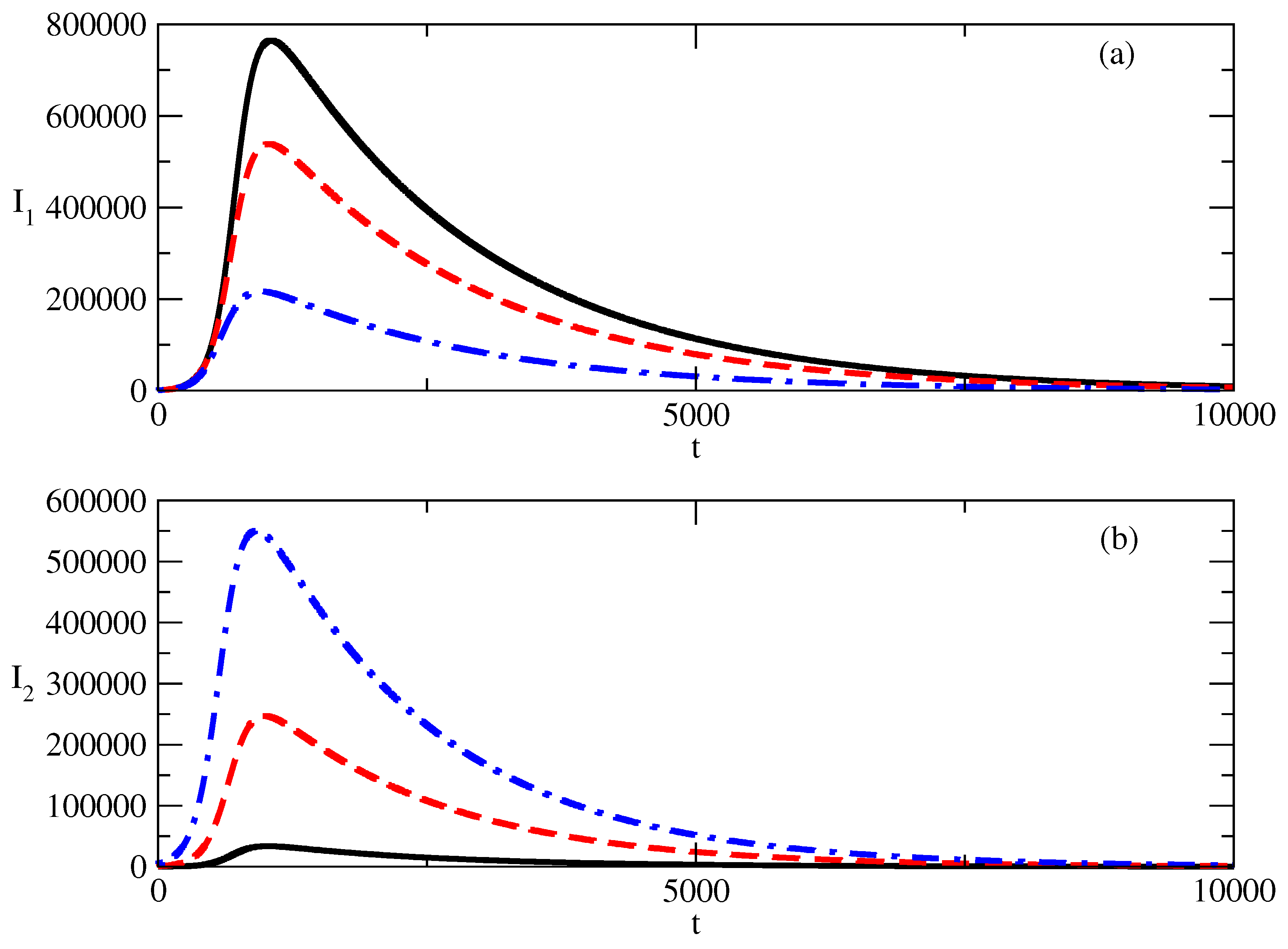
- We observe that for small values of , the positive popularity can decrease and the occurrence of a peak in this popularity happens for values of over a certain threshold.
- Further, an increase in can lead to a jump of positive popularity.
- At the same time, the negative popularity can remain almost unchanged, as can be seen in Figure 5c,d.
- A larger transmission rate means that the negative popularity spreads easily. This influences the positive popularity: the easier spread of negative popularity inhibits the positive popularity. The peak of positive popularity becomes smaller and it occurs earlier.
- Opposite to this, the larger transmission rate for the negative popularity leads to larger negative popularity: the peak of the negative popularity becomes larger and this peak occurs later in time.
- Thus, if we want to suppress positive popularity and increase negative popularity, we have to increase the transmission rate of the negative popularity. This decreases the peak of positive popularity and increases the peak of the negative popularity.
- In addition, the positive popularity will last less (as its peaks will move to an earlier time) and the negative popularity will last longer (as its peak will move to the region of larger times).
- The increase in the value of the recovery rate negatively influences the positive popularity . The value of the peak of this popularity can fall dramatically. In addition, the smaller peak of popularity shifts to the region of smaller times. This means that the positive popularity increases with larger difficulties and decays faster in comparison to the case when the value of the recovery rate is smaller.
- Figure 7b shows the opposite effect on the increase in the value of the recovery rate on the evolution of the negative popularity . The increase in the value of the recovery rate for positive popularity leads to an increase in negative popularity. The peak of the negative popularity can become very large and, in addition, the peak moves to the region of larger times. This means that the negative popularity increases faster and lasts longer.
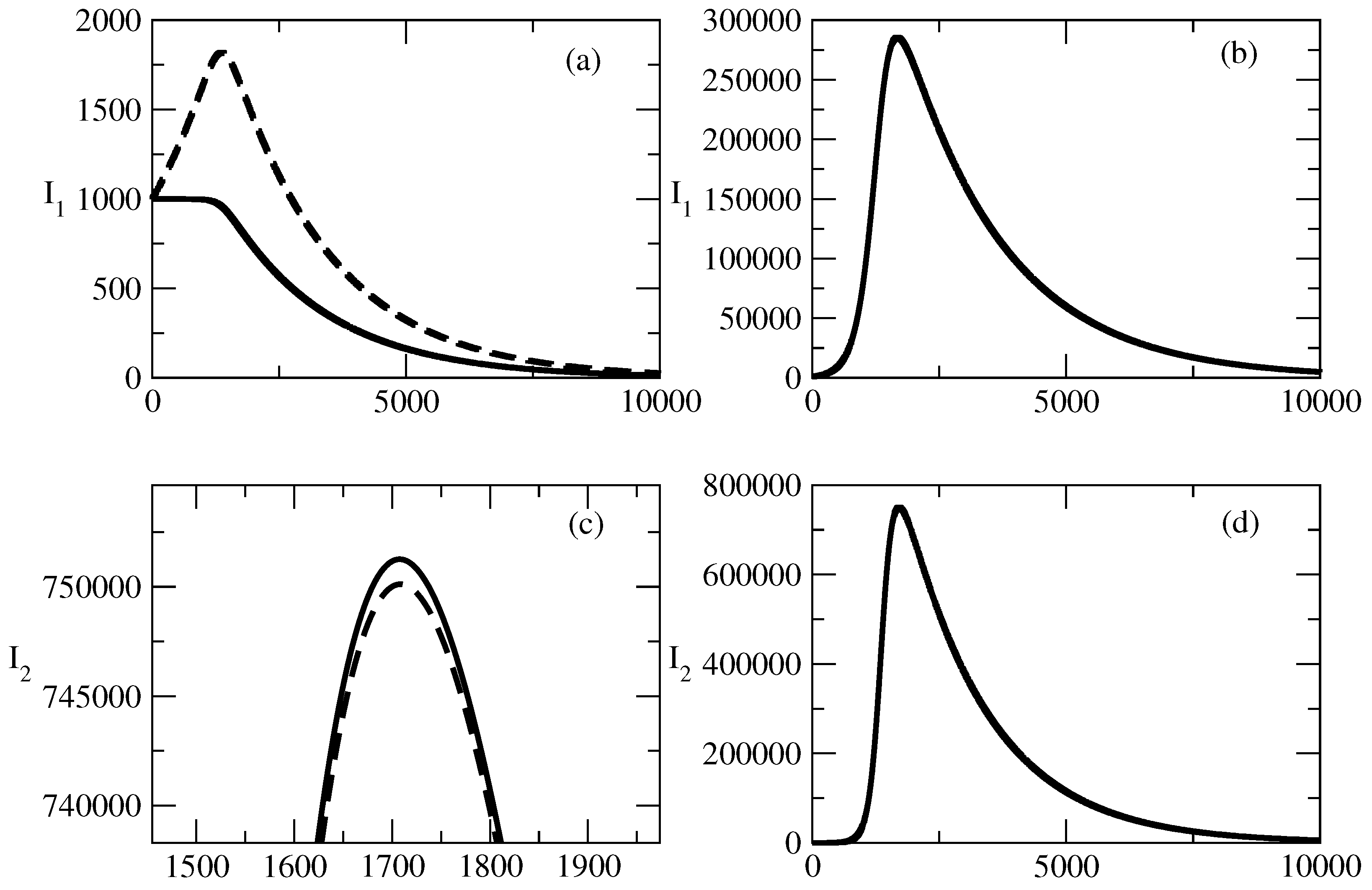
- Figure 8a shows that there is an interval of values for where a change in the value of leads to small changes in positive popularity and this popularity is almost not affected.
- An interesting influence of the change in the value of the recovery rate for negative popularity on the evolution of the negative popularity is shown in Figure 8b. Here we observe a bell-shaped behavior of the curve of positive popularity, and the decrease in the value of leads to reaching a peak value followed by a very slow decrease in the positive popularity.
- The peak of the wave of negative popularity is slightly earlier than the peak of the wave of positive popularity.
- We observe polarization of society with respect to the corresponding person or idea.
- Despite this polarization, in the course of time, popularity decreases and then tends to 0.
- Figure 9b shows the corresponding evolution of the susceptible and recovered individuals. The number of susceptible individuals decreases fast, and then society is divided to groups of infected and indifferent individuals.
- For a short time, popularity prevails over indifference, but as time advances, society loses its interest in the corresponding person or idea.
- In the case of a small number of individuals susceptible to the corresponding popularity, we again observe the effect of suppression: the positive and negative popularity decrease monotonically with increasing time.
- Then, in Figure 11, we observe the “effect of the single peak”. Here, the negative popularity again decreases monotonically, and the positive popularity has a peak before the beginning of its decay. Of course, for different values of the parameters, we can have monotonous decay for positive popularity and a peak for negative popularity.
- With a further increase in the initial number of individuals susceptible to “popularity infection” the curves for positive and negative popularity develop peaks and then there is a decay. We observe again “the effects of forgetting”, “the effect of delay of the peak” and the “windows of dominance”.
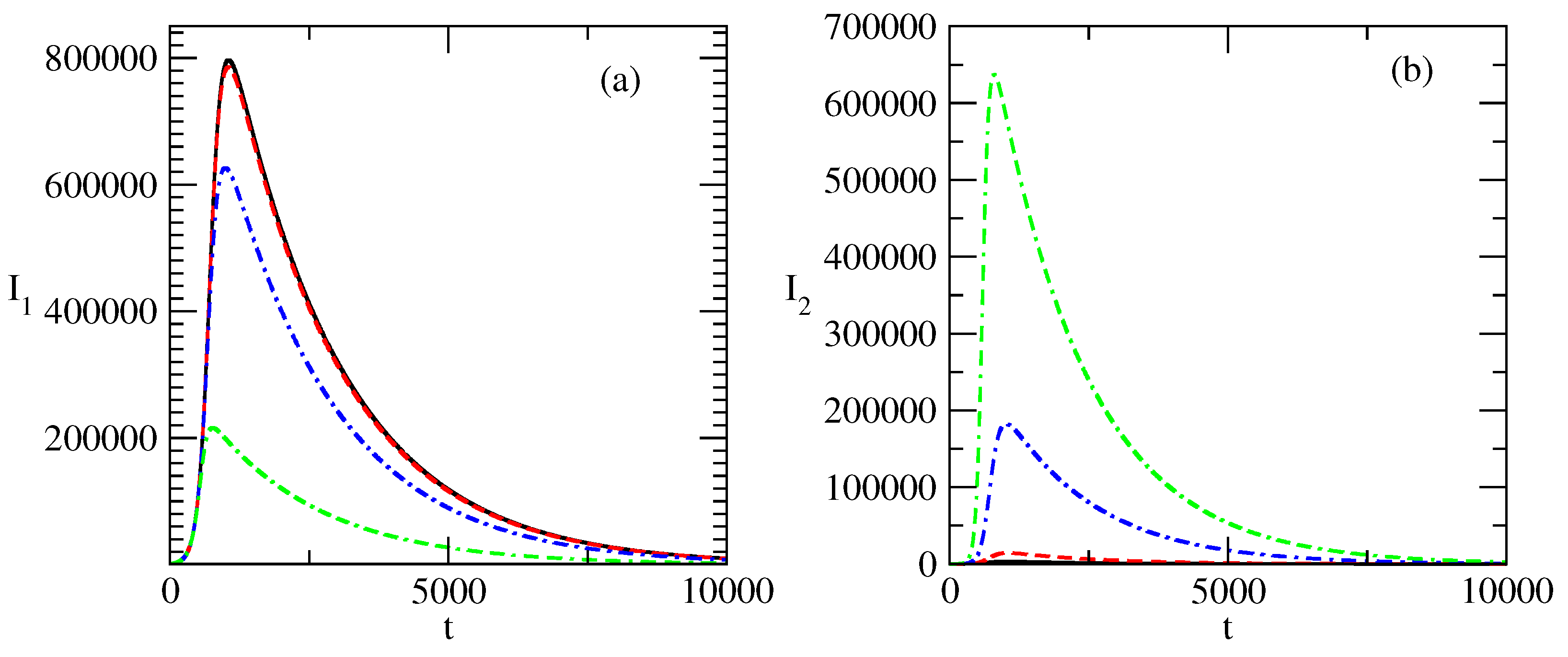
- The increase in the recovery rate for positive popularity negatively influences the positive popularity and positively influences the negative popularity. We observe that the increase in leads to a decrease in the peak of the positive popularity.
- In addition, this peak shifts to the region of earlier times, which means that the positive popularity begins to decrease earlier.
- The second negative effect of the increasing value of is that the positive popularity decreases faster at the times after the peak.
- On the contrary, the increase in the value of the recovery rate for positive popularity positively affects the negative popularity .
- The positive effects are that the peak value of the negative popularity becomes larger. In addition, the peak shifts to the region of larger times, i.e, the wave of negative popularity increases faster and lasts longer.
- Finally, the decay of this wave becomes slow.
- We observe that the increase in the recovery rate for negative popularity leads to a slight increase in the peak of and to a slight shift of this peak to the region of larger times.
- The decrease in leads to an increase in the value of the peak of and to a shift of this peak to the region of larger times.
- In addition, the decay of after the peak is slower.
- The decrease in the value of the transmission rate leads to a decrease in the peak of positive popularity and to increase in the value of the peak for negative popularity.
- With an increasing value of , the decay of the positive popularity after the peak becomes faster and the decay of the negative popularity happens more slowly.
- Thus, the decrease in the transmission rate of positive popularity negatively influences the positive popularity and positively influences the negative popularity.
- The increase in the value of leads to an increase in the value of the peak of negative popularity and to a decrease in the value of the peak of positive popularity.
- The decay of negative popularity after the peak happens more slowly with an increasing value of and, at the same time, the positive popularity decays faster.
6. Concluding Remarks
- If an individual is infected by one of the viruses, then this individual cannot be infected by the second virus;
- The individuals who have recovered from an infection cannot be infected again.
- Arising of bell-shaped profiles of the numbers of supporters of positive popularity and negative popularity;
- Suppression of popularity;
- Faster increase–faster decrease effect for the peaks of the bell-shaped profiles;
- Shift of the peak of popularity in time;
- Effect of forgetting;
- Window of dominance;
- Short-term win–long-term loss effect;
- The effect of the single peak where one kind of popularity decreases steadily and the other kind of popularity increases, then has a peak and, after that, begins to decrease.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Miller, J.H.; Page, S.E. Complex Adaptive Systems: An Introduction to Computational Models of Social Life; Princeton University Press: Princeton, NJ, USA, 2007; ISBN 978-0-691-13096-5. [Google Scholar]
- Latora, V.; Nicosia, V.; Russo, G. Complex Networks. Principles, Methods, and Applications; Cambridge University Press: Cambridge, UK, 2017; ISBN 978-1-107-10318-4. [Google Scholar]
- Chian, A.C.-L. Complex Systems Approach to Economic Dynamics; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-39752-6. [Google Scholar]
- Vitanov, N.K. Science Dynamics and Research Production. Indicators, Indexes, Statistical Laws and Mathematical Models; Springer: Cham, Switzerland, 2016; ISBN 978-3-319-41629-8. [Google Scholar]
- Treiber, M.; Kesting, A. Traffic Flow Dynamics: Data, Models, and Simulation; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-32460-4. [Google Scholar]
- Dimitrova, Z.I. Flows of Substances in Networks and Network Channels: Selected Results and Applications. Entropy 2022, 24, 1485. [Google Scholar] [CrossRef] [PubMed]
- Drazin, P.G. Nonlinear Systems; Cambridge University Press: Cambridge, UK, 1992; ISBN 0-521-40489-4. [Google Scholar]
- Ganji, D.D.; Sabzehmeidani, Y.; Sedighiamiri, A. Nonlinear Systems in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 978-0-12-812024-8. [Google Scholar]
- Yoshida, Z. Nonlinear Science. The Challenge of Complex Systems; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-64203405-3. [Google Scholar]
- Diekmann, O.; Heesterbeek, H.; Britton, T. Mathematical Tools for Understanding Infectious Disease Dynamics; Princeton University Press: Princeton, NJ, USA, 2012; ISBN 978-0-6911-5539-5. [Google Scholar]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematcal Models in Epidemiology; Springer: New York, NY, USA, 2019; ISBN 978-1-4939-9828-9. [Google Scholar]
- Li, M.I. An Introduction to Mathematical Modeling of Infectious Diseases; Springer: Cham, Switzerland, 2018; ISBN 978-3-319-72122-4. [Google Scholar]
- Brauer, F. Mathematical Epidemiology: Past, Present and Future. Infect. Dis. Model. 2017, 2, 113–127. [Google Scholar] [CrossRef] [PubMed]
- Teng, P.S. A Comparison of Simulation Approaches to Epidemic Modeling. Annu. Rev. Phytopathol. 1985, 23, 351–379. [Google Scholar] [CrossRef]
- Britton, T. Stochastic Epidemic Models: A Survey. Math. Biosci. 2010, 225, 24–35. [Google Scholar] [CrossRef]
- Hethcote, H.W. A Thousand and One Epidemic Models. In Frontiers in Mathematical Biology; Levin, S.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 504–515. ISBN 978-3-642-50126-5. [Google Scholar]
- Keeling, M.J.; Eames, K.T. Networks and Epidemic Models. J. R. Soc. Interface 2005, 2, 295–307. [Google Scholar] [CrossRef]
- Capasso, V.; Serio, G. A Generalization of the Kermack- McKendrick Deterministic Epidemic Model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Wang, W.; Tang, M.; Stanley, H.E.; Braunstein, L.A. Unification of Theoretical Approaches for Epidemic Spreading on Complex Networks. Rep. Prog. Phys. 2017, 80, 036603. [Google Scholar] [CrossRef]
- Cifuentes-Faura, J.; Faura-Martínez, U.; Lafuente-Lechuga, M. Mathematical Modeling and the Use of Network Models as Epidemiological Tools. Mathematics 2022, 10, 3347. [Google Scholar] [CrossRef]
- Cui, Q.; Qiu, Z.; Liu, W.; Hu, Z. Complex Dynamics of an SIR Epidemic Model with Nonlinear Saturate Incidence and Recovery Rate. Entropy 2017, 19, 305. [Google Scholar] [CrossRef]
- Rahimi, I.; Gandomi, A.H.; Asteris, P.G.; Chen, F. Analysis and Prediction of COVID-19 Using SIR, SEIQR, and Machine Learning Models: Australia, Italy, and UK Cases. Information 2021, 12, 109. [Google Scholar] [CrossRef]
- Trawicki, M.B. Deterministic Seirs Epidemic Model for Modeling Vital Dynamics, Vaccinations, and Temporary Immunity. Mathematics 2017, 5, 7. [Google Scholar] [CrossRef]
- Frank, T.D. COVID-19 Epidemiology and Virus Dynamics; Springer: Cham, Switzerland, 2022; ISBN 978-3-030-97178-6. [Google Scholar]
- Godio, A.; Pace, F.; Vergnano, A. SEIR Modeling of the Italian Epidemic of SARS-CoV-2 Using Computational Swarm Intelligence. Int. J. Environ. Res. Public Health 2020, 17, 3535. [Google Scholar] [CrossRef] [PubMed]
- Vitanov, N.K.; Ausloos, M.R. Knowledge Epidemics and Population Dynamics Models for Describing Idea Diffusion. In Models of Science Dynamics; Scharnhorst, A., Boerner, K., Besselaar, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 69–125. ISBN 978-3-642-23068-4. [Google Scholar]
- Etxeberria-Etxaniz, M.; Alonso-Quesada, S.; De la Sen, M. On an SEIR Epidemic Model with Vaccination of Newborns and Periodic Impulsive Vaccination with Eventual On-Line Adapted Vaccination Strategies to the Varying Levels of the Susceptible Subpopulation. Appl. Sci. 2020, 10, 8296. [Google Scholar] [CrossRef]
- Al-Shbeil, I.; Djenina, N.; Jaradat, A.; Al-Husban, A.; Ouannas, A.; Grassi, G. A New COVID-19 Pandemic Model including the Compartment of Vaccinated Individuals: Global Stability of the Disease-Free Fixed Point. Mathematics 2023, 11, 576. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, S.E.; Kim, J.-O.; Kim, G.B. Two-Way Contact Network Modeling for Identifying the Route of COVID-19 Community Transmission. Informatics 2021, 8, 22. [Google Scholar] [CrossRef]
- Harjule, P.; Poonia, R.C.; Agrawal, B.; Saudagar, A.K.J.; Altameem, A.; Alkhathami, M.; Khan, M.B.; Hasanat, M.H.A.; Malik, K.M. An Effective Strategy and Mathematical Model to Predict the Sustainable Evolution of the Impact of the Pandemic Lockdown. Healthcare 2022, 10, 759. [Google Scholar] [CrossRef]
- Chen, J.; Yin, T. Transmission Mechanism of Post-COVID-19 Emergency Supply Chain Based on Complex Network: An Improved SIR Model. Sustainability 2023, 15, 3059. [Google Scholar] [CrossRef]
- Almeshal, A.M.; Almazrouee, A.I.; Alenizi, M.R.; Alhajeri, S.N. Forecasting the Spread of COVID-19 in Kuwait Using Compartmental and Logistic Regression Models. Appl. Sci. 2020, 10, 3402. [Google Scholar] [CrossRef]
- Batool, H.; Li, W.; Sun, Z. Extinction and Ergodic Stationary Distribution of COVID-19 Epidemic Model with Vaccination Effects. Symmetry 2023, 15, 285. [Google Scholar] [CrossRef]
- Jitsinchayakul, S.; Humphries, U.W.; Khan, A. The SQEIRP Mathematical Model for the COVID-19 Epidemic in Thailand. Axioms 2023, 12, 75. [Google Scholar] [CrossRef]
- Khorev, V.; Kazantsev, V.; Hramov, A. Effect of Infection Hubs in District-Based Network Epidemic Spread Model. Appl. Sci. 2023, 13, 1194. [Google Scholar] [CrossRef]
- Ni, G.; Wang, Y.; Gong, L.; Ban, J.; Li, Z. Parameters Sensitivity Analysis of COVID-19 Based on the SCEIR Prediction Model. COVID 2022, 2, 1787–1805. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Chmykhov, M.A.; Vigdorowitsch, M. Analytical Features of the SIR Model and their Applications to COVID-19. Appl. Math. Model. 2021, 90, 466–473. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Mak, M.K. Exact Analytical Solutions of the Susceptible-Infected-Recovered (SIR) Epidemic Model and of the SIR Model with Equal Death and Birth Rates. Appl. Math. Comput. 2014, 236, 184–194. [Google Scholar] [CrossRef]
- Leonov, A.; Nagornov, O.; Tyuflin, S. Modeling of Mechanisms of Wave Formation for COVID-19 Epidemic. Mathematics 2023, 11, 167. [Google Scholar] [CrossRef]
- Wang, W.; Xia, Z. Study of COVID-19 Epidemic Control Capability and Emergency Management Strategy Based on Optimized SEIR Model. Mathematics 2023, 11, 323. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Liu, C.-T. A Stochastic Multi-Strain SIR Model with Two-Dose Vaccination Rate. Mathematics 2022, 10, 1804. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Micula, S. Dynamical Strategy to Control the Accuracy of the Nonlinear Bio-Mathematical Model of Malaria Infection. Mathematics 2021, 9, 1031. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Micula, S.; Nieto, J.J. A Novel Technique to Control the Accuracy of a Nonlinear Fractional Order Model of COVID-19: Application of the CESTAC Method and the CADNA Library. Mathematics 2021, 9, 1321. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. Lond. Ser. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Kamo, M.; Sasaki, A. The Effect of Cross-immunity and Seasonal Forcing in a Multi-strain Epidemic Model. Phys. D 2002, 165, 228–241. [Google Scholar] [CrossRef]
- Massard, M.; Eftimie, R.; Perasso, A.; Saussereau, B. A Multi-strain Epidemic Model for COVID-19 with Infected and Asymptomatic Cases: Application to French Data. J. Theor. Biol. 2022, 545, 111117. [Google Scholar] [CrossRef] [PubMed]
- Lazebnik, T.; Bunimovich-Mendrazitsky, S. Generic Approach for Mathematical Model of Multi-strain Pandemics. PLoS ONE 2022, 17, e0260683. [Google Scholar] [CrossRef]
- Khyar, O.; Allali, K. Global Dynamics of a Multi-strain SEIR Epidemic Model with General Incidence Rates: Application to COVID-19 Pandemic. Nonlinear Dyn. 2020, 102, 489–509. [Google Scholar] [CrossRef]
- Arruda, E.F.; Das, S.S.; Dias, C.M.; Pastore, D.H. Modelling and Optimal Control of Multi Strain Epidemics, with Application to COVID-19. PLoS ONE 2021, 16, e0257512. [Google Scholar] [CrossRef]
- Fudolig, M.; Howard, R. The Local Stability of a Modified Multi-strain SIR Model for Emerging Viral Strains. PLoS ONE 2020, 15, e0243408. [Google Scholar] [CrossRef]
- Martcheva, M. A Non-autonomous Multi-strain SIS Epidemic Model. J. Biol. Dyn. 2009, 3, 235–251. [Google Scholar] [CrossRef]
- Kooi, B.W.; Aguiar, M.; Stollenwerk, N. Bifurcation Analysis of a Family of Multi-strain Epidemiology Models. J. Comput. Appl. Math. 2013, 252, 148–158. [Google Scholar] [CrossRef]
- Breban, R.; Drake, J.M.; Rohani, P. A General Multi-strain Model with Environmental Transmission: Invasion Conditions for the Disease-free and Endemic States. J. Theor. Biol. 2010, 264, 729–736. [Google Scholar] [CrossRef]
- Minayev, P.; Ferguson, N. Improving the Realism of Deterministic Multi-strain Models: Implications for Modelling Influenza A. J. R. Soc. Interface 2009, 6, 509–518. [Google Scholar] [CrossRef] [PubMed]
- Pateras, J.; Vaidya, A.; Ghosh, P. Network Thermodynamics-Based Scalable Compartmental Model for Multi-Strain Epidemics. Mathematics 2022, 10, 3513. [Google Scholar] [CrossRef]
- Cai, L.; Xiang, J.; Li, X.; Lashari, A.A. A Two-Strain Epidemic Model with Mutant Strain and Vaccination. J. Appl. Math. Comput. 2021, 40, 125–142. [Google Scholar] [CrossRef]
- Baba, I.A.; Kaymakamzade, B.; Hincal, E. Two-Strain Epidemic Model with Two Vaccinations. Chaos Solitons Fractals 2018, 106, 342–348. [Google Scholar] [CrossRef]
- Otunuga, O.M. Analysis of Multi-Strain Infection of Vaccinated and Recovered Population through Epidemic Model: Application to COVID-19. PLoS ONE 2022, 17, e0271446. [Google Scholar] [CrossRef]
- Ashrafur Rahman, S.M.; Zou, X. Flu Epidemics: A Two-Strain Fu Model with a Single Vaccination. J. Biol. Dyn. 2011, 5, 376–390. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Zhou, Y. Competitive Coexistence in a Two-Strain Epidemic Model with a Periodic Infection Rate. Discret. Dyn. Nat. Soc. 2020, 2020, 7541861. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I.; Vitanov, K.N. Simple Equations Method (SEsM): Algorithm, Connection with Hirota Method, Inverse Scattering Transform Method, and Several Other Methods. Entropy 2021, 23, 10. [Google Scholar] [CrossRef]
- Vitanov, N.K. Simple Equations Method (SEsM): Review and New Results. AIP Conf. Ser. 2022, 2459, 020003. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I. Simple Equations Method and Non-linear Differential Equations with Non-polynomial Non-linearity. Entropy 2021, 23, 1624. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I.; Vitanov, K.N. On the Use of Composite Functions in the Simple Equations Method to Obtain Exact Solutions of Nonlinear Differential Equations. Computation 2021, 9, 104. [Google Scholar] [CrossRef]
- Vitanov, N.K. Simple Equations Method (SEsM): An Effective Algorithm for Obtaining Exact Solutions of Nonlinear Differential Equations. Entropy 2022, 24, 1653. [Google Scholar] [CrossRef] [PubMed]
- Vitanov, N.K.; Vitanov, K.N. Epidemic Waves and Exact solutions of a Sequence of Nonlinear Differential Equations Connected to the SIR model of Epidemics. Entropy 2023, 25, 438. [Google Scholar] [CrossRef] [PubMed]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vitanov, N.K.; Dimitrova, Z.I. Sic Transit Gloria Mundi: A Mathematical Theory of Popularity Waves Based on a SIIRR Model of Epidemic Spread. Entropy 2025, 27, 611. https://doi.org/10.3390/e27060611
Vitanov NK, Dimitrova ZI. Sic Transit Gloria Mundi: A Mathematical Theory of Popularity Waves Based on a SIIRR Model of Epidemic Spread. Entropy. 2025; 27(6):611. https://doi.org/10.3390/e27060611
Chicago/Turabian StyleVitanov, Nikolay K., and Zlatinka I. Dimitrova. 2025. "Sic Transit Gloria Mundi: A Mathematical Theory of Popularity Waves Based on a SIIRR Model of Epidemic Spread" Entropy 27, no. 6: 611. https://doi.org/10.3390/e27060611
APA StyleVitanov, N. K., & Dimitrova, Z. I. (2025). Sic Transit Gloria Mundi: A Mathematical Theory of Popularity Waves Based on a SIIRR Model of Epidemic Spread. Entropy, 27(6), 611. https://doi.org/10.3390/e27060611






