Overcoming Intensity Limits for Long-Distance Quantum Key Distribution
Abstract
1. Introduction
2. Probabilistic Modeling
2.1. QKD Components
2.1.1. Detectors
- (After-pulse): probability of a click given a click in the previous detection window.
- (Efficiency): probability of a click given a single photon.
- (Dark count): probability of a click in the absence of a photon.
- (Misalignment): probability of a detection error due to misalignment.
2.1.2. Fiber-Detector
- is the probability of a click given that k photons reach the detector, as previously derived in Lemma 1.
- is the probability that exactly k photons pass through the fiber, modeled as .
2.1.3. Fiber-Beam Splitter
2.1.4. Pair of Detectors
- : The probability of neither detectors clicking.
- : The probability of only clicking.
- : The probability of only clicking.
- : The probability of both detectors clicking.
2.1.5. Laser-Fiber
2.1.6. Laser-Detector
2.2. PNS Attack
2.2.1. Eavesdropper Assumptions (The Generalized PNS Attack)
- (Distance from Alice): Eve’s interception point is between Alice and Bob, with , where is their total distance.
- (Proportion of intercepted pulses): Eve intercepts a fraction of pulses, , balancing information gain and detection risk.
- (Number of intercepted photons): Eve intercepts photons per intercepted pulse.
- (Channel efficiency): Eve selects a channel efficiency to transmit intercepted pulses, simulating legitimate loss to avoid detection.
- Eve intercepts every pulse ().
- Eve intercepts immediately after Alice ().
- Eve intercepts exactly one photon per pulse ().
2.2.2. PNS Model
Alice to Eve
Eve to Bob
2.2.3. All Possible Detection Events
2.2.4. Marginalization of Unknowns in the Sifting Phase
2.2.5. Multiple Intensities
- : The lowest intensity where, if Eve intercepts a single photon immediately after Alice, she must use a channel with efficiency to avoid detection.
- : The highest intensity that maximizes the proportion of events where occurs, as cases where both detectors either click or do not click provide no useful information and appear uniformly random from Bob’s perspective.
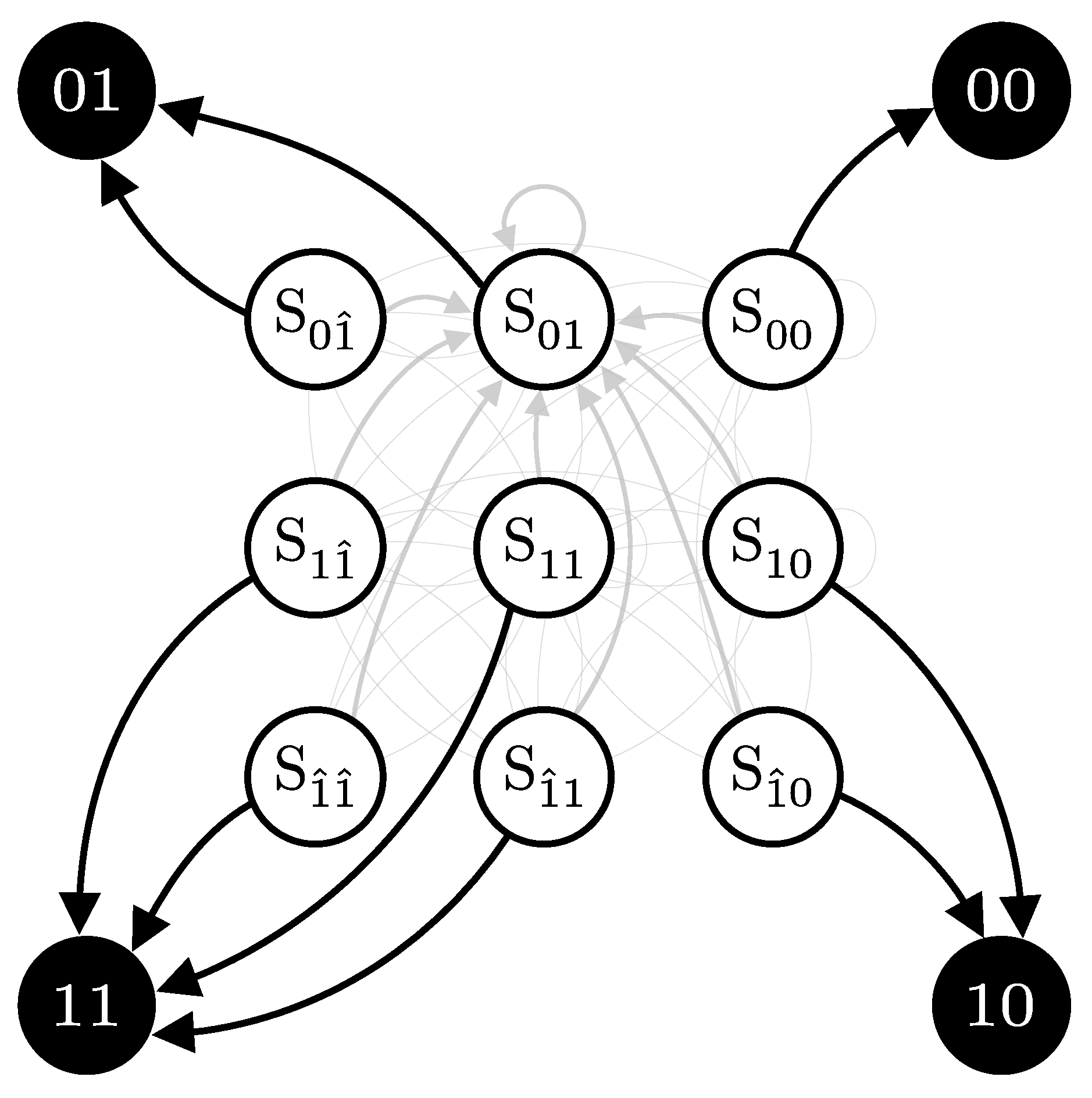
2.3. After-Pulsing
2.3.1. Single Detector, Single Probability
- State : No click occurs, at which it remains in this state with probability , or transition to the state with probability .
- State : A click due to either a signal or a dark count. It will then transition to the after-pulse state with probability q, or with probability transition to state or remain in state with probability .
- State : A click due to an after-pulse effect. This state occurs following a click in the previous detection window (state ). Then, it transitions to the state with probability or state with probability , but it cannot remain in this state.
- Transition matrix (): Probabilities of transitioning from one hidden state to another (gray arrows in Figure 8).
- Emission matrix (): Probabilities of observing specific outputs given the current hidden state (black arrows in Figure 8).
- Initial state probabilities (): Represents the probabilities of starting in each hidden state at the beginning of the process (usually assumed uniform or alwayas starts at a specific state).
2.3.2. Two Detectors, Single Probability
2.3.3. Two Detectors, Multiple Probabilities
- Intra-Mode Transition: With probability , the bit choice remains . The system transitions according to the probabilities defined by the current state’s corresponding entry in . For example, the probability of transitioning from in mode 0 to in mode 0 is given by .
- Inter-Mode Transition: With probability , the bit choice switches to . The system then transitions according to the probabilities defined by the corresponding entry in . For example, the probability of transitioning from in mode 0 to in mode 1 is .
2.3.4. Constructing the Full Transition Matrix
Intensity-Based Transitions
Eavesdropping Transitions
Bit Choice Transitions
Basis Choice Transitions
2.3.5. Extracting the Probabilities of Click Events
2.4. Error and Gain Probabilities
2.4.1. Marginalizing over Eve’s Interception Flag
2.4.2. Gain and Error Probabilities
2.4.3. Marginalizing over Bit Choice
2.4.4. Distribution of Gain and Error Counts
3. Bayesian Inference
3.1. Constructing the Likelihood
HMM Likelihood
3.2. Constructing the Prior
3.2.1. Assumptions and Independence
3.2.2. Priors for Bounded Parameters
3.2.3. Prior for Semi-Bounded Parameters
3.2.4. Selection of Prior Parameters
- : The maximum number of photons Eve can intercept from a pulse immediately emitted by Alice such that she would require a channel efficiency of to avoid detection.
3.2.5. Final Formulation of the Prior
3.3. Constructing the Posterior
Methods for Approximating the Posterior
3.4. From Bounded to Unbounded Variables
3.4.1. Defining Transformations and Their Inverses
3.4.2. Jacobian of the Transformation
3.4.3. Updating the Posterior with the Jacobian
3.5. From Fixed to Random Variables
4. Experimental Results
4.1. Validation Through Simulation
| Algorithm 1 Simulation of QKD detection events under the i.i.d assumption |
|
| 25: |
|
| Algorithm 2 Simulation of QKD detection events under the HMM assumption |
|
4.1.1. Validation of the i.i.d. Model
Comparison with the Decoy-State Protocol
4.1.2. Validation of the HMM Model
4.2. Error Rate Estimation
4.2.1. Simulation Setup and Results
4.2.2. Analysis of Results
4.3. Secure-Key Rate Comparison
4.3.1. Experimental Setup
4.3.2. Secure-Key Rate Calculation
4.3.3. Analysis of Secure-Key Rates
4.4. Testing the Bayesian Framework
4.4.1. Inference of Eve’s Parameters Under the i.i.d. Model
Analysis of the Inference Results
4.4.2. Inference of Eve’s Parameters Under the HMM Model
Results for the HMM Model
Comparison with the i.i.d. Model
Secure-Key Rate Analysis
4.4.3. Testing the Fully Bayesian Model
Experimental Setup
Testing the Fixed-Parameter Assumption
Analysis of Results
5. Time Complexity Analysis
5.1. Computational Complexity for the i.i.d. Model
5.1.1. Function Evaluation
5.1.2. Derivative Evaluations
5.1.3. Total Computational Cost
5.2. Computational Complexity for the HMM Model
5.2.1. Function Evaluation
Transition Matrix
Stationary Distribution
Emission Projection
5.2.2. Derivative Evaluations
5.2.3. Total Computational Cost
5.3. Analysis of Time Complexities
6. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
- Shor, P.W.; Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Huttner, B.; Imoto, N.; Gisin, N.; Mor, T. Quantum cryptography with coherent states. Phys. Rev. A 1995, 51, 1863. [Google Scholar] [CrossRef] [PubMed]
- Gottesman, D.; Lo, H.K.; Lütkenhaus, N.; Preskill, J. Security of quantum key distribution with imperfect devices. Quantum Inf. Comput. 2004, 4, 325–360. [Google Scholar]
- Lo, H.K.; Ma, X.; Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef]
- Hwang, W.Y. Quantum key distribution with high loss: Toward global secure communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef] [PubMed]
- Lo, H.K. Quantum key distribution with vacua or dim pulses as decoy states. In Proceedings of the International Symposium on Information Theory, Chicago, IL, USA, 27 June–2 July 2004; p. 137. [Google Scholar]
- Ma, X.; Qi, B.; Zhao, Y.; Lo, H.K. Practical decoy state for quantum key distribution. Phys. Rev. A—At. Mol. Opt. Phys. 2005, 72, 012326. [Google Scholar] [CrossRef]
- Wang, X.B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 2005, 94, 230503. [Google Scholar] [CrossRef]
- Zhao, Y.; Qi, B.; Ma, X.; Lo, H.K.; Qian, L. Experimental quantum key distribution with decoy states. Phys. Rev. Lett. 2006, 96, 070502. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. SARG04: A secure quantum key distribution protocol against photon number splitting attacks. Phys. Rev. Lett. 2004, 92, 077902. [Google Scholar] [CrossRef]
- Barrett, H.; Becker, F.; Scarani, V. Coherent one-way quantum cryptography with enhanced security. Phys. Rev. A 2005, 72, 052307. [Google Scholar]
- Lim, C.C.W.; Curty, M.; Walenta, N.; Xu, F.; Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 2014, 89, 022307. [Google Scholar] [CrossRef]
- Restelli, A.; Bienfang, J.C.; Clark, C.W. Afterpulse probability and detection efficiency of free-running InGaAs/InP single-photon avalanche diodes. J. Appl. Phys. 2013, 113, 043101. [Google Scholar]
- Yuan, Z.; Sharpe, A.W.; Shields, A.J. Unconditionally secure one-way quantum key distribution using decoy pulses. Appl. Phys. Lett. 2007, 90, 011118. [Google Scholar] [CrossRef]
- Lucamarini, M.; Yuan, Z.; Dynes, J.F.; Shields, A.J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400–403. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern recognition and machine learning. Springer Google Sch. 2006, 2, 1122–1128. [Google Scholar]
- Olver, F.W.J.; Daalhuis Olde, A.B.; Lozier, D.W.; Schneider, B.I.; Boisvert, R.F.; Clark, C.W.; Miller, B.R.; Saunders, B.V.; Cohl, H.S.; McClain, M.A. (Eds.) NIST Digital Library of Mathematical Functions; Release 1.2.2 of 2024-09-15. Available online: https://dlmf.nist.gov/ (accessed on 30 October 2024).
- Murphy, K.P. Dynamic Bayesian Networks: Representation, Inference and Learning. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2002. [Google Scholar]
- Perron, O. Zur Theorie der Matrices. Math. Ann. 1907, 64, 248–263. [Google Scholar] [CrossRef]
- Frobenius, G. Über Matrizen aus nicht negativen Elementen. In Sitzungsberichte; Deutsche Akademie der Wissenschaften zu Berlin: Berlin, Germany, 1912; pp. 456–477. [Google Scholar] [CrossRef]
- Norris, J.R. Markov Chains; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Murphy, K.P. Probabilistic Machine Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Stewart, G. A Krylov-Schur algorithm for large eigenproblems. SIAM J. Matrix Anal. Appl. 2001, 23, 601–614. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 721–741. [Google Scholar] [CrossRef]
- Cowles, M.K.; Carlin, B.P. Markov chain Monte Carlo convergence diagnostics: A comparative review. J. Am. Stat. Assoc. 1996, 91, 883–904. [Google Scholar] [CrossRef]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods; Springer: New York, NY, USA, 2004. [Google Scholar]
- Osborne, M.A.; Garnett, R.; Roberts, S.J. Active learning of model evidence using Bayesian quadrature. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 46–54. [Google Scholar]
- Gunter, T.; Osborne, M.A.; Garnett, R.; Hennig, P.; Roberts, S.J. Sampling for inference in probabilistic models with fast Bayesian quadrature. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2789–2797. [Google Scholar]
- Duane, S.; Kennedy, E.; Pendleton, B.; Roweth, D. Hybrid Monte Carlo. Phys. Lett. B 1987, 195, 216–222. [Google Scholar] [CrossRef]
- Neal, R.M. Chapter 5: MCMC using Hamiltonian dynamics. In Handbook of Markov Chain Monte Carlo; Chapman and Hall/CRC: Boca Raton, FL, USA, 2011; pp. 113–162. [Google Scholar]
- Hoffman, M.D.; Gelman, A. The No-U-Turn Sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Betancourt, M. A conceptual introduction to Hamiltonian Monte Carlo. arXiv 2017, arXiv:1701.02434. [Google Scholar]
- Thompson, M.B.; Neal, R.M. Covariance-adaptive slice sampling. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–11 December 2010; pp. 2244–2252. [Google Scholar]
- Greenwood, M.; Yule, G.U. An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks of disease or of repeated accidents. J. R. Stat. Soc. 1920, 83, 255–279. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- Gobby, C.; Yuan, a.; Shields, A. Quantum key distribution over 122 km of standard telecom fiber. Appl. Phys. Lett. 2004, 84, 3762–3764. [Google Scholar] [CrossRef]
- Hayashi, M. Practical evaluation of security for quantum key distribution. New J. Phys. 2007, 9, 284. [Google Scholar] [CrossRef]
- Tsurumaru, T.; Tamaki, K. Efficient protocol for practical decoy-state quantum key distribution. Phys. Rev. A 2008, 77, 022319. [Google Scholar] [CrossRef]
- Hayashi, M.; Nakayama, R. Upper bounds of eavesdropper’s performances in finite-length code with decoy method. J. Phys. A: Math. Theor. 2016, 49, 165301. [Google Scholar] [CrossRef][Green Version]
- Neal, R.M. CASS: Software for Covariance-Adaptive Slice Sampling. Available online: https://glizen.com/radfordneal/cass.software.html (accessed on 21 November 2024).
- Almosallam, I. Generalized PNS. 2024. Available online: https://github.com/csibrahim/generalized_pns_qkd/ (accessed on 28 December 2024).
- Pan, D.; Lin, Z.; Wu, J.; Zhang, H.; Sun, Z.; Ruan, D.; Yin, L.; Long, G.L. Experimental free-space quantum secure direct communication and its security analysis. Photonics Res. 2020, 8, 1522–1531. [Google Scholar] [CrossRef]






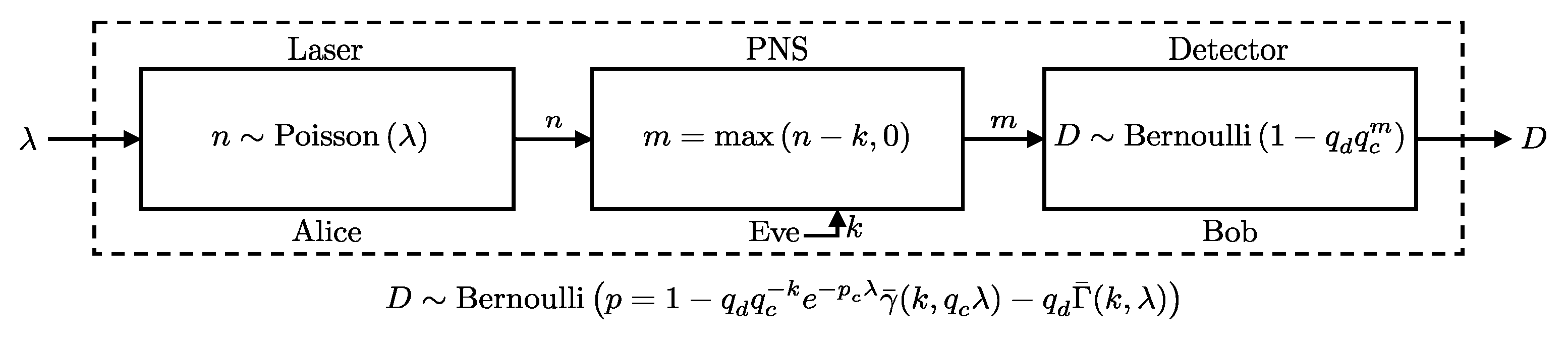



















| Parameter Configuration for the Simulation Experiment | ||
|---|---|---|
| (Alice) | ||
| Parameter | Description | Value |
| Intensity levels | ||
| Channel attenuation (dB/km) | 0.21 | |
| Distance from Alice to Bob (km) | 50 | |
| (Bob) | ||
| Parameter | Description | Value |
| After-pulse probability | 0.1 | |
| Detection efficiency | 0.045 | |
| Dark count probability | ||
| Misalignment probability | 0.033 | |
| (Eve) | ||
| Parameter | Description | Value |
| Distance from Alice to Eve (km) | 10 | |
| Fraction of intercepted pulses | 0.2 | |
| k | Photons intercepted per pulse | 3 |
| Channel efficiency from Eve to Bob (if Eve intercepts) | optimized | |
| (Session) | ||
| Parameter | Description | Value |
| N | Number of pulses per session | 10,000 |
| Number of simulation runs | 10,000 | |
| Detector-Specific Parameter Adjustments | ||
|---|---|---|
| Parameter | ||
| After-pulse probability | ||
| Detection efficiency | ||
| Dark count probability | ||
| Model | Function Evaluation | Derivative Evaluation |
|---|---|---|
| i.i.d. | ||
| HMM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almosallam, I. Overcoming Intensity Limits for Long-Distance Quantum Key Distribution. Entropy 2025, 27, 568. https://doi.org/10.3390/e27060568
Almosallam I. Overcoming Intensity Limits for Long-Distance Quantum Key Distribution. Entropy. 2025; 27(6):568. https://doi.org/10.3390/e27060568
Chicago/Turabian StyleAlmosallam, Ibrahim. 2025. "Overcoming Intensity Limits for Long-Distance Quantum Key Distribution" Entropy 27, no. 6: 568. https://doi.org/10.3390/e27060568
APA StyleAlmosallam, I. (2025). Overcoming Intensity Limits for Long-Distance Quantum Key Distribution. Entropy, 27(6), 568. https://doi.org/10.3390/e27060568







