Assessing Functional Connectivity Dynamics During Cognitive Tasks Involving the Dorsal Stream
Abstract
1. Introduction
2. Materials and Methods
2.1. Patients
2.2. Anatomical Reconstruction of Electrode Positions
2.3. SEEG Data Acquisition
2.4. Cognitive Tasks
2.4.1. Picture-Naming Experiments
2.4.2. Oddball Experiments
2.4.3. ba/pa English/French
2.4.4. Face Recognition
2.4.5. Word vs. Non-Word (W/NW) Discrimination
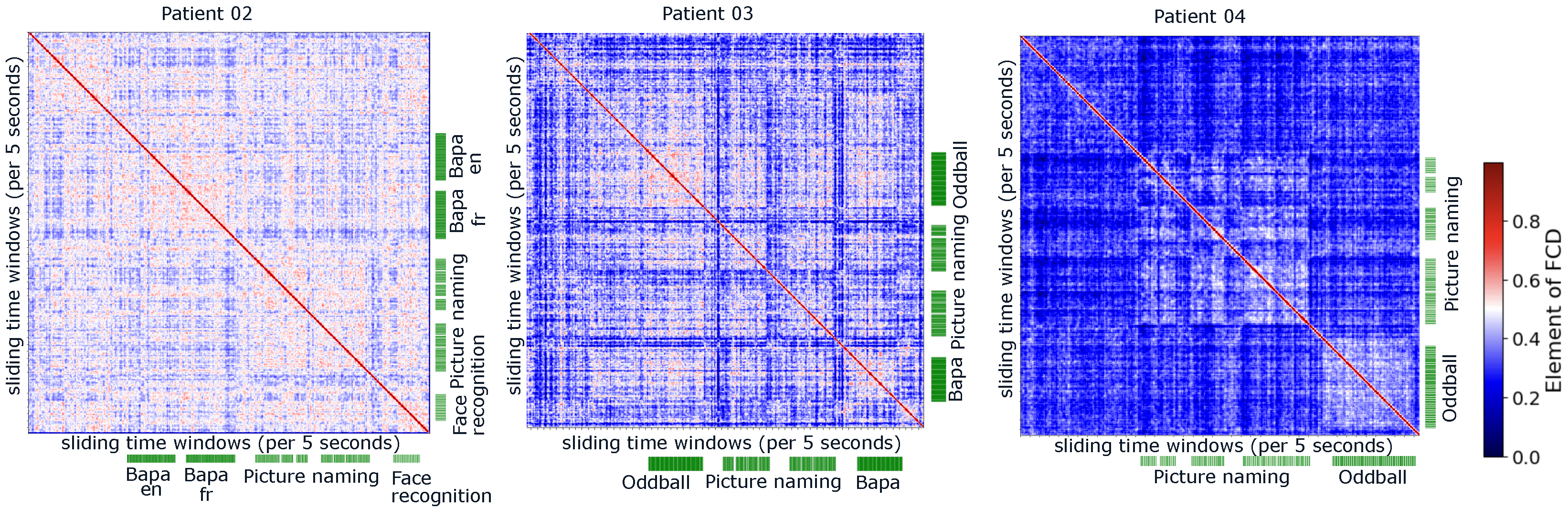
2.5. Functional Connectivity and Its Dynamics
2.6. Clustering Methods for Distinguishable Functional Connectivity
2.7. Machine Learning Methods for Identifiable Tasks
2.8. Performance Metrics
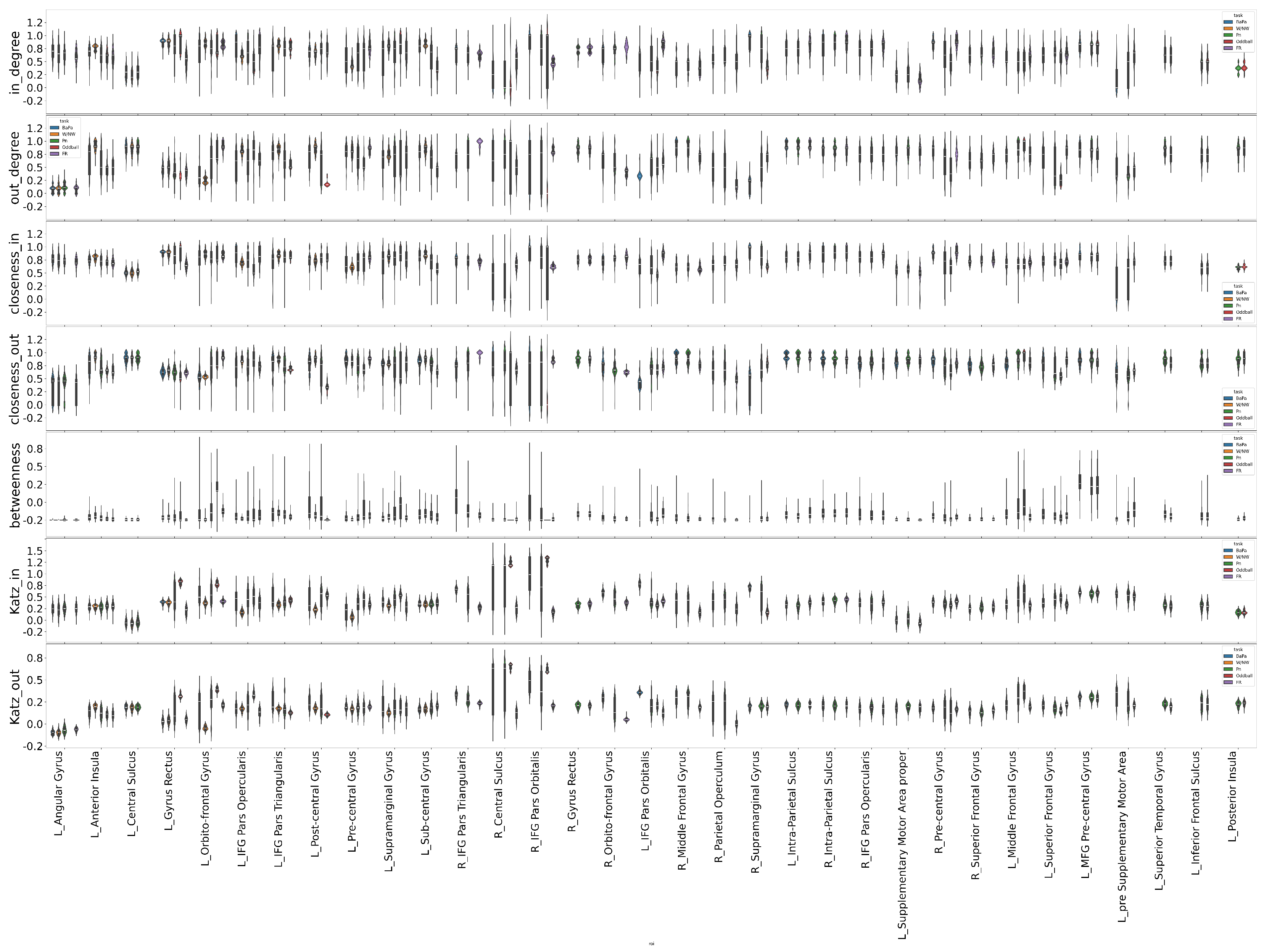
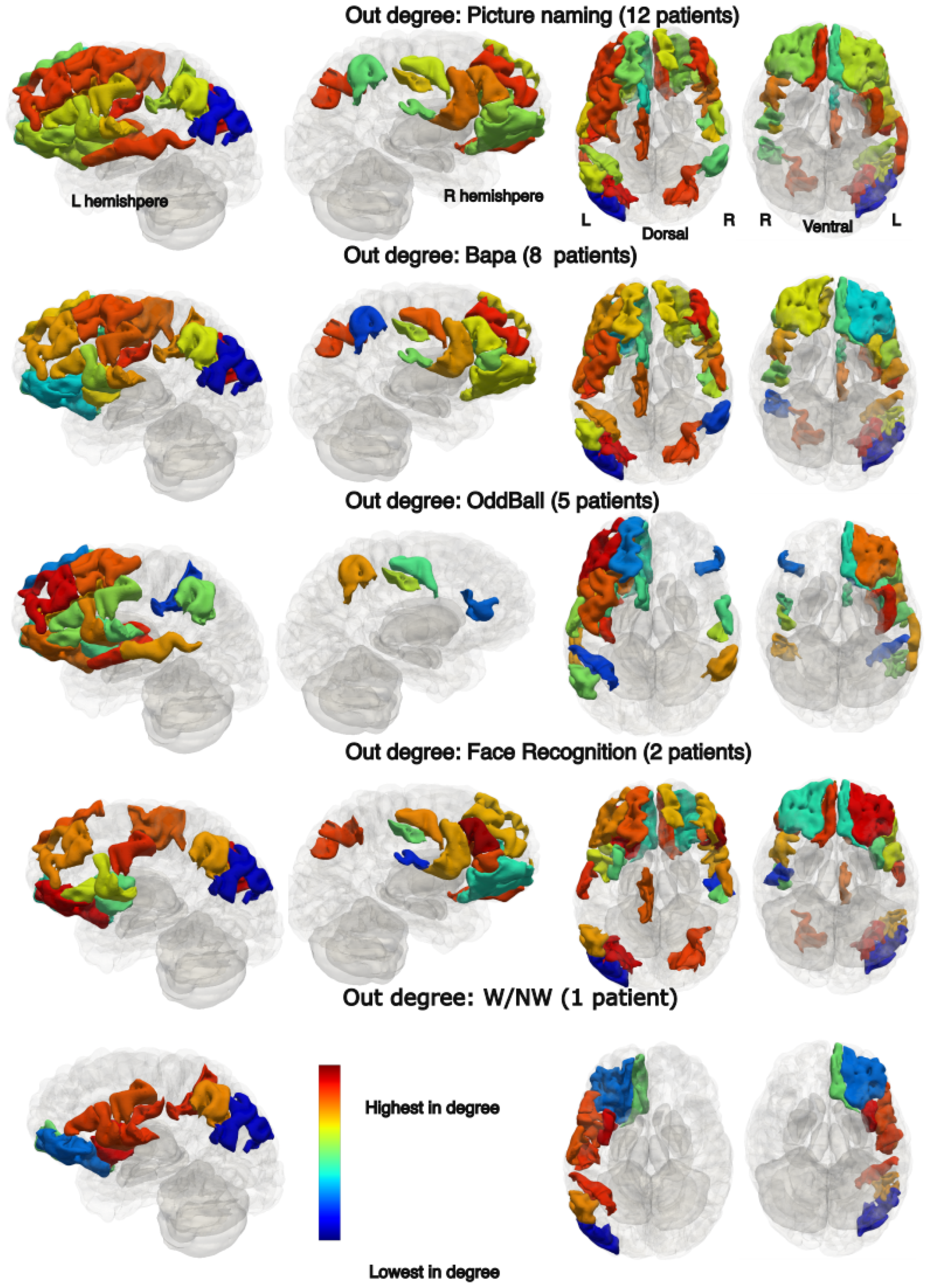
2.9. Network Profile Metrics
3. Results
3.1. Overview of the Analysis and Results
3.2. Distinguishable Functional Connectivity During Different Cognitive Tasks
3.3. Identifiable Cognitive Tasks from Functional Connectivity
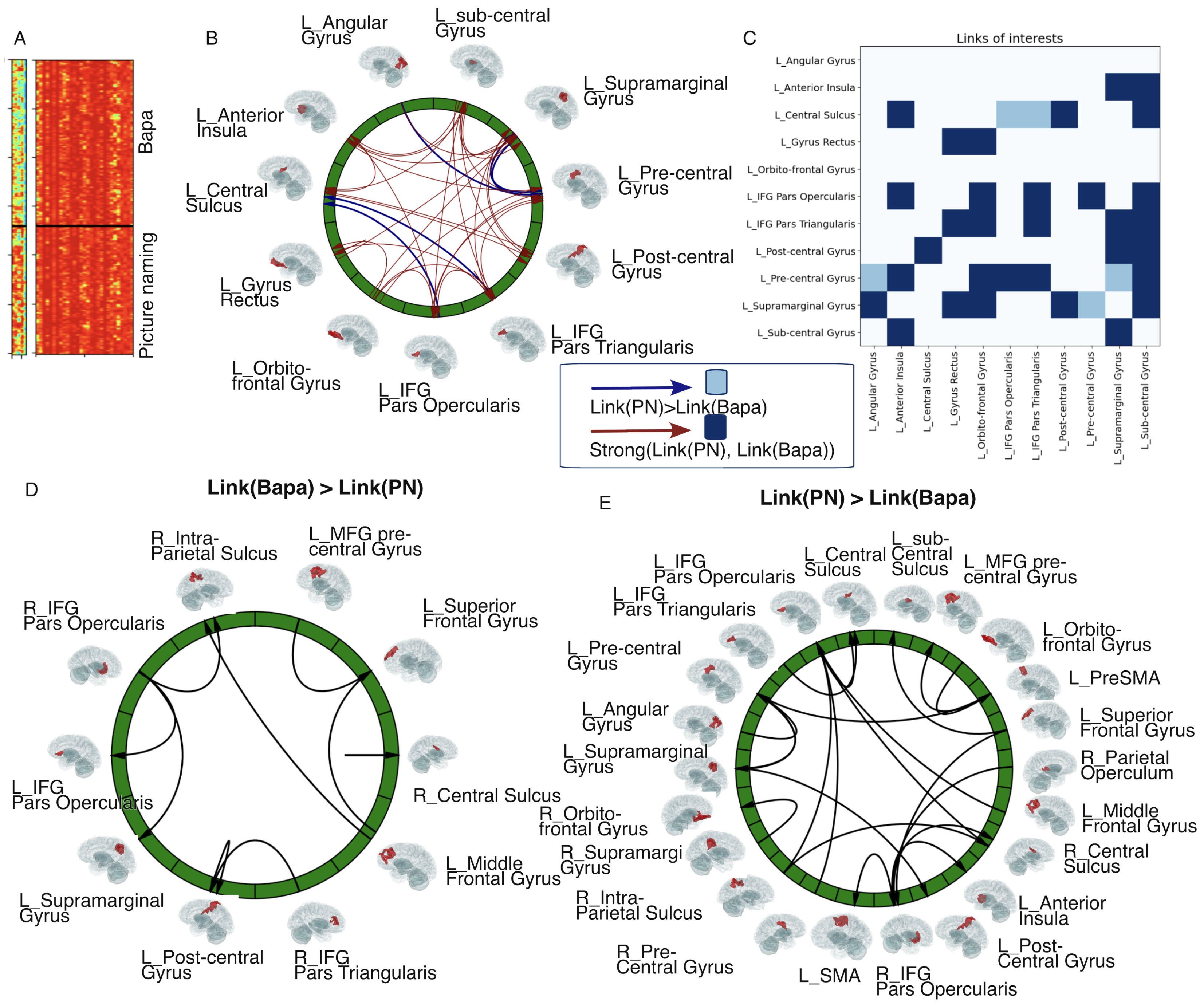
3.4. Links of Interest
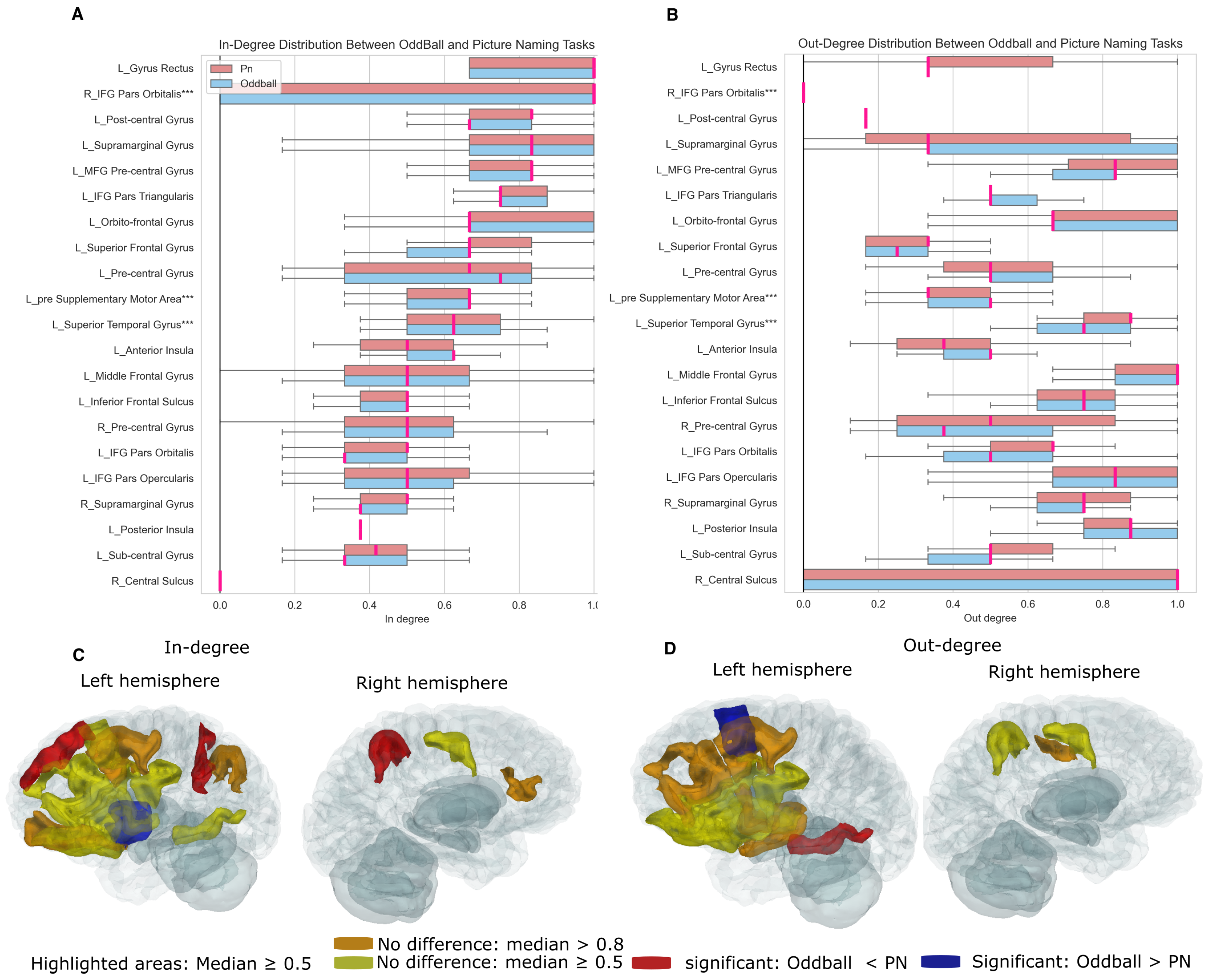
3.5. Connectivity Profiles of Brain Regions During Cognitive Tasks
3.6. Spatial Connectivity Features for Different Tasks
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Case | Age | Sex | Handedness | Language Dominance (Criterion) | Epilepsy | Onset (Years) | Tasks |
|---|---|---|---|---|---|---|---|
| P01 | 41 | F | Right | Left (ictal aphasia & fMRI) | Temporo-parietal | 12 | PN/Ba-pa |
| P02 | 45 | M | Right | NA (Not available) | R MTL | 0.75 | PN/FR |
| P03 | 34 | F | Right | NA | R LTL | 29 | PN/BaPa/OB |
| P04 | 42 | F | Left | Bilateral (Wada) | R MTL | 33 | PN/BaPa |
| P05 | 28 | F | Right | Left (stimulation) | L MTL | 21 | PN/BaPa |
| P06 | 61 | F | Right | Left (stimulation) | L Temporo-Perisylvian | 50 | PN/BaPa/FR |
| P07 | 53 | F | Right | Left | L MTL | 35 | PN/OB |
| P08 | 21 | M | Right | NA | R FT | 13 | PN/BaPa |
| P09 | 48 | F | Left | Left | L MTL | 42 | PN/BaPa/OB |
| P10 | 27 | M | Right | Left (ictal aphasia) | Bi post Insula-temporal operculum | 8 | PN/BaPa |
| P11 | 40 | F | Right | Left (Wada test) | L MTL | 17 | PN/OB |
| P12 | 25 | M | Right | Left (Wada test) | L IFG & OF | 7 | PN/OB |


References
- Friston, K. Functional and effective connectivity: A review. Brain Connect. 2011, 1, 13–24. [Google Scholar] [CrossRef] [PubMed]
- Cole, M.W.; Bassett, D.S.; Power, J.D.; Braver, T.S.; Petersen, S.E. Intrinsic and task-evoked network architectures of the human brain. Neuron 2014, 83, 238–251. [Google Scholar] [CrossRef] [PubMed]
- Hansen, E.C.A.; Battaglia, D.; Spiegler, A.; Deco, G.; Jirsa, V.K. Functional connectivity dynamics: Modeling the switching behavior of the resting state. NeuroImage 2015, 105, 525–535. [Google Scholar] [CrossRef]
- Gallivan, J.P.; Goodale, M.A. Chapter 23—The dorsal “action” pathway. In The Parietal Lobe; Vallar, G., Coslett, H.B., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 151, pp. 449–466. [Google Scholar] [CrossRef]
- Hickok, G.; Poeppel, D. The cortical organization of speech processing. Nat. Rev. Neurosci. 2007, 8, 393–402. [Google Scholar] [CrossRef]
- Hickok, G.; Poeppel, D. Dorsal and ventral streams: A framework for understanding aspects of the functional anatomy of language. Cognition 2004, 92, 67–99. [Google Scholar] [CrossRef] [PubMed]
- Roelofs, A. A dorsal-pathway account of aphasic language production: The WEAVER++/ARC model. Cortex 2014, 59, 33–48. [Google Scholar] [CrossRef]
- Ueno, T.; Saito, S.; Rogers, T.T.; Ralph, M.A.L. Lichtheim 2: Synthesizing Aphasia and the Neural Basis of Language in a Neurocomputational Model of the Dual Dorsal-Ventral Language Pathways. Neuron 2011, 72, 385–396. [Google Scholar] [CrossRef]
- Thompson-Schill, S.L.; D’Esposito, M.; Aguirre, G.K.; Farah, M.J. Role of left inferior prefrontal cortex in retrieval of semantic knowledge: A reevaluation. Proc. Natl. Acad. Sci. USA 1997, 94, 14792–14797. [Google Scholar] [CrossRef]
- Tremblay, P.; Gracco, V.L. Contribution of the pre-SMA to the production of words and non-speech oral motor gestures, as revealed by repetitive transcranial magnetic stimulation (rTMS). Brain Res. 2009, 1268, 112–124. [Google Scholar] [CrossRef]
- Riès, S.K.; Dronkers, N.F.; Knight, R.T. Choosing words: Left hemisphere, right hemisphere, or both? Perspective on the lateralization of word retrieval. Ann. N. Y. Acad. Sci. 2016, 1369, 111–131. [Google Scholar] [CrossRef]
- Heim, S.; Friederici, A.D.; Schiller, N.O.; Rüschemeyer, S.; Amunts, K. The determiner congruency effect in language production investigated with functional MRI. Hum. Brain Mapp. 2009, 30, 928–940. [Google Scholar] [CrossRef] [PubMed]
- Price, C.J. A review and synthesis of the first 20 years of PET and fMRI studies of heard speech, spoken language and reading. Hum. Brain Mapp. 2012, 62, 816–847. [Google Scholar] [CrossRef]
- Liégeois-Chauvel, C.; Dubarry, A.; Wang, I.; Chauvel, P.; Gonzalez-Martinez, J.A.; Alario, F. Inter-individual variability in dorsal stream dynamics during word production. Eur. J. Neurosci. 2022, 56, 5070–5089. [Google Scholar] [CrossRef]
- Duncan, J.; Owen, A.M. Common regions of the human frontal lobe recruited by diverse cognitive demands. Trends Neurosci. 2000, 23, 475–483. [Google Scholar] [CrossRef]
- Criel, Y.; Depuydt, E.; Miatton, M.; Santens, P.; Van Mierlo, P.; De Letter, M. Cortical Generators and Connections Underlying Phoneme Perception: A Mismatch Negativity and P300 Investigation. Brain Topogr. 2024, 37, 1089–1117. [Google Scholar] [CrossRef]
- Polich, J.; Kok, A. Cognitive and Biological Determinants of P300: An Integrative Review. Biol. Psychol. 1995, 41, 103–146. [Google Scholar] [CrossRef]
- Linden, D.E.; Prvulovic, D.; Formisano, E.; Völlinger, M.; Zanella, F.E.; Goebel, R.; Dierks, T. The Functional Neuroanatomy of Target Detection: An fMRI Study of Visual and Auditory Oddball Tasks. Cereb. Cortex 1999, 9, 815–823. [Google Scholar] [CrossRef]
- Duncan, J.S. Imaging in the surgical treatment of epilepsy. Nat. Rev. Neurol. 2010, 6, 537–550. [Google Scholar] [CrossRef] [PubMed]
- Fedorenko, E.; Duncan, J.; Kanwisher, N. Broad domain generality in focal regions of frontal and parietal cortex. Proc. Natl. Acad. Sci. USA 2013, 110, 16616–16621. [Google Scholar] [CrossRef]
- Fedorenko, E.; Duncan, J.; Kanwisher, N. Language-Selective and Domain-General Regions Lie Side by Side within Broca’s Area. Curr. Biol. 2012, 22, 2059–2062. [Google Scholar] [CrossRef]
- Gratton, C.; Sun, H.; Petersen, S.E. Control networks and hubs. Trends Cogn. Sci. 2016, 20, 805–817. [Google Scholar] [CrossRef] [PubMed]
- Lachaux, J.P.; Axmacher, N.; Mormann, F.; Halgren, E.; Crone, N.E. High-Frequency Neural Activity and Human Cognition: Past, Present and Possible Future of Intracranial EEG Research. Prog. Neurobiol. 2012, 98, 279–301. [Google Scholar] [CrossRef]
- Flinker, A.; Piai, V.; Knight, R. Intracranial Electrophysiology in Language Research. In The Oxford Handbook of Psycholinguistics, 2nd ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar] [CrossRef]
- Johnson, E.L.; Kam, J.W.Y.; Tzovara, A.; Knight, R.T. Insights into Human Cognition from Intracranial EEG: A Review of Audition, Memory, Internal Cognition, and Causality. J. Neural Eng. 2020, 17, 051001. [Google Scholar] [CrossRef] [PubMed]
- Lagarde, S.; Roehri, N.; Lambert, I.; Trebuchon, A.; McGonigal, A.; Carron, R.; Scavarda, D.; Milh, M.; Pizzo, F.; Colombet, B.; et al. Interictal stereotactic-EEG functional connectivity in refractory focal epilepsies. Brain 2018, 141, 2966–2980. [Google Scholar] [CrossRef]
- Stergiadis, C.; Halliday, D.M.; Kazis, D.; Klados, M.A. Functional connectivity of interictal iEEG and the connectivity of high-frequency components in epilepsy. Brain Organoid Syst. Neurosci. J. 2023, 1, 3–12. [Google Scholar] [CrossRef]
- Balatskaya, A.; Roehri, N.; Lagarde, S.; Pizzo, F.; Medina, S.; Wendling, F.; Bénar, C.G.; Bartolomei, F. The “Connectivity Epileptogenicity Index ” (cEI), a method for mapping the different seizure onset patterns in StereoElectroEncephalography recorded seizures. Clin. Neurophysiol. 2020, 131, 1947–1955. [Google Scholar] [CrossRef]
- Jerbi, K.; Ossandón, T.; Hamamé, C.M.; Senova, S.; Dalal, S.S.; Jung, J.; Minotti, L.; Bertrand, O.; Berthoz, A.; Kahane, P.; et al. Task-related gamma-band dynamics from an intracerebral perspective: Review and implications for surface EEG and MEG. Hum. Brain Mapp. 2009, 30, 1758–1771. [Google Scholar] [CrossRef]
- Wang, H.E.; Friston, K.J.; Bénar, C.G.; Woodman, M.M.; Chauvel, P.; Jirsa, V.; Bernard, C. MULAN: Evaluation and ensemble statistical inference for functional connectivity. NeuroImage 2018, 166, 167–184. [Google Scholar] [CrossRef]
- Bancaud, J.; Angelergues, R.; Bernouilli, C.; Bonis, A.; Bordas-Ferrer, M.; Bresson, M.; Buser, P.; Covello, L.; Morel, P.; Szikla, G.; et al. Functional stereotaxic exploration (stereo-electroencephalography) in epilepsies. Rev. Neurol. 1969, 120, 448. [Google Scholar]
- Chauvel, P.; Gonzalez-Martinez, J.; Bulacio, J. Presurgical intracranial investigations in epilepsy surgery. Handb. Clin. Neurol. 2019, 161, 45–71. [Google Scholar]
- Gonzalez-Martinez, J.; Mullin, J.; Vadera, S.; Bulacio, J.; Hughes, G.; Jones, S.; Enatsu, R.; Najm, I. Stereotactic placement of depth electrodes in medically intractable epilepsy. J. Neurosurg. 2014, 120, 639–644. [Google Scholar] [CrossRef] [PubMed]
- González-Martínez, J. Convergence of stereotactic surgery and epilepsy: The stereoelectroencephalography method. Neurosurgery 2015, 62, 117–122. [Google Scholar] [CrossRef]
- Trébuchon, A.; Liegeois-Chauvel, C.; Gonzalez-Martinez, J.A.; Alario, F.X. Contributions of electrophysiology for identifying cortical language systems in patients with epilepsy. Epilepsy Behav. 2020, 112, 107407. [Google Scholar] [CrossRef] [PubMed]
- Hickok, G. Computational neuroanatomy of speech production. Nat. Rev. Neurosci. 2012, 13, 135–145. [Google Scholar] [CrossRef]
- Collins, D.; Zijdenbos, A.; Kollokian, V.; Sled, J.; Kabani, N.; Holmes, C.; Evans, A. Design and construction of a realistic digital brain phantom. IEEE Trans. Med. Imaging 1998, 17, 463–468. [Google Scholar] [CrossRef]
- Talairach, J.; Tournoux, P. Co-Planar Stereotaxic Atlas of the Human Brain: 3-Dimensional Proportional System: An Approach to Cerebral Imaging; Thieme Medical Publishers, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Johnson, M.A.; Thompson, S.; Gonzalez-Martinez, J.; Park, H.J.; Bulacio, J.; Najm, I.; Kahn, K.; Kerr, M.; Sarma, S.V.; Gale, J.T. Performing Behavioral Tasks in Subjects with Intracranial Electrodes. J. Vis. Exp. 2014, 92, e51947. [Google Scholar] [CrossRef]
- Snodgrass, J.G.; Vanderwart, M. A standardized set of 260 pictures: Norms for name agreement, image agreement, familiarity, and visual complexity. J. Exp. Psychol. Hum. Learn. Mem. 1980, 6, 174–215. [Google Scholar] [CrossRef]
- Wang, H.E.; Bénar, C.G.; Quilichini, P.P.; Friston, K.J.; Jirsa, V.K.; Bernard, C. A systematic framework for functional connectivity measures. Front. Neurosci. 2014, 8, 1–22. [Google Scholar] [CrossRef]
- Baccalá, L.; Sameshima, K. Partial directed coherence: A new concept in neural structure determination. Biol. Cybern. 2001, 84, 463–474. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: An efficient data clustering method for very large databases. ACM Sigmod Rec. 1996, 25, 103–114. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Fowlkes, E.B.; Mallows, C.L. A Method for Comparing Two Hierarchical Clusterings. J. Am. Stat. Assoc. 1983, 78, 553–569. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Brandes, U. On variants of shortest-path betweenness centrality and their generic computation. Soc. Netw. 2008, 30, 136–145. [Google Scholar] [CrossRef]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- Ramdas, A.; Trillos, N.G.; Cuturi, M. On Wasserstein Two-Sample Testing and Related Families of Nonparametric Tests. Entropy 2017, 19, 47. [Google Scholar] [CrossRef]
- Cabral, J.; Kringelbach, M.L.; Deco, G. Functional connectivity dynamically evolves on multiple time-scales over a static structural connectome: Models and mechanisms. NeuroImage 2017, 160, 84–96. [Google Scholar] [CrossRef] [PubMed]
- Rissman, J.; Gazzaley, A.; D’Esposito, M. Measuring functional connectivity during distinct stages of a cognitive task. NeuroImage 2004, 23, 752–763. [Google Scholar] [CrossRef]
- Smallwood, J.; Bernhardt, B.C.; Leech, R.; Bzdok, D.; Jefferies, E.; Margulies, D.S. The default mode network in cognition: A topographical perspective. Nat. Rev. Neurosci. 2021, 22, 503–513. [Google Scholar] [CrossRef]
- Kaufmann, T.; Alnæs, D.; Brandt, C.L.; Doan, N.T.; Kauppi, K.; Bettella, F.; Lagerberg, T.V.; Berg, A.O.; Djurovic, S.; Agartz, I.; et al. Task modulations and clinical manifestations in the brain functional connectome in 1615 fMRI datasets. NeuroImage 2017, 147, 243–252. [Google Scholar] [CrossRef] [PubMed]
- Flinker, A.; Korzeniewska, A.; Shestyuk, A.Y.; Crone, N.E. Redefining the role of Broca’s area in speech. Proc. Natl. Acad. Sci. USA 2015, 112, 2871–2875. [Google Scholar] [CrossRef]
- Abrahams, S.; Goldstein, L.H.; Simmons, A.; Brammer, M.J.; Williams, S.C.R.; Giampietro, V.P.; Andrew, C.M.; Leigh, P.N. Functional magnetic resonance imaging of verbal fluency and confrontation naming using compressed image acquisition to permit overt responses. Hum. Brain Mapp. 2003, 20, 29–40. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, S.; Honda, M.; Sadato, N. Modality-Specific Cognitive Function of Medial and Lateral Human Brodmann Area 6. J. Neurosci. 2005, 25, 496–501. [Google Scholar] [CrossRef]
- Squires, K.C.; Wickens, C.; Squires, N.K.; Donchin, E. The effect of stimulus sequence on the waveform of the cortical event-related potential. Science 1976, 193, 1142–1146. [Google Scholar] [CrossRef]
- Polich, J. Updating P300: An integrative theory of P3a and P3b. Clin. Neurophysiol. 2007, 118, 2128–2148. [Google Scholar] [CrossRef]
- Kim, H. Involvement of the dorsal and ventral attention networks in oddball stimulus processing: A meta-analysis. Hum. Brain Mapp. 2014, 35, 2265–2284. [Google Scholar] [CrossRef]
- Wang, H.E.; Triebkorn, P.; Breyton, M.; Dollomaja, B.; Lemarechal, J.D.; Petkoski, S.; Sorrentino, P.; Depannemaecker, D.; Hashemi, M.; Jirsa, V.K. Virtual brain twins: From basic neuroscience to clinical use. Natl. Sci. Rev. 2024, 11, nwae079. [Google Scholar] [CrossRef] [PubMed]
- Lavanga, M.; Stumme, J.; Yalcinkaya, B.H.; Fousek, J.; Jockwitz, C.; Sheheitli, H.; Bittner, N.; Hashemi, M.; Petkoski, S.; Caspers, S.; et al. The virtual aging brain: Causal inference supports interhemispheric dedifferentiation in healthy aging. NeuroImage 2023, 283, 120403. [Google Scholar] [CrossRef] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.E.; Gonzalez-Martinez, J.; Jirsa, V.; Chauvel, P.; Alario, F.-X.; Liegeois-Chauvel, C. Assessing Functional Connectivity Dynamics During Cognitive Tasks Involving the Dorsal Stream. Entropy 2025, 27, 566. https://doi.org/10.3390/e27060566
Wang HE, Gonzalez-Martinez J, Jirsa V, Chauvel P, Alario F-X, Liegeois-Chauvel C. Assessing Functional Connectivity Dynamics During Cognitive Tasks Involving the Dorsal Stream. Entropy. 2025; 27(6):566. https://doi.org/10.3390/e27060566
Chicago/Turabian StyleWang, Huifang E., Jorge Gonzalez-Martinez, Viktor Jirsa, Patrick Chauvel, F.-Xavier Alario, and Catherine Liegeois-Chauvel. 2025. "Assessing Functional Connectivity Dynamics During Cognitive Tasks Involving the Dorsal Stream" Entropy 27, no. 6: 566. https://doi.org/10.3390/e27060566
APA StyleWang, H. E., Gonzalez-Martinez, J., Jirsa, V., Chauvel, P., Alario, F.-X., & Liegeois-Chauvel, C. (2025). Assessing Functional Connectivity Dynamics During Cognitive Tasks Involving the Dorsal Stream. Entropy, 27(6), 566. https://doi.org/10.3390/e27060566









