The Origin of Shared Emergent Properties in Discrete Systems
Abstract
1. Introduction
1.1. Entropy as an Emergent Property
1.2. Information Entropy and the Development of CoHSI Theory
1.2.1. Why the Conservation of Information?
1.2.2. Ordered or Heterogeneous Systems
The information content of a message is the log of the number of ways the symbols in the message can be arranged, specifically excluding any intrinsic meaning so that all symbols are equally likely.
1.2.3. Unordered Systems
1.3. On Equilibrium
2. Materials and Methods
2.1. Databases
2.1.1. Biological Datasets
2.1.2. Software Datasets
$ git clone \
git://git.kernel.org/pub/scm/linux/kernel/git/stable/linux.git
$ cd linux
$ git checkout ...
2.2. Computational Methods
2.3. The Canonical CoHSI Distributions
- D1
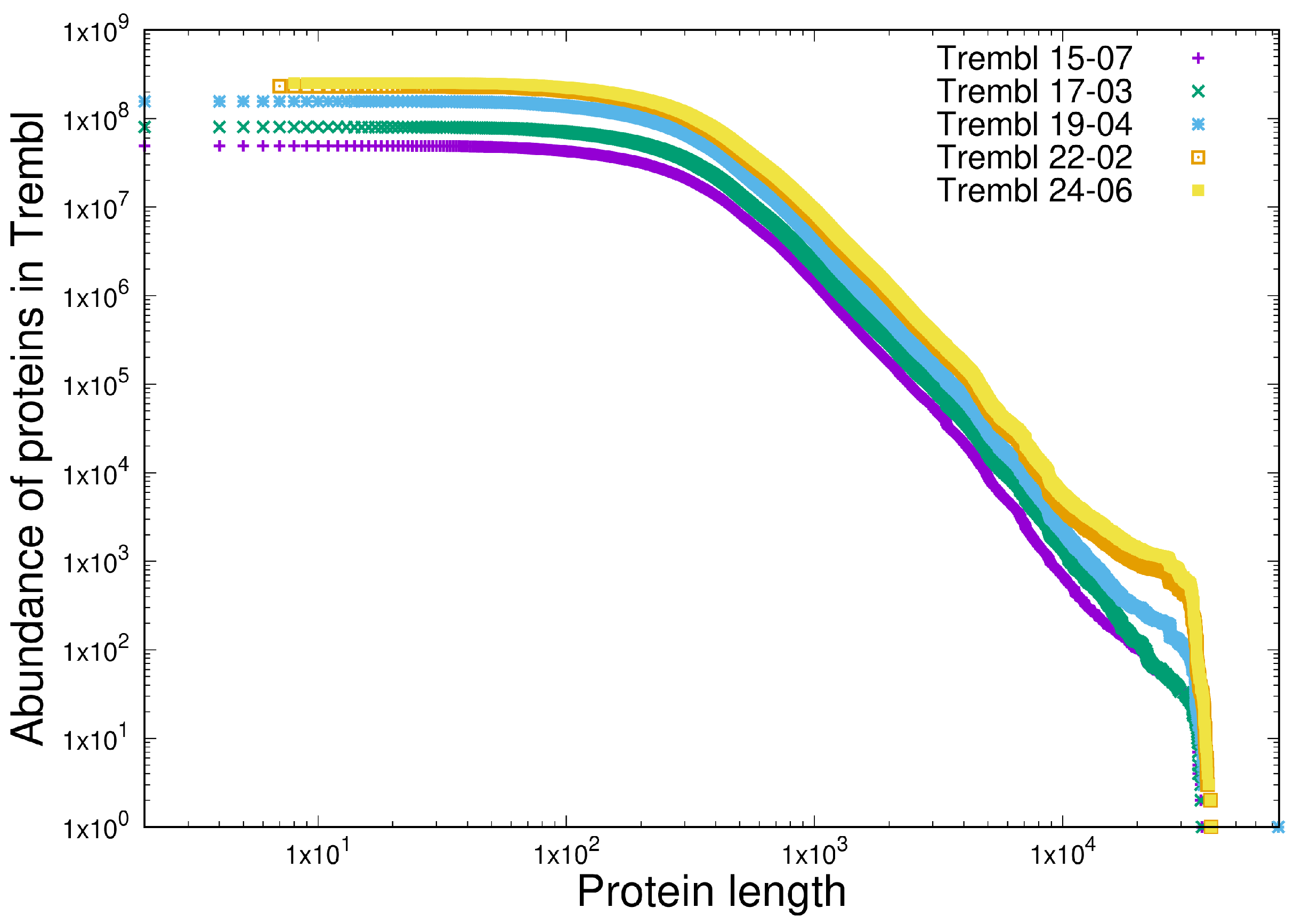
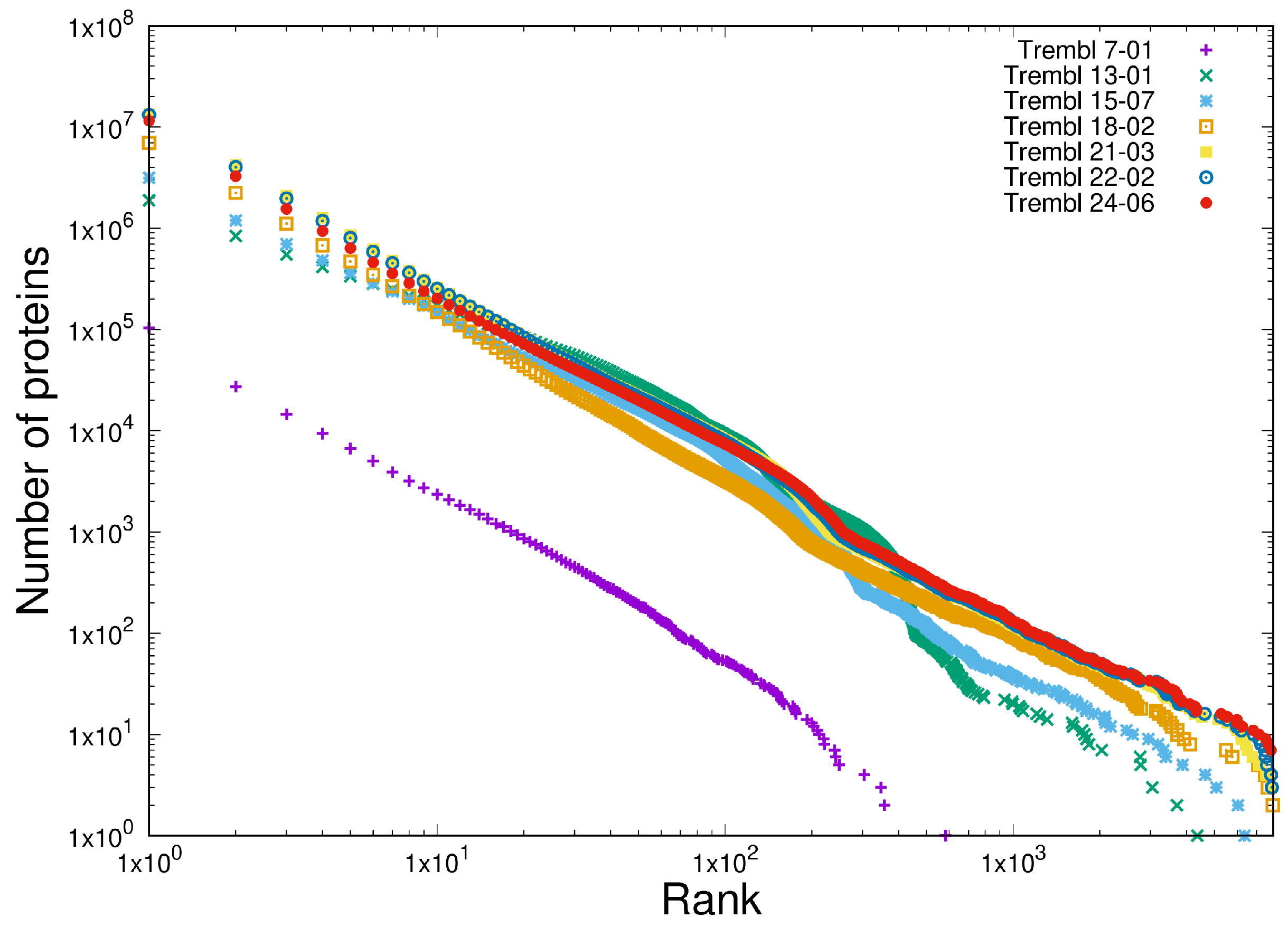
- Shared heterogeneous behaviour between the current latest version of the protein database TrEMBL 24-06 at https://uniprot.org (accessed 22 May 2025) and a set of open source software written in C in the Linux and BSD distributions.
- D2
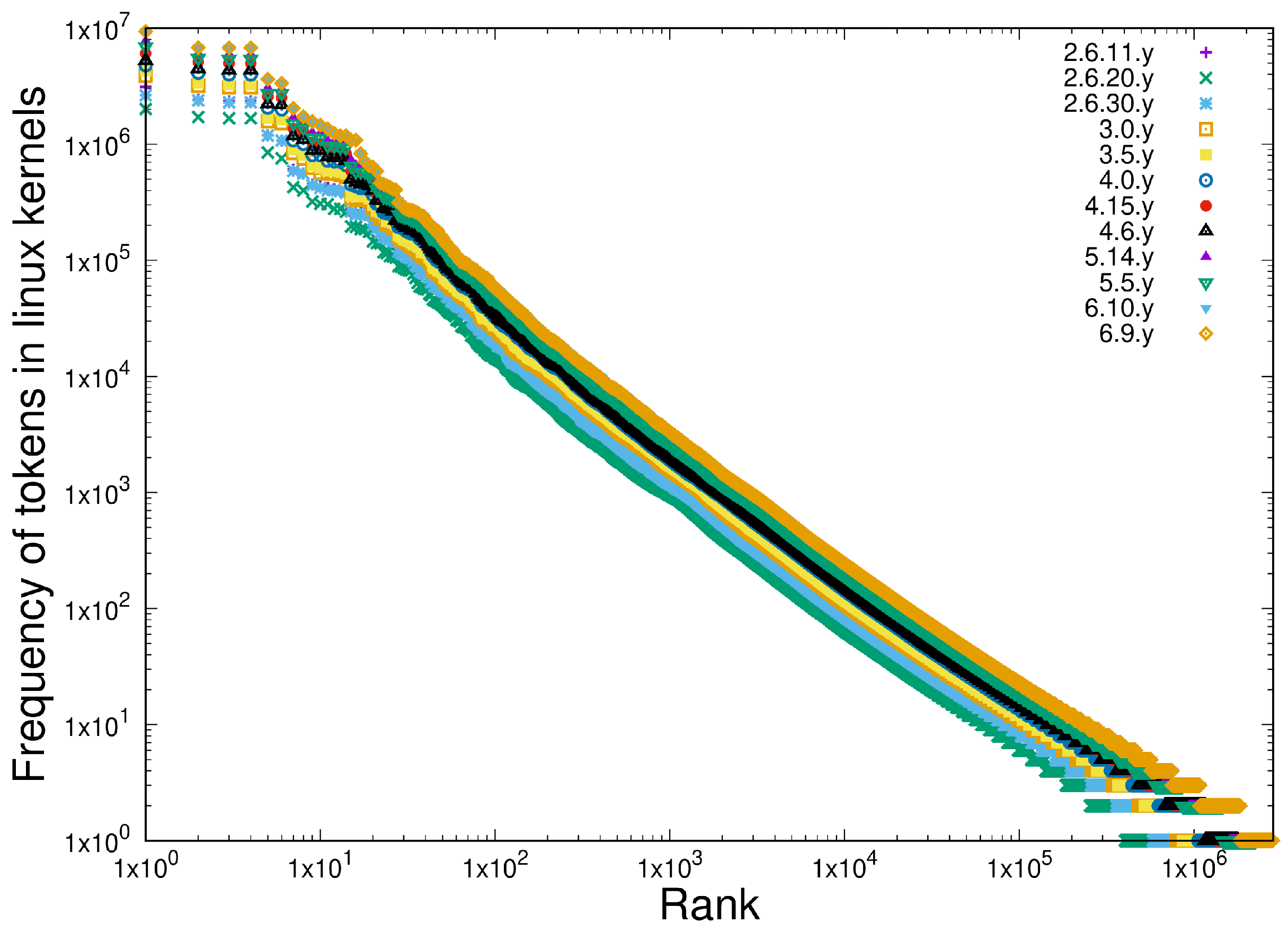
- Scale-independent heterogeneous behaviour in the last 10 years of versions of the TrEMBL protein database and in 12 versions of the Linux kernel distribution in the last 15 years (versions 2.6.11 - 6.9). This is written in C.
- D3
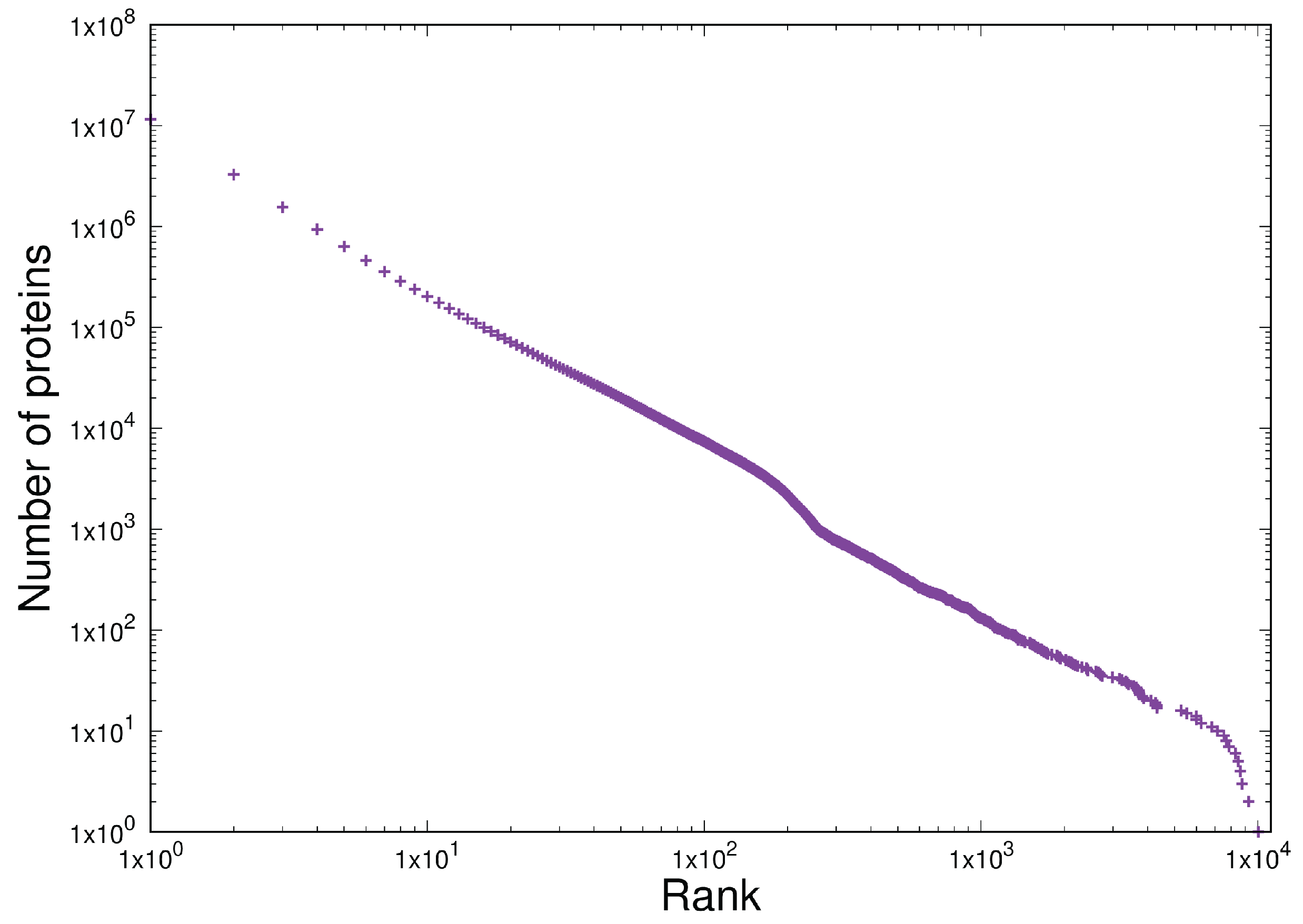
- Shared homogeneous behaviour between the current latest version of the protein database TrEMBL 24-06 at https://uniprot.org (accessed 22 May 2025) and a set of open source software written in C in the Linux and BSD distributions.
- D4
- Scale-independent homogeneous behaviour in the last 10 years of the TrEMBL protein database and 12 versions of the Linux kernel distribution in the last 15 years (versions 2.6.11 - 6.9). This is written in C.
3. Results
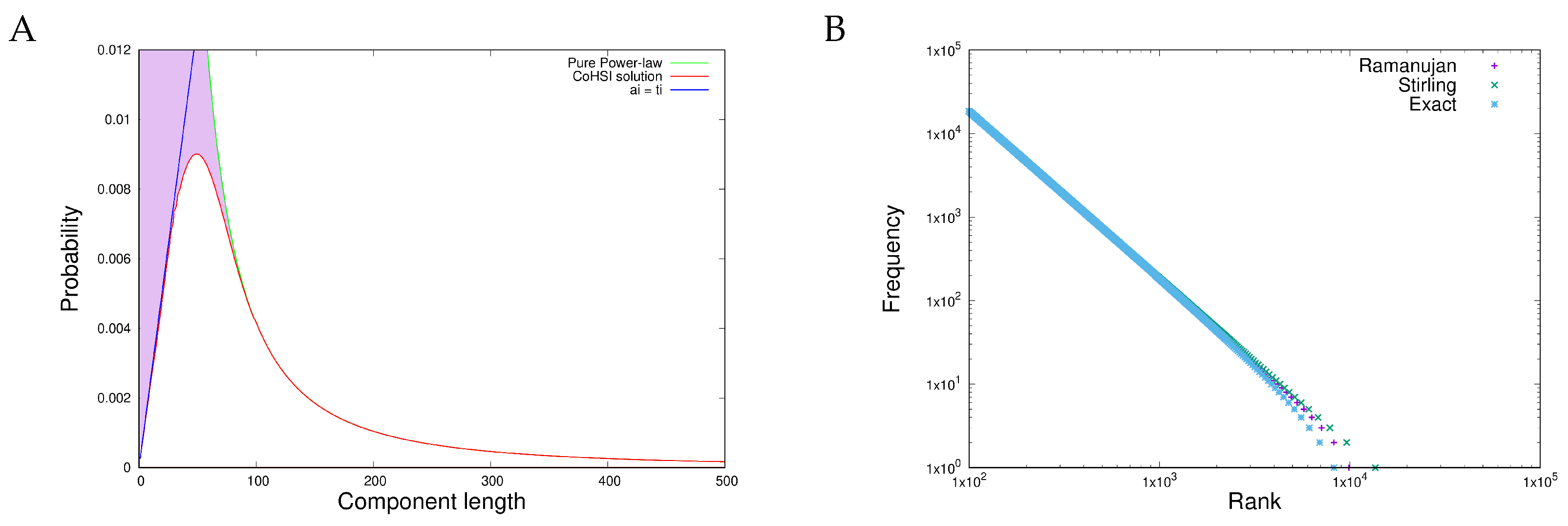
3.1. Item D1
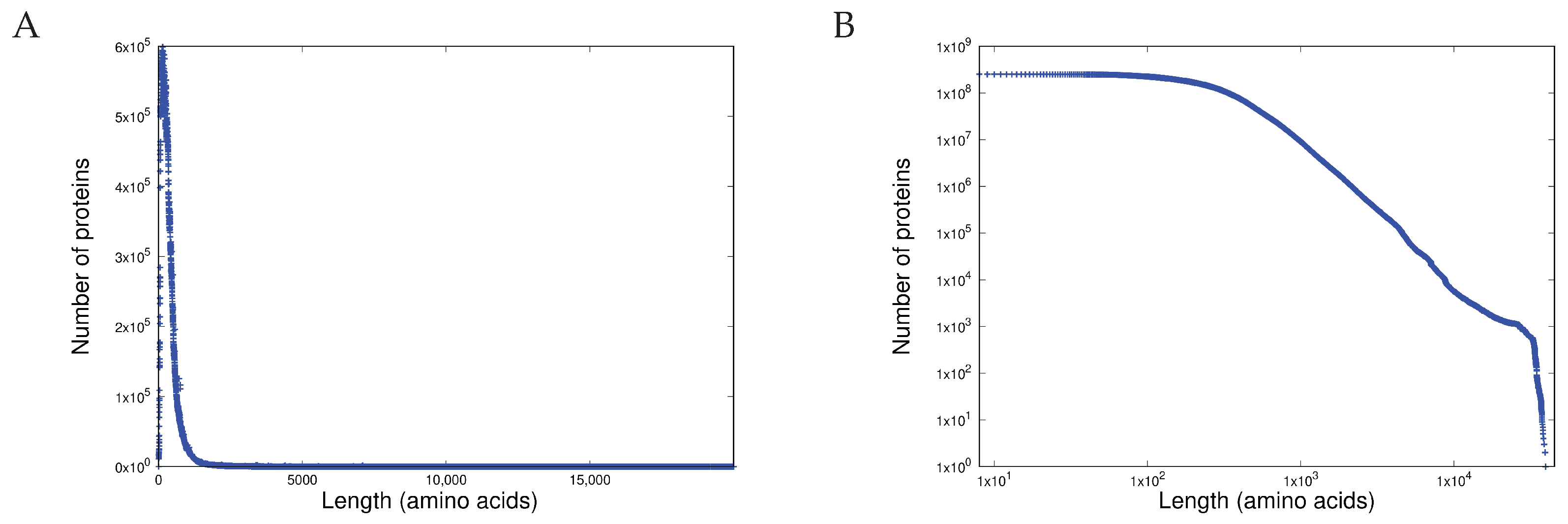
3.2. Item D2
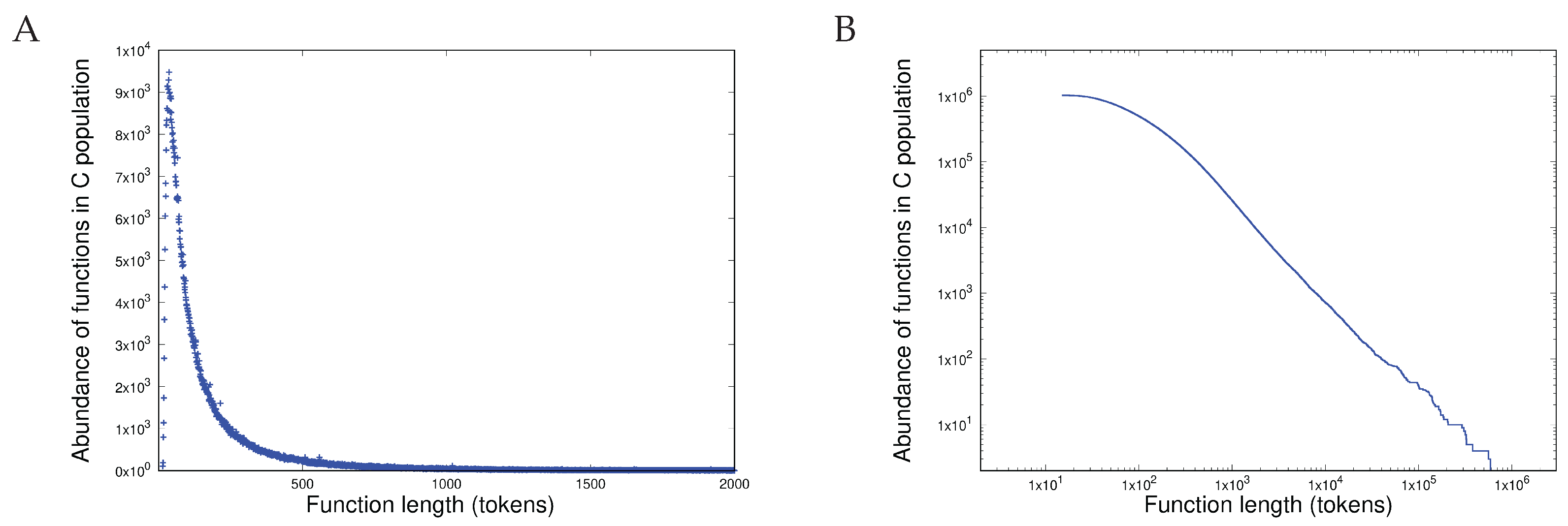
3.3. Item D3
3.4. Item D4
4. Discussion
- The simultaneous existence of two sets of properties: one set pertaining to when intrinsic meaning is considered and one set pertaining to when intrinsic meaning is irrelevant and therefore shared amongst disparate systems.
- Discrete systems tend towards the overwhelmingly most likely equilibrium state defined by CoHSI theory, with the caveat that departures from the equilibrium are permitted by the theory. This latter point can be observed in the minor bumps and bulges that are observable in many of the datasets presented here.
Life’s Emergent Properties: The Most Likely Outcome of Evolution
5. Conclusions
- Heterogeneous behaviour, manifest in length distributions as a sharp unimodal peak followed by a precise power-law, is exhibited both by proteins (measured in amino acids) and in software components (measured in programming language tokens).
- Scale independence is demonstrated in the heterogeneous behaviour of the length distributions of both proteins and software functions.
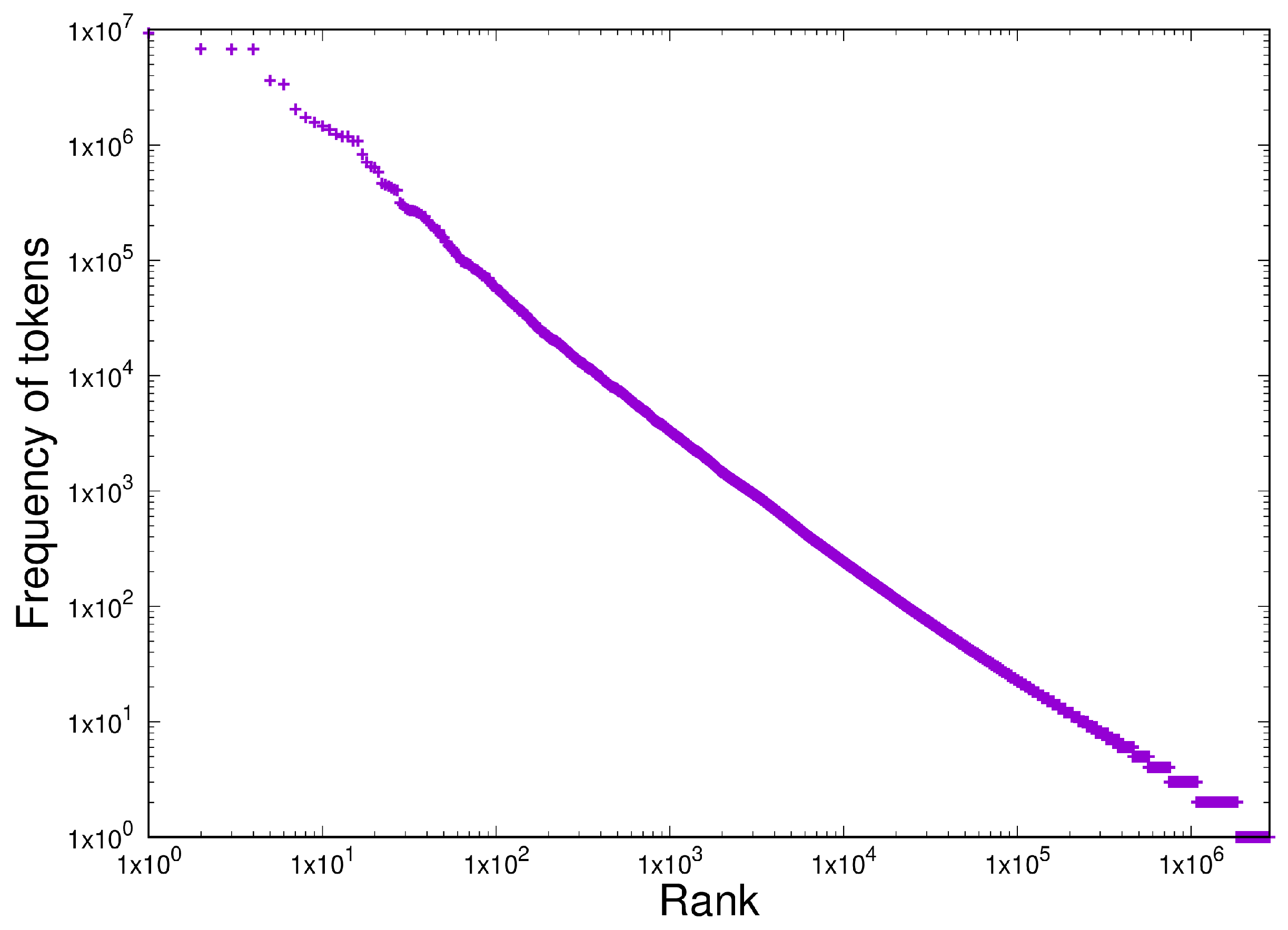
- Homogeneous behaviour (a Zipfian power-law distribution with a droop in the tail) is exhibited in the frequency of multiplicity in proteins and in the frequency of tokens in software.
- Scale independence is demonstrated in the homogeneous behaviour of both protein multiplicity and token frequency in programming languages.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. What Is a Discrete System?
| System | Component | Indivisible Pieces | Size of Alphabet |
|---|---|---|---|
| Genome | Chromosome | Nucleotides, A,C,T,G | 4 1 |
| Transcriptome | Messenger RNA | Nucleotides, A,C,U,G | 4 1 |
| Proteome | Protein | Amino acids | 20 2 |
| Software package | Subroutine | Programming language tokens 3 | Hundreds |
| Written text | Sentence | Words | Hundreds |
Appendix A.2. A Short Note on the CoHSI Derivations
Appendix A.2.1. Heterogeneous
Appendix A.2.2. Homogeneous
References
- Zipf, G.K. Psycho-Biology of Languages: An Introduction to Dynamic Philology; Houghton-Miflin: Boston, MA, USA, 1935. [Google Scholar]
- Newman, M. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Hatton, L.; Warr, G. Exposing Nature’s Bias: The Hidden Clockwork Behind Society, Life and the Universe; Bluespear Publishing: London, UK, 2022; ISBN 978-1-908-42204-0. [Google Scholar]
- Shooman, M. Software Engineering, 2nd ed.; McGraw-Hill: Singapore, 1985. [Google Scholar]
- Cherry, C. On Human Communication; Library of Congress 56-9820; John Wiley Science Editions: Hoboken, NJ, USA, 1963. [Google Scholar]
- Pareto, V. Cours d’économie Politique; Librairie de l’Université de Lausanne: Lausanne, Switzerland, 1896; Volume 1, p. 416. [Google Scholar]
- Cross, C. The size distribution of lunar craters. Mon. Not. Royal Ast. Soc. 1966, 134, 245–252. [Google Scholar] [CrossRef][Green Version]
- Hatton, L.; Warr, G. Strong evidence of an information theoretical conservation principle linking all discrete systems. R. Soc. Open Sci. 2019, 6. [Google Scholar] [CrossRef] [PubMed]
- Lemons, D.S. A Student’s Guide to Entropy, 1st ed.; Cambridge University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Jeffery, K.; Pollack, R.; Rovelli, C. On the Statistical Mechanics of Life: Schroedinger Revisited. Entropy 2019, 21, 1211. [Google Scholar] [CrossRef]
- Noether, E. Invariante Variationsprobleme. Nachrichten der Königlichen Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse. pp. 235–257. Available online: https://arxiv.org/abs/physics/0503066 (accessed on 22 May 2025).
- Sommerfeld, A. Thermodynamics and Statistical Mechanics; Academic Press: New York, NY, USA, 1956. [Google Scholar]
- Glazer, M.A.; Wark, J.S. Statistical MEchanics. A Survival Guide; Oxford University Press: Oxford, UK, 2001; p. 142. [Google Scholar]
- Frank, S.A. The common patterns of nature. J. Evol. Biol. 2009, 22, 1563–1585. [Google Scholar] [CrossRef] [PubMed]
- Hartley, R. Transmission of Information. Bell Syst. Tech. J. 1928, 7, 535. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10. [Google Scholar] [CrossRef]
- Hatton, L.; Spinellis, D.; van Genuchten, M. The long-term growth rate of evolving software: Empirical results and implications. J. Softw. Evol. Process 2017, 29, e1847. [Google Scholar] [CrossRef]
- Aho, A.; Ullman, J. Principles of Compiler Design; Addison-Wesley: Boston, MA, USA, 1977; p. 604. [Google Scholar]
- Aho, A. Software and the Future of Programming Languages. Science 2004, 303, 1331–1333. [Google Scholar] [CrossRef]
- Ramanujan, S. The Lost Notebook and Other Unpublished Papers; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Gillespie, C. Package ‘poweRlaw’. 2019. Available online: https://github.com/csgillespie/poweRlaw (accessed on 22 May 2025).
- Warr, G.; Hatton, L. The Covid-19 Pandemic and the Patterns of Nature. Int. J. Coronaviruses 2024, 5, 10–17. [Google Scholar]
- Hatton, L.; Warr, G. Information Theory and the Length Distribution of all Discrete Systems. arXiv 2017, arXiv:1709.01712. [Google Scholar]
- Hatton, L.; Warr, G. Protein Multiplicity: Exemplifying an Overwhelmingly Likely Pattern of Molecular Evolution? Acad. Biol. 2024, 2. [Google Scholar] [CrossRef]
- Mora, C.; Tittensor, D.P.; Adl, S.; Simpson, A.G.; Worm, B. How Many Species Are There on Earth and in the Ocean? PLoS Biol. 2011, 9, e1001127. [Google Scholar] [CrossRef]
- Jing, G.; Zhang, Y.; Liu, L.; Wang, Z.; Sun, Z.; Knight, R.; Su, X.; Xu, J. A Scale-Free, Fully Connected Global Transition Network Underlies Known Microbiome Diversity. mSystems 2021, 6. [Google Scholar] [CrossRef] [PubMed]
- Koonin, E.V.; Krupovic, M.; Dolja, V.V. The global virome: How much diversity and how many independent origins? Environ. Microbiol. 2023, 25, 40–44. [Google Scholar] [CrossRef]
- Darwin, C. On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life; John Murray: London, UK, 1859; p. 502. [Google Scholar]
- de Jong, M.J.; van Oosterhout, C.; Hoelzel, A.R.; Janke, A. Moderating the neutralist-selectionist debate: Exactly which propositions are we debating, and which arguments are valid? Biol. Rev. 2024, 99, 23–55. [Google Scholar] [CrossRef]
- Kimura, M. The Neutral Theory of Evolution and the World View of the Neutralists. Genome 1989, 31, 24–31. [Google Scholar] [CrossRef]
- Huang, S. The maximum genetic diversity theory of molecular evolution. Commun. Inf. Syst. 2023, 23, 359–392. [Google Scholar] [CrossRef]
- Koonin, E.V. Are There Laws of Genome Evolution? PLoS Comput. Biol. 2011, 7, e1002173. [Google Scholar] [CrossRef]
- Gan, X.; Wang, D.; Han, Z. A growth model that generates an n-tuple Zipf law. Phys. A Stat. Theor. Phys. 2011, 390, 792–800. [Google Scholar] [CrossRef]
- Huynen, M.A.; van Nimwegen, E. The frequency distribution of gene family sizes in complete genomes. Mol. Biol. Evol. 1998, 15, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Kendal, W.S. A scale invariant clustering of genes on human chromosome 7. BMC Evol. Biol. 2004, 4, 3. [Google Scholar] [CrossRef] [PubMed]
- Naryzhny, S.; Maynskova, M.; Zgoda, V.; Archakov, A. Zipf’s law in Proteomics. J. Proteom. Bioinform. 2017, 10, 79–84. [Google Scholar] [CrossRef]
- Motomura, K.; Fujita, T.; Tsutsumi, M.; Kikuzato, S.; Nakamura, M.; Otaki, J.M. Word Decoding of Protein Amino Acid Sequences with Availability Analysis: A Linguistic Approach. PLoS ONE 2012, 7, e50039. [Google Scholar] [CrossRef]
- White, E.P.; Ernest, S.M.; Kerkhoff, A.J.; Enquist, B.J. Relationships between body size and abundance in ecology. Trends Ecol. Evol. 2007, 22, 323–330. [Google Scholar] [CrossRef]
- Speakman, J.R. Body size, energy metabolism and lifespan. J. Exp. Biol. 2005, 208, 1717–1730. [Google Scholar] [CrossRef]
- Rhodes, C.; Anderson, R. Power laws governing epidemics in isolated populations. Nature 1996, 381, 600–602. [Google Scholar] [CrossRef]
- Rhodes, C.J.; Anderson, R.M. A scaling analysis of measles epidemics in a small population. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1996, 351, 1679–1688. [Google Scholar] [CrossRef]
- Xenikos, D.; Asimakopoulos, A. Power-law growth of the COVID-19 fatality incidents in Europe. Infect. Dis. Model. 2021, 6, 743–750. [Google Scholar] [CrossRef] [PubMed]
- Meyer, S.; Held, L. Power-law models for infectious disease spread. Ann. Appl. Stat. 2014, 8, 1612–1639. [Google Scholar] [CrossRef]
- Macarthur, R.; Wilson, E. The Theory of Island Biogeography; Princeton University Press: Princeton, NJ, USA, 1967; p. 203. [Google Scholar]
- Brown, J.H.; Gupta, V.K.; Li, B.L.; Milne, B.T.; Restrepo, C.; West, G.B. The fractal nature of nature: Power laws, ecological complexity and biodiversity. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2002, 357, 619–626. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J.; Roberts, B.W. Mass Extinction: Evolution and the Effects of External Influences on Unfit Species. Proceedings Biol. Sci. 1995, 260, 31–37. [Google Scholar]
- Newman, M.E.J. Self-organized criticality, evolution and the fossil extinction record. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1996, 263, 1605–1610. [Google Scholar] [CrossRef]
- Sepkoski, J.J., Jr. Ten Years in the Library: New Data Confirm Paleontological Patterns. Paleobiology 1993, 9, 43–51. [Google Scholar] [CrossRef]
- Ince, D.C.; Hatton, L.; Graham-Cumming, J. The case for open program code. Nature 2012, 482, 485–488. [Google Scholar] [CrossRef]
- Hatton, L. Conservation of Information: Software’s Hidden Clockwork. IEEE Trans. Softw. Eng. 2014, 40, 450–460. [Google Scholar] [CrossRef]
- Hatton, L.; Warr, G. Protein Structure and Evolution: Are They Constrained Globally by a Principle Derived from Information Theory? PLoS ONE 2015, 10, e0125663. [Google Scholar] [CrossRef]


| Test | Type | Results |
|---|---|---|
| R lm() | Necessary | adjusted = 0.995, p ; slope, i.e., |
| Clauset–Gillespie | Sufficient | p = 1 |
| Test | Type | Results |
|---|---|---|
| R lm() | Necessary | adjusted = 0.99, p , |
| Clauset-Gillespie | Sufficient | p = 1 |
| Release | Longest Protein | Length (aa) |
|---|---|---|
| 7-01 | BACTERIA Chlorobium chlorochromatii | 36,805 |
| 13-01 | BACTERIA Chlorobium chlorochromatii | 36,805 |
| 15-07 | BACTERIA Chlorobium chlorochromatii | 36,805 |
| 17-03 | BACTERIA Chlorobium chlorochromatii | 36,805 |
| 18-02 | EUKARYOTA Patagioenas fasciata | 36,991 |
| 24-06 | EUKARYOTA Hucho hucho (A0A5A9P0L4_9TELE) | 45,354 |
| Test | Type | Results |
|---|---|---|
| R lm() | Necessary | adjusted = 0.995, p , |
| Clauset–Gillespie | Sufficient | p = 1 |
| Test | Type | Results |
|---|---|---|
| R lm() | Necessary | adjusted = 0.997, p , |
| Clauset-Gillespie | Sufficient | p = 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatton, L.; Warr, G. The Origin of Shared Emergent Properties in Discrete Systems. Entropy 2025, 27, 561. https://doi.org/10.3390/e27060561
Hatton L, Warr G. The Origin of Shared Emergent Properties in Discrete Systems. Entropy. 2025; 27(6):561. https://doi.org/10.3390/e27060561
Chicago/Turabian StyleHatton, Les, and Greg Warr. 2025. "The Origin of Shared Emergent Properties in Discrete Systems" Entropy 27, no. 6: 561. https://doi.org/10.3390/e27060561
APA StyleHatton, L., & Warr, G. (2025). The Origin of Shared Emergent Properties in Discrete Systems. Entropy, 27(6), 561. https://doi.org/10.3390/e27060561






