Sinkhorn Distributionally Robust Conditional Quantile Prediction with Fixed Design
Abstract
1. Introduction
2. Preliminaries
3. Problem Setup
3.1. Sinkhorn Distance
3.2. Sinkhorn Distributionally Robust Conditional Quantile Prediction with Fixed Design
4. Tractable Reformulation
- (ii)
- for almost every
- (iii)
- (iv)
- For every joint distribution γ on with a first marginal distribution , it has a regular conditional distribution , given that the value of the first marginal equals
5. Numerical Experiments
- Conditional quantile prediction problem based on the SAA method [8]:
- KL DRCQP problem [19]:
- Type 1-Wasserstein DRCQP problem [9]:
- Type p-Wasserstein () DRCQP problem [37]:
- where , ,
- and
- Catoni’s log-truncated robust quantile regression [43]:where is a robustification parameter to be tuned, and the non-decreasing influence function is
- Cauchy-truncated robust quantile regression [44]:where , and the truncation function is .
5.1. Simulation
5.1.1. Comparison of Out-of-Sample Performance and Computational Time
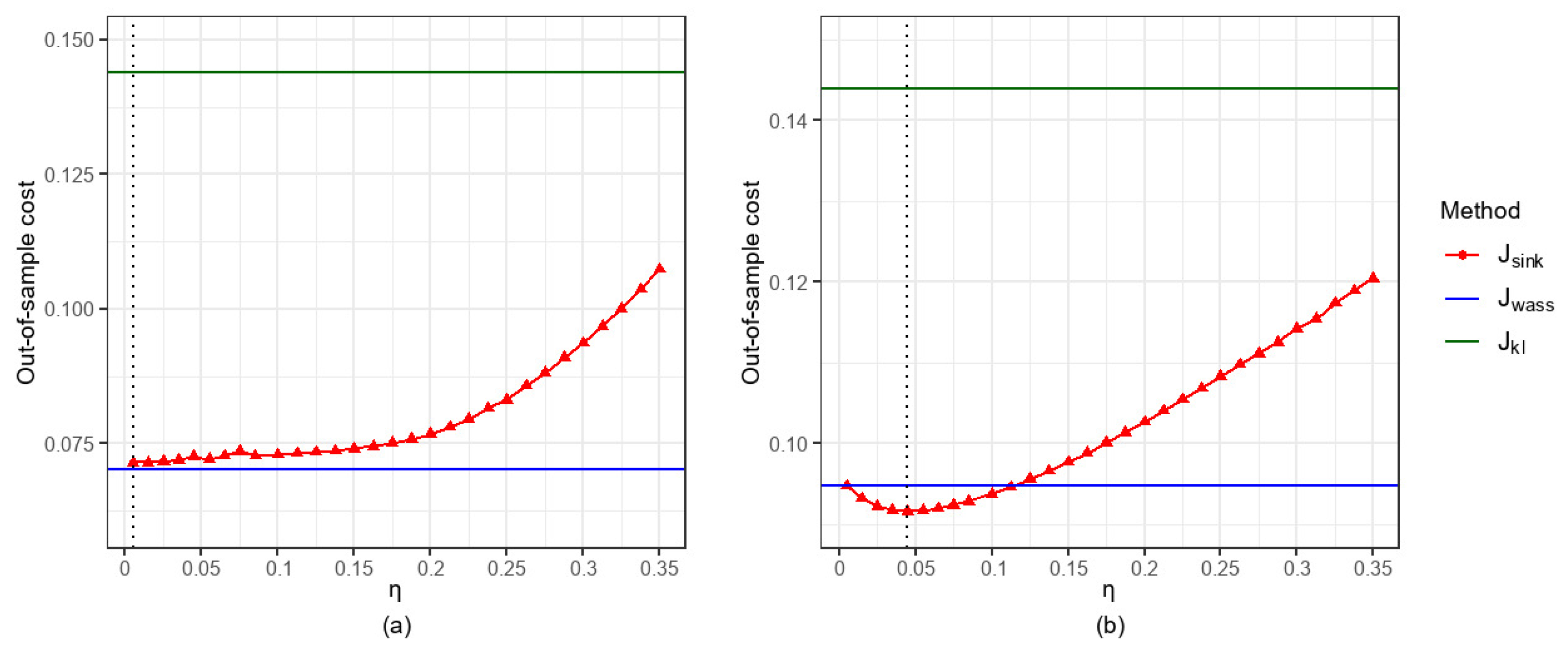
5.1.2. Comparison of the Impacts of Parameter Settings
5.2. Real-World Applications
5.2.1. Data Selection and Reconstruction
- Step 1: Construct a linear regression problem on the preprocessed dataset and use the coefficients estimated using the OLS method as the coefficients for potential true linear relationships, namely ;
- Step 2: Discard the demand column of the dataset and retain only the columns of the covariates. Then, generate new demand observations by adding i.i.d. simulated noise following the normal distribution. Specifically,
- Step 3: Divide the observations into training and testing sets based on time periods. Starting from the 8000-th observation, the next 500 time periods are used as the test set. For any given sample size N, the training set consists of the N observations immediately preceding the start of the test set;
- Step 4: For each observation in the test set, i.i.d. noises are simulated 50 times, resulting in a total of data points for the test set. These data points are used to evaluate the predictive performance of each method.
5.2.2. Comparison of Out-of-Sample Performance and Computational Time
5.2.3. Comparison of the Impacts of Parameter Settings
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| i.i.d. | Independent and identically distributed |
| SAA | Sample average approximation |
| DRO | Distributionally robust optimization |
| KL | Kullback–Leibler |
| OLS | Ordinary least squares |
| DRCQP | Distributionally robust conditional quantile prediction |
References
- Koenker, R.; Bassett, G. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Foster, N. The Impact of Trade Liberalisation on Economic Growth: Evidence from a Quantile Regression Analysis. Kyklos 2008, 61, 543–567. [Google Scholar] [CrossRef]
- Hong, H.G.; Christiani, D.C.; Li, Y. Quantile regression for survival data in modern cancer research: Expanding statistical tools for precision medicine. Precis. Clin. Med. 2019, 2, 90–99. [Google Scholar] [CrossRef] [PubMed]
- Reich, B.J. Spatiotemporal quantile regression for detecting distributional changes in environmental processes. J. R. Stat. Soc. Ser. C Appl. Stat. 2012, 61, 535–553. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision: Revisions to the Basel II Market Risk Framework. 2009. Available online: https://www.bis.org/publ/bcbs158.htm (accessed on 13 July 2009).
- Ban, G.Y.; Rudin, C. The big data newsvendor: Practical insights from machine learning. Oper. Res. 2019, 67, 90–108. [Google Scholar] [CrossRef]
- Rosset, S.; Tibshirani, R.J. From fixed-x to random-x regression: Bias-variance decompositions, covariance penalties, and prediction error estimation. J. Am. Stat. Assoc. 2018, 115, 138–151. [Google Scholar] [CrossRef]
- Kleywegt, A.J.; Shapiro, A.; Homem-de-Mello, T. The sample average approximation method for stochastic discrete optimization. SIAM J. Optim. 2002, 12, 479–502. [Google Scholar] [CrossRef]
- Qi, M.; Cao, Y.; Shen, Z.J. Distributionally robust conditional quantile prediction with fixed-design. Manag. Sci. 2022, 68, 1639–1658. [Google Scholar] [CrossRef]
- Scarf, H.E. Studies in the mathematical theory of inventory and production. In A Min–Max Solution of an Inventory Problem; Arrow, K.J., Karlin, S., Scarf, H.E., Eds.; Stanford University Press: Stanford, CA, USA, 1958; pp. 201–209. Available online: https://www.rand.org/pubs/papers/P910.html (accessed on 28 February 2025).
- Delage, E.; Ye, Y. Distributionally robust optimization under moment uncertainty with application to data-driven problems. Oper. Res. 2010, 58, 595–612. [Google Scholar] [CrossRef]
- Zymler, S.; Kuhn, D.; Rustem, B. Distributionally robust joint chance constraints with second-order moment information. Math. Program. 2013, 137, 167–198. [Google Scholar] [CrossRef]
- Wiesemann, W.; Kuhn, D.; Sim, M. Distributionally robust convex optimization. Oper. Res. 2014, 62, 1358–1376. [Google Scholar] [CrossRef]
- Popescu, I. A semidefinite programming approach to optimal-moment bounds for convex classes of distributions. Math. Oper. Res. 2005, 30, 632–657. [Google Scholar] [CrossRef]
- Van Parys, B.P.; Goulart, P.J.; Kuhn, D. Generalized gauss inequalities via semidefinite programming. Math. Program. 2015, 156, 271–302. [Google Scholar] [CrossRef]
- Natarajan, K.; Song, M.; Teo, C.P. Persistency problem and its applications in choice probleming. Manag. Sci. 2009, 55, 453–469. [Google Scholar] [CrossRef]
- Agrawal, S.; Ding, Y.; Saberi, A.; Ye, Y. Price of correlations in stochastic optimization. Oper. Res. 2012, 60, 150–162. [Google Scholar] [CrossRef]
- Hu, Z.; Hong, L.J. Kullback-Leibler Divergence Constrained Distributionally Robust Optimization. 2012. Available online: https://optimization-online.org/?p=12225 (accessed on 23 November 2012).
- Ben-Tal, A.; den Hertog, D.; De Waegenaere, A.; Melenberg, B.; Rennen, G. Robust solutions of optimization problems affected by uncertain probabilities. Manag. Sci. 2013, 59, 341–357. [Google Scholar] [CrossRef]
- Bayraksan, G.; Love, D.K. Data-driven stochastic programming using phi-divergences. INFORMS TutORials Oper. Res. 2015, 11, 1–19. [Google Scholar] [CrossRef]
- Kuhn, D.; Esfahani, P.M.; Nguyen, V.A.; Shafieezadeh-Abadeh, S. Wasserstein distributionally robust optimization: Theory and applications in machine learning. INFORMS TutORials Oper. Res. 2019, 15, 130–166. [Google Scholar] [CrossRef]
- Blanchet, J.; Murthy, K. Quantifying distributional problem risk via optimal transport. Math. Oper. Res. 2019, 44, 565–600. [Google Scholar] [CrossRef]
- Gao, R.; Kleywegt, A. Distributionally robust stochastic optimization with Wasserstein distance. Math. Oper. Res. 2022, 48, 603–655. [Google Scholar] [CrossRef]
- Staib, M.; Jegelka, S. Distributionally robust optimization and generalization in kernel methods. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 819, pp. 9134–9144. [Google Scholar] [CrossRef]
- Sinkhorn, R. A relationship between arbitrary positive matrices and doubly stochastic matrices. Ann. Math. Stat. 1964, 35, 876–879. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS’13), New York, NY, USA, 5–10 December 2013; Volume 2, pp. 2292–2300. [Google Scholar] [CrossRef]
- Wang, J.; Gao, R.; Xie, Y. Sinkhorn Distributionally Robust Optimization. 2021. Available online: https://arxiv.org/abs/2109.11926 (accessed on 26 March 2025).
- Azizian, W.; Iutzeler, F.; Malick, J. Regularization for wasserstein distributionally robust optimization. ESAIM Control Optim. Calc. Var. 2023, 29, 29–33. [Google Scholar] [CrossRef]
- Courty, N.; Flamary, R.; Tuia, D. Domain adaptation with regularized optimal transport. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Nancy, France, 15–19 September 2014; Volume 8724, pp. 274–289. [Google Scholar] [CrossRef]
- Courty, N.; Flamary, R.; Tuia, D.; Rakotomamonjy, A. Optimal transport for domain adaptation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1853–1865. [Google Scholar] [CrossRef] [PubMed]
- Luise, G.; Rudi, A.; Pontil, M.; Ciliberto, C. Differential properties of sinkhorn approximation for learning with wasserstein distance. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 2–8 December 2018; Volume 31, pp. 5864–5874. [Google Scholar] [CrossRef]
- Patrini, G.; Van den Berg, R.; Forre, P.; Carioni, M.; Bhargav, S.; Welling, M.; Genewein, T.; Nielsen, F. Sinkhorn Autoencoders. In Proceedings of the 35th Uncertainty in Artificial Intelligence Conference, Tel Aviv, Israel, 22–25 July 2019; Volume 115, pp. 733–743. [Google Scholar]
- Lin, T.; Fan, C.; Ho, N.; Cuturi, M.; Jordan, M. Projection robust wasserstein distance and riemannian optimization. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; Volume 787, pp. 9383–9397. [Google Scholar] [CrossRef]
- Wang, J.; Gao, R.; Xie, Y. Two-sample test using projected wasserstein distance. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Melbourne, Australia, 12–20 July 2021; pp. 3320–3325. [Google Scholar] [CrossRef]
- Wang, J.; Gao, R.; Xie, Y. Two-sample test with kernel projected wasserstein distance. In Proceedings of the 25th International Conference on Artificial Intelligence and Statistics, 28–30 March 2022; Volume 151, pp. 3315–3320. [Google Scholar]
- Hu, Y.; Chen, X.; He, N. Sample complexity of sample average approximation for conditional stochastic optimization. SIAM J. Optim. 2023, 30, 2103–2133. [Google Scholar] [CrossRef]
- Cheng, B.; Xie, X. Distributionally Robust Conditional Quantile Prediction with Wasserstein Ball. JUSTC 2023, accepted. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 25–54. [Google Scholar]
- Joseph, T.C.; David, P. Conditioning as disintegration. Stat. Neerl. 1997, 51, 287–317. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, Y.; Lu, Z. A Stochastic Algorithm for Sinkhorn Distance-Regularized Distributionally Robust Optimization. In Proceedings of the OPT2024: 16th Annual Workshop on Optimization for Machine Learning, Vancouver, BC, Canada, 15 December 2024. [Google Scholar]
- Grant, M.; Boyd, S. CVX:Matlab Software for Disciplined Convex Programming. Available online: https://cvxr.com/cvx/ (accessed on 1 January 2020).
- Catoni, O. Challenging the empirical mean and empirical variance: A deviation study. Ann. l’IHP Probab. Stat. 2012, 48, 1148–1185. [Google Scholar] [CrossRef]
- Xu, L.; Yao, F.; Yao, Q.; Zhang, H. Non-asymptotic guarantees for robust statistical learning under infinite variance assumption. J. Mach. Learn. Res. 2023, 24, 1–46. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, S.; Yang, S.; Zhang, C.; Jin, R.; Yang, T. Learning with non-convex truncated losses by SGD. In Proceedings of the Thirty-Fifth Conference on Uncertainty in Artificial Intelligence (UAI 2019), Tel Aviv, Israel, 22–25 July; Volume 115, pp. 701–711. [CrossRef]
- Furer, D.; Kohler, M.; Krzyżak, A. Fixed-design regression estimation based on real and artificial data. J. Nonparametr. Stat. 2013, 25, 223–241. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/dataset/560/seoul+bike+sharing+demand (accessed on 29 February 2020).

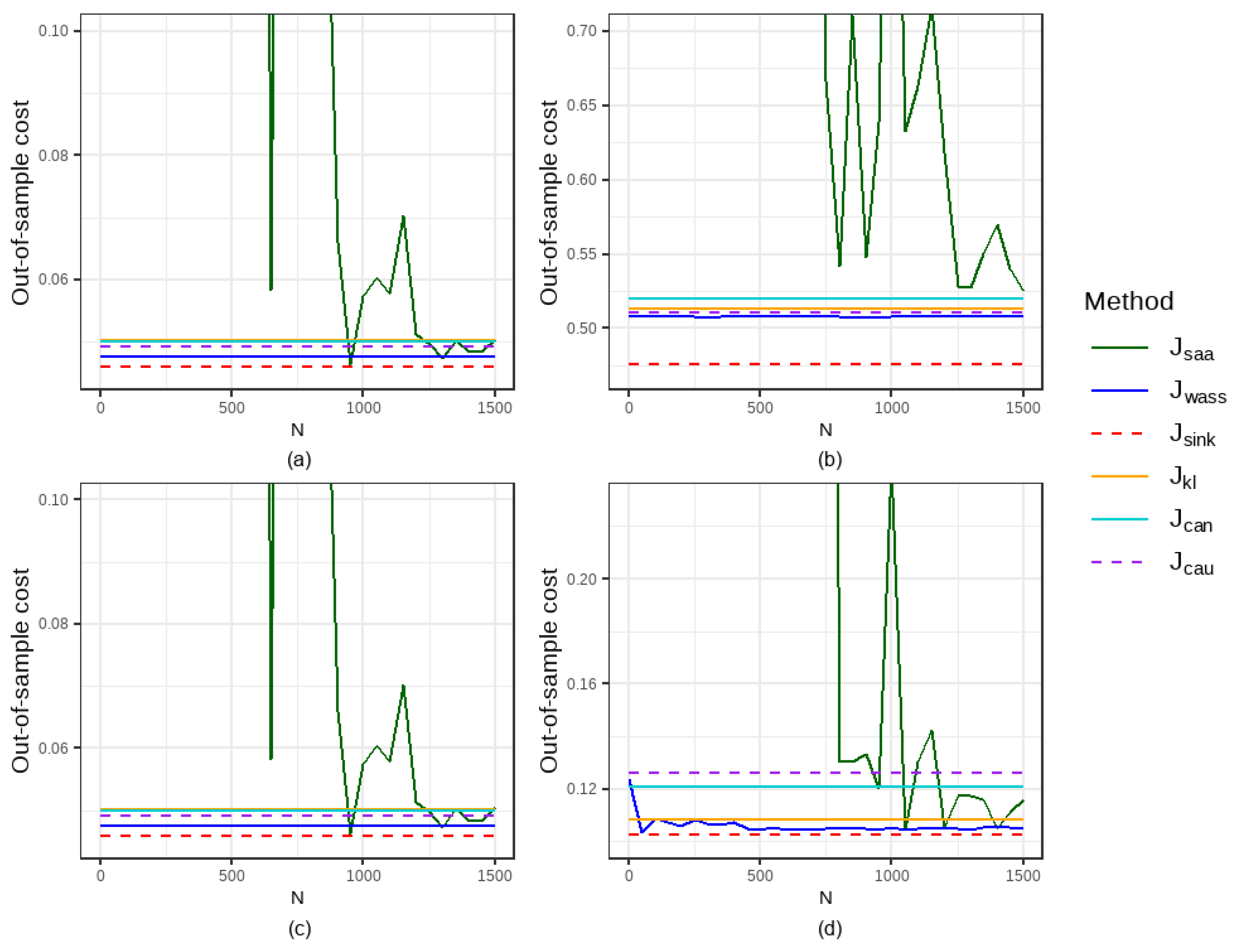
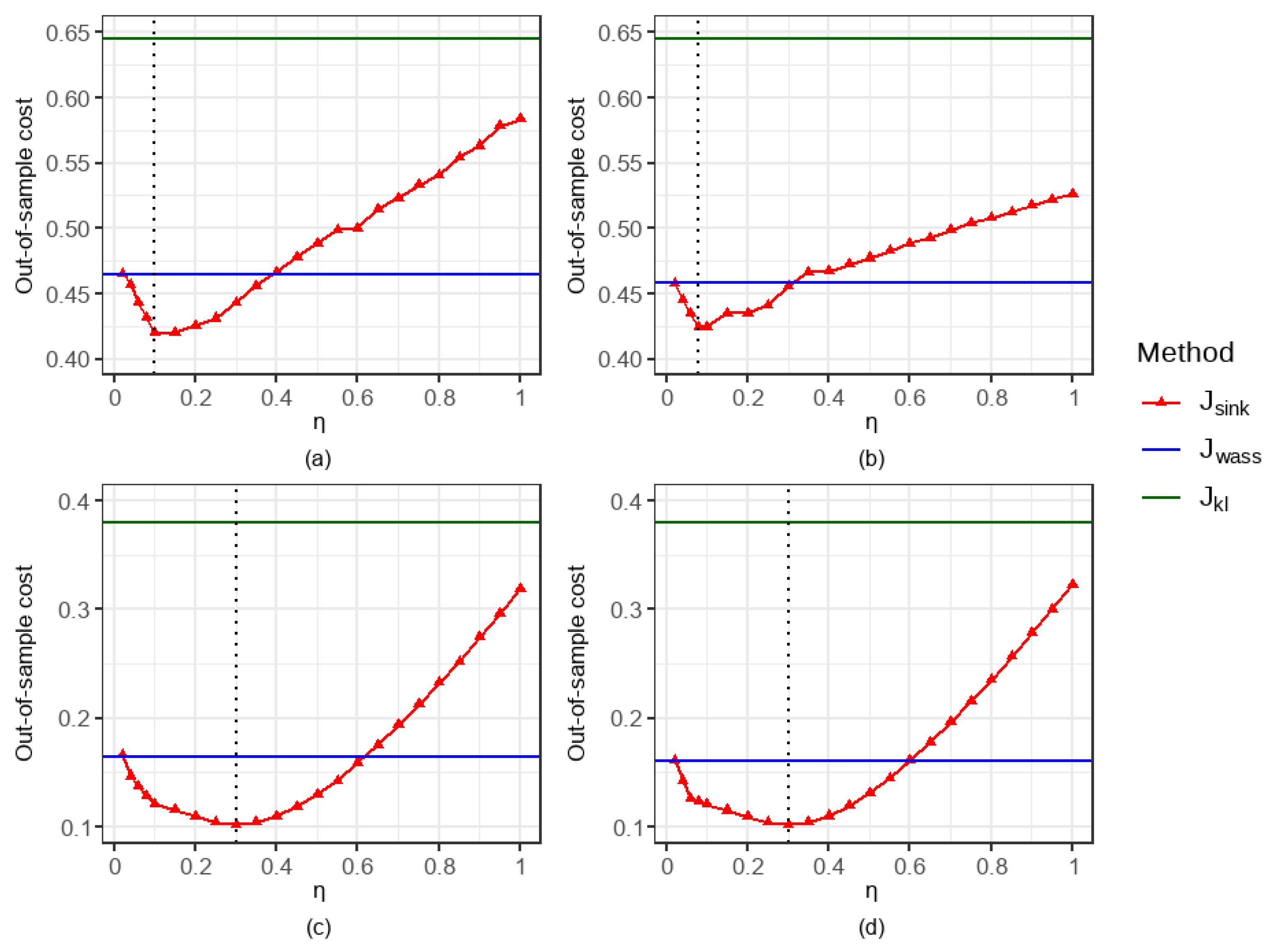
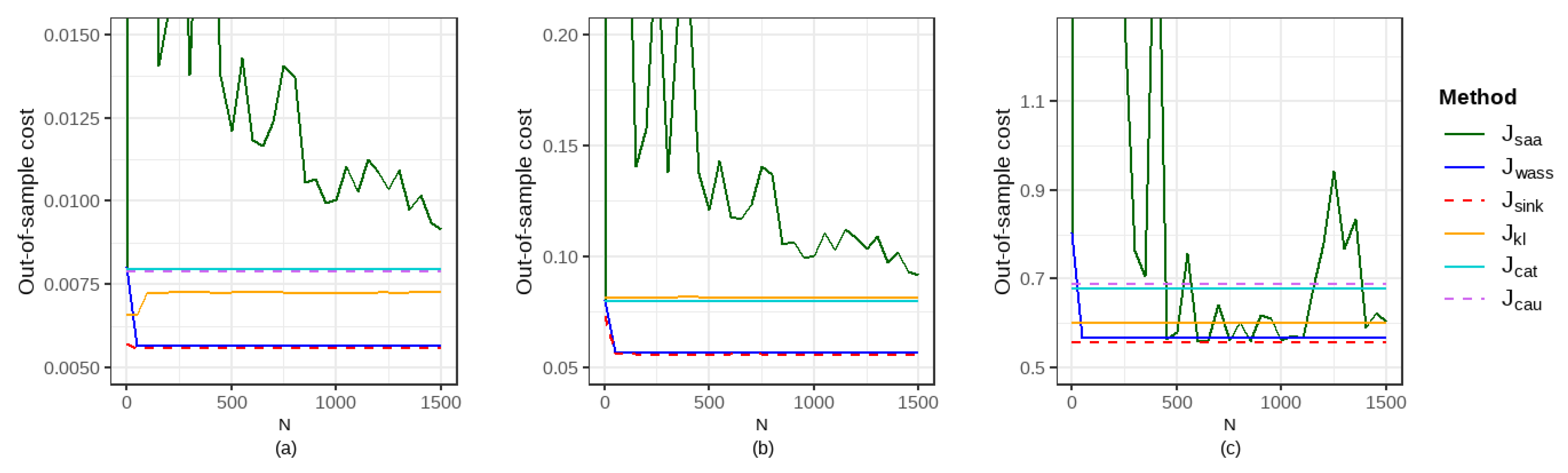

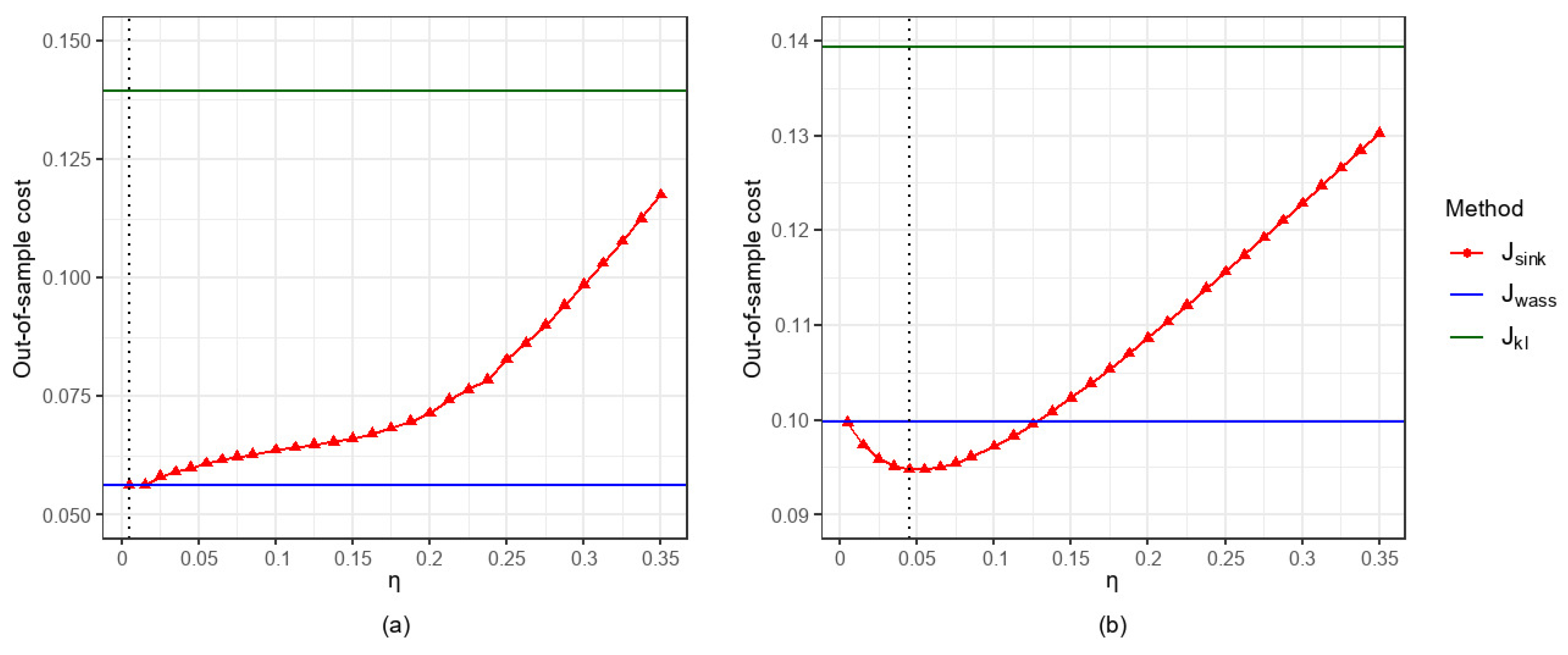
| Noise | N | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| t(2) | 0.2 | 100 | 7.78e+04 | 0.630 | 0.612 | 0.574 (−99.99%) | 0.574 (−99.99%) | 0.559 (−99.99%) | 0.559 (−99.99%) | 0.603 (−99.99%) |
| 800 | 1.060 | 0.630 | 0.612 | 0.587 (−44.63%) | 0.586 (−44.68%) | 0.564 (−46.76%) | 0.559 (−47.31%) | 0.603 (−43.12%) | ||
| 1500 | 0.664 | 0.630 | 0.612 | 0.587 (−11.61%) | 0.581 (−12.55%) | 0.564 (−14.99%) | 0.559 (−15.87%) | 0.603 (−9.18%) | ||
| 0.7 | 100 | 1.75e+04 | 0.688 | 0.660 | 0.667 (−99.99%) | 0.657 (−99.99%) | 0.648 (−99.99%) | 0.635 (−99.99%) | 0.676 (−99.99%) | |
| 800 | 3.842 | 0.688 | 0.660 | 0.664 (−82.71%) | 0.661 (−82.80%) | 0.648 (−83.14%) | 0.635 (−83.48%) | 0.676 (−82.41%) | ||
| 1500 | 0.680 | 0.688 | 0.660 | 0.665 (−2.23%) | 0.659 (−3.14%) | 0.648 (−4.75%) | 0.635 (−6.65%) | 0.676 (−0.62%) | ||
| t(5) | 0.2 | 100 | 8.50e+03 | 0.389 | 0.384 | 0.363 (−99.99%) | 0.371 (−99.99%) | 0.348 (−99.99%) | 0.348 (−99.99%) | 0.362 (−99.99%) |
| 800 | 8.755 | 0.389 | 0.384 | 0.353 (−95.97%) | 0.355 (−95.94%) | 0.348 (−96.03%) | 0.348 (−96.03%) | 0.362 (−95.86%) | ||
| 1500 | 0.364 | 0.389 | 0.384 | 0.351 (−3.42%) | 0.358 (−1.53%) | 0.348 (−4.40%) | 0.348 (−4.40%) | 0.362 (−0.42%) | ||
| 0.7 | 100 | 2.86e+03 | 0.433 | 0.425 | 0.428 (−99.99%) | 0.423 (−99.99%) | 0.418 (−99.99%) | 0.418 (−99.99%) | 0.427 (−99.99%) | |
| 800 | 6.885 | 0.433 | 0.425 | 0.421 (−93.88%) | 0.422 (−93.87%) | 0.418 (−93.93%) | 0.418 (−93.93%) | 0.427 (−93.79%) | ||
| 1500 | 0.436 | 0.433 | 0.425 | 0.421 (−3.59%) | 0.424 (−2.94%) | 0.418 (−4.33%) | 0.418 (−4.31%) | 0.427 (−2.09%) | ||
| P(2,1) | 0.2 | 100 | 2.16e+03 | 0.196 | 0.194 | 0.193 (−99.99%) | 0.193 (−99.99%) | 0.183 (−99.99%) | 0.183 (−99.99%) | 0.194 (−99.99%) |
| 800 | 0.673 | 0.196 | 0.194 | 0.193 (−71.38%) | 0.193 (−71.38%) | 0.183 (−72.82%) | 0.183 (−72.82%) | 0.194 (−71.11%) | ||
| 1500 | 0.194 | 0.196 | 0.194 | 0.193 (−0.97%) | 0.193 (−0.97%) | 0.183 (−5.95%) | 0.183 (−5.95%) | 0.194 (−0.01%) | ||
| 0.7 | 100 | 4.38e+04 | 0.519 | 0.511 | 0.508 (−99.99%) | 0.508 (−99.99%) | 0.476 (−99.99%) | 0.476 (−99.99%) | 0.513 (−99.99%) | |
| 800 | 0.542 | 0.519 | 0.511 | 0.508 (−6.32%) | 0.508 (−6.31%) | 0.476 (−12.20%) | 0.476 (−12.20%) | 0.513 (−5.33%) | ||
| 1500 | 0.525 | 0.519 | 0.511 | 0.508 (−3.33%) | 0.508 (−3.31%) | 0.476 (−9.40%) | 0.476 (−9.40%) | 0.513 (−2.30%) | ||
| P(5,1) | 0.2 | 100 | 1.06e+03 | 0.050 | 0.049 | 0.047 (−99.99%) | 0.049 (−99.99%) | 0.046 (−99.99%) | 0.046 (−99.99%) | 0.050 (−99.99%) |
| 800 | 0.225 | 0.050 | 0.049 | 0.047 (−78.85%) | 0.049 (−78.28%) | 0.046 (−79.56%) | 0.046 (−79.56%) | 0.050 (−77.66%) | ||
| 1500 | 0.050 | 0.050 | 0.049 | 0.047 (−5.89%) | 0.049 (−3.36%) | 0.046 (−9.04%) | 0.046 (−9.04%) | 0.050 (−0.57%) | ||
| 0.7 | 100 | 1.43e+03 | 0.121 | 0.126 | 0.107 (−99.99%) | 0.109 (−99.99%) | 0.102 (−99.99%) | 0.102 (−99.99%) | 0.108 (−99.99%) | |
| 800 | 0.130 | 0.121 | 0.126 | 0.107 (−17.92%) | 0.105 (−19.66%) | 0.102 (−21.46%) | 0.102 (−21.53%) | 0.108 (−16.95%) | ||
| 1500 | 0.116 | 0.121 | 0.126 | 0.107 (−7.60%) | 0.105 (−9.62%) | 0.102 (−11.58%) | 0.102 (−11.67%) | 0.108 (−6.51%) |
| Noise | SAA | CAT | CAU | 1-WDRO | 2-WDRO | 1-SDRO | 2-SDRO | KL-DRO | |
|---|---|---|---|---|---|---|---|---|---|
| t(2) | 0.2 | 2.11e+02 | 3.35e+02 | 5.39e+02 | 1.80e+02 | 1.05e+02 | 4.76e+00 | 3.23e+00 | 1.90e-01 |
| 0.7 | 2.48e+02 | 3.17e+02 | 2.27e+02 | 1.53e+02 | 9.85e+01 | 5.39e+00 | 2.14e+00 | 2.00e-01 | |
| t(5) | 0.2 | 4.18e+02 | 3.40e+02 | 5.13e+02 | 9.43e+01 | 8.89e+01 | 4.58e+00 | 2.12e+00 | 1.70e-01 |
| 0.7 | 3.90e+02 | 3.35e+02 | 4.00e+02 | 9.96e+01 | 9.18e+01 | 4.75e+00 | 2.59e+00 | 1.90e-01 | |
| P(2,1) | 0.2 | 3.26e+02 | 2.91e+02 | 3.16e+02 | 1.29e+02 | 1.38e+02 | 5.08e+00 | 3.17e+00 | 1.50e-01 |
| 0.7 | 3.81e+02 | 1.99e+02 | 2.44e+02 | 9.82e+01 | 1.01e+02 | 4.34e+00 | 1.95e+00 | 2.00e-01 | |
| P(5,1) | 0.2 | 2.88e+02 | 3.38e+02 | 5.05e+02 | 9.67e+01 | 1.03e+02 | 6.62e+00 | 2.37e+00 | 1.50e-01 |
| 0.7 | 3.62e+02 | 3.62e+02 | 3.44e+02 | 8.92e+01 | 9.19e+01 | 5.85e+00 | 3.97e+00 | 1.70e-01 |
| Feature | Type | Value Range | Unit |
|---|---|---|---|
| Temperature | Numeric | (−17.8, 39.4) | °C |
| Humidity | Numeric | (0, 98) | % |
| Wind speed | Numeric | (0, 7.4) | m/s |
| Visibility | Numeric | (270, 20000) | m |
| Dew point temperature | Numeric | (−30.6, 27.2) | °C |
| Solar radiation | Numeric | (0, 3.52) | MJ/m2 |
| Rainfall | Numeric | (0, 35) | mm |
| N | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.02 | 0.2 | 100 | 0.031 | 0.008 | 0.008 | 0.006 (−81.91%) | 0.006 (−81.91%) | 0.006 (−82.13%) | 0.006 (−82.12%) | 0.007 (−76.73%) |
| 550 | 0.014 | 0.008 | 0.008 | 0.006 (−60.53%) | 0.006 (−60.53%) | 0.006 (−60.99%) | 0.006 (−60.97%) | 0.007 (−49.20%) | ||
| 1500 | 0.009 | 0.008 | 0.008 | 0.006 (−38.39%) | 0.006 (−38.39%) | 0.006 (−39.11%) | 0.006 (−39.07%) | 0.007 (−20.71%) | ||
| 0.7 | 100 | 0.041 | 0.008 | 0.008 | 0.007 (−83.03%) | 0.007 (−83.03%) | 0.007 (−83.26%) | 0.007 (−83.26%) | 0.007 (−81.91%) | |
| 550 | 0.007 | 0.008 | 0.008 | 0.007 (0.41%) | 0.007 (0.41%) | 0.007 (−0.59%) | 0.007 (−0.43%) | 0.007 (7.45%) | ||
| 1500 | 0.008 | 0.008 | 0.008 | 0.007 (−7.97%) | 0.007 (−7.97%) | 0.007 (−8.77%) | 0.007 (−8.73%) | 0.007 (−1.40%) | ||
| 0.2 | 0.2 | 100 | 0.312 | 0.080 | 0.080 | 0.057 (−81.85%) | 0.073 (−76.72%) | 0.057 (−81.92%) | 0.058 (−81.57%) | 0.082 (−73.89%) |
| 550 | 0.143 | 0.080 | 0.080 | 0.057 (−60.39%) | 0.075 (−47.31%) | 0.056 (−60.93%) | 0.058 (−59.76%) | 0.082 (−32.75%) | ||
| 1500 | 0.092 | 0.080 | 0.080 | 0.057 (−38.18%) | 0.071 (−22.19%) | 0.056 (−39.04%) | 0.058 (−37.18%) | 0.082 (−18.73%) | ||
| 0.7 | 100 | 0.385 | 0.080 | 0.080 | 0.071 (−81.67%) | 0.090 (−76.71%) | 0.070 (−82.00%) | 0.070 (−81.97%) | 0.089 (−76.97%) | |
| 550 | 0.178 | 0.080 | 0.080 | 0.071 (−60.20%) | 0.081 (−54.40%) | 0.070 (−60.87%) | 0.070 (−60.81%) | 0.089 (−49.93%) | ||
| 1500 | 0.097 | 0.080 | 0.080 | 0.070 (−27.51%) | 0.081 (−16.63%) | 0.070 (−28.61%) | 0.070 (−28.49%) | 0.089 (−8.65%) | ||
| 2 | 0.2 | 100 | 1.715 | 0.677 | 0.687 | 0.567 (−66.94%) | 0.565 (−67.08%) | 0.558 (−67.48%) | 0.558 (−67.48%) | 0.601 (−64.93%) |
| 550 | 0.758 | 0.677 | 0.687 | 0.567 (−25.19%) | 0.568 (−25.04%) | 0.558 (−26.38%) | 0.558 (−26.35%) | 0.601 (−20.65%) | ||
| 1500 | 0.603 | 0.677 | 0.687 | 0.567 (−6.01%) | 0.567 (−5.97%) | 0.558 (−7.48%) | 0.558 (−7.48%) | 0.601 (−0.27%) | ||
| 0.7 | 100 | 4.153 | 0.696 | 0.696 | 0.704 (−83.06%) | 0.707 (−82.98%) | 0.695 (−83.27%) | 0.694 (−83.29%) | 0.745 (−82.06%) | |
| 550 | 1.663 | 0.696 | 0.696 | 0.701 (−57.85%) | 0.705 (−57.61%) | 0.693 (−58.30%) | 0.694 (−58.26%) | 0.745 (−55.19%) | ||
| 1500 | 0.857 | 0.696 | 0.696 | 0.700 (−18.27%) | 0.702 (−18.04%) | 0.694 (−18.98%) | 0.694 (−18.98%) | 0.745 (−13.01%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, G.; Mao, T. Sinkhorn Distributionally Robust Conditional Quantile Prediction with Fixed Design. Entropy 2025, 27, 557. https://doi.org/10.3390/e27060557
Jiang G, Mao T. Sinkhorn Distributionally Robust Conditional Quantile Prediction with Fixed Design. Entropy. 2025; 27(6):557. https://doi.org/10.3390/e27060557
Chicago/Turabian StyleJiang, Guohui, and Tiantian Mao. 2025. "Sinkhorn Distributionally Robust Conditional Quantile Prediction with Fixed Design" Entropy 27, no. 6: 557. https://doi.org/10.3390/e27060557
APA StyleJiang, G., & Mao, T. (2025). Sinkhorn Distributionally Robust Conditional Quantile Prediction with Fixed Design. Entropy, 27(6), 557. https://doi.org/10.3390/e27060557




