Artificial Intelligence Models for Predicting Stock Returns Using Fundamental, Technical, and Entropy-Based Strategies: A Semantic-Augmented Hybrid Approach
Abstract
1. Introduction
2. Literature Review
2.1. AI in Technical Analysis
2.2. AI in Fundamental Analysis
2.3. Sentiment Analysis and NLP Applications
2.4. Fuzzy and Entropy-Based Approaches
2.5. Comparative and Hybrid Modeling
3. Methodology—LLM-Created Scoring Framework
3.1. LLM-Constructed Fundamental Strategy—Learning from Financial Performance Signals
3.2. LLM-Constructed Technical Strategy—Learning from Price Behavior and Return Patterns
3.3. LLM-Constructed Entropy Strategy—Approximating Predictability via Volatility-Based Models
3.4. Construction of Algorithmic Scores and Hybrid Portfolio Optimization
4. Results
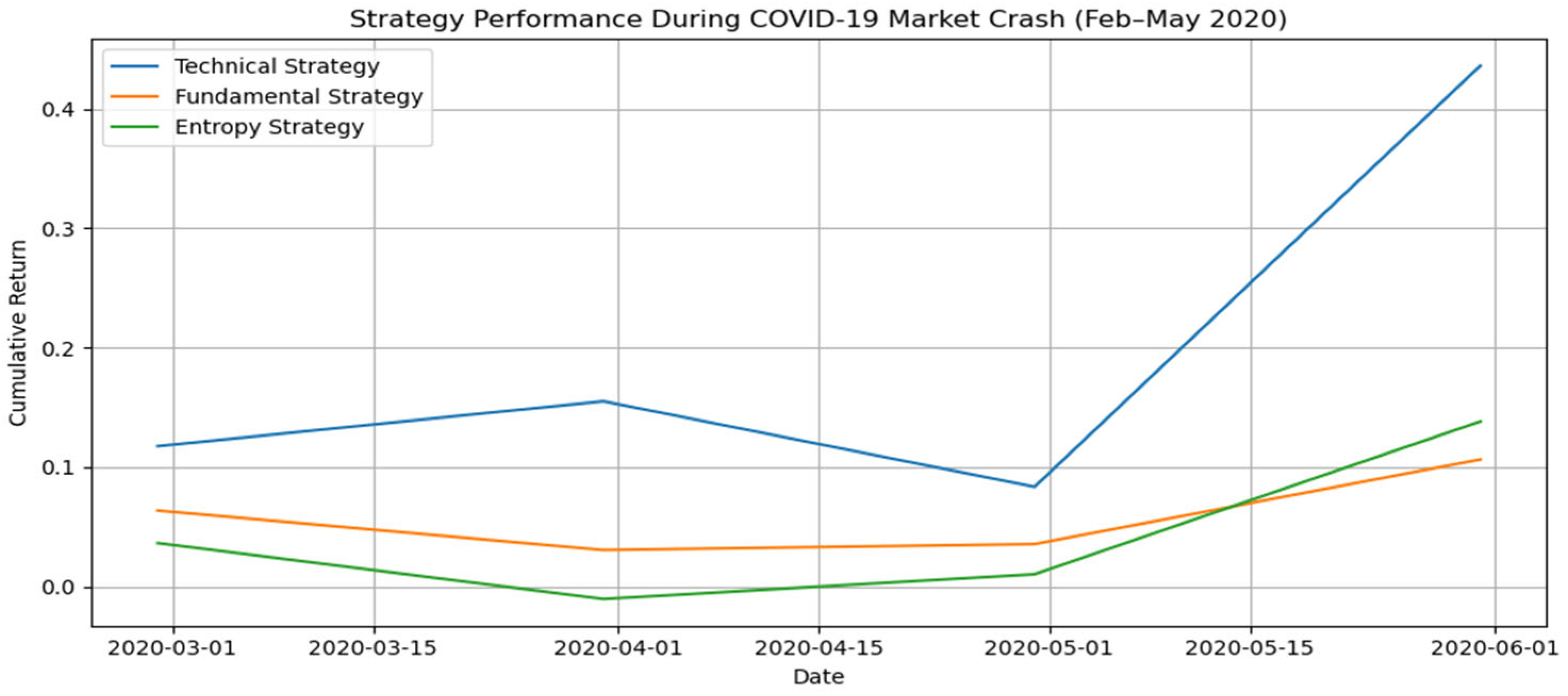
4.1. Performance Under Market Stress: COVID-19 Crash Analysis
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Dey, A. Machine Learning Algorithms: A Review. Int. J. Sci. Res. (IJSR) 2022, 11, 1127–1133. [Google Scholar]
- Kramer, B.; Stang, M.; Doskoc, V.; Schäfers, W.; Friedrich, T. Automated valuation models: Improving model performance by choosing the optimal spatial training level. J. Prop. Res. 2023, 40, 365–390. [Google Scholar] [CrossRef]
- Shi, M.; Zhao, Q. Stock Market Trend Prediction and Investment Strategy by Deep Neural Networks. In Proceedings of the 2020 11th International Conference on Awareness Science and Technology (iCAST), Qingdao, China, 7–9 December 2020; pp. 1–6. [Google Scholar]
- Mokhtari, S.; Kang, K.; Yen, L.J. Effectiveness of artificial intelligence in stock market prediction based on machine learning. Int. J. Comput. Appl. 2021, 183, 1–8. [Google Scholar] [CrossRef]
- Agusta, S.; Rakhman, F.; Mustakini, J.; Wijayana, S. Enhancing the accuracy of stock return movement prediction in Indonesia through recent fundamental value incorporation in multilayer perceptron. Asian J. Account. Res. 2024, 9, 358–377. [Google Scholar] [CrossRef]
- Zhou, Q.; Faff, R. The complementary role of cross-sectional and time-series information in forecasting stock returns. Aust. J. Manag. 2016, 42, 113–139. [Google Scholar] [CrossRef]
- Dawson, E.; Steeley, J. On the existence of visual technical patterns in the UK stock market. J. Bus. Financ. Account. 2003, 30, 263–293. [Google Scholar] [CrossRef]
- Hurriyati, R.; Ana, A.; Sulastri, S.; Lisnawati, L.; Sawangsang, T. Stock market trend analysis and machine learning-based predictive evaluation. J. Wirel. Mob. Netw. Ubiquitous Comput. Dependable Appl. 2023, 14, 267–281. [Google Scholar] [CrossRef]
- Alizadeh, M.; Rada, R.; Jolai, F.; Fotoohi, E. An adaptive neuro-fuzzy system for stock portfolio analysis. Int. J. Intell. Syst. 2010, 26, 99–114. [Google Scholar] [CrossRef]
- Ayyildiz, N.; Iskenderoglu, O. How effective is machine learning in stock market predictions? Heliyon 2024, 10, e24123. [Google Scholar] [CrossRef]
- Souza, M.; Ramos, D.; Pena, M.; Sobreiro, V.; Kimura, H. Examination of the profitability of technical analysis based on moving average strategies in BRICS. Financ. Innov. 2018, 4, 3. [Google Scholar] [CrossRef]
- Neely, C.; Weller, P.; Dittmar, R. Is technical analysis in the foreign exchange market profitable? A genetic programming approach. J. Financ. Quant. Anal. 1997, 32, 405. [Google Scholar] [CrossRef]
- Yoo, P.; Kim, M.; Jan, T. Machine learning techniques and use of event information for stock market prediction: A survey and evaluation. In Proceedings of the International Conference (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; pp. 835–841. [Google Scholar]
- Abraham, R.; Samad, M.; Bakhach, A.; El-Chaarani, H.; Sardouk, A.; Nemar, S.; Jaber, D. Forecasting a stock trend using genetic algorithm and random forest. J. Risk Financ. Manag. 2022, 15, 188. [Google Scholar] [CrossRef]
- Kabbani, T.; Usta, F.E. Predicting The Stock Trend Using News Sentiment Analysis and Technical Indicators in Spark. arXiv 2022, arXiv:2201.12283. [Google Scholar]
- Liu, P.; Yuan, W.; Fu, J.; Jiang, Z.; Hayashi, H.; Neubig, G. Pre-train, Prompt, and Predict: A Systematic Survey of Prompting Methods in Natural Language Processing. ACM Comput. Surv. 2021, 55, 1–35. [Google Scholar] [CrossRef]
- Yan, F.; Wang, J. Research on Sentiment Analysis of Micro-blog based on Attention-BiLSTM. Front. Comput. Intell. Syst. 2024, 7, 49–51. [Google Scholar] [CrossRef]
- Sufi, F.; Khalil, I. Automated Disaster Monitoring from Social Media Posts Using AI-Based Location Intelligence and Sentiment Analysis. IEEE Trans. Comput. Soc. Syst. 2024, 11, 4614–4624. [Google Scholar] [CrossRef]
- Yang, C.W. Investment strategy via analyst report text mining. J. Deriv. Quant. Stud. 2023, 31, 98–120. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, W. Fractional refined composite multiscale fuzzy entropy of international stock indices. Entropy 2019, 21, 914. [Google Scholar] [CrossRef]
- Zhou, R.; Zhan, Y.; Cai, R.; Tong, G. A mean-variance hybrid-entropy model for portfolio selection with fuzzy returns. Entropy 2015, 17, 3319–3331. [Google Scholar] [CrossRef]
- Ramesh, K.P.; Amudha, R.; Prasob, K.; Francis, J. Robo-advisory: An intrinsic convergence of AI in enhancing investment returns—An empirical analysis. Multidiscip. Sci. J. 2023, 5, 2023ss0321. [Google Scholar] [CrossRef]
- Singh, M. A Quantitative Study of Innovation-Driven Investment and its Performance Management on Corporate Fiscal Returns Using AI. In Proceedings of the 2023 12th International Conference on System Modeling & Advancement in Research Trends (SMART), Moradabad, India, 22–23 December 2023; pp. 380–386. [Google Scholar]
- Zhao, Y. Research on momentum strategy and contrarian strategy in AI stock prediction. Appl. Comput. Eng. 2023, 29, 125–132. [Google Scholar] [CrossRef]
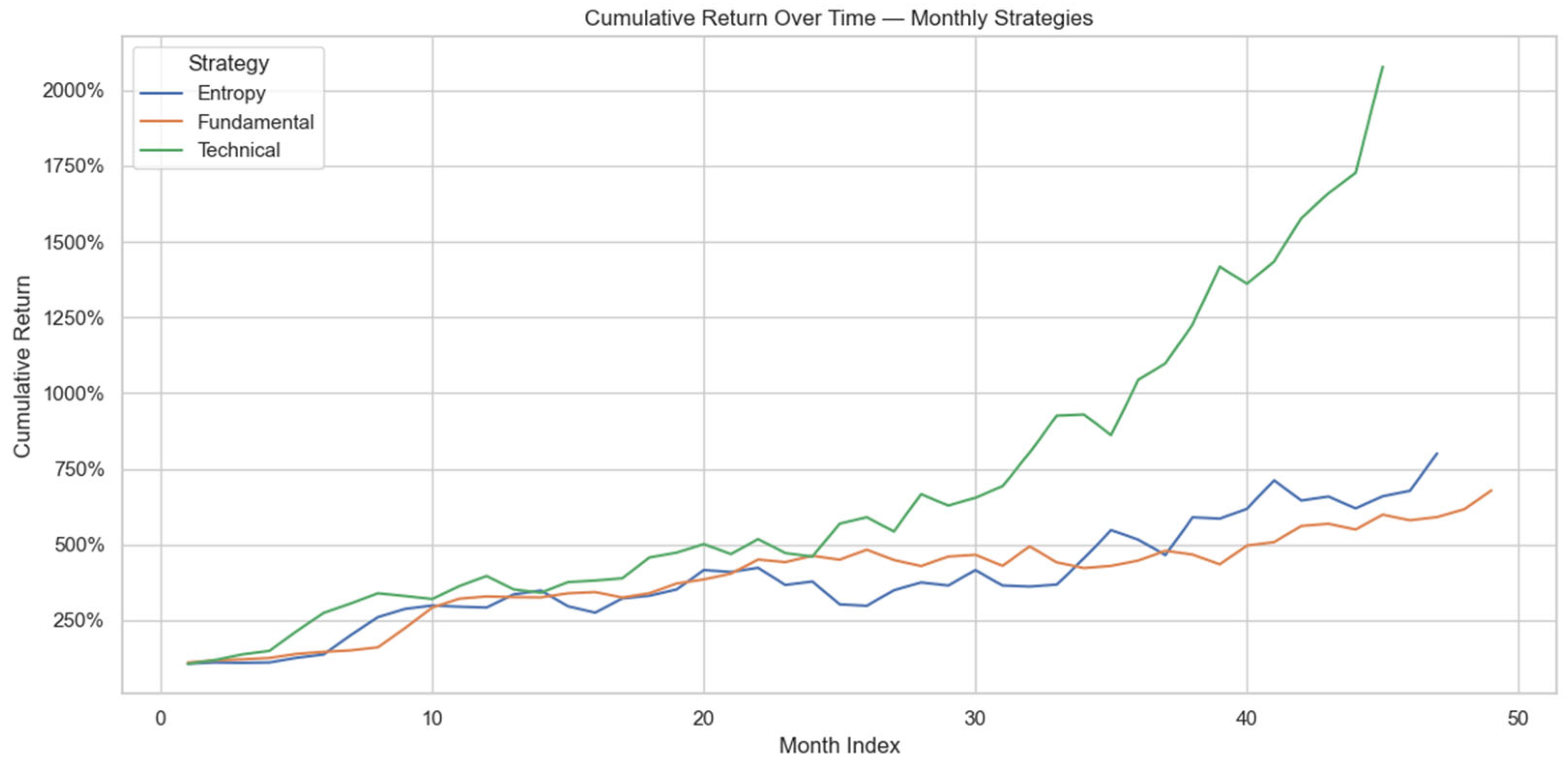


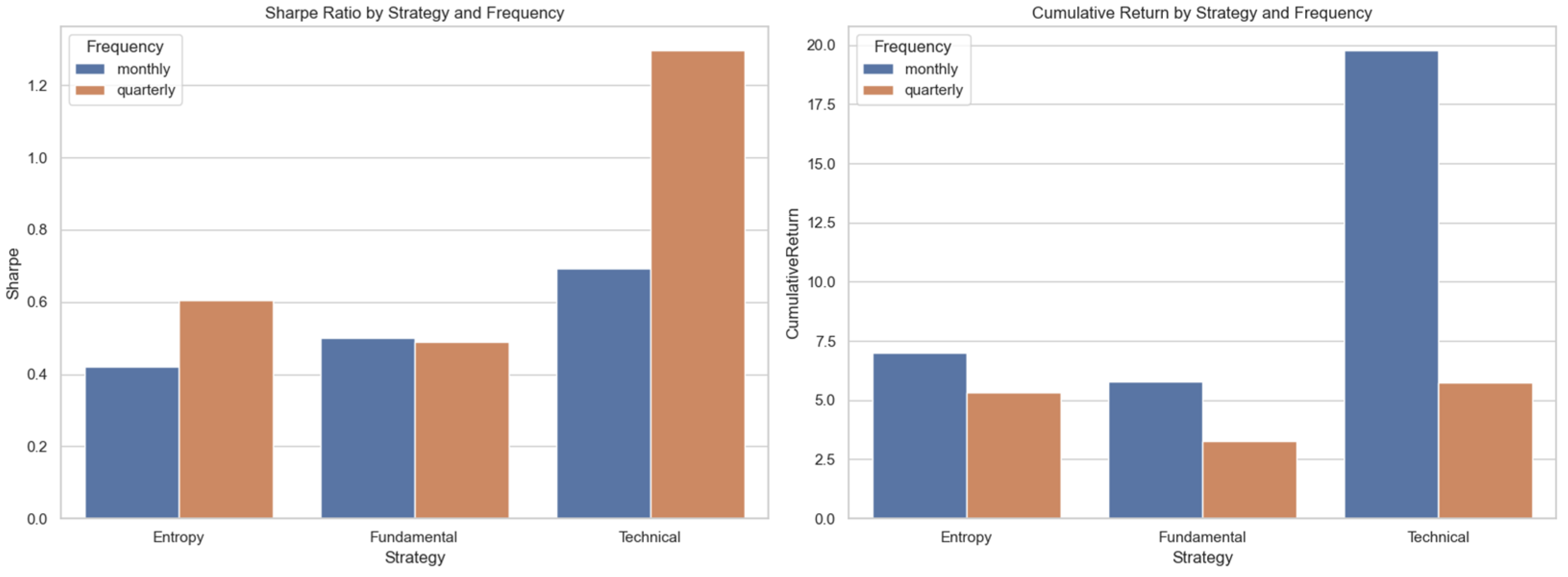
| Strategy | Frequency | ML Weight | Sharpe | Average Return | Volatility | Cumulative Return |
|---|---|---|---|---|---|---|
| Technical | monthly | 1 | 0.6934 | 7.50% | 0.1082 | 1977.71% |
| Entropy | monthly | 0.7 | 0.4207 | 5.23% | 0.1244 | 700.52% |
| Fundamental | monthly | 0.15 | 0.5001 | 4.32% | 0.0863 | 578.40% |
| Technical | quarterly | 0.45 | 1.2967 | 24.99% | 0.1927 | 573.37% |
| Entropy | quarterly | 0.4 | 0.6048 | 20.25% | 0.3348 | 534.36% |
| Fundamental | quarterly | 0 | 0.4899 | 14.71% | 0.3002 | 326.12% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cohen, G.; Aiche, A.; Eichel, R. Artificial Intelligence Models for Predicting Stock Returns Using Fundamental, Technical, and Entropy-Based Strategies: A Semantic-Augmented Hybrid Approach. Entropy 2025, 27, 550. https://doi.org/10.3390/e27060550
Cohen G, Aiche A, Eichel R. Artificial Intelligence Models for Predicting Stock Returns Using Fundamental, Technical, and Entropy-Based Strategies: A Semantic-Augmented Hybrid Approach. Entropy. 2025; 27(6):550. https://doi.org/10.3390/e27060550
Chicago/Turabian StyleCohen, Gil, Avishay Aiche, and Ron Eichel. 2025. "Artificial Intelligence Models for Predicting Stock Returns Using Fundamental, Technical, and Entropy-Based Strategies: A Semantic-Augmented Hybrid Approach" Entropy 27, no. 6: 550. https://doi.org/10.3390/e27060550
APA StyleCohen, G., Aiche, A., & Eichel, R. (2025). Artificial Intelligence Models for Predicting Stock Returns Using Fundamental, Technical, and Entropy-Based Strategies: A Semantic-Augmented Hybrid Approach. Entropy, 27(6), 550. https://doi.org/10.3390/e27060550







