Quantum Exact Response Theory Based on the Dissipation Function
Abstract
1. Introduction
2. Classical and Quantum Response Theory
3. Quantum Dissipation Function for Time-Independent Perturbations
4. Self-Adjoint Quantum Dissipation Operator
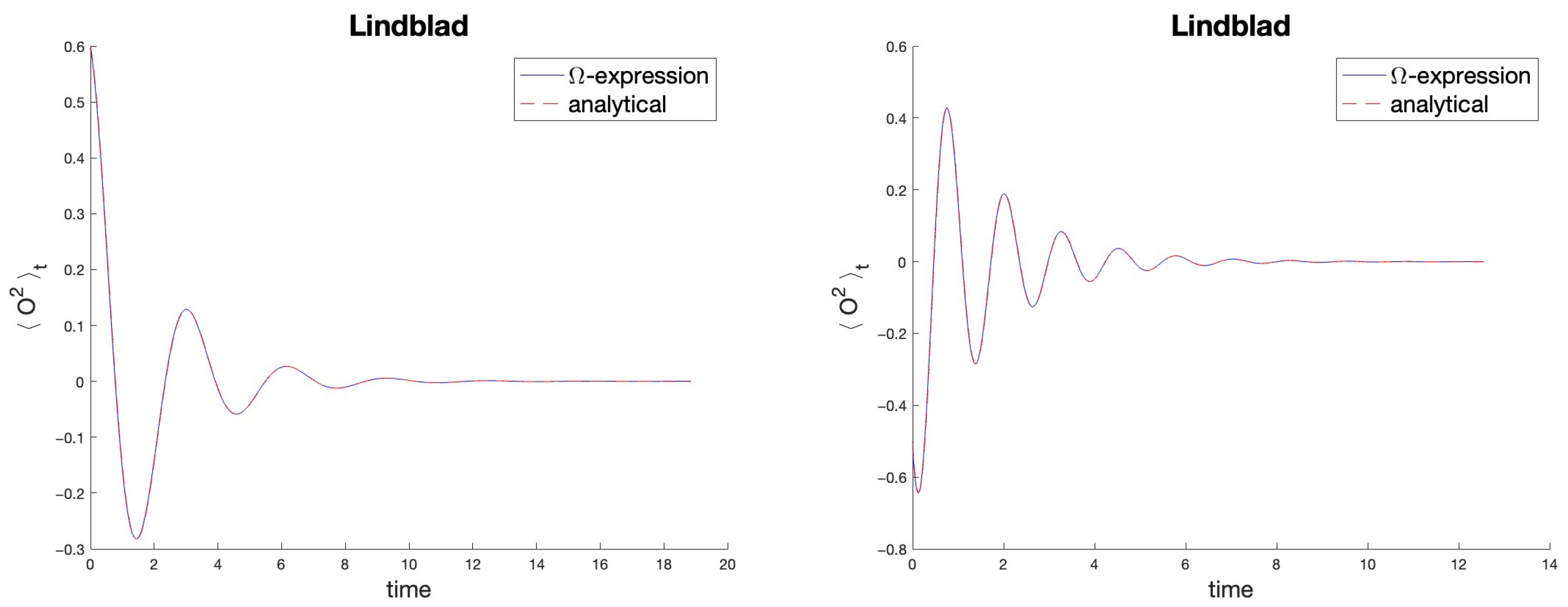
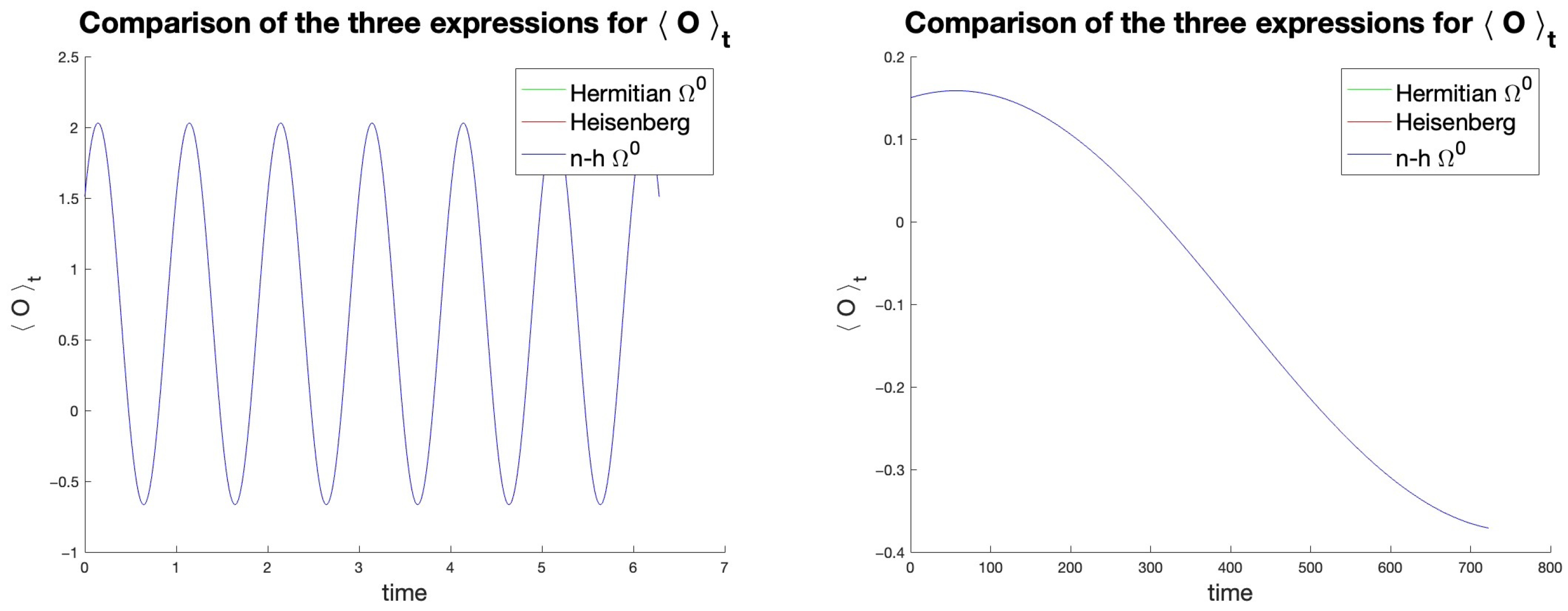
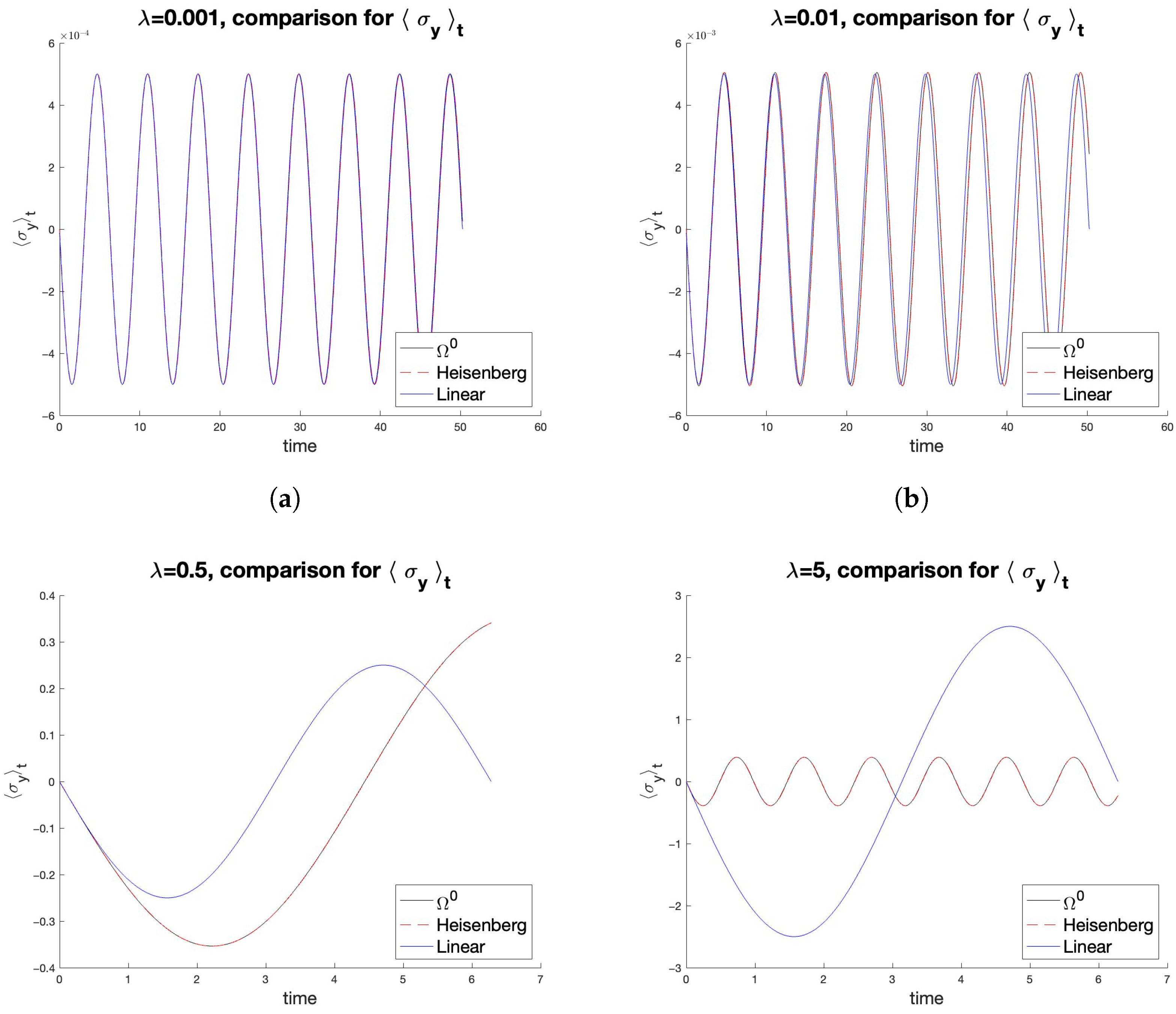
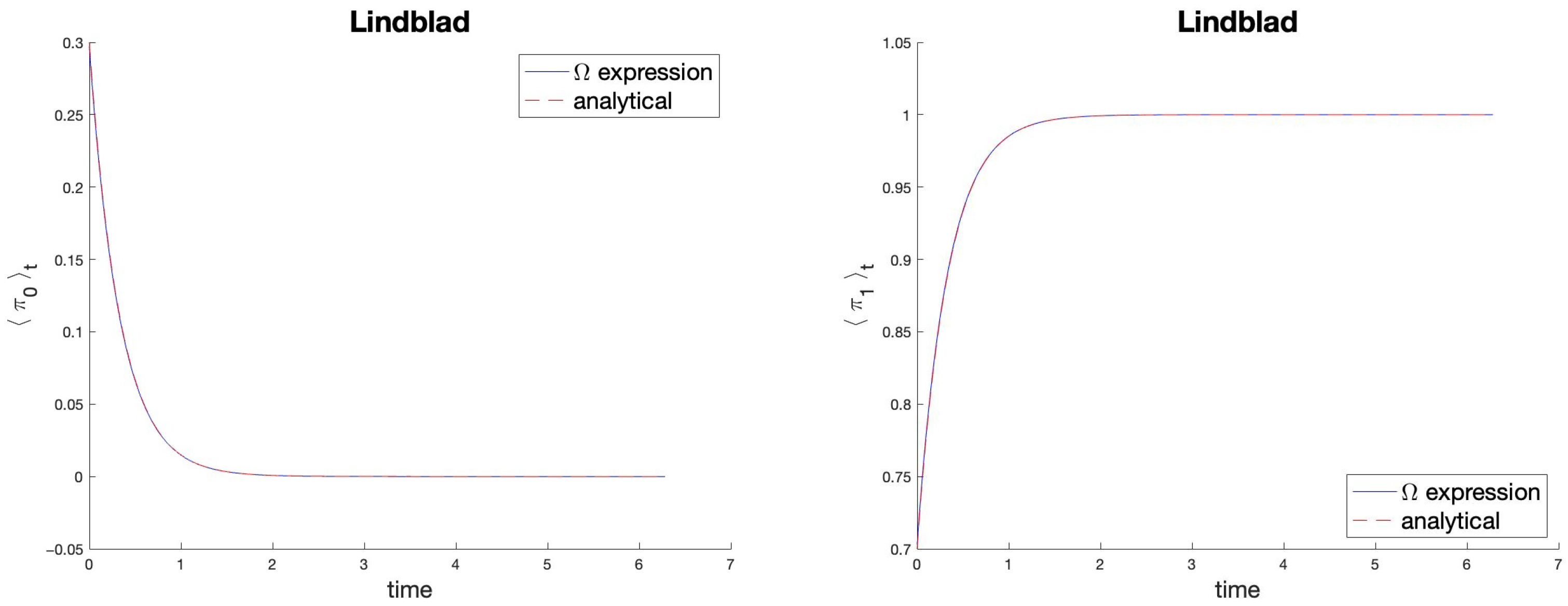
5. Applications to Qubits and Numerical Tests
6. Properties of Dissipation and Time-Dependent Perturbations
7. The Dissipation Operator for Open Quantum Systems
8. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Callen, H.B.; Welton, T.A. Irreversibility and generalized noise. Phys. Rev. 1951, 83, 34. [Google Scholar] [CrossRef]
- Greene, R.F.; Callen, H.B. On the formalism of thermodynamic fluctuation theory. Phys. Rev. 1951, 83, 1231. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Green, M.S. Markoff random processes and the statistical mechanics of time-dependent phenomena. II. Irreversible processes in fluids. J. Chem. Phys. 1954, 22, 398–413. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Marconi, U.M.B.; Puglisi, A.; Rondoni, L.; Vulpiani, A. Fluctuation–dissipation: Response theory in statistical physics. Phys. Rep. 2008, 461, 111–195. [Google Scholar] [CrossRef]
- Evans, D.J.; Morriss, G.P. Statistical Mechanics of Nonequilbrium Liquids; ANU Press: Canberra, Australia, 2007. [Google Scholar]
- Feynman, R.P. Simulating physics with computers. In Feynman and Computation; CRC Press: Boca Raton, FL, USA, 2018; pp. 133–153. [Google Scholar]
- Schaller, G. Open Quantum Systems Far from Equilibrium; Springer: Cham, Switzerland, 2014; Volume 881. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Cai, Z.; Babbush, R.; Benjamin, S.C.; Endo, S.; Huggins, W.J.; Li, Y.; McClean, J.R.; O’Brien, T.E. Quantum error mitigation. Rev. Mod. Phys. 2023, 95, 045005. [Google Scholar] [CrossRef]
- Avron, J.E.; Fraas, M.; Graf, G.M.; Kenneth, O. Quantum response of dephasing open systems. New J. Phys. 2011, 13, 053042. [Google Scholar] [CrossRef][Green Version]
- Avron, J.; Fraas, M.; Graf, G. Adiabatic response for Lindblad dynamics. J. Stat. Phys. 2012, 148, 800–823. [Google Scholar] [CrossRef]
- Narayan, O. Linear response formula for open systems. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2011, 83, 061110. [Google Scholar] [CrossRef]
- Campos Venuti, L.; Zanardi, P. Dynamical response theory for driven-dissipative quantum systems. Phys. Rev. A 2016, 93, 032101. [Google Scholar] [CrossRef]
- Shen, H.; Li, D.; Yi, X. Non-Markovian linear response theory for quantum open systems and its applications. Phys. Rev. E 2017, 95, 012156. [Google Scholar] [CrossRef]
- Konopik, M.; Lutz, E. Quantum response theory for nonequilibrium steady states. Phys. Rev. Res. 2019, 1, 033156. [Google Scholar] [CrossRef]
- Mehboudi, M.; Parrondo, J.M.; Acin, A. Linear response theory for quantum Gaussian processes. New J. Phys. 2019, 21, 083036. [Google Scholar] [CrossRef]
- Levy, A.; Rabani, E.; Limmer, D.T. Response theory for nonequilibrium steady states of open quantum systems. Phys. Rev. Res. 2021, 3, 023252. [Google Scholar] [CrossRef]
- Nakamura, K. Quantum Chaos: A New Paradigm of Nonlinear Dynamics; CUP Archive: Cambridge, UK, 1994; Volume 3. [Google Scholar]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Mukherjee, B.; Sengupta, K.; Majumdar, S.N. Quantum dynamics with stochastic reset. Phys. Rev. B 2018, 98, 104309. [Google Scholar] [CrossRef]
- Cirillo, E.N.; Colangeli, M.; Rondoni, L. Transport in quantum multi-barrier systems as random walks on a lattice. J. Stat. Phys. 2019, 176, 692–709. [Google Scholar] [CrossRef]
- Dubey, V.; Chetrite, R.; Dhar, A. Quantum resetting in continuous measurement induced dynamics of a qubit. J. Phys. Math. Theor. 2023, 56, 154001. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J. Equilibrium microstates which generate second law violating steady states. Phys. Rev. E 1994, 50, 1645. [Google Scholar] [CrossRef]
- Evans, D.; Cohen, E.; Morriss, G. Probability of second law violations in shearing steady flows. Phys. Rev. Lett. 1993, 70, 2401. [Google Scholar] [CrossRef]
- Gallavotti, G.; Cohen, E.G.D. Dynamical ensembles in stationary states. J. Stat. Phys. 1995, 80, 931–970. [Google Scholar] [CrossRef]
- Jarzynski, C.; Wójcik, D.K. Classical and quantum fluctuation theorems for heat exchange. Phys. Rev. Lett. 2004, 92, 230602. [Google Scholar] [CrossRef] [PubMed]
- Searles, D.J.; Rondoni, L.; Evans, D.J. The steady state fluctuation relation for the dissipation function. J. Stat. Phys. 2007, 128, 1337–1363. [Google Scholar] [CrossRef]
- Searles, D.J.; Evans, D.J. Ensemble dependence of the transient fluctuation theorem. J. Chem. Phys. 2000, 113, 3503–3509. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J. The fluctuation theorem. Adv. Phys. 2002, 51, 1529–1585. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J.; Williams, S.R. On the fluctuation theorem for the dissipation function and its connection with response theory. J. Chem. Phys. 2008, 128, 014504. [Google Scholar] [CrossRef]
- Jepps, O.G.; Rondoni, L. A dynamical-systems interpretation of the dissipation function, T-mixing and their relation to thermodynamic relaxation. J. Phys. Math. Theor. 2016, 49, 154002. [Google Scholar] [CrossRef]
- Amadori, D.; Colangeli, M.; Correa, A.; Rondoni, L. Exact response theory and Kuramoto dynamics. Phys. D Nonlinear Phenom. 2022, 429, 133076. [Google Scholar] [CrossRef]
- Iannella, L.; Rondoni, L. Exact Response Theory for Time-Dependent and Stochastic Perturbations. Entropy 2023, 26, 12. [Google Scholar] [CrossRef]
- Maffioli, L.; Smith, E.R.; Ewen, J.P.; Daivis, P.J.; Dini, D.; Todd, B. Slip and stress from low shear rate nonequilibrium molecular dynamics: The transient-time correlation function technique. J. Chem. Phys. 2022, 156, 184111. [Google Scholar] [CrossRef]
- Bernardi, S.; Searles, D.J. Local response in nanopores. Mol. Simul. 2016, 42, 463–473. [Google Scholar] [CrossRef]
- Hunter, M.A.; Demir, B.; Petersen, C.F.; Searles, D.J. New framework for computing a general local self-diffusion coefficient using statistical mechanics. J. Chem. Theory Comput. 2022, 18, 3357–3363. [Google Scholar] [CrossRef]
- Searles, D.J.; Sanderson, S. Fluctuation theorems and distribution functions for polar molecules in an electric field. arXiv 2024, arXiv:2401.02862. [Google Scholar]
- Sanderson, S.; Petersen, C.F.; Searles, D.J. Machine learning a time-local fluctuation theorem for nonequilibrium steady states. Prog. Theor. Exp. Phys. 2023, 2023, 083A01. [Google Scholar] [CrossRef]
- Andrieux, D.; Gaspard, P. Quantum work relations and response theory. Phys. Rev. Lett. 2008, 100, 230404. [Google Scholar] [CrossRef] [PubMed]
- Evans, D.J.; Searles, D.J.; Williams, S.R. Fundamentals of Classical Statistical Thermodynamics: Dissipation, Relaxation, and Fluctuation Theorems; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Touchette, H.; Harris, R.J. Large deviation approach to nonequilibrium systems. In Nonequilibrium Statistical Physics of Small Systems: Fluctuation Relations and Beyond; Wiley: Hoboken, NJ, USA, 2013; pp. 335–360. [Google Scholar]
- Schwabl, F. Quantum Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Teta, A. A Mathematical Primer on Quantum Mechanics; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Sinaĭ, A. Introduction to Ergodic Theory; Princeton University Press: Princeton, NJ, USA, 1976; Volume 18. [Google Scholar]
- Jepps, O.G.; Rondoni, L. Deterministic thermostats, theories of nonequilibrium systems and parallels with the ergodic condition. J. Phys. Math. Theor. 2010, 43, 133001. [Google Scholar] [CrossRef]
- Pan, L.; Chen, X.; Chen, Y.; Zhai, H. Non-Hermitian linear response theory. Nat. Phys. 2020, 16, 767–771. [Google Scholar] [CrossRef]
- Ashida, Y.; Gong, Z.; Ueda, M. Non-hermitian physics. Adv. Phys. 2020, 69, 249–435. [Google Scholar]
- Caruso, S.; Giberti, C.; Rondoni, L. Dissipation function: Nonequilibrium physics and dynamical systems. Entropy 2020, 22, 835. [Google Scholar] [CrossRef]
- Rammer, J. Quantum field theory of non-equilibrium states. In Quantum Field Theory of Non-Equilibrium States; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Stockburger, J.T.; Motz, T. Thermodynamic deficiencies of some simple Lindblad operators: A diagnosis and a suggestion for a cure. Fortschritte Der Phys. 2017, 65, 1600067. [Google Scholar] [CrossRef]
- Levy, A.; Kosloff, R. The local approach to quantum transport may violate the second law of thermodynamics. Europhys. Lett. 2014, 107, 20004. [Google Scholar] [CrossRef]
- De Jong, W.A.; Metcalf, M.; Mulligan, J.; Płoskoń, M.; Ringer, F.; Yao, X. Quantum simulation of open quantum systems in heavy-ion collisions. Phys. Rev. D 2021, 104, L051501. [Google Scholar] [CrossRef]
- Hu, Z.; Xia, R.; Kais, S. A quantum algorithm for evolving open quantum dynamics on quantum computing devices. Sci. Rep. 2020, 10, 3301. [Google Scholar] [CrossRef]
- Santos, J.P.; Céleri, L.C.; Landi, G.T.; Paternostro, M. The role of quantum coherence in non-equilibrium entropy production. npj Quantum Inf. 2019, 5, 23. [Google Scholar] [CrossRef]
- Lindblad, G. Expectations and entropy inequalities for finite quantum systems. Commun. Math. Phys. 1974, 39, 111–119. [Google Scholar] [CrossRef]
- Sasaki, R.; Tateyama, Y.; Searles, D.J. Constant-Current Nonequilibrium Molecular Dynamics Approach for Accelerated Computation of Ionic Conductivity Including Ion-Ion Correlation. PRX Energy 2025, 4, 013005. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Greppi, E.; Rondoni, L. Quantum Exact Response Theory Based on the Dissipation Function. Entropy 2025, 27, 527. https://doi.org/10.3390/e27050527
Greppi E, Rondoni L. Quantum Exact Response Theory Based on the Dissipation Function. Entropy. 2025; 27(5):527. https://doi.org/10.3390/e27050527
Chicago/Turabian StyleGreppi, Enrico, and Lamberto Rondoni. 2025. "Quantum Exact Response Theory Based on the Dissipation Function" Entropy 27, no. 5: 527. https://doi.org/10.3390/e27050527
APA StyleGreppi, E., & Rondoni, L. (2025). Quantum Exact Response Theory Based on the Dissipation Function. Entropy, 27(5), 527. https://doi.org/10.3390/e27050527