Reference Point and Grid Method-Based Evolutionary Algorithm with Entropy for Many-Objective Optimization Problems
Abstract
1. Introduction
- A new algorithm was developed to combine reference point-based and grid-based methods in coping with regular and irregular many-objective optimization problems. The algorithm proposed is to remedy the issue where the reference point-based method has good results in dealing with regular problems but fails to obtain good solutions in dealing with irregular problems, as well as address how the grid-based method has good results in dealing with irregular problems but does not deliver good solutions for regular problems.
- In this paper, an entropy-based criterion, which combines the reference point-based and grid-based methods, is proposed. In order to determine the interval of the calculated entropy value, we introduced a parameter . By comparing the current entropy with the maximum entropy, we can determine whether to adopt the reference-point-based approach or the grid-based approach.
- A comprehensive experimental evaluation was conducted to assess the performance of RGEA. To verify its effectiveness, this paper, using regular and irregular DTLZ1-7 and WFG1-9 test suites for verification, compared RGEA with six evolutionary algorithms without adaptive technology and six evolutionary algorithms with adaptive technology. The large number of experimental results obtained indicate that the proposed algorithm RGEA can achieve good performance on many-objective optimization problems with a regular and irregular Pareto front.
2. Preliminaries
2.1. Definition of the Multi-Objective Optimization Problem
2.2. Definition of Regular and Irregular Problems
2.3. Reference Point-Based Many-Objective Optimization Algorithms
2.4. Grid-Based Many-Objective Optimization Algorithms
3. The Proposed Algorithm
3.1. The Main Idea of the Proposed Algorithm
| Algorithm 1: Framework of RGEA |
| Input: |
| H structured reference ponits or supplied aspiration ponits |
| P: population |
| N: population size |
| maxGen: maximum number of iterations |
| N uniformly distributed weight vectors: |
| div: the size of grid division |
| : the interval for calculating the entropy value |
| Initialization: |
| t = 1 |
| = Initialize(P) |
| Compute maximum entropy: MaxEntropy; |
| Optimization: |
| while t < maxGen do |
| 1: , , |
| 2: = Genetic Recombination and Mutation() |
| 3: |
| 4: = Non-dominated Sorting |
| 5: while do |
| 6: |
| 7: |
| 8: Final Front to Incorporate: |
| 9: if then |
| 10: |
| 11: else |
| 12: |
| 13: Points Selected From |
| 14: if kind = 1 |
| 15: Normalize Objectives and Establish Reference Set : |
| 16: Associate each member of with a reference point: |
| 17: Compute niche count of reference point |
| 18: Choose members one at a time from to construct |
| : |
| 19: else |
| 20: |
| 21: |
| 22: |
| 23: end if |
| 24: if |
| 25: Calculate CurrentEntropy: |
| 26: if MaxEntropy - CurrentEntropy <= 0, then |
| 27: kind = 2 |
| 28: end if |
| 29: end if |
| 30: end if |
| 31: |
| 32: end |
| Output: |
| P |
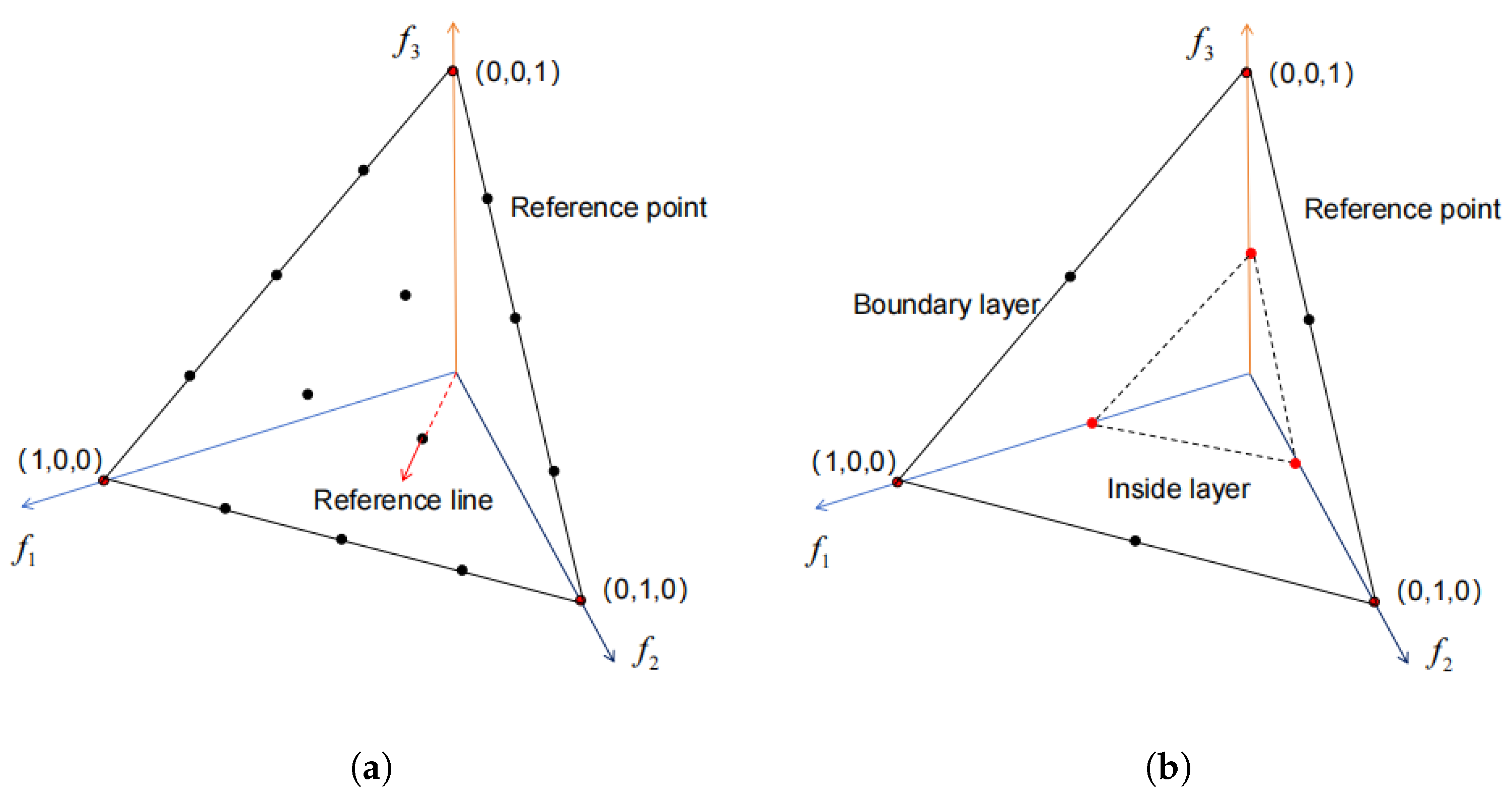
3.2. Generation of Reference Points
3.3. Grid-Based Mechanism
| Algorithm 2: |
| Input: |
| : optimal solution in P |
| : the i-th solution P |
| Optimization: |
| 1: |
| 2: for to do |
| 3: if then |
| 4: |
| 5: else if then |
| 6: if then |
| 7: |
| 8: else if then |
| 9: if then |
| 10: |
| 11: end if |
| 12: end if |
| 13: end if |
| 14: end for |
| Output: |
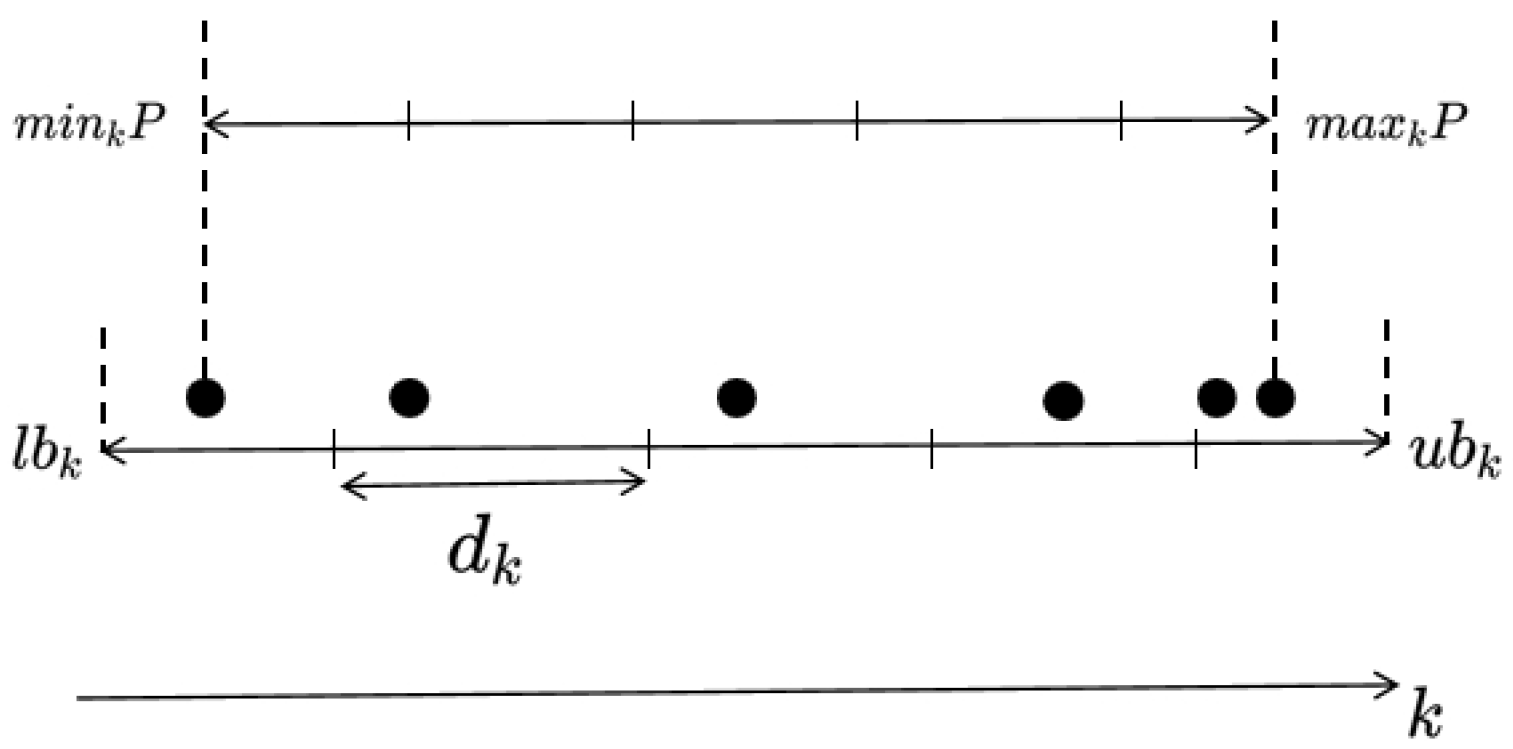
3.4. Entropy Calculation
| Algorithm 3: Calculate the Entropy |
| Input: |
| N: The population size |
| N uniformly distributed weight vectors: |
| : the count of solutions associated with each reference point |
| Association: |
| 1: Measure the distance between each solution and each reference vector: Cosine |
| 2: Match each solution with its closest reference point: pi |
| 3: Compute the count of solutions associated with each reference point: rho |
| Calculate the Entropy: |
| 4: entropy = 0 |
| 5: i = 1 |
| 6: while do |
| 7: if , then , entropy = entropy + |
| 8: end |
| 9: if the loop ends |
| 10: entropy = −entropy |
| 11: end if |
| 12: i = i + 1 |
| 13: end |
| Output: |
| entropy |
3.5. Analysis of Computational Complexity
4. Experiment Design
4.1. Experiment Settings
- (1)
- Characteristics of the test problems: For the test problems involving 3, 5, 8, and 10 objectives, the population sizes are set to 91, 210, 156, and 275, respectively. Each algorithm is independently run 20 times on each benchmark. The algorithms considered all have an equal number of evaluations for the same test problem, and the maximum number of fitness evaluations is detailed in Table 1. Additionally, the stopping criterion for these runs is not specified here, but it is presumably based on reaching the maximum number of evaluations listed in Table 1.
- (2)
- Configuration of genetic operators: In this paper, our primary focus is on the simulated binary crossover operator and the polynomial mutation operator. We set the crossover probability to 1.0 and the mutation probability to , which represents the total number of decision variables. Additionally, the distribution index for both the crossover and mutation operators is set at 20.
- (3)
- Parameters in MOEA/D and GrEA: For MOEA/D, the neighborhood size is determined by rounding of the population size to the nearest integer for the given benchmark problem. In the case of GrEA, the grid division size follows the guidelines outlined in reference [5].
- (4)
- Computation of performance indicators: In this paper, the performance of each algorithm was assessed using the inverted generational distance (IGD) indicator and the hypervolume (HV) indicator, of which the specific calculation reference is in Section 4.4. The average value of these two index values in 20 runs was calculated on each test problem. Another important step in evolutionary computation is to normalize the objective space to a unified scale. The primary approach involves normalizing the objective space to the interval based on the minimum and maximum values of each objective, as derived from the true Pareto front of each benchmark problem. Consequently, the normalized ideal point shifts to a zero vector, while the nadir point transforms into (1, 1, …, 1).
| Test Problems | Objectives (M) | Variables (D) | Evaluations | Pareto Front |
|---|---|---|---|---|
| DTLZ1 | 3, 5, 8, 10 | M-1 + 5 | 50,000 | Regular |
| DTLZ2, DTLZ4 | 3, 5, 8, 10 | M-1 + 10 | 20,000 | Regular |
| DTLZ3 | 3, 5, 8, 10 | M-1 + 10 | 50,000 | Regular |
| DTLZ5, DTLZ6 | 3, 5, 8, 10 | M-1 + 10 | 20,000 | Irregular |
| DTLZ7 | 3, 5, 8, 10 | M-1 + 20 | 20,000 | Irregular |
| WFG1-3 | 3, 5, 8, 10 | 24 | Irregular | |
| WFG4-9 | 3, 5, 8, 10 | 24 | Regular |
4.2. Benchmark
4.3. Algorithms in Comparison
4.4. Selection of Evaluation Metrics
4.5. Nonparametric Statistics Analysis
5. Experimental Results and Analysis
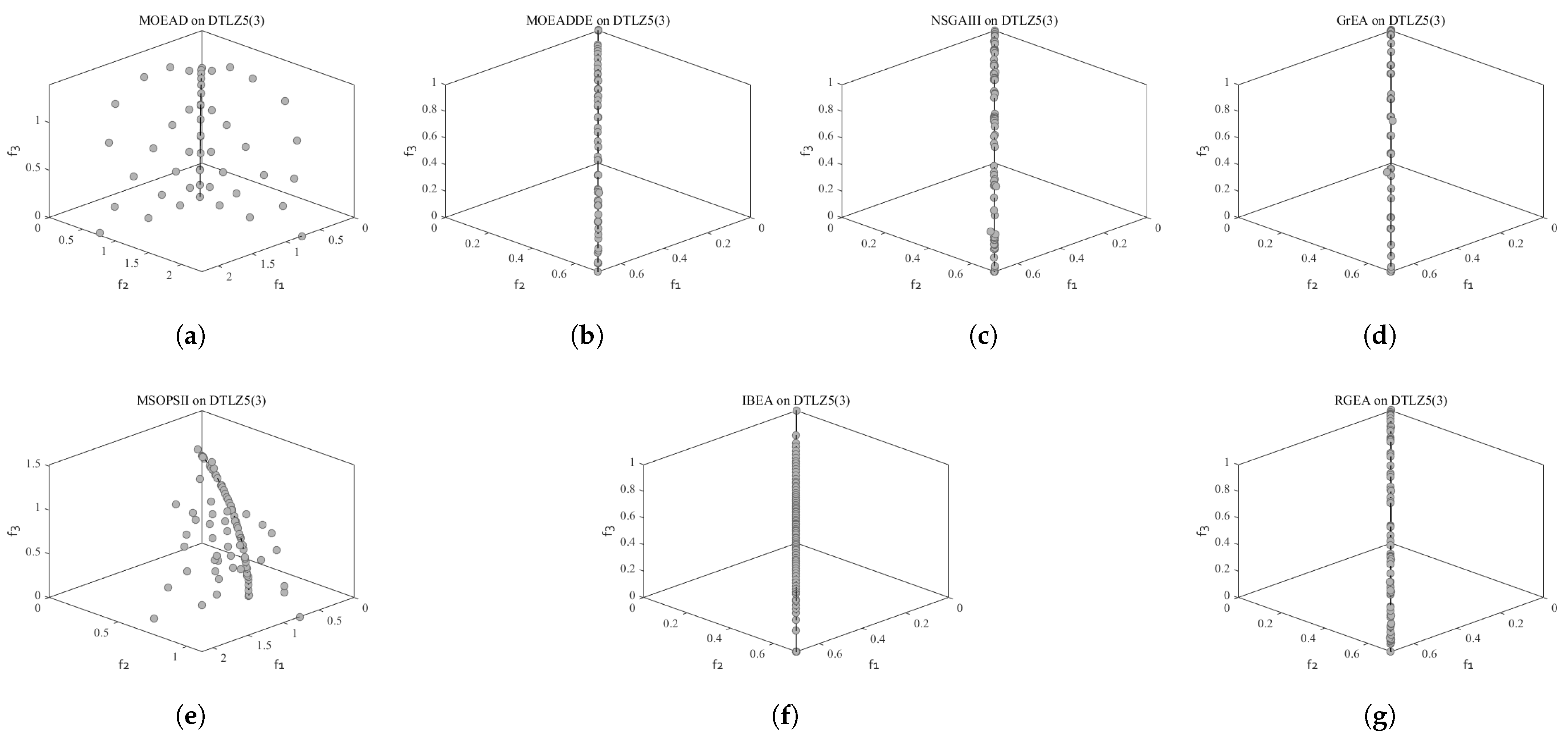
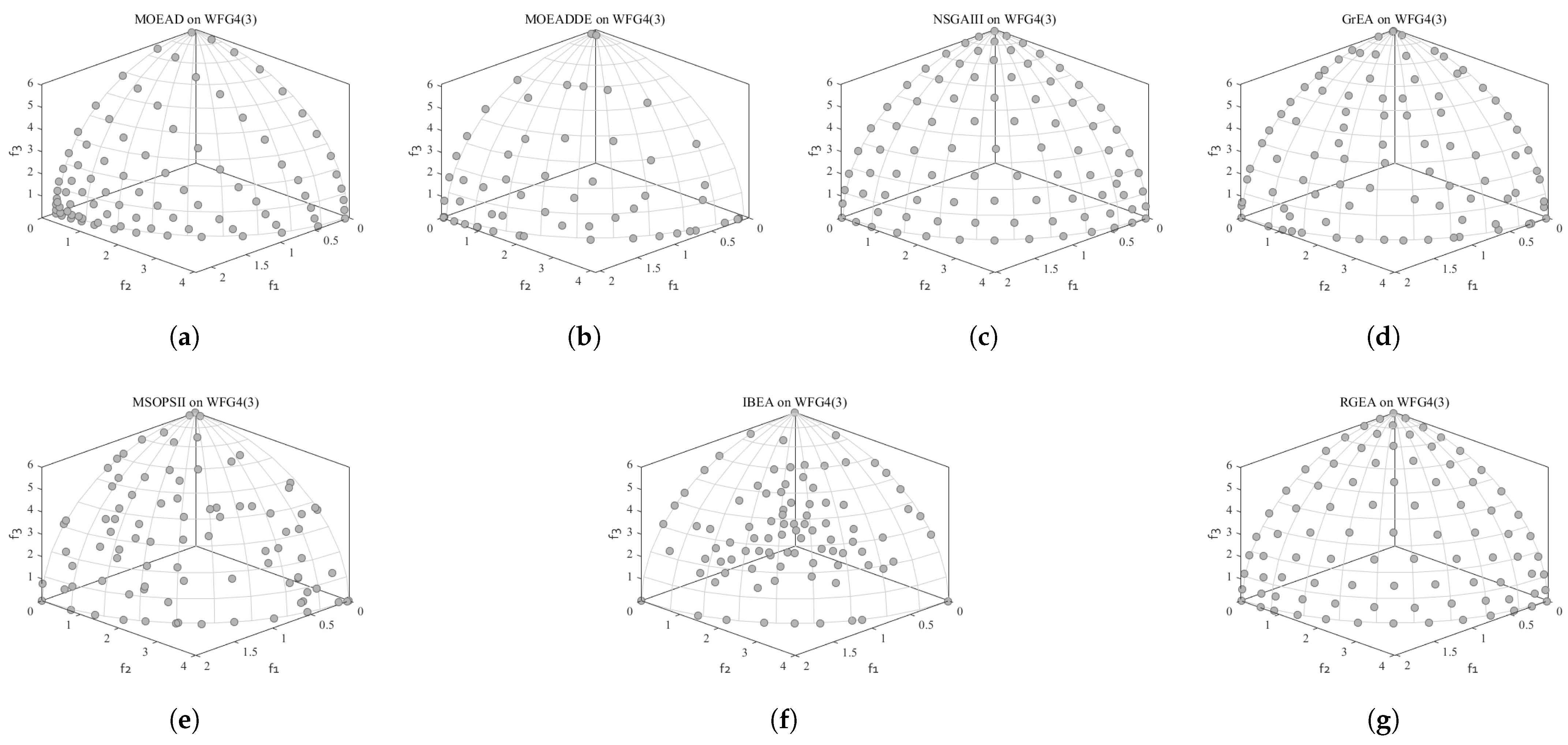
5.1. Comparison with Six Evolutionary Algorithms Without Adaptive Technology
5.2. Comparison with Six Evolutionary Algorithms with Adaptive Technology
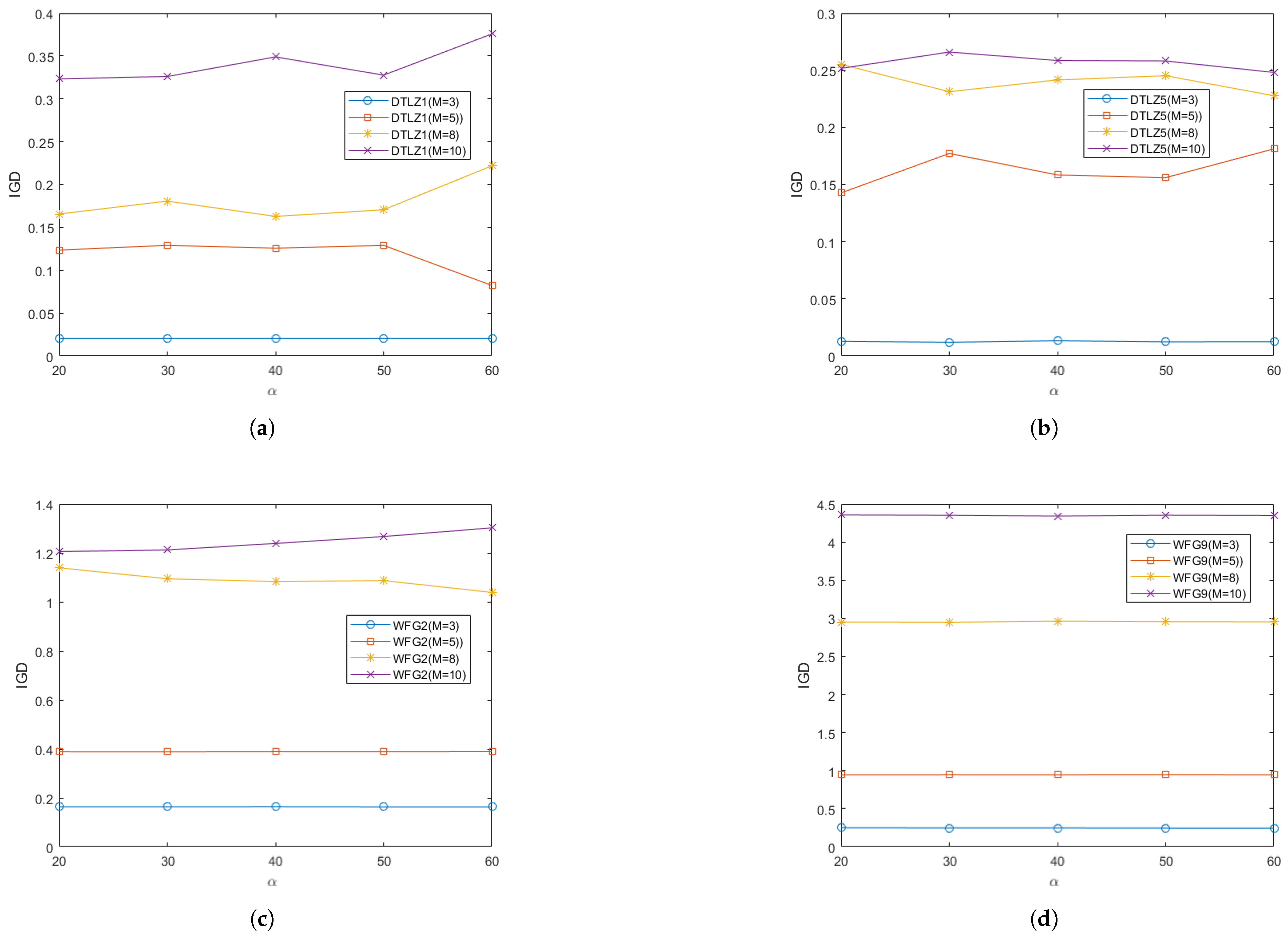
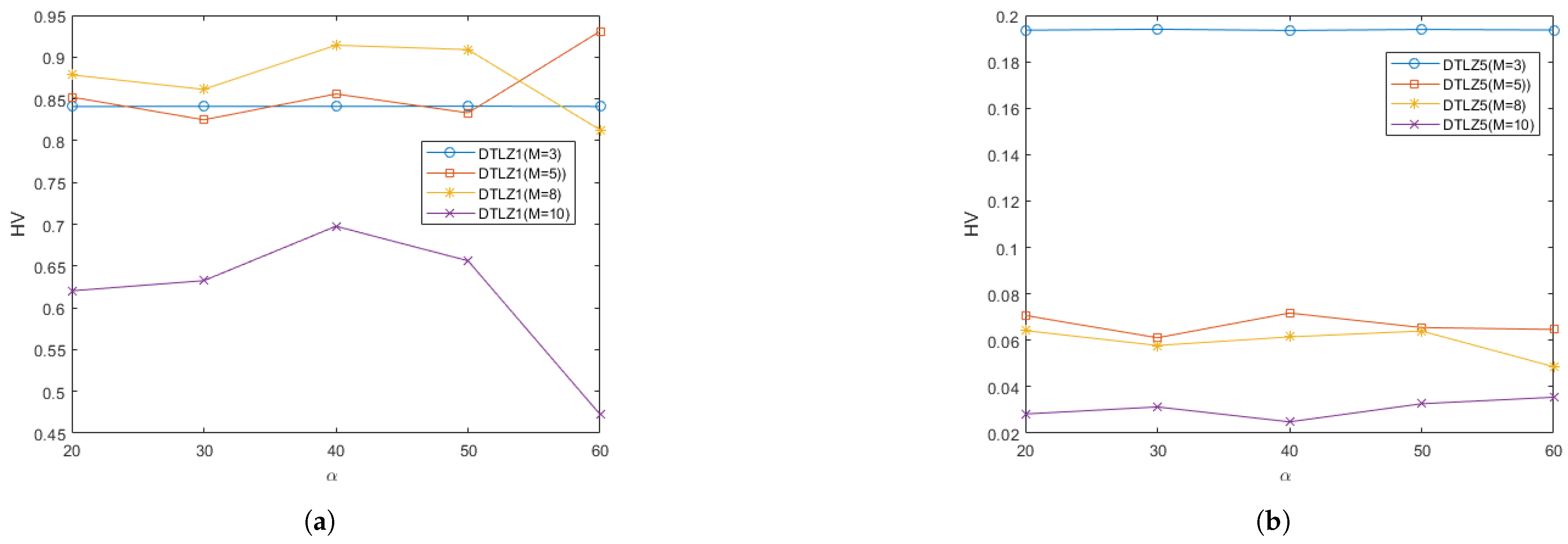
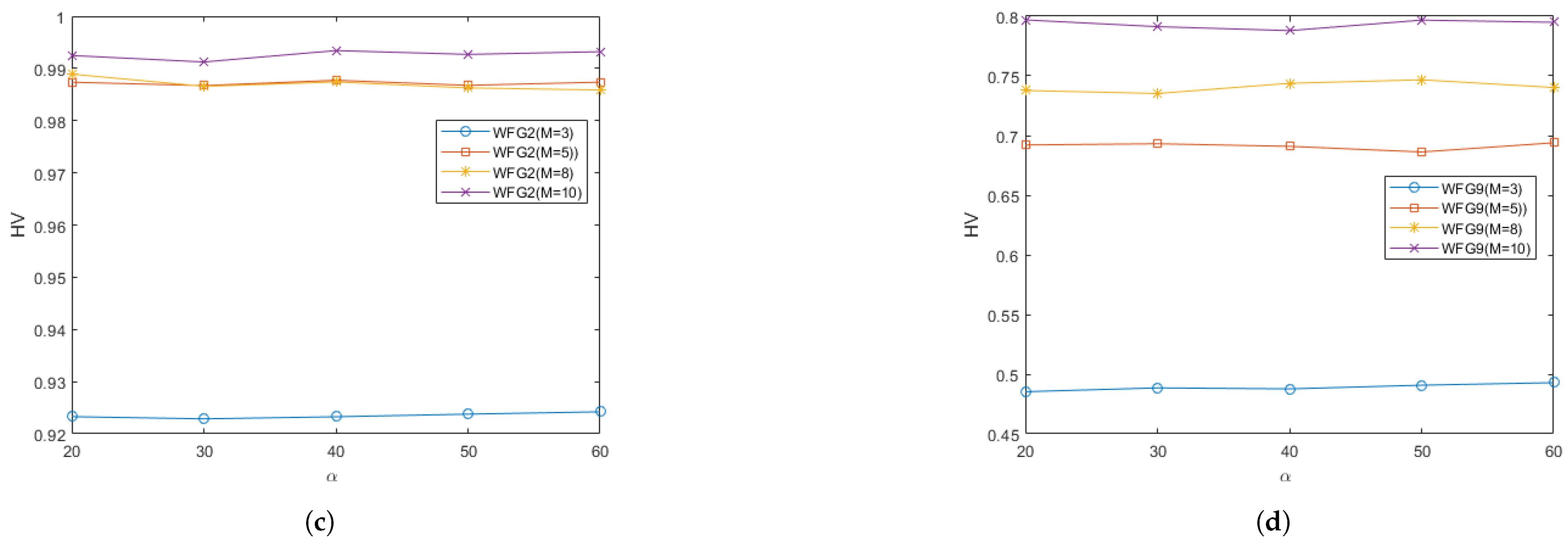
5.3. Analysis of Parameter Sensitivity
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khare, V.; Yao, X.; Deb, K. Performance scaling of multi-objective evolutionary algorithms. In Proceedings of the 2003 EMO, Faro, Portugal, 8–11 April 2003; pp. 376–390. [Google Scholar]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Li, B.; Li, J.; Tang, K.; Yao, X. Many-Objective Evolutionary Algorithms: A Survey. ACM Comput. Surv. 2015, 48, 13. [Google Scholar] [CrossRef]
- Laumanns, M.; Thiele, L.; Deb, K.; Zitzler, E. Combining convergence and diversity in evolutionary multiobjective optimization. Evol. Comput. 2002, 10, 263–282. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Li, M.; Liu, X.; Zheng, J. A Grid-Based Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2013, 17, 721–736. [Google Scholar] [CrossRef]
- He, Z.; Yen, G.G.; Zhang, J. Fuzzy-Based Pareto Optimality for Many-Objective Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2014, 18, 269–285. [Google Scholar] [CrossRef]
- Ikeda, K.; Kita, H.; Kobayashi, S. Failure of Pareto-based MOEAs: Does non-dominated really mean near to optimal? In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Republic of Korea, 27–30 May 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 2, pp. 957–962. [Google Scholar]
- Yuan, Y.; Xu, H.; Wang, B.; Yao, X. A New Dominance Relation-Based Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 16–37. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.; Li, M.; Chen, Z. A Vector Angle-Based Evolutionary Algorithm for Unconstrained Many-Objective Optimization. IEEE Trans. Evol. Comput. 2017, 21, 131–152. [Google Scholar] [CrossRef]
- Li, M.; Yang, S.; Liu, X. Shift-Based Density Estimation for Pareto-Based Algorithms in Many-Objective Optimization. IEEE Trans. Evol. Comput. 2014, 18, 348–365. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Jin, Y. A Knee Point-Driven Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2015, 19, 761–776. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-Based Selection in Multiobjective Search. In Parallel Problem Solving from Nature–PPSN VIII, Proceedings of the 8th International Conference, Birmingham, UK, 18–22 September 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 832–842. [Google Scholar]
- Hernández Gómez, R.; Coello Coello, C.A. Improved Metaheuristic Based on the R2 Indicator for Many-Objective Optimization. In Proceedings of the GECCO ’15: Genetic and Evolutionary Computation Conference, Madrid, Spain, 11–15 July 2015; pp. 679–686. [Google Scholar]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Li, B.; Tang, K.; Li, J.; Yao, X. Stochastic Ranking Algorithm for Many-Objective Optimization Based on Multiple Indicators. IEEE Trans. Evol. Comput. 2016, 20, 924–938. [Google Scholar] [CrossRef]
- Brockhoff, D.; Zitzler, E. Are all objectives necessary? On dimensionality reduction in evolutionary multiobjective optimization. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Reykjavik, Iceland, 9–13 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 533–542. [Google Scholar]
- Saxena, D.K.; Deb, K. Non-linear Dimensionality Reduction Procedures for Certain Large-Dimensional Multi-objective Optimization Problems: Employing Correntropy and a Novel Maximum Variance Unfolding. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2007; pp. 772–787. [Google Scholar]
- Wang, H.; Yao, X. Objective reduction based on nonlinear correlation information entropy. Soft Comput. 2016, 20, 2393–2407. [Google Scholar] [CrossRef]
- Yuan, Y.; Ong, Y.S.; Gupta, A. Objective Reduction in Many-Objective Optimization: Evolutionary Multiobjective Approach and Critical Analysis. IEEE Trans. Evol. Comput. 2017, PP(99), 1–20. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Kluwer: Boston, MA, USA, 1999. [Google Scholar]
- Jaszkiewicz, A. On the performance of multiple-objective genetic local search on the 0/1 knapsack problem—A comparative experiment. IEEE Trans. Evol. Comput. 2002, 6, 402–412. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM J. Optim. 1998, 8, 631–657. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Asafuddoula, M.; Ray, T.; Sarker, R. A Decomposition-Based Evolutionary Algorithm for Many Objective Optimization. IEEE Trans. Evol. Comput. 2015, 19, 445–460. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H.; Wang, B.; Zhang, B.; Yao, X. Balancing Convergence and Diversity in Decomposition-Based Many-Objective Optimizers. IEEE Trans. Evol. Comput. 2016, 20, 180–198. [Google Scholar] [CrossRef]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An Evolutionary Many-Objective Optimization Algorithm Based on Dominance and Decomposition. IEEE Trans. Evol. Comput. 2015, 19, 694–716. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, Z.; Ishibuchi, H.; Liao, T.; Zhang, T. Localized weighted sum method for many-objective optimization. IEEE Trans. Evol. Comput. 2016, 22, 3–18. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A Reference Vector Guided Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 773–791. [Google Scholar] [CrossRef]
- Cai, L.; Qu, S.; Yuan, Y.; Yao, X. A clustering-ranking method for many-objective optimization. Appl. Soft Comput. 2015, 35, 681–694. [Google Scholar] [CrossRef]
- Wang, Z.K.; Zhang, Q.F.; Li, H.; Ishibuchi, H.; Jiao, L.C. On the use of two reference points in decomposition based multiobjective evolutionary algorithms. Swarm Evolut. Comput. 2017, 34, 89–102. [Google Scholar] [CrossRef]
- Ma, X.L.; Yu, Y.; Li, X.D.; Qi, Y.T.; Zhu, Z.X. A survey of weight vector adjustment methods for decomposition-based multiobjective evolutionary algorithms. IEEE Trans. Evolut. Comput. 2020, 24, 634–649. [Google Scholar] [CrossRef]
- Hua, Y.C.; Jin, Y.; Hao, K.R. A clustering-based adaptive evolutionary algorithm for multiobjective optimization with irregular Pareto fronts. IEEE Trans. Cybernet. 2019, 49, 2758–2770. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.Z.; Liu, S.B.; Wong, K.C.; Gong, M.G.; Coello, C.A.C.; Chen, J.Y.; Zhang, J. A clustering-based evolutionary algorithm for many-objective optimization problems. IEEE Trans. Evolut. Comput. 2019, 23, 391–405. [Google Scholar] [CrossRef]
- Cai, X.Y.; Mei, Z.W.; Fan, Z.; Zhang, Q.F. A constrained decomposition approach with grids for evolutionary multiobjective optimization. IEEE Trans. Evolut. Comput. 2018, 22, 564–577. [Google Scholar] [CrossRef]
- Liang, P.; Chen, Y.; Sun, Y.; Huang, Y.; Li, W. An information entropy-driven evolutionary algorithm based on reinforcement learning for many-objective optimization. Expert Syst. Appl. 2024, 238, 122164. [Google Scholar] [CrossRef]
- Cui, Z.; Qu, C.; Zhang, Z.; Jin, Y.; Cai, J.; Zhang, W.; Chen, J. An adaptive interval many-objective evolutionary algorithm with information entropy dominance. Swarm Evol. Comput. 2024, 91, 101749. [Google Scholar] [CrossRef]
- Li, W.; He, L.; Cao, Y. Many-objective evolutionary algorithm with reference point-based fuzzy correlation entropy for energy-efficient job shop scheduling with limited workers. IEEE Trans. Cybern. 2021, 52, 10721–10734. [Google Scholar] [CrossRef]
- Farhang-Mehr, A.; Azarm, S. Diversity assessment of Pareto optimal solution sets: An entropy approach. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 1, pp. 723–728. [Google Scholar]
- Saxena, D.K.; Sinha, A.; Duro, J.A.; Zhang, Q. Entropy-based termination criterion for multiobjective evolutionary algorithms. IEEE Trans. Evol. Comput. 2015, 20, 485–498. [Google Scholar] [CrossRef]
- Zhou, C.; Dai, G.; Zhang, C.; Li, X.; Ma, K. Entropy based evolutionary algorithm with adaptive reference points for many-objective optimization problems. Inf. Sci. 2018, 465, 232–247. [Google Scholar] [CrossRef]
- Tian, Y.; He, C.; Cheng, R.; Zhang, X.Y. A multistage evolutionary algorithm for better diversity preservation in multiobjective optimization. IEEE Trans. Syst. Man Cybernet. Syst. 2019, 51, 5880–5894. [Google Scholar] [CrossRef]
- Moen, H.J.F.; Hansen, N.B.; Hovl, H.; Tørresen, J. Many-Objective Optimization Using Taxi-Cab Surface Evolutionary Algorithm. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7811, pp. 128–142. [Google Scholar]
- Wang, L.; Zhang, Q.; Zhou, A.; Gong, M.; Jiao, L. Constrained Subproblems in a Decomposition-Based Multiobjective Evolutionary Algorithm. IEEE Trans. Evol. Comput. 2016, 20, 475–480. [Google Scholar] [CrossRef]
- Seada, H.; Deb, K. A Unified Evolutionary Optimization Procedure for Single, Multiple, and Many Objectives. IEEE Trans. Evol. Comput. 2016, 20, 358–369. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.; Yang, X.; Huang, H. A Many-Objective Evolutionary Algorithm with Pareto-Adaptive Reference Points. IEEE Trans. Evol. Comput. 2020, 24, 99–113. [Google Scholar] [CrossRef]
- Yu, W.; Liu, J. A Multi-objective Evolutionary Algorithm Based on Q-learning for Adaptive Reference Vectors and Partition Deletion Strategy. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25–27 May 2024; pp. 2284–2289. [Google Scholar]
- Wu, K.E.; Panoutsos, G. A New Method for Generating and Indexing Reference Points in Many Objective Optimisation. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Liu, S.; Lin, Q.; Wong, K.; Coello, C.A.C.; Li, J.; Ming, Z. A Self-Guided Reference Vector Strategy for Many-Objective Optimization. IEEE Trans. Cybern. 2022, 52, 1164–1178. [Google Scholar] [CrossRef]
- Liu, Q.; Jin, Y.; Heiderich, M.; Rodemann, T. Coordinated Adaptation of Reference Vectors and Scalarizing Functions in Evolutionary Many-Objective Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 763–775. [Google Scholar] [CrossRef]
- Knowles, J.; Corne, D. The Pareto archived evolution strategy: A new baseline algorithm for Pareto multiobjective optimisation. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 1, pp. 98–105. [Google Scholar]
- Knowles, J.D.; Corne, D.W. Approximating the nondominated front using the Pareto archived evolution strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef]
- Corne, D.W.; Knowles, J.D.; Oates, M.J. The Pareto envelopebased selection algorithm for multiobjective optimization. In Proceedings of the 6th International Conference Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000; pp. 839–848. [Google Scholar]
- Deb, K.; Mohan, M.; Mishra, S. Evaluating the ε-domination based multi-objective evolutionary algorithm for a quick computation of Pareto-optimal solutions. Evol. Comput. 2005, 13, 501–525. [Google Scholar] [CrossRef] [PubMed]
- Yen, G.G.; Lu, H. Dynamic multiobjective evolutionary algorithm: Adaptive cell-based rank and density estimation. IEEE Trans. Evol. Comput. 2003, 7, 253–274. [Google Scholar] [CrossRef]
- Knowles, J.D.; Corne, D.W. Properties of an adaptive archiving algorithm for storing nondominated vectors. IEEE Trans. Evol. Comput. 2003, 7, 100–116. [Google Scholar] [CrossRef]
- Rachmawati, L.; Srinivasain, D. Dynamic resizing for grid-based archiving in evolutionary multiobjective optimization. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 3975–3982. [Google Scholar]
- Zhou, Y.; He, J. Convergence analysis of a self-adaptive multiobjective evolutionary algorithm based on grids. Inform. Process. Lett. 2007, 104, 117–122. [Google Scholar] [CrossRef]
- Hernández-Díaz, A.G.; Santana-Quintero, L.V.; Coello, C.A.C.; Molina, J. Pareto-adaptive ϵ-dominance. Evol. Comput. 2007, 15, 493–517. [Google Scholar] [CrossRef] [PubMed]
- Karahan, I.; Köksalan, M. A territory defining multiobjective evolutionary algorithm and preference incorporation. IEEE Trans. Evol. Comput. 2010, 14, 636–664. [Google Scholar] [CrossRef]
- Cai, X.; Xiao, Y.; Li, M.; Hu, H.; Ishibuchi, H.; Li, X. A Grid-Based Inverted Generational Distance for Multi/Many-Objective Optimization. IEEE Trans. Evol. Comput. 2021, 25, 21–34. [Google Scholar] [CrossRef]
- He, X.; Dai, C. An Improvement Evolutionary Algorithm Based on Decomposition and Grid-based Pareto Dominance for Many-objective Optimization. In Proceedings of the 2022 Global Conference on Robotics, Artificial Intelligence and Information Technology (GCRAIT), Chicago, IL, USA, 22–31 July 2022; pp. 145–149. [Google Scholar]
- He, M.; Xia, H.; Chen, H.; Ma, L. An Inhomogeneous Grid-Based Evolutionary Algorithm for Many-Objective Optimization. IEEE Access 2022, 10, 60459–60473. [Google Scholar] [CrossRef]
- Palakonda, V.; Kang, J.-M.; Jung, H. Clustering-Aided Grid-Based One-to-One Selection-Driven Evolutionary Algorithm for Multi/Many-Objective Optimization. IEEE Access 2024, 12, 120612–120623. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. In Proceedings of the Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 1, pp. 825–830. [Google Scholar]
- Huband, S.; Hingston, P.; Barone, L.; While, L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. Evol. Comput. 2006, 10, 477–506. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Sakane, Y.; Tsukamoto, N.; Nojima, Y. Evolutionary many-objective optimization by NSGA-II and MOEA/D with large populations. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 1758–1763. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; Wiley: Chichester, UK, 2001. [Google Scholar]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Natural Computing Series; Springer: Secaucus, NJ, USA, 2005. [Google Scholar]
- Hughes, E.J. MSOPS-II: A general-purpose Many-Objective optimiser. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 3944–3951. [Google Scholar]
- Qi, Y.; Ma, X.; Liu, F.; Jiao, L.; Sun, J.; Wu, J. MOEA/D with adaptive weight adjustment. Evol. Comput. 2014, 22, 231–264. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Du, B.; Zhang, L.; Liu, R. ANSGA-III: A Multiobjective Endmember Extraction Algorithm for Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 700–721. [Google Scholar] [CrossRef]
- Liu, Y.; Ishibuchi, H.; Masuyama, N.; Nojima, Y. Adapting reference vectors and scalarizing functions by growing neural gas to handle irregular Pareto fronts. IEEE Trans. Evol. Comput. 2020, 24, 439–453. [Google Scholar] [CrossRef]
- Li, M.; Yao, X. What weights work for you? Adapting weights for any Pareto front shape in decomposition-based evolutionary multiobjective optimisation. Evol. Comput. 2020, 28, 227–253. [Google Scholar] [CrossRef] [PubMed]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; da Fonseca, V.G. Performance assessment of multiobjective optimizers:an analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: A case study on the CEC’2005 Special Session on Real Parameter Optimization. J. Heuristics 2009, 15, 617–644. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]





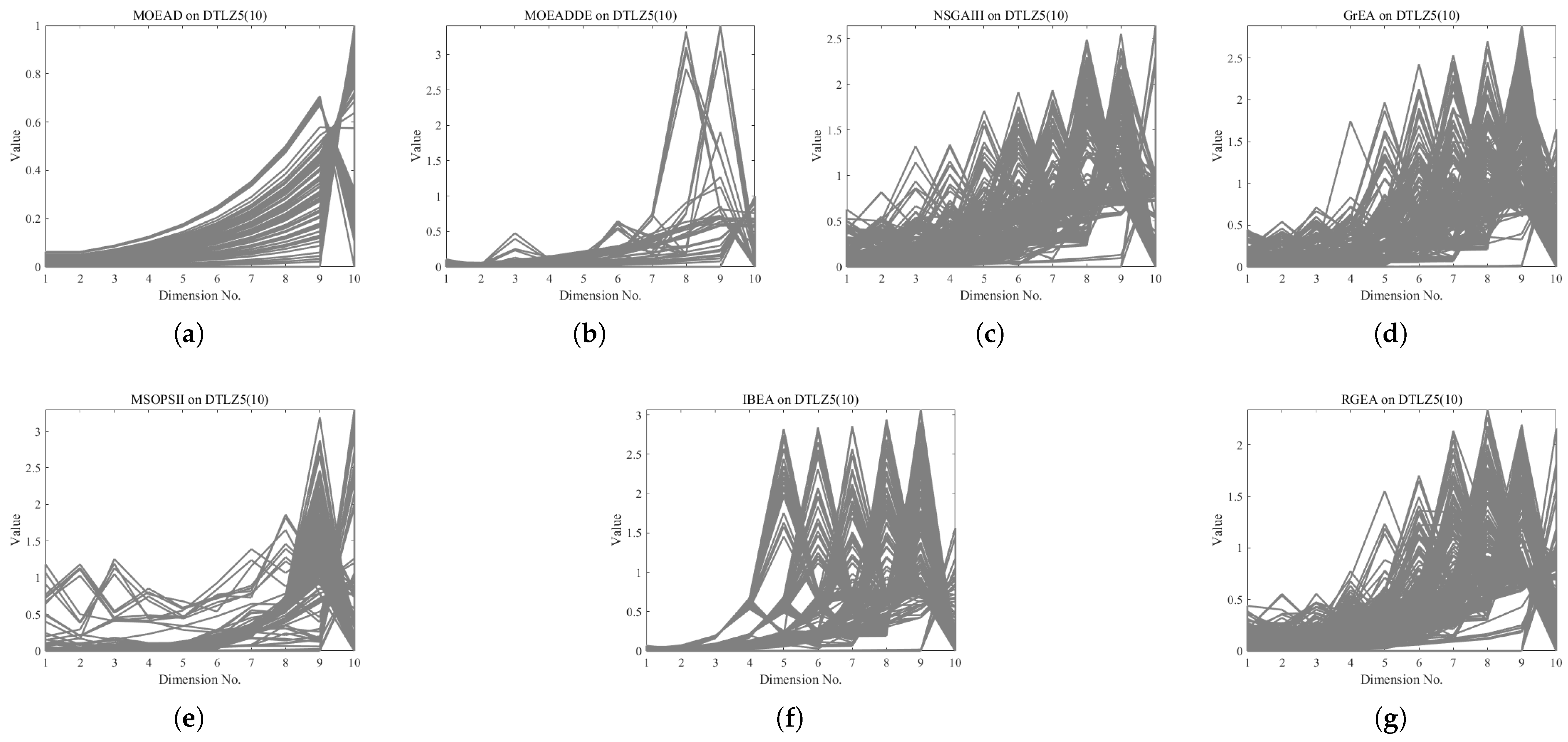

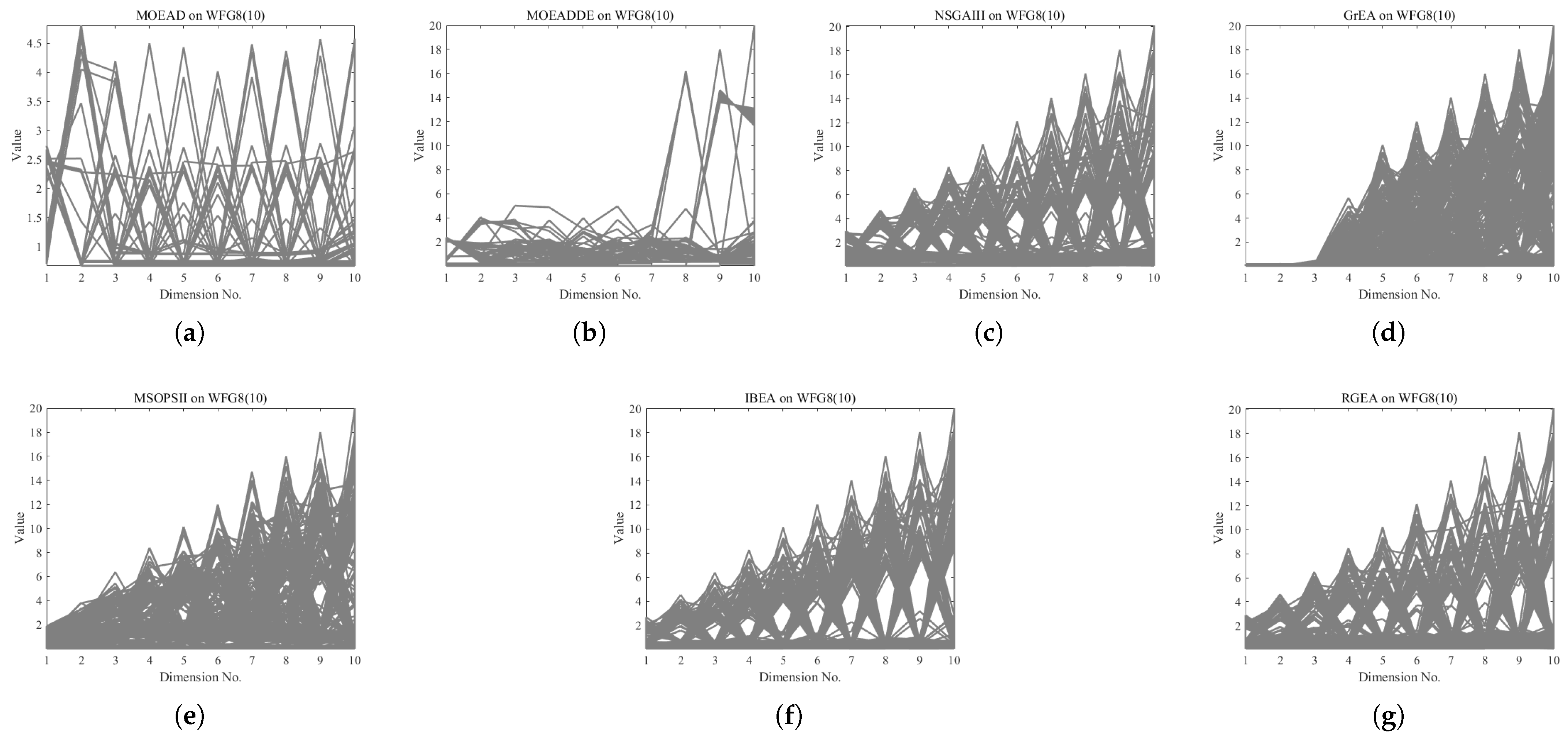


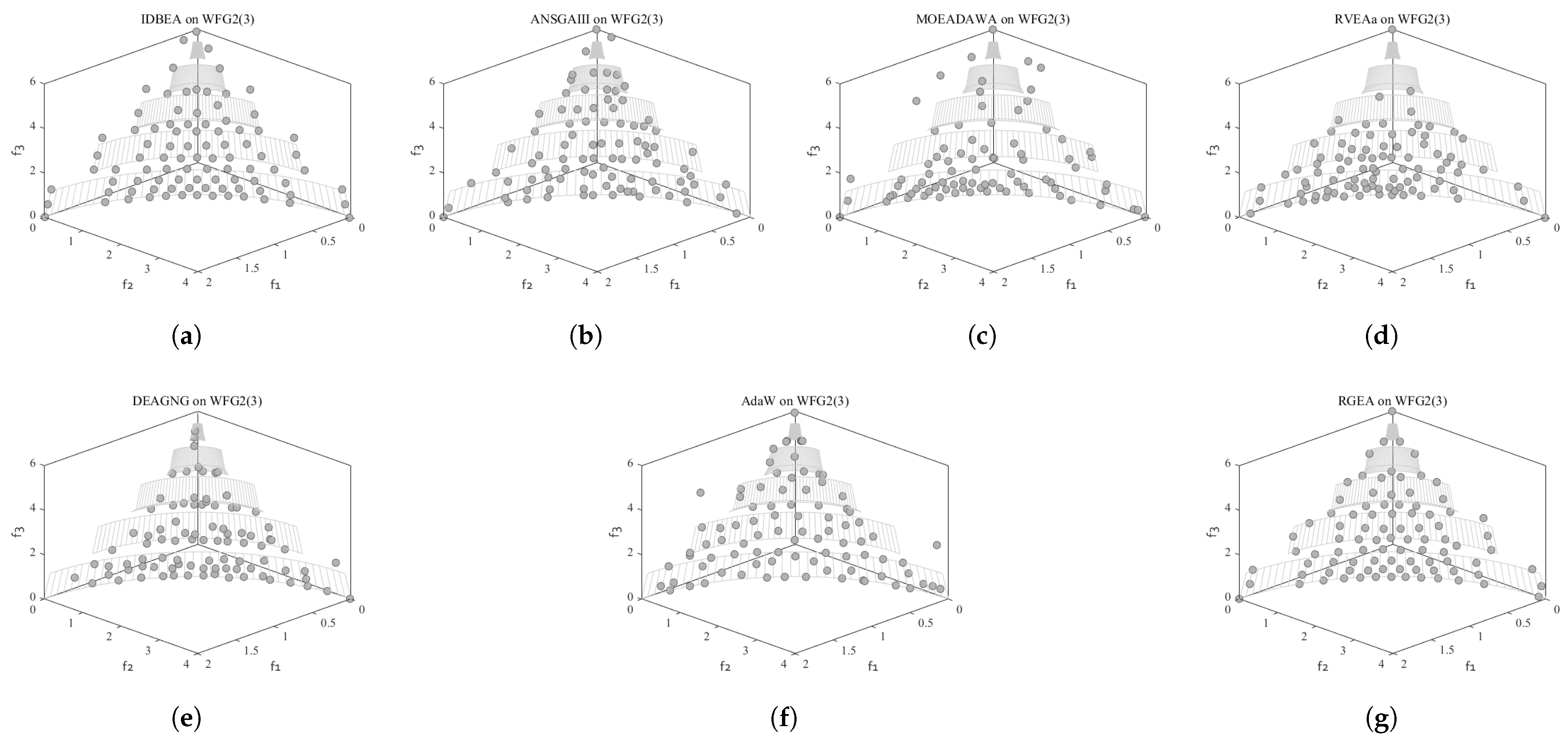
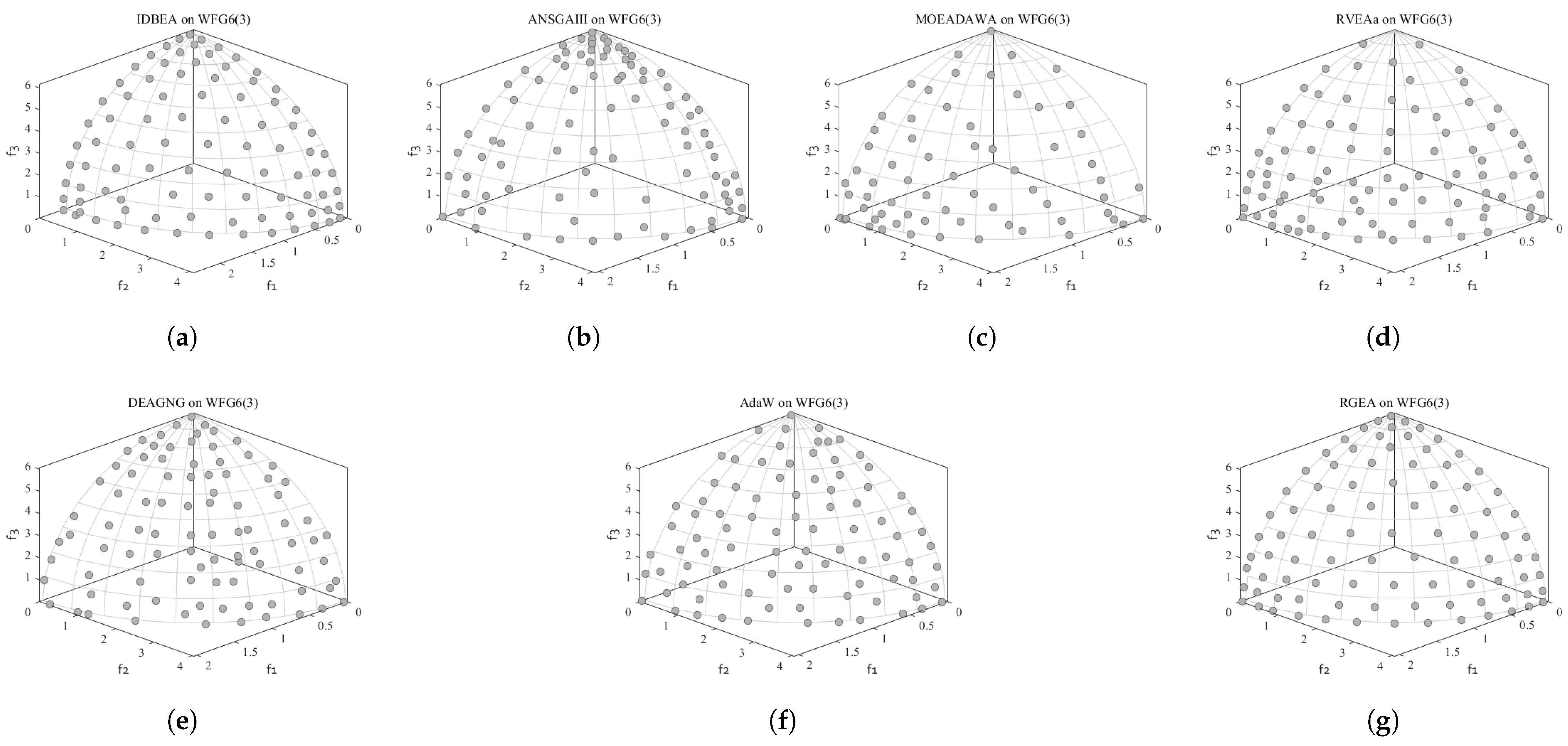
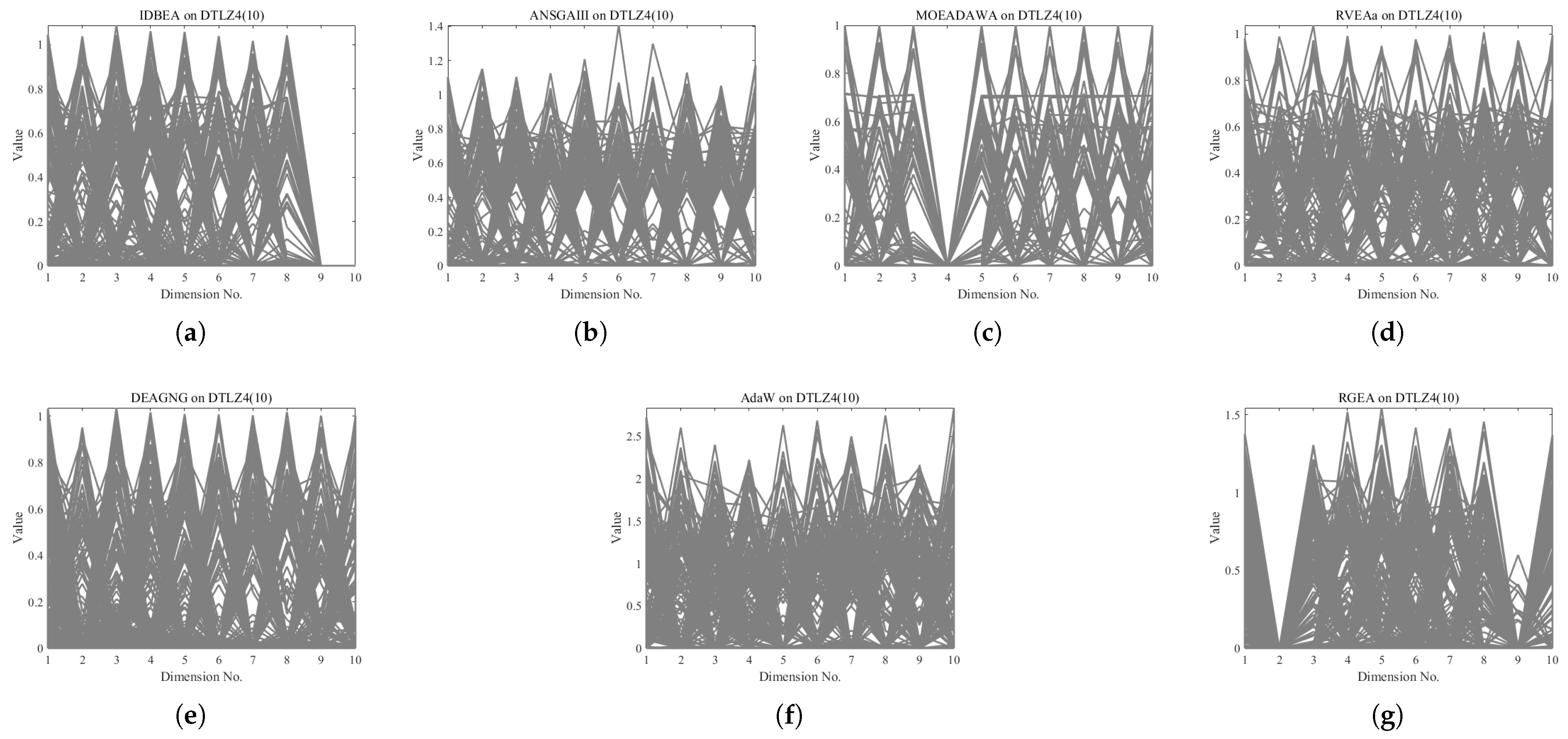

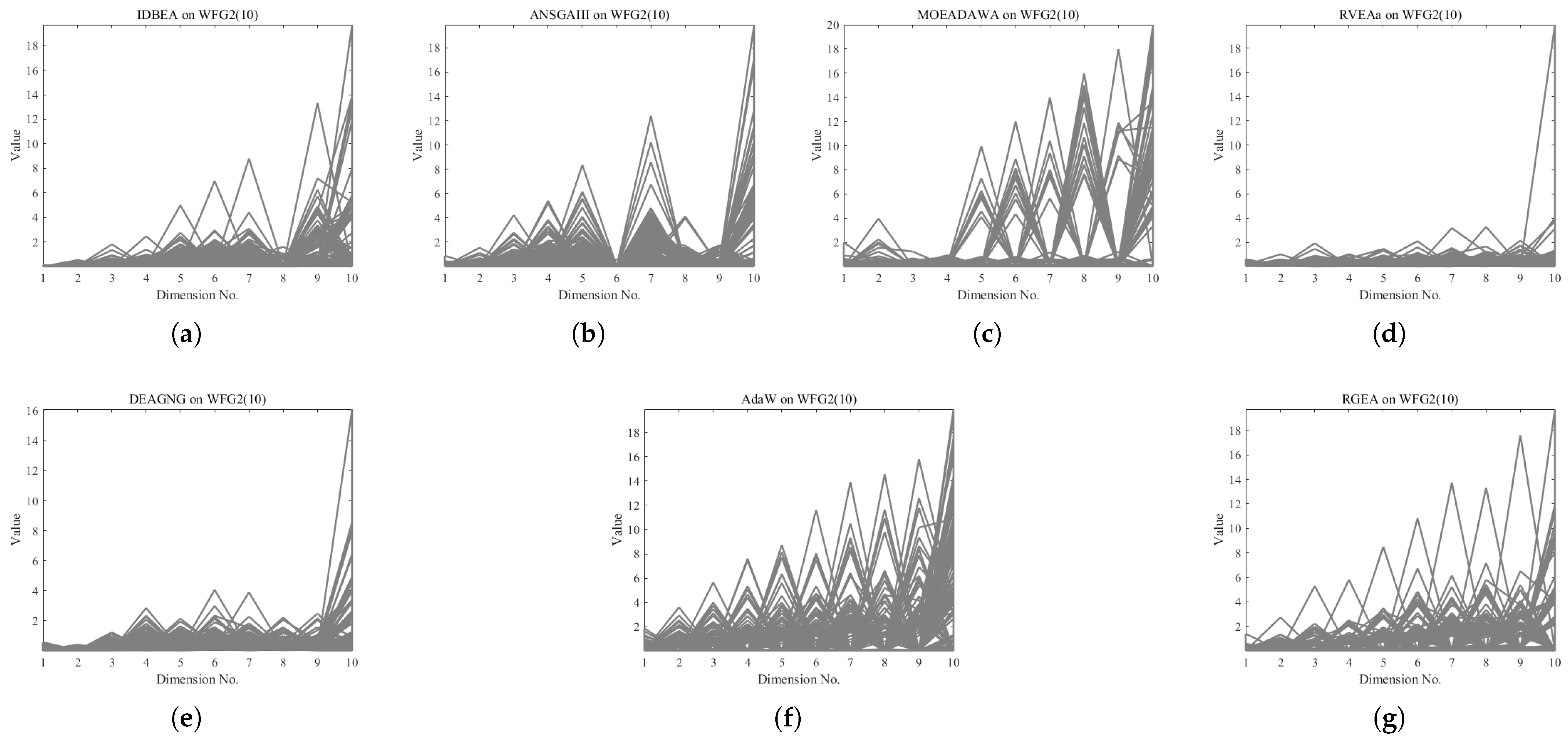
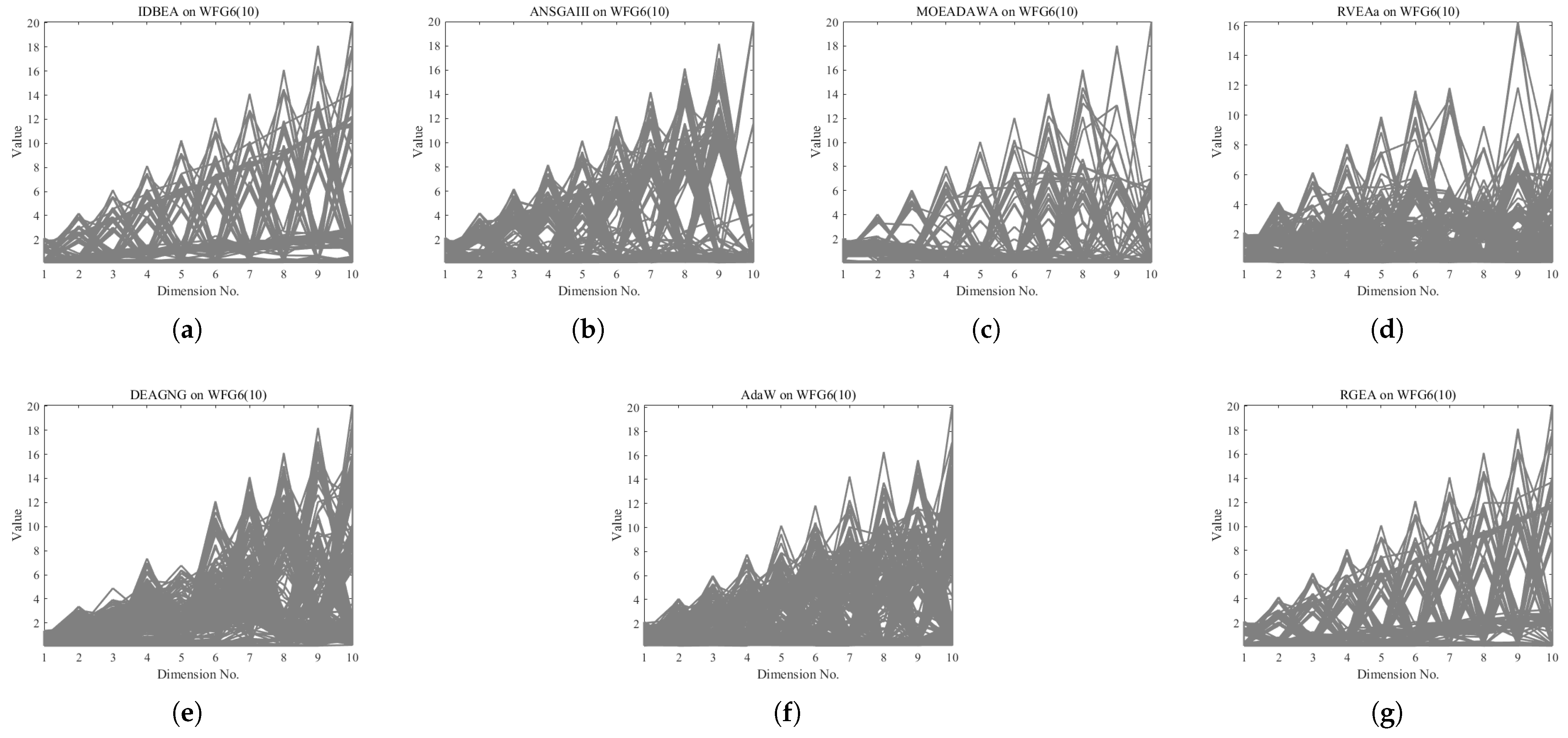
| Problem | MOEAD | MOEADDE | NSGAIII | GrEA | MSOPSII | IBEA | RGEA |
|---|---|---|---|---|---|---|---|
| DTLZ1 | ()= | - | - | - | - | - | (3.38 × 10−5) |
| (1.08 × 10−3)+ | - | + | = | = | - | ||
| (8.93 × 10−4)+ | = | = | - | = | - | ||
| (5.60 × 10−4 | = | = | - | + | ()= | ||
| DTLZ2 | (7.77 × 10−6)+ | - | = | - | - | - | |
| (3.72 × 10−4)+ | - | = | - | - | - | ||
| (9.89 × 10−4)+ | - | - | - | - | - | ||
| ()+ | - | = | (1.34 × 10−3)+ | = | )+ | () | |
| DTLZ3 | (= | (- | (= | (- | (- | - | (3.41 × 10−3) |
| = | - | = | - | (1.64 × 10−2)= | )= | ||
| (+ | (+ | (- | (- | (2.63 × 10−1)+ | )+ | ( | |
| ()+ | (+ | (= | (= | (+ | (6.91 × 10−3 | ( | |
| DTLZ4 | = | + | = | + | - | (1.79 × 10−3 | |
| - | - | (9.71 × 10−4)= | - | - | - | ||
| - | - | = | (1.73 × 10−3)= | - | )= | ||
| - | - | = | (1.23 × 10−3)+ | - | )+ | ||
| DTLZ5 | - | - | = | - | - | - | (1.56 × 10−3) |
| (4.96 × 10−4)+ | + | = | = | + | )+ | ||
| (2.85 × 10−4)+ | + | = | - | + | )+ | ||
| (5.56 × 10−4)+ | + | = | - | + | )+ | ||
| DTLZ6 | - | (5.21 × 10−5)+ | = | - | = | - | |
| (9.44 × 10−4)+ | + | = | + | + | )+ | ||
| + | (2.76 × 10−3)+ | = | + | + | )+ | ||
| (1.49 × 10−3)+ | + | = | + | + | )+ | ||
| DTLZ7 | - | - | = | (4.31 × 10−3)+ | - | )= | |
| - | - | = | (9.49 × 10−3)+ | - | )+ | ||
| - | = | = | + | = | (1.68 × 10−1 | ||
| + | + | = | + | = | (1.71 × 10−1 | ||
| WFG1 | - | - | = | + | - | (1.00 × 10−2 | |
| - | - | = | = | = | (8.99 × 10−3 | ||
| - | - | = | - | + | (2.61 × 10−2 | ||
| - | - | = | + | + | (2.55 × 10−2 | ||
| WFG2 | - | - | = | - | - | - | (9.63 × 10−4) |
| - | - | (2.08 × 10−3)= | - | - | - | ||
| - | - | = | (3.90 × 10−2)= | - | )= | ||
| - | - | = | + | - | (3.36 × 10−2)+ | ||
| WFG3 | - | - | = | + | = | (3.15 × 10−3 | |
| - | - | = | + | (1.37 × 10−2)+ | )+ | ||
| - | - | = | = | (5.23 × 10−2)+ | )+ | ||
| - | - | = | - | (5.77 × 10−2)+ | )+ | ||
| WFG4 | - | - | = | - | - | - | (1.58 × 10−3) |
| - | - | = | = | - | - | (2.31 × 10−3) | |
| - | - | = | (1.75 × 10−2)+ | - | - | ||
| - | - | = | (5.04 × 10−2)+ | + | )+ | ||
| WFG5 | - | - | (1.02 × 10−3)= | - | - | - | |
| - | - | (4.05 × 10−3)= | - | - | - | ||
| - | - | = | (1.82 × 10−2)+ | - | - | ||
| - | - | = | (2.79 × 10−2)+ | + | )= | ||
| WFG6 | - | - | = | - | - | - | (4.50 × 10−3) |
| - | - | = | - | - | - | (2.92 × 10−3) | |
| - | - | = | (2.16 × 10−2)+ | - | - | ||
| - | - | = | (2.50 × 10−2)+ | + | )= | ||
| WFG7 | - | - | (2.29 × 10−3)= | - | - | - | |
| - | - | = | - | - | - | (2.43 × 10−3) | |
| - | - | = | (1.79 × 10−2)+ | - | - | ||
| - | - | = | (3.71 × 10−2)+ | + | )+ | ||
| WFG8 | - | - | = | - | - | - | (4.22 × 10−3) |
| - | - | (3.23 × 10−3)= | - | - | - | ||
| - | - | - | (1.91 × 10−2)+ | - | - | ||
| - | - | = | - | - | (5.62 × 10−2)= | ||
| WFG9 | - | - | - | - | - | - | (1.31 × 10−2) |
| - | - | (7.57 × 10−3)= | = | - | - | ||
| - | - | = | (2.34 × 10−2)+ | - | - | ||
| - | - | = | + | - | (2.78 × 10−2)+ | ||
| +/-/= | 16/44/4 | 11/50/3 | 1/5/58 | 26/29/9 | 18/37/9 | 26/30/8 |
| Problem | IDBEA | ANSGAIII | MOEADAWA | RVEAa | DEAGNG | AdaW | RGEA |
|---|---|---|---|---|---|---|---|
| DTLZ1 | - | - | - | - | - | - | (4.31 × 10−4) |
| = | = | + | = | - | (1.45 × 10−3)+ | ||
| - | = | = | (9.50 × 10−3)+ | - | - | ||
| - | = | (4.97 × 10−3)+ | + | = | - | ) | |
| DTLZ2 | - | - | (5.68 × 10−4)+ | - | - | = | |
| - | - | (1.21 × 10−2)+ | - | - | - | ||
| (2.95 × 10−3)+ | = | - | - | - | - | ||
| (4.30 × 10−3)+ | = | = | - | - | - | ||
| DTLZ3 | - | - | (6.83 × 10−3)= | - | - | = | |
| - | = | (4.28 × 10−2)+ | + | - | = | ||
| + | = | (7.00 × 10−2)+ | + | = | = | ||
| = | = | (5.44 × 10−2)+ | = | = | = | ||
| DTLZ4 | + | + | (7.93 × 10−2)+ | - | + | = | |
| - | = | = | - | - | - | (4.48 × 10−3) | |
| = | + | = | (1.21 × 10−2)+ | = | - | ||
| = | = | + | + | (1.45 × 10−3)+ | - | ||
| DTLZ5 | - | + | + | + | (1.25 × 10−4)+ | + | |
| (2.66 × 10−3)+ | = | + | + | = | - | ||
| - | - | (3.91 × 10−4)+ | + | - | - | ||
| - | = | (2.64 × 10−4)+ | + | = | - | ||
| DTLZ6 | = | + | + | + | (1.52 × 10−4)+ | + | |
| = | = | (2.82 × 10−3)+ | + | + | + | ||
| + | = | (3.16 × 10−4)+ | + | + | = | ||
| = | = | (3.15 × 10−4)+ | + | + | = | ||
| DTLZ7 | - | = | - | + | - | (9.59 × 10−4)+ | |
| + | = | - | = | (4.63 × 10−3)+ | = | ||
| (1.42 × 10−2)+ | = | = | - | + | - | ||
| (2.52 × 10−2)+ | = | + | + | + | - | ||
| WFG1 | - | = | (6.05 × 10−3)+ | - | + | + | |
| = | - | (8.67 × 10−3)+ | - | + | + | ||
| + | + | (4.69 × 10−4)+ | - | + | + | ||
| + | = | (1.09 × 10−5)+ | - | + | = | ||
| WFG2 | - | - | - | - | - | (1.79 × 10−3)+ | |
| - | - | = | - | - | (1.63 × 10−3)+ | ) | |
| - | = | (2.66 × 10−3)+ | - | - | = | ||
| - | = | (8.32 × 10−4)+ | - | - | - | ||
| WFG3 | - | - | (5.54 × 10−3)+ | = | + | = | |
| - | + | (2.28 × 10−2)+ | - | = | - | ||
| (5.23 × 10−3)+ | + | + | = | + | = | ||
| (7.80 × 10−3)+ | = | + | = | = | = | ||
| WFG4 | - | - | - | - | (3.42 × 10−3)= | - | |
| - | - | - | - | - | - | (3.58 × 10−3) | |
| (8.48 × 10−3)= | - | - | - | - | - | ||
| (1.32 × 10−2)+ | - | + | - | - | - | ||
| WFG5 | - | - | - | - | - | - | (2.44 × 10−3) |
| - | - | - | - | - | - | (2.28 × 10−3) | |
| = | - | - | - | - | - | (3.85 × 10−3) | |
| (4.11 × 10−3)= | - | - | - | - | - | ||
| WFG6 | - | - | - | - | (6.67 × 10−3)+ | + | |
| - | - | - | - | - | - | (7.94 × 10−3) | |
| = | - | - | - | - | - | (1.12 × 10−2) | |
| = | )- | - | - | - | - | (1.07 × 10−2) | |
| WFG7 | - | - | - | - | (2.72 × 10−3)+ | + | |
| - | - | - | - | - | - | (3.32 × 10−3) | |
| = | - | - | - | - | - | (9.73 × 10−3) | |
| (3.51 × 10−3)+ | - | - | - | - | - | ||
| WFG8 | - | - | - | - | = | (3.66 × 10−3)+ | |
| - | - | - | - | - | - | (4.60 × 10−3) | |
| - | - | - | - | - | - | (1.47 × 10−2) | |
| - | (3.32 × 10−2)+ | - | - | - | - | ||
| WFG9 | - | - | - | - | (2.24 × 10−2)+ | - | |
| = | - | - | - | (8.38 × 10−3)= | - | ||
| = | - | - | - | - | - | (2.74 × 10−2) | |
| (1.88 × 10−2)= | = | - | - | - | - | ||
| +/-/= | 15/32/17 | 8/31/25 | 29/28/7 | 16/42/6 | 19/34/11 | 13/37/14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leng, Q.; Shan, B.; Zhou, C. Reference Point and Grid Method-Based Evolutionary Algorithm with Entropy for Many-Objective Optimization Problems. Entropy 2025, 27, 524. https://doi.org/10.3390/e27050524
Leng Q, Shan B, Zhou C. Reference Point and Grid Method-Based Evolutionary Algorithm with Entropy for Many-Objective Optimization Problems. Entropy. 2025; 27(5):524. https://doi.org/10.3390/e27050524
Chicago/Turabian StyleLeng, Qi, Bo Shan, and Chong Zhou. 2025. "Reference Point and Grid Method-Based Evolutionary Algorithm with Entropy for Many-Objective Optimization Problems" Entropy 27, no. 5: 524. https://doi.org/10.3390/e27050524
APA StyleLeng, Q., Shan, B., & Zhou, C. (2025). Reference Point and Grid Method-Based Evolutionary Algorithm with Entropy for Many-Objective Optimization Problems. Entropy, 27(5), 524. https://doi.org/10.3390/e27050524











