Scalable Structure for Chiral Quantum Routing
Abstract
1. Introduction
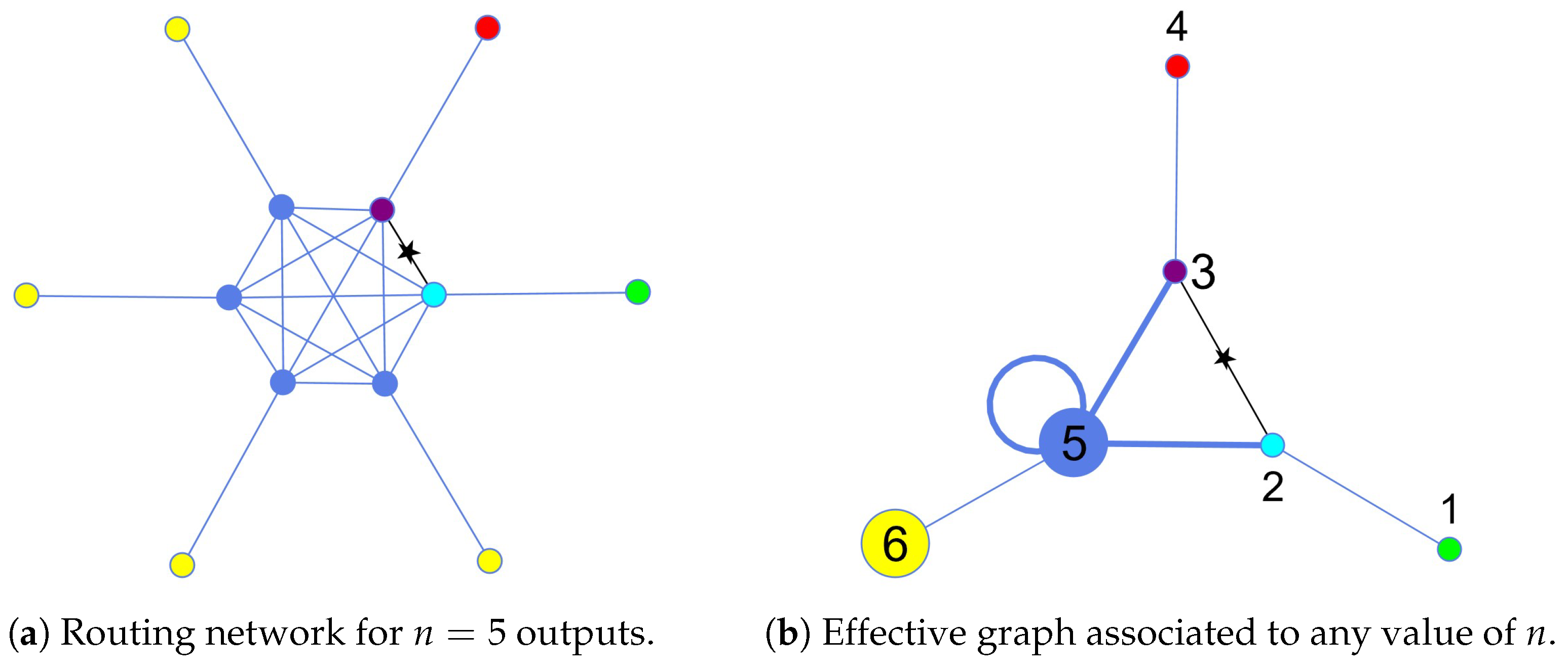
2. Quantum Routing with Quantum Walks
3. Routing Classical Information
3.1. Chiral Optimization
3.2. Edge Weighting Optimization

4. Routing Quantum Information
5. Robustness Against Noise
5.1. Chiral Phase Subject to Static Noise
5.2. Chiral Phase Subject to Dynamical Noise

6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QW | Quantum Walks |
| OU | Ornstein–Uhlenbeck |
References
- Nikolopoulos, G.M.; Jex, I. Quantum State Transfer and Network Engineering; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Yung, M.H.; Bose, S. Perfect state transfer, effective gates, and entanglement generation in engineered bosonic and fermionic networks. Phys. Rev. A 2005, 71, 032310. [Google Scholar] [CrossRef]
- Zwick, A.; Alvarez, G.A.; Stolze, J.; Osenda, O. Robustness of spin-coupling distributions for perfect quantum state transfer. Phys. Rev. A 2011, 84, 022311. [Google Scholar] [CrossRef]
- Shomroni, I.; Rosenblum, S.; Lovsky, Y.; Bechler, O.; Guendelman, G.; Dayan, B. All-optical routing of single photons by a one-atom switch controlled by a single photon. Science 2014, 345, 903–906. [Google Scholar] [CrossRef]
- Pant, M.; Krovi, H.; Towsley, D.; Tassiulas, L.; Jiang, L.; Basu, P.; Englund, D.; Guha, S. Routing entanglement in the quantum internet. Npj Quantum Inf. 2019, 5, 25. [Google Scholar] [CrossRef]
- Bapat, A.; Childs, A.M.; Gorshkov, A.V.; Schoute, E. Advantages and Limitations of Quantum Routing. PRX Quantum 2023, 4, 010313. [Google Scholar] [CrossRef]
- Shi, W.; Malaney, R. Quantum Routing for Emerging Quantum Networks. IEEE Netw. 2024, 38, 140–146. [Google Scholar] [CrossRef]
- Kostak, V.; Nikolopoulos, G.M.; Jex, I. Perfect state transfer in networks of arbitrary topology and coupling configuration. Phys. Rev. A At. Mol. Opt. Phys. 2007, 75, 042319. [Google Scholar] [CrossRef]
- Cavazzoni, S.; Ragazzi, G.; Bordone, P.; Paris, M.G.A. Perfect chiral quantum routing. Phys. Rev. A 2025, 111, 032439. [Google Scholar] [CrossRef]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915–928. [Google Scholar] [CrossRef]
- Mülken, O.; Pernice, V.; Blumen, A. Quantum transport on small-world networks: A continuous-time quantum walk approach. Phys. Rev. E 2007, 76, 051125. [Google Scholar] [CrossRef]
- Mohseni, M.; Rebentrost, P.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 2008, 129, 174106. [Google Scholar] [CrossRef] [PubMed]
- Mülken, O.; Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 2011, 502, 37–87. [Google Scholar] [CrossRef]
- Maciel Cássio, M.; Mendes, C.F.O.; Strunz, W.T.; Galiceanu, M. Quantum transport on generalized scale-free networks. Phys. Rev. A 2020, 102, 032219. [Google Scholar] [CrossRef]
- Cavazzoni, S.; Razzoli, L.; Bordone, P.; Paris, M.G.A. Perturbed graphs achieve unit transport efficiency without environmental noise. Phys. Rev. E 2022, 106, 024118. [Google Scholar] [CrossRef]
- Childs, A.M. Universal Computation by Quantum Walk. Phys. Rev. Lett. 2009, 102, 180501. [Google Scholar] [CrossRef]
- Hines, A.P.; Stamp, P.C.E. Quantum walks, quantum gates, and quantum computers. Phys. Rev. A 2007, 75, 062321. [Google Scholar] [CrossRef]
- Chen, Z.; Li, G.; Li, L. Implementation of a continuous-time quantum walk on a sparse graph. Phys. Rev. A 2024, 110, 052215. [Google Scholar] [CrossRef]
- Childs, A.M.; Goldstone, J. Spatial search by quantum walk. Phys. Rev. A 2004, 70, 022314. [Google Scholar] [CrossRef]
- Malmi, J.; Rossi, M.A.C.; García-Pérez, G.; Maniscalco, S. Spatial search by continuous-time quantum walks on renormalized Internet networks. Phys. Rev. Res. 2022, 4, 043185. [Google Scholar] [CrossRef]
- Candeloro, A.; Benedetti, C.; Genoni, M.G.; Paris, M.G.A. Feedback-Assisted Quantum Search by Continuous-Time Quantum Walks. Adv. Quantum Technol. 2023, 6, 2200093. [Google Scholar] [CrossRef]
- Benedetti, C.; Tamascelli, D.; Paris, M.G.A.; Crespi, A. Quantum Spatial Search in Two-Dimensional Waveguide Arrays. Phys. Rev. Appl. 2021, 16, 054036. [Google Scholar] [CrossRef]
- Portugal, R. Quantum Walks and Search Algorithms; Springer Nature: Cham, Switzerland, 2018. [Google Scholar]
- Seveso, L.; Benedetti, C.; Paris, M.G.A. The walker speaks its graph: Global and nearly-local probing of the tunnelling amplitude in continuous-time quantum walks. J. Phys. A Math. Theo. 2019, 52, 105304. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, S.; Wu, J.; Xu, P. Continuous-time quantum walk based centrality testing on weighted graphs. Sci. Rep. 2022, 12, 6001. [Google Scholar] [CrossRef] [PubMed]
- Gianani, I.; Benedetti, C. Multiparameter estimation of continuous-time quantum walk Hamiltonians through machine learning. AVS Quantum Sci. 2023, 5, 014405. [Google Scholar] [CrossRef]
- Benedetti, C.; Gianani, I. Identifying network topologies via quantum walk distributions. AVS Quantum Sci. 2024, 6, 014412. [Google Scholar] [CrossRef]
- Zimborás, Z.; Faccin, M.; Kádár, Z.; Whitfield, J.D.; Lanyon, B.P.; Biamonte, J. Quantum Transport Enhancement by Time-Reversal Symmetry Breaking. Sci. Rep. 2013, 3, 2361. [Google Scholar] [CrossRef]
- Wong, T.G. Quantum walk search with time-reversal symmetry breaking. J. Phys. A Math. Theor. 2015, 48, 405303. [Google Scholar] [CrossRef]
- Lu, D.; Biamonte, J.D.; Li, J.; Li, H.; Johnson, T.H.; Bergholm, V.; Faccin, M.; Zimborás, Z.; Laflamme, R.; Baugh, J.; et al. Chiral quantum walks. Phys. Rev. A 2016, 93, 042302. [Google Scholar] [CrossRef]
- Frigerio, M.; Benedetti, C.; Olivares, S.; Paris, M.G.A. Generalized quantum-classical correspondence for random walks on graphs. Phys. Rev. A 2021, 104, L030201. [Google Scholar] [CrossRef]
- Bedkihal, S.; Bandyopadhyay, M.; Segal, D. The probe technique far from equilibrium: Magnetic field symmetries of nonlinear transport. Eur. Phys. J. B 2013, 86, 506. [Google Scholar] [CrossRef]
- Kryukov, A.; Abramov, R.; Fedichkin, L.E.; Alodjants, A.; Melnikov, A.A. Supervised graph classification for chiral quantum walks. Phys. Rev. A 2022, 105, 022208. [Google Scholar] [CrossRef]
- Frigerio, M.; Benedetti, C.; Olivares, S.; Paris, M.G.A. Quantum-classical distance as a tool to design optimal chiral quantum walks. Phys. Rev. A 2022, 105, 032425. [Google Scholar] [CrossRef]
- Bottarelli, A.; Frigerio, M.; Paris, M.G.A. Quantum routing of information using chiral quantum walks. AVS Quantum Sci. 2023, 5, 025001. [Google Scholar] [CrossRef]
- Sağlam, U.; Paternostro, M.; Müstecaplıoğlu, O.E. Entanglement transfer via chiral and continuous-time quantum walks on a triangular chain. Phys. A Stat. Mech. Appl. 2023, 612, 128480. [Google Scholar] [CrossRef]
- Wang, Q.; Ren, S.; Yin, R.; Ziegler, K.; Barkai, E.; Tornow, S. First Hitting Times on a Quantum Computer: Tracking vs. Local Monitoring, Topological Effects, and Dark States. Entropy 2024, 26, 869. [Google Scholar] [CrossRef]
- Boada, O.; Novo, L.; Sciarrino, F.; Omar, Y. Quantum walks in synthetic gauge fields with three-dimensional integrated photonics. Phys. Rev. A 2017, 95, 013830. [Google Scholar] [CrossRef]
- Novo, L.; Ribeiro, S. Floquet engineering of continuous-time quantum walks: Toward the simulation of complex and next-nearest-neighbor couplings. Phys. Rev. A 2021, 103, 042219. [Google Scholar] [CrossRef]
- Dalibard, J.; Gerbier, F.; Juzeliūnas, G.; Öhberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 2011, 83, 1523–1543. [Google Scholar] [CrossRef]
- Schreiber, A.; Cassemiro, K.N.; Potoček, V.; Gábris, A.; Jex, I.; Silberhorn, C. Decoherence and Disorder in Quantum Walks: From Ballistic Spread to Localization. Phys. Rev. Lett. 2011, 106, 180403. [Google Scholar] [CrossRef]
- Izaac, J.; Wang, J.; Li, Z. Continuous-time quantum walks with defects and disorder. Phys. Rev. A 2013, 88, 042334. [Google Scholar] [CrossRef]
- Crespi, A.; Osellame, R.; Ramponi, R.; Giovannetti, V.; Fazio, R.; Sansoni, L.; De Nicola, F.; Sciarrino, F.; Mataloni, P. Anderson localization of entangled photons in an integrated quantum walk. Nat. Photonics 2013, 7, 322. [Google Scholar] [CrossRef]
- Benedetti, C.; Buscemi, F.; Bordone, P.; Paris, M.G.A. Non-markovian continuous-time quantum walks on lattices with dynamical noise. Phys. Rev. A 2016, 93, 042313. [Google Scholar] [CrossRef]
- Benedetti, C.; Rossi, M.A.C.; Paris, M.G.A. Continuous-time quantum walks on dynamical percolation graphs. Europhys. Lett. 2019, 124, 60001. [Google Scholar] [CrossRef]
- Bressanini, G.; Benedetti, C.; Paris, M.G.A. Decoherence and classicalization of continuous-time quantum walks on graphs. Quantum Inf. Proc. 2022, 21, 317. [Google Scholar] [CrossRef]
- Kurz, G.; Pfaff, F.; Hanebeck, U.D. Kullback-leibler divergence and moment matching for hyperspherical probability distributions. In Proceedings of the 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2087–2094. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the Theory of the Brownian Motion. Phys. Rev. 1930, 36, 823–841. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact numerical simulation of the Ornstein-Uhlenbeck process and its integral. Phys. Rev. E 1996, 54, 2084–2091. [Google Scholar] [CrossRef]
- Bose, S. Quantum Communication through an Unmodulated Spin Chain. Phys. Rev. Lett. 2003, 91, 207901. [Google Scholar] [CrossRef]
- Kay, A. Perfect, efficient, state transfer and its application as a constructive tool. Int. J. Quantum Inf. 2010, 8, 641–676. [Google Scholar] [CrossRef]
- Meyer, D.A.; Wong, T.G. Connectivity is a poor indicator of fast quantum search. Phys. Rev. Lett. 2015, 114, 110503. [Google Scholar] [CrossRef]
- Razzoli, L.; Paris, M.G.A.; Bordone, P. Transport efficiency of continuous-time quantum walks on graphs. Entropy 2021, 23, 85. [Google Scholar] [CrossRef]
- Jozsa, R. Fidelity for mixed quantum states. J. Mod. Opt. 1994, 41, 2315–2323. [Google Scholar] [CrossRef]
- Raginsky, M. A fidelity measure for quantum channels. Phys. Lett. A 2001, 290, 11–18. [Google Scholar] [CrossRef]
- Gilchrist, A.; Langford, N.K.; Nielsen, M.A. Distance measures to compare real and ideal quantum processes. Phys. Rev. A At. Mol. Opt. Phys. 2005, 71, 062310. [Google Scholar] [CrossRef]
- Chen, H.B.; Gneiting, C.; Lo, P.Y.; Chen, Y.N.; Nori, F. Simulating open quantum systems with Hamiltonian ensembles and the nonclassicality of the dynamics. Phys. Rev. Lett. 2018, 120, 030403. [Google Scholar] [CrossRef]
- Ragazzi, G.; Cavazzoni, S.; Bordone, P.; Paris, M.G.A. Generalized phase estimation in noisy quantum gates. Phys. Rev. A 2024, 110, 052425. [Google Scholar] [CrossRef]
- Cialdi, S.; Benedetti, C.; Tamascelli, D.; Olivares, S.; Paris, M.G.A.; Vacchini, B. Experimental investigation of the effect of classical noise on quantum non-Markovian dynamics. Phys. Rev. A 2019, 100, 052104. [Google Scholar] [CrossRef]
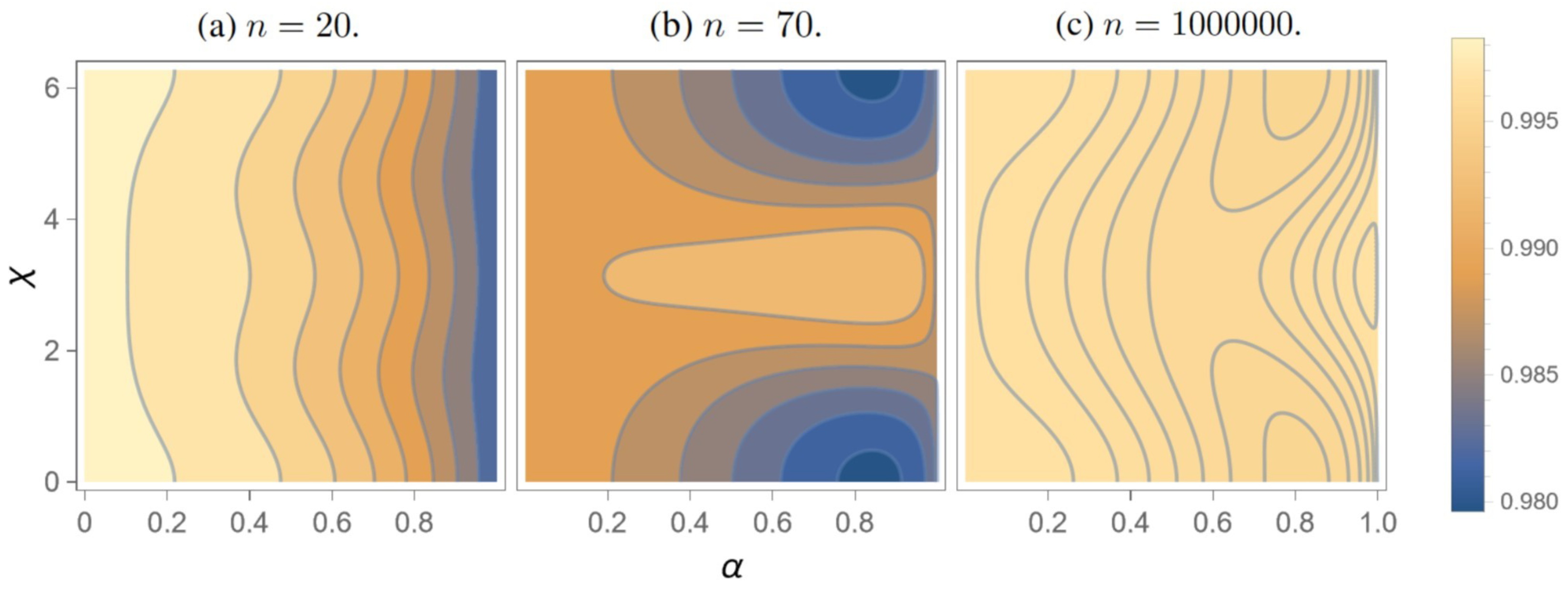
| n | t | (rad) | |
|---|---|---|---|
| 20 | 4.712 | ||
| 4.708 | |||
| 70 | 18.397 | 4.758 | |
| 18.484 | 4.765 | ||
| 40.068 | 4.716 |
| Von Mises | Gaussian | OU |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ragazzi, G.; Cavazzoni, S.; Benedetti, C.; Bordone, P.; Paris, M.G.A. Scalable Structure for Chiral Quantum Routing. Entropy 2025, 27, 498. https://doi.org/10.3390/e27050498
Ragazzi G, Cavazzoni S, Benedetti C, Bordone P, Paris MGA. Scalable Structure for Chiral Quantum Routing. Entropy. 2025; 27(5):498. https://doi.org/10.3390/e27050498
Chicago/Turabian StyleRagazzi, Giovanni, Simone Cavazzoni, Claudia Benedetti, Paolo Bordone, and Matteo G. A. Paris. 2025. "Scalable Structure for Chiral Quantum Routing" Entropy 27, no. 5: 498. https://doi.org/10.3390/e27050498
APA StyleRagazzi, G., Cavazzoni, S., Benedetti, C., Bordone, P., & Paris, M. G. A. (2025). Scalable Structure for Chiral Quantum Routing. Entropy, 27(5), 498. https://doi.org/10.3390/e27050498







