Quantum κ-Entropy: A Quantum Computational Approach
Abstract
1. Introduction
2. Kappa Entropy for Canonical States
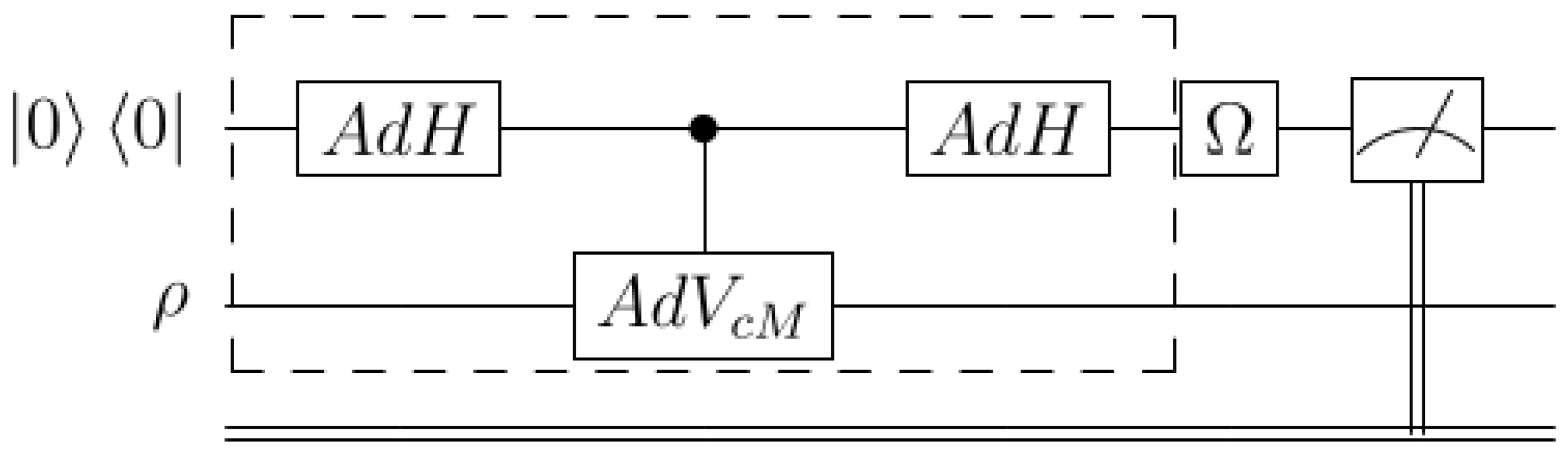
3. Quantum Channels for Entropy
4. Set of Values and Bounds for Entropy
5. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proofs
References
- Kaniadakis, G. Non-linear kinetics underlying generalized statistics. Phys. A 2001, 296, 405–425. [Google Scholar] [CrossRef]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. Phys. Rev. E 2002, 66, 056125. [Google Scholar] [CrossRef] [PubMed]
- Kaniadakis, G. Statistical mechanics in the context of special relativity II. Phys. Rev. E 2005, 72, 036108. [Google Scholar] [CrossRef] [PubMed]
- Kaniadakis, G. Relativistic roots of κ-entropy. Entropy 2024, 26, 406. [Google Scholar] [CrossRef]
- Silva, R. The relativistic statistical theory and Kaniadakis entropy: An approach through a molecular chaos hypothesis. Eur. Phys. J. B 2006, 54, 499–502. [Google Scholar] [CrossRef]
- Silva, R. The H-theorem in κ-statistics: Influence on the molecular chaos hypothesis. Phys. Lett. A 2006, 352, 17–20. [Google Scholar] [CrossRef]
- Wada, T. Thermodynamic stabilities of the generalized Boltzmann entropies. Phys. A 2004, 340, 126–130. [Google Scholar]
- Wada, T. Thermodynamic stability conditions for nonadditive composable entropies. Contin. Mechan. Thermod. 2004, 16, 263–267. [Google Scholar] [CrossRef]
- Naudts, J. Deformed exponentials and logarithms in generalized thermostatistics. Phys. A 2002, 316, 323–334. [Google Scholar] [CrossRef]
- Naudts, J. Continuity of a class of entropies and relative entropies. Rev. Math. Phys. 2004, 16, 809–822. [Google Scholar] [CrossRef]
- Scarfone, A.M.; Wada, T. Canonical partition function for anomalous systems described by the κ-entropy. Prog. Theor. Phys. Suppl. 2006, 162, 45–52. [Google Scholar] [CrossRef]
- Yamano, T. On the laws of thermodynamics from the escort average and on the uniqueness of statistical factors. Phys. Lett. A 2003, 308, 364–368. [Google Scholar] [CrossRef]
- Lucia, U. Maximum entropy generation and kappa-exponential model. Phys. A 2010, 389, 4558–4563. [Google Scholar] [CrossRef]
- Pistone, G. κ-exponential models from the geometrical point of view. Eur. Phys. J. B 2009, 70, 29–37. [Google Scholar] [CrossRef]
- Pistone, G.; Shoaib, M. Kaniadakis’s Information Geometry of Compositional Data. Entropy 2023, 25, 1107. [Google Scholar] [CrossRef]
- Oikonomou, T.; Bagci, G.B. A completness criterion for Kaniadakis, Abe, and two-parameter generalized statistical theories. Rep. Math. Phys. 2010, 66, 137–146. [Google Scholar] [CrossRef]
- Stankovic, M.S.; Marinkovic, S.D.; Rajkovic, P.M. The deformed exponential functions of two variables in the context of various statistical mechanics. Appl. Math. Comput. 2011, 218, 2439–2448. [Google Scholar] [CrossRef]
- Tempesta, P. Group entropies, correlation laws, and zeta functions. Phys. Rev. E 2011, 84, 021121. [Google Scholar] [CrossRef]
- Vigelis, R.F.; Cavalcante, C.C. On φ-Families of probability distributions. J. Theor. Probab. 2013, 26, 870–884. [Google Scholar] [CrossRef]
- Scarfone, A.M. Entropic Forms and Related Algebras. Entropy 2013, 15, 624–649. [Google Scholar] [CrossRef]
- da Costa, B.G.; Gomez, I.S.; Portesi, M. κ-Deformed quantum and classical mechanics for a system with position-dependent effective mass. J. Math. Phys. 2020, 61, 082105. [Google Scholar] [CrossRef]
- Biro, T.S. Kaniadakis Entropy Leads to Particle-Hole Symmetric Distribution. Entropy 2022, 24, 1217. [Google Scholar] [CrossRef] [PubMed]
- Sfetcu, R.-C.; Sfetcu, S.-C.; Preda, V. Some Properties of Weighted Tsallis and Kaniadakis Divergences. Entropy 2022, 24, 1616. [Google Scholar] [CrossRef] [PubMed]
- Sfetcu, R.-C.; Sfetcu, S.-C.; Preda, V. On Tsallis and Kaniadakis Divergences. Math. Phys. An. Geom. 2022, 25, 7. [Google Scholar] [CrossRef]
- Wada, T.; Scarfone, A.M. On the Kaniadakis Distributions Applied in Statistical Physics and Natural Sciences. Entropy 2023, 25, 292. [Google Scholar] [CrossRef]
- Scarfone, A.M.; Wada, T. Multi-Additivity in Kaniadakis Entropy. Entropy 2024, 26, 77. [Google Scholar] [CrossRef]
- Chung1, W.S.; Hassanabadi, H. Investigation of Some Quantum Mechanics Problemswith κ-Translation Symmetry. Int. J. Theor. Phys. 2022, 61, 110. [Google Scholar] [CrossRef]
- Santos, F.F.; Boschi-Filho, H. Black branes in asymptotically Lifshitz spacetimes with arbitrary exponents in κ-Horndeski gravity. Phys. Rev. D 2024, 109, 064035. [Google Scholar] [CrossRef]
- Pereira, F.I.M.; Silva, R.; Alcaniz, J.S. Non-gaussian statistics and the relativistic nuclear equation of state. Nucl. Phys. A 2009, 828, 136–148. [Google Scholar] [CrossRef]
- Santos, A.P.; Silva, R.; Alcaniz, J.S.; Anselmo, D.H.A.L. Kaniadakis statistics and the quantum H-theorem. Phys. Lett. A 2011, 375, 352–355. [Google Scholar] [CrossRef]
- Santos, A.P.; Silva, R.; Alcaniz, J.S.; Anselmo, D.H.A.L. Generalized quantum entropies. Phys. Lett. A 2011, 375, 3119–3123. [Google Scholar] [CrossRef]
- Santos, A.P.; Silva, R.; Alcaniz, J.S.; Anselmo, D.H.A.L. Non-Gaussian effects on quantum entropies. Phys. A 2012, 391, 2182–2192. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A.; Barboza, E.M.; Nunes, R.C. Jeans instability criterion from the viewpoint of Kaniadakis statistics. EPL 2016, 114, 55001. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A.; Barboza, E.M.; Nunes, R.C. Tsallis and Kaniadakis statistics from the viewpoint of entropic gravity formalism. Int. J. Mod. Phys. 2017, 32, 1750028. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, S.X.; Liu, S.Q. Jeans gravitational instability with kappa-deformed Kaniadakis distribution. Chin. Phys. Lett. 2017, 34, 075101. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A.; Mendes, A.C.R.; Bonilla, A. Tsallis and Kaniadakis statistics from a point of view of the holographic equipartition law. EPL 2018, 121, 45002. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A.; Mendes, A.C.R.; Bonilla, A.; de Paula, R.M. Cosmological considerations in Kaniadakis statistics. EPL 2018, 124, 30003. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A.; Mendes, A.C.R.; de Paula, R.M. Loop quantum gravity Immirzi parameter and the Kaniadakis statistics. Chaos Sol. Fractals 2019, 118, 307–310. [Google Scholar] [CrossRef]
- Yang, W.; Xiong, Y.; Chen, H.; Liu, S. Jeans instability of dark-baryonic matter model in the context of Kaniadakis’ statistic distribution. J. Taibah Univ. Sci. 2022, 16, 337–343. [Google Scholar] [CrossRef]
- He, K.-R. Jeans analysis with κ-deformed Kaniadakis distribution in f (R) gravity. Phys. Scr. 2022, 97, 025601. [Google Scholar] [CrossRef]
- Moradpour, H.; Javaherian, M.; Namvar, E.; Ziaie, A.H. Gamow Temperature in Tsallis and Kaniadakis Statistics. Entropy 2022, 24, 797. [Google Scholar] [CrossRef] [PubMed]
- Luciano, G.G. Modified Friedmann equations from Kaniadakis entropy and cosmological implications on baryogenesis and 7Li -abundance. Eur. Phys. J. C 2022, 82, 314. [Google Scholar] [CrossRef]
- Luciano, G.G.; Saridakis, E.N. P-v criticalities, phase transitions and geometrothermodynamics of charged AdS black holes from Kaniadakis statistics. J. High Energy Phys. 2023, 2023, 114. [Google Scholar] [CrossRef]
- Lambiase, G.; Luciano, G.G.; Sheykhi, A. Slow-roll inflation and growth of perturbations in Kaniadakis modification of Friedmann cosmology. Eur. Phys. J. C 2023, 83, 936. [Google Scholar] [CrossRef]
- Sheykhi, A. Corrections to Friedmann equations inspired by Kaniadakis entropy. Phys. Lett. 2024, 850, 138495. [Google Scholar] [CrossRef]
- Wilde, M.M. Quantum Information Theory; Cambridge University Press: Cambridge, UK, 2017; Available online: https://www.markwilde.com (accessed on 2 April 2025).
- Wang, Y.X.; Mu, L.; Vedral, V.; Fan, H. Entanglement Renyi alpha entropy. Phys. Rev. A 2016, 93, 022324. [Google Scholar] [CrossRef]
- Cui, J.; Gu, M.; Kwek, L.C.; Santos, M.F.; Vedral, H.F. Quantum phases with differing computational power. Nat. Commun. 2012, 3, 812. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013; Chapter 8. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Meyer, C.D. Matrix Analysis and Applied Linear Algebra; SIAM: Philadelphia, PA, USA, 2000; Chapter 8. [Google Scholar]
- Kraus, K. States, Effects, and Operations: Fundamental Notions of Quantum Theory; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1983; Volume 190. [Google Scholar]
- Aharonov, D.; Jones, V.; Landau, V. A Polynomial Quantum Algorithm for Approximating the Jones Polynomial. Algorithmica 2009, 55, 395. [Google Scholar] [CrossRef]
- Weisstein, E. Sinhc Function—From MathWorld, A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/SinhcFunction.html (accessed on 16 April 2025).
- Sa’nchez-Reyes, J. The Hyperbolic Sine Cardinal and the Catenary. College Math. J. 2012, 43, 285–290. [Google Scholar] [CrossRef]
- Merca, M. Asymptotics of the Chebyshev–Stirling numbers of the first kind. Integral Trans. Spec. Fun. 2015. [Google Scholar] [CrossRef]
- Merca, M. The cardinal sine function and the Chebyshev–Stirling numbers. J. Number Theory 2016, 160, 19–31. [Google Scholar] [CrossRef]
- Bosyk, G.M.; Zozor, S.; Holik, F.; Portesi, M.; Lamberti, P.W. A family of generalized quantum entropies: Definition and properties. Quantum Inf. Process 2016, 15, 3393. [Google Scholar] [CrossRef]
- Bosyk, G.M.; Zozor, S.; Holik, F.; Portesi, M.; Lamberti, P.W. Comment on Quantum Kaniadakis entropy under projective measurement. Phys. Rev. E 2016, 94, 026103. [Google Scholar] [CrossRef]
- Ourabah, K.; Hamici-Bendimerad, A.H.; Tribeche, M. Quantum entanglement and Kaniadakis entropy. Phys. Scr. 2015, 90, 045101. [Google Scholar] [CrossRef]
- Bhatia, R. Matrix Analysis; Springer: New York, NY, USA, 1997. [Google Scholar]
- Alberti, P.M.; Uhlmann, A. Stochasticity and Partial Order: Double Stochastic Map and Unitary Mixing; Dordrecht: Boston, MA, USA, 1982. [Google Scholar]
- Nielsen, M.A. An Introduction to Majorization and Its Applications to Quantum Mechanics. Available online: http://michaelnielsen.org/papers/maj-book-notes.pdf (accessed on 16 April 2025).
- Ellinas, D.; Floratos, E.G. Prime factorization and correlation measure for finite quantum systems. J. Phys. A Math. Gen. 1999, 32, L63–L69. [Google Scholar] [CrossRef]
- Ellinas, D. SL (2,C) multilevel dynamics. Phys. Rev. A 1992, 45, 1822–1828. [Google Scholar] [CrossRef]
- Brennen, G.K.; Ellinas, D.; Kendon, V.; Pachos, J.K.; Tsohantjis, I.; Wang, Z. Anyonic Quantum Walks. Ann. Phys. 2010, 325, 664–681. [Google Scholar] [CrossRef]
- Barnett, M.; Ellinas, D.; Dupertuis, M.A. Berry’s phase in coherent excitation of atoms. J. Mod. Opt. 1988, 35, 565–574. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. Inequalities: Theory of Majorization and Its Applications; Academic: New York, NY, USA, 1979. [Google Scholar]
- Bracken, A.J.; Ellinas, D.; Tsojantjis, I. Pseudo memory effects, majorization and entropy in quantum random walks. J. Phys. A Math. Gen. 2004, 37, L91–L97. [Google Scholar] [CrossRef]
- Langville, A.N.; Meyer, C.D. Google’s PageRank and Beyond: The Science of Search Engine Rankings; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ellinas, D.; Kaniadakis, G. Quantum κ-Entropy: A Quantum Computational Approach. Entropy 2025, 27, 482. https://doi.org/10.3390/e27050482
Ellinas D, Kaniadakis G. Quantum κ-Entropy: A Quantum Computational Approach. Entropy. 2025; 27(5):482. https://doi.org/10.3390/e27050482
Chicago/Turabian StyleEllinas, Demosthenes, and Giorgio Kaniadakis. 2025. "Quantum κ-Entropy: A Quantum Computational Approach" Entropy 27, no. 5: 482. https://doi.org/10.3390/e27050482
APA StyleEllinas, D., & Kaniadakis, G. (2025). Quantum κ-Entropy: A Quantum Computational Approach. Entropy, 27(5), 482. https://doi.org/10.3390/e27050482







