The Knudsen Layer in Modeling the Heat Transfer at Nanoscale: Bulk and Wall Contributions to the Local Heat Flux
Abstract
1. Introduction
2. The Theoretical Model
3. Longitudinal Heat Transfer in Steady-State Situations
3.1. The Case of a Two-Dimensional Nanolayer
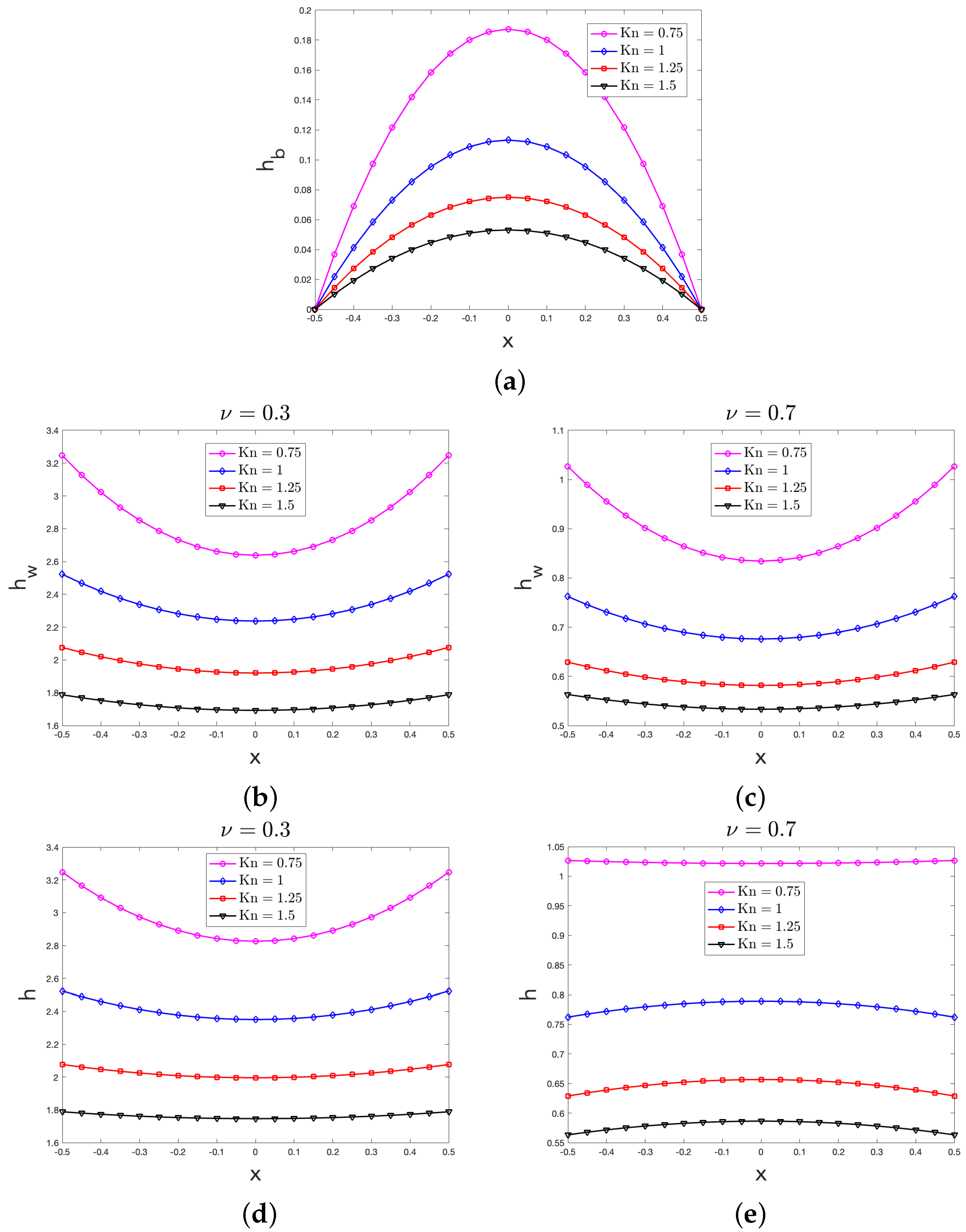
3.1.1. The Behavior of the Heat Flux Vectors
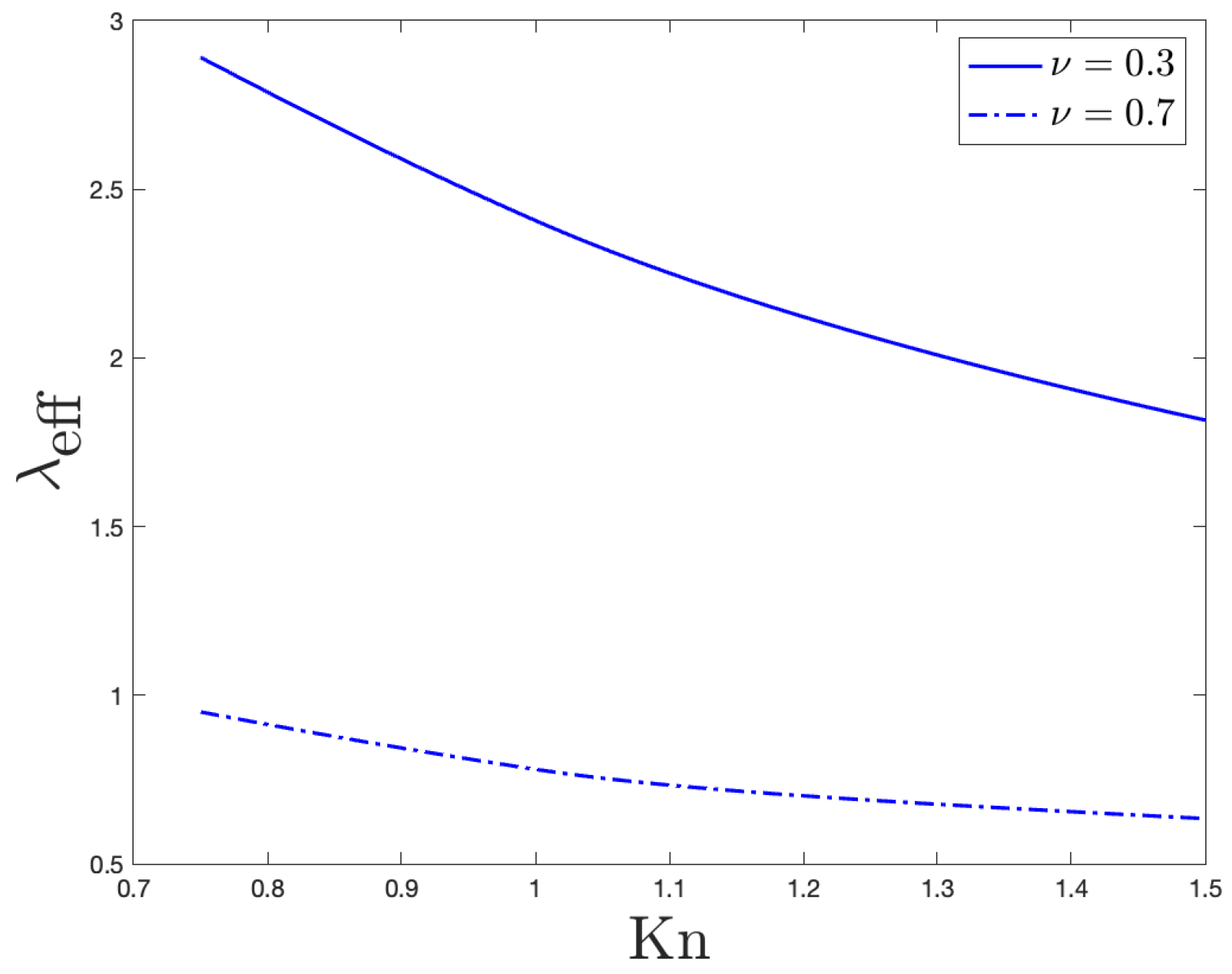
3.1.2. The Effective Thermal Conductivity
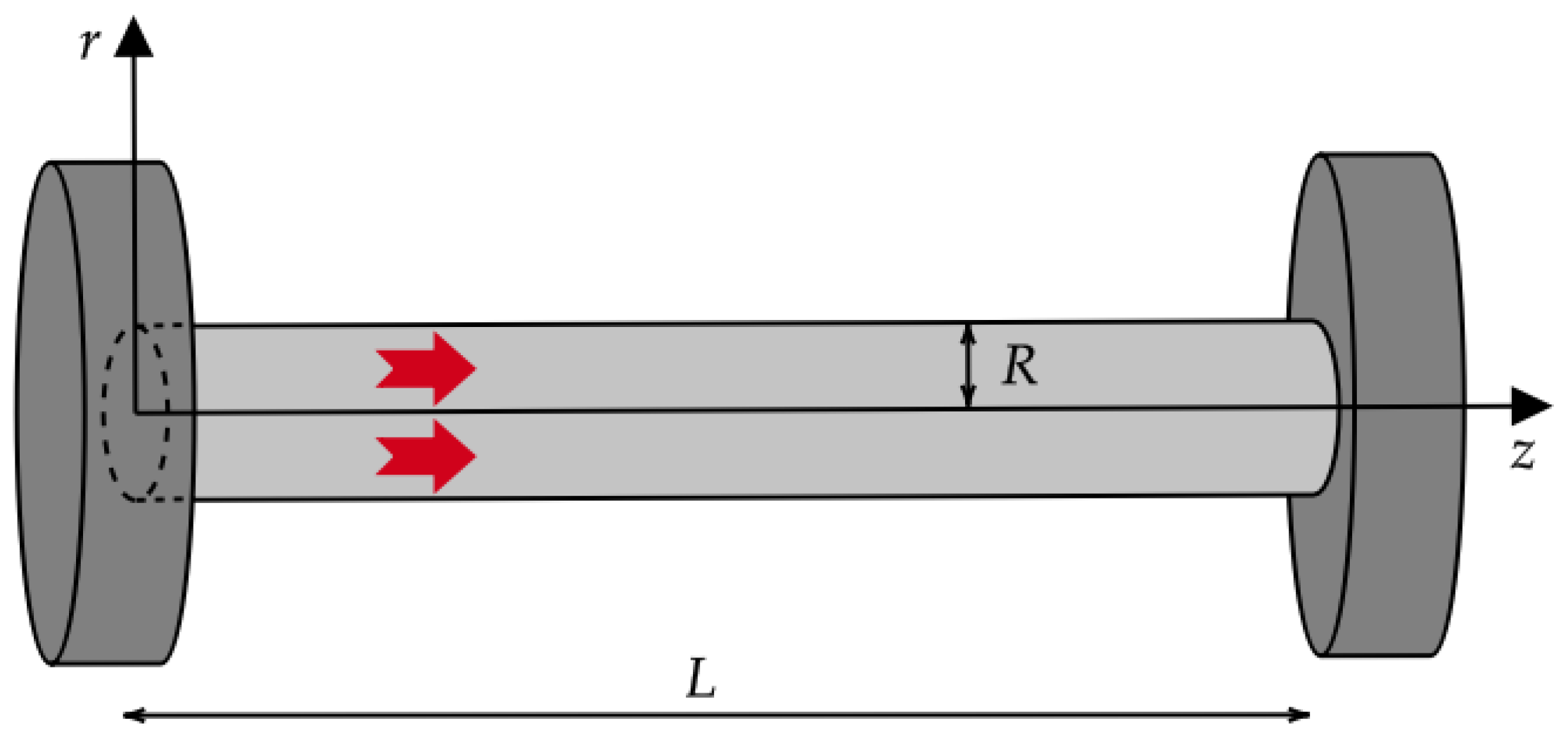
3.2. The Case of a Nanowire
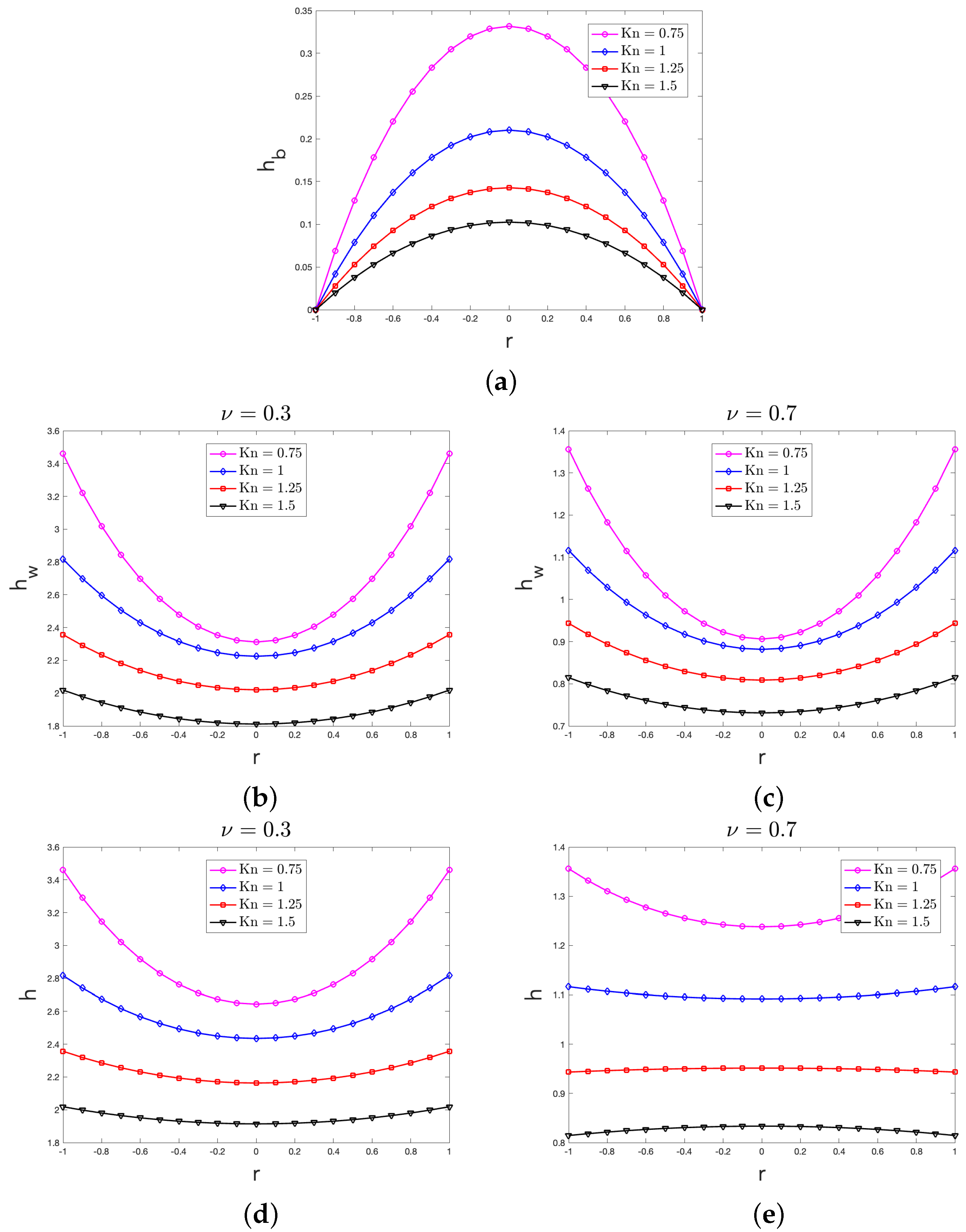
3.2.1. The Behavior of the Heat Flux Vector
3.2.2. The Effective Thermal Conductivity
4. Summary and Conclusions
4.1. Comments on the Bulk Heat Flux Profile
4.2. Comments on the Wall Heat Flux Profile
4.3. Comments on the Heat Flux Profile
4.4. Comments on the Effective Thermal Conductivity
4.5. Final Remark
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Meaning | Unit of Measurement |
| non-equilibrium temperature | K | |
| value of at the wall | K | |
| local-equilibrium temperature | K | |
| reference temperature | K | |
| e | specific internal energy | |
| local heat flux | ||
| bulk heat flux | ||
| flux of | ||
| deviatoric (traceless) part of | ||
| volumetric part of | ||
| wall heat flux | ||
| flux of | ||
| deviatoric (traceless) part of | ||
| volumetric part of | ||
| relaxation time of | s | |
| relaxation time of | s | |
| relaxation time of | s | |
| relaxation time of | s | |
| relaxation time of | s | |
| relaxation time of | s | |
| thermal conductivity | ||
| ℓ | mean-free path of phonons | m |
| s | specific entropy per unit volume | |
| specific-entropy flux per unit volume | ||
| specific-entropy production per unit volume | ||
| non-equilibrium temperature | ||
| temperature gradient | ||
| bulk heat flux | ||
| wall heat flux | ||
| total heat flux | ||
| Kn | Knudsen number | |
| parameters accounting for the reflections of the | ||
| heat carriers at the walls | ||
| p | ||
| momentum accommodation coefficient | ||
| parameter accounting for the possible difference | ||
| of ℓ in the bulk and in the Knudsen layer | ||
| effective thermal conductivity |
References
- Chen, G. Nanoscale Energy Transport and Conversion—A Parallel Treatment of Electrons, Molecules, Phonons, and Photons; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Ván, P. Weakly nonlocal irreversible thermodynamics—The Guyer-Krumhansl and the Cahn-Hilliard equations. Phys. Lett. A 2001, 290, 88–92. [Google Scholar] [CrossRef]
- Cao, B.-Y.; Guo, Z.-Y. Equation of motion of a phonon gas and non-Fourier heat conduction. J. Appl. Phys. 2007, 102, 053503. [Google Scholar] [CrossRef]
- Lebon, G.; Jou, D.; Casas-Vázquez, J. Understanding Non-Equilibrium Thermodynamics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 4th revised ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Tzou, D.Y. Macro- to Microscale Heat Transfer: The Lagging Behaviour, 2nd ed.; Wiley: Chichester, UK, 2014. [Google Scholar]
- Cahill, D.G.; Braun, P.V.; Chen, G.; Clarke, D.R.; Fan, S.; Goodson, K.E.; Keblinski, P.; King, W.P.; Mahan, G.D.; Majumdar, A.; et al. Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 2014, 1, 011305. [Google Scholar] [CrossRef]
- Dong, Y. Dynamical Analysis of Non-Fourier Heat Conduction and Its Application in Nanosystems; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2016. [Google Scholar]
- Sellitto, A.; Cimmelli, V.A.; Jou, D. Linear and Nonlinear Heat-Transport Equations. In Mesoscopic Theories of Heat Transport in Nanosystems; SEMA SIMAI Springer Series; Springer International Publishing: Cham, Switzerland, 2016; Colume 6; pp. 31–51. [Google Scholar]
- Kovács, R.; Madjarević, D.; Simić, S.; Ván, P. Non-equilibrium theories of rarefied gases: Internal variables and extended thermodynamics. Continuum Mech. Thermodyn. 2021, 33, 307–325. [Google Scholar] [CrossRef]
- Fugallo, G.; Lazzeri, M.; Paulatto, L.; Mauri, F. Ab initio variational approach for evaluating lattice thermal conductivity. Phys. Rev. B 2013, 88, 045430. [Google Scholar] [CrossRef]
- Li, W.; Carrete, J.; Katcho, N.A.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Zou, J.-H.; Cao, B.-Y. Phonon thermal properties of graphene on h-BN from molecular dynamics simulations. J. Appl. Phys. 2017, 110, 103106. [Google Scholar] [CrossRef]
- He, J.; Li, D.; Ying, Y.; Feng, C.; He, J.; Zhong, C.; Zhou, H.; Zhou, P.; Zhang, G. Orbitally driven giant thermal conductance associated with abnormal strain dependence in hydrogenated graphene-like borophene. npj Comput. Mater. 2019, 5, 47. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, M. Phonon hydrodynamics and its applications in nanoscale heat transport. Phys. Rep. 2015, 595, 1–44. [Google Scholar] [CrossRef]
- Sellitto, A.; Cimmelli, V.A.; Jou, D. Mesoscopic Description of Boundary Effects and Effective Thermal Conductivity in Nanosystems: Phonon Hydrodynamics. In Mesoscopic Theories of Heat Transport in Nanosystems; SEMA SIMAI Springer Series; Springer International Publishing: Cham, Switzerland, 2016; Volume 6, pp. 53–89. [Google Scholar]
- Guo, Y.; Wang, M. Phonon hydrodynamics for nanoscale heat transport at ordinary temperatures. Phys. Rev. B 2018, 97, 035421. [Google Scholar] [CrossRef]
- Beardo, A.; Hennessy, M.G.; Sendra, L.; Camacho, J.; Myers, T.G.; Bafaluy, J.; Alvarez, F.X. Phonon hydrodynamics in frequency-domain thermoreflectance experiments. Phys. Rev. B 2020, 101, 075303. [Google Scholar] [CrossRef]
- Lee, S.; Broido, D.; Esfarjani, K.; Chen, G. Hydrodynamic phonon transport in suspended graphene. Nat. Comm. 2015, 6, 6290. [Google Scholar] [CrossRef]
- Bochicchio, I.; Giannetti, F.; Sellitto, A. Heat transfer at nanoscale and boundary conditions. Z. Angew. Math. Phys. 2022, 73, 147. [Google Scholar] [CrossRef]
- Bochicchio, I.; Sellitto, A.; Munafó, C.F. Phonon-boundary scattering and second-order boundary conditions: Application to the heat transfer in one-dimensional nanosystems. J. Therm. Stresses 2025, 1–16. [Google Scholar] [CrossRef]
- Lebon, G.; Jou, D.; Dauby, P.C. Beyond the Fourier heat conduction law and the thermal non-slip condition. Phys. Lett. A 2012, 376, 2842–2846. [Google Scholar] [CrossRef]
- Xu, M. Slip boundary condition of heat flux in Knudsen layers. Proc. R. Soc. A 2014, 470, 20130578. [Google Scholar] [CrossRef]
- Hua, Y.-C.; Cao, B.-Y. Slip Boundary Conditions in Ballistic-Diffusive Heat Transport in Nanostructures. Nanoscale Microscale Thermophys. Eng. 2017, 21, 159–176. [Google Scholar] [CrossRef]
- Xu, M. Phonon hydrodynamic transport and Knudsen minimum in thin graphite. Phys. Lett. A 2021, 389, 127076. [Google Scholar] [CrossRef]
- Xu, M. Boundary effect and heat vortices of hydrodynamic heat conduction in graphene. Phys. Lett. A 2023, 492, 129231. [Google Scholar] [CrossRef]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Interscience: New York, NY, USA, 1961. [Google Scholar]
- Verhás, J. Thermodynamics and Rheology; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Smith, G.F. On isotropic functions of symmetric tensors, skew-symmetric tensors and vectors. Int. J. Engng. Sci. 1971, 9, 899–916. [Google Scholar] [CrossRef]
- Di Domenico, M.; Jou, D.; Sellitto, A. Nonlinear heat waves and some analogies with nonlinear optics. Int. J. Heat Mass Transf. 2020, 156, 119888. [Google Scholar] [CrossRef]
- Guyer, R.A.; Krumhansl, J.A. Solution of the linearized phonon Boltzmann equation. Phys. Rev. 1966, 148, 766–778. [Google Scholar] [CrossRef]
- Xu, M. The Modified Guyer-Krumhansl Equations Derived From the Linear Boltzmann Transport Equation. J. Heat Mass Transf. ASME 2024, 146, 102501. [Google Scholar] [CrossRef]
- Xu, M. Effect of inflow boundary conditions on phonon transport in suspended graphene. Phys. Lett. A 2022, 428, 127944. [Google Scholar] [CrossRef]
- Sellitto, A.; Carlomagno, I.; Jou, D. Two-dimensional phonon hydrodynamics in narrow strips. Proc. R. Soc. A 2015, 471, 20150376. [Google Scholar] [CrossRef]
- Ferry, D.K.; Goodnick, S.M. Transport in Nanostructures, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Luo, T.; Chen, G. Nanoscale heat transfer—From computation to experiment. Phys. Chem. Chem. Phys. 2013, 15, 3389–3412. [Google Scholar] [CrossRef]
- Asheghi, M.; Leung, Y.K.; Wong, S.S.; Goodson, K.E. Phonon-boundary scattering in thin silicon layers. Appl. Phys. Lett. 1997, 71, 1798–1800. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Fan, R.; Yang, P.; Majumdar, A. Thermal conductivity of Si/SiGe superlattice nanowires. Appl. Phys. Lett. 2003, 83, 3186. [Google Scholar] [CrossRef]
- Liu, W.; Asheghi, M. Phonon-boundary scattering in ultrathin single-crystal silicon layers. Appl. Phys. Lett. 2004, 84, 3819–3821. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munafò, C.F.; Nunziata, M.; Sellitto, A. The Knudsen Layer in Modeling the Heat Transfer at Nanoscale: Bulk and Wall Contributions to the Local Heat Flux. Entropy 2025, 27, 469. https://doi.org/10.3390/e27050469
Munafò CF, Nunziata M, Sellitto A. The Knudsen Layer in Modeling the Heat Transfer at Nanoscale: Bulk and Wall Contributions to the Local Heat Flux. Entropy. 2025; 27(5):469. https://doi.org/10.3390/e27050469
Chicago/Turabian StyleMunafò, Carmelo Filippo, Martina Nunziata, and Antonio Sellitto. 2025. "The Knudsen Layer in Modeling the Heat Transfer at Nanoscale: Bulk and Wall Contributions to the Local Heat Flux" Entropy 27, no. 5: 469. https://doi.org/10.3390/e27050469
APA StyleMunafò, C. F., Nunziata, M., & Sellitto, A. (2025). The Knudsen Layer in Modeling the Heat Transfer at Nanoscale: Bulk and Wall Contributions to the Local Heat Flux. Entropy, 27(5), 469. https://doi.org/10.3390/e27050469






