Phase Stability and Transitions in High-Entropy Alloys: Insights from Lattice Gas Models, Computational Simulations, and Experimental Validation
Abstract
1. Introduction
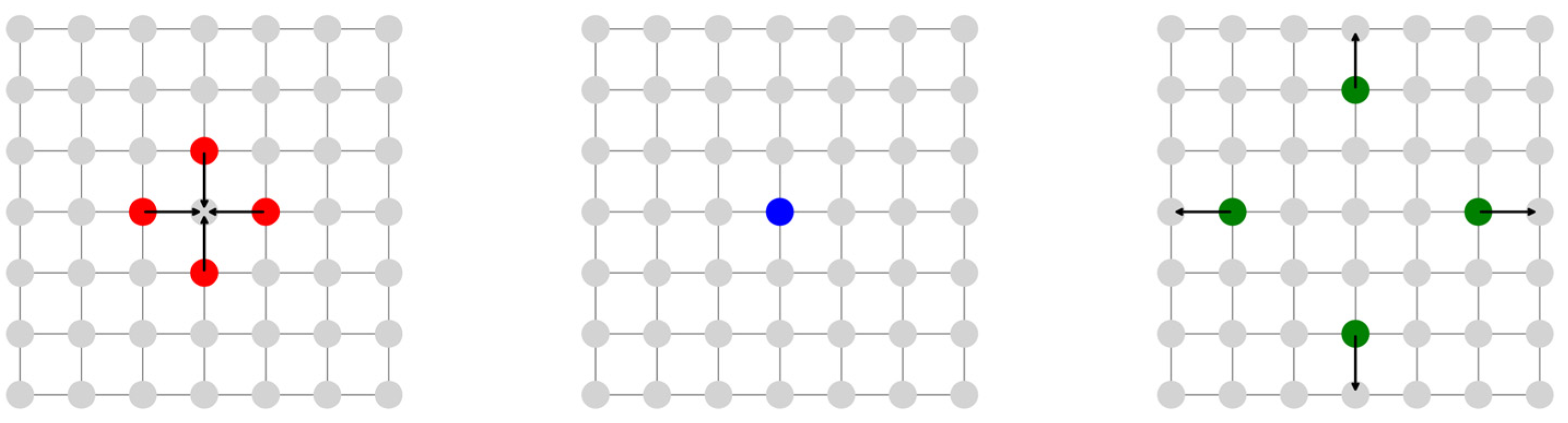
2. Fundamentals of Lattice Gas Models
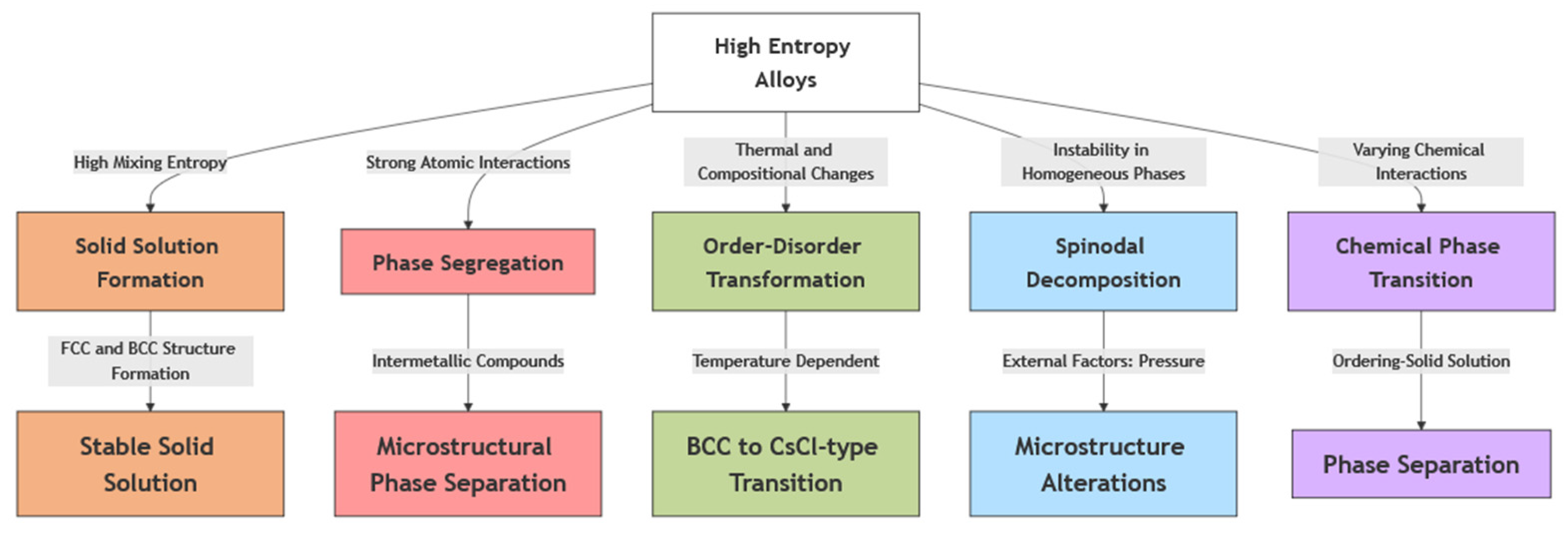
3. Phase Transitions in High-Entropy Alloys
4. Application of Lattice Gas Models to HEA Phase Transitions
5. Computational and Simulation Techniques
5.1. Monte Carlo and Kinetic Monte Carlo Simulations in HEAs
5.2. Molecular Dynamics Integration with Lattice Gas Models
5.3. Machine Learning and Artificial Intelligence in Lattice Gas-Based Phase Prediction
5.4. Multi-Scale Modeling Strategies for HEA Phase Transitions
6. Experimental Validation and Real-World Applications
6.1. Comparison of Lattice Gas Predictions with Experimental Phase Diagrams of HEAs
6.2. Case Studies of Lattice Gas Applications in HEA Design and Optimization
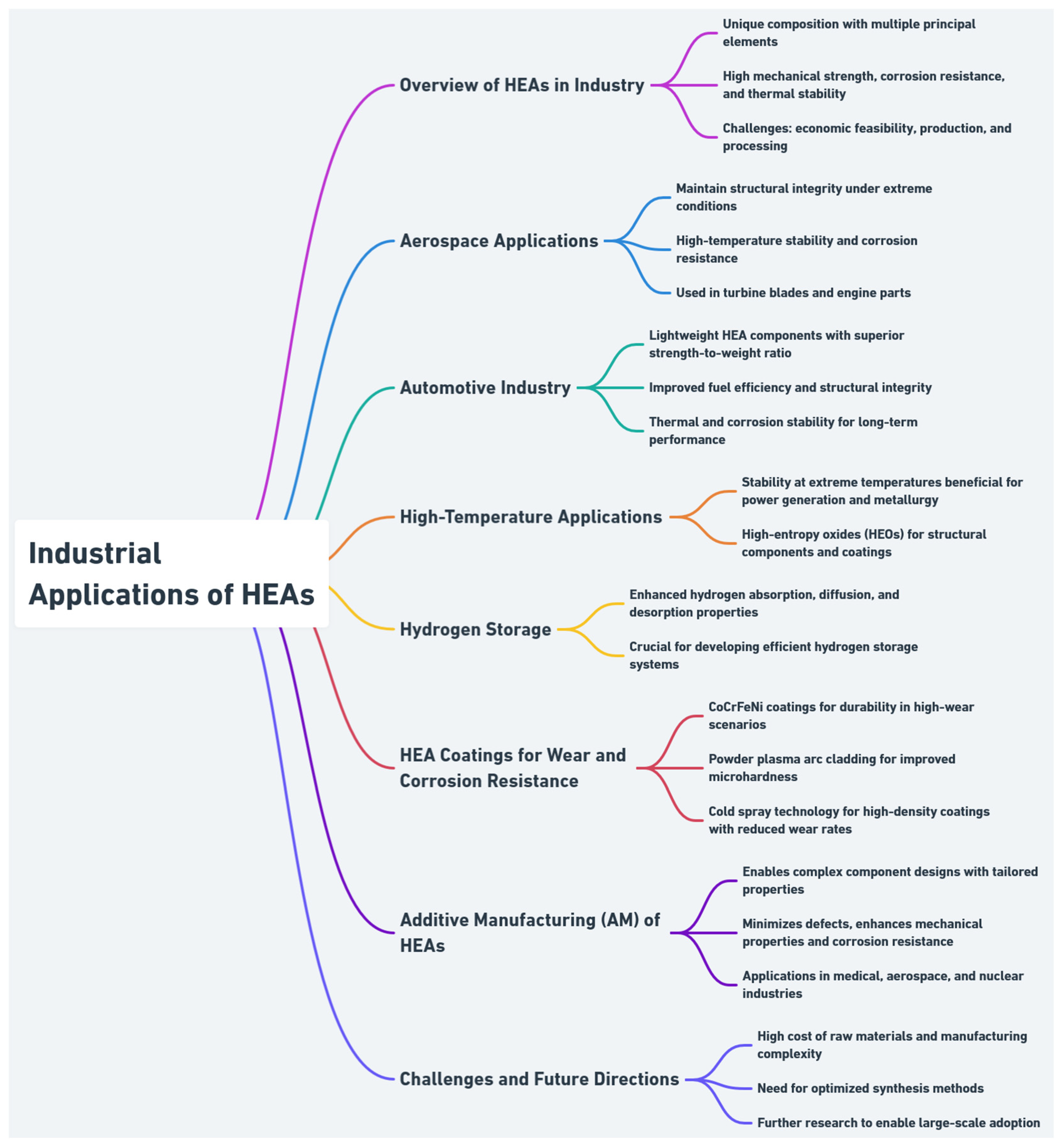
6.3. Industrial Applications
7. Challenges and Future Perspectives
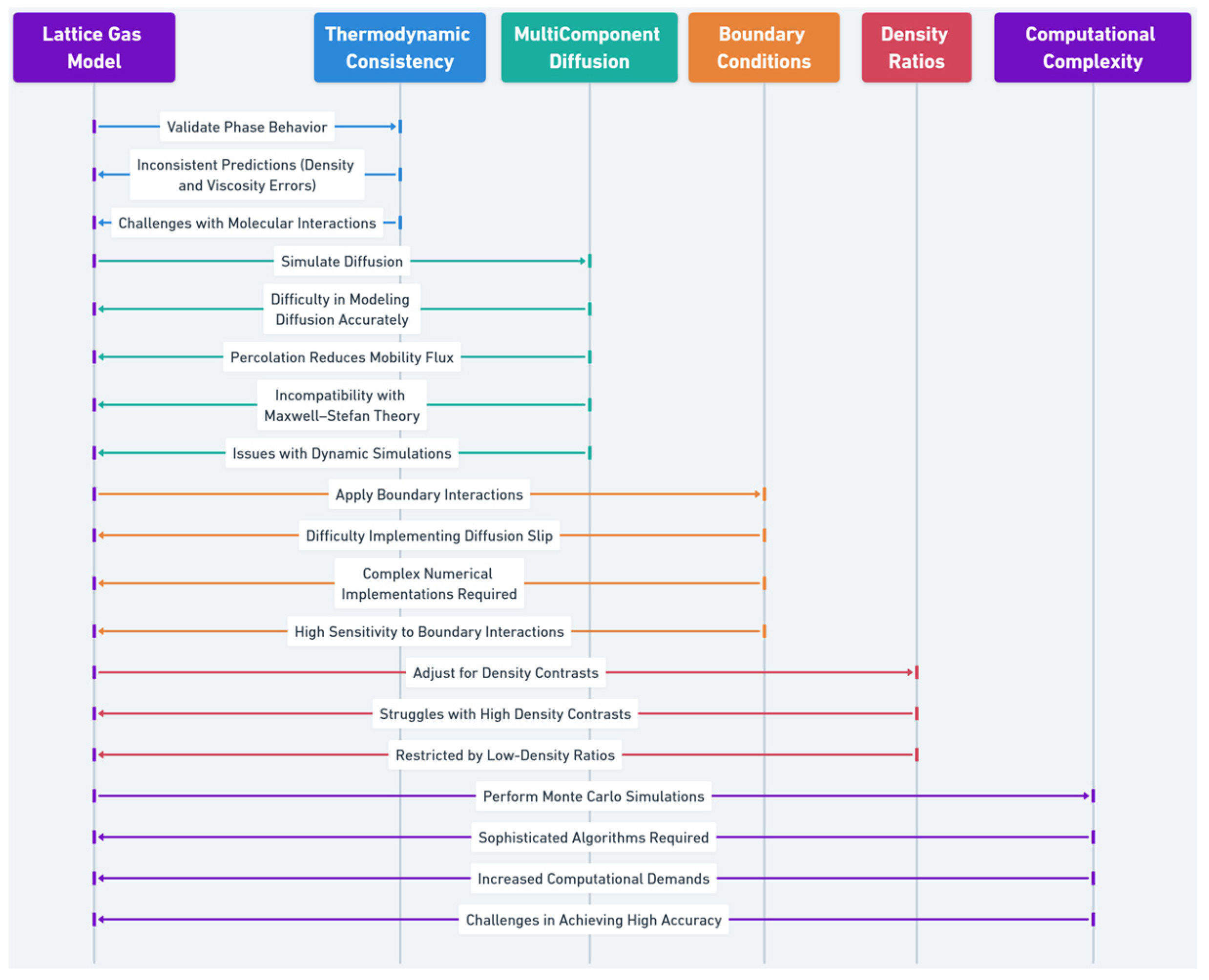
7.1. Limitations of Lattice Gas Models for Multi-Component Alloy Systems
7.2. Opportunities for Hybrid Modeling Approaches
7.3. Future Research Directions in HEA Phase Transformation Modeling
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- George, E.P.; Curtin, W.A.; Tasan, C.C. High entropy alloys: A focused review of mechanical properties and deformation mechanisms. Acta Mater. 2020, 188, 435–474. [Google Scholar] [CrossRef]
- Ikeda, Y.; Grabowski, B.; Körmann, F. Ab initio phase stabilities and mechanical properties of multicomponent alloys: A comprehensive review for high entropy alloys and compositionally complex alloys. Mater. Charact. 2019, 147, 464–511. [Google Scholar] [CrossRef]
- Li, W.; Xie, D.; Li, D.; Zhang, Y.; Gao, Y.; Liaw, P.K. Mechanical behavior of high-entropy alloys. Prog. Mater. Sci. 2021, 118, 100777. [Google Scholar] [CrossRef]
- Dai, J.H.; Li, W.; Song, Y.; Vitos, L. Theoretical investigation of the phase stability and elastic properties of TiZrHfNb-based high entropy alloys. Mater. Des. 2019, 182, 108033. [Google Scholar] [CrossRef]
- Harrington, T.J.; Gild, J.; Sarker, P.; Toher, C.; Rost, C.M.; Dippo, O.F.; McElfresh, C.; Kaufmann, K.; Marin, E.; Borowski, L.; et al. Phase stability and mechanical properties of novel high entropy transition metal carbides. Acta Mater. 2019, 166, 271–280. [Google Scholar] [CrossRef]
- Silva, D.D.S.; Bertoli, G.; Neto, N.D.C.; Schell, N.; Clarke, K.D.; Kaufman, M.J.; Clarke, A.J.; Coury, F.G.; Bolfarini, C. Computational thermodynamics-guided alloy design and phase stability in CoCrFeMnNi-based medium-and high-entropy alloys: An experimental-theoretical study. Scr. Mater. 2024, 252, 116264. [Google Scholar] [CrossRef]
- Qin, G.; Chen, R.; Mao, H.; Yan, Y.; Li, X.; Schönecker, S.; Vitos, L.; Li, X. Experimental and theoretical investigations on the phase stability and mechanical properties of Cr7Mn25Co9Ni23Cu36 high-entropy alloy. Acta Mater. 2021, 208, 116763. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, R.; Xiao, B.; Zhang, Z.; Li, S.; Qiao, J.; Bai, S.; Zhang, Y.; Liaw, P.K. A review on the dynamic-mechanical behaviors of high-entropy alloys. Prog. Mater. Sci. 2023, 135, 101090. [Google Scholar] [CrossRef]
- Li, J.; Fang, Q.; Liaw, P.K. Microstructures and Properties of High-Entropy Materials: Modeling, Simulation, and Experiments. Adv. Eng. Mater. 2021, 23, 2001044. [Google Scholar] [CrossRef]
- Schuster, M.D.; Memarsadeghi, N. Lattice Gas Cellular Automata Fluid Dynamics Case Study. Comput. Sci. Eng. 2020, 22, 87–91. [Google Scholar] [CrossRef]
- Vikhrenko, V.S.; Bokun, G.S.; Groda, Y.G. Thermodynamics and Kinetics of Lattice Gases: Statistical Mechanics Perspective. In New Trends in Intercalation Compounds for Energy Storage; Springer: Dordrecht, The Netherlands, 2002; pp. 641–642. ISBN 978-94-010-0389-6. [Google Scholar]
- d’Humières, D.; Lallemand, P.; Qian, Y.H. Review of flow simulations using lattice gases. In Proceedings of the Nonlinear Hyperbolic Problems. Lecture Notes in Mathematics, Bordeaux, France, 13–17 June 1988; Springer: Berlin/Heidelberg, Germany, 1989; pp. 56–68. [Google Scholar]
- Khotimah, S.N.; Arif, I.; Liong, T.H. Lattice-gas automata for the problem of kinetic theory of gas during free expansion. Int. J. Mod. Phys. C 2002, 13, 1033–1045. [Google Scholar] [CrossRef]
- Hamilton, M.; Lynch, I.; Lee, D. Lattice gas models derived from effective field theory. Phys. Rev. C Nucl. Phys. 2004, 71, 044005. [Google Scholar] [CrossRef]
- Yepez, J.; Seeley, G.P.; Margolus, N. Lattice-Gas Automata Fluids on Parallel Supercomputers. arXiv 1994, arXiv:comp-gas/9403005v1. [Google Scholar] [CrossRef]
- Cook, N.D. Is the lattice gas model a unified model of nuclear structure? J. Phys. G Nucl. Part. Phys. 1999, 25, 1213. [Google Scholar] [CrossRef]
- Fonio, N.O.; Sagaut, P.; Di Molfetta, G. A Fully Quantum Algorithm for Hydrodynamic Lattice Gas Cellular Automata. arXiv 2023, arXiv:2310.07362v1. [Google Scholar] [CrossRef]
- Love, P. On Quantum Extensions of Hydrodynamic Lattice Gas Automata. Condens. Matter 2019, 4, 48. [Google Scholar] [CrossRef]
- Zamora, A.D.B.; Budinski, L.; Niemimäki, O.; Lahtinen, V. Efficient quantum lattice gas automata. Comput. Fluids 2025, 286, 106476. [Google Scholar] [CrossRef]
- Schubert, D.; Richter, J.; Jin, F.; Michielsen, K.; De Raedt, H.; Steinigeweg, R. Quantum versus classical dynamics in spin models: Chains, ladders, and square lattices. Phys. Rev. B 2021, 104, 054415. [Google Scholar] [CrossRef]
- Occhialini, C.A.; Handunkanda, S.U.; Curry, E.B.; Hancock, J.N. Classical, quantum, and thermodynamics of a lattice model exhibiting structural negative thermal expansion. Phys. Rev. B 2017, 95, 094106. [Google Scholar] [CrossRef]
- Yepez, J. Quantum lattice gas algorithmic representation of gauge field theory. In Proceedings of the SPIE 9996, Quantum Information Science and Technology II, Edinburgh, UK, 26–29 September 2016. [Google Scholar]
- Lewis, D.G.; Kempf, A.; Menicucci, N.C. Quantum lattice models that preserve continuous translation symmetry. Phys. Rev. D 2023, 108, 096024. [Google Scholar] [CrossRef]
- Åstrand, P.-O.; de Miguel, R. Lattice Models in Molecular Thermodynamics: Merging the Configurational and Translational Entropies. J. Phys. Chem. B 2024, 128, 12752–12759. [Google Scholar] [CrossRef] [PubMed]
- Agranov, T.; Cates, M.E.; Jack, R.L. Entropy production and its large deviations in an active lattice gas. J. Stat. Mech. Theory Exp. 2022, 2022, 123201. [Google Scholar] [CrossRef]
- Ramirez-Pastor, A.J.; Romá, F.J.; Riccardo, J.L. Configurational entropy in generalized lattice-gas models. Int. J. Mod. Phys. B 2009, 23, 4589–4627. [Google Scholar] [CrossRef]
- Kaburagi, M.; Ebina, K.; Tonegawa, T. Multicomponent alloy with random interactions. J. Non–Cryst. Solids 1990, 117–118 Pt 2, 543–546. [Google Scholar] [CrossRef]
- Levine, H.B. Equations for a Lattice Gas. II. Multio-Cmponent Systems. J. Chem. Phys. 1957, 27, 335–342. [Google Scholar] [CrossRef]
- Goff, J.M.; Li, B.Y.; Sinnott, S.B.; Dabo, I. Quantifying multipoint ordering in alloys. Phys. Rev. B 2021, 104, 054109. [Google Scholar] [CrossRef]
- Kehr, K.W.; Binder, K.; Reulein, S.M. Mobility, interdiffusion, and tracer diffusion in lattice-gas models of two-component alloys. Phys. Rev. B 1989, 39, 4891. [Google Scholar] [CrossRef]
- Barroso-Luque, L.; Ceder, G. The cluster decomposition of the configurational energy of multicomponent alloys. npj Comput. Mater. 2024, 10, 158. [Google Scholar] [CrossRef]
- Zakharov, A.Y.; Schneider, A.A.; Udovsky, A.L.; Baykov, A.A. Variable-lattice model of multi-component systems. 1. General consideration. arXiv 2010, arXiv:1003.2731v1. [Google Scholar] [CrossRef]
- Murty, B.S.; Yeh, J.W.; Ranganathan, S. High-Entropy Alloy Solid Solutions. In High-Entropy Alloys; Butterworth Heinemann: Oxford, UK, 2014; pp. 91–118. [Google Scholar] [CrossRef]
- Kumar, A.; Chopkar, M. Effects of Mutual Interaction between Constituent Elements on Phase Formation of High Entropy Alloys. J. Mater. Sci. Nanotechnol. 2017, 5, 201. [Google Scholar] [CrossRef]
- Ustinovshikov, Y. “Chemical” phase transition in alloys: Ordering–phase separation. Curr. Opin. Solid State Mater. Sci. 2010, 14, 7–20. [Google Scholar] [CrossRef]
- Eisenbach, M.; Pei, Z.; Liu, X. First-principles study of order-disorder transitions in multicomponent solid-solution alloys. J. Phys. Condens. Matter 2019, 31, 273002. [Google Scholar] [CrossRef]
- Widom, M. First-principles study of the order-disorder transition in the AlCrTiV high entropy alloy. arXiv 2024, arXiv:2407.00865v1. [Google Scholar] [CrossRef]
- Dong, D.; Min, R.; Zhu, D.; Huo, J.; Deng, Y.; Ma, T.; Wang, X. Spinodal decomposition, ordering, and precipitation transformation in CoCrFeNiAl HEAs under GPa pressure. J. Mater. Res. Technol. 2024, 28, 2660–2670. [Google Scholar] [CrossRef]
- Abe, T.; Han, K.; Goto, Y.; Ohnuma, I.; Koyama, T. Stabilization of Equiatomic Solutions Due to High-Entropy Effect. Mater. Trans. 2023, 64, 877–884. [Google Scholar] [CrossRef]
- Hatzenbichler, L.; Zeisl, S.; Clemens, H.; Holec, D. Phase stability of TiAl-based BCC high entropy alloys. Intermetallics 2023, 158, 107893. [Google Scholar] [CrossRef]
- Fu, X.; Li, Y.; Hou, C.; Lu, H.; Song, X. Phase stability and transition of CrTaVW high-entropy alloy. J. Alloys Compd. 2024, 1002, 175481. [Google Scholar] [CrossRef]
- Coduri, M.; Magnaghi, L.R.; Fracchia, M.; Biesuz, R.; Anselmi-Tamburini, U. Assessing Phase Stability in High-Entropy Materials by Design of Experiments: The Case of the (Mg,Ni,Co,Cu,Zn)O System. Chem. Mater. 2024, 36, 720–729. [Google Scholar] [CrossRef]
- Pope, A.D.; Iwan, S.; Clay, M.P.; Ren, J.; Yang, W.; Chen, W.; Vohra, Y.K. Phase stability of a eutectic high entropy alloy under extremes of pressures and temperatures. AIP Adv. 2024, 14, 025239. [Google Scholar] [CrossRef]
- Li, D.; Yu, D.; Zhang, G.; Du, A.; Ye, Z.; Jia, Y.; Hou, W.; Xu, T.; Li, F.; Chi, S.; et al. High Configuration Entropy Promises Electrochemical Stability of Chloride Electrolytes for High-Energy, Long-Life All-Solid-State Batteries. Angew. Chemie Int. Ed. 2025, 64, e202419735. [Google Scholar] [CrossRef]
- Wang, Z.; Pattamatta, A.S.L.S.; Han, J.; Srolovitz, D.J. Scaling laws for lattice distortions: Application to high entropy alloys. PNAS Nexus 2024, 3, page117. [Google Scholar] [CrossRef] [PubMed]
- Kumar, J.; Linda, A.; Biswas, K. Lattice distortion in FCC HEAs and its effect on mechanical properties: Critical analysis and way forward. J. Appl. Phys. 2023, 133, 155102. [Google Scholar] [CrossRef]
- Spurling, R.J.; Lass, E.A.; Wang, X.; Page, K. Entropy-driven phase transitions in complex ceramic oxides. Phys. Rev. Mater. 2022, 6, 090301. [Google Scholar] [CrossRef]
- Ding, N.; Jiang, H.H.; Xu, C.R.; Shao, L.; Tang, B.Y. Lattice distortion and the influence on mechanical and thermodynamic properties of high entropy (HfZrTaNbTi)X (X=C, N, NC) by Ab initio investigation. Ceram. Int. 2022, 48, 35353–35364. [Google Scholar] [CrossRef]
- San, S.; Tong, Y.; Bei, H.; Kombaiah, B.; Zhang, Y.; Ching, W.Y. First-principles calculation of lattice distortions in four single phase high entropy alloys with experimental validation. Mater. Des. 2021, 209, 110071. [Google Scholar] [CrossRef]
- Georgescu, A.B.; Millis, A.J. Quantifying the role of the lattice in metal–insulator phase transitions. Commun. Phys. 2022, 5, 135. [Google Scholar] [CrossRef]
- Wang, R.; Tang, Y.; Li, S.; Ai, Y.; Li, Y.; Xiao, B.; Zhu, L.; Liu, X.; Bai, S. Effect of lattice distortion on the diffusion behavior of high-entropy alloys. J. Alloys Compd. 2020, 825, 154099. [Google Scholar] [CrossRef]
- Liu, W.H.; Tong, Y.; Chen, S.W.; Xu, W.W.; Wu, H.H.; Zhao, Y.L.; Yang, T.; Wang, X.L.; Liu, X.; Kai, J.J.; et al. Unveiling the Electronic Origin for Pressure-Induced Phase Transitions in High-Entropy Alloys. Matter 2020, 2, 751–763. [Google Scholar] [CrossRef]
- Yang, W.C.; Tsubota, M.; Del Campo, A.; Zeng, H.B. Universal defect density scaling in an oscillating dynamic phase transition. Phys. Rev. B 2023, 108, 174518. [Google Scholar] [CrossRef]
- Wang, X.; Deng, Y.; Zhu, D.; Dong, D.; Ma, T. GPa level pressure-induced phase transitions and enhanced corrosion resistance of AlCrMoSiTi high-entropy alloys. J. Mater. Res. Technol. 2023, 26, 6389–6404. [Google Scholar] [CrossRef]
- Fang, Z.; Gong, M.; Guo, G.-C.; Fu, Y.; Xiong, L. Distance between two manifolds, topological phase transitions and scaling laws. arXiv 2024, arXiv:2405.03323v1. [Google Scholar] [CrossRef]
- Sekkal, W.; Besson, R.; Legris, A. Atomic scale modeling of structural phase transformations in AlCrFeMnMo high-entropy alloys during thermal treatments. J. Alloys Compd. 2021, 876, 160201. [Google Scholar] [CrossRef]
- Basu, S.S.; Jana, P.P.; Ghosh, M. A new insight into the phase stability in high entropy alloys. Mater. Today Commun. 2023, 37, 107394. [Google Scholar] [CrossRef]
- Berti, A.; Bochicchio, I. A mathematical model for phase separation: A generalized Cahn-Hilliard equation. Math. Methods Appl. Sci. 2011, 34, 1193–1201. [Google Scholar] [CrossRef]
- Chang, H.; Tao, Y.; Liaw, P.K.; Ren, J. Phase prediction and effect of intrinsic residual strain on phase stability in high-entropy alloys with machine learning. J. Alloys Compd. 2022, 921, 166149. [Google Scholar] [CrossRef]
- Butler, T.M.; Weaver, M.L. Investigation of the phase stabilities in AlNiCoCrFe high entropy alloys. J. Alloys Compd. 2017, 691, 119–129. [Google Scholar] [CrossRef]
- Saal, J.E.; Berglund, I.S.; Sebastian, J.T.; Liaw, P.K.; Olson, G.B. Equilibrium high entropy alloy phase stability from experiments and thermodynamic modeling. Scr. Mater. 2018, 146, 5–8. [Google Scholar] [CrossRef]
- Liang, F.; Du, J.; Su, G.; Xu, C.; Zhang, C.; Kong, X. Phase Stability and Mechanical Properties Analysis of AlCoxCrFeNi HEAs Based on First Principles. Metals 2022, 12, 1860. [Google Scholar] [CrossRef]
- Evans, D.; Chen, J.; Bokas, G.; Chen, W.; Hautier, G.; Sun, W. Visualizing temperature-dependent phase stability in high entropy alloys. npj Comput. Mater. 2021, 7, 151. [Google Scholar] [CrossRef]
- Maiti, S.; Steurer, W. Phase stability, local chemical disorder and its effect on the mechanical properties of refractory high-entropy alloys. arXiv 2016, arXiv:1601.06015v1. [Google Scholar] [CrossRef]
- Wang, X.S.; Wang, Y.J. Disorder-order transition in multiprincipal element alloy: A free energy perspective. Phys. Rev. Mater. 2023, 7, 033606. [Google Scholar] [CrossRef]
- Zhao, S. Local Ordering Tendency in Body-Centered Cubic (BCC) Multi-Principal Element Alloys. J. Phase Equilibria Diffus. 2021, 42, 578–591. [Google Scholar] [CrossRef]
- Qu, N.; Liu, Y.; Zhang, Y.; Yang, D.; Han, T.; Liao, M.; Lai, Z.; Zhu, J.; Zhang, L. Machine learning guided phase formation prediction of high entropy alloys. Mater. Today Commun. 2022, 32, 104146. [Google Scholar] [CrossRef]
- Mohammadi, A.; Tsang, J.; Huang, X.; Kearsey, R. Phase Prediction Methodologies for Rapid Screening of High Entropy Alloys. In Proceedings of the ASME Turbo Expo 2024: Turbomachinery Technical Conference and Exposition, London, UK, 24–28 June 2024. [Google Scholar]
- Singh, P.; Johnson, D.D.; Tiarks, J.; White, E.M.H.; Kustas, A.B.; Pegues, J.W.; Jones, M.R.; Lim, H.; DelRio, F.W.; Carroll, J.D.; et al. Theory-guided design of duplex-phase multi-principal-element alloys. Acta Mater. 2024, 272, 119952. [Google Scholar] [CrossRef]
- Li, J.; Chen, Y.; Xie, B.; Lu, W.; Fang, Q. Deformation Behaviour and Strengthening Mechanism of High-Entropy Alloys Using Model and Simulation. In Proceedings of the International Conference on Computational & Experimental Engineering and Sciences; Computers, Materials and Continua. Tech Science Press: Henderson, NV, USA, 2023; Volume 25, pp. 1–2. [Google Scholar]
- Moniri, S.; Yang, Y.; Yuan, Y.; Zhou, J.; Yang, L.; Zhu, F.; Liao, Y.; Yao, Y.; Hu, L.; Ercius, P.; et al. Three-dimensional atomic positions and local chemical order of medium- and high-entropy alloys. arXiv 2023, arXiv:2305.14123v1. [Google Scholar] [CrossRef]
- Cao, P.Y.; Liu, F.; Yuan, F.P.; Ma, E.; Wu, X.L. Multiple potential phase-separation paths in multi-principal element alloys. Mater. Today Nano 2024, 28, 100511. [Google Scholar] [CrossRef]
- Baumgaertner, A.; Narasimhan, S.L. Phase transitions in the driven lattice gas (TASEP) with repulsive energies. J. Phys. A Math. Theor. 2023, 56, 355001. [Google Scholar] [CrossRef]
- Schmidt, J.; Schütz, G.M.; van Beijeren, H. A lattice Gas Model for Generic One-Dimensional Hamiltonian Systems. J. Stat. Phys. 2021, 183, 8. [Google Scholar] [CrossRef]
- He, Q.; Huang, W.; Yin, Y.; Li, D.; Wang, Y. A lattice Boltzmann model for liquid-vapor-solid flow with thermal phase change. Comput. Math. Appl. 2022, 114, 60–72. [Google Scholar] [CrossRef]
- Chen, T.; Wang, W.; Tu, Y.; Hua, X. Modelling Unidirectional Crowd Motion in a Corridor with Statistical Characteristics of Pedestrian Movements. Math. Probl. Eng. 2020, 2020, 7483210. [Google Scholar] [CrossRef]
- Su, W.-Y.; Liu, Y.-J.; Ma, N.; Cheng, C. Probing phase transitions with correlations in configuration space. Phys. Rev. B 2024, 110, 195108. [Google Scholar] [CrossRef]
- Akimenko, S.S. Tensor network construction for lattice gas models: Hard-core and triangular lattice models. Phys. Rev. E 2023, 107, 054116. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Yang, Y. The CALPHAD approach for HEAs: Challenges and opportunities. MRS Bull. 2022, 47, 158–167. [Google Scholar] [CrossRef]
- Scherr, R.; Liepold, P.; Markl, M.; Körner, C. A CALPHAD-Informed Enthalpy Method for Multicomponent Alloy Systems with Phase Transitions. Modelling 2024, 5, 367–391. [Google Scholar] [CrossRef]
- Moitzi, F.; Romaner, L.; Ruban, A.V.; Peil, O.E. Accurate ab initio modeling of solid solution strengthening in high entropy alloys. Phys. Rev. Mater. 2022, 6, 103602. [Google Scholar] [CrossRef]
- Wang, Y.; Curtarolo, S.; Jiang, C.; Arroyave, R.; Wang, T.; Ceder, G.; Chen, L.Q.; Liu, Z.K. Ab initio lattice stability in comparison with CALPHAD lattice stability. Calphad 2004, 28, 79–90. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Y.; Liu, Z.K.; Zhong, Y. Ab initio simulations on the pure Cr lattice stability at 0K: Verification with the Fe-Cr and Ni-Cr binary systems. Calphad 2021, 75, 102359. [Google Scholar] [CrossRef]
- Eisele, S.; Grieshammer, S. MOCASSIN: Metropolis and kinetic Monte Carlo for solid electrolytes. J. Comput. Chem. 2020, 41, 2663–2677. [Google Scholar] [CrossRef]
- Adjanor, G.; Athènes, M.; Domain, C.; Mousseau, N. Overview of kinetic Monte Carlo methods used to simulate microstructural evolution of materials under irradiation. EPJ Web Conf. 2024, 302, 06005. [Google Scholar] [CrossRef]
- Pagonis, V. Kinetic Monte Carlo Simulations. In Luminescence: Data Analysis and Modeling Using R; Springer: Cham, Switzerland, 2021; pp. 261–273. [Google Scholar]
- Huang, W.; Farkas, D.; Bai, X.M. High-throughput machine learning—Kinetic Monte Carlo framework for diffusion studies in Equiatomic and Non-equiatomic FeNiCrCoCu high-entropy alloys. Materialia 2023, 32, 101966. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, J.; Ma, S.; Xiong, Y.; Huang, S.; Kai, J.J.; Zhao, S. Revealing the crucial role of rough energy landscape on self-diffusion in high-entropy alloys based on machine learning and kinetic Monte Carlo. Acta Mater. 2022, 234, 118051. [Google Scholar] [CrossRef]
- Martins, R.; Gonçalves, A.P.; Correia, J.B.; Galatanu, A.; Alves, E.; Tejado, E.; Pastor, J.Y.; Dias, M. Simulation, Structural, Thermal and Mechanical Properties of the FeTiTaVW High Entropy Alloy. Metals 2024, 14, 436. [Google Scholar] [CrossRef]
- Ye, Q.; Yang, B.; Yang, G.; Zhao, J.; Gong, Z. Stability prediction of AlCoCrFeMo0.05Ni2 high entropy alloy by Kinetic Monte Carlo method. Mater. Lett. 2022, 306, 130907. [Google Scholar] [CrossRef]
- Shen, Z.; Du, J.P.; Shinzato, S.; Sato, Y.; Yu, P.; Ogata, S. Kinetic Monte Carlo simulation framework for chemical short-range order formation kinetics in a multi-principal-element alloy. Comput. Mater. Sci. 2021, 198, 110670. [Google Scholar] [CrossRef]
- Nellis, C.; Hin, C. Kinetic Monte Carlo Modeling of Helium Bubble Nucleation onto Oxides in the Fe-Ti-Y-O System. Small Sci. 2025, 5, 2400462. [Google Scholar] [CrossRef] [PubMed]
- Novick, A.; Nguyen, Q.; Garnett, R.; Toberer, E.; Stevanović, V. Simulating high-entropy alloys at finite temperatures: An uncertainty-based approach. Phys. Rev. Mater. 2023, 7, 063801. [Google Scholar] [CrossRef]
- Sato, K.; Hayashi, G.; Ogushi, K.; Okabe, S.; Suzuki, K.; Terai, T.; Fukushima, T. Computational Materials Design of High-Entropy Alloys Based on Full Potential Korringa-Kohn-Rostoker Coherent Potential Approximation and Machine Learning Techniques. Mater. Trans. 2023, 64, 2174–2178. [Google Scholar] [CrossRef]
- Zhou, X.W.; Hui, C.S.Y.; Robinson, D.B.; Sugar, J.D. Accelerated kinetic Monte Carlo method for simulations of helium bubble formation in metals. J. Comput. Phys. 2025, 523, 113666. [Google Scholar] [CrossRef]
- Jiang, D.; Li, Y.; Wang, L.; Zhang, L.C. Accelerating the Exploration of High-Entropy Alloys: Synergistic Effects of Integrating Computational Simulation and Experiments. Small Struct. 2024, 5, 2400110. [Google Scholar] [CrossRef]
- Gao, W.H.; Qiao, L.; Zhao, D.; Wang, J.J.; Fang, H.Q.; Zhang, W.Y.; Ma, S.G.; Zhang, T.W.; Wang, Z.H. A molecular dynamics investigation of nano-twins and nano-precipitates effects in CoCrFeNi-based high-entropy alloys. Phys. Scr. 2024, 99, 115407. [Google Scholar] [CrossRef]
- Dujana, W.A.; Ahmad, S.; Noman, M.N.H.; Kabir, M.H. The effect of changing constituents on tensile mechanical properties of HfNbTaTiZr high entropy alloy: A molecular dynamics study. Heliyon 2024, 10, e38350. [Google Scholar] [CrossRef] [PubMed]
- Ehsan, M.T.; Zafar, S.; Sarker, A.; Das Suvro, S.; Hasan, M.N. Graph neural network framework for energy mapping of hybrid monte-carlo molecular dynamics simulations of Medium Entropy Alloys. arXiv 2024, arXiv:2411.13670v1. [Google Scholar] [CrossRef]
- Bordoloi, P.; Hazarika, M.P.; Tripathi, A.; Chakraborty, S.N. Plasticity and strength of an equiatomic and a non-equiatomic HfNbTaTiZr high entropy alloy during uniaxial loading: A molecular dynamics simulation study. Mater. Res. Express 2024, 11, 096517. [Google Scholar] [CrossRef]
- Riazul Islam, M.; Islam, J.; Hasan, R.; Hasan, M. Effect of alloying element content, temperature, and strain rate on the mechanical behavior of NbTiZrMoV high entropy alloy: A molecular dynamics study. Mater. Today Commun. 2024, 40, 110071. [Google Scholar] [CrossRef]
- Thürmer, D.; Deluigi, O.R.; Urbassek, H.M.; Bringa, E.M.; Merkert, N. Atomistic Simulations of the Shock and Spall Behavior of the Refractory High-Entropy Alloy HfNbTaTiZr. High Entropy Alloy. Mater. 2024, 2, 321–331. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Z.; Deng, Y. Molecular Dynamics Study on Wear Resistance of High Entropy Alloy Coatings Considering the Effect of Temperature. Materials 2024, 17, 3911. [Google Scholar] [CrossRef] [PubMed]
- Miao, L.; Cao, Y.; Liu, J.; Xu, Y.; Sun, L.; Zhou, S. Effects of Cu on the high-entropy alloys of CuxCoCrFeNi: Experiment and molecular dynamics simulations. Vacuum 2024, 227, 113369. [Google Scholar] [CrossRef]
- Li, G.; Zhao, Y.; Zhang, F.; Tang, Q.; Wang, R.; Ma, J.; Wang, D. Different TBS and Grain Numbers on Mechanical Behavior of FeNiCrCoCu High-Entropy Alloys: A Molecular Dynamics Simulation. Nano 2024, 19, 2450065. [Google Scholar] [CrossRef]
- Singh, S.K.; Mahanta, B.K.; Rawat, P.; Kumar, S. Machine learning-assisted design of high-entropy alloys for optimal strength and ductility. J. Alloys Compd. 2024, 1007, 176282. [Google Scholar] [CrossRef]
- Jung, S.G.; Jung, G.; Cole, J.M. Predictive Modeling of High-Entropy Alloys and Amorphous Metallic Alloys Using Machine Learning. J. Chem. Inf. Model. 2024, 64, 7313–7336. [Google Scholar] [CrossRef]
- Akinwekomi, A.D. Prediction of High-Entropy Alloy Phases Using Soft Computing Techniques. Adv. Sci. Technol. 2024, 154, 3–12. [Google Scholar] [CrossRef]
- Hareharen, K.; Panneerselvam, T.; Raj Mohan, R. Improving the performance of machine learning model predicting phase and crystal structure of high entropy alloys by the synthetic minority oversampling technique. J. Alloys Compd. 2024, 991, 174494. [Google Scholar] [CrossRef]
- Liu, G.; Yang, S.; Zhong, Y. High-Entropy Materials Design by Integrating the First-Principles Calculations and Machine Learning: A Case Study in the Al-Co-Cr-Fe-Ni System. High Entropy Alloy Mater. 2024, 2, 307–320. [Google Scholar] [CrossRef]
- Swateelagna, S.; Singh, M.; Rahul, M.R. Explainable Machine Learning based approach for the design of new refractory high entropy alloys. Intermetallics 2024, 167, 108198. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, Z.; Zhao, J.; Jia, Y.; Cao, S.; Wang, D.; Lei, Y. Machine-Learning-Assisted Design of Novel TiZrNbVAl Refractory High-Entropy Alloys with Enhanced Ductility. Metals 2024, 14, 894. [Google Scholar] [CrossRef]
- Amin, M.T.; Bin Noor, W. Advancements in machine learning for predicting phases in high-entropy alloys: A comprehensive review. Futur. Sustain. 2024, 2, 8–19. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, W.; Yi, X.; Zhang, Y.; Duan, H. Multiscale modeling of dislocation-mediated plasticity of refractory high entropy alloys. J. Mech. Phys. Solids 2024, 187, 105640. [Google Scholar] [CrossRef]
- Farkas, D. The role of compositional complexity in the increased fracture resistance of high entropy alloys: Multi-scale atomistic simulations. Comput. Mater. Sci. 2024, 235, 112758. [Google Scholar] [CrossRef]
- Tan, F.; Li, L.; Li, J.; Liu, B.; Liaw, P.K.; Fang, Q. Multiscale modelling of irradiation damage behavior in high entropy alloys. Adv. Powder Mater. 2023, 2, 100114. [Google Scholar] [CrossRef]
- Jiang, D.; Xie, L.; Wang, L. Current application status of multi-scale simulation and machine learning in research on high-entropy alloys. J. Mater. Res. Technol. 2023, 26, 1341–1374. [Google Scholar] [CrossRef]
- Oropesa, W.G.C.; Nascimento, E.S.; Vieira, A.P. Phase behavior of a lattice-gas model for biaxial nematics. Phys. Rev. E 2022, 105, 044705. [Google Scholar] [CrossRef] [PubMed]
- Almarza, N.G.; Capitán, J.A.; Cuesta, J.A.; Lomba, E. Phase diagram of a two-dimensional lattice gas model of a ramp system. J. Chem. Phys. 2009, 131, 124506. [Google Scholar] [CrossRef]
- Bakr, M.; Syarif, J.; Hashem, I.A.T. Prediction of phase and hardness of HEAs based on constituent elements using machine learning models. Mater. Today Commun. 2022, 31, 103407. [Google Scholar] [CrossRef]
- Hou, S.; Li, Y.; Bai, M.; Sun, M.; Liu, W.; Wang, C.; Tetik, H.; Lin, D. Phase Prediction of High-Entropy Alloys by Integrating Criterion and Machine Learning Recommendation Method. Materials 2022, 15, 3321. [Google Scholar] [CrossRef]
- Singh, S.; Katiyar, N.K.; Goel, S.; Joshi, S.N. Phase prediction and experimental realisation of a new high entropy alloy using machine learning. Sci. Rep. 2023, 13, 4811. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Huang, X.; Luo, A.A. Phase formations in low density high entropy alloys. Calphad 2017, 56, 19–28. [Google Scholar] [CrossRef]
- Mohammadzdeh, A.; De Nardi, A.; Omidbakhsh, F.; Garbiec, D.; Fardan, A.; Hryha, E.; Mostafaei, A.; Torralba, J.M. A novel alloy design approach in developing CoNi-based high entropy superalloy using high entropy alloys thermodynamic and spark plasma sintering. Mater. Sci. Eng. A 2024, 909, 146841. [Google Scholar] [CrossRef]
- Segbenu Joseph Zosu; Cyril Anosike Amaghionyeodiwe; Kasali Aderinmoye Adedeji Optimization of high-entropy alloys (HEAS) for lightweight automotive components: Design, fabrication, and performance enhancement. Glob. J. Eng. Technol. Adv. 2024, 21, 064–072. [CrossRef]
- Wang, X.; Zhu, L.; Sun, L.; Li, N. A study of functionally graded lattice structural design and optimisation. In Proceedings of the 2020 6th International Conference on Mechanical Engineering and Automation Science, Moscow, Russia, 29–31 October 2020; pp. 50–55. [Google Scholar]
- Hanks, B.; Frecker, M. Lattice Structure Design for Additive Manufacturing: Unit Cell Topology Optimization. In Proceedings of the 45th Design Automation Conference, Proceedings of the ASME Design Engineering Technical Conference, Anaheim, CA, USA, 18–21 August 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 2A-2019. [Google Scholar]
- Xu, L.; Ruan, Q.; Shen, Q.; Xi, L.; Gao, J.; Li, Y. Optimization Design of Lattice Structures in Internal Cooling Channel with Variable Aspect Ratio of Gas Turbine Blade. Energies 2021, 14, 3954. [Google Scholar] [CrossRef]
- Ma, Y.; Li, M.; Mu, Y.; Wang, G.; Lu, W. Accelerated Design for High-Entropy Alloys Based on Machine Learning and Multiobjective Optimization. J. Chem. Inf. Model. 2023, 63, 6029–6042. [Google Scholar] [CrossRef]
- Du, C.; Firmansyah, I.; Yamaguchi, Y. High-performance computation of lgca fluid dynamics on an FPGA-based platform. In Proceedings of the ICCCS 2020, Proceedings of the 2020 5th International Conference on Computer and Communication Systems, Shanghai, China, 15–18 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 520–525. [Google Scholar]
- Harris, C.D.; Schroeder, K.K.; Black, J. A lattice-based method for optimization in continuous spaces with genetic algorithms. Acta Astronaut. 2025, 228, 957–971. [Google Scholar] [CrossRef]
- Hareancz, F.; Juhász, G.; Fábián, R.E.; Vida, Á. Applicability of High-Entropy Alloys. Solid State Phenom. 2024, 363, 71–79. [Google Scholar] [CrossRef]
- Caramarin, S.; Badea, I.C.; Mosinoiu, L.F.; Mitrica, D.; Serban, B.A.; Vitan, N.; Cursaru, L.M.; Pogrebnjak, A. Structural Particularities, Prediction, and Synthesis Methods in High-Entropy Alloys. Appl. Sci. 2024, 14, 7576. [Google Scholar] [CrossRef]
- Lee, J.Y.; Cai, W. From fabrication to mechanical properties: Exploring high-entropy oxide thin films and coatings for high-temperature applications. Front. Coat. Dyes Interface Eng. 2024, 2. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, W. High Entropy Alloys: Emerging Materials for Advanced Hydrogen Storage. Energy Technol. 2024, 12, 2401061. [Google Scholar] [CrossRef]
- Ding, Z.; Li, Y.; Jiang, H.; Zhou, Y.; Wan, H.; Qiu, J.; Jiang, F.; Tan, J.; Du, W.; Chen, Y.; et al. The integral role of high-entropy alloys in advancing solid-state hydrogen storage. Interdiscip. Mater. 2025, 4, 75–108. [Google Scholar] [CrossRef]
- Sivaraman, S.; Radhika, N. Predictive analytics of wear performance in high entropy alloy coatings through machine learning. Phys. Scr. 2024, 99, 076014. [Google Scholar] [CrossRef]
- Chai, Q.; Jiang, C.; Zhang, C.; Yin, S. Microstructure and wear resistance of cold sprayed CoCrFeNi HEA coatings: Influence of powder particle size and spraying temperature. Surf. Eng. 2024, 40, 793–803. [Google Scholar] [CrossRef]
- Ni, J.; Wen, M.; Jayalakshmi, S.; Geng, Y.; Chen, X. Investigation on microstructure, wear and friction properties of CoCrFeNiMox high-entropy alloy coatings deposited by powder plasma arc cladding. Mater. Today Commun. 2024, 39, 108807. [Google Scholar] [CrossRef]
- Ragunath, S.; Radhika, N.; Saleh, B. Advancements and future prospects of additive manufacturing in high-entropy alloy applications. J. Alloys Compd. 2024, 997, 174859. [Google Scholar] [CrossRef]
- Bao, J.; Schaefer, L. Lattice Boltzmann equation model for multi-component multi-phase flow with high density ratios. Appl. Math. Model. 2013, 37, 1860–1871. [Google Scholar] [CrossRef]
- Deng, H.; Jiao, K.; Hou, Y.; Park, J.W.; Du, Q. A lattice Boltzmann model for multi-component two-phase gas-liquid flow with realistic fluid properties. Int. J. Heat Mass Transf. 2019, 128, 536–549. [Google Scholar] [CrossRef]
- Langenbach, K.; Browarzik, D.; Sailer, J.; Enders, S. New formulation of the lattice cluster theory equation of state for multi-component systems. Fluid Phase Equilib. 2014, 362, 196–212. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Li, N.; Bao, C.; Feng, D.; Jiang, Z.; Zhang, X. An approach combining the lattice boltzmann method and maxwell-stefan equation for modeling multi-component diffusion. Phys. Fluids 2021, 33, 082010. [Google Scholar] [CrossRef]
- Benes, N.E.; Bouwmeester, H.J.M.; Verweij, H. Multi-component lattice gas diffusion. Chem. Eng. Sci. 2002, 57, 2673–2678. [Google Scholar] [CrossRef]
- Bennett, S.; Asinari, P.; Dellar, P.J. A lattice Boltzmann model for diffusion of binary gas mixtures that includes diffusion slip. Int. J. Numer. Methods Fluids 2012, 69, 171–189. [Google Scholar] [CrossRef]
- Van de Wall, A.; Asta, M. Self-driven lattice-model Monte Carlo simulations of alloy thermodynamic properties and phase diagrams. Model. Simul. Mater. Sci. Eng. 2002, 10, 521. [Google Scholar] [CrossRef]
- Coe, J.P. Lattice Density-Functional Theory for Quantum Chemistry. Phys. Rev. B 2019, 99, 165118. [Google Scholar] [CrossRef]
- Ko, H.Y.; Calegari Andrade, M.F.; Sparrow, Z.M.; Zhang, J.A.; DiStasio, R.A. High-Throughput Condensed-Phase Hybrid Density Functional Theory for Large-Scale Finite-Gap Systems: The SeA Approach. J. Chem. Theory Comput. 2023, 19, 4182–4201. [Google Scholar] [CrossRef]
- Pulicharla, M.R. Hybrid Quantum-Classical Machine Learning Models: Powering the Future of AI. J. Sci. Technol. 2023, 4, 40–65. [Google Scholar] [CrossRef]
- Laqua, H.; Dietschreit, J.C.B.; Kussmann, J.; Ochsenfeld, C. Accelerating Hybrid Density Functional Theory Molecular Dynamics Simulations by Seminumerical Integration, Resolution-of-the-Identity Approximation, and Graphics Processing Units. J. Chem. Theory Comput. 2022, 18, 6010–6020. [Google Scholar] [CrossRef] [PubMed]
- Rogers, A.W.; Zhang, D. Hybrid Model Construction. In Machine Learning and Hybrid Modelling for Reaction Engineering; Royal Society of Chemistry: London, UK, 2024; pp. 56–84. [Google Scholar]
- Bradley, W.; Kim, J.; Kilwein, Z.; Blakely, L.; Eydenberg, M.; Jalvin, J.; Laird, C.; Boukouvala, F. Perspectives on the integration between first-principles and data-driven modeling. Comput. Chem. Eng. 2022, 166, 107898. [Google Scholar] [CrossRef]
- Liang, W.Z.; Pei, Z.; Mao, Y.; Shao, Y. Evaluation of molecular photophysical and photochemical properties using linear response time-dependent density functional theory with classical embedding: Successes and challenges. J. Chem. Phys. 2022, 156, 210901. [Google Scholar] [CrossRef]
- Srivastava, A.; Tiwari, S.P.; Miyashita, O.; Tama, F. Integrative/Hybrid Modeling Approaches for Studying Biomolecules. J. Mol. Biol. 2020, 432, 2846–2860. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Joshi, S.N.; Goel, S. Summary of Efforts in Phase Prediction of High Entropy Alloys Using Machine Learning. In Low Cost Manufacturing Technologies: Proceedings of NERC 2022; Springer: Singapore, 2023; pp. 43–57. [Google Scholar]
- Soltani, M.; Ferdousi, S.; Haridas, R.S.; Mishra, R.S.; Jiang, Y. A Crystal Plasticity Finite Element—Machine Learning Combined Approach for Phase Transformation Prediction in High Entropy Alloy. Int. J. Appl. Mech. 2024, 16, 2450024. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, X.; Zhou, D.; Wang, P.; Pan, D.; Wang, H. Tunability of Martensitic Transformation with Cohesive Energies for Fe80−xMnxCo10Cr10 High-Entropy Alloys. Metals 2024, 14, 728. [Google Scholar] [CrossRef]
- Lee, S.Y.; Byeon, S.; Kim, H.S.; Jin, H.; Lee, S. Deep learning-based phase prediction of high-entropy alloys: Optimization, generation, and explanation. Mater. Des. 2021, 197, 109260. [Google Scholar] [CrossRef]
- Kadirvel, K.; Fraser, H.L.; Wang, Y. Microstructural design via spinodal-mediated phase transformation pathways in high-entropy alloys (HEAs) using phase-field modelling. Acta Mater. 2023, 243, 118438. [Google Scholar] [CrossRef]
- Huang, X.; Liu, L.; Liao, W.; Huang, J.; Sun, H.; Yu, C. Characterization of Nucleation Behavior in Temperature-Induced BCC-to-HCP Phase Transformation for High Entropy Alloy. Acta Metall. Sin. Engl. Lett. 2021, 34, 1546–1556. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, L.; Bai, C.; Zhao, J.; Wang, L.; Guo, W.; Tu, J.; Wan, Q. Bidirectional phase transformation facilitated by ε-martensite bands interaction in metastable Fe50Mn30Co10Cr10 dual-phase high entropy alloys. Mater. Charact. 2024, 208, 113655. [Google Scholar] [CrossRef]
- Peivaste, I.; Jossou, E.; Tiamiyu, A.A. Data-driven analysis and prediction of stable phases for high-entropy alloy design. Sci. Rep. 2023, 13, 22556. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Fang, Q.; Liu, B.; Liu, Y. Transformation induced softening and plasticity in high entropy alloys. Acta Mater. 2018, 147, 35–41. [Google Scholar] [CrossRef]
- Zhang, H.F.; Yan, H.L.; Fang, F.; Jia, N. Reverse Transformation in [110]-Oriented Face-Centered-Cubic Single Crystals Studied by Atomic Simulations. Acta Metall. Sin. (Engl. Lett.) 2022, 35, 1631–1640. [Google Scholar] [CrossRef]
- Fu, G.; Liu, X.; Yi, X.; Zhang, S.; Cao, X.; Meng, X.; Gao, Z.; Wang, H. Development of High-Entropy Shape-Memory Alloys: A Review. Metals 2023, 13, 1279. [Google Scholar] [CrossRef]


| Aspect | Classical Lattice Gas | Quantum Lattice Gas |
|---|---|---|
| Computational Complexity | O(N)—Linear Complexity | O(log N)—Logarithmic Complexity |
| Scaling Behavior | Scales linearly with system size | Scales logarithmically with system size |
| Efficiency | Computationally expensive for large systems | Exponential efficiency gain for large systems |
| Memory Usage | High, increases with system size | Low, due to quantum parallelism |
| Simulation Type | Cellular automata based on rule-based updates | Quantum algorithms leveraging entanglement |
| Parallelism | Limited paralel processing | Inherent quantum parallelism |
| Key Advantage | Simple, well-studied for fluid dynamics | Massive speedup for large simulations |
| Limitation | Limited scalability; high computational cost | Requires advanced quantum hardware; noise-sensitive |
| Real-World Applications | Computational fluid dynamics, turbulence modeling | Quantum fluid dynamics, quantum field theory, Dirac equation simulations |
| Energy Efficiency | High energy consumption due to large computations | Lower energy consumption due to computational efficiency |
| Experimental Implementation | Easily implemented on classical supercomputers | Requires quantum computers with high coherence times |
| Error Sensitivity | Low; numerical precision issues in high-resolution simulations | High; noise and decoherence affect computations |
| Hardware Requirements | Traditional CPU/GPU clusters, supercomputers | Quantum processors (e.g., superconducting qubits, trapped ions) |
| Boundary Condition | Description | Applications in HEA Modeling | Effect on Simulation |
|---|---|---|---|
| Periodic Boundary Conditions (PBCs) | The system repeats itself at the boundaries, simulating an infinite medium. | Spinodal decomposition, Ordering/disordering transitions, KMC/MD/MC simulations. | Eliminates artificial boundaries, mimicking an infinite system. Prevents finite-size effects, ensuring realistic phase behavior. |
| Fixed/Dirichlet Boundary Conditions | The values at the boundary are fixed, representing external constraints. | Ordering/disordering transitions, Interfaces/surfaces, Stress-induced phase transitions. | Models fixed temperature, concentration, or stress conditions. Simulates experimental constraints like boundary layers in coatings. |
| Reflective/Neumann Boundary Conditions | No flux condition at the boundary, ensuring no particle or energy flow across it. | Spinodal decomposition, KMC simulations, Defect evolution. | Ensures no loss of mass or energy. Useful for modeling confined HEA nanostructures. Prevents artificial interactions with an external environment. |
| Open Boundary Conditions (OBCs) | Allows mass or energy exchange with the surroundings. | Spinodal decomposition, KMC simulations, Nonequilibrium HEA systems. | Models external interactions like evaporation, adsorption, or material influx. Captures real-world experimental conditions better. |
| Mixed (Robin) Boundary Conditions | A combination of Dirichlet and Neumann conditions, balancing function values and their derivatives. | Interfaces and surfaces, Gradient-driven transitions. | Controls interactions at interfaces. Allows gradual diffusion between regions instead of sharp discontinuities. |
| Absorbing Boundary Conditions | Particles or energy reaching the boundary are removed from the system. | Defect migration, Interfacial reactions, Surface evaporation models. | Models processes where materials are lost, such as oxidation or desorption. Simulates degradation effects in HEA coatings. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łach, Ł. Phase Stability and Transitions in High-Entropy Alloys: Insights from Lattice Gas Models, Computational Simulations, and Experimental Validation. Entropy 2025, 27, 464. https://doi.org/10.3390/e27050464
Łach Ł. Phase Stability and Transitions in High-Entropy Alloys: Insights from Lattice Gas Models, Computational Simulations, and Experimental Validation. Entropy. 2025; 27(5):464. https://doi.org/10.3390/e27050464
Chicago/Turabian StyleŁach, Łukasz. 2025. "Phase Stability and Transitions in High-Entropy Alloys: Insights from Lattice Gas Models, Computational Simulations, and Experimental Validation" Entropy 27, no. 5: 464. https://doi.org/10.3390/e27050464
APA StyleŁach, Ł. (2025). Phase Stability and Transitions in High-Entropy Alloys: Insights from Lattice Gas Models, Computational Simulations, and Experimental Validation. Entropy, 27(5), 464. https://doi.org/10.3390/e27050464







