Improving the Protection of Step-Down Transformers by Utilizing Percentage Differential Protection and Scale-Dependent Intrinsic Entropy
Abstract
1. Introduction
2. Method
2.1. Percentage Differential Protection
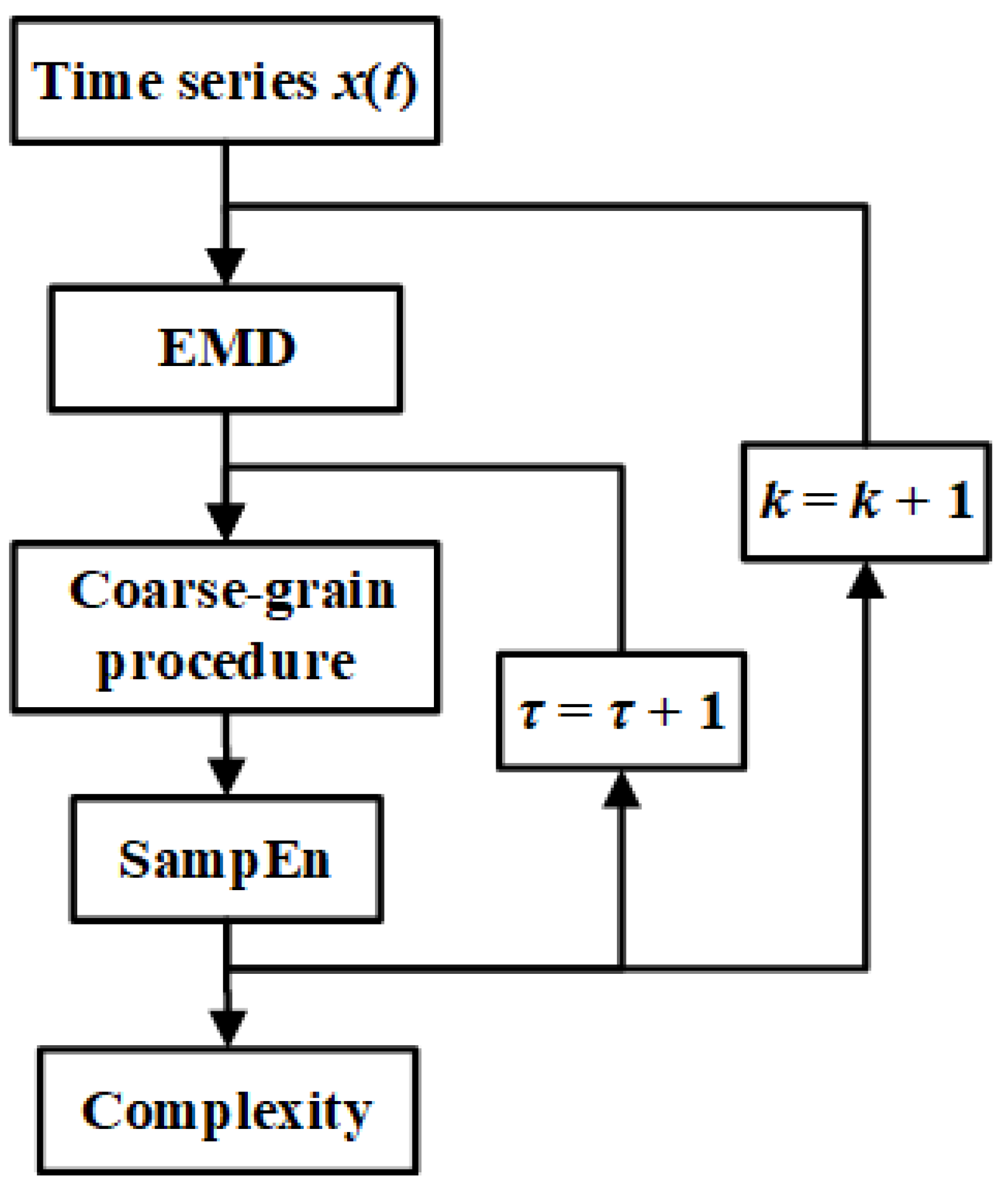
2.2. Scale-Dependent Intrinsic Entropy
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Shahbazi, N.; Bagheri, S.; Gharehpetian, G.B. Transformer differential protection scheme based on self-adaptive biased characteristic curve and considering cross-country faults. Int. J. Circuit Theory Appl. 2023, 51, 1110–1131. [Google Scholar] [CrossRef]
- Bhalja, H.; Bhalja, B.R.; Agarwal, P.; Malik, O.P. Time-frequency decomposition based protection scheme for power transformer- simulation and experimental validation. IEEE Trans. Ind. Electron. 2024, 71, 5296–5306. [Google Scholar] [CrossRef]
- Sahebi, A.; Askarian-Abyaneh, H.; Sadeghi, S.H.H.; Samet, H.; Malik, O.P. Efficient practical method for differential protection of power transformer in the presence of the fault current limiters. IET Gener. Transm. Distrib. 2023, 17, 3861–3871. [Google Scholar] [CrossRef]
- Xian, R.; Wang, L.; Zhang, B.; Li, J.; Xian, R.; Li, J. Identification Method of Interturn Short Circuit Fault for Distribution Transformer Based on Power Loss Variation. IEEE Trans. Ind. Inform. 2024, 20, 2444–2454. [Google Scholar] [CrossRef]
- Yuan, J.; Li, P.; Jiang, Z.; Chen, H.; Wu, X. Monitoring method of high voltage power system’s leapfrog tripping prevention based on differential protection. Int. J. Power Energy Convers. 2023, 14, 121–132. [Google Scholar] [CrossRef]
- Nazari, A.A.; Hosseini, S.A.; Taheri, B. Improving the performance of differential relays in distinguishing between high second harmonic faults and inrush current. Electr. Power Syst. Res. 2023, 223, 109675. [Google Scholar] [CrossRef]
- Ahmadzadeh-Shooshtari, B.; Rezaei-Zare, A. Transformer Differential Protection During Geomagnetic Disturbances: A Hybrid Protection Scheme and Real-Time Validation Tests. IEEE Trans. Power Deliv. 2024, 39, 13–28. [Google Scholar] [CrossRef]
- Shakeri, S.; Koochi, M.H.R.; Esmaeili, S. Optimal harmonic resonance monitoring in electrical network considering area of harmonic pollution and system uncertainty. IET Gener. Transm. Distrib. 2024, 18, 2570–2586. [Google Scholar] [CrossRef]
- Baker, E.; Nese, S.V.; Dursun, E. Hybrid Condition Monitoring System for Power Transformer Fault Diagnosis. Energies 2023, 16, 1151. [Google Scholar] [CrossRef]
- Koloushani, S.M.; Taher, S.A. A new virtual consensus-based wide area differential protection, IET Generation. Transm. Distrib. 2024, 18, 1906–1918. [Google Scholar] [CrossRef]
- Key, S.; Son, G.-W.; Nam, S.-R. Deep Learning-Based Algorithm for Internal Fault Detection of Power Transformers during Inrush Current at Distribution Substations. Energies 2024, 17, 963. [Google Scholar] [CrossRef]
- Kakolaki, S.E.H.; Hakimian, V.; Sadeh, J.; Rakhshani, E. Comprehensive Study on Transformer Fault Detection via Frequency Response Analysis. IEEE Access 2023, 11, 81852–81881. [Google Scholar] [CrossRef]
- Hsu, W.-T.; Huang, C.-W. Analysis of Symmetrical and Unsymmetrical Faults Using the EEMD and Scale-Dependent Intrinsic Entropies. Fluct. Noise Lett. 2022, 21, 3. [Google Scholar] [CrossRef]
- Peng, F.; Gao, H.; Huang, J.; Guo, Y.; Liu, Y. Power Differential Protection for Transformer Based on Fault Component Network. IEEE Trans. Power Deliv. 2023, 38, 2464–2477. [Google Scholar] [CrossRef]
- Chandra, A.; Singh, G.K.; Pant, V. A Novel High Impedance Fault Detection Strategy for Microgrid Based on Differential Energy Signal of Current Signatures and Entropy Estimation. Electr. Power Compon. Syst. 2024, 52, 532–554. [Google Scholar] [CrossRef]
- Chen, Y.B.; Cui, H.S.; Huang, C.W.; Hsu, W.T. Improving transmission line fault diagnosis based on EEMD and power spectral entropy. Entropy 2024, 26, 806. [Google Scholar] [CrossRef] [PubMed]
- Moravej, Z.; Ebrahimi, A.; Pazoki, M.; Barati, M. Time domain differential protection scheme applied to power transformers. Int. J. Electr. Power Energy Syst. 2023, 154, 109465. [Google Scholar] [CrossRef]
- Saleh, S.A.; Ozkop, E.; Valdes, M.E.; Yuksel, A.; Jewett, D.; Al-Durra, A. Experimental Assessment of Ground Fault Protection in Frequency-Selective Grounded Systems Fed by a Single Transformer. IEEE Trans. Ind. Appl. 2023, 59, 2386–2399. [Google Scholar] [CrossRef]
- Duan, J.; Zhao, M.; Lei, Y.; Guan, X. A Novel Transient Saturation Detection Method for P-Class Current Transformer Using Improved Hausdorff Distance Algorithm. IEEE Trans. Instrum. Meas. 2024, 73, 9003812. [Google Scholar] [CrossRef]
- Zheng, T.; Zhang, R.; Chen, Y.; Ai, J.; Sun, Y. Improved scheme based on memory voltage for transformer differential protection considering the effects of PLL. IET Gener. Transm. Distrib. 2024, 18, 214–225. [Google Scholar] [CrossRef]
- Liu, P.; Jiao, B.; Zhang, P.; Du, S.; Zhu, J.; Song, Y. Countermeasure to prevent transformer differential protection from false operations. IEEE Access 2023, 11, 45950–45960. [Google Scholar] [CrossRef]
- Yigang, S.K.H.; Lei, W. Fault identification of transformer based on multiscale entropy analysisand improved SVM. J. Electron. Meas. Instrum. 2022, 36, 161–168. [Google Scholar]
- Liang, J.; Zhang, K.; Al-Durra, A.; Zhou, D. A Multi-Information Fusion Algorithm to Fault Diagnosis of Power Converter in Wind Power Generation Systems. IEEE Trans. Ind. Inform. 2024, 20, 1167–1179. [Google Scholar] [CrossRef]
- Bounoua, W.; Aftab, M.F.; Omlin, C.W.P. Online detrended fluctuation analysis and improved empirical wavelet transform for real-time oscillations detection in industrial control loops. Comput. Chem. Eng. 2023, 172, 108173. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, N.; Hou, Y. Comparison of empirical modal decomposition class techniques applied in noise cancellation for building heating consumption prediction based on time-frequency analysis. Energy Build. 2023, 284, 112853. [Google Scholar] [CrossRef]
- Das, J.C. Short Circuits in AC and DC Systems ANSI, IEEE, and IEC Standards, 1st ed.; CRC press: Boca Raton, FL, USA, 2021. [Google Scholar]

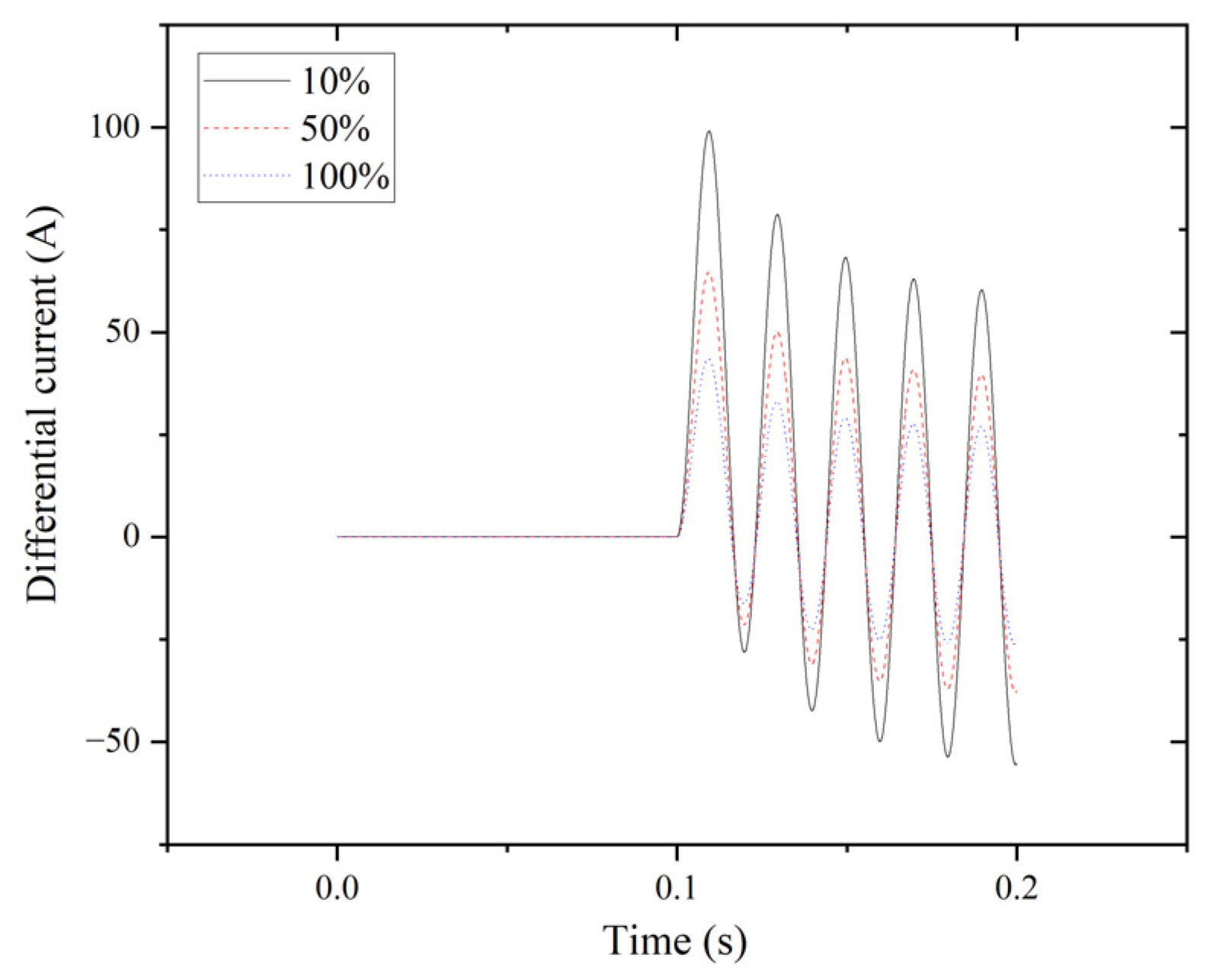
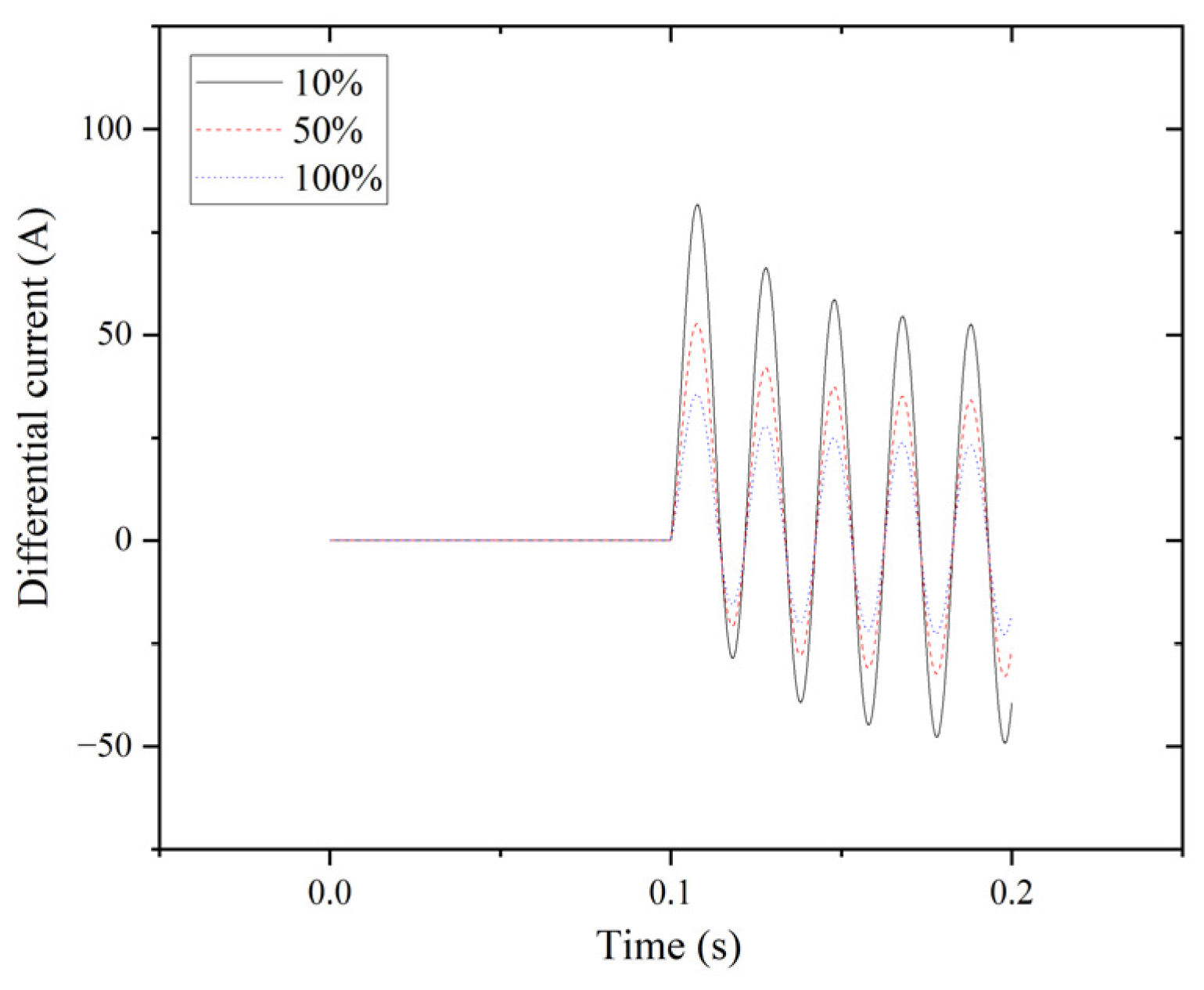

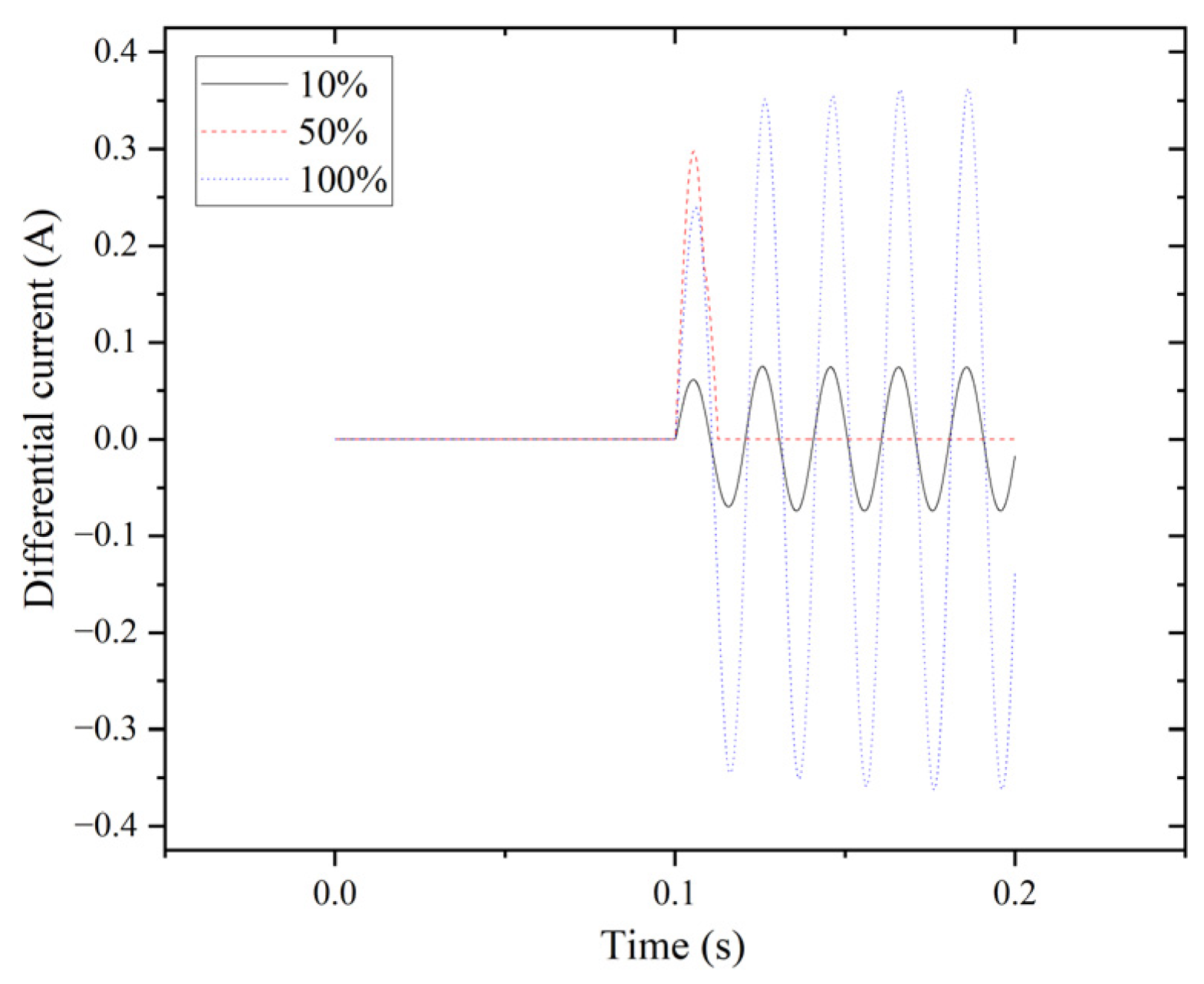
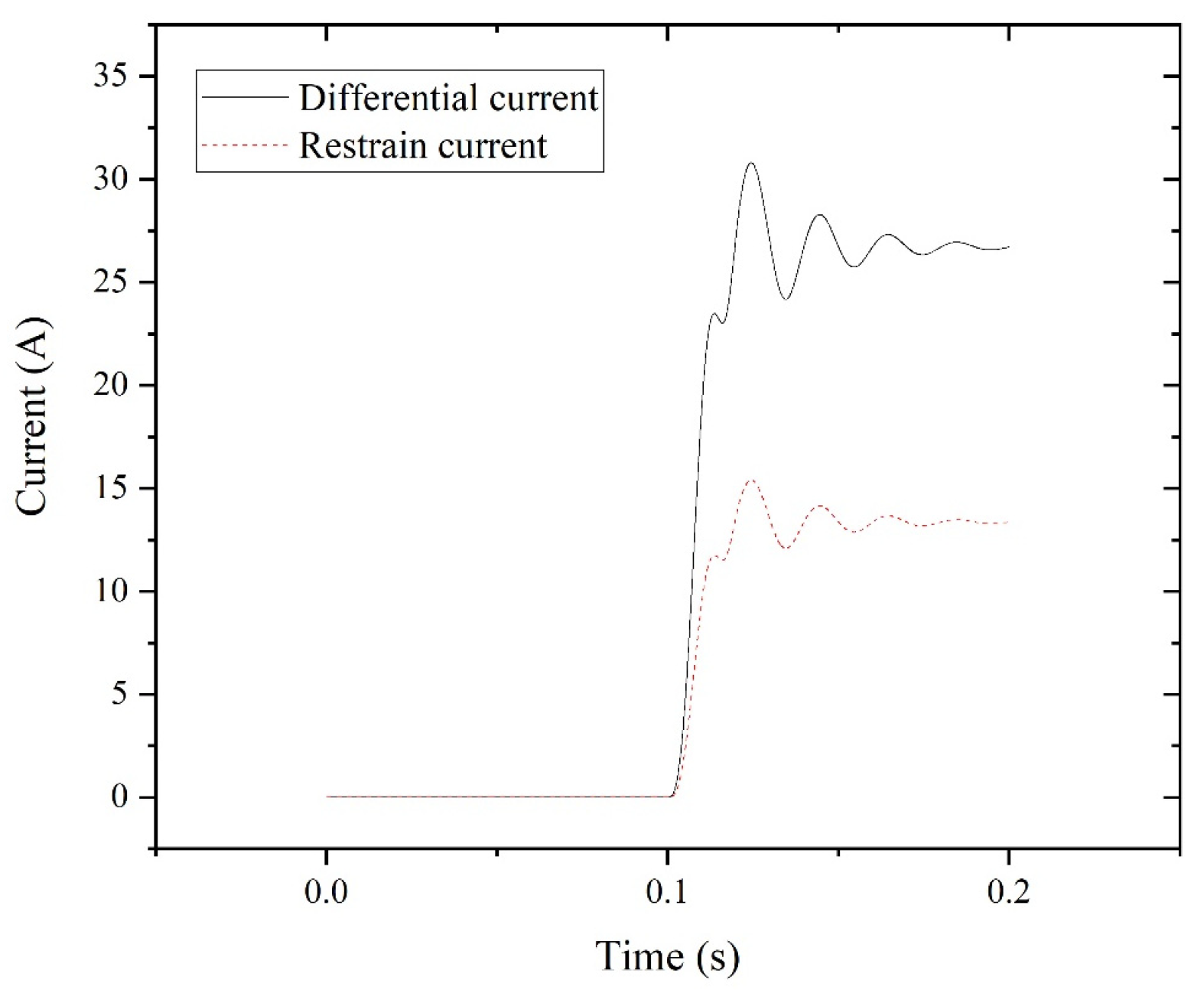
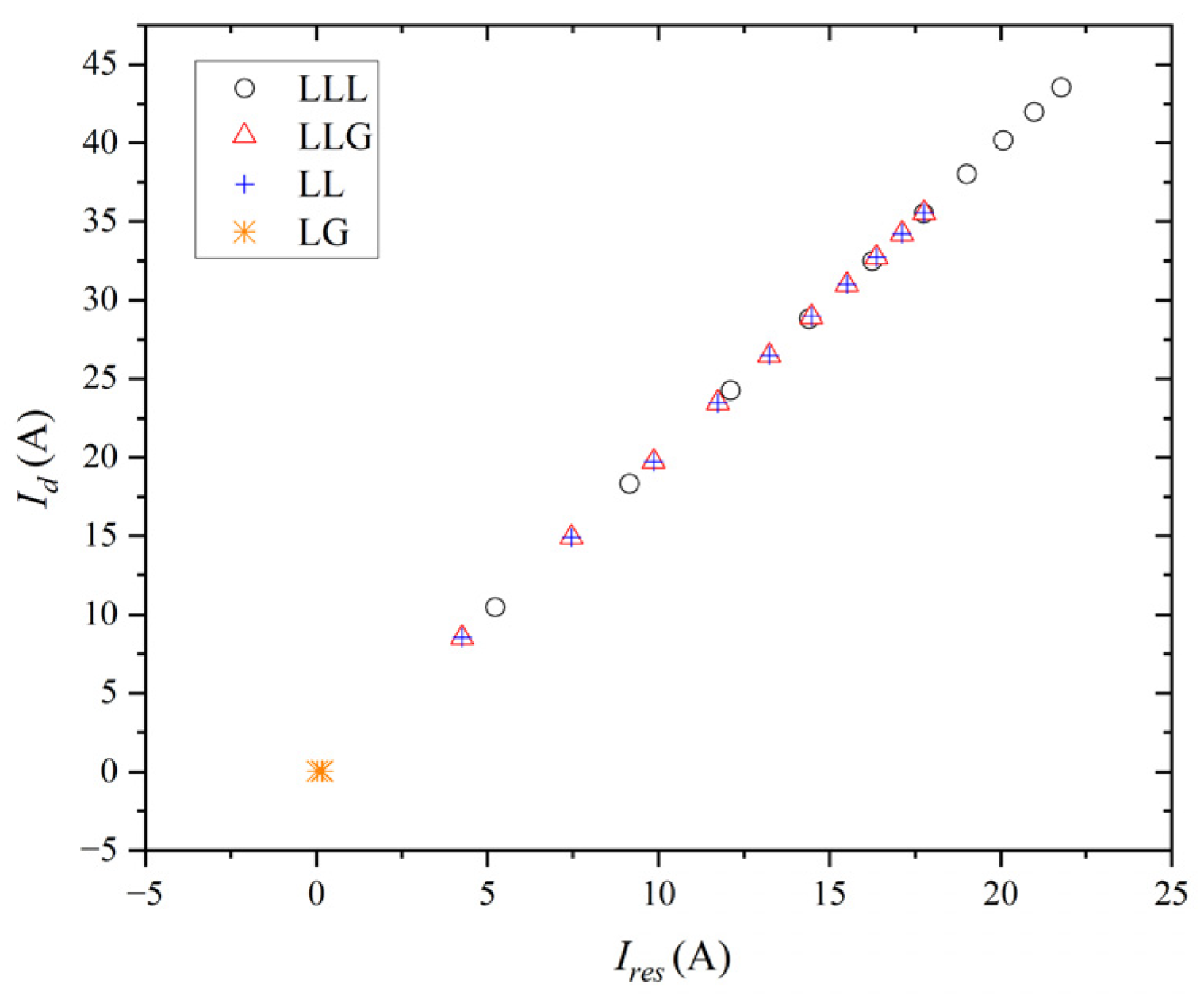
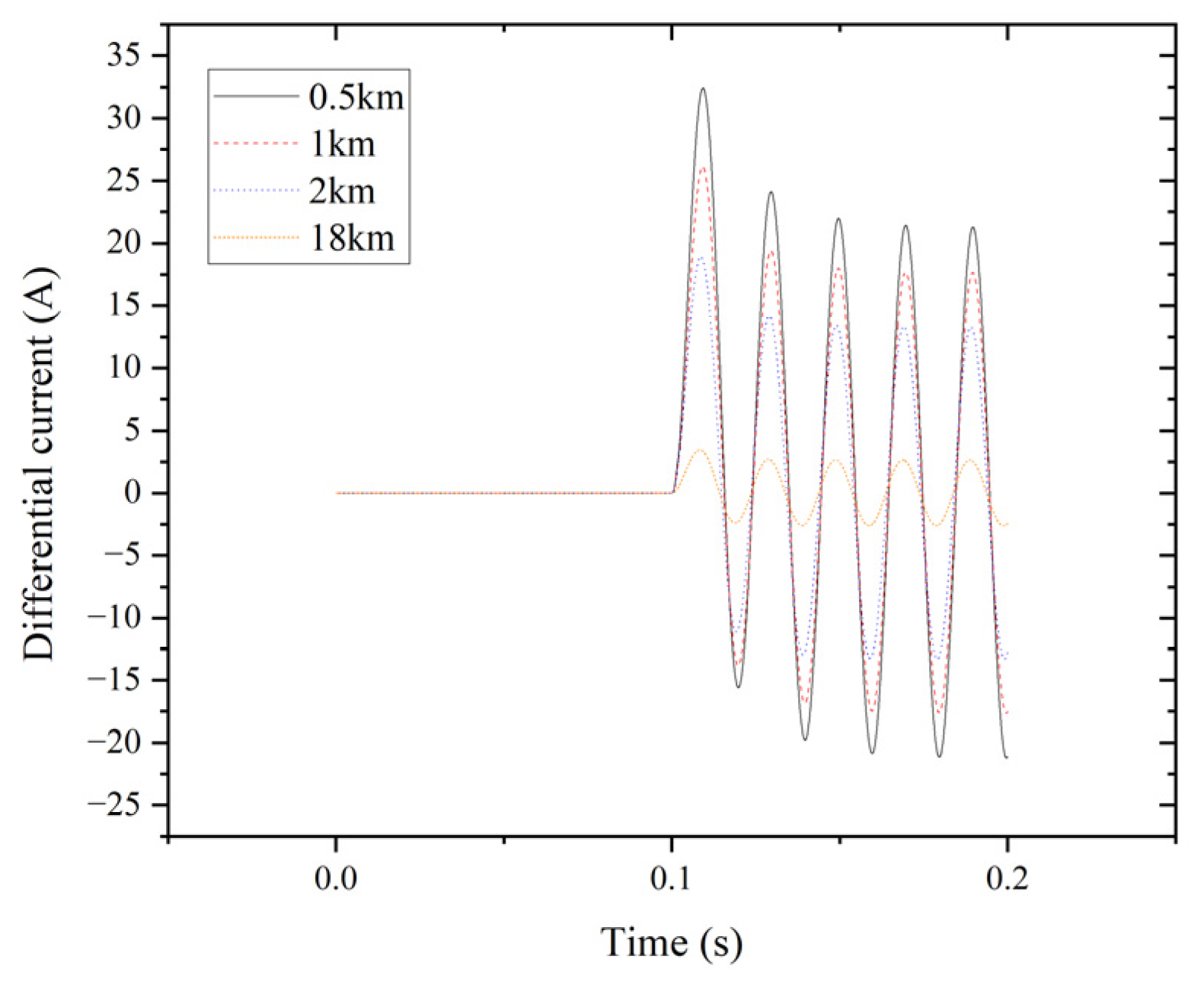

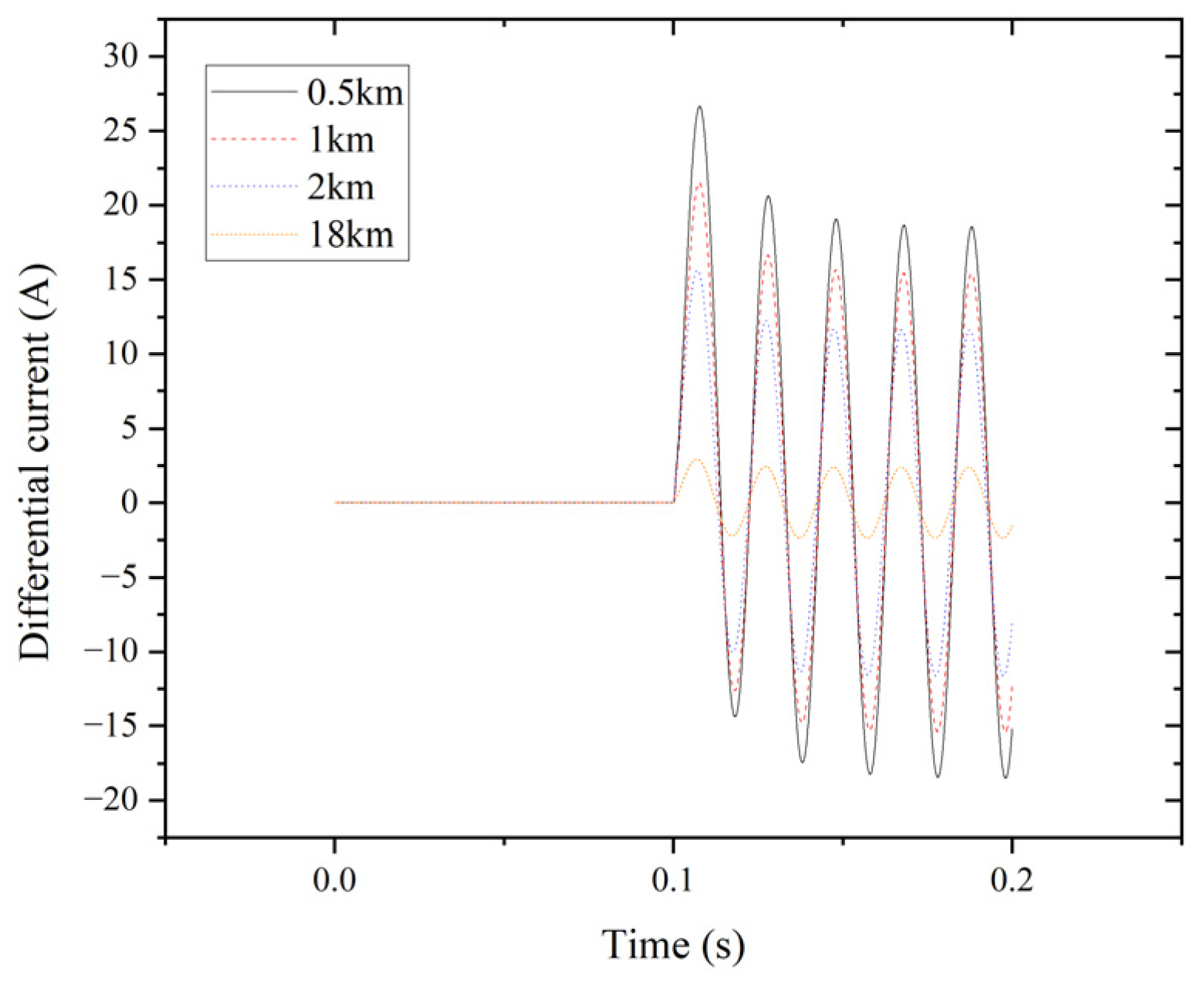
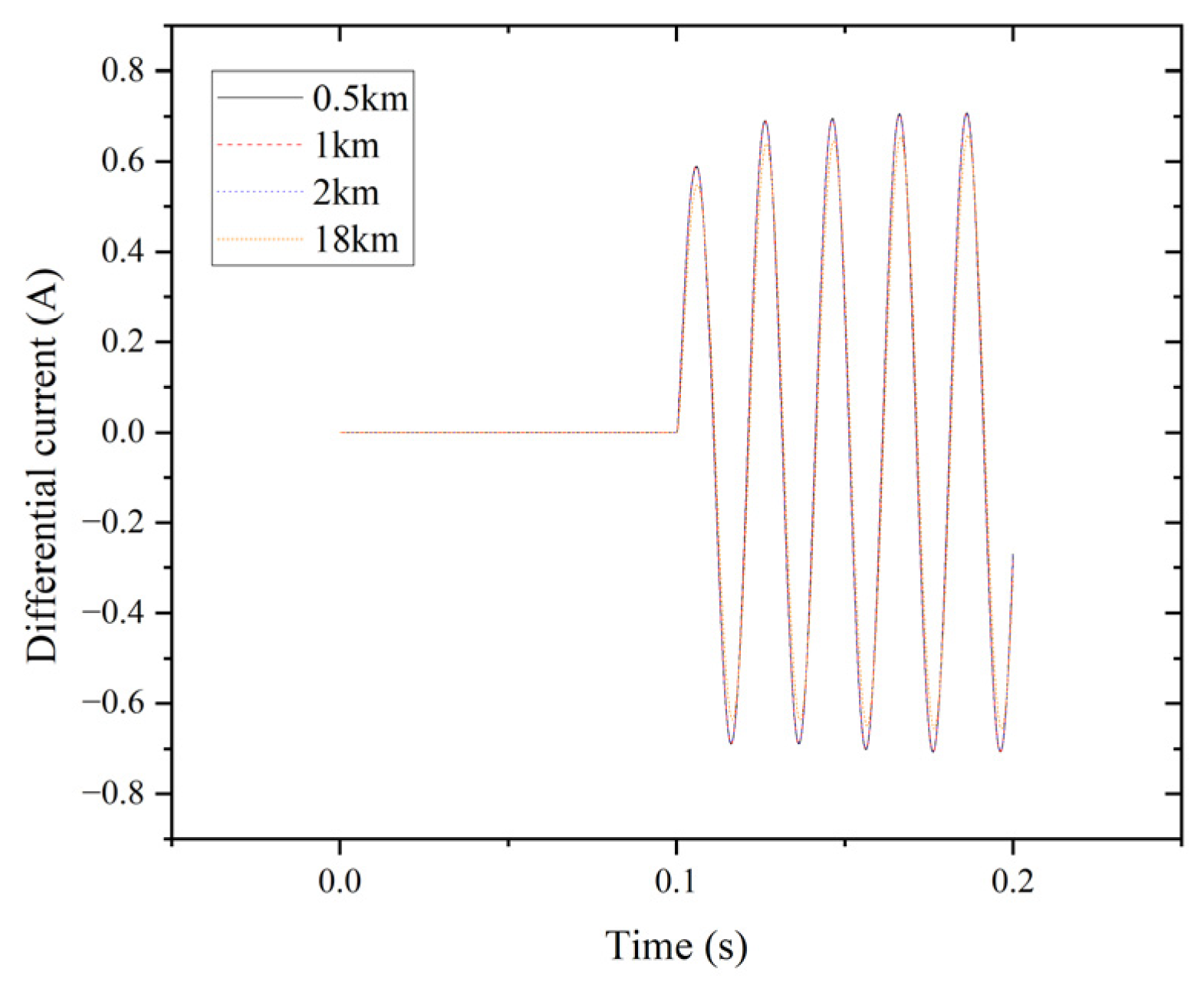
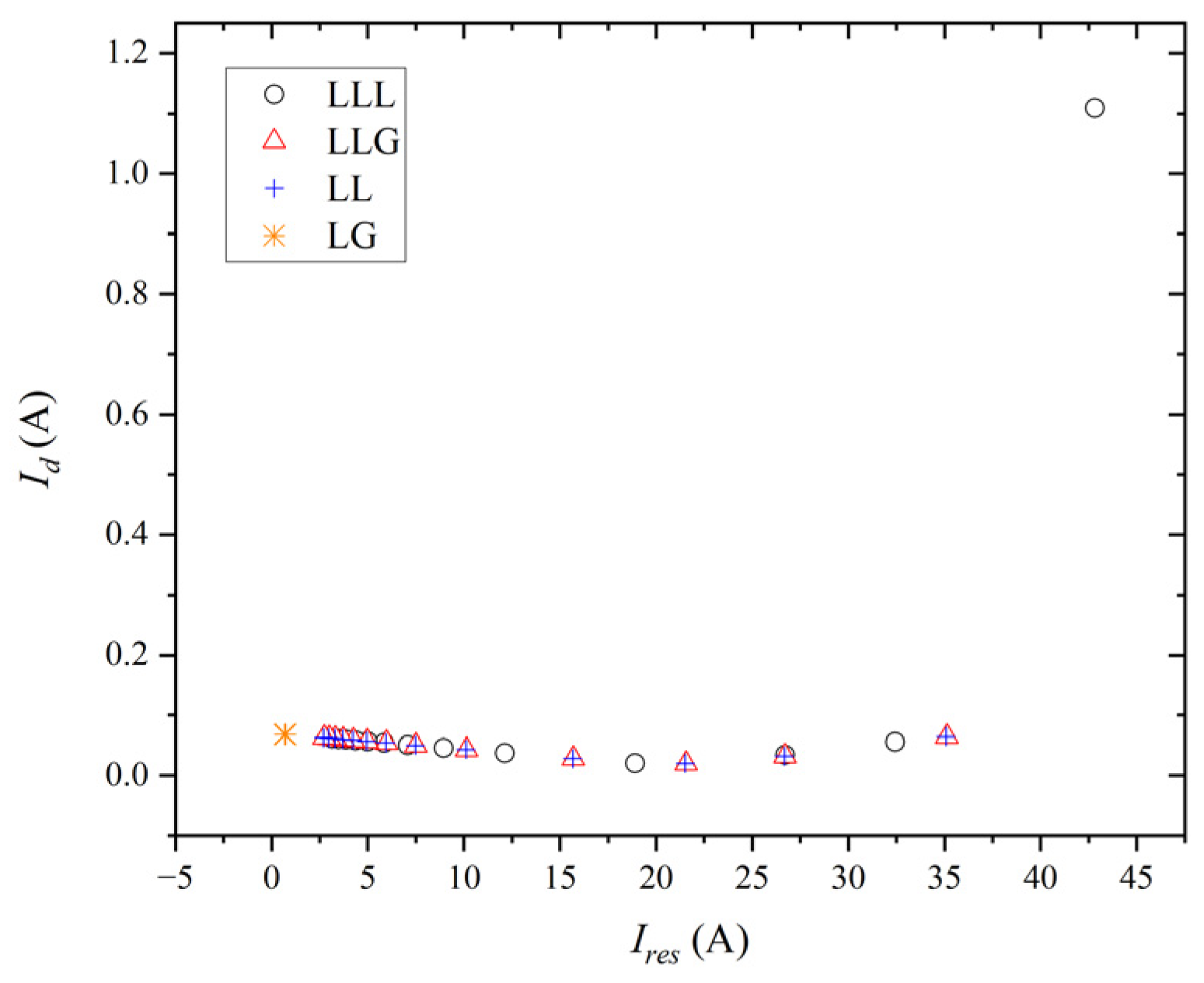
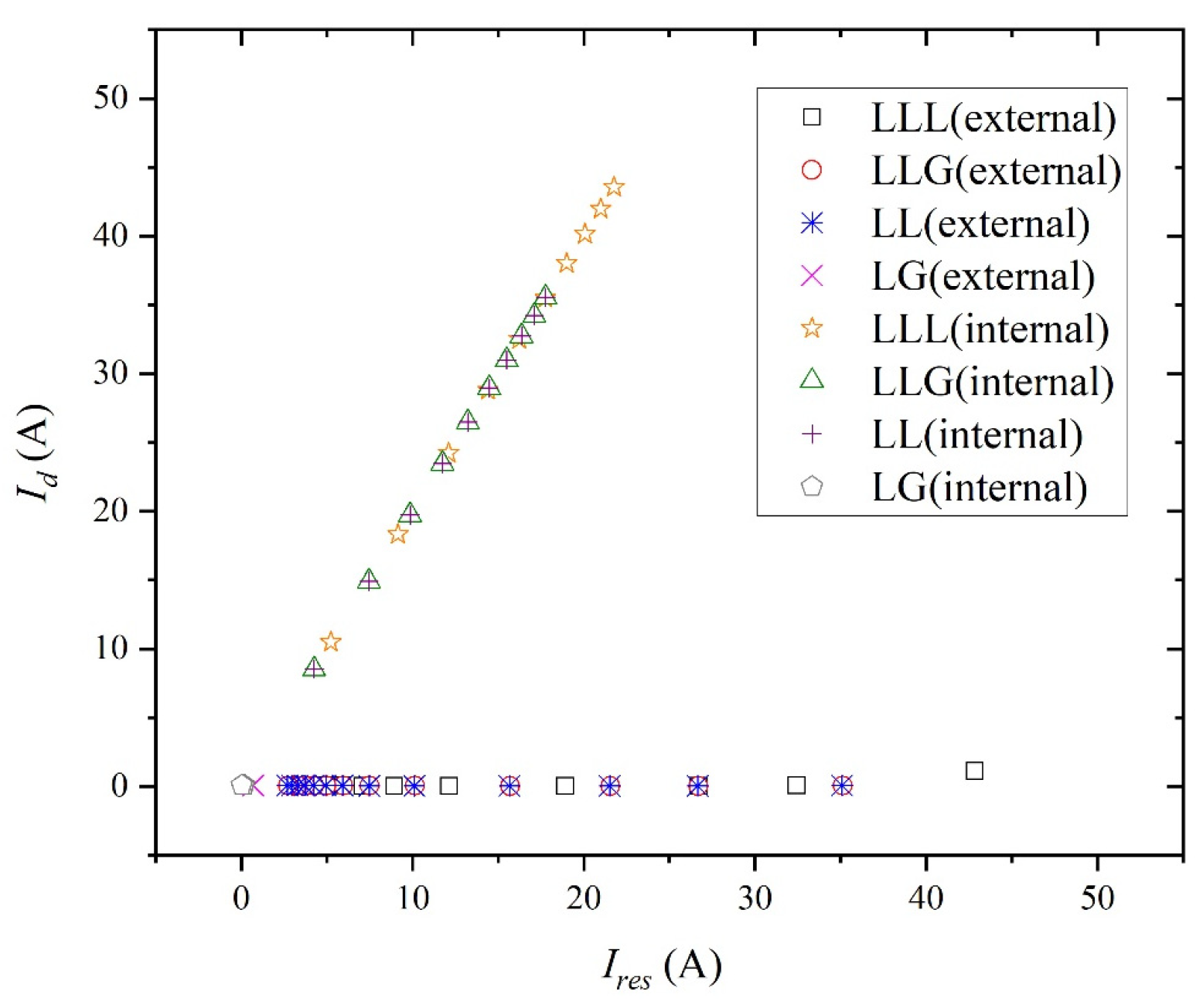
| Tap | Fault Phase A | Non-Faulty Phase B | Non-Faulty Phase C | Normal Phase A | Normal Phase B | Normal Phase C |
|---|---|---|---|---|---|---|
| 10% | 1.4661 | 1.5531 | 1.4039 | 1.0778 | 1.0694 | 1.0667 |
| 20% | 1.4761 | 1.5631 | 1.3064 | 1.0778 | 1.0694 | 1.0667 |
| 30% | 1.4875 | 1.5743 | 1.2236 | 1.0778 | 1.0694 | 1.0667 |
| 40% | 1.5002 | 1.5788 | 1.1779 | 1.0778 | 1.0694 | 1.0667 |
| 50% | 1.5152 | 1.5690 | 1.1471 | 1.0778 | 1.0694 | 1.0667 |
| 60% | 1.5341 | 1.5409 | 1.1252 | 1.0778 | 1.0694 | 1.0667 |
| 70% | 1.5760 | 1.5047 | 1.1124 | 1.0778 | 1.0694 | 1.0667 |
| 80% | 1.6133 | 1.4483 | 1.1091 | 1.0778 | 1.0694 | 1.0667 |
| 90% | 1.6270 | 1.3550 | 1.1176 | 1.0778 | 1.0694 | 1.0667 |
| 100% | 1.6391 | 1.2432 | 1.1357 | 1.0778 | 1.0694 | 1.0667 |
| Tap | Fault Phase A | Non-Faulty Phase B | Non-Faulty Phase C | Normal Phase A | Normal Phase B | Normal Phase C |
|---|---|---|---|---|---|---|
| 10% | 0.268 | 1.4729 | 1.4733 | 1.0842 | 1.0615 | 1.0612 |
| 20% | 0.2679 | 1.4863 | 1.4874 | 1.0842 | 1.0615 | 1.0612 |
| 30% | 0.268 | 1.501 | 1.5027 | 1.0842 | 1.0615 | 1.0612 |
| 40% | 0.2679 | 1.5165 | 1.5193 | 1.0842 | 1.0615 | 1.0612 |
| 50% | 0.268 | 1.5336 | 1.5373 | 1.0842 | 1.0615 | 1.0612 |
| 60% | 0.2679 | 1.5525 | 1.557 | 1.0842 | 1.0615 | 1.0612 |
| 70% | 0.2679 | 1.5733 | 1.5789 | 1.0842 | 1.0615 | 1.0612 |
| 80% | 0.268 | 1.5857 | 1.5966 | 1.0842 | 1.0615 | 1.0612 |
| 90% | 0.268 | 1.4428 | 1.455 | 1.0842 | 1.0615 | 1.0612 |
| 100% | 0.2681 | 1.1942 | 1.2036 | 1.0842 | 1.0615 | 1.0612 |
| Tap#B | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tap#A | |||||||||||
| 2 | 1.4467 | 1.4382 | 1.4314 | 1.4258 | 1.418 | 1.4116 | 1.4067 | 1.4031 | 1.4005 | 1.3987 | |
| 2.1 | 1.4686 | 1.4581 | 1.4494 | 1.4424 | 1.4334 | 1.4259 | 1.42 | 1.4154 | 1.412 | ||
| 2.2 | 1.4891 | 1.4769 | 1.4669 | 1.4584 | 1.4482 | 1.4398 | 1.433 | 1.4276 | |||
| 2.3 | 1.5087 | 1.4947 | 1.4832 | 1.4737 | 1.4626 | 1.4532 | 1.4456 | ||||
| 2.4 | 1.5293 | 1.5119 | 1.499 | 1.4883 | 1.4756 | 1.4663 | |||||
| 2.5 | 1.5514 | 1.5303 | 1.5142 | 1.5024 | 1.4897 | ||||||
| 2.6 | 1.5743 | 1.5497 | 1.5311 | 1.5162 | |||||||
| 2.7 | 1.5938 | 1.5695 | 1.5483 | ||||||||
| 2.8 | 1.4878 | 1.5901 | |||||||||
| 2.9 | 1.2421 | ||||||||||
| Normal | 1.0778 | 1.0778 | 1.0778 | 1.0778 | 1.0778 | 1.0778 | 1.0778 | 1.0778 | 1.0778 | 1.0778 | |
| Tap#B | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tap#A | |||||||||||
| 2 | 0.2766 | 0.268 | 0.268 | 0.268 | 0.268 | 0.268 | 0.268 | 0.268 | 0.268 | 0.268 | |
| 2.1 | 0.6533 | 0.5453 | 0.4465 | 0.3579 | 0.2791 | 0.2644 | 0.2644 | 0.2643 | 0.2643 | ||
| 2.2 | 1.0128 | 0.9503 | 0.8967 | 0.8459 | 0.7967 | 0.7481 | 0.6984 | 0.6434 | |||
| 2.3 | 1.1724 | 1.1176 | 1.071 | 1.0282 | 0.9881 | 0.9502 | 0.9141 | ||||
| 2.4 | 1.276 | 1.2258 | 1.1825 | 1.1427 | 1.1057 | 1.0711 | |||||
| 2.5 | 1.3526 | 1.3045 | 1.2635 | 1.2258 | 1.1909 | ||||||
| 2.6 | 1.4138 | 1.3661 | 1.3267 | 1.2906 | |||||||
| 2.7 | 1.4699 | 1.4187 | 1.3785 | ||||||||
| 2.8 | 1.5241 | 1.4571 | |||||||||
| 2.9 | 1.5703 | ||||||||||
| Normal | 1.0842 | 1.0842 | 1.0842 | 1.0842 | 1.0842 | 1.0842 | 1.0842 | 1.0842 | 1.0842 | 1.0842 | |
| Distance | Fault Phase A | Non-Faulty Phase B | Non-Faulty Phase C | Normal Phase A | Normal Phase B | Normal Phase C |
|---|---|---|---|---|---|---|
| 0 km | 1.4236 | 1.544 | 1.4808 | 1.0778 | 1.0694 | 1.0667 |
| 0.5 km | 1.4243 | 1.545 | 1.4819 | 1.0778 | 1.0694 | 1.0667 |
| 1 km | 1.425 | 1.546 | 1.483 | 1.0778 | 1.0694 | 1.0667 |
| 2 km | 1.4263 | 1.5481 | 1.485 | 1.0778 | 1.0694 | 1.0667 |
| 4 km | 1.4291 | 1.5522 | 1.4891 | 1.0778 | 1.0694 | 1.0667 |
| 6 km | 1.4319 | 1.5563 | 1.4927 | 1.0778 | 1.0694 | 1.0667 |
| 8 km | 1.4347 | 1.5607 | 1.4954 | 1.0778 | 1.0694 | 1.0667 |
| 10 km | 1.4376 | 1.5651 | 1.4977 | 1.0778 | 1.0694 | 1.0667 |
| 12 km | 1.4405 | 1.5696 | 1.4994 | 1.0778 | 1.0694 | 1.0667 |
| 14 km | 1.4435 | 1.5743 | 1.5008 | 1.0778 | 1.0694 | 1.0667 |
| 16 km | 1.4464 | 1.5791 | 1.5017 | 1.0778 | 1.0694 | 1.0667 |
| 18 km | 1.4493 | 1.583 | 1.5024 | 1.0778 | 1.0694 | 1.0667 |
| 20 km | 1.4524 | 1.5853 | 1.5027 | 1.0778 | 1.0694 | 1.0667 |
| Distance | Fault Phase A | Non-Faulty Phase B | Non-Faulty Phase C | Normal Phase A | Normal Phase B | Normal Phase C |
|---|---|---|---|---|---|---|
| 0 km | 0.2574 | 1.4607 | 1.4604 | 1.0842 | 1.0615 | 1.0612 |
| 0.5 km | 0.2573 | 1.4619 | 1.4604 | 1.0842 | 1.0615 | 1.0612 |
| 1 km | 0.2572 | 1.4632 | 1.4604 | 1.0842 | 1.0615 | 1.0612 |
| 2 km | 0.257 | 1.4658 | 1.4605 | 1.0842 | 1.0615 | 1.0612 |
| 4 km | 0.2617 | 1.471 | 1.4608 | 1.0842 | 1.0615 | 1.0612 |
| 6 km | 0.5707 | 1.4762 | 1.4611 | 1.0842 | 1.0615 | 1.0612 |
| 8 km | 0.7652 | 1.4816 | 1.4616 | 1.0842 | 1.0615 | 1.0612 |
| 10 km | 0.8758 | 1.4872 | 1.4621 | 1.0842 | 1.0615 | 1.0612 |
| 12 km | 0.9542 | 1.4929 | 1.4627 | 1.0842 | 1.0615 | 1.0612 |
| 14 km | 1.0162 | 1.4987 | 1.4635 | 1.0842 | 1.0615 | 1.0612 |
| 16 km | 1.0671 | 1.5046 | 1.4643 | 1.0842 | 1.0615 | 1.0612 |
| 18 km | 1.1101 | 1.5106 | 1.4651 | 1.0842 | 1.0615 | 1.0612 |
| 20 km | 1.1473 | 1.5167 | 1.466 | 1.0842 | 1.0615 | 1.0612 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-W.; Fang, C.-C.; Hsu, W.-T.; Yang, C.-C.; Zhou, L.-T. Improving the Protection of Step-Down Transformers by Utilizing Percentage Differential Protection and Scale-Dependent Intrinsic Entropy. Entropy 2025, 27, 444. https://doi.org/10.3390/e27040444
Huang C-W, Fang C-C, Hsu W-T, Yang C-C, Zhou L-T. Improving the Protection of Step-Down Transformers by Utilizing Percentage Differential Protection and Scale-Dependent Intrinsic Entropy. Entropy. 2025; 27(4):444. https://doi.org/10.3390/e27040444
Chicago/Turabian StyleHuang, Chia-Wei, Chih-Chiang Fang, Wei-Tai Hsu, Chih-Chung Yang, and Li-Ting Zhou. 2025. "Improving the Protection of Step-Down Transformers by Utilizing Percentage Differential Protection and Scale-Dependent Intrinsic Entropy" Entropy 27, no. 4: 444. https://doi.org/10.3390/e27040444
APA StyleHuang, C.-W., Fang, C.-C., Hsu, W.-T., Yang, C.-C., & Zhou, L.-T. (2025). Improving the Protection of Step-Down Transformers by Utilizing Percentage Differential Protection and Scale-Dependent Intrinsic Entropy. Entropy, 27(4), 444. https://doi.org/10.3390/e27040444








