Robust Smoothing Cardinalized Probability Hypothesis Density Filter-Based Underwater Multi-Target Direction-of-Arrival Tracking with Uncertain Measurement Noise
Abstract
1. Introduction
2. Multi-Target Tracking Model
2.1. Kinematic Model of the Underwater Target by the Bearing Angle
2.2. Measurement Model
3. GM-CPHD Filter for Multi-Target DOA Tracking
- Step 1. Prediction
- Step 2. Update
- Step 3. Managing Mixture Components
- Step 4. State Estimation
4. Saga–Husa CPHD Filter (SH-CPHD Filter) for Multi-Target DOA Tracking
5. Smoothing SH-CPHD Filter for Robust Multi-Target DOA Tracking
5.1. Smoothing CPHD Filter
5.2. Algorithm of Smoothing SH-CPHD Filter
| Algorithm 1: Smoothing SH-CPHD filter for robust multi-target DOA tracking |
| 1. Initialize the components of Gaussian mixture model and cardinalized distribution ; For Prediction: 2. Calculate the predicted cardinalized distribution according to Equation (3); 3. Calculate the components of survival targets: For , , ; End 4. Add the components of birth targets ; 5. Express the predicted GM components as , where ; Update: 6. Update the cardinality distribution to by using Equation (10); 7. The DOA estimation method is used to process these extracted signals to estimate the bearing angle of the target, and the bearing angle measurement set is obtained. 8. Update GM components of targets: For , , ; end For For , , , , ; End End 9. , prune, merge and limit the components to obtain new components; 10. Express the updated GM components as ; 11. The estimate of target number is the n corresponding to the maximum of ; 12. The corresponding to the components with the largest weights are the estimates of target states. End Smoothing: 13. Initialize , , , ; For 14. Smooth the PHD For For 15. , prune, merge and limit the components to obtain new components; End End |
6. Simulations
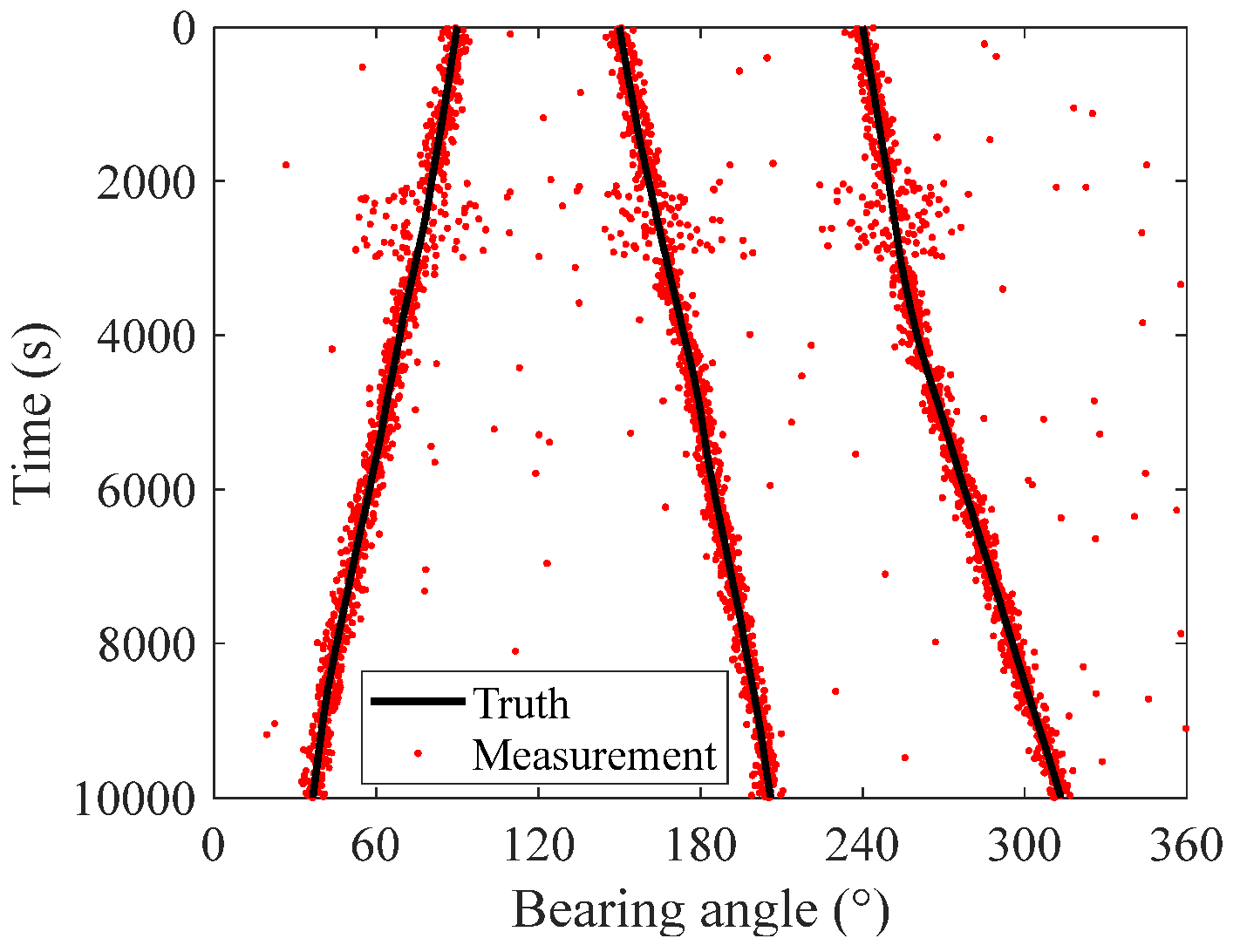
6.1. Simulation Scenario
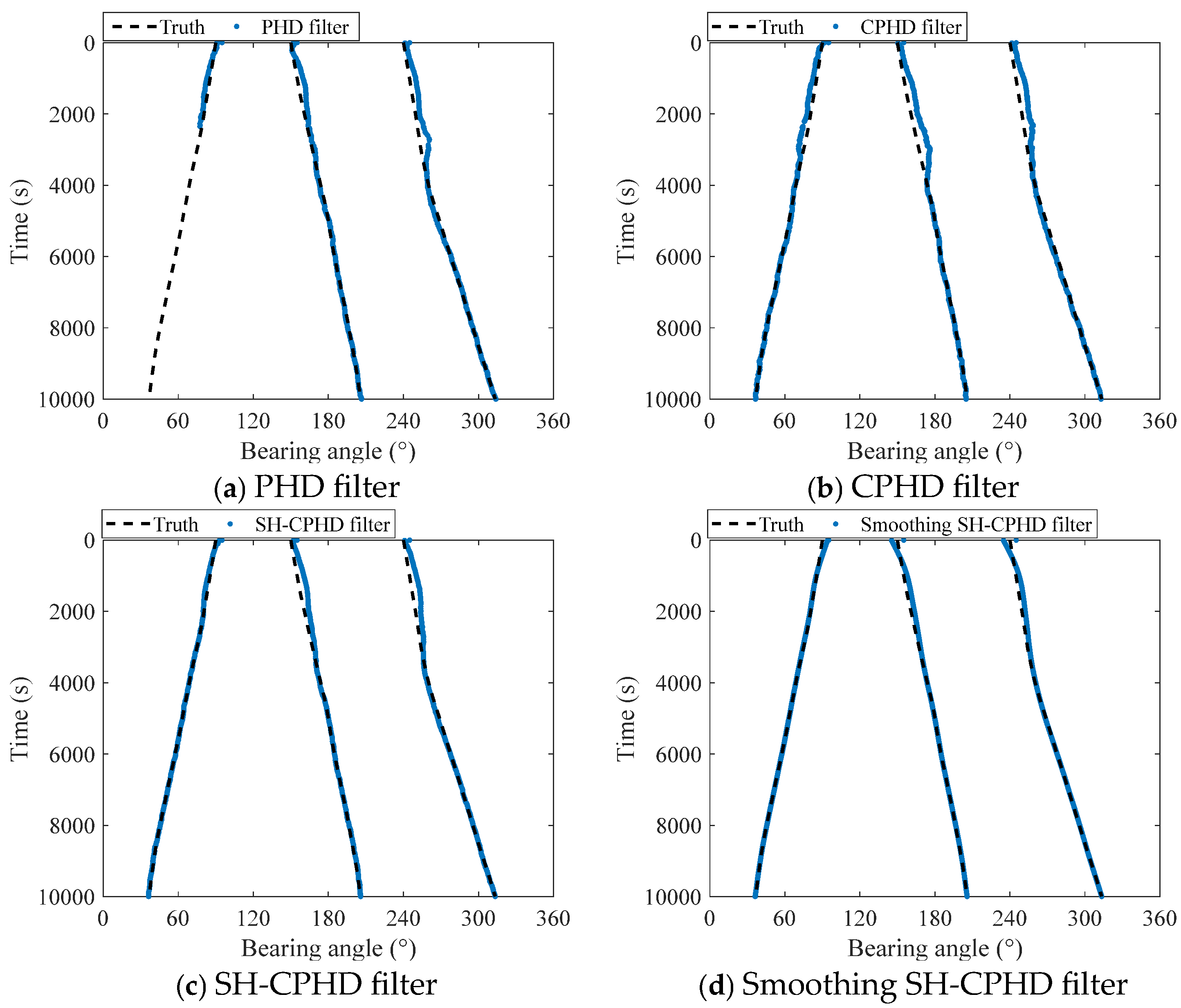
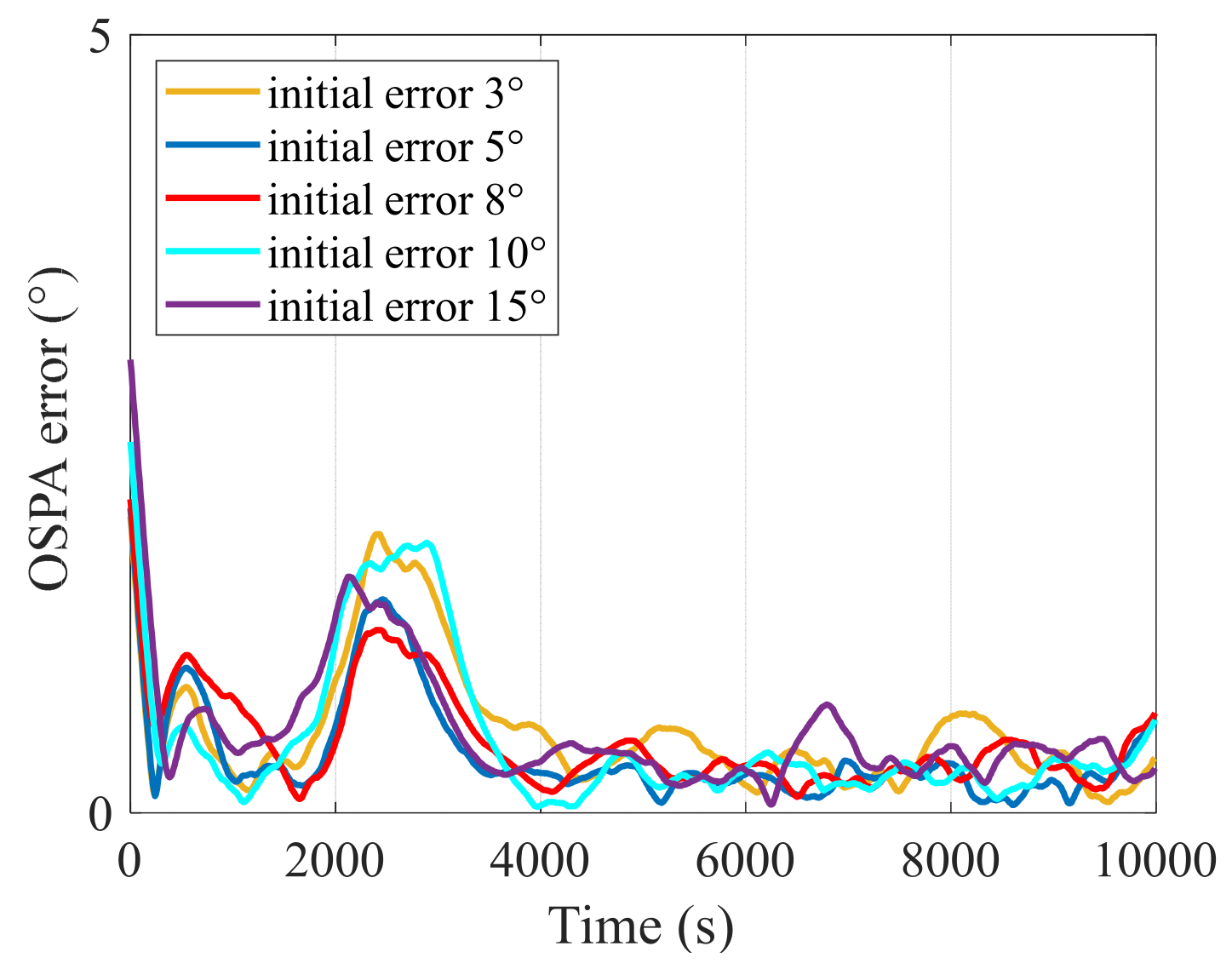
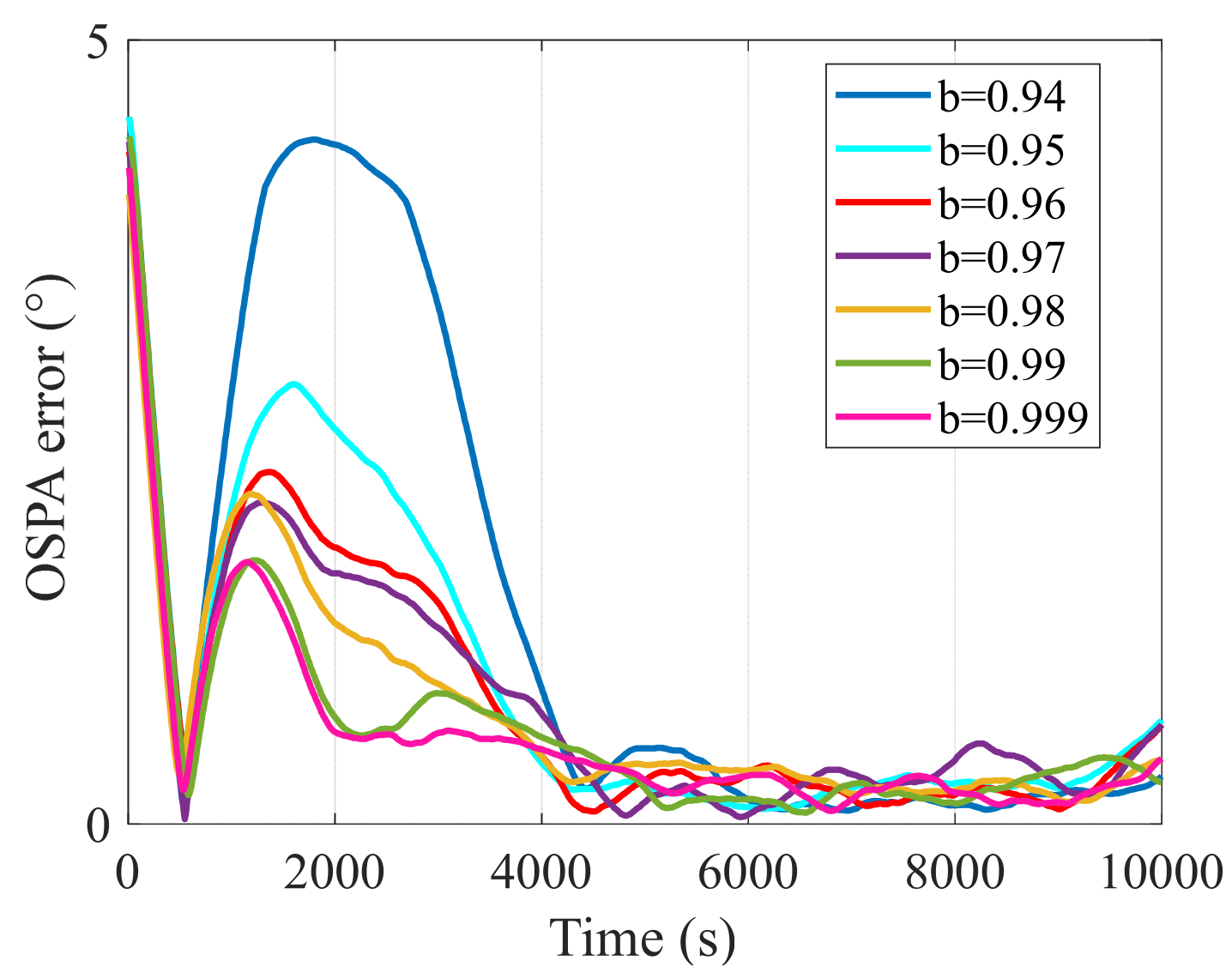
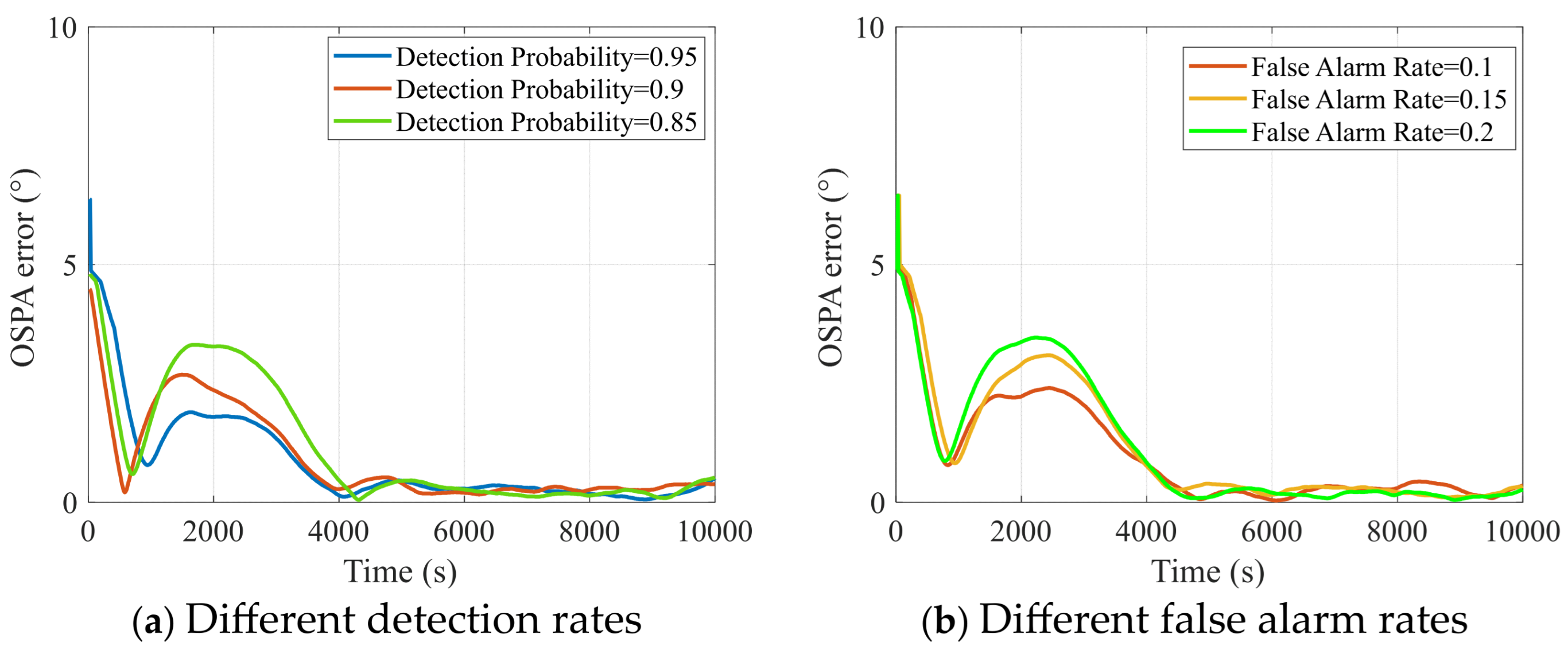
6.2. Verification of the Smoothing SH-CPHD Filter for Robust Multi-Target DOA Tracking
7. Experimental Results
7.1. Experimental Setup and Description
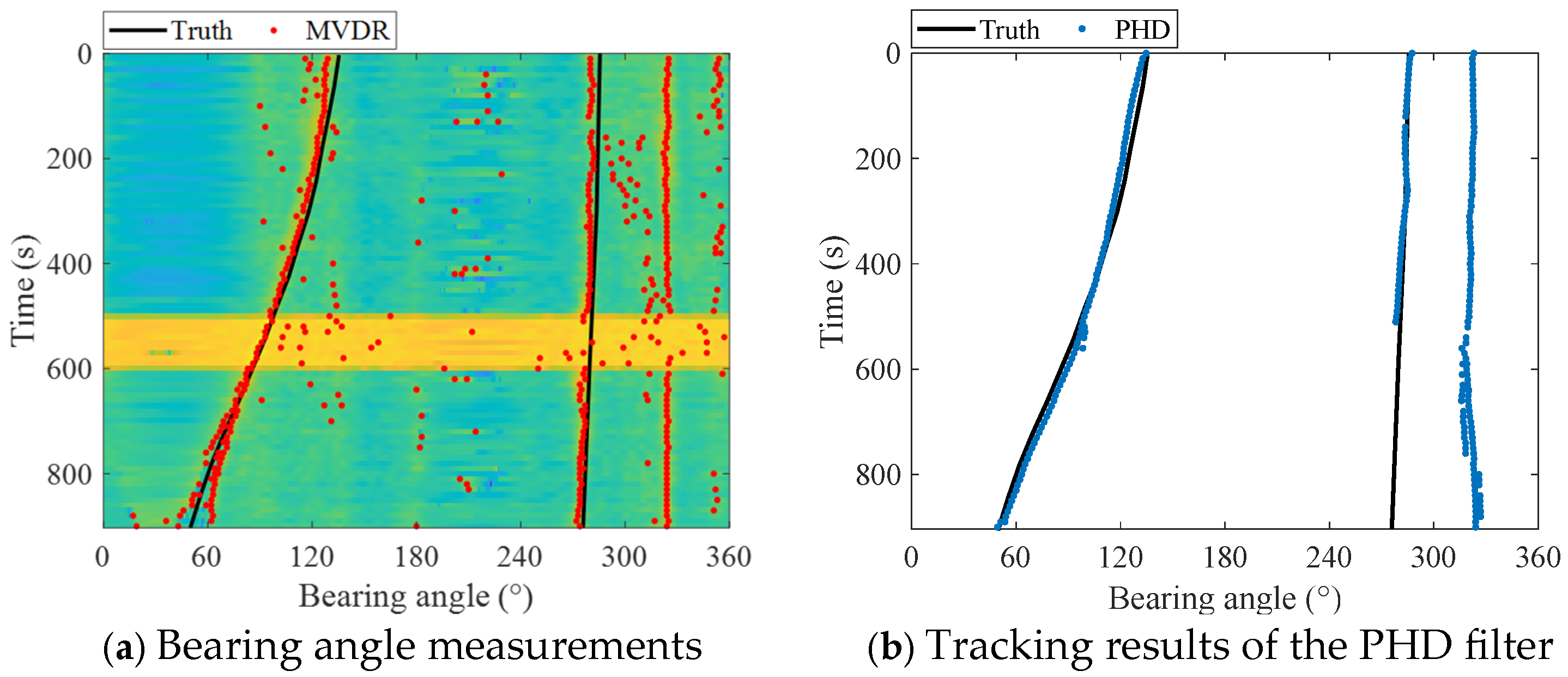
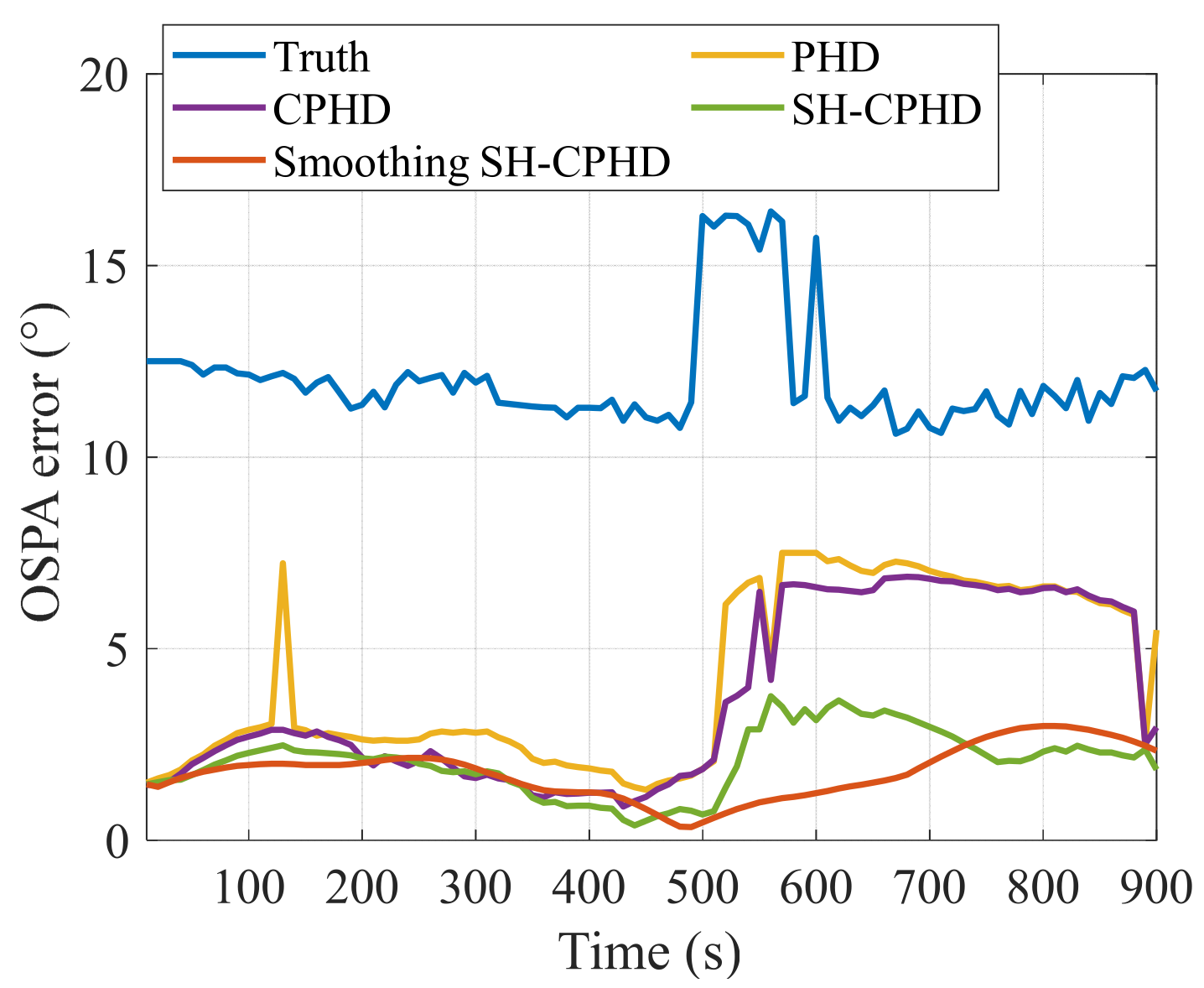
7.2. Verification of the Smoothing SH-CPHD Filter for Robust Multi-Target DOA Tracjing by Using Experimental Data
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, H.; Fan, H.H. Signal-Selective DOA Tracking for Wideband Cyclostationary Sources. IEEE Trans. Signal Process. 2007, 55, 2007–2015. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, W.; Wu, Y.; Chen, T.; Hu, Z. Joint Algorithm Based on Interference Suppression and Kalman Filter for Bearing-Only Weak Target Robust Tracking. IEEE Access 2019, 7, 131653–131662. [Google Scholar] [CrossRef]
- Zhang, B.; Hou, X.; Yang, Y. Robust Underwater Direction-of-Arrival Tracking with Uncertain Environmental Disturbances Using a Uniform Circular Hydrophone Array. J. Acoust. Soc. Am. 2022, 151, 4101–4113. [Google Scholar] [CrossRef] [PubMed]
- Saucan, A.A.; Chonavel, T.; Sintes, C.; Le Caillec, J.M. CPHD-DOA tracking of multiple extended sonar targets in impulsive environments. IEEE Trans. Signal Process. 2016, 64, 1147–1160. [Google Scholar] [CrossRef]
- Masnadi-Shirazi, A.; Rao, B.D. A Covariance-Based Superpositional CPHD Filter for Multisource DOA Tracking. IEEE Trans. Signal Process. 2018, 66, 309–323. [Google Scholar] [CrossRef]
- Zhao, J.; Gui, R.; Dong, X. A new measurement association mapping strategy for DOA tracking. Digit. Signal Process. 2021, 118, 103228. [Google Scholar] [CrossRef]
- Battaglia, G.M.; Isernia, T.; Palmeri, R.; Maisto, M.A.; Solimene, R.; Morabito, A.F. Near-Field Synthesis of 1-D Shaped Patterns through Spectral Factorization and Minimally-Redundant Array-Like Representations. IEEE Trans. Antennas Propag. 2025. [Google Scholar] [CrossRef]
- Kong, D.; Chun, J. A fast DOA tracking algorithm based on the extended Kalman filter. In Proceedings of the IEEE 2000 National Aerospace and Electronics Conference. NAECON 2000. Engineering Tomorrow (Cat. No. 00CH37093), Dayton, OH, USA, 10–12 October 2000; pp. 235–238. [Google Scholar] [CrossRef]
- Orton, M.; Fitzgerald, W. A Bayesian approach to tracking multiple targets using sensor arrays and particle filters. IEEE Trans. Signal Process. 2002, 50, 216–223. [Google Scholar] [CrossRef]
- Mahler, R. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Clark, D.E.; Panta, K.; Vo, B.N. The GM-PHD filter multiple target Tracker. In Proceedings of the 2006 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; pp. 1–8. [Google Scholar]
- Vo, B.N.; Singh, S.; Doucet, A. Sequential Monte Carlo methods for multitarget filtering with random finite sets. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1224–1245. [Google Scholar]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Hou, X.; Zhou, J.; Yang, Y.; Yang, L.; Qiao, G. Adaptive Two-Step Bearing-Only Underwater Uncooperative Target Tracking with Uncertain Underwater Disturbances. Entropy 2021, 23, 907. [Google Scholar] [CrossRef] [PubMed]
- Hou, X.; Qiao, Y.; Zhang, B.; Yang, Y. Robust Underwater Direction-of-Arrival Tracking Based on Variational Bayesian Extended Kalman Filter. JASA Express Lett. 2023, 3, 014801. [Google Scholar] [CrossRef]
- Hou, X.; Qiao, Y.; Zhang, B.; Yang, Y. Robust Underwater Direction-of-Arrival Tracking Based on AI-Aided Variational Bayesian Extended Kalman Filter. Remote Sens. 2023, 15, 420. [Google Scholar] [CrossRef]
- Sage, A.P.; Husa, G.W. Adaptive filtering with unknown prior statistics. In Joint Automatic Control Conference, Las Vegas, NV, USA, 5 August 1969; IEEE: Boulder, CO, USA; pp. 760–769.
- Zhang, B.; Yang, Y.; Hou, X. Robust underwater multi-target direction-of-arrival tracking with uncertain measurement noise. Acta Acust. 2023, 48, 605–617. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Mahler, R. A theory of PHD filters of higher order in target number. Proc. SPIE Int. Soc. Opt. Eng. 2006, 6235, 193–204. [Google Scholar]
- Song, Y.; Hu, Z.; Li, T.; Fan, H. Performance evaluation metrics and approaches for target tracking: A survey. Sensors 2022, 22, 793. [Google Scholar] [CrossRef] [PubMed]
- Booth, N.O.; Hodgkiss, W.S.; Ensberg, D.E. SWellEx-96 Experiment Acoustic Data; UC San Diego Library Digital Collections: La Jolla, CA, USA, 2015. [Google Scholar]

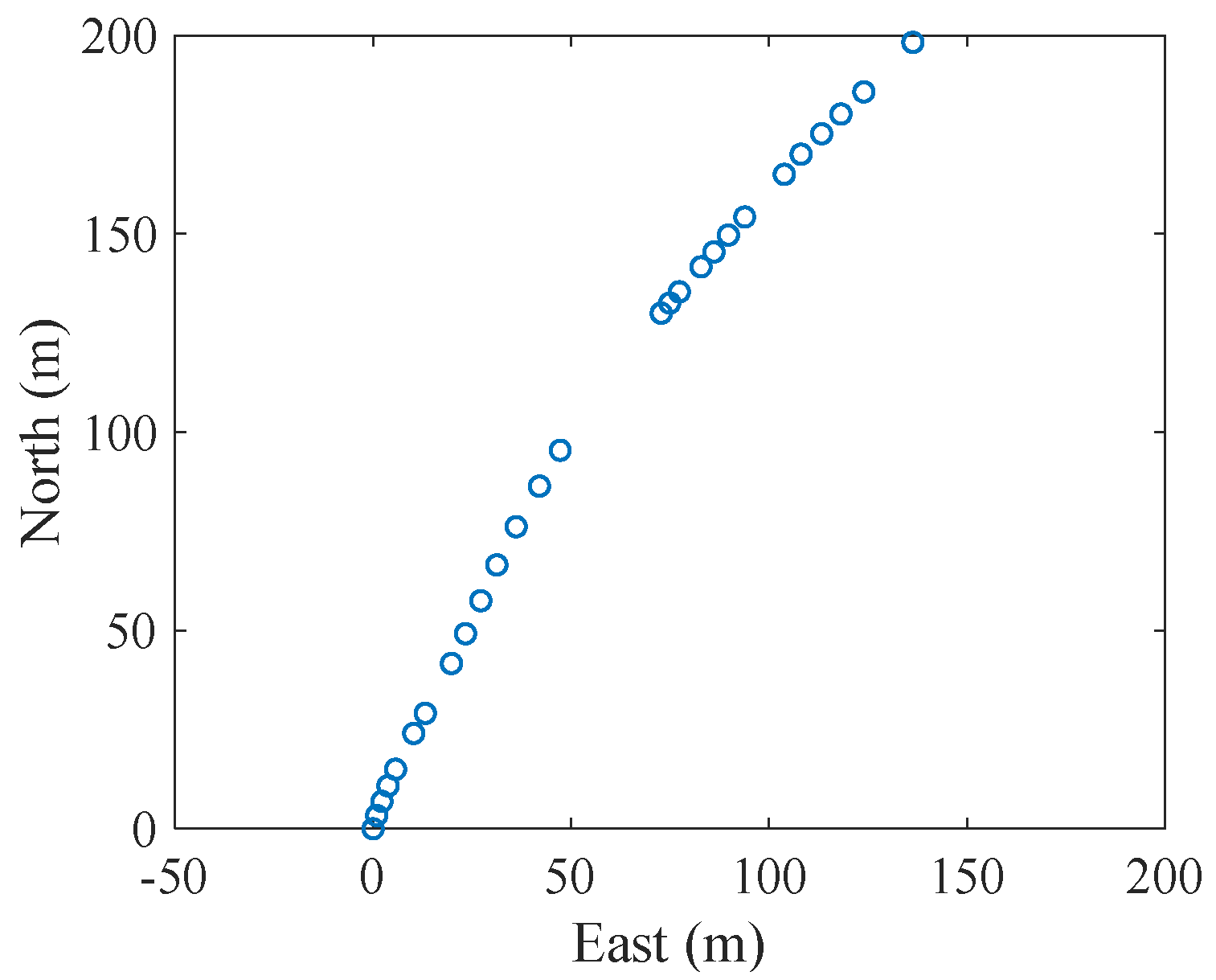

| MVDR | PHD | CPHD | SH-CPHD | Smoothing SH-CPHD Filter | |
|---|---|---|---|---|---|
| Average OSPA error when (°) | 5.70 | 2.46 | 1.30 | 0.71 | 0.48 |
| Average OSPA error when (°) | 6.05 | 3.84 | 1.58 | 0.72 | 0.56 |
| Average OSPA error when (°) | 6.37 | 5.01 | 3.02 | 0.72 | 0.61 |
| b | 0.94 | 0.95 | 0.96 | 0.97 | 0.98 | 0.99 | 0.999 |
|---|---|---|---|---|---|---|---|
| Average OSPA Error (°) | 1.33 | 0.95 | 0.77 | 0.73 | 0.69 | 0.59 | 0.54 |
| MVDR | PHD | CPHD | SH-CPHD | Smoothing SH-CPHD | |
|---|---|---|---|---|---|
| Average OSPA error (°) | 4.26 | 4.22 | 3.71 | 2.49 | 2.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, X.; Hou, X.; Zhang, B.; Yang, Y.; Du, S. Robust Smoothing Cardinalized Probability Hypothesis Density Filter-Based Underwater Multi-Target Direction-of-Arrival Tracking with Uncertain Measurement Noise. Entropy 2025, 27, 438. https://doi.org/10.3390/e27040438
Gu X, Hou X, Zhang B, Yang Y, Du S. Robust Smoothing Cardinalized Probability Hypothesis Density Filter-Based Underwater Multi-Target Direction-of-Arrival Tracking with Uncertain Measurement Noise. Entropy. 2025; 27(4):438. https://doi.org/10.3390/e27040438
Chicago/Turabian StyleGu, Xinyu, Xianghao Hou, Boxuan Zhang, Yixin Yang, and Shuanping Du. 2025. "Robust Smoothing Cardinalized Probability Hypothesis Density Filter-Based Underwater Multi-Target Direction-of-Arrival Tracking with Uncertain Measurement Noise" Entropy 27, no. 4: 438. https://doi.org/10.3390/e27040438
APA StyleGu, X., Hou, X., Zhang, B., Yang, Y., & Du, S. (2025). Robust Smoothing Cardinalized Probability Hypothesis Density Filter-Based Underwater Multi-Target Direction-of-Arrival Tracking with Uncertain Measurement Noise. Entropy, 27(4), 438. https://doi.org/10.3390/e27040438






