A New Discrete Analogue of the Continuous Muth Distribution for Over-Dispersed Data: Properties, Estimation Techniques, and Application
Abstract
1. Introduction
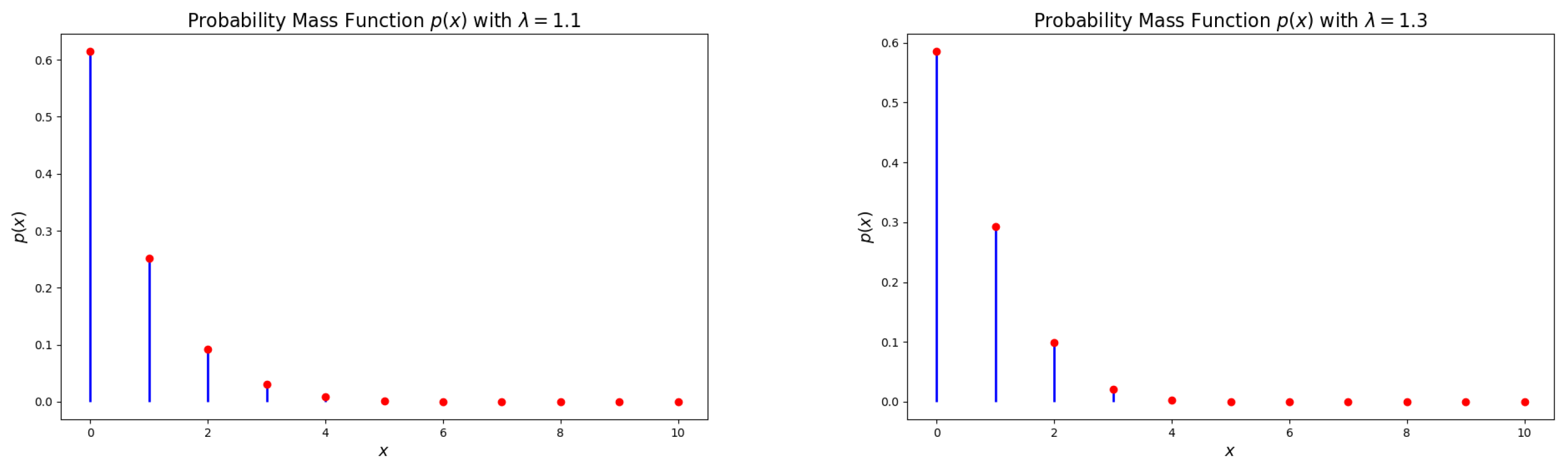
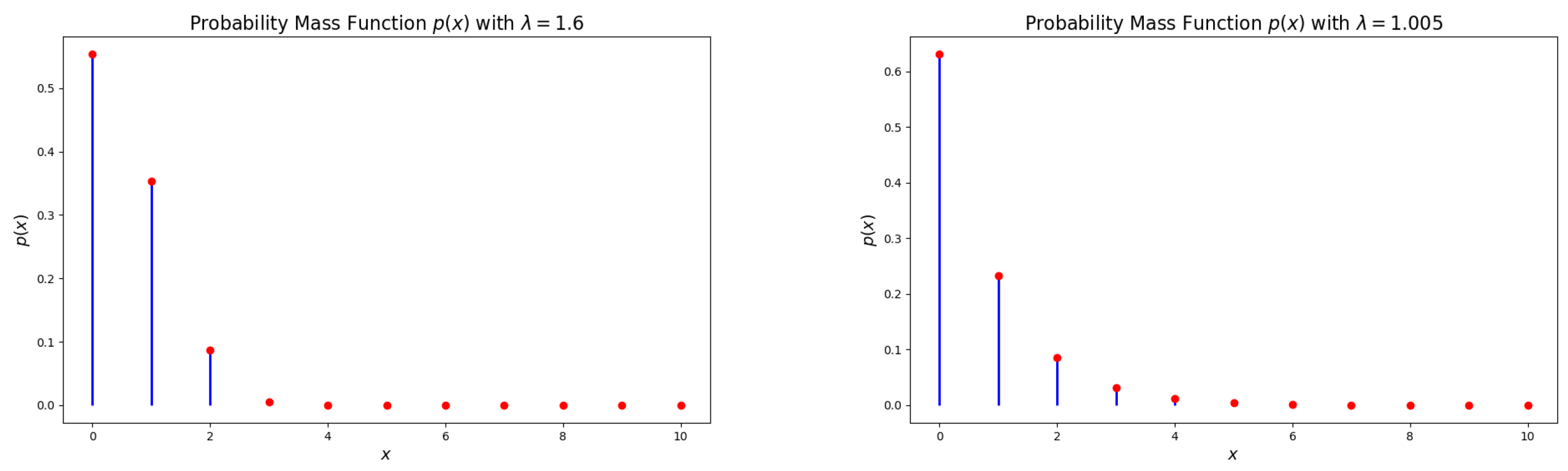
2. The DsMuth Distribution
3. Some Properties of the DsMuth Distribution
3.1. Probability Generating Function (PGF)
- First factorial moment of the DsMuth Distribution
- Second factorial moment: Differentiating once more with respect to and setting , we obtain
- Third factorial moment: Differentiating once more with respect to and setting , we have
- Fourth factorial moment: Differentiating once more with respect to and putting , we obtain
- If DI < 1, the model is appropriate for under-dispersed data.
- If DI > 1, the model is appropriate for over-dispersed data.
- As the parameter increases, the mean and variance of the DsMuth distribution gradually decline.
- The dispersion index (DI) rises as increases, implying that the distribution becomes more dispersed with higher values of .
- Skewness reduces as increases, implying that the distribution becomes less positively skewed for larger values of .
- Kurtosis declines with increasing , meaning the distribution becomes less peaked (less leptokurtic) as grows.
| Measure | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.1 | 1.2 | 1.3 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 | 2.4 | |
| Mean | 0.575 | 0.568 | 0.562 | 0.556 | 0.545 | 0.535 | 0.526 | 0.517 | 0.510 |
| Variance | 0.772 | 0.671 | 0.597 | 0.540 | 0.456 | 0.398 | 0.356 | 0.324 | 0.300 |
| Dispersion Index (DI) | 0.744 | 0.846 | 0.941 | 1.030 | 1.194 | 1.342 | 1.476 | 1.596 | 1.700 |
| Skewness | 1.806 | 1.532 | 1.337 | 1.187 | 0.964 | 0.799 | 0.664 | 0.539 | 0.418 |
| Kurtosis | 13.14 | 11.239 | 10.041 | 9.176 | 7.916 | 6.954 | 6.110 | 5.246 | 4.330 |
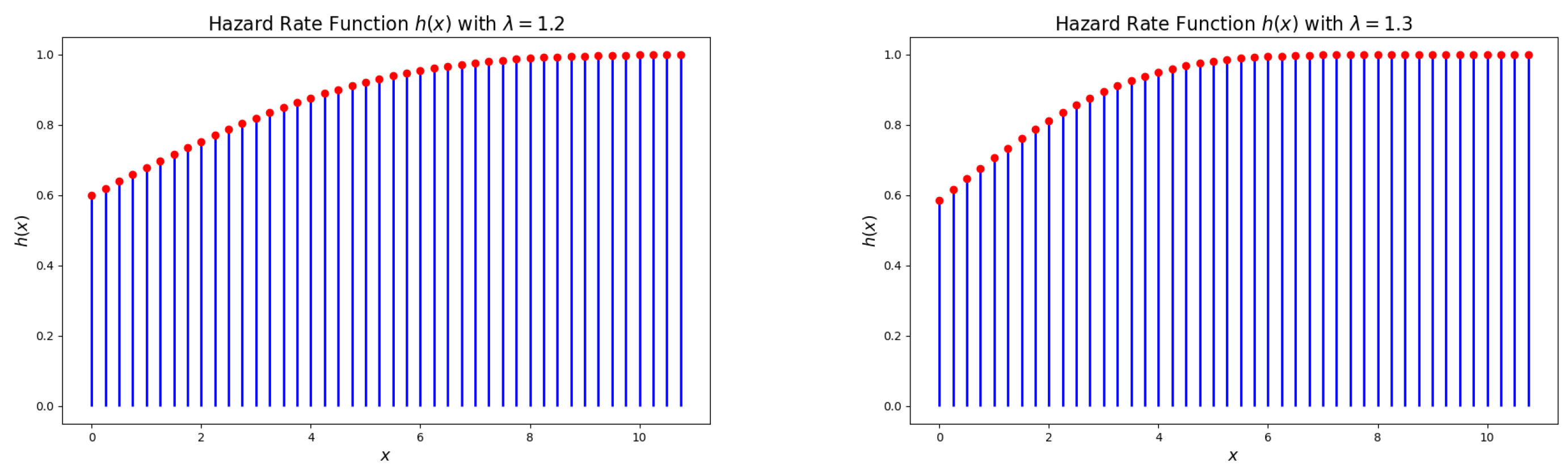
3.2. Mean Residual Life (MRL)
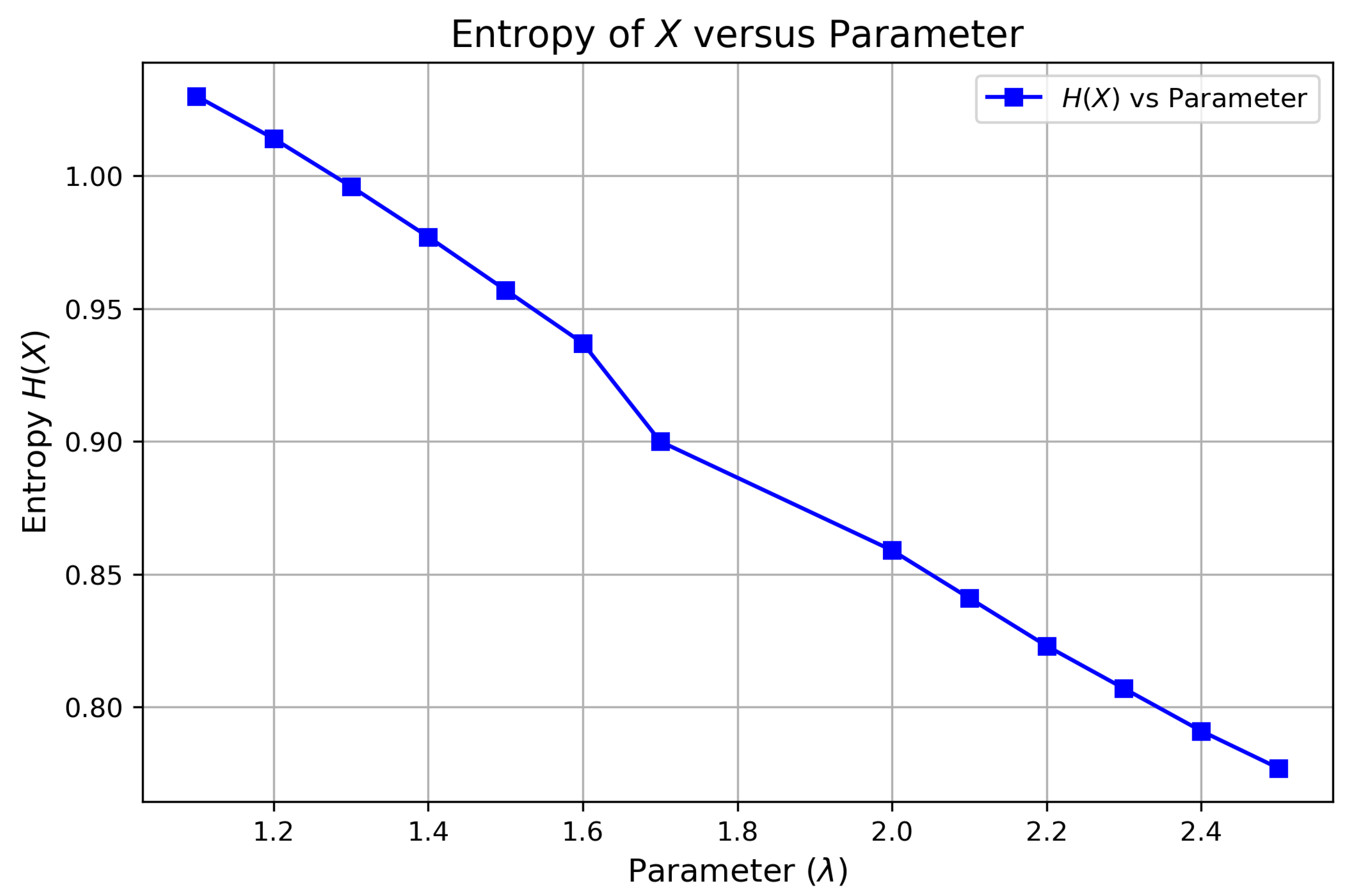
4. Entropy
5. Quantiles of a Discrete Random Variable
6. Estimation Methods
6.1. Maximum Likelihood Estimation
6.2. Method of Moment Estimation
6.3. Method of Proportion Estimation
7. Simulation Study
- Generate 10,000 samples of size from DsMuth(), considering different values: DsMuth(1.1), DsMuth(1.2), DsMuth(1.7), DsMuth(1.8), DsMuth(2.2), and DsMuth(2.5), respectively. This simulation is performed using Mathcad Software.
- Compute the MLEs, MMEs, and PEs for the 10,000 samples, denoted as for .
- Compute the bias (B), mean square errors (MSEs), and mean relative error (MRE) of by employing three methods, specifically MLE, MME, and PE, using the following formulas:
- Improved Accuracy with Larger Sample Sizes:The estimates of get closer to their true values as the sample size n increases across all estimation methods. This demonstrates the asymptotic property of the estimators, meaning they improve as more data become available.
- Bias Reduction:The bias of the parameter decreases toward zero as the sample size increases in all estimation methods. This indicates that the estimators are unbiased or asymptotically unbiased, ensuring greater accuracy in large samples.
- Mean Squared Error (MSE) Decrease:The MSE values decrease as n increases for all estimation methods. This confirms the consistency of the estimators, indicating that as more data is used, the estimates become more precise and less variable.
- Mean Relative Error (MRE) Decrease:The MRE also declines as n increases, further supporting the consistency of the estimators. This metric highlights how estimation errors become smaller in proportion to the true parameter value.
- MLE as the Most Effective Method:Among the three estimation techniques, Maximum Likelihood Estimation (MLE) performs best. It consistently provides estimates with the lowest bias, smallest MSE, and smallest MRE compared to the Method of Moments (MME) and Proportion Estimation (PE) methods. This suggests that MLE is the most efficient method for estimating in the DsMuth distribution.
| Parameter | n | AE | Bias | MSE | MRE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MLE | MME | PE | MLE | MME | PE | MLE | MME | PE | MLE | MME | PE | ||
| 50 | 1.054 | 0.773 | 0.931 | −0.046 | −0.327 | −0.169 | 0.042 | 0.323 | 0.147 | 0.137 | 0.389 | 0.238 | |
| 100 | 1.054 | 0.806 | 1.011 | −0.046 | −0.294 | −0.089 | 0.020 | 0.297 | 0.070 | 0.099 | 0.363 | 0.158 | |
| 150 | 1.075 | 0.795 | 1.027 | −0.025 | −0.305 | −0.073 | 0.010 | 0.296 | 0.056 | 0.071 | 0.367 | 0.151 | |
| 200 | 1.079 | 0.881 | 1.022 | −0.021 | −0.219 | −0.078 | 0.006 | 0.203 | 0.045 | 0.060 | 0.290 | 0.131 | |
| 300 | 1.091 | 0.905 | 1.057 | −0.009 | −0.195 | −0.043 | 0.004 | 0.184 | 0.027 | 0.047 | 0.276 | 0.112 | |
| 500 | 1.098 | 0.938 | 1.079 | −0.002 | −0.162 | −0.021 | 0.002 | 0.129 | 0.013 | 0.034 | 0.234 | 0.081 | |
| 50 | 1.153 | 0.873 | 1.028 | −0.047 | −0.327 | −0.172 | 0.045 | 0.322 | 0.149 | 0.143 | 0.389 | 0.239 | |
| 100 | 1.167 | 0.899 | 1.087 | −0.033 | −0.301 | −0.113 | 0.017 | 0.292 | 0.085 | 0.087 | 0.364 | 0.180 | |
| 150 | 1.180 | 0.903 | 1.123 | −0.020 | −0.297 | −0.077 | 0.012 | 0.274 | 0.060 | 0.076 | 0.352 | 0.151 | |
| 200 | 1.184 | 0.959 | 1.138 | −0.016 | −0.241 | −0.062 | 0.008 | 0.224 | 0.040 | 0.063 | 0.307 | 0.131 | |
| 300 | 1.189 | 0.976 | 1.158 | −0.011 | −0.224 | −0.042 | 0.005 | 0.200 | 0.027 | 0.049 | 0.290 | 0.108 | |
| 500 | 1.194 | 1.014 | 1.172 | −0.006 | −0.186 | −0.028 | 0.003 | 0.158 | 0.017 | 0.038 | 0.257 | 0.089 | |
| 50 | 1.646 | 1.655 | 1.753 | −0.054 | −0.045 | 0.053 | 0.112 | 0.439 | 0.155 | 0.131 | 0.374 | 0.217 | |
| 100 | 1.670 | 1.637 | 1.717 | −0.030 | −0.063 | 0.017 | 0.033 | 0.401 | 0.119 | 0.083 | 0.351 | 0.185 | |
| 150 | 1.684 | 1.609 | 1.727 | −0.016 | −0.091 | 0.027 | 0.022 | 0.375 | 0.106 | 0.071 | 0.335 | 0.173 | |
| 200 | 1.684 | 1.631 | 1.704 | −0.016 | −0.069 | 0.004 | 0.017 | 0.357 | 0.094 | 0.062 | 0.326 | 0.164 | |
| 300 | 1.703 | 1.653 | 1.697 | −0.003 | −0.047 | −0.003 | 0.010 | 0.307 | 0.077 | 0.046 | 0.294 | 0.145 | |
| 500 | 1.698 | 1.655 | 1.698 | −0.002 | −0.045 | −0.002 | 0.006 | 0.250 | 0.059 | 0.038 | 0.258 | 0.127 | |
| 50 | 1.713 | 1.771 | 1.998 | −0.087 | −0.029 | 0.198 | 0.199 | 0.427 | 0.195 | 0.141 | 0.341 | 0.193 | |
| 100 | 1.755 | 1.826 | 1.911 | −0.045 | 0.026 | 0.111 | 0.046 | 0.387 | 0.119 | 0.089 | 0.317 | 0.156 | |
| 150 | 1.775 | 1.823 | 1.891 | −0.025 | 0.023 | 0.091 | 0.026 | 0.364 | 0.095 | 0.069 | 0.301 | 0.141 | |
| 200 | 1.779 | 1.779 | 1.881 | −0.021 | −0.021 | 0.081 | 0.020 | 0.338 | 0.092 | 0.059 | 0.290 | 0.140 | |
| 300 | 1.784 | 1.799 | 1.852 | −0.016 | −0.001 | 0.052 | 0.013 | 0.272 | 0.063 | 0.049 | 0.248 | 0.114 | |
| 500 | 1.713 | 1.771 | 1.998 | −0.009 | −0.000 | 0.004 | 0.199 | 0.427 | 0.195 | 0.141 | 0.341 | 0.193 | |
| 50 | 1.947 | 2.356 | 2.673 | −0.253 | 0.156 | 0.473 | 0.845 | 0.752 | 0.337 | 0.231 | 0.361 | 0.213 | |
| 100 | 2.132 | 2.231 | 2.627 | −0.068 | 0.031 | 0.427 | 0.135 | 0.573 | 0.268 | 0.104 | 0.306 | 0.192 | |
| 150 | 2.160 | 2.233 | 2.591 | −0.040 | 0.033 | 0.391 | 0.068 | 0.512 | 0.215 | 0.084 | 0.284 | 0.176 | |
| 200 | 2.180 | 2.227 | 2.557 | −0.020 | 0.027 | 0.357 | 0.038 | 0.428 | 0.175 | 0.066 | 0.254 | 0.161 | |
| 300 | 2.183 | 2.222 | 2.547 | −0.017 | 0.022 | 0.347 | 0.025 | 0.419 | 0.156 | 0.055 | 0.257 | 0.156 | |
| 500 | 2.185 | 2.170 | 2.507 | −0.015 | −0.030 | 0.307 | 0.014 | 0.296 | 0.113 | 0.041 | 0.208 | 0.138 | |
| 50 | 2.113 | 2.733 | 3.214 | −0.387 | 0.233 | 0.714 | 1.049 | 0.704 | 0.630 | 0.269 | 0.298 | 0.290 | |
| 100 | 2.295 | 2.684 | 3.131 | −0.205 | 0.184 | 0.631 | 0.413 | 0.596 | 0.470 | 0.155 | 0.269 | 0.256 | |
| 150 | 2.406 | 2.634 | 3.108 | −0.094 | 0.134 | 0.608 | 0.201 | 0.487 | 0.425 | 0.110 | 0.243 | 0.247 | |
| 200 | 2.445 | 2.612 | 3.075 | −0.055 | 0.112 | 0.575 | 0.081 | 0.405 | 0.371 | 0.084 | 0.223 | 0.234 | |
| 300 | 2.469 | 2.568 | 3.063 | −0.031 | 0.068 | 0.563 | 0.041 | 0.341 | 0.352 | 0.063 | 0.203 | 0.229 | |
| 500 | 2.481 | 2.539 | 3.020 | −0.019 | 0.039 | 0.520 | 0.020 | 0.254 | 0.286 | 0.045 | 0.174 | 0.211 | |
8. Empirical Study
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Roy, D. The discrete normal distribution. Commun. Stat. Theory Methods 2003, 32, 1871–1883. [Google Scholar] [CrossRef]
- Roy, D. Discrete Rayleigh Distribution. IEEE Trans. Reliab. 2004, 53, 255–260. [Google Scholar] [CrossRef]
- Kemp, A.W. The discrete half-normal distribution. In Advances in Mathematical and Statistical Modeling; Springer: Berlin/Heidelberg, Germany, 2008; pp. 353–360. [Google Scholar] [CrossRef]
- Krishna, H.; Pundir, P.S. Discrete Burr and discrete Pareto distributions. J. Stat. Methodol. 2009, 6, 177–188. [Google Scholar] [CrossRef]
- Afify, A.Z.; Ahsan-ul-Haq, M.; Aljohani, H.M.; Alghamdi, A.S.; Babar, A.; Gòmez, H.W. A new one-parameter discrete exponential distribution: Properties, inference, and applications to COVID-19 data. J. King Saud Univ.-Sci. 2022, 34, 102199. [Google Scholar] [CrossRef]
- Jazi, M.A.; Lai, C.; Alamatsaz, M.H. A discrete inverse Weibull distribution and estimation of its parameters. Stat. Methodol. 2010, 7, 121–132. [Google Scholar] [CrossRef]
- Alghamdi, A.S.; Ahsan-ul-Haq, M.; Babar, A.; Aljohani, H.M.; Afify, A.Z. The discrete power-Ailamujia distribution: Properties, inference, and applications. AIMS Math. 2022, 7, 8344–8360. [Google Scholar] [CrossRef]
- Aboraya, M.A.; Yousof, H.Y.; Hamedani, G.G.; Ibrahim, M. New Family of Discrete Distributions with Mathematical Properties, Characterizations, Bayesian and Non-Bayesian Estimation Methods. Mathematics 2020, 8, 1648. [Google Scholar] [CrossRef]
- Gómez-Déniz, E. Another generalization of the geometric distribution. Test 2010, 19, 399–415. [Google Scholar] [CrossRef]
- Gómez-Déniz, E.; Calderín-Ojeda, E. The discrete Lindley distribution: Properties and applications. J. Stat. Comput. Simul. 2011, 81, 1405–1416. [Google Scholar] [CrossRef]
- Para, B.A. Discrete Generalized Burr-Type XII Distribution. J. Mod. Appl. Stat. Methods 2014, 13, 244–258. [Google Scholar] [CrossRef]
- AL-Huniti, A.A.; AL-Dayian, G.R. Discrete Burr type Iii distribution. Am. J. Math. Stat. 2012, 2, 145–152. [Google Scholar] [CrossRef]
- Hussain, T.; Aslam, M.; Ahmad, M. A Two Parameter Discrete Lindley Distribution. Rev. Colomb. Estad. 2016, 39, 45–61. [Google Scholar] [CrossRef]
- Para, B.A.; Jan, T.R. Discrete Version of Log-Logistic Distribution and its Applications in Genetics. Int. J. Mod. Math. Sci. 2016, 14, 407–422. [Google Scholar]
- Bakouch, H.S.; Jazi, M.A.; Nadarajah, S. A new discrete distribution. J. Theor. Appl. Stat. 2012, 48, 200–240. [Google Scholar] [CrossRef]
- Hassan, A.; Shalbaf, G.A.; Sheikh, S.B.; Rashid, A. A New Flexible Discrete Distribution with Applications to Count Data. J. Stat. Theory Appl. 2020, 19, 102–108. [Google Scholar] [CrossRef][Green Version]
- Almetwally, E.M.; Ibrahim, G.I. Discrete Alpha Power Inverse Lomax Distribution with Application of COVID-19 Data. J. Appl. Math. Stat. Sci. 2020, 9, 11–22. [Google Scholar]
- Aljohani, H.M.; Akdoğan, Y.; Cordeiro, G.M.; Afify, A. The Uniform Poisson—Ailamujia Distribution: Actuarial Measures and Applications in Biological Science. Symmetry 2021, 13, 1258. [Google Scholar] [CrossRef]
- Barbiero, A.; Hitaj, A. A Discrete Analogue of the Half-Logistic Distribution. In Proceedings of the International Conference on Decision Aid Sciences and Application (DASA), Sakheer, Bahrain, 8–9 November 2020; pp. 64–67. [Google Scholar] [CrossRef]
- Opone, F.C.; Izekor, E.A.; Akata, I.U.; Osagiede, F.E.U. A Discrete Analogue of the Continuous Marshall-Olkin Weibull Distribution with Application to Count Data. J. Math. Sci. 2021, 5, 415–428. [Google Scholar] [CrossRef]
- Eliwa, M.S.; Alhussain, Z.A.; El-Morshedy, M. Discrete Gompertz-G Family of Distributions for Over-and Under-Dispersed Data with Properties, Estimation, and Applications. Mathematics 2020, 8, 358. [Google Scholar] [CrossRef]
- Altun, E.; El-Morshedy, M.; Eliwa, M.S. A Study on Discrete Bilal Distribution with Properties and Applications on Integer-Valued Autoregressive Process. Revstat-Stat. J. 2022, 20, 501–528. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.S.; Altun, E. Discrete Burr-Hatke Distribution with Properties, Estimation Methods and Regression Model. IEEE Access 2020, 8, 74359–74370. [Google Scholar] [CrossRef]
- Eliwa, M.S.; Altun, E.; El-Dawoody, M.; El-Morshedy, M. A New Three-Parameter Discrete Distribution with Associated INAR(1) Process and Applications. IEEE Accesss 2020, 8, 91150–91162. [Google Scholar] [CrossRef]
- Al-Babtain, A.A.; Ahmed, A.H.N.; Afify, A.Z. A New Discrete Analog of The Continuous Lindley Distribution, with Reliability Applications. Entropy 2020, 22, 603. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.S.; Nagy, H. A new two-parameter exponentiated discrete Lindley distribution: Properties, estimation and applications. J. Appl. Stat. 2020, 47, 354–375. [Google Scholar] [CrossRef] [PubMed]
- El-Morshedy, M.; Altun, E.; Eliwa, M.S. A new statistical approach to model the counts of novel coronavirus cases. Math. Sci. 2022, 16, 37–50. [Google Scholar] [CrossRef]
- Chakraborty, S.; Chakravarty, D.; Mazucheli, J.; Bertoli, W. A discrete analog of Gumbel distribution: Properties, parameter estimation and applications. J. Appl. Stat. 2021, 48, 712–737. [Google Scholar] [CrossRef]
- Eldeeb, A.S.; Ahsan-Ul-Haq, M.; Babar, A.A. Discrete Analog of Inverted Topp-Leone Distribution: Properties, Estimation and Applications. Int. J. Anal. Appl. 2021, 19, 695–708. [Google Scholar] [CrossRef]
- Eldeeb, A.S.; Ahsan-Ul-Haq, M.; Eliwa, M.S. A discrete Ramos-Louzada distribution for asymmetric and over-dispersed data with leptokurtic-shaped: Properties and various estimation techniques with inference. AIMS Math. 2021, 7, 1726–1741. [Google Scholar] [CrossRef]
- Nekoukhou, V.; Alamatsaz, M.H.; Bidram, H. A Discrete generalized exponential distribution of a second type. Statistics 2013, 47, 876–887. [Google Scholar] [CrossRef]
- Hussain, T.; Ahmad, M. Discrete inverse Rayleigh distribution. J. Stat. 2014, 30, 203–222. [Google Scholar]
- Muth, E.J. Reliability models with positive memory derived from the mean residual life function. In The Theory and Applications of Reliability; Tsokos, C.P., Shimi, I., Eds.; Academic Press, Inc.: Cambridge, MA, USA, 1977; Volume 2, pp. 401–435. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Labs Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rohatgi, V.K.; Saleh, A.K.M.E. An Introduction to Probability and Statistics; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Khaliqu, K.A.; Abouammoh, A.M. On estimating parameters in a discrete Weibull distribution. IEEE Trans. Reliab. 1989, 38, 348–350. [Google Scholar] [CrossRef]
- Sarhan, A.M.; Tadj, L.; Hamilton, D.C. A New Lifetime Distribution and its Power Transformation. J. Probab. Stat. 2014, 6, 532024. [Google Scholar] [CrossRef]
- Eliwa, M.S.; El-Morshedy, M. A one-parameter discrete distribution for over dispersed data: Statistical and reliability properties with applications. J. Appl. Stat. 2022, 49, 2467–2487. [Google Scholar] [CrossRef]
- Poisson, S.D. Probabilité des Jugements en Matière Criminelle et en Matière Civile: Précédées des Règles Générales du Calcul des Probabilités; Bachelier: Paris, France, 1837; pp. 206–207. [Google Scholar]
- Sankaran, M. The Discrete Poisson-Lindley Distribution. Biometrics 1970, 26, 145–149. [Google Scholar] [CrossRef]
- Kumar, C.; Tripathi, Y.M.; Rastogi, M.K. On a Discrete Analogue of Linear Failure Rate Distribution. Am. J. Math. Manag. Sci. 2017, 36, 229–246. [Google Scholar] [CrossRef]



| Parameter | Parameter | ||
|---|---|---|---|
| 1.1 | 1.030 | 1.7 | 0.900 |
| 1.2 | 1.014 | 2.0 | 0.859 |
| 1.3 | 0.996 | 2.1 | 0.841 |
| 1.4 | 0.977 | 2.2 | 0.823 |
| 1.5 | 0.957 | 2.3 | 0.807 |
| 1.6 | 0.937 | 2.4 | 0.791 |
| Distribution | Abbreviation | Author | Pmf |
|---|---|---|---|
| Discrete-Rayleigh | DsR | [3] | |
| Discrete Inverse-Rayleigh | DsIR | [33] | |
| Discrete Lindley | DsLi | [11] | |
| Poisson | Poi | [40] | |
| Discrete Poisson-Lindley | PoiLi | [41] | |
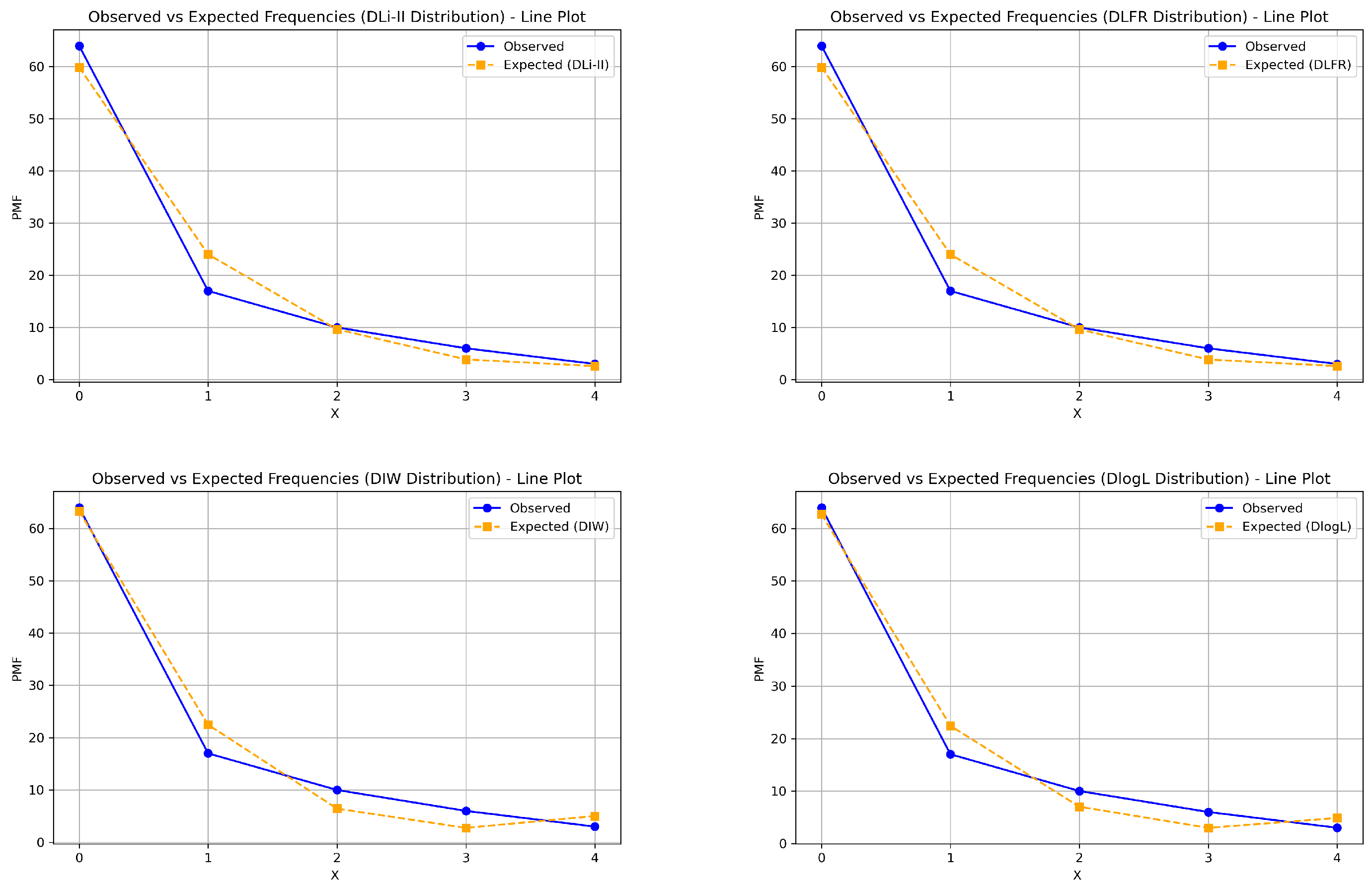
| Discrete Lindley-Two Parameter | DLi-II | [14] | |
| Discrete linear failure rate | DLFR | [42] | |
| Discrete Inverse Weibull | DIW | [7] | |
| Discrete Log-logistic | DLog-L | [15] |
| X | Obs. Freq. | One-Parameter | Two-Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| DsMuth | DR | DIR | DLi | Poi | PoiLi | DLi-II | DLFR | DIW | DLLogL | ||
| 0 | 64 | 63.21 | 33.50 | 62.50 | 57.13 | 51.17 | 37.50 | 59.88 | 59.90 | 63.30 | 62.73 |
| 1 | 17 | 23.25 | 46.94 | 26.41 | 26.88 | 34.28 | 25.00 | 24.02 | 24.01 | 22.48 | 22.42 |
| 2 | 10 | 8.556 | 17.01 | 5.99 | 10.45 | 11.49 | 15.63 | 9.64 | 9.63 | 6.44 | 7.01 |
| 3 | 6 | 3.147 | 2.39 | 2.19 | 3.71 | 2.57 | 9.38 | 3.87 | 3.86 | 2.76 | 2.98 |
| ≥4 | 3 | 1.583 | 0.16 | 2.91 | 1.83 | 0.49 | 12.49 | 2.59 | 2.60 | 5.02 | 4.86 |
| Total | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| MLE | 1.001 | 0.665 | 0.625 | 0.274 | 0.670 | 1.998 | 0.401 | 0.401 | 0.633 | 0.745 | |
| Std-er | 0.01 | 0.029 | 0.049 | 0.029 | 0.082 | 0.263 | 0.269 | 0.056 | 0.049 | 0.101 | |
| L.C.I | 1.000 | 0.608 | 0.529 | 0.217 | 0.509 | 1.481 | 0.000 | 0.291 | 0.537 | 0.546 | |
| U.C.I | 1.019 | 0.722 | 0.721 | 0.331 | 0.831 | 2.514 | 0.928 | 0.511 | 0.729 | 0.944 | |
| 3.934 | 66.07 | 9.056 | 6.638 | 23.65 | 30.889 | 3.347 | 3.340 | 3.503 | 2.783 | ||
| DF | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | |
| p-value | 0.140 | <0.001 | 0.011 | 0.036 | <0.001 | <0.001 | 0.067 | 0.068 | 0.061 | 0.095 | |
| −log Lik. | 112.8 | 205.3 | 118.4 | 113.1 | 120.3 | 112.1 | 112.47 | 112.47 | 116.27 | 115.47 | |
| AIC | 227.7 | 412.6 | 238.9 | 230.8 | 242.7 | 226.2 | 228.95 | 228.94 | 236.55 | 234.94 | |
| BIC | 230.3 | 415.2 | 241.5 | 230.8 | 245.3 | 228.8 | 234.16 | 234.15 | 241.76 | 240.15 | |
| HQIC | 228.7 | 413.7 | 240.0 | 229.2 | 243.8 | 227.3 | 231.06 | 231.05 | 238.66 | 237.04 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsayed, H.; Hussein, M. A New Discrete Analogue of the Continuous Muth Distribution for Over-Dispersed Data: Properties, Estimation Techniques, and Application. Entropy 2025, 27, 409. https://doi.org/10.3390/e27040409
Elsayed H, Hussein M. A New Discrete Analogue of the Continuous Muth Distribution for Over-Dispersed Data: Properties, Estimation Techniques, and Application. Entropy. 2025; 27(4):409. https://doi.org/10.3390/e27040409
Chicago/Turabian StyleElsayed, Howaida, and Mohamed Hussein. 2025. "A New Discrete Analogue of the Continuous Muth Distribution for Over-Dispersed Data: Properties, Estimation Techniques, and Application" Entropy 27, no. 4: 409. https://doi.org/10.3390/e27040409
APA StyleElsayed, H., & Hussein, M. (2025). A New Discrete Analogue of the Continuous Muth Distribution for Over-Dispersed Data: Properties, Estimation Techniques, and Application. Entropy, 27(4), 409. https://doi.org/10.3390/e27040409





