InfoMat: Leveraging Information Theory to Visualize and Understand Sequential Data †
Abstract
1. Introduction
Contributions
2. Background and Preliminaries
2.1. Notation
2.2. Sequential Information Measures
2.3. Information Decomposition and Conservation
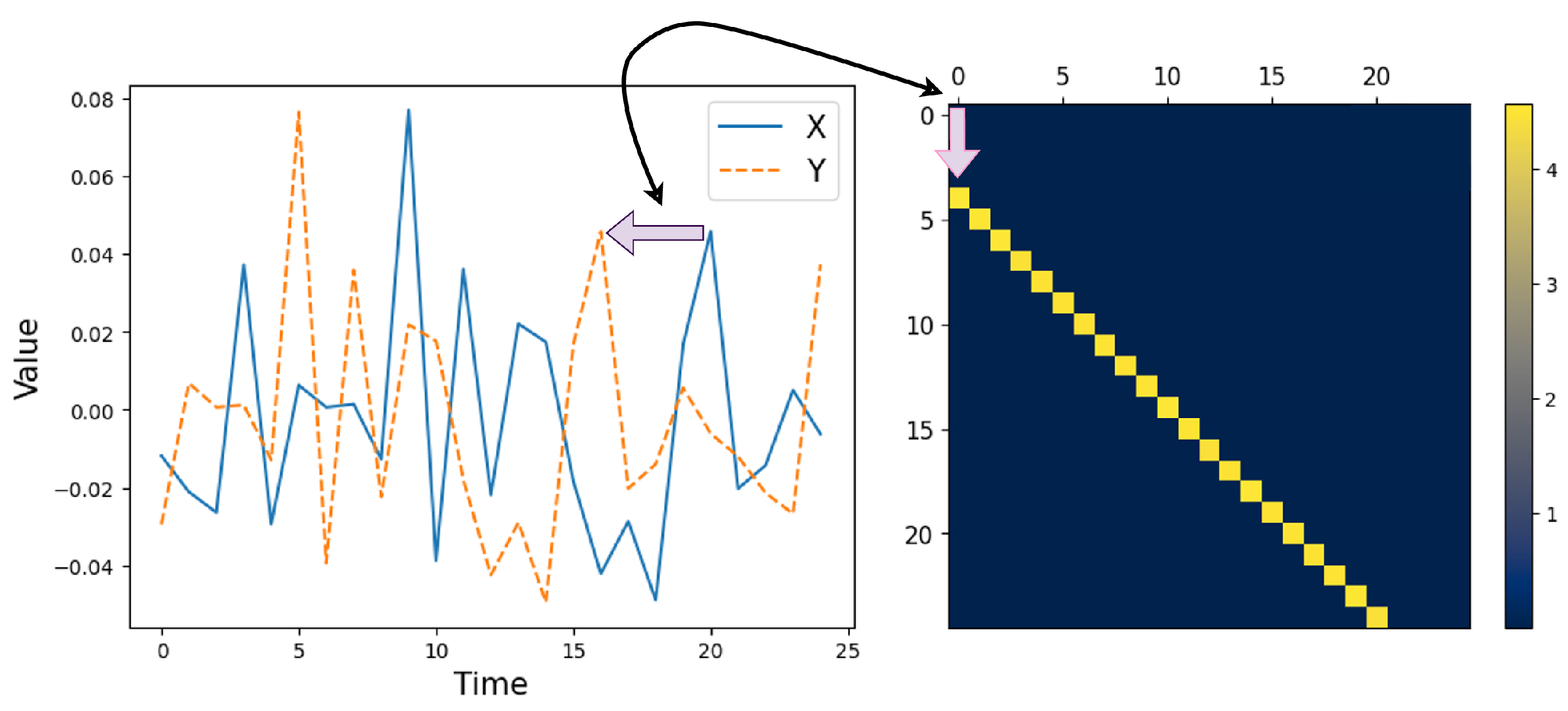
3. Information Matrix
3.1. Visualizing Sequential Information Measures
3.2. Capturing Information Conservation Laws
3.3. Developing New Information-Theoretic Relations
3.4. Relating Dependency Structures and Visual Patterns in the InfoMat
4. InfoMat Estimation via Gaussian Mutual Information
4.1. Proposed Estimator
| Algorithm 1 Gaussian InfoMat Estimation |
input: Data , matrix length m output: Gaussian estimate of |
|
- 1.
- Bias:
- 2.
- Variance:
4.2. InfoMat Estimation for Discrete Datasets
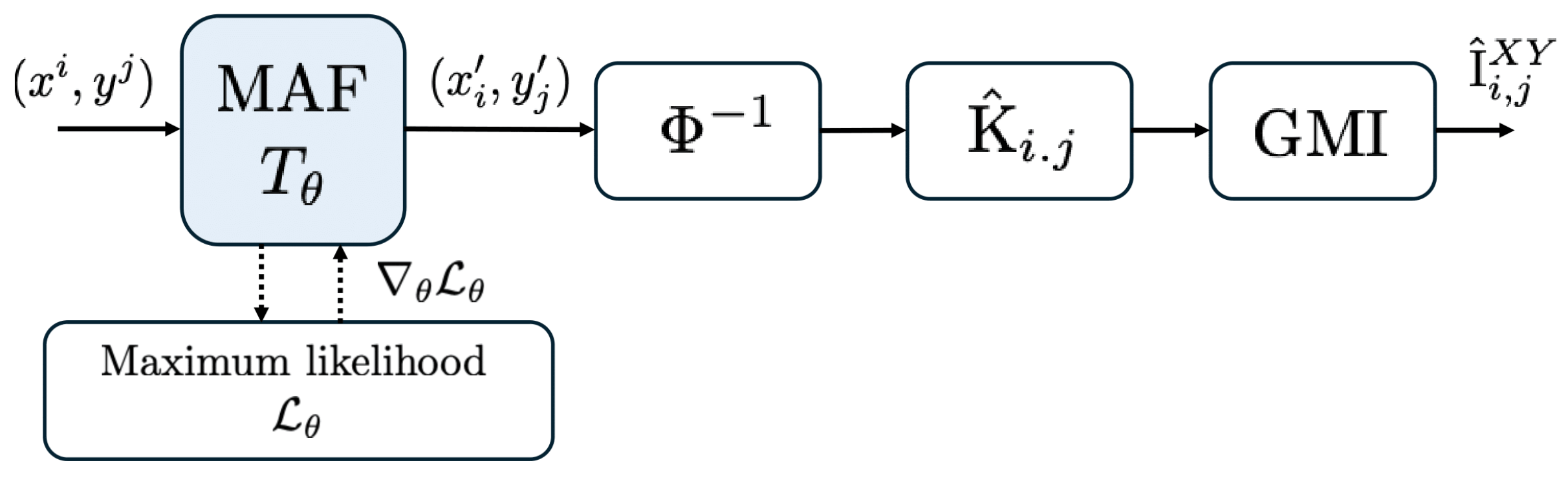
5. Beyond Gaussian—Neural Estimation
5.1. Masked Autoregressive Flows
5.2. Proposed Estimator
| Algorithm 2 Neural InfoMat Estimation |
input: Data , matrix length m, number of epochs N. output: Neural estimate of |
6. Visualization of Information Transfer
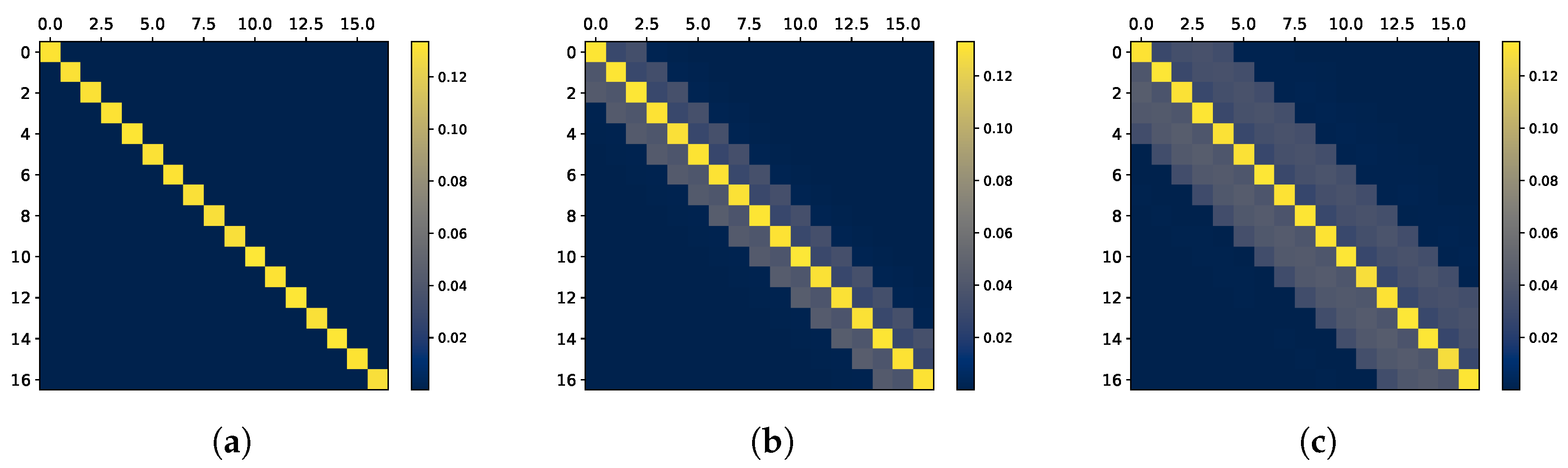
6.1. Synthetic Data—Gaussian Processes
6.2. Expressiveness of Neural Estimation
6.3. Visualizing Information Flow in Physiological Data
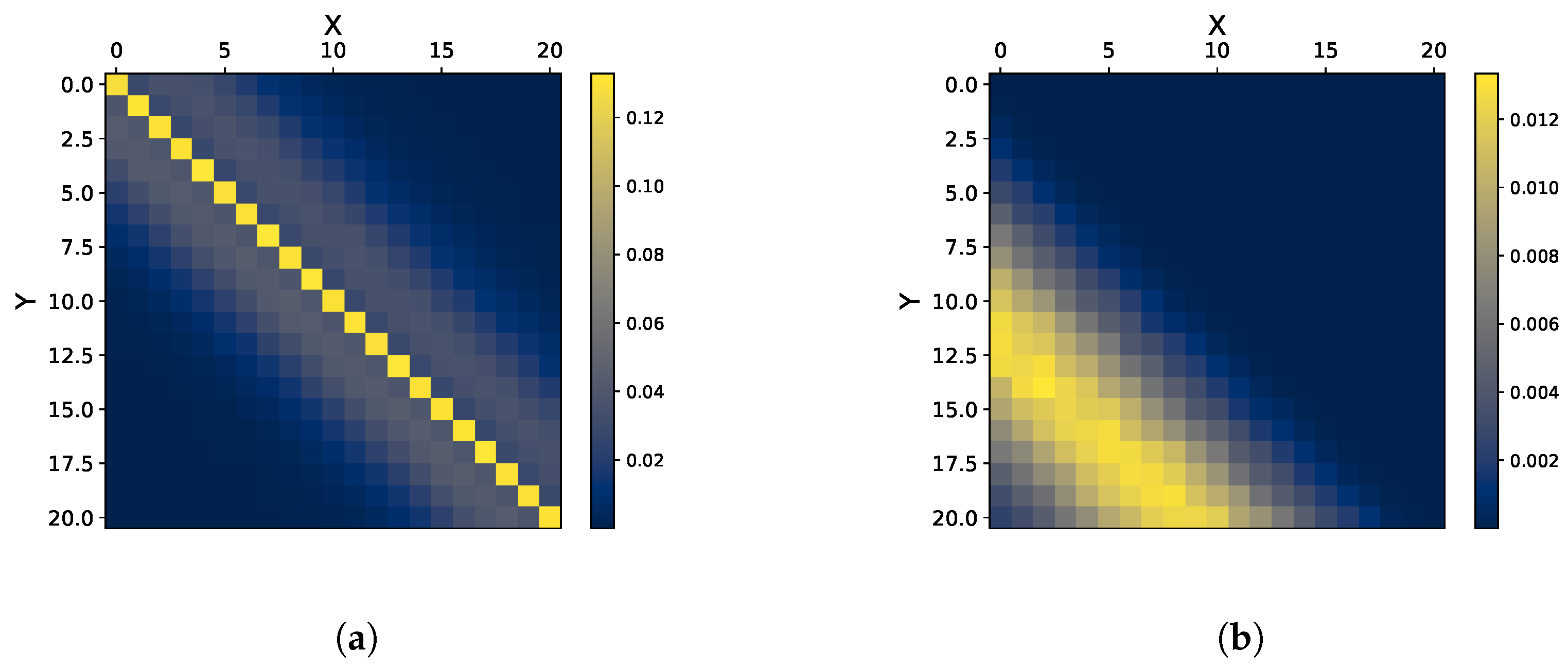
6.4. Visualizing Coding Schemes Effect
6.4.1. Ising Channel
6.4.2. Trapdoor Channel
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Proofs
Appendix A.1.1. Proof of Proposition 2
Appendix A.1.2. Proof of Proposition 3
Appendix A.1.3. Proof of Proposition 4
Appendix A.1.4. Proof of Lemma 1
Appendix A.2. Analysis of the Gap Between Mutual Information and Gaussian Mutual Information
Appendix A.3. Additional Information on Plug-In Entropy Estimator
References
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar]
- Viola, P.; Wells, W.M., III. Alignment by maximization of mutual information. Int. J. Comput. Vis. 1997, 24, 137–154. [Google Scholar]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. arXiv 2000, arXiv:physics/0004057. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Massey, J. Causality, feedback and directed information. In Proceedings of the International Symposium on Information Theory and Its Applications (ISITA-90), Waikiki, Hawaii, 27–30 November 1990; pp. 303–305. [Google Scholar]
- Permuter, H.H.; Kim, Y.H.; Weissman, T. Interpretations of directed information in portfolio theory, data compression, and hypothesis testing. IEEE Trans. Inf. Theory 2011, 57, 3248–3259. [Google Scholar]
- Permuter, H.; Cuff, P.; Van Roy, B.; Weissman, T. Capacity of the trapdoor channel with feedback. IEEE Trans. Inf. Theory 2008, 54, 3150–3165. [Google Scholar]
- Wibral, M.; Vicente, R.; Lizier, J.T. Directed Information Measures in Neuroscience; Springer: Berlin/Heidelberg, Germany, 2014; Volume 724. [Google Scholar]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [PubMed]
- Wibral, M.; Vicente, R.; Lindner, M. Transfer entropy in neuroscience. In Directed Information Measures in Neuroscience; Springer: Berlin/Heidelberg, Germany, 2014; pp. 3–36. [Google Scholar]
- Tanaka, T.; Esfahani, P.M.; Mitter, S.K. LQG control with minimum directed information: Semidefinite programming approach. IEEE Trans. Autom. Control 2017, 63, 37–52. [Google Scholar]
- Tiomkin, S.; Tishby, N. A unified bellman equation for causal information and value in markov decision processes. arXiv 2017, arXiv:1703.01585. [Google Scholar]
- Sabag, O.; Tian, P.; Kostina, V.; Hassibi, B. Reducing the LQG Cost with Minimal Communication. IEEE Trans. Autom. Control 2022. [Google Scholar]
- Klyubin, A.S.; Polani, D.; Nehaniv, C.L. Empowerment: A universal agent-centric measure of control. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; Volume 1, pp. 128–135. [Google Scholar]
- Salge, C.; Glackin, C.; Polani, D. Empowerment—An introduction. In Guided Self-Organization: Inception; Springer: Berlin/Heidelberg, Germany, 2014; pp. 67–114. [Google Scholar]
- Raginsky, M. Directed information and pearl’s causal calculus. In Proceedings of the 2011 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 28–30 September 2011; pp. 958–965. [Google Scholar]
- Shu, Y.; Zhao, J. Data-driven causal inference based on a modified transfer entropy. Comput. Chem. Eng. 2013, 57, 173–180. [Google Scholar]
- Wieczorek, A.; Roth, V. Information theoretic causal effect quantification. Entropy 2019, 21, 975. [Google Scholar] [CrossRef]
- Zhou, Y.; Spanos, C.J. Causal meets submodular: Subset selection with directed information. Adv. Neural Inf. Process. Syst. 2016, 29. Available online: https://proceedings.neurips.cc/paper_files/paper/2016/file/81ca0262c82e712e50c580c032d99b60-Paper.pdf (accessed on 20 March 2025).
- Kalajdzievski, D.; Mao, X.; Fortier-Poisson, P.; Lajoie, G.; Richards, B. Transfer Entropy Bottleneck: Learning Sequence to Sequence Information Transfer. arXiv 2022, arXiv:2211.16607. [Google Scholar]
- Bonetti, P.; Metelli, A.M.; Restelli, M. Causal Feature Selection via Transfer Entropy. arXiv 2023, arXiv:2310.11059. [Google Scholar]
- Friendly, M. Corrgrams: Exploratory displays for correlation matrices. Am. Stat. 2002, 56, 316–324. [Google Scholar]
- Correa, C.D.; Lindstrom, P. The mutual information diagram for uncertainty visualization. Int. J. Uncertain. Quantif. 2013, 3, 187–201. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar]
- Chen, M.; Feixas, M.; Viola, I.; Bardera, A.; Shen, H.W.; Sbert, M. Information Theory Tools for Visualization; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kramer, G. Directed Information for Channels with Feedback; Citeseer: Princeton, NJ, USA, 1998. [Google Scholar]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar]
- Bossomaier, T.; Barnett, L.; Harré, M.; Lizier, J.T.; Bossomaier, T.; Barnett, L.; Harré, M.; Lizier, J.T. Transfer Entropy; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time-series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Massey, J.L.; Massey, P.C. Conservation of mutual and directed information. In Proceedings of the Proceedings. International Symposium on Information Theory, 2005. ISIT 2005, Adelaide, SA, Australia, 4–9 September 2005; pp. 157–158. [Google Scholar]
- Amblard, P.O.; Michel, O.J. On directed information theory and Granger causality graphs. J. Comput. Neurosci. 2011, 30, 7–16. [Google Scholar] [CrossRef]
- Quinn, C.J.; Coleman, T.P.; Kiyavash, N.; Hatsopoulos, N.G. Estimating the directed information to infer causal relationships in ensemble neural spike train recordings. J. Comput. Neurosci. 2011, 30, 17–44. [Google Scholar] [CrossRef] [PubMed]
- Jiao, J.; Permuter, H.H.; Zhao, L.; Kim, Y.H.; Weissman, T. Universal estimation of directed information. IEEE Trans. Inf. Theory 2013, 59, 6220–6242. [Google Scholar] [CrossRef]
- Luxembourg, O.; Tsur, D.; Permuter, H. TREET: TRansfer Entropy Estimation via Transformer. arXiv 2024, arXiv:2402.06919. [Google Scholar]
- Cai, T.T.; Liang, T.; Zhou, H.H. Law of log determinant of sample covariance matrix and optimal estimation of differential entropy for high-dimensional Gaussian distributions. J. Multivar. Anal. 2015, 137, 161–172. [Google Scholar] [CrossRef]
- Duong, B.; Nguyen, T. Diffeomorphic information neural estimation. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 7468–7475. [Google Scholar]
- Knief, U.; Forstmeier, W. Violating the normality assumption may be the lesser of two evils. Behav. Res. Methods 2021, 53, 2576–2590. [Google Scholar] [CrossRef]
- Belghazi, M.I.; Baratin, A.; Rajeshwar, S.; Ozair, S.; Bengio, Y.; Courville, A.; Hjelm, D. Mutual information neural estimation. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 531–540. [Google Scholar]
- Sreekumar, S.; Goldfeld, Z. Neural estimation of statistical divergences. J. Mach. Learn. Res. 2022, 23, 1–75. [Google Scholar]
- Tsur, D.; Aharoni, Z.; Goldfeld, Z.; Permuter, H. Neural estimation and optimization of directed information over continuous spaces. IEEE Trans. Inf. Theory 2023, 69, 4777–4798. [Google Scholar] [CrossRef]
- Tsur, D.; Aharoni, Z.; Goldfeld, Z.; Permuter, H. Data-driven optimization of directed information over discrete alphabets. IEEE Trans. Inf. Theory 2023, 70, 1652–1670. [Google Scholar] [CrossRef]
- Papamakarios, G.; Pavlakou, T.; Murray, I. Masked autoregressive flow for density estimation. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/6c1da886822c67822bcf3679d04369fa-Paper.pdf (accessed on 20 March 2025).
- Rosenblatt, M. Remarks on a multivariate transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar]
- Papamakarios, G.; Nalisnick, E.; Rezende, D.J.; Mohamed, S.; Lakshminarayanan, B. Normalizing flows for probabilistic modeling and inference. J. Mach. Learn. Res. 2021, 22, 2617–2680. [Google Scholar]
- Butakov, I.; Tolmachev, A.; Malanchuk, S.; Neopryatnaya, A.; Frolov, A.; Andreev, K. Mutual Information Estimation via Normalizing Flows. arXiv 2024, arXiv:2403.02187. [Google Scholar]
- Bossomaier, T.R.J.; Barnett, L.C.; Harré, M.S.; Lizier, J.T. An Introduction to Transfer Entropy; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Rigney, D.; Goldberger, A.; Ocasio, W.; Ichimaru, Y.; Moody, G.; Mark, R. Multi-channel physiological data: Description and analysis. In Time Series Prediction: Forecasting the Future and Understanding the Past; Weigend, A., Gershenfeld, N., Eds.; Addison-Wesley: Reading, MA, USA, 1993; pp. 105–129. [Google Scholar]
- Goldberger, A.; Amaral, L.; Glass, L.; Hausdorff, J.; Ivanov, P.; Mark, R.; Stanley, H. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [PubMed]
- Ising, E. Beitrag zur Theorie des Ferro-und Paramagnetismus. Ph.D. Thesis, Grefe & Tiedemann, Hamburg, Germany, 1924. [Google Scholar]
- Elishco, O.; Permuter, H. Capacity and coding for the Ising channel with feedback. IEEE Trans. Inf. Theory 2014, 60, 5138–5149. [Google Scholar]
- Tallini, L.G.; Al-Bassam, S.; Bose, B. On the capacity and codes for the Z-channel. In Proceedings of the IEEE International Symposium on Information Theory, Lausanne, Switzerland, 30 June–5 July 2002; p. 422. [Google Scholar]
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf (accessed on 20 March 2025).
- Tsur, D.; Goldfeld, Z.; Greenewald, K. Max-sliced mutual information. Adv. Neural Inf. Process. Syst. 2023, 36, 80338–80351. [Google Scholar]
- Tsur, D.; Permuter, H. InfoMat: A Tool for the Analysis and Visualization Sequential Information Transfer. arXiv 2024, arXiv:2405.16463. [Google Scholar]
- Goldfeld, Z.; Greenewald, K.; Nuradha, T.; Reeves, G. k-Sliced Mutual Information: A Quantitative Study of Scalability with Dimension. Adv. Neural Inf. Process. Syst. 2022, 35, 15982–15995. [Google Scholar]
- Antos, A.; Kontoyiannis, I. Convergence properties of functional estimates for discrete distributions. Random Struct. Algorithms 2001, 19, 163–193. [Google Scholar]
- Basharin, G.P. On a statistical estimate for the entropy of a sequence of independent random variables. Theory Probab. Its Appl. 1959, 4, 333–336. [Google Scholar]
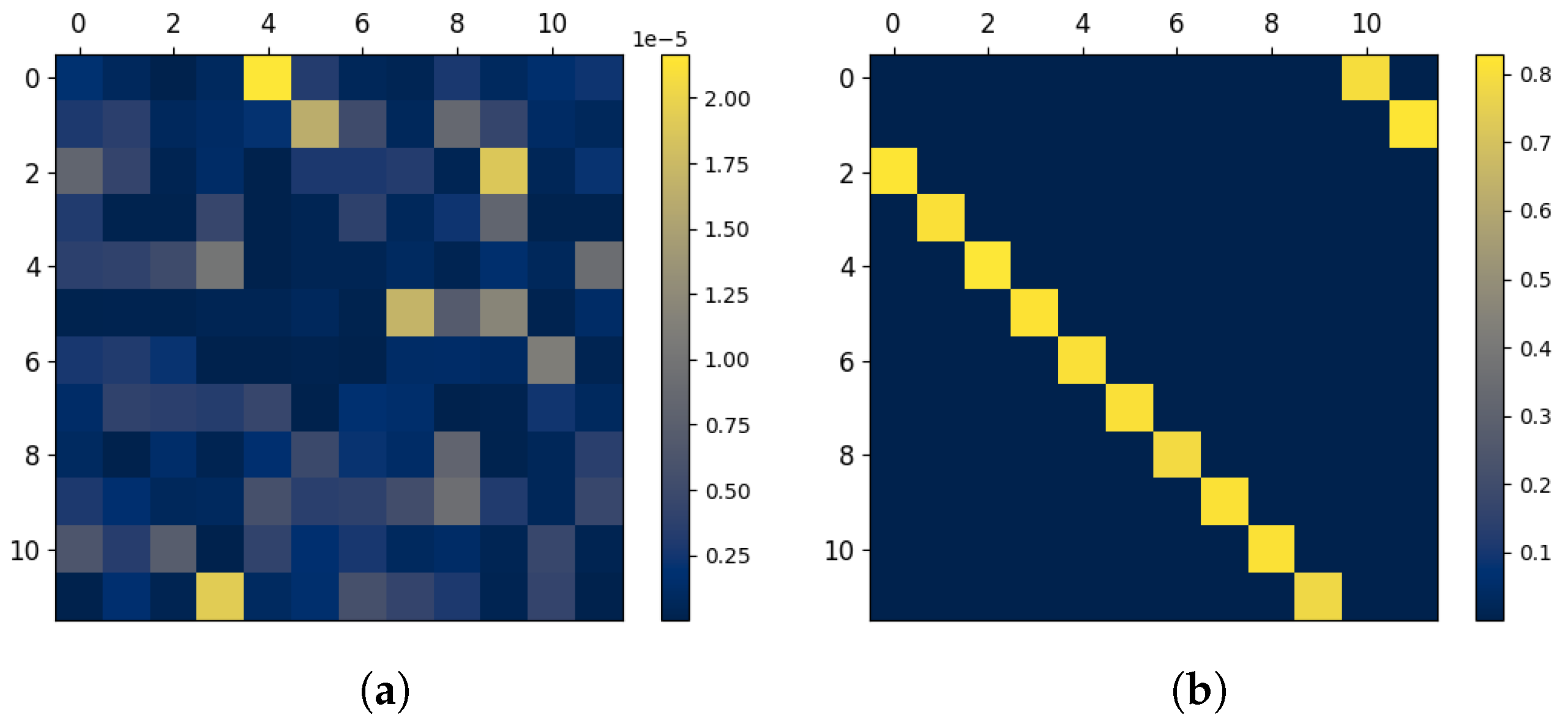
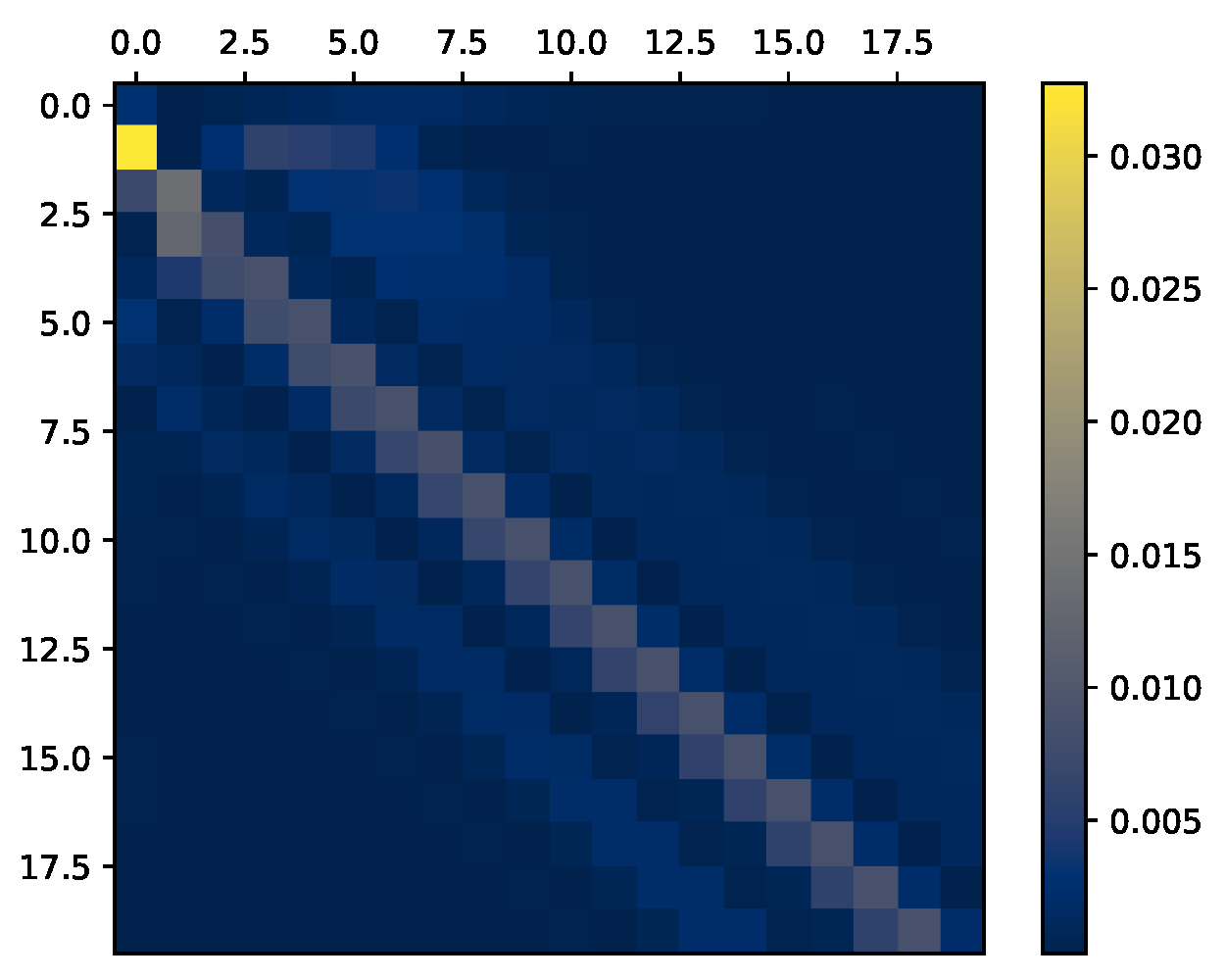
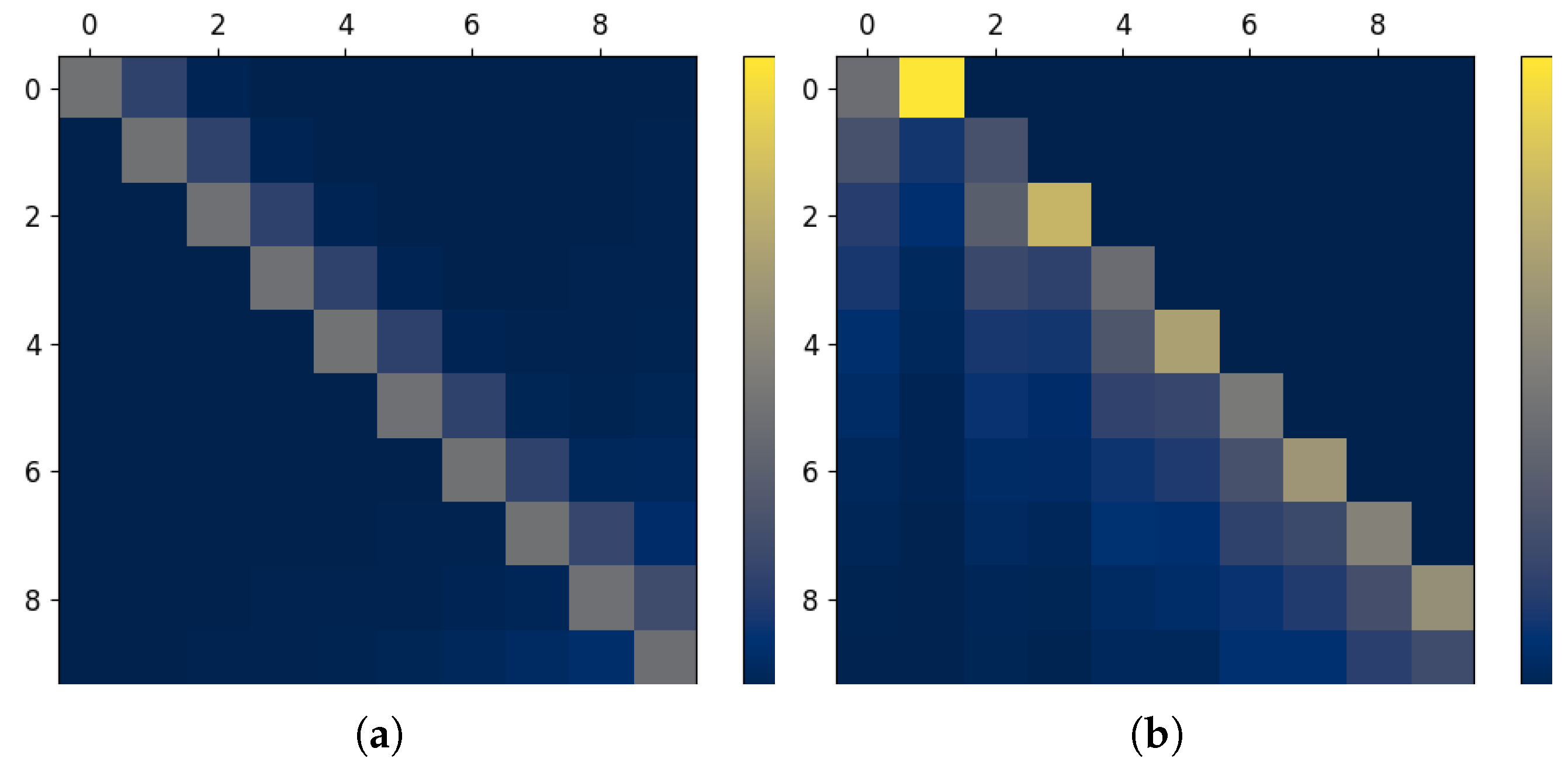
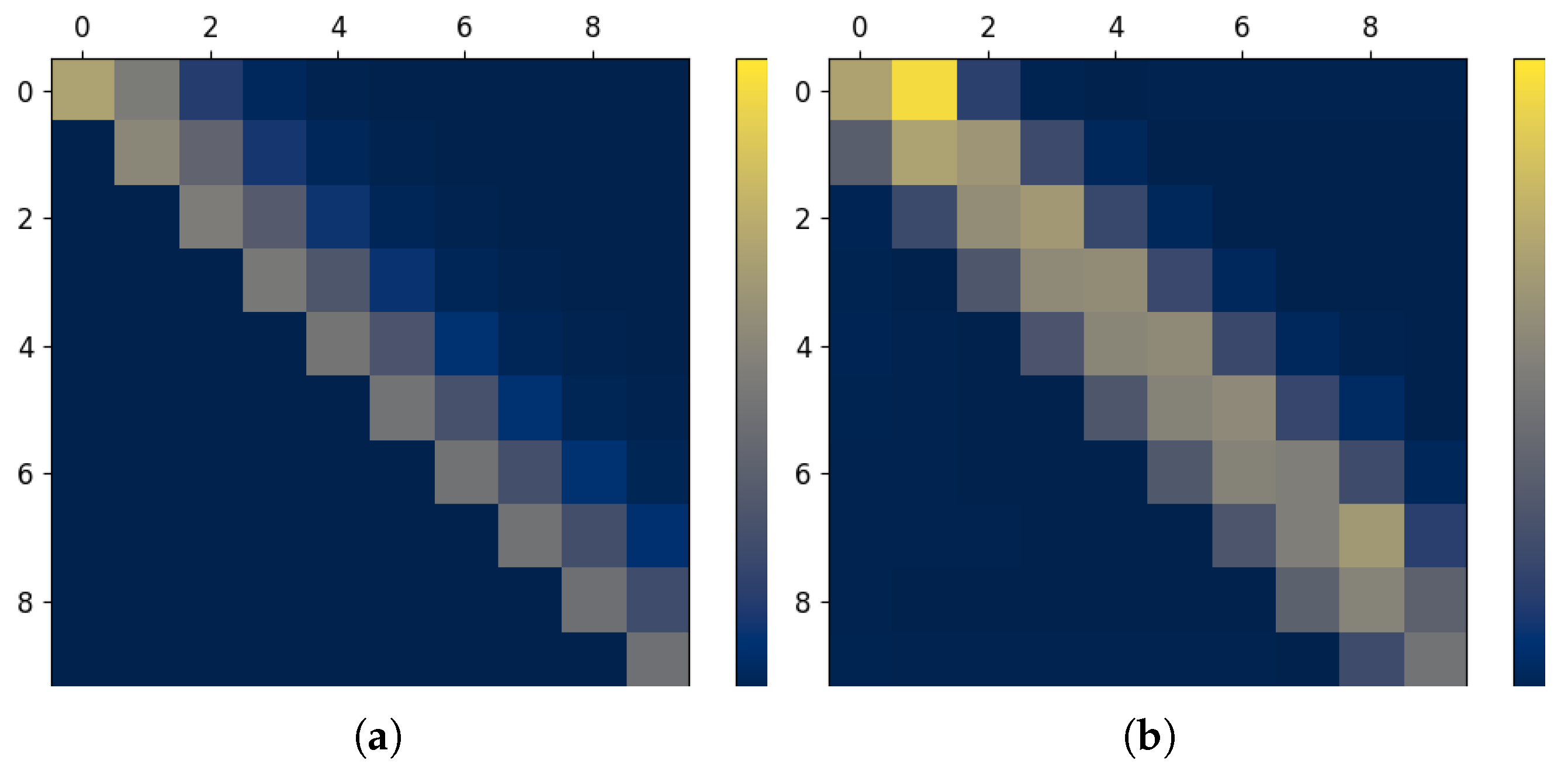
| Information measure | Visual pattern in |
| Upper triangular with diagonal | |
| Upper triangular, side | |
| Col. in row with length i |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsur, D.; Permuter, H. InfoMat: Leveraging Information Theory to Visualize and Understand Sequential Data. Entropy 2025, 27, 357. https://doi.org/10.3390/e27040357
Tsur D, Permuter H. InfoMat: Leveraging Information Theory to Visualize and Understand Sequential Data. Entropy. 2025; 27(4):357. https://doi.org/10.3390/e27040357
Chicago/Turabian StyleTsur, Dor, and Haim Permuter. 2025. "InfoMat: Leveraging Information Theory to Visualize and Understand Sequential Data" Entropy 27, no. 4: 357. https://doi.org/10.3390/e27040357
APA StyleTsur, D., & Permuter, H. (2025). InfoMat: Leveraging Information Theory to Visualize and Understand Sequential Data. Entropy, 27(4), 357. https://doi.org/10.3390/e27040357





