Multiscale Sample Entropy-Based Feature Extraction with Gaussian Mixture Model for Detection and Classification of Blue Whale Vocalization
Abstract
1. Introduction
2. Methods
2.1. Blue Whale Calls
2.2. Data Description and Annotations
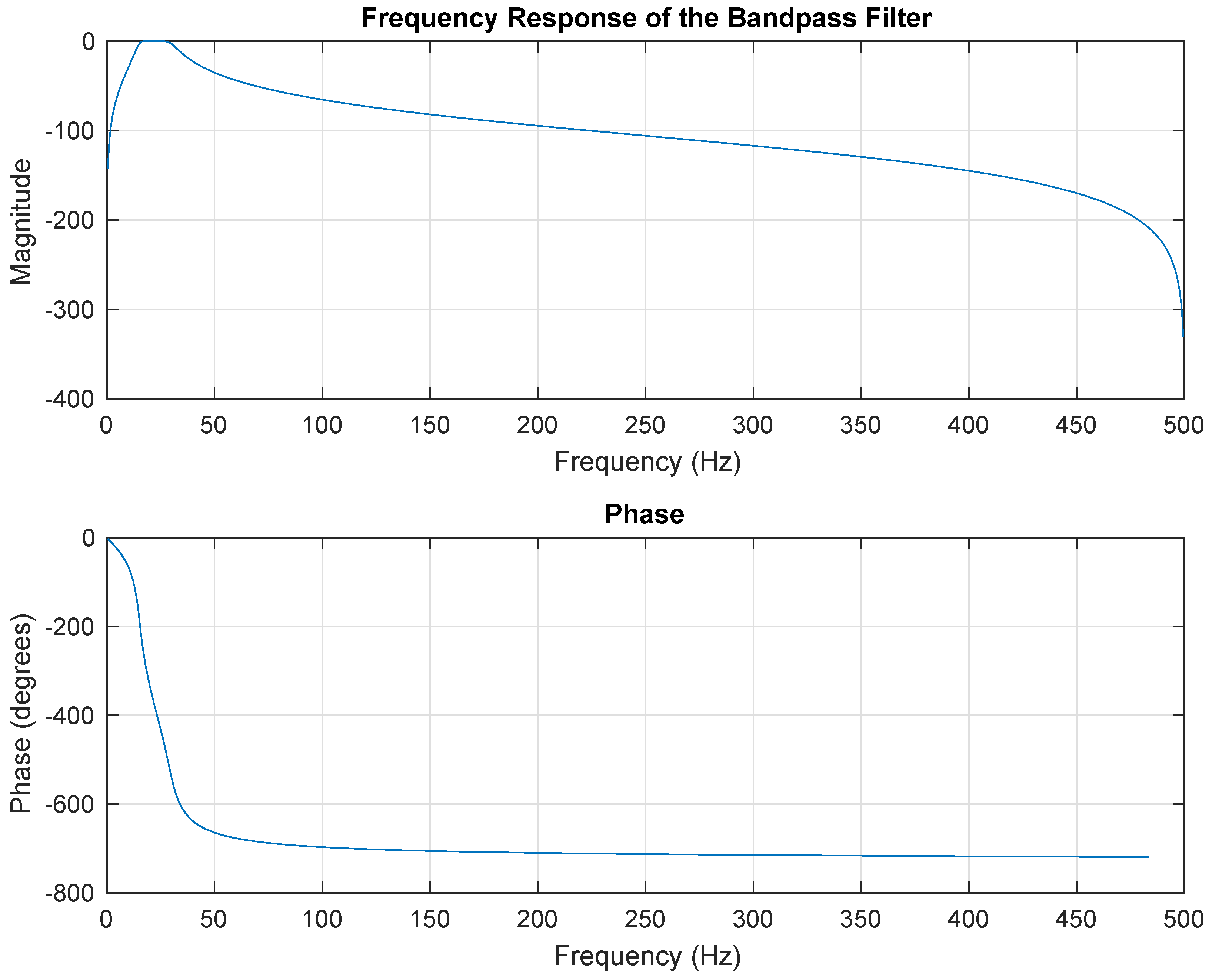
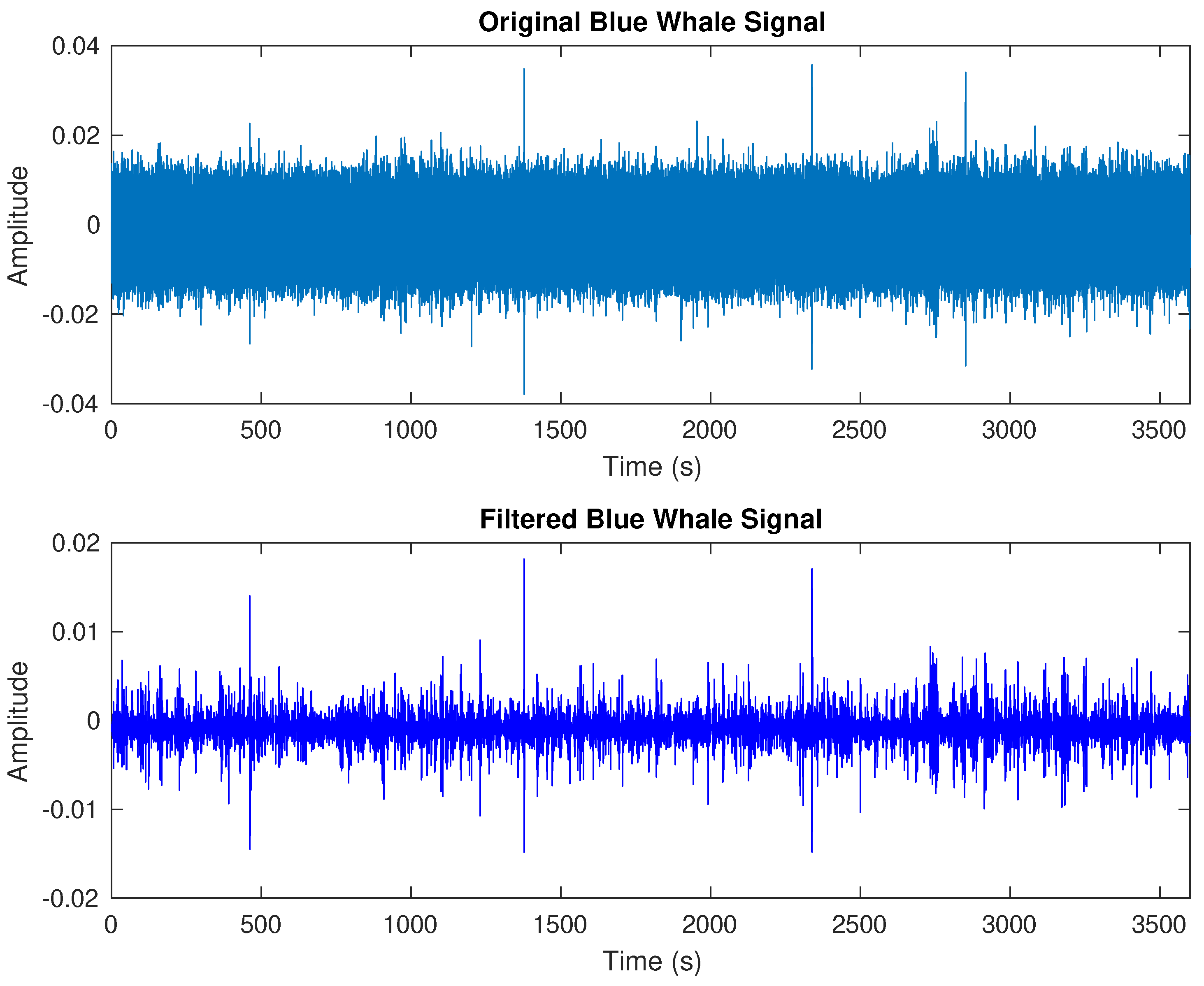
2.3. Data Preprocessing
2.4. Exisiting Feature Extraction Techniques for Whale Vocalizations
2.4.1. PCA-Based Feature Extraction Method
2.4.2. DMD-Based Feature Extraction Method
2.5. Wavelet Transform-Based Feature Extraction Method
2.6. Proposed MSE-Based Feature Extraction Method
2.6.1. Data Segmentation and Coarse-Grained Series Construction
2.6.2. Feature Matrix Construction
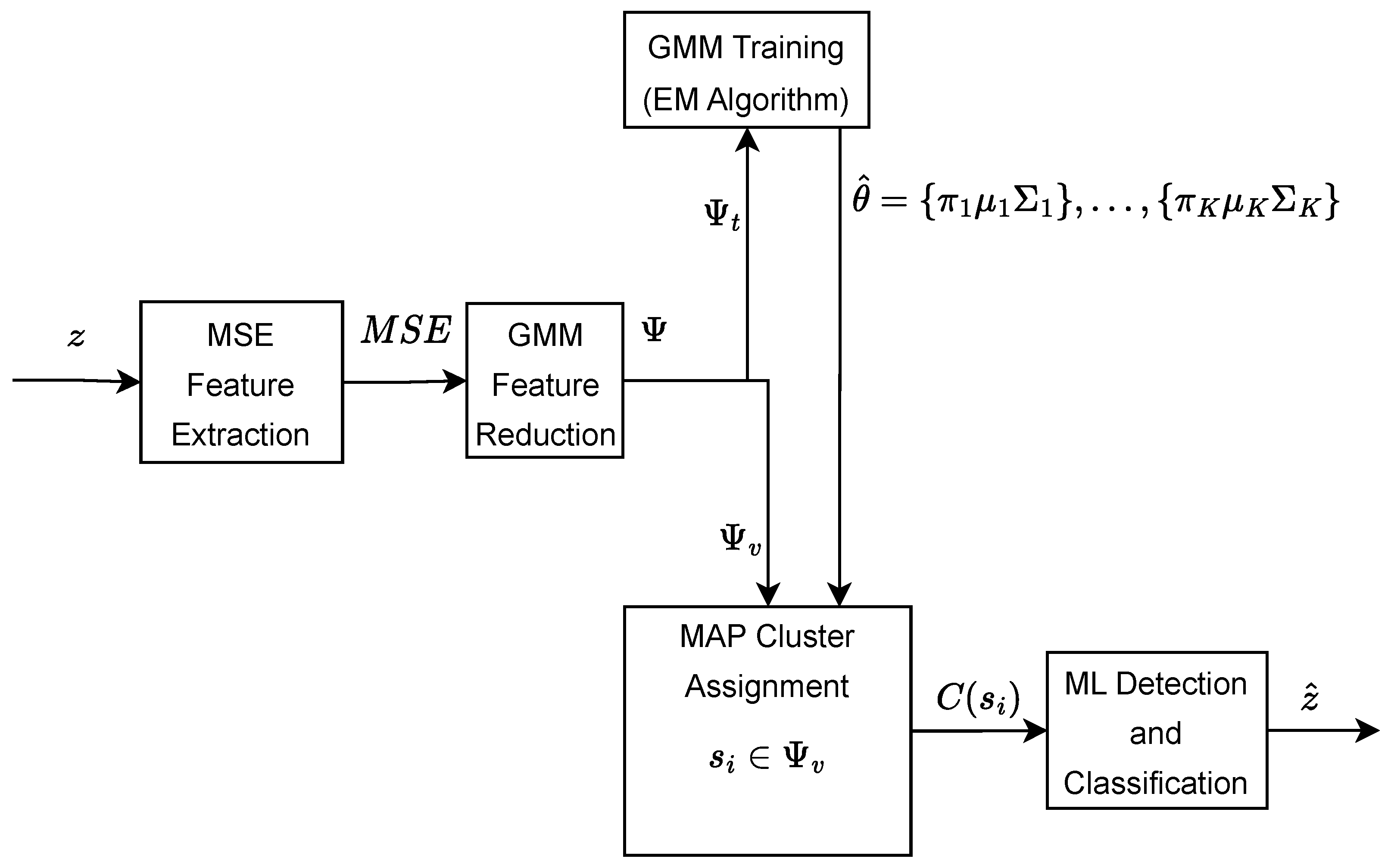
2.7. GMM-Based Feature Reduction
2.8. GMM Training
2.9. GMM Testing, Clustering, and Classification
GMM Clustering
2.10. GMM Classification
| Algorithm 1 GMM-based feature reduction and classification |
Require: MSE feature matrix with s samples and features, number of GMM components K, number of top-ranked features
|
3. Experimental Set-Ups
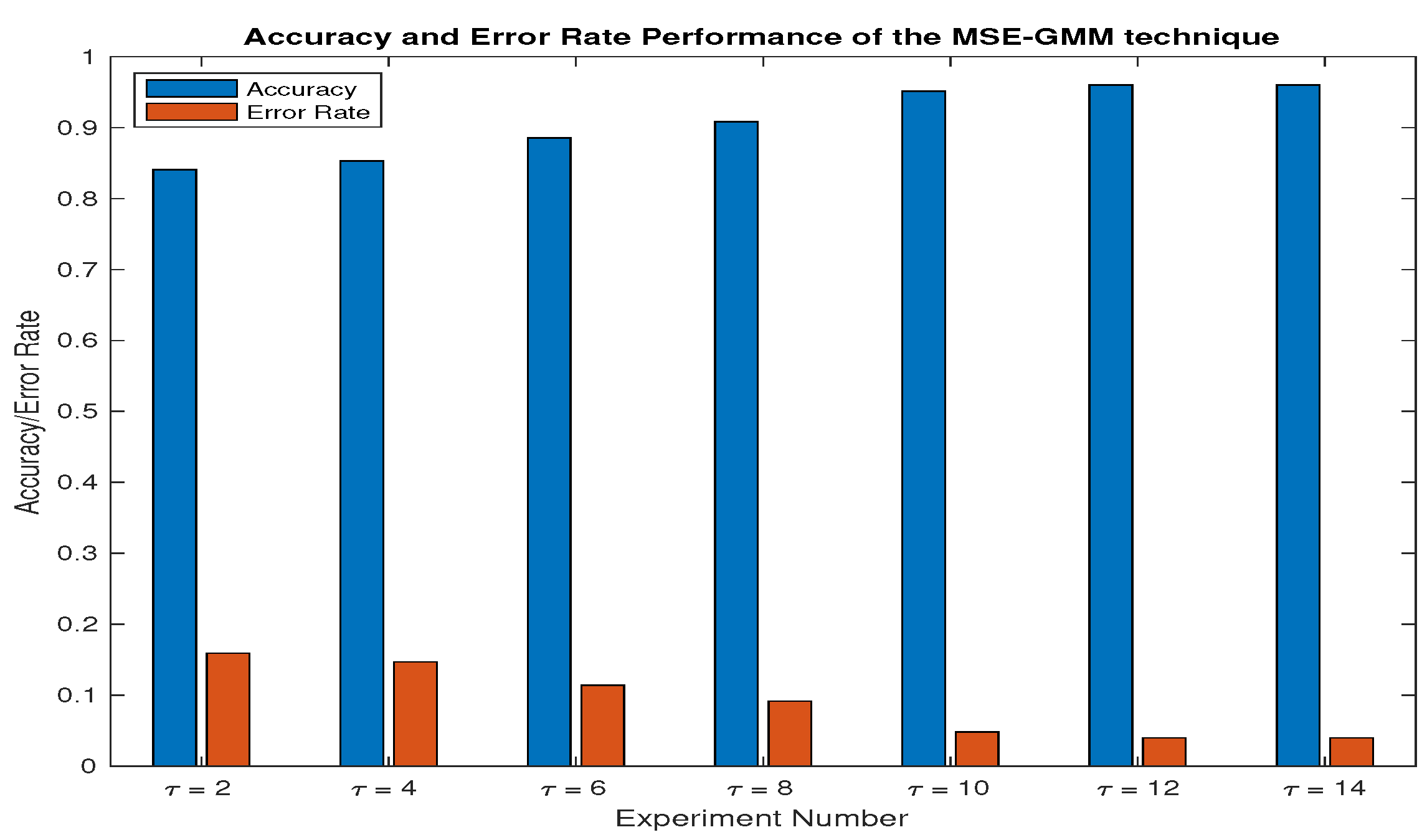
3.1. Simulation Parameter Selection
3.2. Computational Complexity
4. Results and Discussion
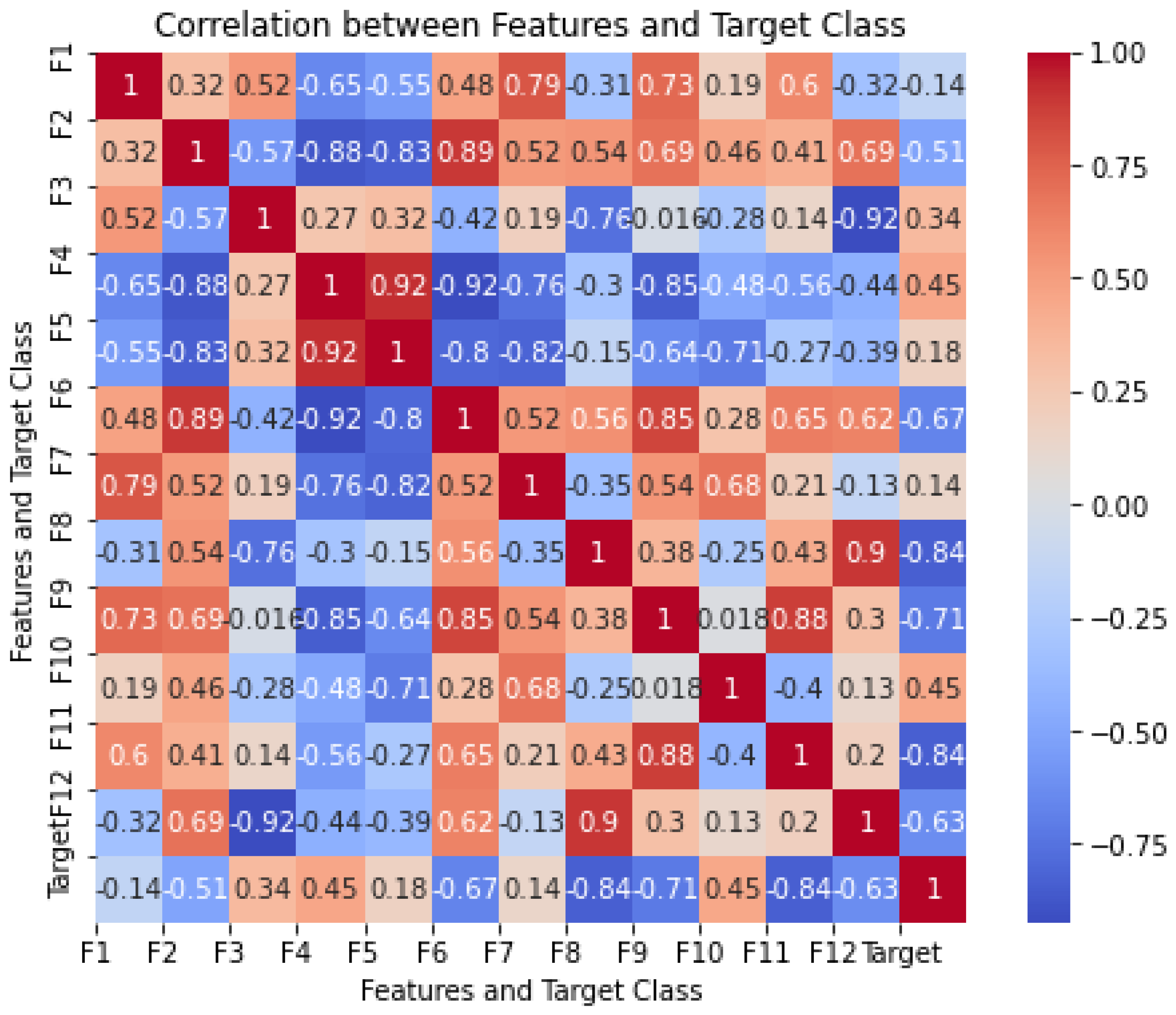
4.1. Correlation Analysis Between Features and Target Class
4.2. Detection and Classification Performance Comparison
4.3. Detection Performance Comparison
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cooke, J. Balaenoptera musculus ssp. Intermedia. The IUCN Red List of Threatened Species, e. T41713A50226962. 2018. Available online: https://www.iucnredlist.org/species/41713/50226962 (accessed on 20 February 2023).
- Širović, A.; Oleson, E. The Bioacoustics of Blue Whales—Global Diversity and Behavioral Variability in a Foraging Specialist. In Ethology and Behavioral Ecology of Mysticetes; Springer: Cham, Switzerland, 2022; pp. 195–221. [Google Scholar] [CrossRef]
- Stimpert, A.K.; DeRuiter, S.L.; Falcone, E.A.; Joseph, J.; Douglas, A.B.; Moretti, D.J.; Friedlaender, A.S.; Calambokidis, J.; Gailey, G.; Tyack, P.L.; et al. Sound production and associated behavior of tagged fin whales (Balaenoptera physalus) in the Southern California Bight. Anim. Biotelem. 2015, 3, 23. [Google Scholar] [CrossRef]
- Fournet, M.E.; Szabo, A.; Mellinger, D.K. Repertoire and classification of non-song calls in Southeast Alaskan humpback whales (Megaptera novaeangliae). J. Acoust. Soc. Am. 2015, 137, 1–10. [Google Scholar] [PubMed]
- Cazau, D.; Adam, O.; Aubin, T.; Laitman, J.T.; Reidenberg, J.S. A study of vocal nonlinearities in humpback whale songs: From production mechanisms to acoustic analysis. Sci. Rep. 2016, 6, 31660. [Google Scholar]
- Richman, J.; Moorman, J. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Moorman, J.; Carlo, W.; Kattwinkel, J.; Schelonka, R.; Porcelli, P.; Navarrete, C.; Bancalari, E.; Aschner, J.; Walker, M.; Perez, J.; et al. Mortality Reduction by Heart Rate Characteristic Monitoring in Very Low Birth Weight Neonates: A Randomized Trial. J. Pediatr. 2011, 159, 900–906.e1. [Google Scholar] [CrossRef]
- Keller, K.; Unakafov, A.; Unakafova, V. Ordinal Patterns, Entropy, and EEG. Entropy 2014, 16, 6212–6239. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar]
- Siddagangaiah, S. Complexity-entropy based approach for detection of fish choruses. J. Acoust. Soc. Am. 2018, 144, 1692–1693. [Google Scholar] [CrossRef]
- Siddagangaiah, S.; Chen, C.F.; Hu, W.C.; Akamatsu, T.; McElligott, M.; Lammers, M.; Pieretti, N. Automatic detection of dolphin whistles and clicks based on entropy approach. Ecol. Indic. 2020, 117, 106559. [Google Scholar] [CrossRef]
- Ogundile, O.; Usman, A.; Babalola, O.; Versfeld, D. A hidden Markov model with selective time domain feature extraction to detect inshore Bryde’s whale short pulse calls. Ecol. Inform. 2020, 57, 101087. [Google Scholar] [CrossRef]
- Babalola, O.P.; Usman, A.M.; Ogundile, O.O.; Versfeld, D.J.J. Detection of Bryde’s whale short pulse calls using time domain features with hidden Markov models. SAIEE Afr. Res. J. 2021, 112, 15–23. [Google Scholar] [CrossRef]
- Ibrahim, A.K.; Zhuang, H.; Erdol, N.; Muhamed Ali, A. Feature Extraction Methods for the Detection of North Atlantic Right Whale Up-Calls. In Proceedings of the 2018 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 12–14 December 2018; pp. 179–185. [Google Scholar] [CrossRef]
- Peso Parada, P.; Cardenal, A. Using Gaussian mixture models to detect and classify dolphin whistles and pulses. J. Acoust. Soc. Am. 2014, 135, 3371–3380. [Google Scholar] [CrossRef]
- Bahoura, M.; Simard, Y. Blue whale calls classification using short-time Fourier and wavelet packet transforms and artificial neural network. Digit. Signal Process. 2010, 20, 1256–1263. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Ogundile, O.; Usman, A.; Babalola, O.; Versfeld, D. Dynamic mode decomposition: A feature extraction technique based hidden Markov model for detection of Mysticetes’ vocalisations. Ecol. Inform. 2021, 63, 101306. [Google Scholar]
- Bartholomew, D. Principal Components Analysis. In International Encyclopedia of Education, 3rd ed.; Peterson, P., Baker, E., McGaw, B., Eds.; Elsevier: Oxford, UK, 2010; pp. 374–377. [Google Scholar] [CrossRef]
- Ogundile, O.O.; Babalola, O.P.; Odeyemi, S.G.; Rufai, K.I. Hidden Markov models for detection of Mysticetes vocalisations based on principal component analysis. Bioacoustics 2022, 31, 710–738. [Google Scholar] [CrossRef]
- Babalola, O.P.; Versfeld, J. Wavelet-based feature extraction with hidden Markov model classification of Antarctic blue whale sounds. Ecol. Inform. 2024, 80, 102468. [Google Scholar] [CrossRef]
- Usman, A.; Versfeld, D. Detection of baleen whale species using kernel dynamic mode decomposition-based feature extraction with a hidden Markov model. Ecol. Inform. 2022, 71, 101766. [Google Scholar] [CrossRef]
- Brown, J.C.; Smaragdis, P. Hidden Markov and Gaussian mixture models for automatic call classification. J. Acoust. Soc. Am. 2009, 125, EL221–EL224. [Google Scholar] [CrossRef]
- Roch, M.A.; Soldevilla, M.S.; Hoenigman, R.; Wiggins, S.M.; Hildebrand, J.A. Comparison of machine learning techniques for the classification of echolocation clicks from three species of odontocetes. Can. Acoust. 2008, 36, 41–47. [Google Scholar]
- Jiang, J.-J.; Bu, L.-R.; Duan, F.-J.; Wang, X.-Q.; Liu, W.; Sun, Z.-B.; Li, C.-Y. Whistle detection and classification for whales based on convolutional neural networks. Appl. Acoust. 2019, 150, 169–178. [Google Scholar] [CrossRef]
- Bermant, P.; Bronstein, M.; Wood, R.; Gero, S.; Gruber, D. Deep Machine Learning Techniques for the Detection and Classification of Sperm Whale Bioacoustics. Sci. Rep. 2019, 9, 12588. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Wang, C.C.; Lee, K.Y. Time Series Analysis Using Composite Multiscale Entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Shabangu, F.W.; Yemane, D.; Best, G.; Estabrook, B.J. Acoustic detectability of whales amidst underwater noise off the west coast of South Africa. Mar. Pollut. Bull. 2022, 184, 114122. [Google Scholar] [CrossRef]
- Miller, B.S.; Stafford, K.M.; Van Opzeeland, I.; Harris, D.; Samaran, F.; Širović, A.; Buchan, S.; Findlay, K.; Balcazar, N.; Nieukirk, S.; et al. An open access dataset for developing automated detectors of Antarctic baleen whale sounds and performance evaluation of two commonly used detectors. Sci. Rep. 2021, 11, 806. [Google Scholar] [CrossRef]
- Leroy, E.C.; Samaran, F.; Bonnel, J.; Royer, J.Y. Seasonal and diel vocalization patterns of Antarctic blue whale (Balaenoptera musculus intermedia) in the Southern Indian Ocean: A multi-year and multi-site study. PLoS ONE 2016, 11, e0163587. [Google Scholar] [CrossRef]
- Širović, A.; Branch, T.; Brownell, R.; Buchan, S.; Cerchio, S.; Findlay, K.; Lang, A.; Miller, B.; Olson, P.; Rogers, T.; et al. Blue Whale Song Occurrence in the Southern Hemisphere; IWC Paper SC/67b/SH11; IWC: Impington, UK, 2018; 12p, Available online: https://archive.iwc.int/pages/download_progress.php?ref=9330&size=&ext=pdf&k= (accessed on 16 May 2022).
- Van Opzeeland, L.; Samaran, F.; Stafford, K.; Findlay, K.; Gedamke, J.; Harris, D.; Miller, B.S. Towards collective circum-Antarctic passive acoustic monitoring: The Southern Ocean hydrophone network (SOHN). Polarforschung 2013, 83, 47–61. [Google Scholar]
- Shabangu, F.W.; Andrew, R.K.; Yemane, D.; Findlay, K.P. Acoustic seasonality, behaviour and detection ranges of Antarctic blue and fin whales under different sea ice conditions off Antarctica. Endanger. Species Res. 2020, 43, 21–37. [Google Scholar] [CrossRef]
- Edds-Walton, P.L. Acoustic Communication Signals of Mysticete Whales. Bioacoustics 1997, 8, 47–60. [Google Scholar] [CrossRef]
- Oleson, E.M.; Wiggins, S.M.; Hildebrand, J.A. Temporal separation of blue whale call types on a southern California feeding ground. Anim. Behav. 2007, 74, 881–894. [Google Scholar]
- Leroy, E.C.; Royer, J.Y.; Bonnel, J.; Samaran, F. Long-term and seasonal changes of large whale call frequency in the southern Indian Ocean. J. Geophys. Res. Oceans 2018, 123, 8568–8580. [Google Scholar] [CrossRef]
- Oleson, E.M.; Calambokidis, J.; Burgess, W.C.; Mcdonald, M.A.; Leduc, C.A.; Hildebrand, J.A. Behavioral context of call production by eastern North Pacific blue whales. Mar. Ecol. Prog. Ser. 2011, 330, 269–284. [Google Scholar] [CrossRef]
- Lewis, L.A.; Calambokidis, J.; Stimpert, A.K.; Fahlbusch, J.; Friedlaender, A.S.; McKenna, M.F.; Mesnick, S.L.; Oleson, E.M.; Southall, B.L.; Szesciorka, A.R.; et al. Context-dependent variability in blue whale acoustic behaviour. R. Soc. Open Sci. 2018, 5, 180241. [Google Scholar] [CrossRef]
- McDonald, M.A.; Mesnick, S.L.; Hildebrand, J.A. Biogeographic characterisation of blue whale song worldwide: Using song to identify populations. J. Cetacean Res. Manag. 2023, 8, 55–65. [Google Scholar] [CrossRef]
- Shannon, R.; Ljungblad, D.; Clark, C.; Kato, H. Vocalisations of Antarctic blue whales, Balaenoptera musculus intermedia, recorded during the 2001/2002 and 2002/2003 IWC/SOWER circumpolar cruises, Area V, Antarctica. J. Cetacean Res. Manag. 2005, 7, 13–20. [Google Scholar]
- Schall, E.; Di Iorio, L.; Berchok, C.; Filún, D.; Bedriñana-Romano, L.; Buchan, S.J.; Van Opzeeland, I.; Sears, R.; Hucke-Gaete, R. Visual and passive acoustic observations of blue whale trios from two distinct populations. Mar. Mammal Sci. 2020, 36, 365–374. [Google Scholar] [CrossRef]
- Miller, B.S.; Stafford, K.M.; Van Opzeel, I.; Harris, D.; Samaran, F.; šIrović, A.; Buchan, S.; Findlay, K.; Balcazar, N.; Nieukirk, S.; et al. An Annotated Library of Underwater Acoustic Recordings for Testing and Training Automated Algorithms for Detecting Antarctic Blue and Fin Whale Sounds; Australian Antarctic Data Centre: Kingston, TAS, Australia, 2020. [Google Scholar] [CrossRef]
- Raven Pro: Interactive Sound Analysis Software, version 1.6.4; K. Lisa Yang Center for Conservation Bioacoustics at the Cornell Lab of Ornithology: Ithaca, NY, USA, 2023.
- Shenoi, B.A. Introduction to Digital Signal Processing and Filter Design; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Han, J.; Kamber, M.J. Data Mining: Concepts and Techniques, 3rd ed.; The Morgan Kaufmann Series in Data Management Systems; Elsevier Science, Morgan Kaufmann: Burlington, MA, USA, 2012. [Google Scholar]
- Hwan, K.C.; Aggarwal, R. Wavelet transform in power systems: Part 1 General introduction to the wavelet transform. IEE Eng. J. 2000, 14, 81–87. [Google Scholar]
- Cantrell, C.D. Modern Mathematical Methods for Physicists and Engineers, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Costa, M.D.; Goldberger, A.L. Generalized multiscale entropy analysis: Application to quantifying the complex volatility of human heartbeat time series. Entropy 2015, 17, 1197–1203. [Google Scholar] [CrossRef]
- Feng, C.; Wang, H.; Lu, N.; Chen, T.; He, H.; Lu, Y.; Tu, X.M. Log-transformation and its implications for data analysis. Shanghai Arch. Psychiatry 2014, 26, 105–109. [Google Scholar]
- Godino-Llorente, J.I.; Gomez-Vilda, P.; Blanco-Velasco, M. Dimensionality reduction of a pathological voice quality assessment system based on Gaussian mixture models and short-term cepstral parameters. IEEE Trans. Biomed. Eng. 2006, 53, 1943–1953. [Google Scholar] [CrossRef] [PubMed]
- Majidnezhad, V.; Kheidorov, I. A novel GMM-based feature reduction for vocal fold pathology diagnosis. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 2245–2254. [Google Scholar] [CrossRef]
- Bhat, H.S.; Kumar, N. On the Derivation of the Bayesian Information Criterion. Available online: https://faculty.ucmerced.edu/hbhat/BICderivation.pdf (accessed on 3 December 2022).
- McLachlan, G.J.; Rathnayake, S. On the number of components in a Gaussian mixture model. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 341–355. [Google Scholar] [CrossRef]
- Stone, J.V. Bayes’ Rule: A Tutorial Introduction to Bayesian Analysis; Sebtel Press: Sheffield, UK, 2013. [Google Scholar]
- Reynolds, D. Gaussian mixture models. In Encyclopedia of Biometrics; Springer: Boston, MA, USA, 2009; pp. 659–663. [Google Scholar] [CrossRef]
- Gauvain, J.L.; Lee, C.H. Maximum a posteriori estimation for multivariate Gaussian mixture observations of Markov chains. IEEE Trans. Speech Audio Process. 1994, 2, 291–298. [Google Scholar] [CrossRef]
- Wan, H.; Wang, H.; Scotney, B.; Liu, J. A novel gaussian mixture model for classification. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 3298–3303. [Google Scholar]


| Processing Step | PCA-GMM | DMD-GMM | WT-GMM | MSE-GMM |
|---|---|---|---|---|
| Data segmentation | N/A | N/A | N/A | per segment |
| Feature transformation | ||||
| Feature extraction | ||||
| Feature selection | ||||
| Total feature extraction complexity | ||||
| GMM parameter estimation (EM) | ||||
| Posterior probability computation | ||||
| Feature selection via MPP ranking |
| Method | Computational Complexity |
|---|---|
| PCA-GMM | |
| DMD-GMM | |
| WT-GMM | |
| MSE-GMM |
| Accuracy Across 10 Trials (%) | Error Rate Across 10 Trials (%) | ||||||
|---|---|---|---|---|---|---|---|
| Mean | Highest | Lowest | Mean | Highest | Lowest | ||
| MSE-GMM | 86.20 | 88.15 | 83.26 | 6.82 | 8.50 | 4.12 | 4 |
| PCA-GMM | 73.41 | 81.01 | 69.42 | 15.39 | 21.63 | 9.89 | 7 |
| DMD-GMM | 81.24 | 86.47 | 77.96 | 9.72 | 14.25 | 5.11 | 5 |
| WF-GMM | 83.77 | 85.01 | 81.95 | 8.35 | 12.69 | 4.53 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babalola, O.P.; Ogundile, O.O.; Balyan, V. Multiscale Sample Entropy-Based Feature Extraction with Gaussian Mixture Model for Detection and Classification of Blue Whale Vocalization. Entropy 2025, 27, 355. https://doi.org/10.3390/e27040355
Babalola OP, Ogundile OO, Balyan V. Multiscale Sample Entropy-Based Feature Extraction with Gaussian Mixture Model for Detection and Classification of Blue Whale Vocalization. Entropy. 2025; 27(4):355. https://doi.org/10.3390/e27040355
Chicago/Turabian StyleBabalola, Oluwaseyi Paul, Olayinka Olaolu Ogundile, and Vipin Balyan. 2025. "Multiscale Sample Entropy-Based Feature Extraction with Gaussian Mixture Model for Detection and Classification of Blue Whale Vocalization" Entropy 27, no. 4: 355. https://doi.org/10.3390/e27040355
APA StyleBabalola, O. P., Ogundile, O. O., & Balyan, V. (2025). Multiscale Sample Entropy-Based Feature Extraction with Gaussian Mixture Model for Detection and Classification of Blue Whale Vocalization. Entropy, 27(4), 355. https://doi.org/10.3390/e27040355







