Quantifying Deviations from Gaussianity with Application to Flight Delay Distributions
Abstract
1. Introduction
2. Ordinal Patterns and the Permutation of Jensen–Shannon Distance
3. Numerical Analysis
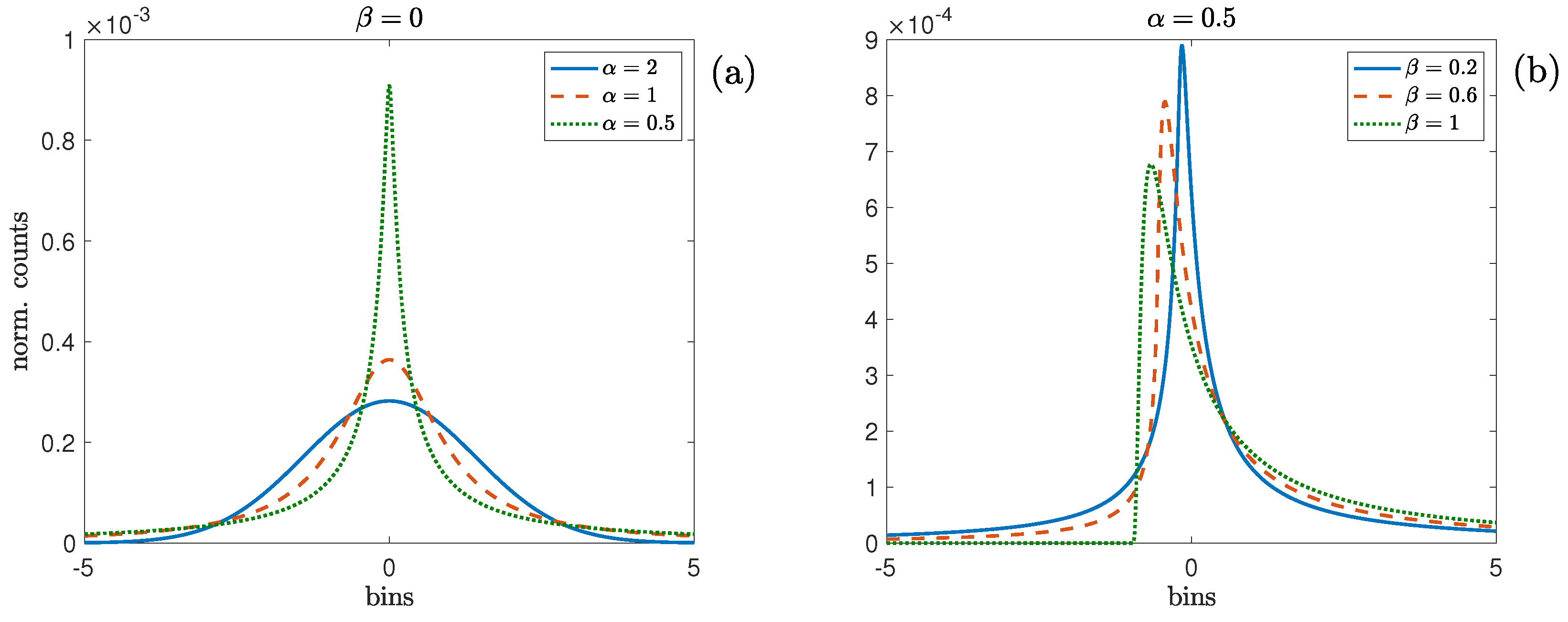
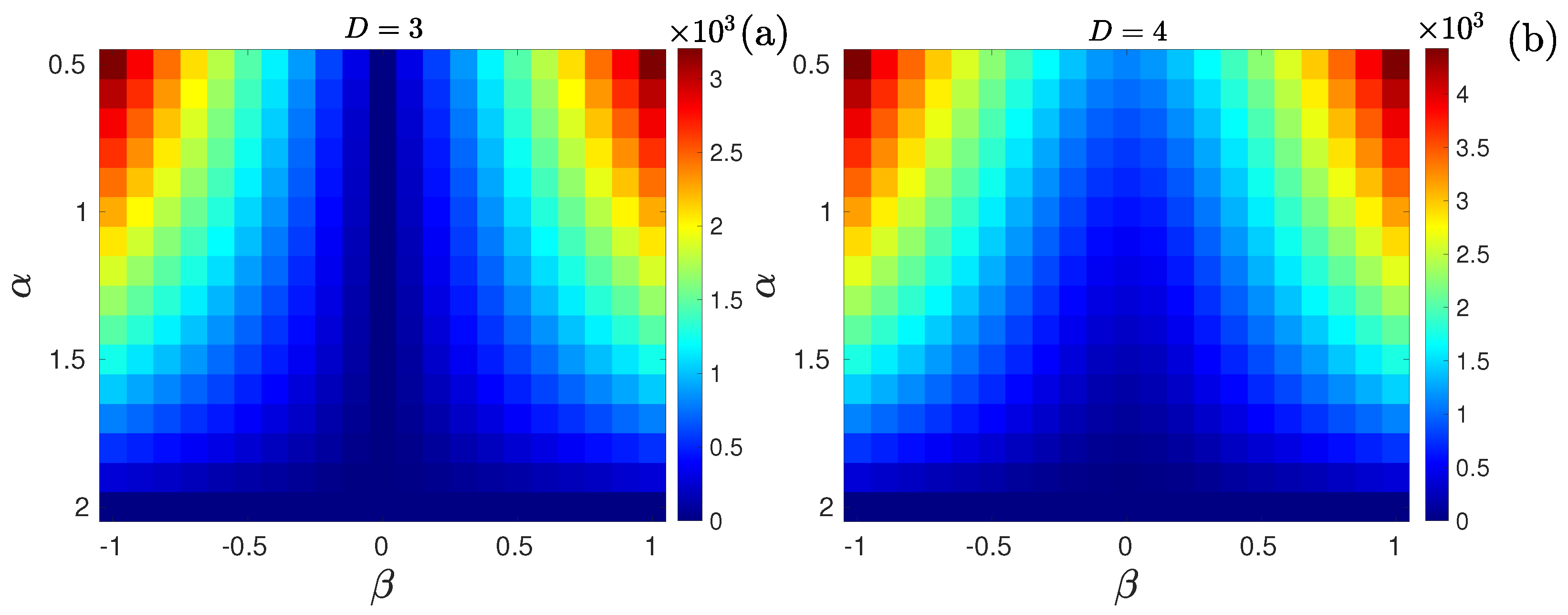
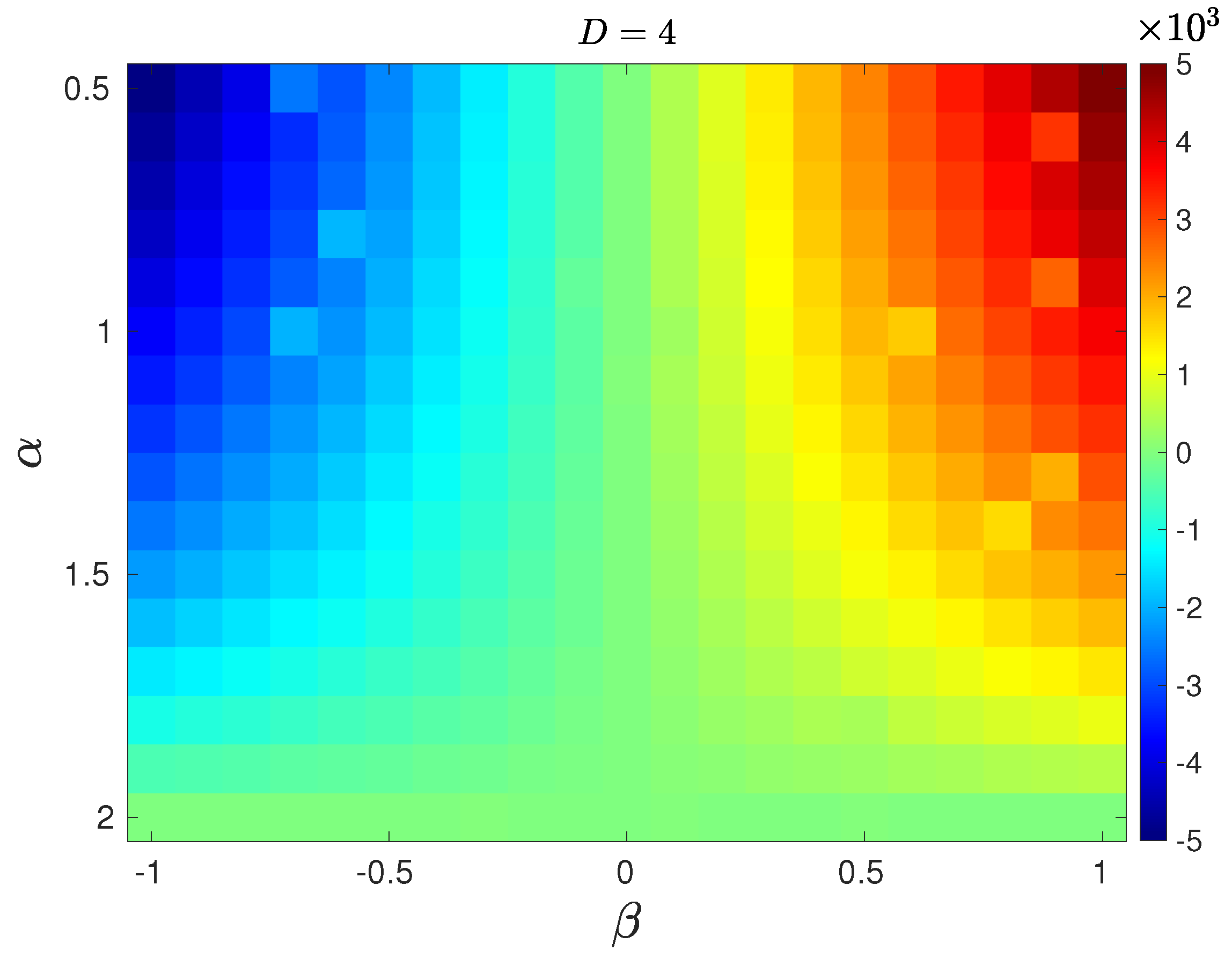
3.1. Stable Distributions
3.2. Synthetic Data Generation
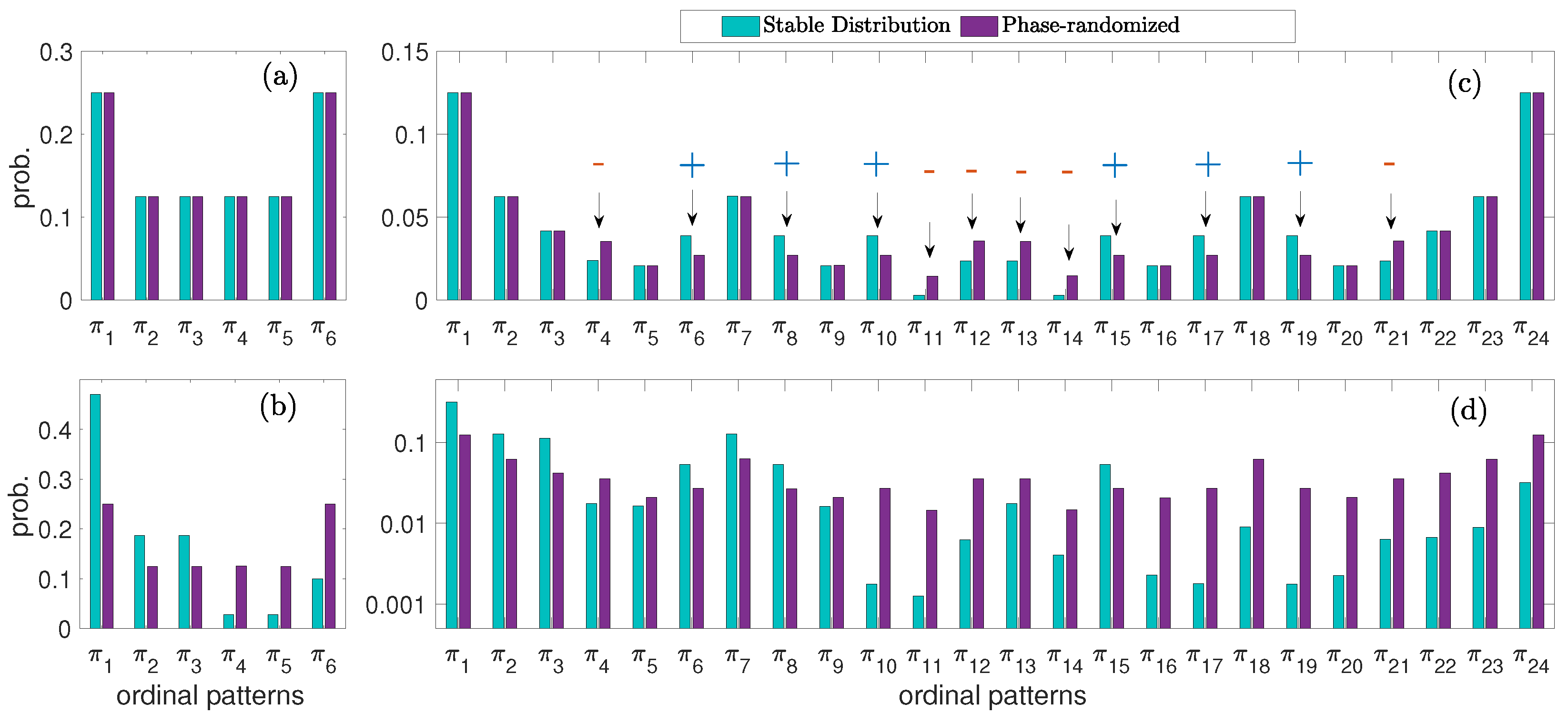
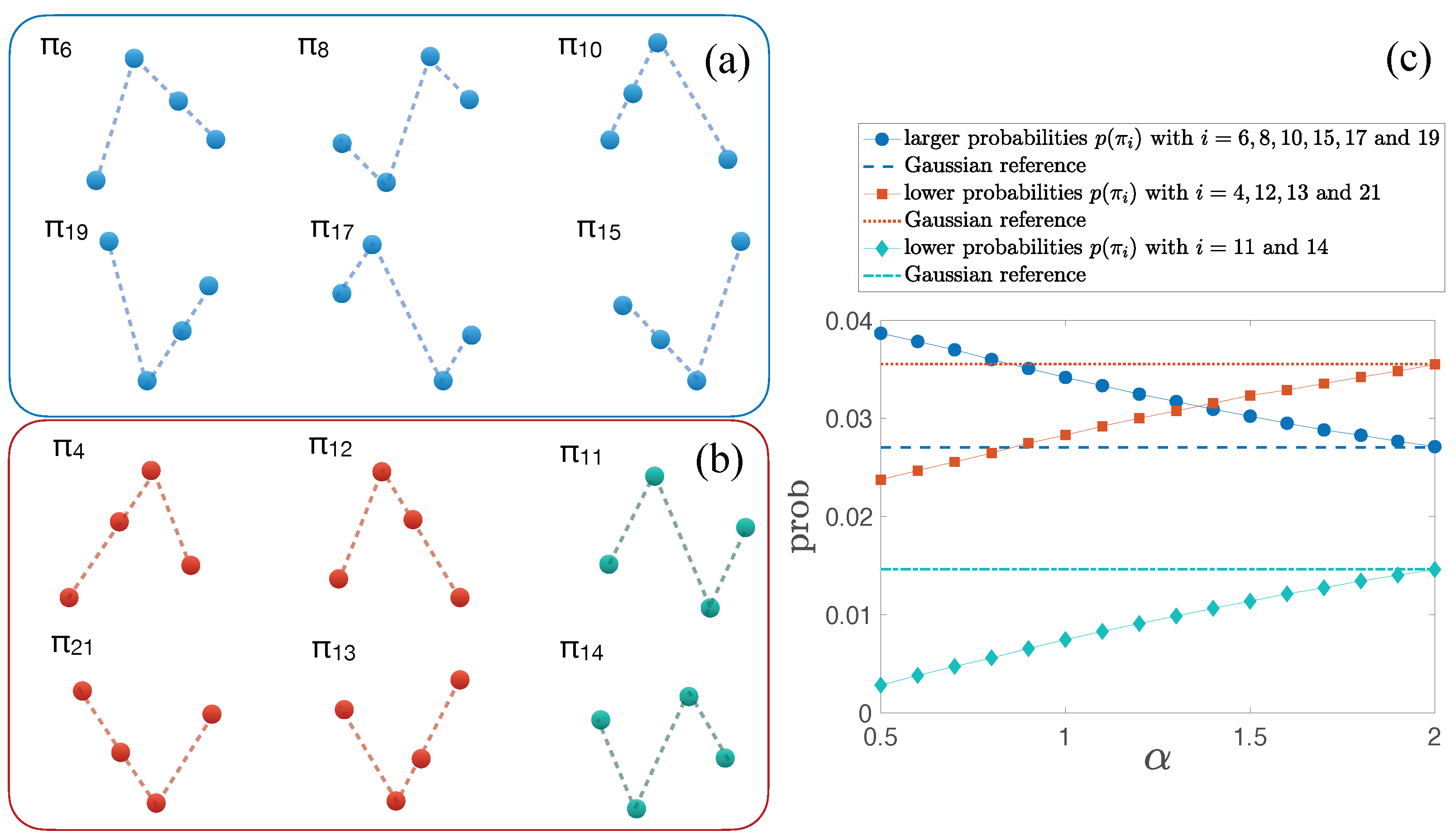
3.3. Surrogate Analysis
4. Application to Flight Delays Distributions
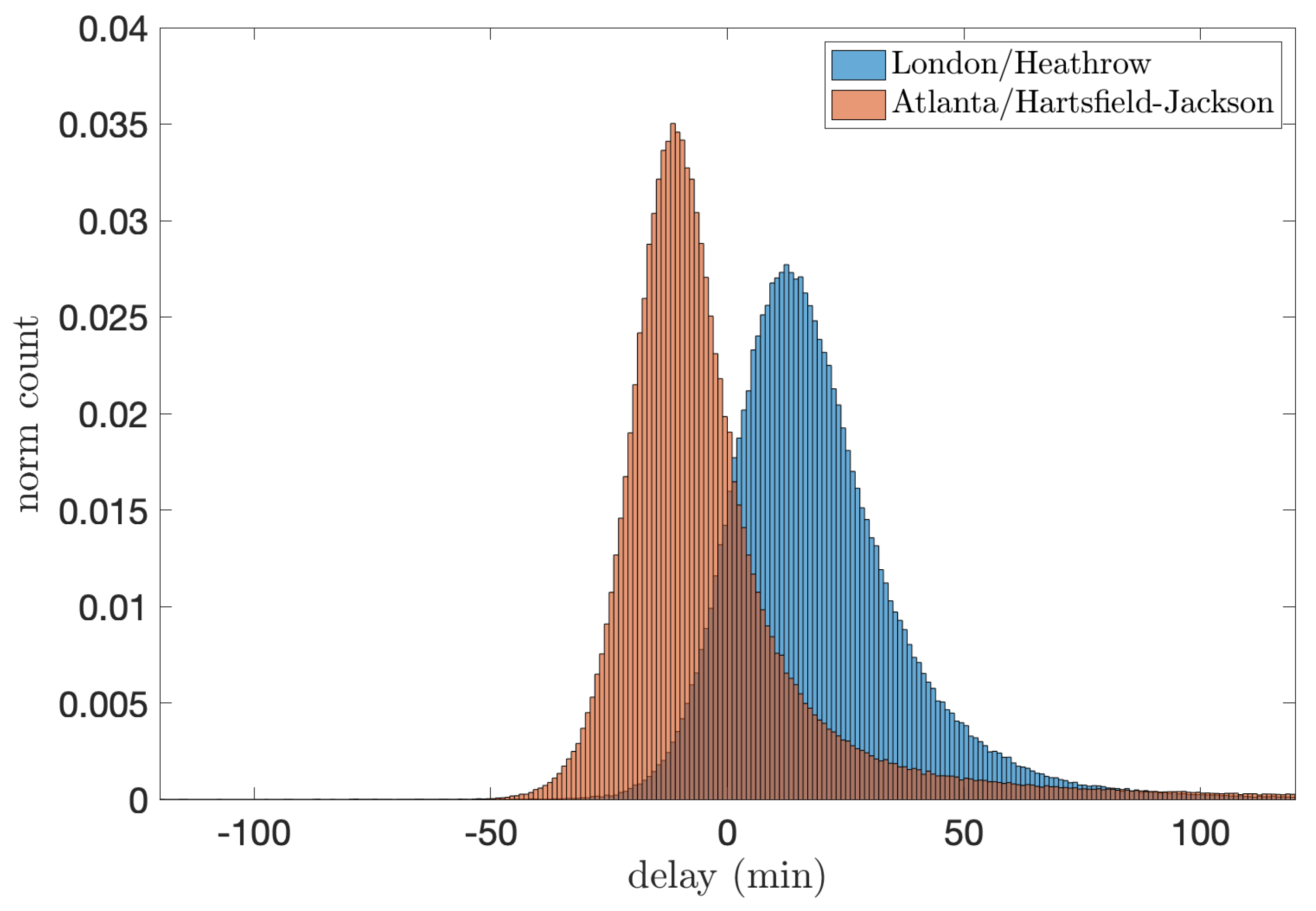
4.1. Analysis of Delay Distributions
4.2. Real Operational Data
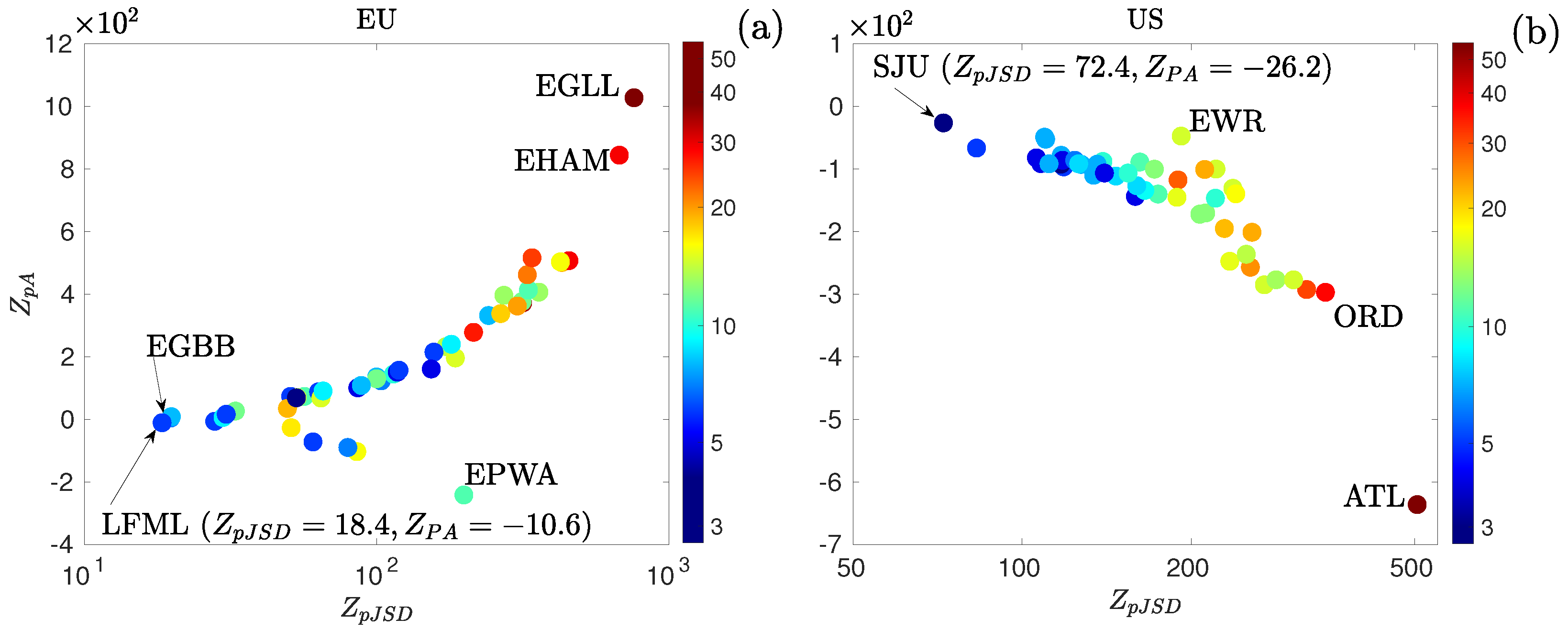
4.3. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, L.; Lv, H.; Yang, F.; Yu, L. Complexity testing techniques for time series data: A comprehensive literature review. Chaos Solitons Fractals 2015, 81, 117–135. [Google Scholar] [CrossRef]
- Olivares, F.; Plastino, A.; Rosso, O.A. Ambiguities in Bandt–Pompe’s methodology for local entropic quantifiers. Phys. A Stat. Mech. Its Appl. 2012, 391, 2518–2526. [Google Scholar] [CrossRef]
- Powell, G.; Percival, I. A spectral entropy method for distinguishing regular and irregular motion of Hamiltonian systems. J. Phys. A Math. Gen. 1979, 12, 2053. [Google Scholar] [CrossRef]
- Rosso, O.A.; Blanco, S.; Yordanova, J.; Kolev, V.; Figliola, A.; Schürmann, M.; Başar, E. Wavelet entropy: A new tool for analysis of short duration brain electrical signals. J. Neurosci. Methods 2001, 105, 65–75. [Google Scholar] [CrossRef] [PubMed]
- De Micco, L.; González, C.; Larrondo, H.; Martin, M.; Plastino, A.; Rosso, O. Randomizing nonlinear maps via symbolic dynamics. Phys. A Stat. Mech. Its Appl. 2008, 387, 3373–3383. [Google Scholar] [CrossRef]
- Mischaikow, K.; Mrozek, M.; Reiss, J.; Szymczak, A. Construction of symbolic dynamics from experimental time series. Phys. Rev. Lett. 1999, 82, 1144. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Amigó, J.M.; Rosso, O.A. Ordinal methods: Concepts, applications, new developments, and challenges—In memory of Karsten Keller (1961–2022). Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 080401. [Google Scholar] [CrossRef]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Leyva, I.; Martínez, J.H.; Masoller, C.; Rosso, O.A.; Zanin, M. 20 years of ordinal patterns: Perspectives and challenges. Europhys. Lett. 2022, 138, 31001. [Google Scholar] [CrossRef]
- Cuesta Frau, D. Permutation entropy: Influence of amplitude information on time series classification performance. Math. Biosci. Eng. 2019, 16, 6842–6857. [Google Scholar] [CrossRef] [PubMed]
- Fadlallah, B.; Chen, B.; Keil, A.; Príncipe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Escudero, J. Amplitude-aware permutation entropy: Illustration in spike detection and signal segmentation. Comput. Methods Programs Biomed. 2016, 128, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Xiao-Feng, L.; Yue, W. Fine-grained permutation entropy as a measure of natural complexity for time series. Chin. Phys. B 2009, 18, 2690. [Google Scholar] [CrossRef]
- Zanin, M. Continuous ordinal patterns: Creating a bridge between ordinal analysis and deep learning. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 033114. [Google Scholar] [CrossRef]
- Zunino, L.; Olivares, F.; Ribeiro, H.V.; Rosso, O.A. Permutation Jensen-Shannon distance: A versatile and fast symbolic tool for complex time-series analysis. Phys. Rev. E 2022, 105, 045310. [Google Scholar] [CrossRef] [PubMed]
- Nolan, J.P. Univariate stable distributions. Springer Ser. Oper. Res. Financ. Eng. 2020, 10, 978-3. [Google Scholar]
- Mandelbrot, B. New methods in statistical economics. J. Political Econ. 1963, 71, 421–440. [Google Scholar] [CrossRef]
- Mitsokapas, E.; Schäfer, B.; Harris, R.J.; Beck, C. Statistical characterization of airplane delays. Sci. Rep. 2021, 11, 7855. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Zhu, C.; Wu, F.; Hu, M.; Duong, V.; Watkins, M.; Barzel, B.; Stanley, H.E. Universal patterns in passenger flight departure delays. Sci. Rep. 2020, 10, 6890. [Google Scholar] [CrossRef]
- Tu, Y.; Ball, M.O.; Jank, W.S. Estimating flight departure delay distributions—A statistical approach with long-term trend and short-term pattern. J. Am. Stat. Assoc. 2008, 103, 112–125. [Google Scholar]
- Szabó, Z. Non-Linear Transitions in Air Transport Delays: Models and Data. Master’s Thesis, . Universitat de les Illes Balears, Palma de Mallorca, Spain, 2023. [Google Scholar]
- Mueller, E.; Chatterji, G. Analysis of aircraft arrival and departure delay characteristics. In Proceedings of the AIAA’s Aircraft Technology, Integration, and Operations (ATIO) 2002 Technical Forum, Los Angeles, CA, USA, 1–3 October 2002; p. 5866. [Google Scholar]
- Wang, Z.; Liao, C.; Hang, X.; Li, L.; Delahaye, D.; Hansen, M. Distribution prediction of strategic flight delays via machine learning methods. Sustainability 2022, 14, 15180. [Google Scholar] [CrossRef]
- Wang, F.; Bi, J.; Xie, D.; Zhao, X. Flight delay forecasting and analysis of direct and indirect factors. IET Intell. Transp. Syst. 2022, 16, 890–907. [Google Scholar] [CrossRef]
- Hatıpoğlu, I.; Tosun, Ö. Predictive Modeling of Flight Delays at an Airport Using Machine Learning Methods. Appl. Sci. 2024, 14, 5472. [Google Scholar] [CrossRef]
- Song, C.; Guo, J.; Zhuang, J. Analyzing passengers’ emotions following flight delays-a 2011–2019 case study on SKYTRAX comments. J. Air Transp. Manag. 2020, 89, 101903. [Google Scholar] [CrossRef]
- Zunino, L.; Soriano, M.C.; Fischer, I.; Rosso, O.A.; Mirasso, C.R. Permutation-information-theory approach to unveil delay dynamics from time-series analysis. Phys. Rev. E 2010, 82, 046212. [Google Scholar] [CrossRef]
- Zunino, L.; Soriano, M.C.; Rosso, O.A. Distinguishing chaotic and stochastic dynamics from time series by using a multiscale symbolic approach. Phys. Rev. E 2012, 86, 046210. [Google Scholar] [CrossRef]
- Olivares, F.; Zunino, L. Multiscale dynamics under the lens of permutation entropy. Phys. A Stat. Mech. Its Appl. 2020, 559, 125081. [Google Scholar] [CrossRef]
- Olivares, F.; Zunino, L.; Zanin, M. Markov-modulated model for landing flow dynamics: An ordinal analysis validation. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.A.; Martin, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Zunino, L. Revisiting the Characterization of Resting Brain Dynamics with the Permutation Jensen–Shannon Distance. Entropy 2024, 26, 432. [Google Scholar] [CrossRef] [PubMed]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. D Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Bandt, C.; Shiha, F. Order patterns in time series. J. Time Ser. Anal. 2007, 28, 646–665. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar]
- Cook, A.J.; Tanner, G. European Airline Delay Cost Reference Values; Technical Report; EUROCONTROL Performance Review Unit: Brussels, Belgium, 2011. [Google Scholar]
- Duytschaever, D. The Development and Implementation of the EUROCONTROL Central Air Traffic Flow Management Unit (CFMU). J. Navig. 1993, 46, 343–352. [Google Scholar] [CrossRef]
- Carlier, S.; De Lépinay, I.; Hustache, J.C.; Jelinek, F. Environmental impact of air traffic flow management delays. In Proceedings of the 7th USA/Europe Air Traffic Management Research and Development Seminar (ATM2007), Barcelona, Spain, 2–5 July 2007; Volume 2, p. 16. [Google Scholar]
- Cao, Y.; Zhu, C.; Wang, Y.; Li, Q. A method of reducing flight delay by exploring internal mechanism of flight delays. J. Adv. Transp. 2019, 2019, 7069380. [Google Scholar] [CrossRef]
- Olivares, F.; Zanin, M. Corrupted bifractal features in finite uncorrelated power-law distributed data. Phys. A Stat. Mech. Its Appl. 2022, 603, 127828. [Google Scholar]
- Olivares, F.; Sun, X.; Wandelt, S.; Zanin, M. Measuring landing independence and interactions using statistical physics. Transp. Res. Part E Logist. Transp. Rev. 2023, 170, 102998. [Google Scholar] [CrossRef]
- Cook, A. European Air Traffic Management: Principles, Practice, and Research; Ashgate Publishing, Ltd.: Aldershot, UK, 2007. [Google Scholar]
- Kuhn, K.D. Ground delay program planning: Delay, equity, and computational complexity. Transp. Res. Part C Emerg. Technol. 2013, 35, 193–203. [Google Scholar] [CrossRef]
- EUROCONTROL. 2017 Comparison of ATM-Related Performance: U.S.–Europe; Technical Report; European Organisation for the Safety of Air Navigation: Brussels, Belgium, 2018. [Google Scholar]
- Pejovic, T.; Netjasov, F.; Crnogorac, D. Relationship between air traffic demand, safety and complexity in high-density airspace in Europe. In Risk Assessment in Air Traffic Management; IntechOpen: London, UK, 2020. [Google Scholar]
- Francis, G.; Humphreys, I.; Fry, J. The benchmarking of airport performance. J. Air Transp. Manag. 2002, 8, 239–247. [Google Scholar] [CrossRef]
- Zografos, K.; Andreatta, G.; Odoni, A. Modelling and Managing Airport Performance; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Yu, C. Airport Performance-a multifarious review of literature. J. Air Transp. Res. Soc. 2023, 1, 22–39. [Google Scholar] [CrossRef]
- Humphreys, I.; Francis, G. Traditional airport performance indicators: A critical perspective. Transp. Res. Rec. 2000, 1703, 24–30. [Google Scholar] [CrossRef]
- Oreschko, B.; Kunze, T.; Schultz, M.; Fricke, H.; Kumar, V.; Sherry, L. Turnaround prediction with stochastic process times and airport specific delay pattern. In Proceedings of the International Conference on Research in Airport Transportation (ICRAT), Berkeley, CA, USA, 22–26 January 2012. [Google Scholar]
- Jain, A.; Nghiem, T.; Morari, M.; Mangharam, R. Learning and control using Gaussian processes. In Proceedings of the 2018 ACM/IEEE 9th International Conference on Cyber-Physical Systems (ICCPS), Porto, Portugal, 11–13 April 2018; pp. 140–149. [Google Scholar]
- Kwon, Y.; Zhang, R.; Moon, I. Analyzing airline delay propagation and delay cause using a Gaussian network. Int. J. Ind. Eng. 2023, 30, 1328. [Google Scholar]
- Rak, R.; Grech, D. Quantitative approach to multifractality induced by correlations and broad distribution of data. Phys. A Stat. Mech. Its Appl. 2018, 508, 48–66. [Google Scholar] [CrossRef]
- Peng, C.K.; Mietus, J.; Hausdorff, J.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 1993, 70, 1343. [Google Scholar] [CrossRef]
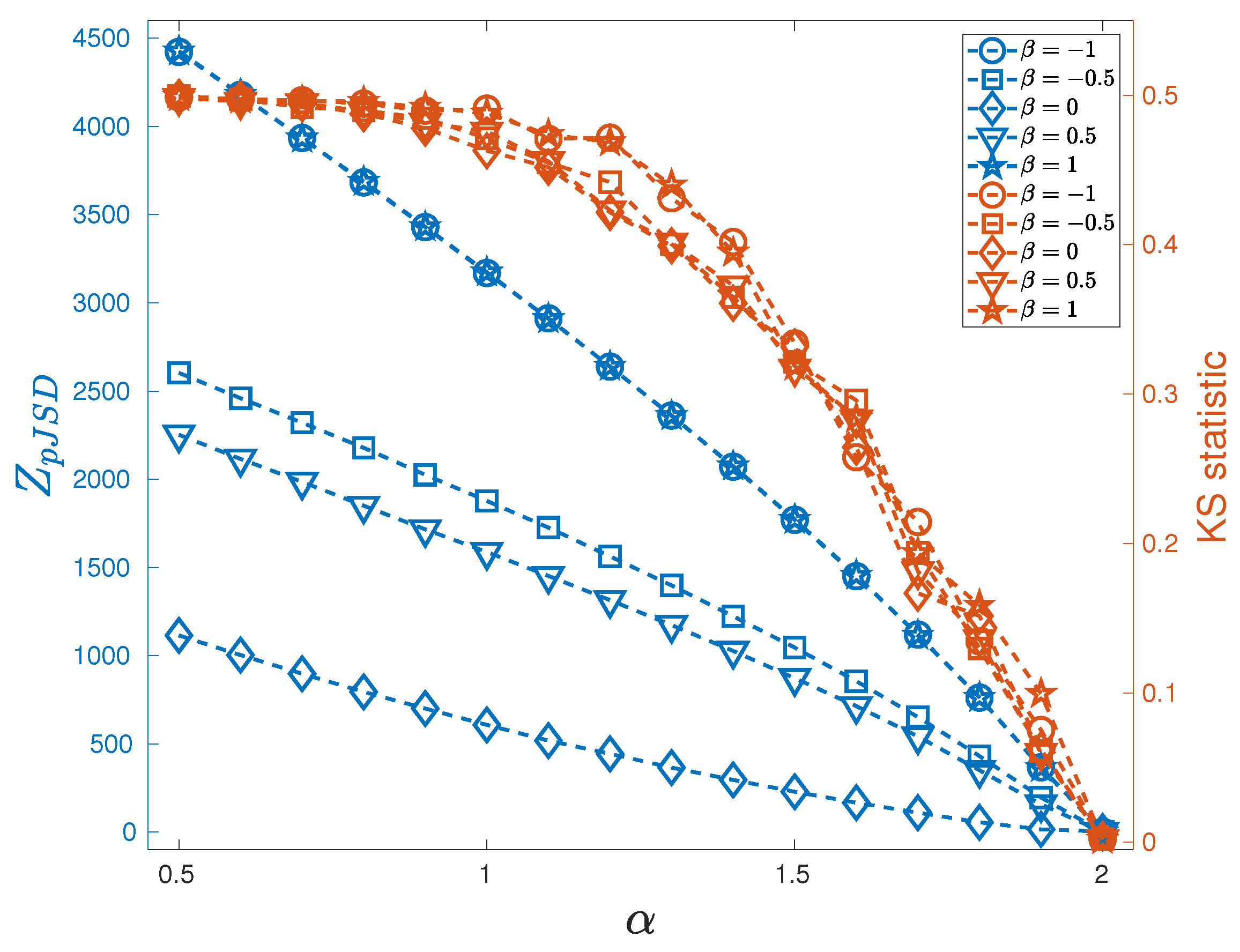

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olivares, F.; Zanin, M. Quantifying Deviations from Gaussianity with Application to Flight Delay Distributions. Entropy 2025, 27, 354. https://doi.org/10.3390/e27040354
Olivares F, Zanin M. Quantifying Deviations from Gaussianity with Application to Flight Delay Distributions. Entropy. 2025; 27(4):354. https://doi.org/10.3390/e27040354
Chicago/Turabian StyleOlivares, Felipe, and Massimiliano Zanin. 2025. "Quantifying Deviations from Gaussianity with Application to Flight Delay Distributions" Entropy 27, no. 4: 354. https://doi.org/10.3390/e27040354
APA StyleOlivares, F., & Zanin, M. (2025). Quantifying Deviations from Gaussianity with Application to Flight Delay Distributions. Entropy, 27(4), 354. https://doi.org/10.3390/e27040354






