Entropy of Volatility Changes: Novel Method for Assessment of Regularity in Volatility Time Series
Abstract
1. Introduction
2. Methodological Background
2.1. Volatility Estimators Based on Daily Data
- Open–close returns:
- Open–high returns:
- Open–low returns:
2.2. Symbolic Encoding of Volatility Time Series
- , where is the volatility estimator given by Definition 1.
- , where is the volatility estimator given by Definition 2,
- , where is the volatility estimator given by Definition 3.
2.3. Entropy of Volatility Changes
3. Experimental Studies: Results and Discussion
3.1. Data Description
- The pre-COVID-19 pandemic period from January 2017 to February 2020 (38 months);
- The COVID-19 pandemic period from March 2020 to April 2023 (38 months).
3.2. Discretization of Time Series of Volatility Changes
3.3. Symbol-Sequence Histograms of Encoded Series of Volatility Changes
3.4. Empirical Results Within the Whole Sample Period: The Modified Shannon Entropy of Volatility Changes, Histograms, and Symbol-Sequence Statistics
3.5. The Comparative Empirical Findings for the Pre-COVID-19 and COVID-19 Periods: The Modified Shannon Entropy of Volatility Changes, Histograms, and Statistics
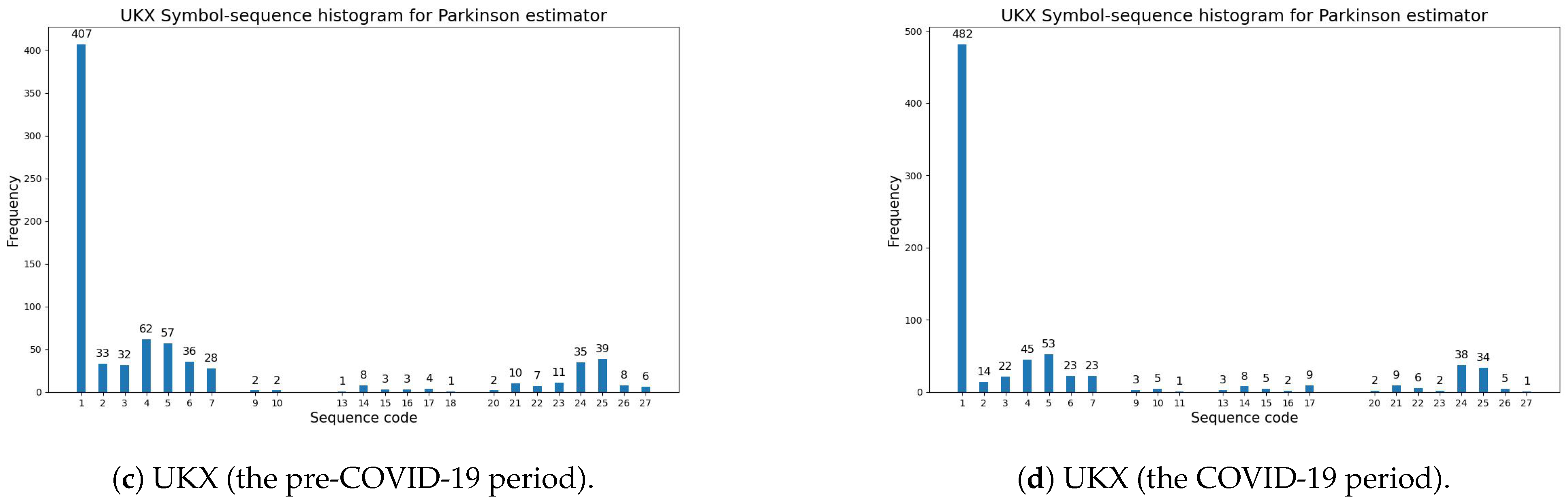
3.5.1. The Comparative Empirical Findings for the Parkinson Volatility Estimator
3.5.2. Comparative Empirical Findings for the Garman–Klass Volatility Estimator
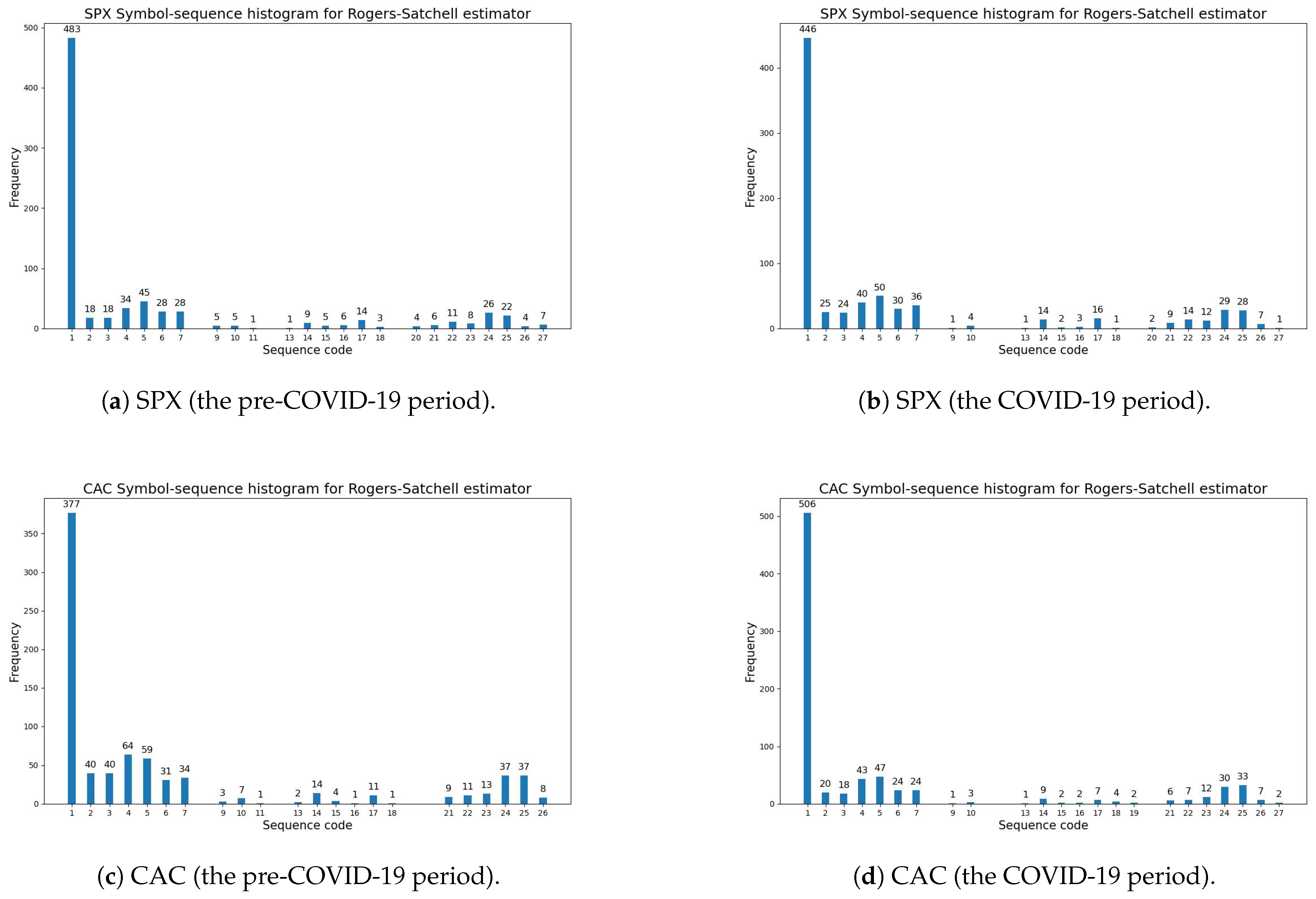
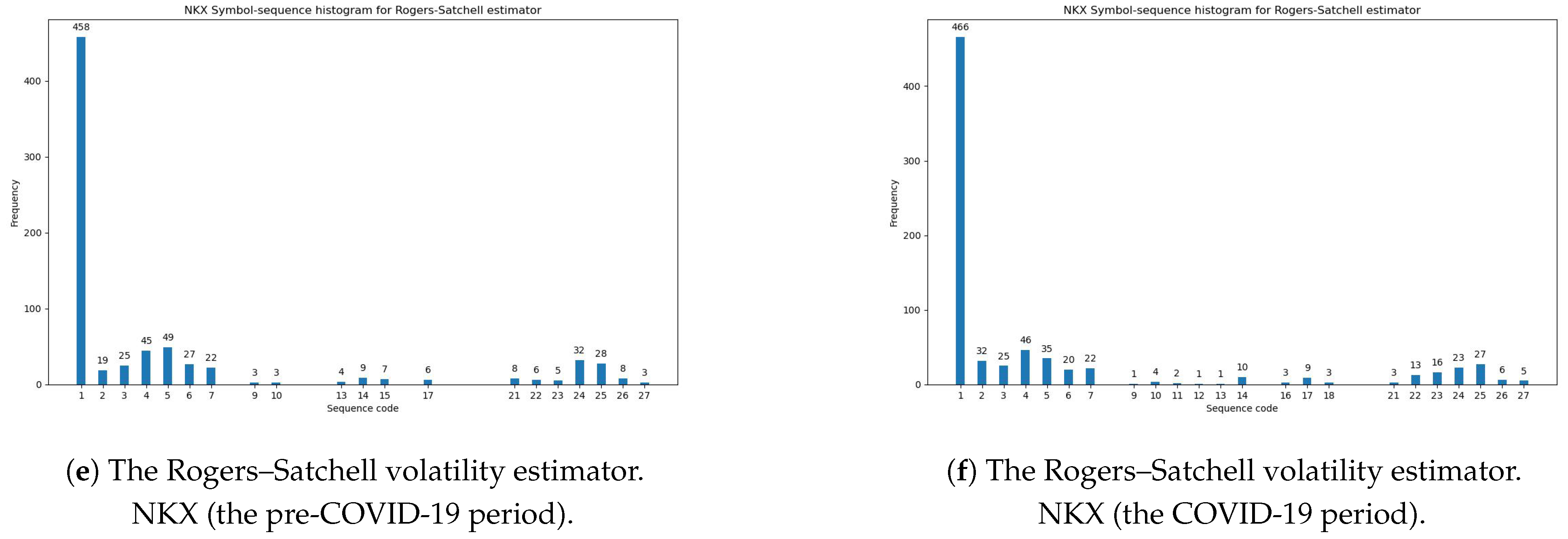
3.5.3. Comparative Empirical Findings for the Rogers–Satchell Volatility Estimator
3.5.4. Statistical Comparison of Symbol-Sequence Histograms
4. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Symbol-Sequence Statistics: Additional Comparative Results
| The Sequences with Zero Frequency Within the Pre-COVID-19 Period | |||||
|---|---|---|---|---|---|
| SPX | CAC | UKX | DAX | NKX | |
| Parkinson | No. 12, No. 18 | No. 8, No. 11, | No. 8, No. 11, | No. 8, No. 11, | No. 8, No. 12, |
| Estimator | No. 12, No. 18 | No. 12, No. 19 | No. 12, No. 13 | No. 19, No. 20 | |
| No. 19 | |||||
| Garman–Klass | No. 8, No. 12 | No. 8, No. 11, | No. 8, No. 11, | No. 8, No. 12 | No. 8, No. 11, |
| Estimator | No. 12 | No. 12, No. 18 | No. 12, No. 18, | ||
| No. 19 | |||||
| Rogers–Satchell | No. 8, No. 12, | No. 8, No. 12, | No. 8, No. 12, | No. 8, No. 12, | No. 8, No. 11, |
| Estimator | No. 19 | No. 19, No. 20 | No. 19, No. 20 | No. 19 | No. 12, No. 16, |
| No. 18, No. 19, | |||||
| No. 20 | |||||
| The Sequences with Zero Frequency Within the COVID-19 Pandemic Period | |||||
|---|---|---|---|---|---|
| SPX | CAC | UKX | DAX | NKX | |
| Parkinson | No. 8, No. 12, | No. 8, No. 12, | No. 8, No. 12, | No. 8, No. 12, | No. 8, No. 19 |
| Estimator | No. 19 | No. 18, No. 19 | No. 18, No. 19 | No. 13, No. 19 | |
| Garman–Klass | No. 8, No. 12 | No. 8, No. 12, | No. 8, No. 12, | No. 8, No. 12, | No. 8, No. 9, |
| Estimator | No. 16, No. 20 | No. 20 | No. 19 | No. 11, No. 13, | |
| No. 15, No. 19 | |||||
| Rogers–Satchell | No. 8, No. 11, | No. 8, No. 11, | No. 8, No. 9, | No. 8, No. 9, | No. 8, No. 15, |
| Estimator | No. 12, No. 19 | No. 12, No. 20 | No. 10, No. 12 | No. 11, No. 12, | No. 19, No. 20 |
| No. 19 | |||||
| The Three Most Frequently Observed Sequences Within the Pre-COVID-19 Period | |||||
|---|---|---|---|---|---|
| SPX | CAC | UKX | DAX | NKX | |
| Parkinson | No. 1 (467 times) | No. 1 (406 times) | No. 1 (407 times) | No. 1 (387 times) | No. 1 (430 times) |
| Estimator | No. 5 (50 times) | No. 4 (60 times) | No. 4 (62 times) | No. 4 (61 times) | No. 5 (53 times) |
| No. 4 (39 times) | No. 5 (54 times) | No. 5 (57 times) | No. 5 (61 times) | No. 4 (51 times) | |
| Garman–Klass | No. 1 (478 times) | No. 1 (365 times) | No. 1 (364 times) | No. 1 (360 times) | No. 1 (440 times) |
| Estimator | No. 5 (53 times) | No. 4 (60 times) | No. 4 (66 times) | No. 5 (64 times) | No. 5 (50 times) |
| No. 4 (47 times) | No. 5 (51 times) | No. 5 (63 times) | No. 4 (59 times) | No. 4 (49 times) | |
| Rogers–Satchell | No. 1 (483 times) | No. 1 (377 times) | No. 1 (399 times) | No. 1 (379 times) | No. 1 (458 times) |
| Estimator | No. 5 (45 times) | No. 4 (64 times) | No. 4 (59 times) | No. 4 (62 times) | No. 5 (49 times) |
| No. 4 (34 times) | No. 5 (59 times) | No. 5 (50 times) | No. 5 (60 times) | No. 4 (45 times) | |
| The Three Most Frequently Observed Sequences Within the COVID-19 Pandemic Period | |||||
|---|---|---|---|---|---|
| SPX | CAC | UKX | DAX | NKX | |
| Parkinson | No. 1 (405 times) | No. 1 (454 times) | No. 1 (482 times) | No. 1 (426 times) | No. 1 (416 times) |
| Estimator | No. 5 (55 times) | No. 4 (55 times) | No. 5 (53 times) | No. 4 (60 times) | No. 5 (54 times) |
| No. 4 (54 times) | No. 5 (49 times) | No. 4 (45 times) | No. 5 (54 times) | No. 4 (50 times) | |
| Garman–Klass | No. 1 (412 times) | No. 1 (459 times) | No. 1 (426 times) | No. 1 (451 times) | No. 1 (483 times) |
| Estimator | No. 5 (49 times) | No. 5 (57 times) | No. 5 (60 times) | No. 5 (56 times) | No. 5 (46 times) |
| No. 4 (46 times) | No. 4 (39 times) | No. 4 (51 times) | No. 4 (46 times) | No. 4 (38 times) | |
| Rogers–Satchell | No. 1 (446 times) | No. 1 (506 times) | No. 1 (483 times) | No. 1 (473 times) | No. 1 (466 times) |
| Estimator | No. 5 (50 times) | No. 5 (47 times) | No. 4 (42 times) | No. 5 (53 times) | No. 4 (46 times) |
| No. 4 (40 times) | No. 4 (43 times) | No. 5 (42 times) | No. 4 (39 times) | No. 5 (35 times) | |
References
- Brooks, C. Introductory Econometrics for Finance, 4th ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Tsay, R. Analysis of Financial Time Series; John Wiley: New York, NY, USA, 2010. [Google Scholar]
- Nelson, D. Modelling stock market volatility changes. In Modelling Stock Market Volatility: Bridging the Gap to Continous Time; Rossi, P., Ed.; Academic Press, Inc.: Cambridge, MA, USA, 1996; pp. 3–15. [Google Scholar]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Brida, J.; Punzo, L. Symbolic time series analysis and dynamic regimes. Struct. Chang. Econ. Dyn. 2003, 14, 159–183. [Google Scholar] [CrossRef]
- Bühlmann, P. Extreme events from the return-volume process: A discretization approach for complexity reduction. Appl. Financ. Econ. 1998, 8, 267–278. [Google Scholar] [CrossRef]
- Daw, C.; Finney, C.; Tracy, E. A review of symbolic analysis of experimental data. Rev. Sci. Instrum. 2003, 74, 915–930. [Google Scholar] [CrossRef]
- Ahn, K.; Lee, D.; Sohn, S.; Yang, B. Stock market uncertainty and economic fundamentals: An entropy-based approach. Quant. Financ. 2019, 19, 1151–1163. [Google Scholar] [CrossRef]
- Finney, C.; Green, J., Jr.; Daw, C. Symbolic time-series analysis of engine combustion measurement. SAE Trans. 1998, 107, 880–897. [Google Scholar]
- Olbryś, J.; Komar, N. Symbolic encoding methods with entropy-based applications to financial time series analyses. Entropy 2023, 25, 1009. [Google Scholar] [CrossRef]
- Shternshis, A.; Mazzarisi, P.; Marmi, S. Measuring market efficiency: The Shannon entropy of high-frequency financial time series. Chaos Soliton Fract. 2022, 162, 112403. [Google Scholar] [CrossRef]
- Olbrys, J. Extreme events and stock market efficiency: The modified Shannon entropy approach. In Applied Economic Research and Trends; Tsounis, N., Vlachvei, A., Eds.; Springer Proceedings in Business and Economics; Springer Nature Switzerland AG: Cham, Switzerland, 2024; pp. 77–89. [Google Scholar] [CrossRef]
- Risso, W. Symbolic time series analysis and its application in social sciences. In Time Series Analysis and Applications; Mohamudally, N., Ed.; IntechOpen: Rijeka, Croatia, 2018. [Google Scholar] [CrossRef][Green Version]
- Olbrys, J. Incorporating volatility into symbolic encoding with thresholds: New entropy-based approach to market efficiency assessment. Proc. Comp. Sci. 2024, 246, 48–57. [Google Scholar] [CrossRef]
- Schittenkopf, C.; Tino, P.; Dorffner, G. The benefit of information reduction for trading strategies. Appl. Econ. 2002, 34, 917–930. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, Q. Drift-independent volatility estimation based on high, low, open, and close prices. J. Bus. 2000, 73, 477–491. [Google Scholar] [CrossRef]
- Garman, M.; Klass, M. On the estimation of security price volatilities from historical data. J. Bus. 1980, 53, 67–78. [Google Scholar] [CrossRef]
- Parkinson, M. The extreme value method for estimating the variance of the rate of return. J. Bus. 1980, 53, 61–65. [Google Scholar] [CrossRef]
- Rogers, L.; Satchell, S. Estimating variance from high, low and closing prices. Ann. Appl. Probab. 1991, 1, 504–512. [Google Scholar] [CrossRef]
- Molnár, P. Properties of range-based volatility estimators. Int. Rev. Financ. Anal. 2012, 23, 20–29. [Google Scholar] [CrossRef]
- Fiszeder, P.; Perczak, G. A new look at variance estimation based on low, high and closing prices taking into account the drift. Stat. Neerl. 2013, 67, 456–481. [Google Scholar] [CrossRef]
- Fiszeder, P.; Perczak, G. Low and high prices can improve volatility forecasts during periods of turmoil. Int. J. Forecast. 2016, 32, 398–410. [Google Scholar] [CrossRef]
- Shu, J.; Zhang, J. Testing range estimators of historical volatility. J. Futur. Mark. 2006, 26, 297–313. [Google Scholar] [CrossRef]
- Wiggins, J.B. Empirical tests of the bias and efficiency of the extreme-value variance estimator for common stocks. J. Bus. 1991, 64, 417–432. [Google Scholar] [CrossRef]
- Fałdziński, M.; Fiszeder, P.; Molnár, P. Improving volatility forecasts: Evidence from range-based models. N. Am. J. Econ. Financ. 2024, 69, 102019. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inform. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- WHO. Timeline of WHO’s Response to COVID-19. 2022. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/interactive-timeline (accessed on 31 December 2022).
- WHO. Statement on the Fifteenth Meeting of the IHR (2005) Emergency Committee on the COVID-19 Pandemic. 2023. Available online: https://www.who.int/news/item/05-05-2023-statement-on-the-fifteenth-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-coronavirus-disease-(covid-19)-pandemic (accessed on 31 December 2023).
- Oh, G.; Kim, H.; Ahn, S.W.; Kwak, W. Analyzing the financial crisis using the entropy density function. Physica A 2015, 419, 464–469. [Google Scholar] [CrossRef]
- Brunelli, R.; Mich, O. Histograms analysis for image retrieval. Pattern Recogn. 2001, 34, 1625–1637. [Google Scholar] [CrossRef]
- Cha, S.H.; Srihari, S. On measuring the distance between histograms. Pattern Recogn. 2002, 35, 1355–1370. [Google Scholar] [CrossRef]
- Olbryś, J.; Majewska, E. Regularity in stock market indices within turbulence periods: The sample entropy approach. Entropy 2022, 24, 921. [Google Scholar] [CrossRef] [PubMed]
- Ozkan, O. Impact of COVID-19 on stock market efficiency: Evidence from developed countries. Res. Int. Bus. Financ. 2021, 58, 101445. [Google Scholar] [CrossRef]
- Papla, D.; Siedlecki, R. Entropy as a tool for the analysis of stock market efficiency during periods of crisis. Entropy 2024, 26, 1079. [Google Scholar] [CrossRef]
- Risso, W. The informational efficiency and the financial crashes. Res. Int. Bus. Financ. 2008, 22, 396–408. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X. COVID-19 and financial market efficiency: Evidence from an entropy-based analysis. Financ. Res. Lett. 2021, 42, 101888. [Google Scholar] [CrossRef]
- Chou, R.Y.; Chou, H.C.; Liu, N. Range volatility: A review of models and empirical studies. In Handbook of Financial Econometrics and Statistics; Lee, C.F., Lee, J.C., Eds.; Springer: New York, NY, USA, 2015; pp. 2029–2050. [Google Scholar] [CrossRef]
- Liebi, L. The effect of ETFs on financial markets: A literature review. Financ. Mark. Portf. Manag. 2020, 34, 165–178. [Google Scholar] [CrossRef]
- Calcagnile, L.; Corsi, F.; Marmi, S. Entropy and efficiency of the ETF market. Comput. Econ. 2020, 55, 143–184. [Google Scholar] [CrossRef]




| Country | Index | The Whole Sample | Pre-COVID-19 | COVID-19 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | Mean | Std. Dev. | N | Mean | Std. Dev. | N | Mean | Std. Dev. | ||
| USA | SPX | 1759 | 0.003 | 793 | 0.002 | 797 | 0.003 | |||
| France | CAC | 1791 | 0.003 | 806 | 0.002 | 813 | 0.003 | |||
| U.K. | UKX | 1765 | 0.003 | 799 | 0.002 | 797 | 0.004 | |||
| Germany | DAX | 1774 | 0.003 | 795 | 0.003 | 807 | 0.004 | |||
| Japan | NKX | 1774 | 0.003 | 769 | 0.003 | 775 | 0.003 | |||
| Country | Index | The Whole Sample | Pre-COVID-19 | COVID-19 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | Mean | Std. Dev. | N | Mean | Std. Dev. | N | Mean | Std. Dev. | ||
| USA | SPX | 1759 | 0.004 | 793 | 0.003 | 797 | 0.005 | |||
| France | CAC | 1791 | 0.004 | 806 | 0.003 | 813 | 0.005 | |||
| U.K. | UKX | 1765 | 0.004 | 799 | 0.003 | 797 | 0.004 | |||
| Germany | DAX | 1774 | 0.004 | 795 | 0.003 | 807 | 0.005 | |||
| Japan | NKX | 1774 | 0.004 | 769 | 0.004 | 775 | 0.004 | |||
| Country | Index | The Whole Sample | Pre-COVID-19 | COVID-19 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | Mean | Std. Dev. | N | Mean | Std. Dev. | N | Mean | Std. Dev. | ||
| USA | SPX | 1759 | 0.005 | 793 | 0.004 | 797 | 0.006 | |||
| France | CAC | 1791 | 0.005 | 806 | 0.003 | 813 | 0.006 | |||
| U.K. | UKX | 1765 | 0.005 | 799 | 0.003 | 797 | 0.006 | |||
| Germany | DAX | 1774 | 0.005 | 795 | 0.004 | 807 | 0.006 | |||
| Japan | NKX | 1774 | 0.004 | 769 | 0.004 | 775 | 0.005 | |||
| The Codes of Sequences for the Alphabet and |
|---|
| Country | Index | Parkinson Estimator (Definition 1) | Garman–Klass Estimator (Definition 2) | Rogers–Satchell Estimator (Definition 3) |
|---|---|---|---|---|
| USA | SPX | 0.584 | 0.577 | 0.557 |
| France | CAC | 0.592 | 0.580 | 0.547 |
| U.K. | UKX | 0.516 | 0.571 | 0.524 |
| Germany | DAX | 0.606 | 0.601 | 0.576 |
| Japan | NKX | 0.560 | 0.536 | 0.540 |
| Min | – | 0.516 | 0.536 | 0.524 |
| Max | – | 0.606 | 0.601 | 0.576 |
| The Sequences with Zero Frequency Within the Whole Sample Period | |||||
|---|---|---|---|---|---|
| SPX | CAC | UKX | DAX | NKX | |
| Parkinson | No. 12 (2,2,2) | No. 8 (0,0,0) | No. 12 (2,2,2) | No. 8 (0,0,0) | No. 8 (0,0,0) |
| Estimator | No. 12 (2,2,2) | No. 19 (2,2,1) | No. 12 (2,2,2) | ||
| Garman–Klass | No. 8 (0,0,0) | No. 8 (0,0,0) | No. 8 (0,0,0) | No. 8 (0,0,0) | No. 8 (0,0,0) |
| Estimator | No. 12 (2,2,2) | No. 12 (2,2,2) | No. 12 (2,2,2) | No. 12 (2,2,2) | |
| No. 19 (2,2,1) | |||||
| Rogers–Satchell | No. 8 (0,0,0) | No. 8 (0,0,0) | No. 8 (0,0,0) | No. 8 (0,0,0) | No. 8 (0,0,0) |
| Estimator | No. 12 (2,2,2) | No. 11 (1,0,0) | No. 12 (2,2,2) | No. 12 (2,2,2) | |
| No. 19 (2,2,1) | No. 19 (2,2,1) | ||||
| The Five Most Frequently Observed Sequences Within the Whole Sample Period | |||||
|---|---|---|---|---|---|
| SPX | CAC | UKX | DAX | NKX | |
| Parkinson | No. 1 (981 times) | No. 1 (971 times) | No. 1 (1084 times) | No. 1 (921 times) | No. 1 (994 times) |
| Estimator | No. 5 (104 times) | No. 4 (119 times) | No. 5 (113 times) | No. 4 (135 times) | No. 4 (117 times) |
| No. 4 (90 times) | No. 5 (113 times) | No. 4 (107 times) | No. 5 (117 times) | No. 5 (117 times) | |
| No. 6 (73 times) | No. 25 (81 times) | No. 24 (81 times) | No. 25 (92 times) | No. 24 (88 times) | |
| No. 7 (69 times) | No. 24 (76 times) | No. 25 (81 times) | No. 24 (87 times) | No. 25 (86 times) | |
| Garman–Klass | No. 1 (1015 times) | No. 1 (985 times) | No. 1 (998 times) | No. 1 (951 times) | No. 1 (1043 times) |
| Estimator | No. 5 (100 times) | No. 5 (115 times) | No. 5 (116 times) | No. 5 (118 times) | No. 5 (115 times) |
| No. 4 (86 times) | No. 4 (109 times) | No. 4 (113 times) | No. 4 (112 times) | No. 4 (109 times) | |
| No. 7 (67 times) | No. 24 (78 times) | No. 24 (75 times) | No. 24 (78 times) | No. 24 (83 times) | |
| No. 6 (66 times) | No. 25 (78 times) | No. 3 (67 times) | No. 25 (76 times) | No. 25 (78 times) | |
| Rogers–Satchell | No. 1 (1055 times) | No. 1 (1055 times) | No. 1 (1094 times) | No. 1 (1007 times) | No. 1 (1055 times) |
| Estimator | No. 5 (92 times) | No. 5 (107 times) | No. 5 (101 times) | No. 5 (107 times) | No. 4 (107 times) |
| No. 4 (77 times) | No. 4 (105 times) | No. 4 (87 times) | No. 4 (102 times) | No. 5 (93 times) | |
| No. 7 (66 times) | No. 25 (69 times) | No. 7 (64 times) | No. 7 (69 times) | No. 24 (68 times) | |
| No. 6 (64 times) | No. 6 (65 times) | No. 6 (63 times) | No. 6 (65 times) | No. 25 (68 times) | |
| The Parkinson Volatility Estimator: The Modified Shannon Entropy of Volatility Changes | ||||
|---|---|---|---|---|
| Country | Index | Pre-COVID-19 | COVID-19 | Change in Entropy |
| USA | SPX | 0.557 | 0.628 | 0.071 ↑ |
| France | CAC | 0.637 | 0.583 | −0.054 ↓ |
| U.K. | UKX | 0.622 | 0.538 | −0.084 ↓ |
| Germany | DAX | 0.650 | 0.611 | −0.039 ↓ |
| Japan | NKX | 0.578 | 0.591 | 0.013 ↑ |
| – | Min | 0.557 | 0.538 | – |
| – | Max | 0.650 | 0.628 | – |
| The Garman–Klass Volatility Estimator: The Modified Shannon Entropy of Volatility Changes | ||||
|---|---|---|---|---|
| Country | Index | Pre-COVID-19 | COVID-19 | Change in Entropy |
| USA | SPX | 0.536 | 0.624 | 0.088 ↑ |
| France | CAC | 0.677 | 0.579 | −0.098 ↓ |
| U.K. | UKX | 0.674 | 0.601 | −0.073 ↓ |
| Germany | DAX | 0.660 | 0.580 | −0.080 ↓ |
| Japan | NKX | 0.576 | 0.533 | −0.043 ↓ |
| – | Min | 0.536 | 0.533 | – |
| – | Max | 0.677 | 0.624 | – |
| The Rogers–Satchell Volatility Estimator: The Modified Shannon Entropy of Volatility Changes | ||||
|---|---|---|---|---|
| Country | Index | Pre-COVID-19 | COVID-19 | Change in Entropy |
| USA | SPX | 0.551 | 0.591 | 0.040 ↑ |
| France | CAC | 0.669 | 0.525 | −0.144 ↓ |
| U.K. | UKX | 0.649 | 0.547 | −0.102 ↓ |
| Germany | DAX | 0.644 | 0.565 | −0.079 ↓ |
| Japan | NKX | 0.573 | 0.553 | −0.020 ↓ |
| – | Min | 0.551 | 0.525 | – |
| – | Max | 0.669 | 0.591 | – |
| Country | Index | The Euclidean Norm (Equation (11)) | The Manhattan Norm (Equation (12)) | ||||
|---|---|---|---|---|---|---|---|
| Parkinson Estimator | Garman–Klass Estimator | Rogers–Satchell Estimator | Parkinson Estimator | Garman–Klass Estimator | Rogers–Satchell Estimator | ||
| USA | SPX | 67.65 | 73.09 | 42.19 | 154 | 174 | 122 |
| France | CAC | 54.55 | 103.24 | 135.78 | 144 | 222 | 268 |
| U.K. | UKX | 82.35 | 68.98 | 89.22 | 186 | 164 | 198 |
| Germany | DAX | 47.33 | 95.44 | 103.11 | 128 | 190 | 222 |
| Japan | NKX | 21.86 | 49.32 | 29.33 | 74 | 134 | 106 |
| Min | 21.86 | 49.32 | 29.33 | 74 | 134 | 106 | |
| Max | 82.35 | 103.24 | 135.78 | 186 | 222 | 268 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olbryś, J. Entropy of Volatility Changes: Novel Method for Assessment of Regularity in Volatility Time Series. Entropy 2025, 27, 318. https://doi.org/10.3390/e27030318
Olbryś J. Entropy of Volatility Changes: Novel Method for Assessment of Regularity in Volatility Time Series. Entropy. 2025; 27(3):318. https://doi.org/10.3390/e27030318
Chicago/Turabian StyleOlbryś, Joanna. 2025. "Entropy of Volatility Changes: Novel Method for Assessment of Regularity in Volatility Time Series" Entropy 27, no. 3: 318. https://doi.org/10.3390/e27030318
APA StyleOlbryś, J. (2025). Entropy of Volatility Changes: Novel Method for Assessment of Regularity in Volatility Time Series. Entropy, 27(3), 318. https://doi.org/10.3390/e27030318






