Controlled Double-Direction Cyclic Quantum Communication of Arbitrary Two-Particle States
Abstract
1. Introduction
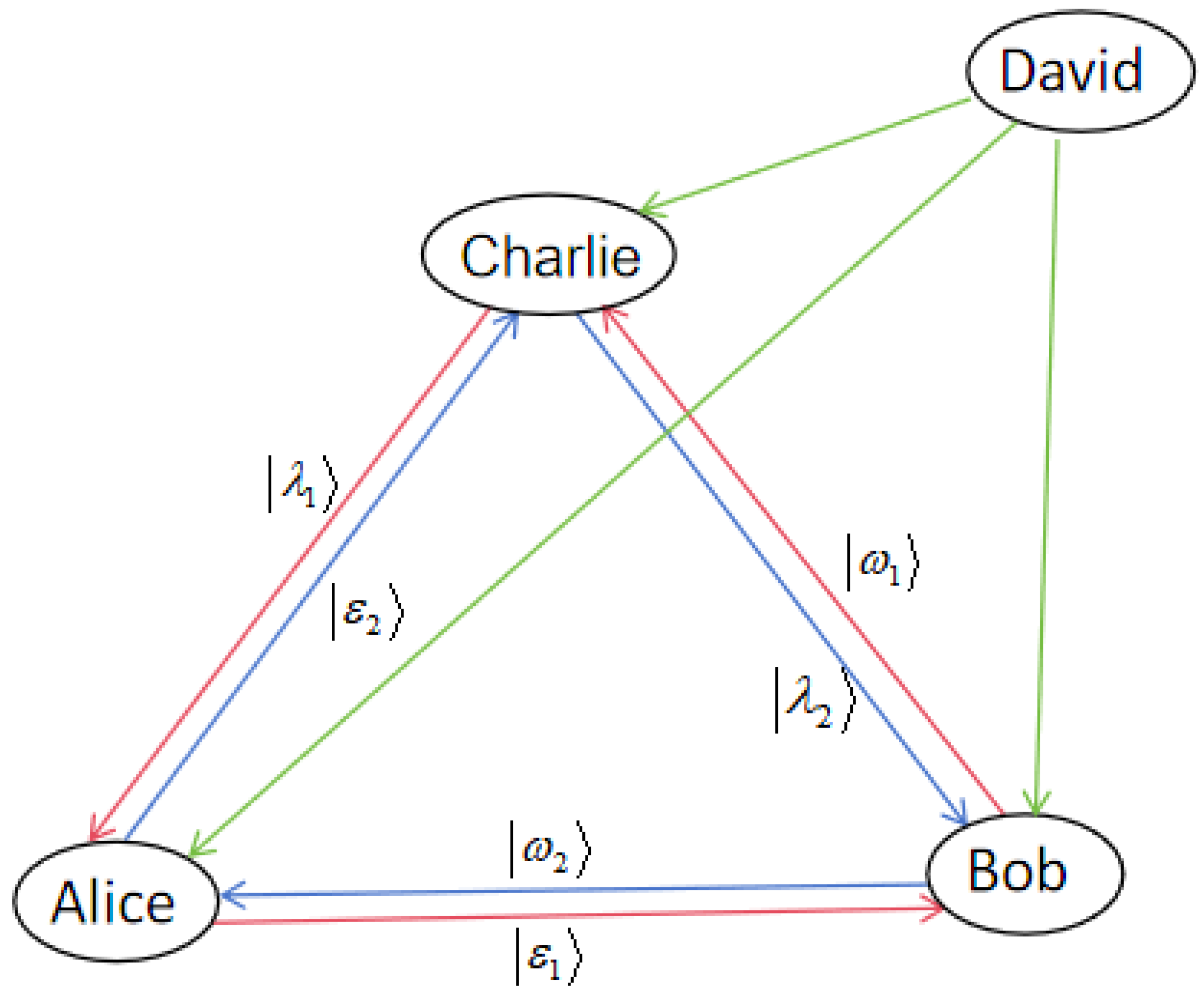
2. Double-Direction Cyclic Controlled Quantum Teleportation of Arbitrary Two-Particle States
2.1. Construction of the Quantum Channel
2.2. Four-Party DDC Controlled Quantum Teleportation Protocol
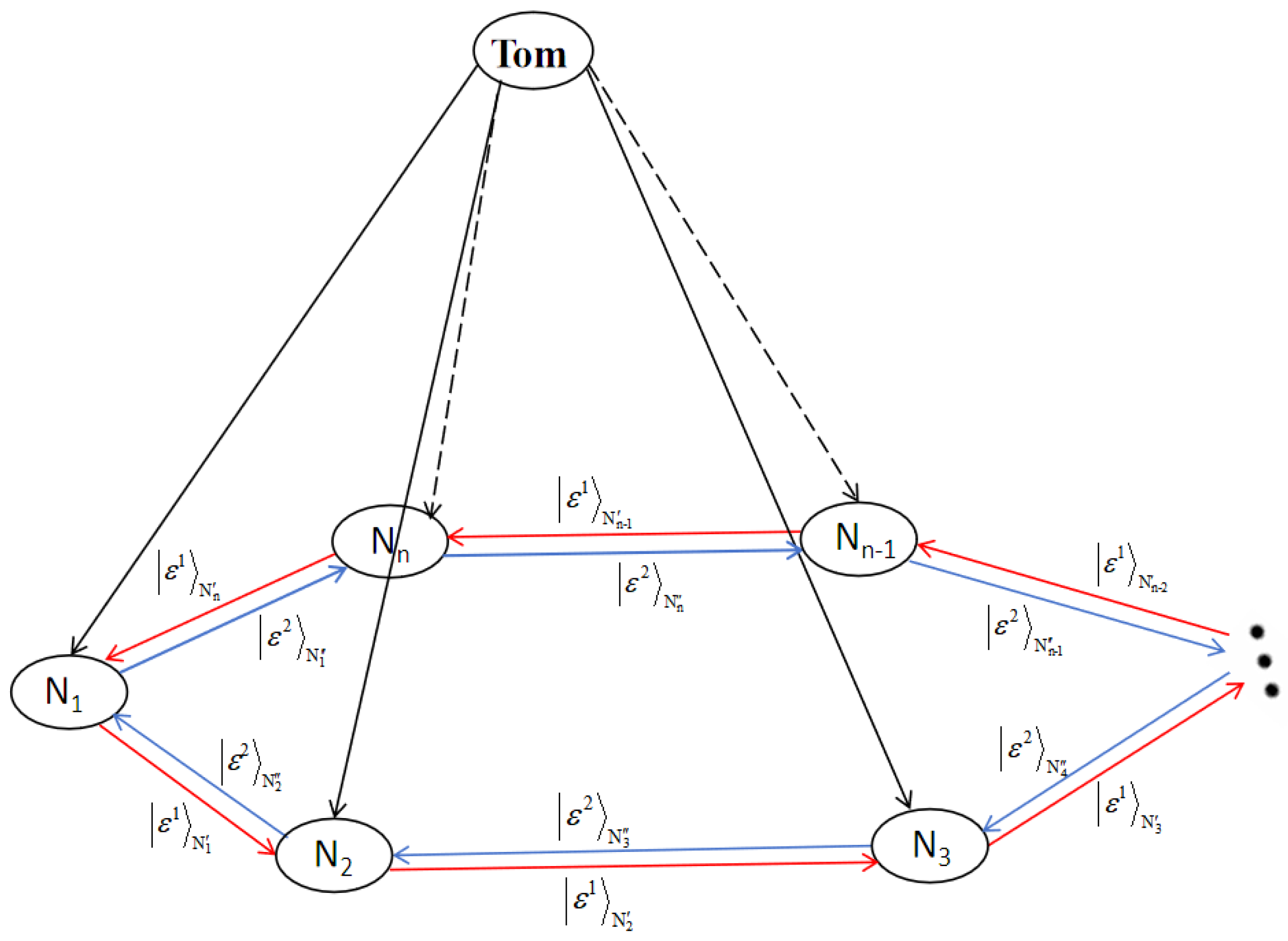
2.3. Generalized DDC Controlled Quantum Teleportation Scheme
3. DDC Controlled RSP of Arbitrary Two-Particle States
3.1. Four-Party DDC Controlled RSP Scheme
3.2. Generalized DDC Controlled RSP Scheme
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed Derivation of the Relevant Equations
Appendix B. Detailed Fidelity Derivation
References
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Li, X.H.; Deng, F.G.; Zhou, H.Y. Multiparty-controlled teleportation of an arbitrary m-qubit state with a pure entangled quantum channel. J. Phys. A Math. Theor. 2007, 40, 13121–13130. [Google Scholar] [CrossRef]
- Gangopadhyay, S.; Wang, T.; Mashatan, A.; Ghose, S. Controlled quantum teleportation in the presence of an adversary. Phys. Rev. A 2022, 106, 052433. [Google Scholar] [CrossRef]
- Kumar, A.; Haddadi, S.; Pourkarimi, M.R.; Behera, B.K.; Panigrahi, P.K. Experimental realization of controlled quantum teleportation of arbitrary qubit states via cluster states. Sci. Rep. 2020, 10, 13608. [Google Scholar] [CrossRef]
- Hassanpour, S.; Houshm, M. Bidirectional teleportation of a pure EPR state by using GHZ states. Quantum Inf. Process. 2016, 15, 905–912. [Google Scholar] [CrossRef]
- Yang, G.; Lian, B.W.; Nie, M.; Jin, J. Bidirectional multi-qubit quantum teleportation in noisy channel aided with weak measurement. Chin. Phys. B 2017, 26, 040305. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Zha, X.W.; Yu, Y. Asymmetric bidirectional controlled teleportation via seven-qubit cluster state. Int. J. Theor. Phys. 2016, 55, 4197–4204. [Google Scholar] [CrossRef]
- Jiang, S.X.; Zhou, R.G.; Luo, G.F.; Liang, X.Z.; Fan, P. Controlled bidirectional quantum teleportation of arbitrary single qubit via a non-maximally entangled state. Int. J. Theor. Phys. 2020, 59, 2966–2983. [Google Scholar] [CrossRef]
- Wu, F.; Bai, M.Q.; Zhang, Y.C.; Liu, R.J.; Mo, Z.W. Cyclic quantum teleportation of an unknown multi-particle high-dimension state. Mod. Phys. Lett. B 2020, 34, 2050073. [Google Scholar] [CrossRef]
- Zhou, R.G.; Qian, C.; Lan, H. Cyclic and bidirectional quantum teleportation via pseudo multi-qubit states. IEEE Access 2019, 7, 42445–42449. [Google Scholar] [CrossRef]
- Sang, Z.W. Cyclic controlled teleportation by using a seven-qubit entangled state. Int. J. Theor. Phys. 2019, 57, 3835–3838. [Google Scholar] [CrossRef]
- Yang, B. Hierarchical controlled cyclic quantum teleportation. Phys. Scr. 2023, 98, 115125. [Google Scholar] [CrossRef]
- Peng, J.Y.; He, Y. Annular controlled teleportation. Int. J. Theor. Phys. 2019, 58, 3271–3281. [Google Scholar] [CrossRef]
- Lo, H.K. Classical-communication cost in distributed quantum-information processing: A generalization of quantum-communication complexity. Phys. Rev. A 2000, 62, 012313. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, N.; Pei, C.X. Multicast-based multiparty remote state prepartion schemes of two-qubit states. Quantum Inf. Process. 2019, 18, 319. [Google Scholar] [CrossRef]
- Chen, X.B.; Ma, S.Y.; Su, Y.; Zhang, R.; Yang, Y.X. Controlled remote state preparation of arbitrary two and three qubit states via the Brown state. Quantum Inf. Process. 2012, 11, 1653–1667. [Google Scholar] [CrossRef]
- Ma, P.C.; Chen, G.B.; Li, X.W.; Zhan, Y.B. Hierarchically controlled remote state preparation of an arbitrary single-qubit state by using a four-qubit |χ〉 entangled state. Quantum Inf. Process. 2018, 17, 105. [Google Scholar] [CrossRef]
- An, N.B.; Kim, J. Joint remote state preparation. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 095501. [Google Scholar]
- Peng, J.Y.; Luo, M.X.; Mo, Z.W.; Liu, H.W. Flexible deterministic joint remote state preparation of some states. Int. J. Quantum Inf. 2013, 11, 1350044. [Google Scholar] [CrossRef]
- Peng, J.Y.; Bai, M.Q.; Mo, Z.W. Joint remote state preparation of arbitrary two-particle states via GHZ-type states. Quantum Inf. Process. 2013, 12, 2325–2342. [Google Scholar] [CrossRef]
- Shukla, C.; Thapliyal, K.; Pathak, A. Hierarchical joint remote state preparation in noisy environment. Quantum Inf. Process. 2017, 16, 205. [Google Scholar] [CrossRef]
- Peng, J.Y.; Bai, M.Q.; Mo, Z.W. Joint remote state preparation of a four-dimensional quantum stste. Chin. Phys. Lett. 2014, 31, 010301. [Google Scholar] [CrossRef]
- Lv, S.X.; Zhao, Z.W.; Zhou, P. Multiparty-controlled joint remote preparation of an arbitrary m-qubit state with d-dimensional Greenberger-Horne-Zeilinger states. Int. J. Theor. Phys. 2018, 57, 148–158. [Google Scholar] [CrossRef]
- Zhang, D.; Zha, X.W.; Duan, Y.J.; Yang, Y.Q. Deterministic controlled bidirectional remote state preparation via a six-qubit entangled state. Quantum Inf. Process. 2016, 15, 2169. [Google Scholar] [CrossRef]
- Peng, J.Y.; Bai, M.Q.; Mo, Z.W. Bidirectional controlled joint remote state preparation. Quantum Inf. Process. 2015, 14, 4263–4278. [Google Scholar] [CrossRef]
- Sharma, V.; Shukla, C.; Banerjee, S.; Pathak, A. Controlled bidirectional remote state preparation in noisy environment: A generalized view. Quantum Inf. Process. 2015, 14, 3441–3464. [Google Scholar] [CrossRef]
- Gu, J.R.; Liu, J.M. Deterministic controlled bidirectional remote state preparation in dissipative environments. Commun. Theor. Phys. 2022, 74, 075101. [Google Scholar] [CrossRef]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef]
- Jiang, J.L.; Luo, M.X.; Ma, S.Y. The network capacity of entangled quantum Internet. IEEE J. Sel. Area Commun. 2024, 42, 1900–1918. [Google Scholar] [CrossRef]
- Luo, M.X. Computationally Efficient Nonlinear Bell Inequalities for Quantum Networks. Phys. Rev. Lett. 2018, 120, 140402. [Google Scholar] [CrossRef]
- Azuma, K.; Economou, S.E.; Elkouss, D.; Hilaire, P.; Jiang, L.; Lo, H.K.; Tzitrin, I. Quantum repeaters: From quantum networks to the quantum internet. Rev. Mod. Phys. 2023, 95, 045006. [Google Scholar] [CrossRef]
- Castelvecchi, D. The quantum internet has arrived (and it hasn’t). Nature 2018, 554, 289–292. [Google Scholar] [CrossRef]
- Luo, M.X. Fully device-independent model on quantum networks. Phys. Rev. Res. 2022, 4, 013203. [Google Scholar] [CrossRef]
- Chen, Y.X.; Du, J.; Liu, S.Y.; Wang, X.H. Cyclic quantum teleportation. Quantum Inf. Process. 2017, 16, 201. [Google Scholar] [CrossRef]
- Shao, Z.L.; Long, Y.X. Circular controlled quantum teleportation by a genuine seven-qubit entangled state. Int. J. Theor. Phys. 2019, 58, 1957–1967. [Google Scholar] [CrossRef]
- Verma, V. Symmetric and asymmetric cyclic controlled quantum teleportation via nine-qubit entangled state. Mod. Phys. Lett. B 2021, 35, 2150249. [Google Scholar] [CrossRef]
- Peng, J.Y.; Lei, H.X. Cyclic remote state preparation. Int. J. Theor. Phys. 2021, 60, 1593–1602. [Google Scholar]
- Zhang, C.Y.; Bai, M.Q.; Zhou, S.Q. Cyclic joint remote state preparation in noisy environment. Quantum Inf. Process. 2018, 17, 146. [Google Scholar] [CrossRef]
- Wang, M.M.; Yang, C.; Mousoli, R. Controlled cyclic remote state preparation of arbitrary qubit states. CMC-Comput. Mater. Contin. 2018, 55, 321–329. [Google Scholar]
- Houshm, M.; Jami, S.; Haghparast, M. General controlled cyclic remote state preparations and their analysis. Quantum Inf. Process. 2024, 23, 372. [Google Scholar] [CrossRef]
- Jiang, S.X.; Zhou, R.G.; Xu, R.Q.; Luo, G.F. Cyclic hybrid double-channel quantum communication via Bell-state and GHZ-state in noisy environments. IEEE Access 2019, 7, 80530–80541. [Google Scholar] [CrossRef]
- Sun, S.Y.; Zhang, H.S. Quantum double-direction cyclic controlled communication via a thirteen-qubit entangled state. Quantum Inf. Process. 2020, 19, 120. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, N. General quantum broadcast and multi-cast communications based on entanglement. Opt. Express 2018, 26, 29296–29310. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.Y.; Liu, M.; Yang, Z.; Tang, L.; Tang, J.G. Double-direction cyclic controlled quantum communication of single-particle states. Phys. A Stat. Mech. Its Appl. 2023, 632, 129343. [Google Scholar] [CrossRef]
- Sun, S.Y.; Zhang, H.S. Double-direction quantum cyclic controlled remote state preparation of two-qubit states. Quantum Inf. Process. 2021, 20, 211. [Google Scholar] [CrossRef]
- Yuan, H.; Liu, Y.M.; Zhang, W.; Zhang, Z.J. Optimizing resource con sumption, operation complexity and efficiency in quantum-state sharing. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 145506. [Google Scholar] [CrossRef]
- Yang, C.; Guo, G.C. Disentanglement-free state of two pairs of two-level atoms. Phys. Rev. A 1999, 59, 4217. [Google Scholar] [CrossRef]
- Deng, F.G.; Long, G.L.; Liu, X.S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 2003, 68, 042317. [Google Scholar] [CrossRef]
- Hu, M.L. Disentanglement, Bell-nonlocality violation and teleportation capacity of the decaying tripartite states. Ann. Phys. 2012, 327, 2332–2342. [Google Scholar]
- Jung, E.; Hwang, M.R.; Ju, Y.H.; Kim, M.S.; Yoo, S.K.; Kim, H.; Park, D.; Son, J.W.; Tamaryan, S.; Cha, S.K. Greenberger-Horne-Zeilinger versus W states: Quantum teleportation through noisy channels. Phys. Rev. A At. Mol. Opt. Phys. 2008, 78, 012312. [Google Scholar]
- Li, X.H.; Ghose, S. Control power in perfect controlled teleportation via partially entangled channels. Phys. Rev. A 2014, 90, 052305. [Google Scholar] [CrossRef]
- Li, X.H.; Ghose, S. Analysis of control power in controlled remote state preparation schemes. Int. J. Theor. Phys. 2017, 56, 667–677. [Google Scholar] [CrossRef]
- Ikram, M.; Zhu, S.Y.; Zubairy, M.S. Quantum teleportation of an entangled state. Phys. Rev. A 2000, 62, 022307. [Google Scholar] [CrossRef]
- Riebe, M.; Häffner, H.; Roos, C.F.; Hänsel, W.; Benhelm, J.; Lancaster, G.P.T.; Körber, T.W.; Becher, C.; Schmidt-Kaler, F.; James, D.F.V.; et al. Deterministic quantum teleportation with atoms. Nature 2004, 429, 734. [Google Scholar] [CrossRef] [PubMed]
- Boschi, D.; Branca, S.; Martini, F.D.; Hardy, L.; Popescu, S. Experimental realization of teleporting an unknown pur quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1998, 80, 1121. [Google Scholar] [CrossRef]

| Scheme | ||||
|---|---|---|---|---|
| Ref. [44] (Single-particle) | 6 | 13 + 15 | – | |
| Ref. [44] (Multiparty) | ||||
| the schemes in Section 2.2 | 12 | 25 + 15 | – | |
| the schemes in Section 2.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maihemuti, N.; Chen, Z.; Peng, J.; Aisan, Y.; Tang, J. Controlled Double-Direction Cyclic Quantum Communication of Arbitrary Two-Particle States. Entropy 2025, 27, 292. https://doi.org/10.3390/e27030292
Maihemuti N, Chen Z, Peng J, Aisan Y, Tang J. Controlled Double-Direction Cyclic Quantum Communication of Arbitrary Two-Particle States. Entropy. 2025; 27(3):292. https://doi.org/10.3390/e27030292
Chicago/Turabian StyleMaihemuti, Nueraminaimu, Zhanheng Chen, Jiayin Peng, Yimamujiang Aisan, and Jiangang Tang. 2025. "Controlled Double-Direction Cyclic Quantum Communication of Arbitrary Two-Particle States" Entropy 27, no. 3: 292. https://doi.org/10.3390/e27030292
APA StyleMaihemuti, N., Chen, Z., Peng, J., Aisan, Y., & Tang, J. (2025). Controlled Double-Direction Cyclic Quantum Communication of Arbitrary Two-Particle States. Entropy, 27(3), 292. https://doi.org/10.3390/e27030292








