BoxesZero: An Efficient and Computationally Frugal Dots-and-Boxes Agent
Abstract
1. Introduction
- Addressing the Sparse Reward Problem: In traditional RL, agents often require multiple steps to obtain a reward, which increases the difficulty of learning. Our backward training method prioritizes learning the values of states near the end of the game and gradually progresses forward, significantly mitigating the sparse reward problem.
- Mitigating Data Scarcity: Typically, in traditional MCTS, only data from the root node are used for training, which may overlook high-quality nodes and necessitate a large number of simulations, thereby wasting computational resources. To address this, we introduce a constraint mechanism to filter out frequently visited high-quality nodes in MCTS for training. Experiments show that this method greatly improves the learning efficiency of the agent’s value network during the early stages of training. However, during the reinforcement training phase, we eliminate this data extraction method in the tree to enhance the policy network.
- Incorporating Domain Knowledge: In reinforcement learning, effectively utilizing prior knowledge without hindering exploration embodies the balance between exploration [24] and exploitation, which is a significant challenge. In our MCTS process, we introduce a bias constraint to balance exploration with the avoidance of unreasonable moves, focusing computational resources on common game states and improving efficiency. Additionally, we utilize forced endings (endgame theorems) to accelerate MCTS and enable it to obtain more accurate rewards.
- Solving Endgames with 1-Chains and 2-Chains: The existing endgame theorem for Boxes only applies to cases with long chains (length and long loops (length . However, in actual gameplay, cases with 1-chains and 2-chains are very common. Therefore, we provide endgame theorems and proofs involving cases with 1-chains and 2-chains. This extension significantly improves the hit rate of endgame situations in MCTS.
2. Related Work
2.1. Deep Reinforcement Learning Algorithm for Boxes
- Selection: During the selection phase, the algorithm begins at the root node and utilizes the Upper Confidence Bound for Trees (UCT) [30,31] formula to select child nodes along an already expanded path until it encounters a non-expanded node. The UCT formula balances exploration and exploitation by selecting the optimal child node. It is expressed mathematically as follows:where represents the average value of the action taken at state s, denotes the prior probability of taking action a in state s (as provided by the neural network), is the visit count for state s, is the visit count for the action a in state s, and is a constant parameter that determines the exploration factor. This formula facilitates a trade-off between exploring less-visited paths and exploiting those believed to yield high rewards.
- Expansion: Upon reaching a non-expanded node during the selection phase, the expansion phase commences. At this stage, the search tree is augmented by adding unexplored child nodes, thus increasing the search space and allowing for a more comprehensive exploration of possible actions.
- Evaluation: At the newly added nodes, the neural network evaluates the current state and generates two outputs: the policy vector p (indicating the probabilities of each action) and the value v (representing the expected outcome from that state). This evaluation informs future decision-making processes and helps refine the strategy.
- Backpropagation: After the evaluation step, the results are backpropagated from the current node to the root node along the path traversed during selection. The search counts and state value v for each node are updated based on the propagated results. This mechanism reflects the win rates or returns of the current strategy, effectively informing the model about the success of actions taken during the simulation.
2.2. Traditional Search Algorithm for Boxes
3. Game of Dots-and-Boxes
3.1. Basic Rules of Boxes
- Capture all the boxes in the chain or loop.
- Capture part of the chain (all but two boxes) or part of the loop (all but four boxes), leaving the remaining boxes for your opponent.
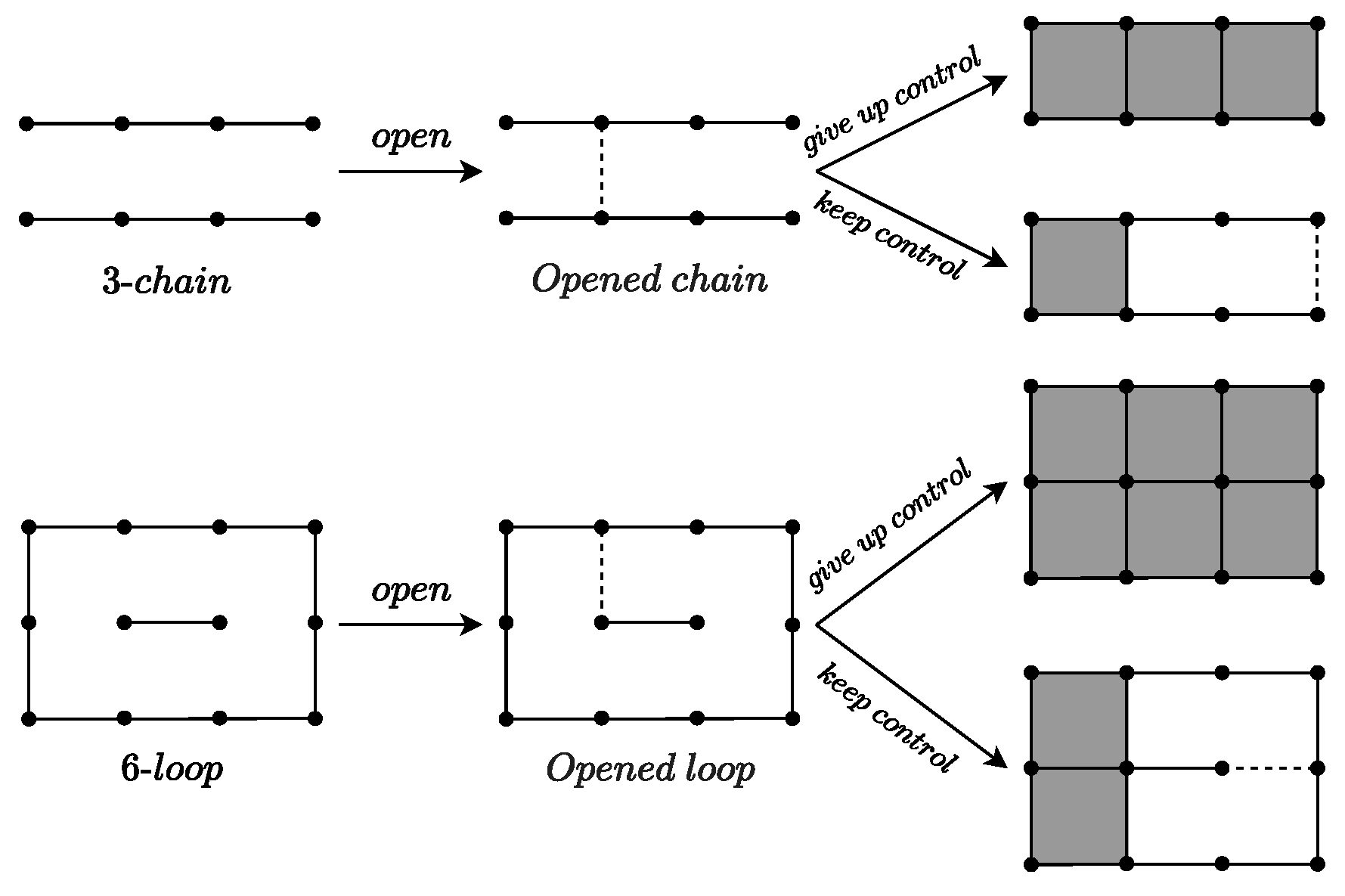
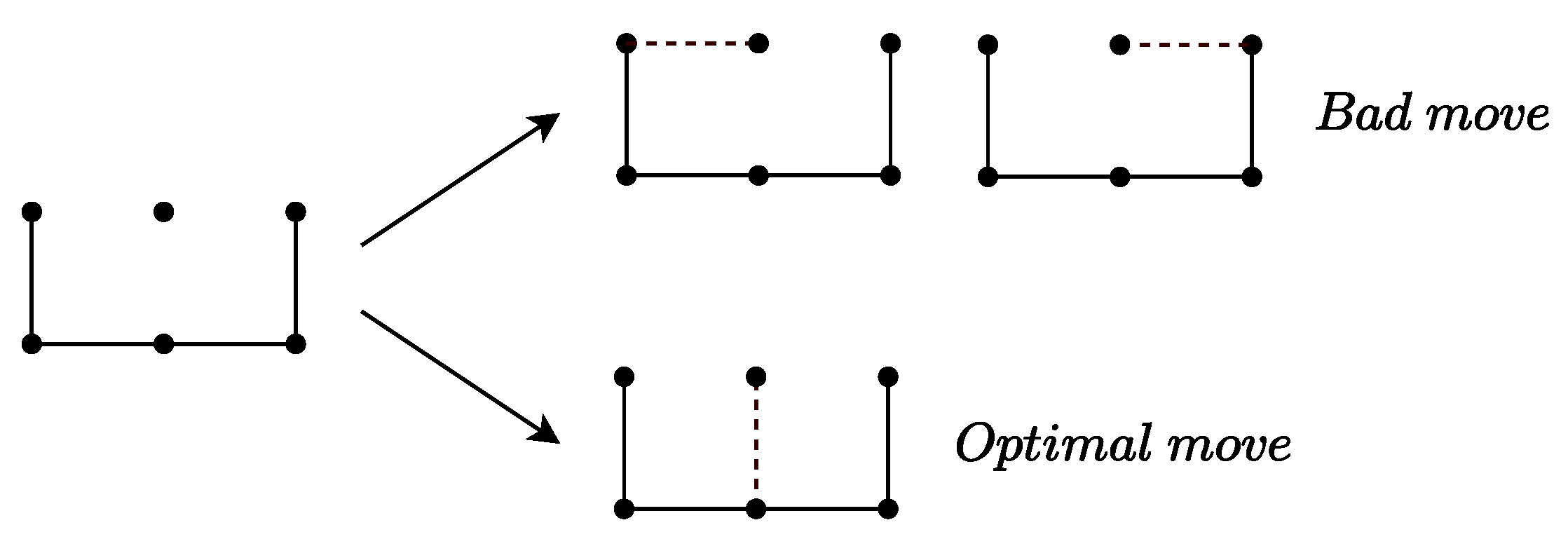
3.2. Endgame Theorems
- 1.
- 2 and 3+ (one or more loops);
- 2.
- 0, ±1} and 4l + (anything except 3 + 3 + 3);
- 3.
- 2 and 4l + 3 , where 4 and H has no 3-chains.
- 1.
- if 2, then ;
- 2.
- if 0, G has a 4-loop, and 4l + 3 + 3, then 0;
- 3.
- if 0, or if 1 and 34, then
4. Methodology
4.1. Reinforcement Learning in BoxesZero
4.2. Overview of Backward Training
4.2.1. Backward Self-Play
4.2.2. Model Advancement Conditions
4.3. Data Augmentation
4.4. Improved Endgame Theorems
- 1.
- If k is odd and n is odd: 1;
- 2.
- If k is odd and n is even: 1 ;
- 3.
- If k is even and n is odd: 2 ;
- 4.
- If k is even and n is even: .
4.5. Pruning in MCTS
- Endgame Theorem Pruning: During the search process, if a node’s position s meets the definition of an endgame, Theorems 3 and 5 can be directly applied to calculate the value . Taking into account the current territory situation, we can calculate the score of state s as follows: . The positive and negative values of correspond to in the MCTS nodes, thus achieving the purpose of pruning. This allows the search tree to encounter actual rewards earlier. It has been verified that for a Dots-and-Boxes game, which consists of 60 moves in total, MCTS can start detecting endgames around the 30th move, enabling effective reward propagation.
- Chain-Loop Pruning: In the tree, if the current position contains an opened chain or opened loop, the forced-move strategy mentioned in Section 3.1 can be applied to execute multiple consecutive moves, thereby reducing the search depth of MCTS. This leads to faster encounters with the endgame, thus mitigating the issue of sparse rewards and significantly improving search efficiency and decision quality.
5. Implementation Details
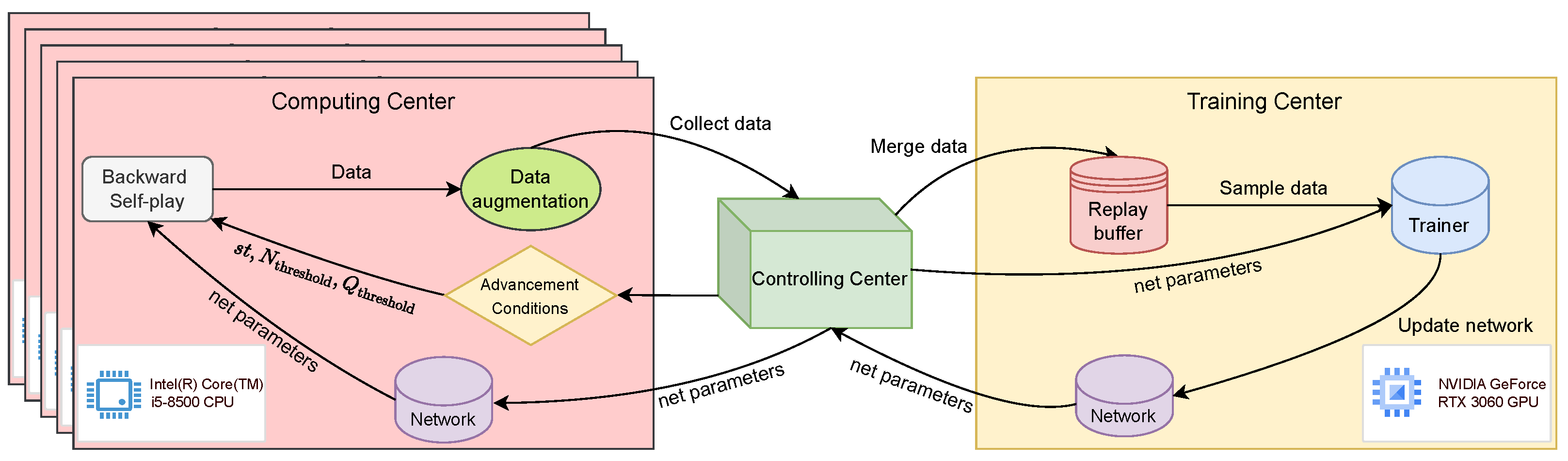
5.1. System Overview
5.2. Neural Network Training Process
5.3. Neural Network Architecture
- The first channel represents the edges, where positions with edges are marked as 1, and those without edges are marked as 0.
- The second channel represents the boxes, where the positions with boxes are marked as 1, and those without boxes are marked as 0.
- The third channel represents the relative scores, calculated as follows:
6. Experiments
6.1. Experiment Setups
6.1.1. Baselines
6.1.2. Metrics
6.1.3. Experimental Environment
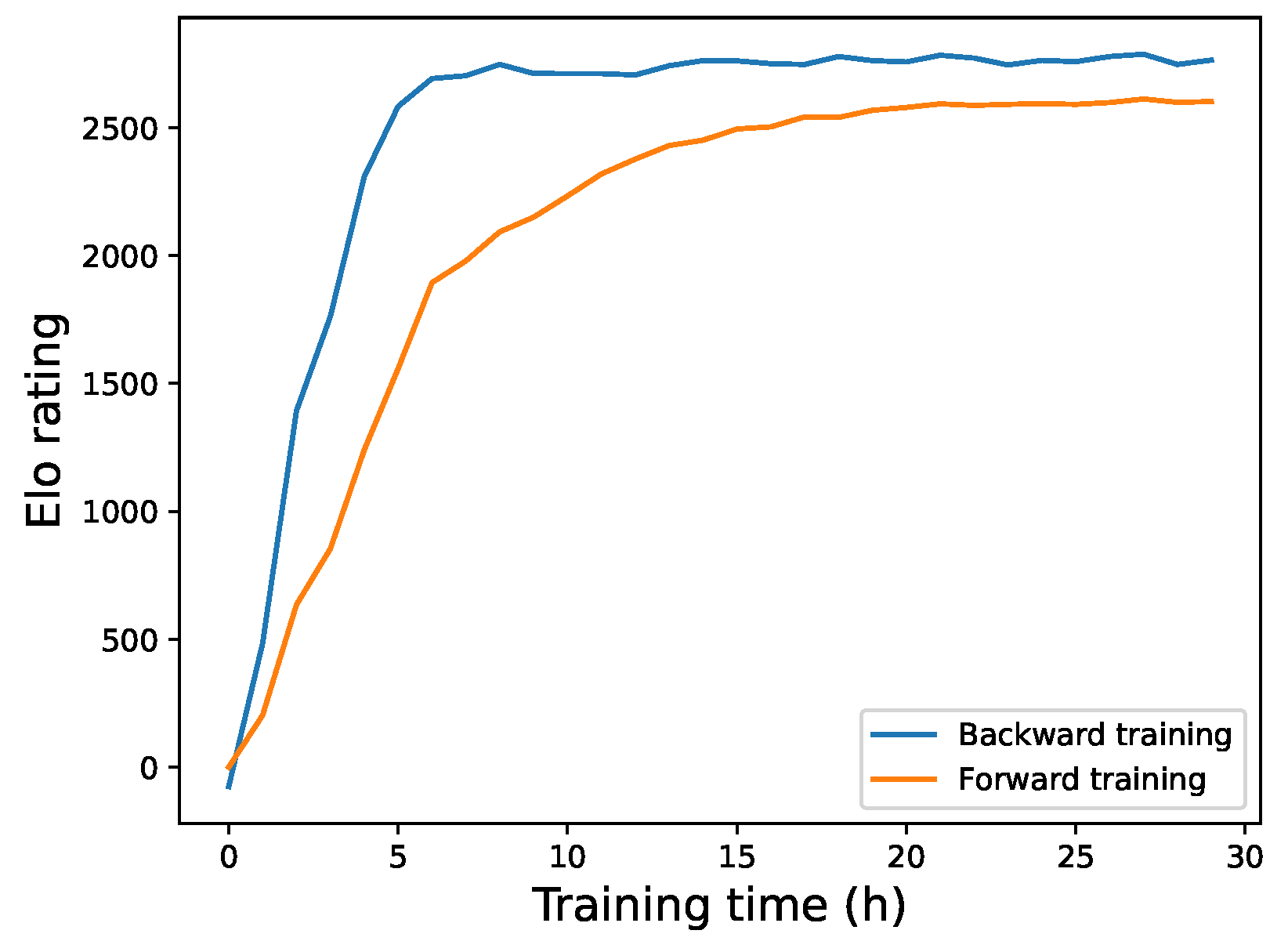
6.2. Comparative Evaluation of Backward Training
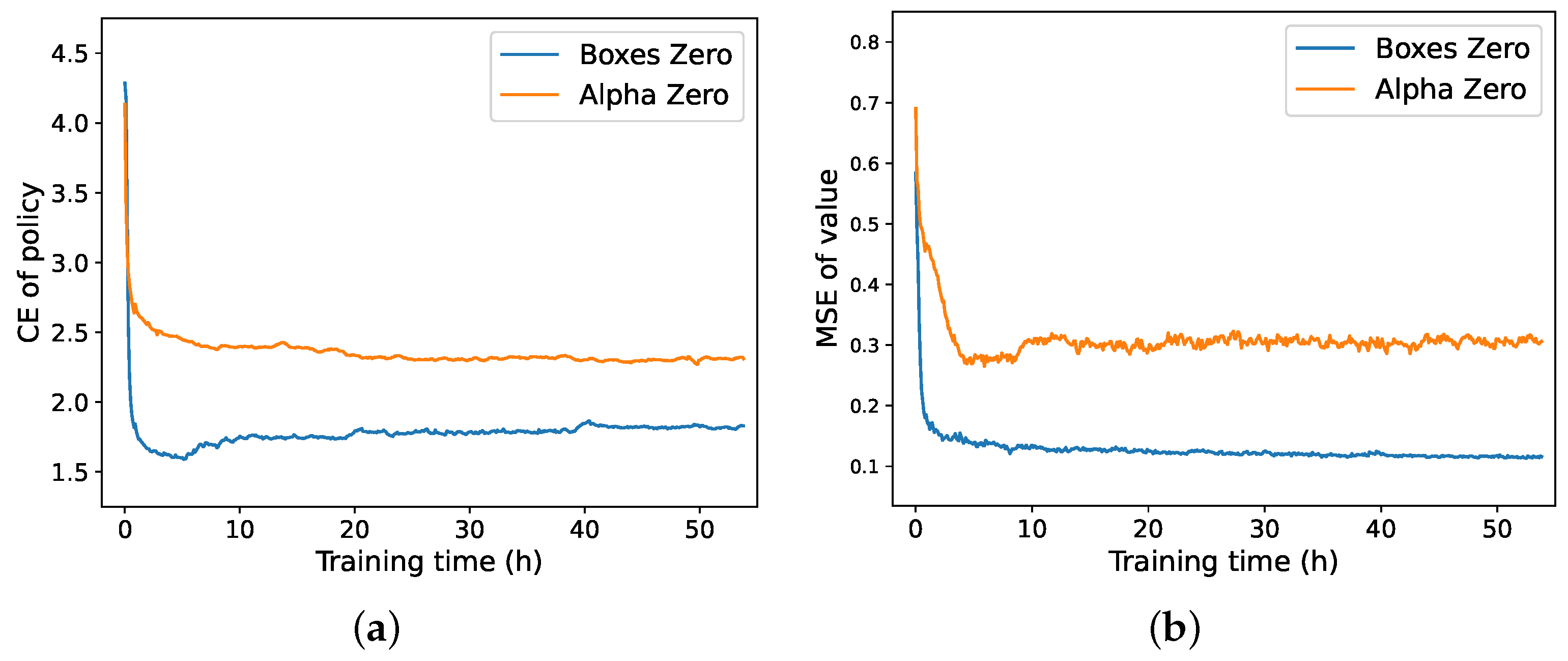
6.3. Analysis of Loss Function Curve
6.4. Ablation Studies
6.5. Evaluation of Model’s Predictive Capabilities at Different Steps
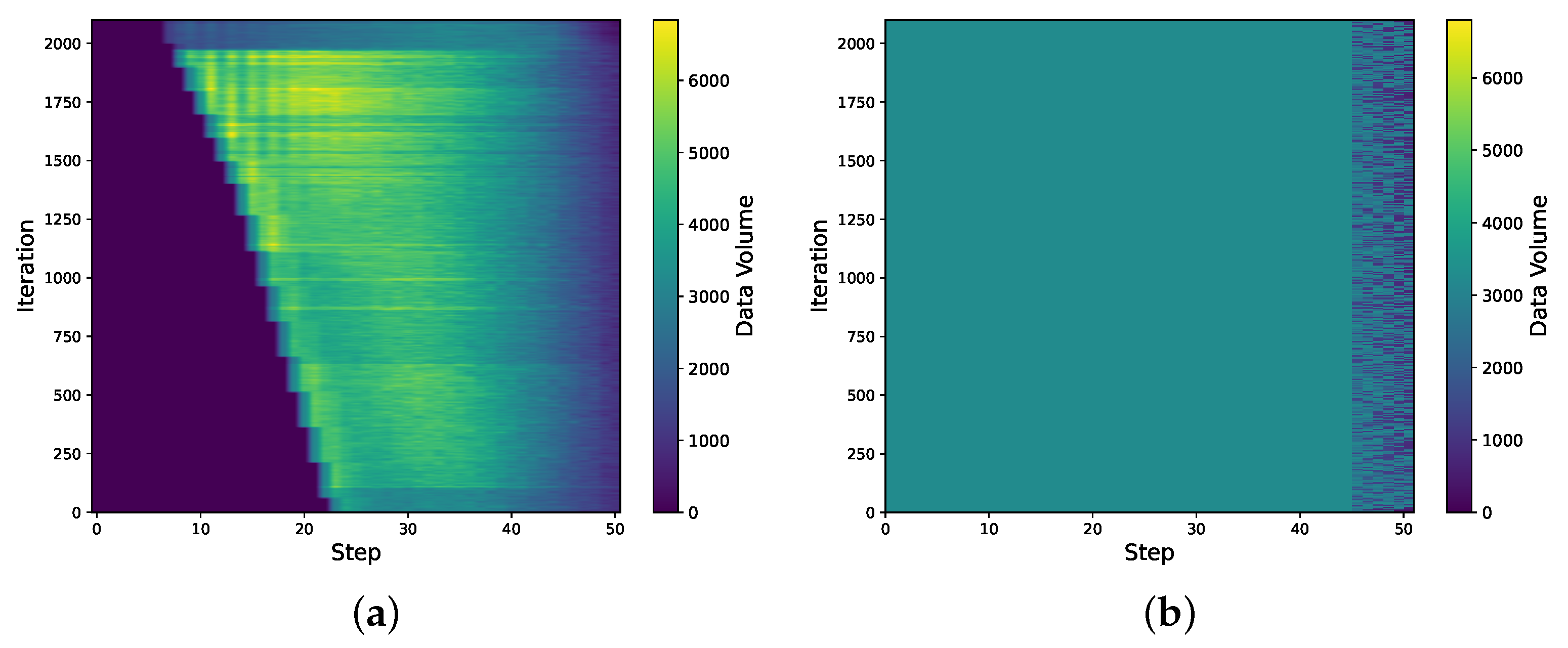
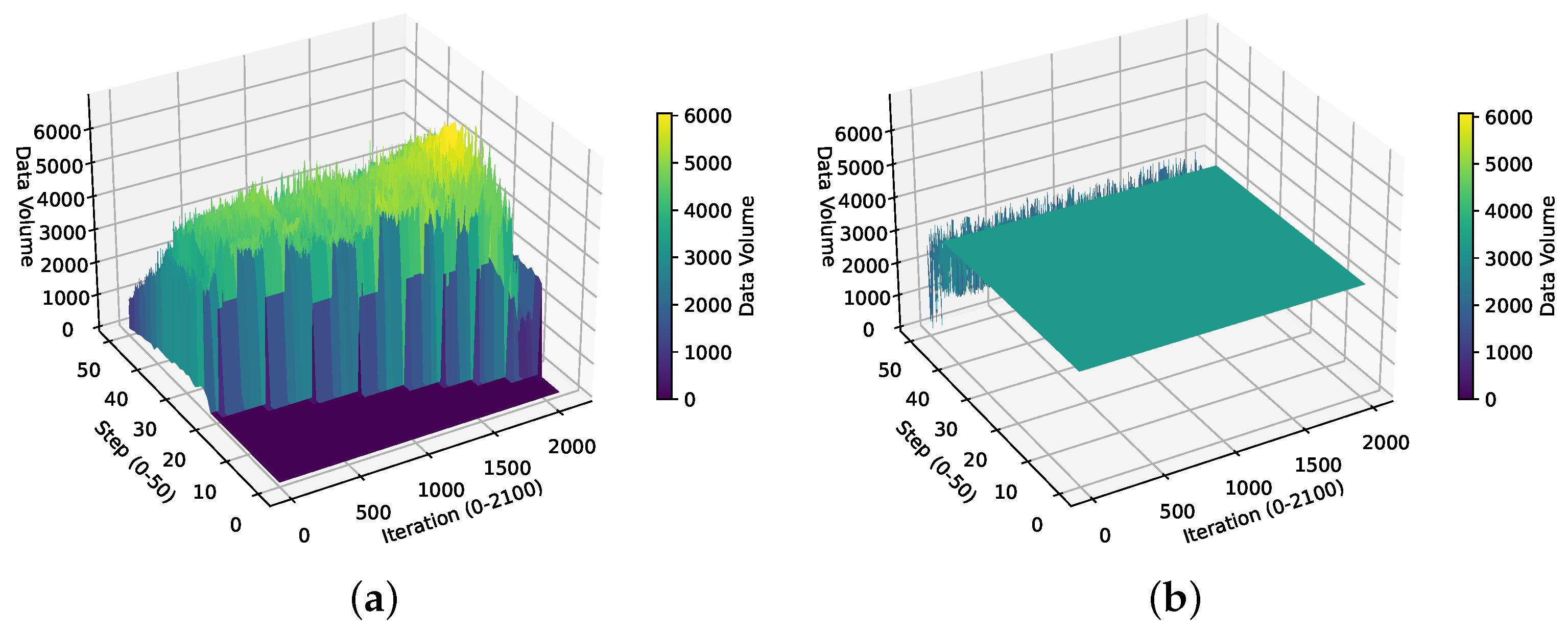
6.6. Analysis of BoxesZero and AlphaZero Data Distributions
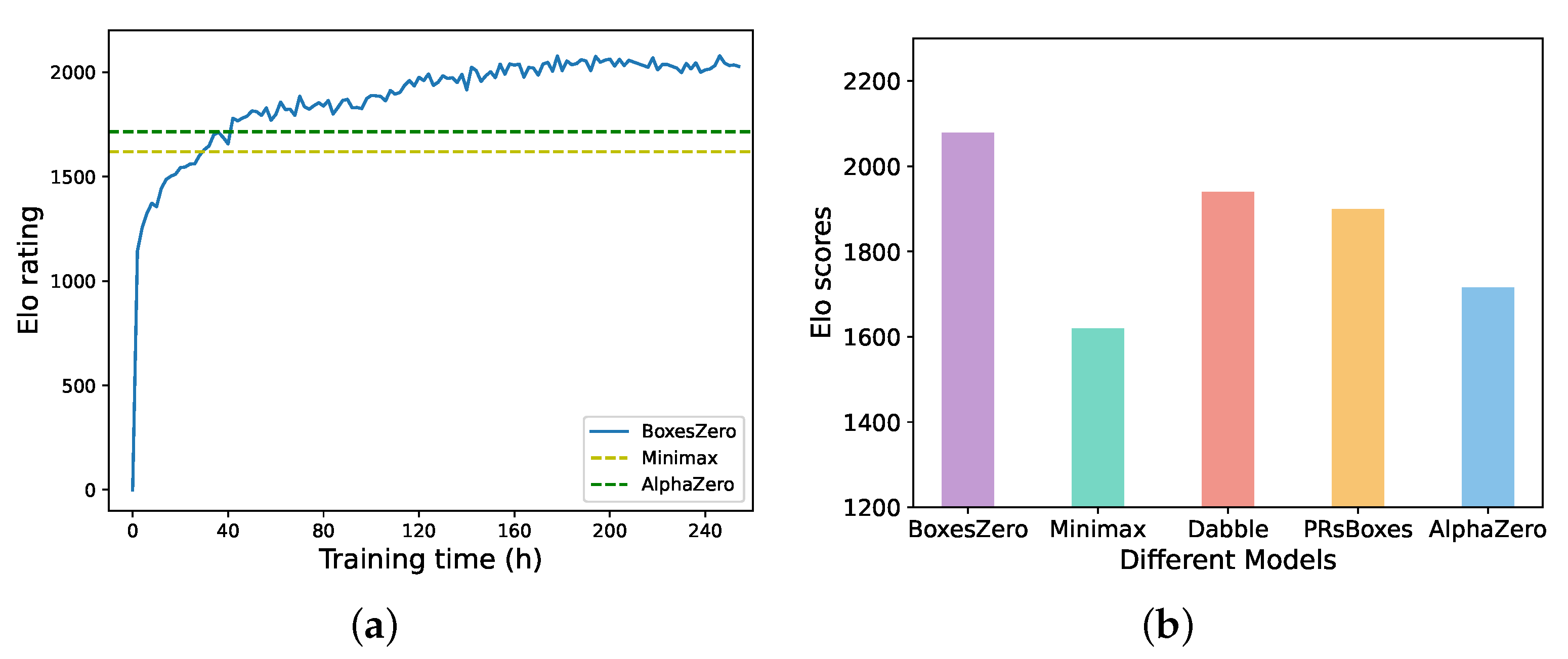
6.7. Final Performance
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Analysis of Q Rate

Appendix B. Winning Rate Analysis

Appendix C. Proof of Extended Endgame Theorem
- If is even, the proof is similar to the case for 1-chains, and it is evident that opening a 2-chain is optimal.
- If is odd, the proof is analogous to the case for , and opening a 2-chain is optimal.
- If o is odd and t is odd, the simplified sequence is , is even, and the player does not change. Thus, .
- If o is odd and t is even, the simplified sequence is , is odd, and the player changes. Therefore, .
- If o is even and t is odd, the simplified sequence is , is odd, and the player changes. Hence, .
- If o is even and t is even, the simplified sequence is , is even, and the player does not change. Thus, .
Appendix D. From Foolishness to Success: Turning Points in BoxesZero’s Gameplay
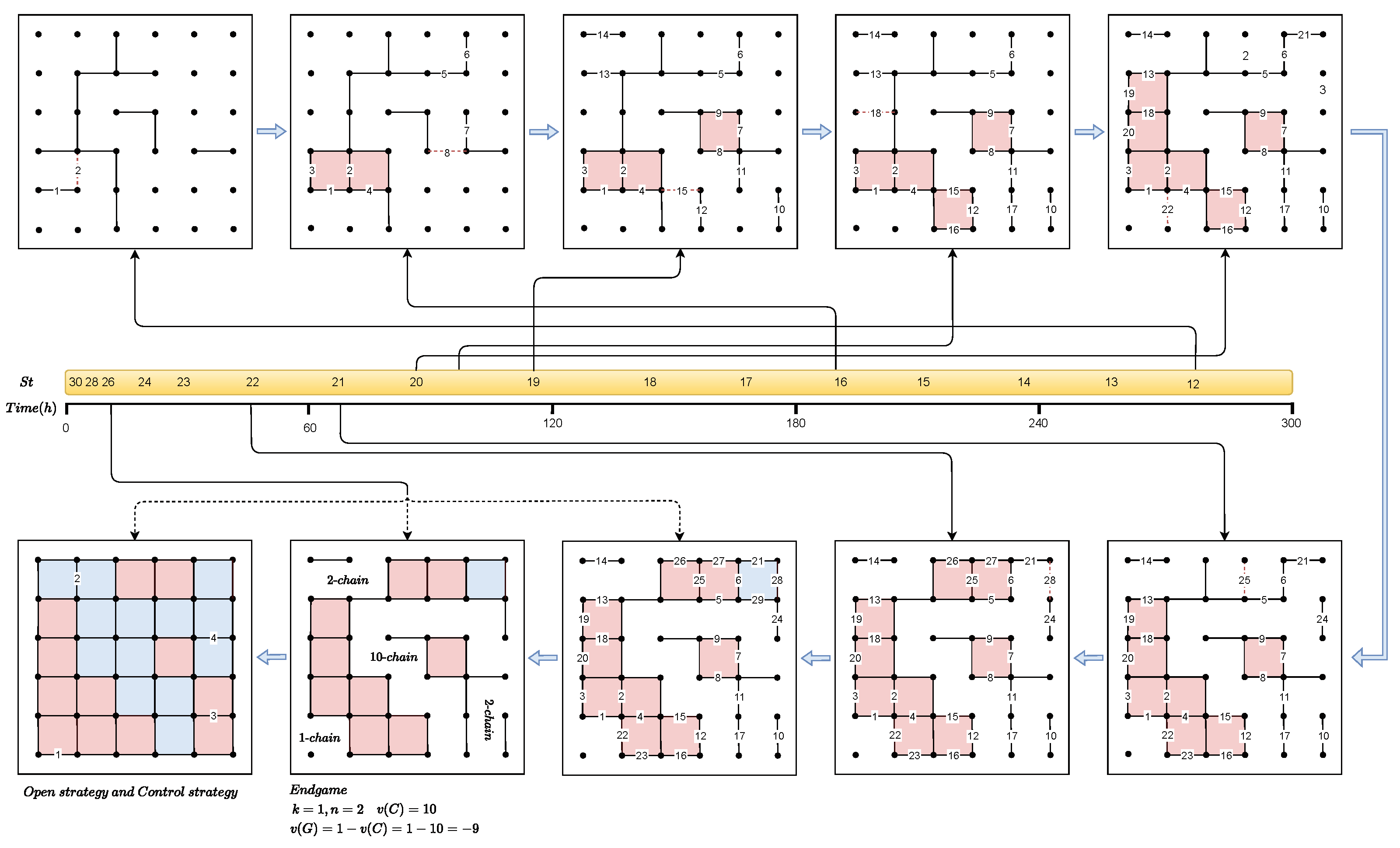
Appendix E. Details of Training
Appendix E.1. AlphaZero Training Details
| Hyperparameter | Description | Value |
|---|---|---|
| D | Number of recent iterations stored in the replay buffer. | 5 |
| Data decay factor | 0.98 | |
| lr | Learning rate | 0.001 |
| epochs | Number of epochs per batch | 5 |
| batch size | Batch size for training | 1024 |
| N | MCTS search nodes | 800 |
| Ngame | Number of self-play games in one iteration | 50 |
| Exploration constant | 2 |
- Policy Loss: This is used to measure the difference between the predicted policy and the true policy, which is represented by cross-entropy loss, as shown in the following equation:where is the true policy distribution, and is the model’s output policy distribution.
- Value Loss: This is used to evaluate the accuracy of the model’s prediction of the value of the state, which is represented by the mean squared error, as shown in the following equation:where z is the actual value of the state, and is the value predicted by the model.
- Regularization Loss: This is used to prevent overfitting the model, which is typically represented by L2 regularization, as shown in the following equation:where is the regularization parameter and are the weights of the model.
- Total Loss Function: Combining the above three components, the total loss function for AlphaZero can be expressed as follows:
Appendix E.2. BoxesZero Training Details
| Step Range | () | |
|---|---|---|
| 0.15 | 0.5 | |
| 0.2 | 0.6 | |
| 0.21 | 0.7 | |
| 0.22 | 0.8 | |
| 0.23 | 0.85 |
Appendix E.3. Dataset Construction Methods
References
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. Int. Conf. Mach. Learn. 2018, 80, 1861–1870. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the Game of Go without Human Knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Hsueh, C.-H.; Ikeda, K.; Wu, I.-C.; Chen, J.-C.; Hsu, T. Analyses of Tabular AlphaZero on Strongly-Solved Stochastic Games. IEEE Access 2023, 11, 18157–18182. [Google Scholar] [CrossRef]
- Wu, D.J. Accelerating Self-Play Learning in Go. arXiv 2019, arXiv:1902.10565. [Google Scholar]
- Schrittwieser, J.; Antonoglou, I.; Hubert, T.; Simonyan, K.; Sifre, L.; Schmitt, S.; Guez, A.; Lockhart, E.; Hassabis, D.; Graepel, T.; et al. Mastering Atari, Go, Chess and Shogi by planning with a learned model. Nature 2020, 588, 604–609. [Google Scholar] [CrossRef]
- Coulom, R. Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search. In International Conference on Computers and Games; Springer: Berlin/Heidelberg, Germany, 2006; pp. 72–83. [Google Scholar]
- Świechowski, M.; Godlewski, K.; Sawicki, B.; Mańdziuk, J. Monte Carlo Tree Search: A Review of Recent Modifications and Applications. Artif. Intell. Rev. 2023, 56, 2497–2562. [Google Scholar] [CrossRef]
- McGrath, T.; Kapishnikov, A.; Tomašev, N.; Pearce, A.; Wattenberg, M.; Hassabis, D.; Kim, B.; Paquet, U.; Kramnik, V. Acquisition of chess knowledge in AlphaZero. Proc. Natl. Acad. Sci. USA 2022, 119, e2206625119. [Google Scholar] [CrossRef] [PubMed]
- Zahavy, T.; Veeriah, V.; Hou, S.; Waugh, K.; Lai, M.; Leurent, E.; Tomasev, N.; Schut, L.; Hassabis, D.; Singh, S. Diversifying AI: Towards Creative Chess with AlphaZero. arXiv 2024, arXiv:2308.09175. [Google Scholar]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science 2018, 362, 1140–1144. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All You Need. In Advances in Neural Information Processing Systems (NeurIPS); Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2017; pp. 5998–6008. [Google Scholar]
- Tjong, E.; Huang, J.; Zhang, K.; Wang, W.; Li, H. A Transformer-based Mahjong AI via Hierarchical Decision-Making and Fan Backward. In Proceedings of the 2021 CAAI Conference on Artificial Intelligence (CAAI), Hangzhou, China, 5–6 June 2021; pp. 123–130. [Google Scholar]
- Badia, A.P.; Piot, B.; Kapturowski, S.; Sprechmann, P.; Vitvitskyi, A.; Guo, Z.D.; Blundell, C. Agent57: Outperforming the Atari Human Benchmark. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020. [Google Scholar]
- Fan, L.; Wang, G.; Jiang, Y.; Mandlekar, A.; Yang, Y.; Zhu, H.; Tang, A.; Huang, D.; Zhu, Y.; Anandkumar, A. Minedojo: Building open-ended embodied agents with internet-scale knowledge. arXiv 2022, arXiv:2206.08853. [Google Scholar]
- Buzzard, K.; Ciere, M. Playing Simple Loony Dots-and-Boxes Endgames Optimally. Integers 2013, 14, G8. [Google Scholar]
- Barker, J.; Korf, R. Solving dots-and-boxes. In Proceedings of the AAAI Conference on Artificial Intelligence, Toronto, ON, Canada, 22–26 July 2012. [Google Scholar]
- Knuth, D.E.; Moore, R.W. An analysis of alpha-beta pruning. Artif. Intell. 1975, 6, 293–326. [Google Scholar] [CrossRef]
- Catacora Ocana, J.M.; Capobianco, R.; Nardi, D. An Overview of Environmental Features that Impact Deep Reinforcement Learning in Sparse-Reward Domains. J. Artif. Intell. Res. 2023, 76, 1181–1218. [Google Scholar] [CrossRef]
- Allcock, D. Best Play in Dots and Boxes Endgames. Int. J. Game Theory 2021, 50, 671–693. [Google Scholar] [CrossRef]
- Ladosz, P.; Weng, L.; Kim, M.; Oh, H. Exploration in deep reinforcement learning: A survey. Inf. Fusion 2022, 85, 1–22. [Google Scholar] [CrossRef]
- Cazenave, T. EMCTS: Enhanced Monte Carlo Tree Search. In Proceedings of the Conference on Artificial Intelligence and Interactive Digital Entertainment (AIIDE), Snowbird, UT, USA, 5–9 October 2007. [Google Scholar]
- Rivest, R.L. Game tree searching by min/max approximation. Artif. Intell. 1987, 34, 77–96. [Google Scholar] [CrossRef]
- Allis, L.V.; van der Meulen, M.; van den Herik, H.J. Proof-number search. Artif. Intell. 1994, 66, 91–124. [Google Scholar] [CrossRef]
- Qi, Z.; Huang, X.; Shen, Y.; Shi, J. Optimization of connect6 based on principal variation search and transposition tables algorithms. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; Curran Associates, Inc.: Red Hook, NY, USA, 2020. [Google Scholar]
- Cazenave, T. Generalized rapid action value estimation. In Proceedings of the 24th International Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; AAAI Press: Washington, DC, USA, 2015. [Google Scholar]
- Kocsis, L.; Szepesvári, C. Bandit based monte-carlo planning. In European Conference on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Gelly, S.; Wang, Y. Exploration exploitation in go: UCT for Monte-Carlo go. In NIPS: Neural Information Processing Systems Conference On-line trading of Exploration and Exploitation Workshop; HAL: Bengaluru, India, 2006. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; IEEE: New York City, NY, USA, 2015. [Google Scholar]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Coulom, R. Whole-history rating: A Bayesian rating system for players of time-varying strength. In Proceedings of the International Conference on Computers and Games, Beijing, China, 29 September 2008; Volume 5131, pp. 113–124. [Google Scholar]





| Function | Description |
|---|---|
| Number of boxes not yet claimed | |
| Number of 3-chains | |
| Number of 4-loops | |
| Number of 6-loops | |
| Optimal value | |
| Controlled value | |
| Terminal bonus |
| Parameter | Description | Value |
|---|---|---|
| mqth | MCTS Q threshold at the root node, used to assess the overall capability of the network. | 0.85 |
| nvth | Network v threshold is used to evaluate the network’s predictive ability. | 0.75 |
| nvr | The ratio of the number of game states in self-play that satisfy the following conditions to the total number of states: and . | — |
| mqr | The ratio of the number of game states in self-play that satisfy the following conditions to the total number of states: . | — |
| mqrth | The required value of mqr for the model to advance. | 0.75 |
| nvrth | The required value of nvr for the model to advance. | 0.85 |
| mit | The maximum iteration limit per step. | 150 |
| The number of steps the model advances each time. | 1 |
| Step | Full Component | No Endgame Theorem | No Dada Augmentation | No Chain Loop | Random | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1 K Games) | 10 (h) | 20 (h) | 30 (h) | 10 (h) | 20 (h) | 30 (h) | 10 (h) | 20 (h) | 30 (h) | 10 (h) | 20 (h) | 30 (h) | |
| 24 | 0.570 | 0.675 | 0.701 | 0.437 | 0.554 | 0.695 | 0.374 | 0.486 | 0.620 | 0.355 | 0.391 | 0.435 | 0.112 |
| 25 | 0.744 | 0.785 | 0.795 | 0.615 | 0.671 | 0.792 | 0.471 | 0.665 | 0.760 | 0.410 | 0.425 | 0.545 | 0.134 |
| 26 | 0.793 | 0.844 | 0.872 | 0.783 | 0.840 | 0.865 | 0.575 | 0.755 | 0.765 | 0.445 | 0.512 | 0.610 | 0.151 |
| 27 | 0.876 | 0.891 | 0.912 | 0.865 | 0.875 | 0.901 | 0.755 | 0.850 | 0.900 | 0.565 | 0.690 | 0.821 | 0.170 |
| 28 | 0.930 | 0.971 | 0.979 | 0.924 | 0.933 | 0.934 | 0.851 | 0.925 | 0.940 | 0.615 | 0.840 | 0.904 | 0.215 |
| 29 | 0.971 | 0.974 | 0.987 | 0.965 | 0.972 | 0.980 | 0.925 | 0.955 | 0.971 | 0.832 | 0.941 | 0.952 | 0.263 |
| 30 | 0.980 | 0.987 | 0.992 | 0.973 | 0.985 | 0.990 | 0.954 | 0.965 | 0.989 | 0.931 | 0.960 | 0.972 | 0.291 |
| Step (1 K Games) | BoxesZero (6b) | AlphaZero (6b) | Random | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 10 (h) | 30 (h) | 60 (h) | 90 (h) | 10 (h) | 30 (h) | 60 (h) | 90 (h) | ||
| 22 | 0.407 | 0.453 | 0.645 | 0.671 | 0.315 | 0.355 | 0.365 | 0.37 | 0.115 |
| 24 | 0.475 | 0.64 | 0.72 | 0.745 | 0.355 | 0.365 | 0.38 | 0.385 | 0.125 |
| 26 | 0.67 | 0.83 | 0.85 | 0.88 | 0.38 | 0.397 | 0.405 | 0.425 | 0.13 |
| 28 | 0.923 | 0.953 | 0.971 | 0.975 | 0.533 | 0.532 | 0.605 | 0.635 | 0.217 |
| 30 | 0.984 | 0.995 | 1.0 | 1.0 | 0.75 | 0.778 | 0.82 | 0.834 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, X.; Liu, Q.; Chen, W.; Zheng, Y.; Jin, Z. BoxesZero: An Efficient and Computationally Frugal Dots-and-Boxes Agent. Entropy 2025, 27, 285. https://doi.org/10.3390/e27030285
Niu X, Liu Q, Chen W, Zheng Y, Jin Z. BoxesZero: An Efficient and Computationally Frugal Dots-and-Boxes Agent. Entropy. 2025; 27(3):285. https://doi.org/10.3390/e27030285
Chicago/Turabian StyleNiu, Xuefen, Qirui Liu, Wei Chen, Yujiao Zheng, and Zhanggen Jin. 2025. "BoxesZero: An Efficient and Computationally Frugal Dots-and-Boxes Agent" Entropy 27, no. 3: 285. https://doi.org/10.3390/e27030285
APA StyleNiu, X., Liu, Q., Chen, W., Zheng, Y., & Jin, Z. (2025). BoxesZero: An Efficient and Computationally Frugal Dots-and-Boxes Agent. Entropy, 27(3), 285. https://doi.org/10.3390/e27030285






